REGISTRO DOI: 0.5281/zenodo.11224181
Carmem Mereth dos Santos,
Drº. José Amauri Siqueira da Silva,
Suzana Gusmão Lima
RESUMO
Este artigo aborda a “Dificuldade de Aprendizagem na Disciplina de Matemática nos 4º e 5º anos do Ensino Fundamental I na Escola Municipal Dom Pedro II, no Distrito de Santo Antônio de Matupi/Manicoré-Amazonas, Brasil”. Ao identificar essa problemática na instituição de ensino, o objetivo geral foi identificar as possíveis causas que levam os alunos a enfrentarem grandes dificuldades de aprendizado na disciplina em estudo. A justificativa para a realização deste estudo surgiu da necessidade de compreender melhor a realidade escolar, com foco no ensino de matemática como uma disciplina prática e relevante para o cotidiano dos estudantes. Reconhecendo a importância da matemática como uma ciência aplicada, buscamos explorar como ela se relaciona com a vida diária dos alunos e como isso pode influenciar sua aprendizagem. Para atingir esse objetivo, realizamos entrevistas com professores e alunos, buscando conhecer os desafios enfrentados no ensino e aprendizagem da Matemática. A pesquisa adotou uma metodologia experimental, que incluiu a aplicação de questionários estruturados. Esses questionários foram elaborados para abordar questões tanto abertas quanto fechadas, permitindo uma análise abrangente dos dados coletados. Essa abordagem refletiu uma perspectiva quantitativa, alinhada à filosofia determinista do paradigma pós-positivista. Dentro desse paradigma, buscamos examinar as causas e entender como diferentes fatores interagem e influenciam os resultados. A metodologia foi tipicamente dedutiva, envolvendo a redução de ideias a variáveis mensuráveis, com ênfase na observação, medição e interpretação cuidadosa da realidade objetiva para a obtenção de conhecimento. As dificuldades encontradas durante a pesquisa serviram de motivação para o desenvolvimento e elaboração deste estudo. A seção de resultados apresenta uma análise das concepções e recursos a serem utilizados no ensino-aprendizagem da matemática, culminando na conclusão deste trabalho.
Palavras chaves: Aprendizagem, Escola, Professor, Aluno e Matemática
1 INTRODUÇÃO
Este artigo teve como propósito investigar os desafios que foram enfrentados por professores e alunos no processo de aprendizagem da disciplina de matemática, especialmente nos 4º e 5º anos do Ensino Fundamental I na Escola Municipal Dom Pedro II. O ambiente escolar, concebido como um espaço motivador e acolhedor, deveria ter sido um cenário propício para o desenvolvimento do aluno como agente ativo de seu próprio aprendizado.
A escolha desse tema foi motivada pela urgência em compreender os obstáculos que permeavam o ensino e a aprendizagem da matemática nesse contexto específico. Embora diversos estudos já tivessem sido realizados nessa área, esta pesquisa se destacou por focar de forma particular nas experiências vivenciadas na escola mencionada.
Dentro desse contexto, esta investigação assumiu um papel de suma importância para o aprimoramento da educação, visando preparar os alunos para participarem ativamente na sociedade como indivíduos capazes de construir seu próprio conhecimento. O ambiente escolar foi delimitado como o principal campo de estudo, sendo os alunos o foco central da pesquisa, enquanto aprendizes em constante processo de desenvolvimento.
É importante ressaltar que não existia uma abordagem única e definitiva para o ensino de matemática, como apontado pelos Parâmetros Curriculares Nacionais (PCN’s) de 1997. No entanto, a familiaridade dos professores com diversas estratégias pedagógicas era essencial para enriquecer suas práticas de ensino e promover uma aprendizagem significativa e eficaz.
1.1 ABORDAGEM DO PROBLEMA
Este artigo teve como objetivo conhecer os desafios enfrentados em sala de aula por professores e alunos no processo de aprendizagem da disciplina de matemática. Nesse sentido, esperava-se que o ambiente escolar fosse um lugar motivador e acolhedor, onde o processo de ensino-aprendizagem contribuísse para o desenvolvimento do aluno como sujeito de seu próprio aprendizado
1.2 PERGUNTA GERAL
Quais as dificuldades de aprendizagem na disciplina de matemática nos 4º e 5º anos do ensino fundamental I na Escola Municipal Dom Pedro II?
1.3 OBJETIVO GERAL
Identificar possíveis causas das dificuldades de aprendizagem na disciplina de matemática nos 4º e 5º anos do ensino fundamental I na Escola Municipal Dom Pedro II.
1.4 JUSTIFICATIVA
Esta pesquisa teve seu início a partir da necessidade de buscar uma melhor compreensão da realidade escolar, tendo como foco o ensino de matemática como uma ciência prática do cotidiano do estudante. Vale ressaltar que a existência da escola só se dava porque havia uma clientela a ser atendida. Compreendendo isso, era necessário repensar o ato de ensinar como um direito da criança e dever da escola de proporcionar um ambiente atrativo, motivador, acolhedor e, acima de tudo, humano, onde “Aquele que ensina aprende ao ensinar e aquele que aprende ensina ao aprender” (FREIRE, 1999).
Além de transmitir o conhecimento, era papel do docente verificar quais eram as dificuldades de aprendizagem na disciplina de matemática percebidas em sala de aula, de modo que o aluno saísse sabendo utilizar em seu dia a dia na sociedade em que vivia os conhecimentos propostos pela referida disciplina.
1.5 LIMITAÇÕES DA PESQUISA
A educação tanto no contexto mundial como no brasileiro evoluiu com uma diversidade de pesquisas que são realizadas e aplicadas nas escolas visando contribuir com a formação dos professores e com novas metodologias que podem ser utilizadas, no intuito de tornar a sala de aula mais atrativa. Mas, a existência de novas metodologias de ensino não garante que os problemas que surgirem serão sanados em todas as escolas, e que, as pesquisas desenvolvidas serão propícias para aplicação em qualquer realidade de educação vivenciada, as metodologias, por si, são tem o potencial de garantir a aprendizagem dos alunos, é a ação do professor em sala de aula, a sua compreensão sobre a metodologia e do gerenciamento desta, em sala, que permite que uma determinada metodologia atinja os objetivos educacionais que se esperam ou não. Cyrino, Passerini (2009), Santos-Wagner, Nasser e Tinoco (1997) afirmam que, para muitos, o rendimento insatisfatório dos alunos em avaliações de aprendizagem escolar, está associado à má qualidade de ensino e ao despreparo dos professores para a prática letiva, assim segundo Garcia (2002) a formação de professores é definida como um fator decisivo na melhoria do ensino e, portanto, com grande influência no conhecimento social, jurídico, político e pedagógico de seu trabalho.
Em virtude do contexto apresentado, acredita-se que, a formação inicial de professores é uma etapa do processo de desenvolvimento profissional, o qual deve se estender ao longo de todo o período de atuação, além de que o conjunto de conhecimentos adquiridos durante essa etapa juntamente com os conhecimentos que esses futuros professores trazem de suas experiências quando estudantes, servirá de referência para sua prática em sala de aula. Assim, surge a necessidade de conhecer melhor as compreensões dos futuros professores que estão nas etapas finais de conclusão do Curso de Licenciatura em Matemática, acerca de uma metodologia em específico, a Resolução de Problemas.
Procedente da pesquisa, neste artigo, será apresentado o referencial teórico, a metodologia utilizada na pesquisa, bem como a análise dos dados e os resultados obtidos acerca das potencialidades e limitações do uso da Metodologia de Resolução de Problemas em sala de aula, segundo a visão desses futuros professores.
2. METODOLOGIA
2.1 Desenho de investigação:
A pesquisa foi conduzida de forma experimental, utilizando entrevistas com questionários contendo questões abertas e fechadas relacionadas à temática em estudo.
A abordagem foi tipicamente dedutiva, onde a maioria das ideias ou conceitos foi reduzida a variáveis e as relações entre elas foram testadas. O conhecimento resultante baseou-se em observação, medição e interpretação cuidadosa da realidade objetiva.
Por outro lado, o desenho de pesquisa qualitativa baseou-se no paradigma naturalístico. A abordagem do estudo foi indutiva, ao contrário de dedutiva, partindo da suposição de que a realidade é subjetiva, não objetiva, e que podem existir múltiplas realidades.
2.2 Enfoque
A pesquisa teve como objetivo analisar, explicar e prever fenômenos a partir de dados quantificáveis em uma realidade numérica, de maneira geral. Suas características incluíram análise estatística (cálculos e parâmetros), análise sistêmica (relação e interdependências das partes com o todo), procedimentos comparativos e realidades objetivas.
Para esse enfoque, as técnicas de pesquisa mais comuns foram medidas de opinião, entrevistas, questionários, experimentos, análise de dados e observação.
A investigação para a construção desta referida dissertação se conduziu de forma quantitativa.
2.3 Alcance
O alcance dessa pesquisa foi do tipo descritivo, nos moldes da exposição de Sampieiri, Colado e Lucio (2010, p. 80), segundo os quais:
No alcance descritivo, a meta do investigador consiste em descrever fenômenos, situações, contextos e eventos, detalhar como são e se manifestam os estudos descritivos. Buscam especificar as propriedades, as características e os perfis de pessoas, grupos, comunidades, processos, objetos ou qualquer outro fenômeno que se submeta a análise. É dizer, unicamente, que pretende medir ou reconhecer informações de maneira independente ou conjunta sobre os conceitos ou as variáveis a que se referem.
Os estudos elaborados a respeito do Autismo na Educação Infantil contavam com uma ampla gama de informações pertinentes, trazendo um amplo conjunto de variáveis que buscavam propor planos de ações e melhorias, explicando e traduzindo em palavras a realidade cotidiana vivenciada pelos principais atores que atuavam nesse contexto. No entanto, a abordagem proposta nesta pesquisa se amparou em uma ampla bibliografia para descrever os fenômenos, tendo em vista um fim mais específico: medir e avaliar a eficácia do tratamento dado ao aluno com autismo na educação infantil enquanto política pública e privada. Nesse sentido, o alcance que melhor se encaixou a este objetivo foi o descritivo. É importante destacar que esse alcance investigativo descritivo buscava “[…] especificar propriedades, características e cortes importantes de qualquer fenômeno que se analisasse” (SAMPIERI; COLADO; LUCIO, 2010, p. 80).
2.4 Fonte de dados
Na elaboração deste estudo, foram realizadas consultas em documentos como o Projeto Político Pedagógico (PPP), entrevistas com questionários e observações em salas de aula. A entrevista, técnica de pesquisa amplamente utilizada no meio social, permite que pesquisador e pesquisado interajam, esclarecendo questões e observando expressões, conforme destaca Gil (1999) e Marconi e Lakatos (2010).
2.5 População e amostra
O estudo em questão adota uma abordagem quantitativa, utilizando uma estratégia de análise transformadora. Isso implica na coleta e análise dos dados quase simultaneamente, com ênfase em uma teoria específica. A amostragem probabilística é direcionada mais por objetivos específicos do que por técnicas estatísticas tradicionais de representatividade. Além disso, destaca-se que se trata de uma amostragem mista, com ênfase na abordagem qualitativa, conforme sugerido por Sampieri. Colado; Lucio (2010, p. 394):
A amostra no processo de investigação quantitativa, é um grupo de pessoas, eventos, sucessos, comunidades etc., sobre o qual haverá uma coleta de dados sem que necessariamente seja representativa do universo ou população que se estuda.
O ambiente escolar será o foco deste estudo, centrando-se nos professores que trabalham na instituição de ensino em questão. Para conduzir a pesquisa de forma eficaz, será crucial obter informações básicas dos entrevistados, como origem, idade, sexo e outras características pertinentes. Os participantes serão devidamente informados sobre os motivos para sua participação ao responderem aos questionários propostos
2.6 Sujeito
O questionário para a entrevista foi aplicado com foco principal nos alunos, considerando que eles estavam em processo de formação e construção do conhecimento.
2.7 Amostra e procedimentos de amostra
Para a construção da referida pesquisa, foram realizadas entrevistas com 10 professores da instituição de ensino mencionada. Para tanto, foram construídos questionários a serem aplicados aos profissionais da educação que atuavam na escola escolhida como campo de estudo para a coleta de dados desta dissertação de mestrado.
2.8 Técnica e instrumento de coletas de dados
Ao desenvolver a pesquisa, os dados foram coletados por meio de consultas em documentos como o PPP (Projeto Político Pedagógico), entrevistas contendo questionários e observação em sala de aula.
2.9 Procedimento de coleta de dados
O método utilizado para a coleta de dados durante a construção desta pesquisa foi a aplicação de questionários por meio de entrevistas pessoais, nas quais cada entrevistado respondeu às questões propostas relacionadas ao tema em estudo. Além disso, o PPP (Projeto Político Pedagógico) foi consultado para obter informações sobre a escola, que é o campo de estudo desta pesquisa. Para complementar, foi realizada observação em sala de aula, onde foram registrados os métodos utilizados durante as aulas.
2.10 Técnica de análise de dados
Os resultados obtidos durante a pesquisa de campo serão apresentados por meio de gráficos.
3. DISCUSSÃO E ANÁLISES DOS RESULTADOS
Segue abaixo os gráficos contendo informações referente ao questionário aplicado durante a construção desta dissertação de mestrado. As questões foram elaboradas com base nos estudos teóricos realizados no decorrer da elaboração desta pesquisa.
1) Sobre a sua área de formação, responda.
- ( ) Formação em área específica.
- ( ) Formação em Normal Superior ou Pedagogia
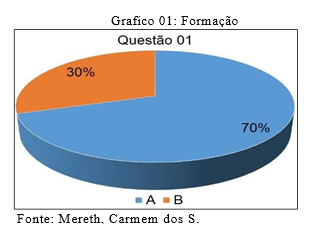
A maioria dos entrevistados tem formação na área em que lecionam. O debate atual sobre a formação de professores destaca a importância de integrar a prática pedagógica à formação, sem distinguir entre disciplinas didático-pedagógicas e específicas.
2) Considera a matemática importante? Por quê?
- ( ) Sim.
- ( ) Não.

Na questão número 2, todos os entrevistados responderam afirmativamente. Suas justificativas destacam a importância da matemática no dia a dia e em diversas profissões, enfatizando sua presença constante em diferentes aspectos da vida. Essa unanimidade reflete a percepção de que a matemática é uma ferramenta essencial, presente em todas as áreas da educação e fundamental para uma formação completa.
Conforme Souza (2001), o ensino da Matemática é fundamental na formação humanística e o currículo escolar deve levar a essa boa formação, logo o ensino da matemática é indispensável para que esta formação seja completa.
3) Durante quanto tempo estudou matemática?
A ( ) Ensino básico 9 anos.
B ( ) Ensino secundário 12 anos ou mais
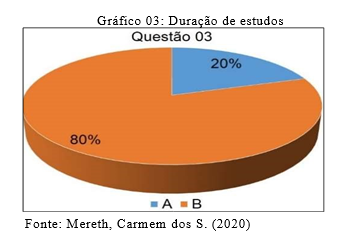
Na questão 03, os entrevistados foram solicitados a indicar por quanto tempo estudaram matemática, seja durante o ensino básico (9 anos) ou durante o ensino secundário (12 anos ou mais). Essa pergunta destaca a importância de que tanto os professores quanto os alunos possuam habilidades matemáticas para resolver problemas do cotidiano, modelar fenômenos em outras áreas do conhecimento, compreender a natureza da matemática como ciência, apreciar sua importância no desenvolvimento científico e tecnológico, e reconhecer sua relevância como um conhecimento social e historicamente construído.
[…] saibam usar a Matemática para resolver problemas práticos do cotidiano; para modelar fenômenos em outras áreas do conhecimento; compreendam que a Matemática é uma ciência com características próprias, que se organiza via teoremas e demonstrações; percebam a Matemática como um conhecimento social e historicamente construído; saibam apreciar a importância da Matemática no desenvolvimento científico e tecnológico (BRASIL, 2006, p. 69).
4) Gosta de matemática?
A ( ) Sim.
B ( ) Não.
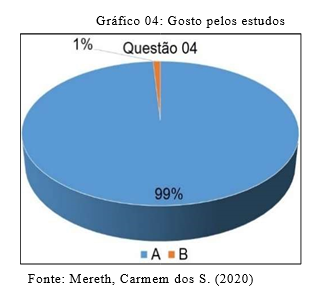
No gráfico acima, observa-se que apenas 1% dos entrevistados não demonstram gostar de matemática, apesar de reconhecerem sua importância na vida escolar e além dela. Essa realidade reflete a percepção de Ávila (2000, p. 61), que ressalta que
Apesar dos esforços empenhados por parte dos professores para explicar conteúdos, na maioria das vezes o estudante sai mal nas provas, rotulando a matemática como vilã, considerando-a difícil e fora de sua realidade. Uma simples pesquisa que se faça em sala de aula demonstra que é raro algum aluno afirmar que goste de matemática, é quase unanimidade a aversão por essa matéria, e os alunos dizem que só estudam por ser um mal necessário.
5) Assinale cada uma das seguintes frases, de acordo com o seu grau de acordo/desacordo, numa escala entre 1 (discordo em absoluto) e 5 (concordo totalmente)
Quadro 02: Pregunta 05
1 2 3 4 5 A Matemática é uma disciplina difícil. 60% 20% 20% A Matemática é uma forma de comunicação. 100% A Matemática é um mal necessário. 80% 20% A Matemática faz parte do nosso dia-a-dia. 100% Posso passar bem sem Matemática. 100% A Matemática é útil apenas nalgumas situações. 100% Qualquer um “tem jeito” para a Matemática. 30% 10% 60% Só os melhores sabem matemática. 100% Saber Matemática é saber a tabuada. 60% 20% 20% Saber Matemática é saber resolver problemas. 25% 20% 25% 30% Saber Matemática é fazer contas. 20% 40% 40% Posso saber matemática mesmo não sabendo realizar os algoritmos das quatro operações. 40% 20% 40%
Na questão número 05, há uma variedade de respostas entre os entrevistados, com poucos consensos evidentes. Isso destaca a presença de diferentes opiniões dentro do mesmo contexto. Essa diversidade de perspectivas reflete a complexidade e a subjetividade envolvidas em questões educacionais e pedagógicas.
Aprender matemática é mais do que manejar fórmulas, saber fazer contas ou marcar x nas respostas: é interpretar, criar significados, construir seus próprios instrumentos para resolver problemas, estar preparado para perceber estes mesmos problemas, desenvolver o raciocínio lógico, a capacidade de conceber, projetar e transcender o imediatamente sensível (PARANÁ, 1990, p.66)
6) Em que situações lhe parece que a Matemática é um instrumento facilitador?
A ( ) Somente no ambiente escolar.
B ( ) Somente em casa.
C ( ) Somente em situações que se use números.
D ( ) Faz parte do cotidiano em toda e qualquer situação.

É importante que a presença do conhecimento matemático seja percebida, e claro, analisada e aplicada às inúmeras situações que circundam o mundo, visto que a matemática desenvolve o raciocínio, garante uma forma de 25 pensamento, possibilita a criação e amadurecimento de ideias, o que traduz uma liberdade, fatores estes que estão intimamente ligados a sociedade.
Por isso, ela favorece e facilita a interdisciplinaridade, bem como a sua relação com outras áreas do conhecimento (filosofia, sociologia, literatura, música, arte, política etc.) (RODRIGUES, 2005, p.5)
7) E quando lhe parece que a Matemática pode constituir um obstáculo? Professor A – “Quando o professor não consegue “passar”, ministrar o conteúdo ao aluno.”
Professor B – “Quando não há interesse em aprender.”
Professor C – “Nas resoluções de algumas fórmulas.”
Professor D – “Nunca.”
Professor E – “Quando se deparamos com determinadas situações problemas.”
A Matemática enquanto ciência pode se constituir um obstáculo por diversos fatores, entretanto, cabe ao professor proporcionar metodologias que possa minimizar a distância entre o ensinar e o aprender. Desta forma “os papéis dos intervenientes se alteram significativamente, tornando-se o aluno ‘o agente da sua própria aprendizagem’ e o professor o ‘dinamizador’ do trabalho, o ‘negociador de intenções’, e o companheiro de descobertas’”, (VASCONCELOS, 2008, p. 16)
8) Quais as principais dificuldades que sente ao ensinar Matemática?
Os entrevistados destacaram diferentes dificuldades ao ensinar Matemática:
Professor A observou que os alunos têm dificuldade nas quatro operações básicas.
Professor B mencionou o tabu de que a matemática é difícil.
Professor C citou como dificuldade o ensino de fórmulas, expressões e frações.
Professor D indicou que não trabalha com Matemática.
Professor E revelou dificuldades específicas com porcentagens.
É de fundamental importância que o professor, como mediador no processo ensino-aprendizagem, tenha domínio dos conteúdos a serem ministrados, garantindo segurança e responsabilidade. Muitos ainda veem o ensino da matemática como algo distante da realidade dos alunos, o que pode criar barreiras ao aprendizado. Cunha (2008, p. 11) ressalta o papel do professor nas seguintes palavras “Cabe ao professor mostrar (…) que [a matemática] pode ser fácil, pela diversidade de estratégias, pela adequação à realidade, embora sinta que há coisas nos programas que, se calhar não cumprem esses objetivos”.
9) Quais as principais dificuldades se podem observar em seus alunos?
Os professores identificaram diversas dificuldades entre os alunos. Destacaram a falta de interesse, especialmente devido à forma como o ensino foi conduzido no passado. Além disso, problemas com o reconhecimento dos sinais das operações e desafios com cálculos foram mencionados. Essas observações ressaltam a necessidade de abordagens pedagógicas que incentivem o interesse dos alunos e fortaleçam suas habilidades em matemática. Certamente, a falta de motivação dos alunos é um dos desafios mais persistentes enfrentados pelos professores em sala de aula. Essa falta de interesse pode levar a atitudes de resistência ao aprendizado, dificultando a eficácia do ensino. Neste caso, Barbosa (2008) enfatiza que:
A presença de um obstáculo no processo de aprendizagem não indica a existência de dificuldades permanentes, mas, sim, a forma que o sujeito encontrou de autorregular seus esquemas de aprendizagem. Neste sentido, a busca da superação desses obstáculos deve acontecer não como uma proposta de cura, mas como um encontro para a ampliação de recursos a serem utilizados neste movimento de busca de equilíbrio e de autorregulação (BARBOSA, 2008, p.55).
10) É possível que essas dificuldades possam se repercutir noutras áreas? Como?
Os professores expressam diversas opiniões sobre a correlação entre leitura e habilidades em matemática. O Professor A destaca a presença da matemática em todos os conteúdos, muitas vezes de forma oculta. Já o Professor B acredita que alunos que leem muito não têm dificuldade em matemática ou em outras disciplinas. O Professor C ressalta a importância do bom trabalho e da entrega adequada dos conteúdos, enquanto o Professor D sugere que a falta de interesse em uma disciplina pode afetar outras áreas também. Por fim, o Professor E sugere o uso de jogos e brincadeiras como uma forma de melhorar o ensino de matemática. É válido ressaltar que quando o professor transforma o ensino de matemática utilizando cada vez mais recursos e meios reais, para maior aproveitamento dessa disciplina ela se torna menos temida pelos alunos. Nessa conexão, D’AMBRÓSIO (2002), infere de modo enfático:
A matemática é sem dúvida uma das matérias mais temidas pelos alunos em geral, e como tal, pode-se ver que quanto mais recursos e meios reais forem utilizados numa aula, maior será o aproveitamento da matéria. A escola não justifica pela apresentação do conhecimento obsoleto e ultrapassado e, sim em fala rem ciências e tecnologia (D’AMBRÓSIO, 2002, p. 67).
CONCLUSÃO
Com base nos resultados desta pesquisa, é evidente que os desafios enfrentados diariamente durante o processo de busca por conhecimento são variados e significativos. Isso ressalta a importância de desenvolver habilidades para lidar com esses desafios, pois o sucesso está intrinsecamente ligado à capacidade de resolvê-los.
Por outro lado, compreender a resolução de problemas como uma metodologia de ensino e aprendizagem de matemática pode ter um impacto significativo na prática pedagógica dos professores. As dificuldades encontradas nesse processo devem ser constantemente questionadas e analisadas, visando sempre aprimorar o processo de ensino.
Recomenda-se, portanto, que os professores que ensinam matemática busquem informações e sugestões para melhorar o processo de ensino-aprendizagem, a fim de modificar a percepção que muitos estudantes têm dessa disciplina. Para os alunos com desempenho insatisfatório em matemática, é imprescindível que os professores utilizem metodologias que despertem seu interesse, considerando a importância dessa ciência em todos os aspectos da vida cotidiana.
Essas atitudes não apenas fortalecerão o papel social e humano do professor, mas também da própria matemática. O papel do docente não se limitará mais à transmissão de conhecimento; ele será responsável por conduzir os alunos à problematização e ao raciocínio crítico, promovendo uma percepção ativa e relevante do que estão estudando e aprendendo.
REFERÊNCIAS
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS (ABNT NBR 14724). Informação e documentação — Trabalhos acadêmicos — Apresentação. 3. ed. Rio de Janeiro – RJ: PETROBRAS, v. s.v., 2011. 11 p. ISBN 978-85-07-02680-8.
ÁVILA, Iraci Vieira: A dificuldade em aprender matemática. Revista do curso de especialização em Educação Brasileira, Rio Grande do Sul, RS, v3, p. 61-65, 2000.
BARBOSA, A. M. (Org.). Inquietações e mudanças no Ensino da Arte. São Paulo: Editora Cortez, 4 ed., 2008.
BRASIL. Ministério da Educação, Secretaria de Educação Básica. Orientações curriculares para o ensino médio: Ciências da natureza, matemática e suas tecnologias. Brasília, 2006.
D’AMBROSIO, Ubiratã. Educação matemática: da teoria à prática. 8. ed. Campinas: Papirus, 2012.
FREIRE, Paulo. Pedagogia da Autonomia. Saberes Necessários à Prática Educativa. Rio de Janeiro: Paz e terra, 1999.
PARANÁ. Secretaria de Estado da Educação. Superintendência da Educação. Departamento de Ensino Fundamental. Orientações Pedagógicas, matemática: sala de apoio à aprendizagem. Curitiba: SEED-PR.2005, p.130.
VASCONCELOS, Cláudia Cristina. Ensino–aprendizagem da matemática: velhos problemas, novos desafios. Revista Milenium, v. 20, 2008.
