REGISTRO DOI: 10.5281/zenodo.12601223
Edilmar Almeida Resende
Higor da Silva Baraúna
Judson Trindade Ramos
Resumo
Nos cálculos judiciais relacionados a financiamentos e empréstimos, a escolha correta do método de cálculo de juros é fundamental para garantir precisão e justiça nos resultados. Este artigo apresenta uma comparação detalhada entre dois métodos de amortização de empréstimos: o Método de Gauss e o Método de Equivalência a Juros Simples. O Método de Gauss, apesar de ser amplamente reconhecido na matemática financeira, apresenta limitações significativas quando utilizado em cálculos de juros simples em processos judiciais. Essas limitações podem resultar em inconsistências e distorções que afetam a justiça das decisões judiciais. Em contraste, o Método de Equivalência a Juros Simples, fundamentado em princípios matemáticos sólidos, oferece maior transparência e simplicidade, sendo mais adequado para a maioria dos cálculos judiciais.
Para ilustrar essas diferenças, este estudo inclui um estudo de caso detalhado envolvendo um financiamento de R$ 50.000,00 com prazo de 15 meses e taxa de juros mensal de 1,5%. A análise mostra que o Método de Equivalência a Juros Simples proporciona maior precisão e consistência nos cálculos. O método garante que o valor presente das prestações seja igual ao valor financiado, refletindo corretamente o montante de juros pagos. Por outro lado, o Método de Gauss pode levar a resultados distorcidos, onde o valor presente das prestações não corresponde ao capital financiado, indicando uma falha na aplicação dos juros simples.
Os resultados destacam a importância de escolher o método de cálculo de juros adequado em processos judiciais para evitar distorções financeiras e garantir decisões justas. Este estudo oferece uma análise detalhada das características de cada método, suas implicações financeiras e judiciais, além de fornecer recomendações práticas para a escolha do método mais adequado em cálculos judiciais. A aplicação correta dos métodos de cálculo de juros é essencial para assegurar a exatidão e a justiça nas decisões judiciais, protegendo os interesses das partes envolvidas e garantindo a integridade dos processos financeiros.
Palavras-chave: Juros Simples, Método de Gauss, Método de Equivalência a Juros Simples, Amortização de Empréstimos.
1. Introdução
Nos cálculos judiciais que envolvem a aplicação de juros, a escolha do método adequado é de extrema importância para garantir a justiça e precisão nos resultados. Em muitos processos judiciais, especialmente aqueles relacionados a financiamentos e empréstimos, a correta aplicação dos juros pode determinar o valor final devido, afetando diretamente as partes envolvidas. Dentre os métodos de cálculo de juros, destacam-se o método de Gauss e o método de equivalência a juros simples. Ambos possuem características distintas, e a escolha entre eles pode influenciar significativamente os resultados financeiros em processos judiciais.
O método de Gauss, amplamente conhecido na matemática financeira, é frequentemente aplicado em cálculos financeiros devido à sua precisão em determinados contextos. Contudo, quando utilizado para cálculos de juros simples em processos judiciais, esse método apresenta diversas limitações. Por outro lado, o método de equivalência a juros simples, baseado na aplicação direta da fórmula de juros simples, oferece maior transparência e simplicidade, sendo mais adequado para a maioria dos cálculos judiciais.
A escolha do método de cálculo de juros em processos judiciais não é uma questão trivial. É crucial para garantir que os valores calculados reflitam com precisão os montantes devidos, evitando distorções financeiras que possam prejudicar qualquer uma das partes envolvidas. Neste contexto, a importância de utilizar métodos adequados e juridicamente aceitos torna-se evidente, sendo este estudo relevante para contadores, advogados, juízes e outros profissionais envolvidos em litígios financeiros.
Este artigo tem como principal objetivo comparar o método de Gauss e o método de equivalência a juros simples, demonstrando que o método de Gauss não é recomendado para cálculos judiciais que envolvem juros simples. A escolha inadequada do método pode resultar em imprecisões nos cálculos, afetando a justiça das decisões judiciais. Assim, este estudo busca oferecer uma análise detalhada das características de cada método, suas implicações judiciais e financeiras, e apresentar um caso prático para ilustrar as diferenças nos resultados obtidos.
A justificativa para este estudo reside na necessidade de assegurar a exatidão nos cálculos judiciais. Em processos onde grandes somas de dinheiro estão em jogo, a precisão dos cálculos é fundamental para garantir que as partes recebam o que lhes é devido, sem prejuízos decorrentes de métodos inadequados. A aplicação de métodos complexos, como o de Gauss, em situações que exigem simplicidade e clareza, como os cálculos de juros simples, pode levar a resultados confusos e potencialmente injustos.
A estrutura do artigo está organizada de forma a proporcionar uma compreensão clara e detalhada do tema. Iniciaremos com uma revisão da literatura, abordando conceitos fundamentais como juros simples, juros compostos, capitalização simples e composta, além de detalhar os métodos de equivalência a juros simples e o método de Gauss. Em seguida, apresentaremos um estudo de caso onde aplicaremos ambos os métodos a uma demanda judicial fictícia, analisando e comparando os resultados obtidos. A análise dos resultados destacará as vantagens e desvantagens de cada método, seguidas por uma discussão sobre as preferências dos magistrados em decisões judiciais recentes. Por fim, concluiremos com recomendações práticas para a escolha do método mais adequado em cálculos judiciais.
A metodologia adotada para este estudo inclui uma revisão de literatura abrangente, a aplicação prática dos métodos em um caso simulado, e a análise dos resultados comparativos. A revisão da literatura fornecerá a base teórica necessária para a compreensão dos conceitos e métodos abordados, enquanto o estudo de caso permitirá uma análise prática e detalhada das diferenças entre os métodos. A análise dos resultados será fundamentada em critérios de precisão, transparência e aplicabilidade jurídica, oferecendo uma visão crítica e embasada das implicações de cada método.
Em resumo, este artigo busca contribuir para a discussão sobre a escolha de métodos de cálculo de juros em processos judiciais, oferecendo uma análise comparativa detalhada entre o método de Gauss e o método de equivalência a juros simples. Acreditamos que, ao final deste estudo, ficará claro que o método de equivalência a juros simples é a melhor opção para garantir a justiça e a precisão nos cálculos judiciais, enquanto o método de Gauss, apesar de sua aplicabilidade em outros contextos, apresenta limitações significativas quando aplicado a juros simples.
2. Revisão da Literatura
2.1. Regimes de Capitalização dos Juros
No contexto econômico, cada transação envolvendo capital, bens duráveis, serviços, entre outros, requer uma contrapartida, ou seja, um pagamento. Diferentes tipos de transações são associados a diferentes termos de remuneração. Por exemplo, na locação de um imóvel, temos o aluguel; para serviços prestados, utilizamos honorários; e no uso do capital, aplicam-se os juros. Segundo Casarotto Filho e Kopittke (1996), os juros podem ser vistos como o preço da moeda ou da liquidez, representando o custo do capital ou do dinheiro. Puccini (1973) define juros como “dinheiro pago pelo uso de dinheiro emprestado” ou “remuneração do capital empregado em atividades produtivas”. Esses conceitos destacam a importância dos juros na economia, permitindo a comparação de capitais em diferentes datas e facilitando o fluxo de capital de investidores para tomadores. Além disso, os juros são cruciais para a análise de viabilidade de projetos e investimentos, pois refletem o custo de oportunidade do capital empregado.
Os juros são fundamentais na matemática financeira, pois possibilitam a transformação de valores ao longo do tempo, facilitando a comparação de capitais em diferentes datas (Kuhnen e Bauer, 2001). Na economia, os juros permitem que detentores de capital disponibilizem recursos a quem necessita, a um preço acordado, e permitem investimentos com retorno esperado sob a forma de taxa de juros. Ferreira (1993) define capitalizar como “converter em capital” ou “acumular”. Assim, capitalização de juros refere-se à forma como os juros são calculados e adicionados ao capital inicial.
Pilão e Hummel (2004) classificam os juros em: antecipados, postecipados, reais, efetivos, nominais, simples e compostos. Juros antecipados são cobrados no início de cada período, enquanto juros postecipados são cobrados no final de cada período. O mercado geralmente utiliza juros postecipados e compostos, comuns em financiamentos imobiliários, mas algumas operações utilizam juros antecipados, como no desconto de duplicatas. Juros antecipados são também conhecidos como juros vencidos, enquanto juros postecipados são conhecidos como anuidades ordinárias.
2.1.1. Juros Reais
Hoji (2001) explica que pode haver diferença entre inflação estimada e efetiva. Quando a taxa de juros bruta é maior que a inflação do período de capitalização, a taxa de juros real é positiva; caso contrário, é negativa. A taxa de juros reais exclui o efeito da inflação, que reduz o poder de compra da moeda. A inflação diminui o valor real do dinheiro ao longo do tempo, e a taxa de juros real ajusta essa perda de valor. Assim, a taxa de juros real é um indicador crucial para entender o verdadeiro retorno de um investimento, descontando os efeitos da inflação.
Por exemplo, se a inflação anual é de 4% e a taxa de juros nominal é de 6%, a taxa de juros real será aproximadamente 2%, indicando um ganho real no poder de compra. Compreender a diferença entre juros reais e nominais é essencial para investidores e tomadores de empréstimos, pois afeta diretamente a análise de rentabilidade e custo de oportunidade. A taxa de juros real, portanto, oferece uma visão mais precisa do retorno de um investimento, ajustando as expectativas para um cenário inflacionário. Isso é especialmente importante em economias com alta volatilidade inflacionária, onde a taxa de juros real pode flutuar significativamente, impactando decisões de investimento e financiamento.
2.1.2. Juros Nominais
Hoji (2001) define a taxa nominal como a taxa de juros contratada em uma operação financeira, calculada com base no valor nominal da aplicação ou do empréstimo, ou seja, no valor explicitado no título ou no contrato. A taxa nominal é utilizada para determinar os pagamentos periódicos de juros ao longo da vida de um empréstimo ou investimento. No entanto, a taxa nominal não considera os efeitos da inflação, diferindo da taxa de juros real que ajusta esses efeitos.
Por exemplo, se um título oferece uma taxa nominal de 5% ao ano, essa é a taxa utilizada para calcular os pagamentos periódicos de juros. No entanto, se a inflação no mesmo período for de 3%, o ganho real do investidor será reduzido para aproximadamente 2%. Portanto, a taxa nominal é uma medida essencialmente administrativa e contratual, enquanto a taxa real é mais relevante para a avaliação do poder de compra e retorno efetivo do investimento.
Além disso, a taxa nominal é fundamental para a estruturação de contratos financeiros e a definição das condições de pagamento em operações de crédito. Ela serve como base para cálculos de juros e amortizações em diversos tipos de financiamento, desde empréstimos pessoais até hipotecas e financiamentos empresariais. A compreensão da taxa nominal é essencial para avaliar a viabilidade de projetos de investimento e para a gestão de passivos financeiros.
2.1.3. Juros Efetivos
Hoji (2001) explica que a taxa efetiva é a taxa de juros do período de capitalização que realmente será aplicada sobre o capital, independentemente da taxa nominal. Quando o período de aplicação da taxa de juros é igual ao período contratado, a taxa nominal e a taxa efetiva serão iguais. A taxa efetiva reflete a verdadeira taxa de retorno sobre um investimento, considerando a frequência de capitalização. Assim, ela pode diferir da taxa nominal, especialmente em regimes de capitalização composta onde os juros são calculados e adicionados ao principal mais frequentemente do que uma vez por ano.
Por exemplo, um investimento com uma taxa nominal anual de 12%, capitalizada mensalmente, resultará em uma taxa efetiva anual de aproximadamente 12,68%. Essa diferença ocorre devido à capitalização dos juros ao longo do ano, o que aumenta o montante final acumulado. A compreensão da taxa efetiva é crucial para avaliar o custo real dos empréstimos e o retorno dos investimentos. A taxa efetiva oferece uma medida mais precisa do impacto dos juros compostos ao longo do tempo, refletindo o verdadeiro custo ou retorno de uma operação financeira.
2.1.4. Regime Simples de Juros
Hoji (2001) define juros simples como aqueles calculados sobre o capital inicial, proporcionalmente ao número de capitalizações. Os juros simples são aplicados linearmente sobre o capital inicial, resultando em um crescimento linear do montante. A fórmula básica dos juros simples é:
J=P⋅i⋅t
Onde:
- J é o valor dos juros,
- P é o principal,
- i a taxa de juros,
- t é o tempo.
A acumulação do capital e juros resulta no montante (M):
M=P+J=P+(P⋅i⋅t)
Neste regime, os juros de cada período não são incorporados ao saldo devedor, evitando a capitalização dos juros. Francisco (1985) define juro simples como aquele produzido unicamente pelo capital inicial. Puccini (2006) esclarece que, na capitalização simples, os juros de cada período são calculados em função do capital inicial, sem somar os juros ao capital para o cálculo de novos juros nos períodos seguintes. Simonsen e Ewald (1990) afirmam que os juros simples são adequados apenas quando os juros são pagos período a período.
As taxas em capitalização simples podem ser classificadas como proporcionais ou equivalentes, sendo que, neste regime, taxas proporcionais são equivalentes. As taxas podem ser apresentadas sob forma unitária ou percentual. Esse regime é frequentemente utilizado em empréstimos de curto prazo, onde o cálculo simples e direto dos juros facilita a gestão e a transparência financeira. A simplicidade do regime de juros simples o torna ideal para situações onde os períodos de capitalização são relativamente curtos e a complexidade adicional dos juros compostos não é necessária.
2.1.5. Regime Composto de Juros
Segundo Hoji (2001), no regime de juros compostos, os juros produzidos em cada período de capitalização são integrados ao capital constituído no início dos respectivos períodos, gerando novos juros nos períodos seguintes. A fórmula de cálculo dos juros compostos é:
M=P(1+i)t
Onde:
- M é o montante final,
- P é o principal,
- i é a taxa de juros,
- t é o tempo.
Neste regime, uma taxa incide sobre o principal, gerando juros que são incorporados ao capital e produzem novos juros no período seguinte. Casarotto Filho e Kopittke (1996) explicam que, após cada período de capitalização, os juros são somados à dívida anterior e passam a render juros no período seguinte. Puccini (2006) esclarece que, na capitalização composta, os juros de cada período são somados ao capital, rendendo novos juros.
Esse regime é amplamente utilizado em financiamentos e investimentos de longo prazo devido ao efeito multiplicador dos juros sobre juros. A capitalização composta resulta em um crescimento exponencial do montante, proporcionando maiores retornos em investimentos e maior custo em financiamentos ao longo do tempo. Esse regime é especialmente relevante em investimentos de longo prazo, como fundos de pensão e hipotecas, onde os efeitos da composição podem ter um impacto significativo no valor final acumulado ou no montante total a ser pago. A aplicação de juros compostos é vantajosa para investidores que buscam maximizar retornos ao longo de períodos prolongados, aproveitando o efeito acumulativo dos juros ao longo do tempo.
2.1.6. Distinção entre os Regimes de Juros Simples e Compostos
Brealey e Myers (1992) destacam a diferença fundamental entre juros compostos e juros simples: nos juros compostos, os juros vencidos são reinvestidos para obter mais juros nos períodos seguintes, enquanto nos juros simples, essa oportunidade não existe. Em termos práticos, a diferença pode ser visualizada através de um gráfico comparativo onde o regime simples é linear, enquanto o regime composto segue uma função exponencial.
Isso significa que, no longo prazo, os juros compostos proporcionam um crescimento significativamente maior do montante em comparação aos juros simples, devido ao efeito cumulativo dos juros sobre juros. Por exemplo, um investimento de R$1.000 a uma taxa de 10% ao ano resultará em R$1.100 após um ano tanto em juros simples quanto em compostos. No entanto, após dois anos, o investimento a juros simples será de R$1.200, enquanto a juros compostos será de R$1.210. Com o tempo, essa diferença se torna mais pronunciada, destacando a importância da capitalização composta para maximizar retornos ou minimizar custos em financiamentos de longo prazo.
Em financiamentos, a escolha entre juros simples e compostos pode ter um impacto significativo no valor total a ser pago pelo tomador de empréstimo. Os juros compostos aumentam o montante devido de forma mais rápida, refletindo um custo total maior ao longo do tempo. Por isso, é crucial que tomadores de empréstimos compreendam as implicações de cada regime para tomar decisões financeiras informadas.
2.1.7. Efeito do Prazo sobre as Taxas de Juros
A periodicidade da capitalização pode influenciar significativamente a taxa efetiva. Quanto maior o número de capitalizações, maior será a taxa efetiva. Rezende (2003) apresenta uma tabela comparando uma taxa nominal de 12% ao ano, capitalizada por diversos períodos até atingir o limite da capitalização contínua. A tabela demonstra que a taxa efetiva aumenta com a frequência da capitalização, atingindo um limite teórico na capitalização contínua.
Por exemplo, uma taxa nominal de 12% ao ano capitalizada mensalmente resulta em uma taxa efetiva anual de aproximadamente 12,68%. Se capitalizada diariamente, a taxa efetiva seria cerca de 12,75%, e na capitalização contínua, atingiria aproximadamente 12,74%. Este fenômeno é crucial para investidores e tomadores de empréstimos, pois afeta diretamente o custo real do capital ao longo do tempo. A compreensão deste efeito é vital para a tomada de decisões financeiras informadas, tanto para maximizar os retornos sobre investimentos quanto para minimizar os custos de empréstimos.
A variação das taxas de juros em função do período de capitalização é uma consideração importante em qualquer análise financeira, especialmente em contextos de inflação alta ou volatilidade econômica. A capitalização frequente de juros pode resultar em um custo total substancialmente maior para os tomadores de empréstimos, ou um retorno significativamente maior para os investidores. Este efeito é amplamente utilizado em produtos financeiros como contas de poupança, certificados de depósito e empréstimos, onde a frequência de capitalização é uma variável chave.
2.1.7.1. Capitalização Contínua
Assaf Neto (2001) define capitalização contínua como um regime que se processa em intervalos de tempo infinitesimais, promovendo grande frequência de capitalização. Embora a capitalização contínua eleve a taxa efetiva, esse aumento tende a um limite, conforme a fórmula da taxa proporcional:
Cᶦeᶜᵗ
onde:
e = base do logaritmo natural (Lₙ), vale aproximadamente 2,7182,
iϲ = taxa instantânea e
t = período de capitalização.
A capitalização contínua é um conceito teórico que ilustra o efeito máximo da frequência de capitalização sobre a taxa efetiva, fornecendo uma perspectiva sobre como pequenas variações na frequência de capitalização podem impactar significativamente o montante acumulado ao longo do tempo. No entanto, na prática, a capitalização contínua é raramente utilizada devido à complexidade de cálculos e à necessidade de tecnologias avançadas para monitorar continuamente o crescimento do montante. Essa abordagem é mais relevante em contextos acadêmicos e teóricos, onde serve como uma ferramenta para entender os limites e comportamentos dos modelos de capitalização ao extremo. A compreensão da capitalização contínua ajuda a esclarecer os limites teóricos do crescimento de um investimento ou do custo de um empréstimo, proporcionando insights valiosos para a formulação de estratégias financeiras eficazes.
2.2. Equivalência de Capitais
A questão do valor do dinheiro no tempo é fundamental na matemática financeira. O valor temporal do dinheiro baseia-se na premissa de que um real hoje vale mais do que um real no futuro, devido ao seu potencial de ganho. Essa premissa é crucial para a tomada de decisões financeiras, sejam elas relacionadas a investimentos, empréstimos ou financiamentos. Puccini (2006) observa que a matemática financeira está diretamente ligada ao valor do dinheiro no tempo e às taxas de juros, preceituando que valores de uma mesma data podem ser comparados e somados algebricamente. Mathias e Gomes (2002) esclarecem que capitais com datas de vencimento diferentes são equivalentes se, quando levados para uma mesma data focal à mesma taxa de juros, tiverem valores iguais. Essa equivalência de capitais é essencial para comparar e analisar diferentes fluxos de caixa ao longo do tempo, facilitando a avaliação de alternativas de investimento e financiamentos.
2.2.1. Equivalência de Capitais a Juros Simples
Na equivalência de capitais a juros simples, existem divergências quanto à data focal, ou seja, a data na qual os valores serão comparados. Assaf Neto (2001) afirma que a definição da data focal deve ser acordada pelas partes envolvidas na transação, pois não há um consenso técnico definitivo. Ele argumenta que, na prática, a data focal é decidida naturalmente, dependendo dos interesses das partes, sendo comum que o credor prefira uma data que maximize os pagamentos enquanto o devedor prefira uma data que minimize esses pagamentos. Francisco (1985) defende que capitais realizáveis em datas distintas são equivalentes se seus valores atuais na data zero forem iguais, implicando que a equivalência deve ser verificada na data de hoje. Faro (1989) observa que capitais equivalentes em determinada data podem não o ser em outra, dependendo da maximização ou minimização dos pagamentos por credores ou devedores, o que indica que a equivalência é sensível ao período escolhido para a comparação. Essa sensibilidade à data focal faz com que a escolha dessa data seja um ponto crítico em negociações financeiras, pois pode afetar significativamente o resultado da equivalência dos capitais envolvidos.
2.2.2. Equivalência de Capitais a Juros Compostos
A equivalência de capitais a juros compostos tem uma definição mais clara e aceita. Mathias e Gomes (2002) afirmam que capitais equivalentes sob juros compostos em uma data focal são equivalentes em qualquer data focal, desde que a mesma taxa de juros seja aplicada. Isso ocorre porque, no regime de juros compostos, os juros são reinvestidos ao longo do tempo, acumulando-se sobre o capital inicial e sobre os juros já acumulados, o que garante que a equivalência financeira seja mantida independentemente da data de referência escolhida. Assaf Neto (2001) confirma que a equivalência financeira pode ser verificada em qualquer momento tomado como referência, reforçando a ideia de que a data focal pode ser escolhida de forma arbitrária sem comprometer a análise de equivalência. Faro (1989) destaca que, em juros compostos, capitais equivalentes em uma data serão equivalentes em outra, desde que a mesma taxa de juros seja aplicada, o que facilita a comparação e a análise de diferentes fluxos de caixa ao longo do tempo. Essa propriedade dos juros compostos torna a equivalência de capitais mais flexível e robusta, permitindo uma análise mais precisa e consistente de investimentos e financiamentos.
2.2.3. Equivalência de Fluxos de Caixa
Para clarificar a equivalência de fluxos de caixa, é essencial traçar uma linha do tempo, demonstrando as entradas e saídas de caixa ao longo do período considerado. Puccini (2006) esclarece que dois ou mais fluxos de caixa são equivalentes a uma determinada taxa de juros se seus valores presentes (PV), calculados com essa mesma taxa de juros, forem iguais. Traçar uma linha do tempo ajuda a visualizar quando e como os fluxos ocorrem, permitindo uma comparação direta entre diferentes alternativas de investimento ou financiamento. A equivalência de fluxos de caixa facilita a avaliação de projetos, permitindo que gestores e investidores comparem diferentes opções de financiamento ou investimento com base no valor presente de seus fluxos de caixa futuros.
2.2.3.1. Valor Presente (PV)
Gitman (2002) define o valor presente como o valor atual de um montante futuro em unidades monetárias, considerando a taxa de juros e o período especificado. O valor presente (PV) é uma ferramenta fundamental na análise de investimentos, pois permite trazer todos os fluxos de caixa futuros para o valor de hoje, facilitando a comparação e a tomada de decisão. O valor presente de um fluxo a juros compostos pode ser encontrado pela fórmula:
PV = FV/(1+i)t
Onde:
- PV é o valor presente,
- FV é o valor futuro,
- i é a taxa de juros,
- t é o tempo.
Essa fórmula mostra como o valor presente diminui à medida que o tempo ou a taxa de juros aumenta, refletindo o conceito de valor temporal do dinheiro. O valor presente a juros simples está relacionado à fórmula de juros simples:
PV = FV/1(i*t)
A principal diferença entre as fórmulas de juros simples e compostos é a maneira como os juros são acumulados ao longo do tempo. Em juros compostos, os juros são acumulados sobre os juros já ganhos, enquanto em juros simples, os juros são calculados apenas sobre o capital inicial. Compreender essas diferenças é crucial para a correta avaliação de alternativas de investimento e financiamento.
2.2.3.2. Valor Presente Líquido (VPL)
O valor presente líquido (VPL) de um fluxo representa a diferença entre o valor presente das entradas de caixa e o valor presente das saídas de caixa, descontadas a uma determinada taxa de juros. Rezende (2003) destaca que o VPL é uma medida essencial para avaliar a viabilidade de projetos de investimento. Puccini (2006) explica que o VPL de um fluxo de caixa é igual ao valor presente de suas parcelas futuras, descontadas a uma determinada taxa, somado à grandeza colocada no ponto zero. Um VPL positivo indica que o investimento é viável e deve gerar um retorno superior ao custo do capital, enquanto um VPL negativo sugere que o investimento não é atraente, pois os fluxos de caixa esperados não compensam o custo do capital. A análise do VPL é amplamente utilizada em decisões de investimento, pois fornece uma medida clara e quantificável da rentabilidade esperada de um projeto.
2.2.3.3. Taxa Interna de Retorno (TIR)
Gitman (2002) define a taxa interna de retorno (TIR) como a taxa de desconto que iguala o valor presente das entradas de caixa ao investimento inicial referente a um projeto. A TIR é uma medida crucial na análise de investimentos, pois representa a taxa de retorno esperada de um projeto. A TIR pode ser calculada por meio de software, calculadora financeira ou tentativa e erro. Brigham, Gapenski e Ehrhardt (2001) destacam que a TIR de um projeto é sua taxa de retorno esperada e que exceder o custo dos fundos usados para financiar o projeto resulta em lucro para os acionistas.
A TIR é frequentemente utilizada em conjunto com o VPL para avaliar a atratividade de projetos de investimento. Se a TIR de um projeto excede o custo do capital, o projeto é considerado viável e deve ser aceito. Por outro lado, se a TIR é inferior ao custo do capital, o projeto deve ser rejeitado, pois não gerará retorno suficiente para compensar o custo dos fundos investidos. A TIR é uma ferramenta poderosa na avaliação de investimentos, pois permite comparar diretamente a rentabilidade esperada de diferentes projetos, facilitando a tomada de decisão informada.
Em resumo, a equivalência de capitais e fluxos de caixa é uma questão central na matemática financeira, essencial para a correta avaliação e comparação de alternativas de investimento e financiamento. A compreensão dos conceitos de valor presente, valor presente líquido e taxa interna de retorno permite a tomada de decisões financeiras mais informadas e eficazes, maximizando os retornos e minimizando os riscos associados aos investimentos e financiamentos.
2.3. Sistemas de Amortização de Empréstimos
Amortização, do latim “mors” que significa morte, implica na extinção gradual de uma dívida ao longo do tempo, conforme explicado por Brigham, Gapenski e Ehrhardt (2001). Ferreira (1993) define amortizar como “extinguir (dívida) aos poucos”, enquanto Veras (1991) afirma que as formas de pagamento dos empréstimos são chamadas sistemas de amortização. Neves (1982) complementa, indicando que a série de pagamentos deve ser financeiramente equivalente ao valor da dívida, considerando a taxa de juros do empréstimo.
Chaves (2009) descreve três critérios fundamentais para caracterizar um sistema de amortização:
- O valor de cada prestação é formado por duas parcelas: amortização e juros.
- Os juros de cada prestação são calculados sobre o saldo devedor do período anterior, com base na taxa de juros contratada.
- Havendo capital e juros vencidos, o pagamento é primeiro imputado nos juros vencidos e depois no capital, conforme as regras da matemática financeira.
Ayres Jr. (1981) destaca a importância de elaborar uma tabela de amortização, que indique claramente a parte que pertence aos juros e à amortização em cada pagamento. Mathias e Gomes (2002) afirmam que nos sistemas de amortização estudados, os juros são calculados sobre o saldo devedor, significando que consideram apenas os regimes de juros compostos. Isso reflete a prática comum de calcular os juros sobre o montante residual da dívida, garantindo precisão na distribuição dos pagamentos ao longo do tempo.
2.3.1. Sistema Price
O sistema Price, amplamente utilizado no Brasil, foi desenvolvido por Richard Price em 1769. Este sistema é baseado nas tábuas de mortalidade e utiliza uma metodologia específica para os pagamentos periódicos e a recuperação do capital. As prestações (Pmt) são constantes ao longo do tempo e compostas por duas parcelas: amortização e juros. Os juros são calculados sobre o saldo devedor do período anterior. No início do plano de pagamento, uma parte maior da prestação é destinada ao pagamento de juros e uma parte menor à amortização do principal. Com o passar do tempo, essa proporção se inverte, aumentando a parcela destinada à amortização e diminuindo a parcela dos juros. Essa característica torna o sistema Price eficiente para empréstimos de longo prazo, pois distribui o peso dos juros de forma gradual.
2.3.2. Sistema de Amortização Constante (SAC)
No Sistema de Amortização Constante (SAC), a principal característica é a constância do valor das amortizações ao longo do período do empréstimo. Isso significa que, em cada período, uma parte fixa do principal é amortizada. As prestações, por sua vez, decrescem em uma progressão aritmética, pois os juros são calculados sobre o saldo devedor remanescente, que diminui gradualmente. No SAC, a prestação inicial é mais alta, devido à maior parcela de juros calculada sobre o saldo devedor total. No entanto, à medida que o principal é amortizado, o saldo devedor diminui e, consequentemente, a parcela de juros também diminui, resultando em prestações menores ao longo do tempo. Essa característica torna o SAC especialmente atrativo para quem prefere iniciar com prestações mais altas que vão diminuindo com o tempo, facilitando o planejamento financeiro a longo prazo.
2.3.3. Sistema de Amortização Misto (SAM)
O Sistema de Amortização Misto (SAM) combina características do SAC e do Price, buscando oferecer uma solução equilibrada entre os dois sistemas. A prestação inicial no SAM é calculada como a média aritmética das prestações dos sistemas SAC e Price, criando um ponto de partida intermediário entre os dois métodos. As prestações no SAM decrescem conforme a constante do SAC dividida por dois, proporcionando uma redução mais gradual das prestações ao longo do tempo. Os juros no SAM são calculados sobre o saldo devedor do período anterior, e a amortização é determinada pela diferença entre a prestação e os juros. Esse sistema é projetado para oferecer maior flexibilidade e suavidade na variação das prestações, tornando-o uma opção interessante para aqueles que buscam um meio-termo entre os sistemas SAC e Price.
2.3.4. Sistema de Amortização Crescente (SACRE)
O Sistema de Amortização Crescente (SACRE) foi criado pela Caixa Econômica Federal e tem características únicas que o distinguem dos outros sistemas. No SACRE, a prestação é recalculada a cada 12 meses, com atualização mensal do saldo devedor. A prestação é composta por uma parcela de amortização constante e juros, que são recalculados periodicamente. Esse sistema foi reintroduzido em 2010 como uma opção para empréstimos habitacionais no Programa Minha Casa Minha Vida, oferecendo uma estrutura que permite a correção anual das prestações de acordo com a inflação e outras variáveis econômicas. O recalculo periódico das prestações no SACRE visa ajustar os pagamentos às mudanças no saldo devedor e nas condições econômicas, oferecendo maior flexibilidade e adaptabilidade ao longo do tempo.
2.3.5. Sistema de Amortização Americano (SAA)
No Sistema de Amortização Americano (SAA), a dívida é liquidada ao final do período do empréstimo com um pagamento único. Durante o período do empréstimo, apenas os juros são pagos periodicamente, sem incorporação ao capital. Assaf Neto (2001) explica que o capital emprestado é devolvido ao final do período contratado, sem amortizações intermediárias. Isso significa que o saldo devedor permanece constante ao longo do período do empréstimo, e o pagamento do principal é feito integralmente na última prestação. Esse sistema é útil em situações onde o devedor espera receber um montante significativo de dinheiro no futuro, permitindo que ele mantenha pagamentos mensais baixos durante a vida do empréstimo. No entanto, é importante planejar adequadamente para garantir que o montante total estará disponível para o pagamento final.
2.3.6. Método Linear Ponderado (Método de Gauss)
Desenvolvido pelo matemático Johann Carl Friedrich Gauss, o Método Linear Ponderado é uma técnica utilizada para liquidar o saldo devedor através de prestações periódicas e constantes. No regime de juros simples, este método tem sido adotado como substituto para métodos como Price e SAC em alguns contextos judiciais, especialmente onde há controvérsias sobre a legalidade da capitalização composta de juros. A constância das prestações no Método de Gauss é obtida pela soma dos termos de uma progressão aritmética (PA). A amortização é encontrada pela soma dos termos da PA, e os juros são a diferença entre a prestação e a amortização. Esse método garante que cada prestação é composta por uma parte fixa destinada à amortização do principal e uma parte variável destinada ao pagamento dos juros. A abordagem linear ponderada oferece uma forma equitativa e previsível de amortizar a dívida ao longo do tempo, sendo particularmente útil em situações onde a simplicidade e a transparência são desejadas.
3. Estudo de Caso
Neste capítulo, analisaremos um financiamento de R$ 50.000,00 com prazo de 15 meses, taxa de juros mensal de 1,5%, taxa de juros anual efetiva de 25,0232% e taxa nominal de 22,5%. Utilizaremos os métodos de amortização de Gauss e Equivalência a Juros Simples para realizar as simulações e comparações necessárias. Nosso objetivo é demonstrar as diferenças e implicações de cada método no cálculo das prestações e na amortização da dívida, proporcionando uma análise aprofundada que permitirá uma compreensão completa dos impactos financeiros de cada abordagem.
A amortização de empréstimos é um processo fundamental na gestão de financiamentos, envolvendo a devolução gradual do valor emprestado, acrescido de juros. Existem diversos métodos para amortizar um empréstimo, cada um com suas próprias características, vantagens e desvantagens. No contexto brasileiro, dois métodos frequentemente discutidos são o Método de Gauss e o Método de Equivalência a Juros Simples. Este estudo de caso tem como objetivo analisar detalhadamente como cada um desses métodos se comporta em um cenário específico de financiamento, fornecendo uma base sólida para comparações e decisões financeiras mais informadas.
A amortização não é apenas o processo de pagamento de uma dívida ao longo do tempo; ela influencia diretamente a carga financeira sobre o tomador do empréstimo, afetando seu fluxo de caixa e capacidade de planejamento financeiro. Compreender os diferentes métodos de amortização é crucial para escolher a melhor opção para cada situação específica. A escolha do método pode impactar significativamente o montante total pago em juros, a estrutura das prestações ao longo do tempo e, consequentemente, a saúde financeira do tomador de empréstimo.
No Brasil, dois métodos que se destacam são o Método de Gauss e o Método de Equivalência a Juros Simples. O Método de Gauss, embora menos comum, oferece uma alternativa interessante com suas próprias peculiaridades de cálculo e impacto financeiro. Já o Método de Equivalência a Juros Simples é amplamente utilizado e reconhecido por sua robustez matemática e previsibilidade. Ambos os métodos serão explorados em profundidade, destacando suas características, processos de cálculo e implicações financeiras.
Para uma análise completa, é essencial partir de dados claros e bem definidos sobre o financiamento em questão. Abaixo estão os parâmetros do financiamento que utilizaremos para nossas simulações e comparações.
- Valor Financiado: R$ 50.000,00
- Prazo: 15 meses
- Taxa de Juros Mensal: 1,5%
- Taxa Anual Efetiva: 25,0232%
- Taxa Nominal: 22,5%
O valor financiado é a quantia total emprestada ao tomador. Neste caso, estamos considerando um valor de R$ 50.000,00. Este valor será amortizado ao longo de 15 meses, com a aplicação das taxas de juros mencionadas.
O prazo de 15 meses refere-se ao período total durante o qual o financiamento será amortizado. Este prazo é relativamente curto, o que pode influenciar a escolha do método de amortização, uma vez que prazos mais curtos geralmente resultam em prestações maiores, mas menos juros pagos no total.
A taxa de juros mensal de 1,5% é aplicada sobre o saldo devedor em cada período. Essa taxa será fundamental para os cálculos de amortização e para a determinação do montante de juros pagos ao longo do tempo.
A taxa anual efetiva de 25,0232% considera a capitalização dos juros ao longo do ano, refletindo de forma mais precisa o custo real do financiamento. Esta taxa é importante para comparar com outras opções de financiamento que o tomador possa estar considerando.
A taxa nominal de 22,5% é a taxa de juros anual sem considerar a capitalização dos juros. Esta taxa é útil para entendimento dos cálculos de juros de forma simplificada, mas não representa o custo total do financiamento, que é melhor refletido pela taxa anual efetiva.
O Método de Gauss utiliza uma progressão aritmética adaptada para calcular as prestações e a amortização dos financiamentos. Embora seja uma técnica alternativa, não possui fundamentação sólida na ciência financeira e pode apresentar inconsistências quando comparada a outros métodos. Este método propõe um cálculo baseado em uma sequência aritmética que distribui os pagamentos de forma que cada parcela é composta de uma parte de amortização crescente e uma parte de juros decrescente.
As prestações pelo Método de Gauss são calculadas considerando uma progressão aritmética. A fórmula básica para determinar o pagamento periódico constante (PMT) é:
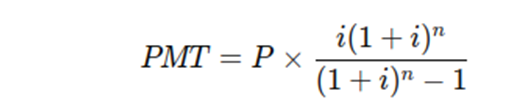
onde:
- PMT é o pagamento periódico constante.
- P é o valor principal do empréstimo ou financiamento.
- i é a taxa de juros por período.
- n é o número total de pagamentos.
Esta fórmula é derivada de uma progressão aritmética onde cada parcela é composta por uma fração crescente do valor principal e uma fração decrescente dos juros. Ao longo do tempo, a parte de amortização aumenta, enquanto a parte de juros diminui, resultando em um saldo devedor que decresce de forma não linear.
A tabela de amortização para o Método de Gauss é construída considerando os valores de juros e amortização calculados em cada período. Abaixo, apresentamos a tabela com as prestações detalhadas para o financiamento de R$ 50.000,00 ao longo de 15 meses.
Nº. de Parcelas Amortização Juros Parcela Devida Saldo Devedor 0 0,00 0,00 0,00 50.000,00 1 3.016,59 678,73 3.695,32 46.983,41 2 3.061,84 633,48 3.695,32 43.921,57 3 3.107,09 588,24 3.695,32 40.814,48 4 3.152,34 542,99 3.695,32 37.662,14 5 3.197,59 497,74 3.695,32 34.464,56 6 3.242,84 452,49 3.695,32 31.221,72 7 3.288,08 407,24 3.695,32 27.933,63 8 3.333,33 361,99 3.695,32 24.600,30 9 3.378,58 316,74 3.695,32 21.221,72 10 3.423,83 271,49 3.695,32 17.797,89 11 3.469,08 226,24 3.695,32 14.328,81 12 3.514,33 181,00 3.695,32 10.814,48 13 3.559,58 135,75 3.695,32 7.254,90 14 3.604,83 90,50 3.695,32 3.650,08 15 3.650,08 45,25 3.695,32 0,00 Total 50.000,00 5.429,86 55.429,86
A tabela de amortização mostra claramente como os componentes de amortização e juros variam ao longo do tempo. Inicialmente, a maior parte da parcela é composta de juros, mas à medida que o saldo devedor diminui, a parte de amortização aumenta. Isso pode ser benéfico para tomadores de empréstimos que esperam uma melhoria na sua capacidade de pagamento ao longo do tempo, uma vez que as prestações são menores no início do período de financiamento.
O Método de Gauss apresenta vantagens como flexibilidade inicial, com prestações menores no início do período de financiamento, proporcionando alívio financeiro inicial ao tomador. Além disso, a amortização crescente aumenta a proporção do principal pago ao longo do tempo, o que pode ser vantajoso para quem espera aumento de renda futura. No entanto, possui desvantagens significativas, como inconsistência financeira, pois o método não possui uma fundamentação sólida e pode apresentar inconsistências quando comparado a métodos mais tradicionais. Além disso, o cálculo é mais complexo e pode ser menos intuitivo para quem não possui conhecimentos financeiros avançados.
O Método de Equivalência a Juros Simples é amplamente utilizado para cálculos financeiros e é baseado em princípios matemáticos robustos. Este método propõe um cálculo linear e direto dos juros, tornando-o uma escolha popular para muitos tipos de financiamento. Ele é particularmente conhecido por sua simplicidade e previsibilidade nos cálculos.
O cálculo das prestações no Método de Equivalência a Juros Simples envolve várias etapas que asseguram a distribuição adequada dos juros e da amortização ao longo do tempo.
O primeiro passo é calcular o Fator de Valor Atual (FVA), que é a base de distribuição que incide sobre o valor da parcela com o objetivo de apurar o valor da amortização mês a mês. A fórmula para calcular o FVA é:
FVA=(1/(1+(Taxa de juros x Número da parcela))
Depois de calculado o FVA, o próximo passo é determinar o valor da parcela a ser paga no contrato. O valor fixo da parcela é obtido dividindo o valor base do financiamento pela soma de todos os FVAs do contrato.
A amortização ou o capital pago é calculado multiplicando o FVA de cada mês pelo valor da parcela fixa apurada no passo anterior. Os juros que incidem em cada parcela são obtidos subtraindo a amortização do valor da parcela fixa.
A tabela de amortização para o Método de Equivalência a Juros Simples é construída com base nos juros e amortizações calculados para cada período. Abaixo, apresentamos a tabela detalhada.
Tabela de Amortização para o Método de Equivalência a Juros Simples
Nº. de Parcelas Fator de Valor Atual Amortização Juros Parcela Devida Saldo Devedor 0 – 0,00 0,00 0,00 50.000,00 1 98,522% 3.665,81 54,99 3.720,80 46.334,19 2 97,087% 3.612,43 108,37 3.720,80 42.721,76 3 95,694% 3.560,57 160,23 3.720,80 39.161,19 4 94,340% 3.510,19 210,61 3.720,80 35.651,00 5 93,023% 3.461,21 259,59 3.720,80 32.189,79 6 91,743% 3.413,58 307,22 3.720,80 28.776,21 7 90,498% 3.367,24 353,56 3.720,80 25.408,97 8 89,286% 3.322,14 398,66 3.720,80 22.086,83 9 88,106% 3.278,24 442,56 3.720,80 18.808,59 10 86,957% 3.235,48 485,32 3.720,80 15.573,11 11 85,837% 3.193,82 526,98 3.720,80 12.379,29 12 84,746% 3.153,22 567,58 3.720,80 9.226,07 13 83,682% 3.113,64 607,16 3.720,80 6.112,43 14 82,645% 3.075,04 645,76 3.720,80 3.037,39 15 81,633% 3.037,39 683,41 3.720,80 0,00 Total – 50.000,00 5.812,00 55.812,00
A tabela de amortização mostra um padrão mais linear e previsível, com a parcela de amortização sendo constante ao longo do tempo. Isso proporciona uma visão clara de como a dívida está sendo reduzida, facilitando o planejamento financeiro e a previsão de custos futuros.
O Método de Equivalência a Juros Simples apresenta vantagens como simplicidade, com cálculos mais diretos e intuitivos, facilitando a compreensão e a aplicação. A previsibilidade é outra vantagem, pois a estrutura de amortização linear proporciona uma visão clara do pagamento da dívida ao longo do tempo. Além disso, o método é baseado em princípios matemáticos sólidos, garantindo precisão e consistência nos cálculos. No entanto, a constância dos juros pagos pode não ser tão atraente para alguns tomadores quanto a redução progressiva dos juros oferecida por outros métodos, e a linearidade pode ser menos vantajosa para quem espera variabilidade na sua capacidade de pagamento ao longo do tempo.
A comparação entre os dois métodos revela diferenças significativas nos valores das prestações, juros totais e saldos devedores ao longo do tempo. Vamos explorar essas diferenças detalhadamente para entender suas implicações financeiras.
Sob a ótica do valor presente, o fluxo de caixa descontado (FCD) pelo método de juros simples é uma técnica usada para avaliar a viabilidade de um investimento, determinando o valor presente de uma série de fluxos de caixa futuros. Ao descontar o fluxo de caixa com juros simples, a taxa de desconto é aplicada diretamente ao valor principal em cada período, sem composto dos juros. Para calcular o fluxo de caixa descontado de uma única parcela de financiamento usando o método de juros simples, você pode seguir os passos abaixo:
A fórmula para calcular o valor presente de uma única parcela usando juros simples é:
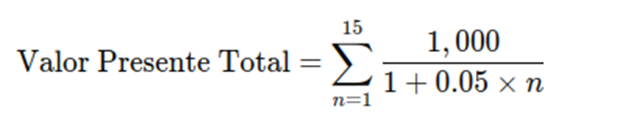
Onde:
- Valor PresenteTotal: É a soma dos valores presentes de todas as parcelas ao longo de 15 períodos, descontados por uma taxa de juros simples.
- ∑n=115: O somatório de n=1 até n=15 indica que estamos somando os valores presentes de 15 parcelas.
- 1,000: O valor de cada parcela futura que será paga ao final de cada período (ano, mês, etc.).
- n: Representa o número do período específico (variando de 1 a 15).
- 0.05: A taxa de juros simples por período (neste caso, 5% ao ano).
- 1+0.05×n1,000: A fórmula para calcular o valor presente de uma parcela específica. Aqui, o valor da parcela futura (1,000) é dividido pela expressão 1+0.05×n, que representa o fator de desconto para o n-ésimo período.
Ao aplicar o método de fluxo de caixa descontado para obter o valor presente de cada parcela, os resultados para os dois métodos de cálculo – Método de Equivalência a Juros Simples e Método de Gauss – foram significativamente diferentes. Abaixo, apresentamos uma análise detalhada de cada método, mostrando como cada parcela foi calculada e quais são as implicações desses cálculos.
Valor Presente das Parcelas Calculadas pelo Método de Equivalência a Juros Simples
Período até o pagamento da parcela Parcela Devida Valor presente 1 3.720,80 3.665,81 2 3.720,80 3.612,43 3 3.720,80 3.560,57 4 3.720,80 3.510,19 5 3.720,80 3.461,21 6 3.720,80 3.413,58 7 3.720,80 3.367,24 8 3.720,80 3.322,14 9 3.720,80 3.278,24 10 3.720,80 3.235,48 11 3.720,80 3.193,82 12 3.720,80 3.153,22 13 3.720,80 3.113,64 14 3.720,80 3.075,04 15 3.720,80 3.037,39 Total 55.812,00 50.000,00
Valor presente das parcelas calculados pelo Método de Gauss:
Período até o pagamento da parcela Parcela Devida Valor presente 1 3.695,32 3.640,71 2 3.695,32 3.587,69 3 3.695,32 3.536,20 4 3.695,32 3.486,15 5 3.695,32 3.437,51 6 3.695,32 3.390,21 7 3.695,32 3.344,18 8 3.695,32 3.299,40 9 3.695,32 3.255,79 10 3.695,32 3.213,33 11 3.695,32 3.171,95 12 3.695,32 3.131,63 13 3.695,32 3.092,32 14 3.695,32 3.053,99 15 3.695,32 3.016,59 Total 55.429,86 49.657,65
No Método de Equivalência a Juros Simples, o somatório das prestações calculadas e trazidas a valor presente (PV) resulta no montante de R$ 50.000,00, idêntico ao capital financiado. Tecnicamente, isso significa que o capital emprestado pelo regime simples foi retornado integralmente. No Método de Gauss, entretanto, o somatório das prestações calculadas e trazidas a valor presente (PV) resulta no montante de R$ 49.657,65, que é inferior ao capital emprestado de R$ 50.000,00. Tecnicamente, isso indica que o capital emprestado pelo regime simples não foi totalmente retornado, refletindo uma inconsistência do método.
Ao analisar as prestações, observa-se que o Método de Gauss apresenta prestações ligeiramente maiores no início e menores no final do período, em comparação ao Método de Equivalência a Juros Simples. Isso ocorre devido à natureza progressiva do cálculo no Método de Gauss. Essa diferença pode influenciar significativamente a gestão do fluxo de caixa dos tomadores de empréstimos. Por outro lado, o Método de Equivalência a Juros Simples mantém as prestações mais constantes, facilitando o planejamento financeiro.
O total de juros pago pelo Método de Gauss (R$ 5.429,86) é ligeiramente menor que o total pago pelo Método de Equivalência a Juros Simples (R$ 5.812,00), o que equivale a uma variação de aproximadamente 7%. Essa diferença, pode ter implicações significativas em financiamentos de maior valor ou prazo. A diferença nos juros pagos pode ser atribuída à forma como os juros são calculados e acumulados ao longo do tempo. A compreensão dessa diferença é crucial para tomadores que buscam minimizar o custo total do financiamento.
Os saldos devedores ao longo do tempo apresentam um padrão de decrescimento mais uniforme no Método de Equivalência a Juros Simples, enquanto no Método de Gauss, há uma variação mais acentuada no início, estabilizando-se nos períodos finais. Esse comportamento pode influenciar a percepção de quão rapidamente a dívida está sendo amortizada. Para muitos tomadores, ver uma redução constante e uniforme no saldo devedor pode ser psicologicamente mais confortante e motivador.
Este estudo de caso evidencia que o Método de Gauss, embora uma alternativa interessante, pode apresentar distorções e inconsistências quando comparado ao Método de Equivalência a Juros Simples. Para financiamentos de maior valor ou prazo, a escolha do método de amortização pode ter implicações significativas nos custos totais e na gestão financeira. É crucial que tanto credores quanto tomadores de empréstimos compreendam essas diferenças para tomar decisões financeiras mais informadas e eficazes. A escolha do método de amortização deve ser feita com base em uma análise cuidadosa das necessidades financeiras e dos objetivos a longo prazo do tomador de empréstimo. Por fim, entender as nuances de cada método permitirá uma melhor preparação e planejamento, evitando surpresas e garantindo uma gestão financeira mais eficiente e sustentável.
4. Conclusão
Este estudo comparativo entre o Método de Gauss e o Método de Equivalência a Juros Simples revelou diferenças significativas na forma como cada método calcula as prestações e os juros ao longo do tempo. O Método de Equivalência a Juros Simples mostrou-se mais consistente e matematicamente robusto, oferecendo maior transparência e previsibilidade nos cálculos. Em contraste, o Método de Gauss, embora interessante e aplicável em certos contextos, apresentou inconsistências que podem resultar em distorções financeiras, especialmente em cálculos judiciais.
Os resultados do estudo de caso com o financiamento de R$ 50.000,00 ao longo de 15 meses mostraram que o Método de Equivalência a Juros Simples, ao trazer as prestações a valor presente, iguala exatamente o valor financiado, garantindo que o capital emprestado seja integralmente retornado. Já o Método de Gauss, ao calcular as prestações e trazê-las a valor presente, resultou em um montante inferior ao capital financiado, indicando uma falha no retorno completo do capital.
A análise das prestações mostrou que o Método de Gauss oferece prestações menores no início e maiores no final, o que pode ser vantajoso para tomadores que esperam uma melhoria na capacidade de pagamento ao longo do tempo. No entanto, essa progressividade também pode levar a um aumento no custo total do financiamento, uma vez que os juros são pagos de forma diferente ao longo do tempo.
Por outro lado, o Método de Equivalência a Juros Simples mantém uma estrutura de prestações mais constante e previsível, facilitando o planejamento financeiro e proporcionando uma visão clara de como a dívida está sendo amortizada. Esta constância é particularmente útil em contextos judiciais, onde a precisão e a transparência são essenciais para evitar disputas e garantir a justiça nas decisões.
Sob a ótica do valor presente, o Método de Equivalência a Juros Simples demonstrou ser superior, garantindo que o valor das prestações descontadas iguale o valor do financiamento, enquanto o Método de Gauss apresentou uma diferença que pode ser considerada inconsistente e prejudicial para o cálculo correto dos juros.
Além disso, a análise dos juros totais pagos ao longo do período de financiamento destacou que, embora a diferença entre os dois métodos seja pequena, ela pode ter implicações significativas em financiamentos de maior valor ou prazo. O Método de Equivalência a Juros Simples, ao calcular juros de forma linear, garante que o custo do financiamento seja distribuído de maneira mais justa e equilibrada ao longo do tempo.
A escolha do método de amortização não deve ser feita de forma arbitrária. É essencial considerar as características específicas do financiamento, as necessidades financeiras do tomador e a finalidade do cálculo, especialmente em contextos judiciais. O Método de Equivalência a Juros Simples se mostrou uma opção mais segura e confiável, proporcionando resultados mais precisos e justos.
Portanto, a recomendação final deste estudo é que o Método de Equivalência a Juros Simples seja preferido em cálculos judiciais e em contextos onde a precisão, transparência e justiça são primordiais. Embora o Método de Gauss possa ser utilizado em outros contextos financeiros, sua aplicação em cálculos judiciais deve ser cuidadosamente avaliada para evitar possíveis inconsistências e distorções.
A escolha do método de amortização pode ter um impacto significativo no montante total pago ao longo do tempo, na distribuição das prestações e na compreensão do fluxo de caixa para o tomador de empréstimos. A análise detalhada dos métodos de Gauss e de Equivalência a Juros Simples, conforme apresentada neste estudo, evidencia que a metodologia escolhida pode influenciar diretamente a justiça e a precisão das decisões judiciais, bem como a gestão financeira de indivíduos e empresas.
Compreender os diferentes métodos de amortização é crucial para a tomada de decisões financeiras informadas. Este estudo contribui para essa compreensão, oferecendo uma análise detalhada e recomendações práticas que podem orientar contadores, advogados, juízes e outros profissionais envolvidos em litígios financeiros na escolha do método mais adequado para garantir a justiça e a precisão nos cálculos judiciais.
A aplicação correta dos métodos de cálculo de juros é essencial para assegurar a exatidão e a justiça nas decisões judiciais, protegendo os interesses das partes envolvidas e garantindo a integridade dos processos financeiros. Este estudo evidencia a importância da escolha criteriosa do método de amortização, destacando o Método de Equivalência a Juros Simples como a melhor opção para garantir resultados precisos e justos em cálculos judiciais.
Referências Bibliográficas
Assaf Neto, A. (2001). Finanças Corporativas e Valor. São Paulo: Atlas.
Ayres Jr., F. (1981). Matemática Financeira. São Paulo: Atlas.
Brealey, R. A., & Myers, S. C. (1992). Princípios de Finanças Corporativas. São Paulo: McGraw-Hill.
Brigham, E. F., Gapenski, L. C., & Ehrhardt, M. C. (2001). Administração Financeira: Teoria e Prática. São Paulo: Atlas.
Casarotto Filho, N., & Kopittke, B. H. (1996). Análise de Investimentos: Matemática Financeira. São Paulo: Atlas.
Chaves, A. (2009). Matemática Financeira. São Paulo: Saraiva.
Faro, F. P. (1989). Matemática Financeira. Rio de Janeiro: Forense Universitária.
Ferreira, A. B. H. (1993). Novo Dicionário Aurélio da Língua Portuguesa. Rio de Janeiro: Nova Fronteira.
Francisco, W. (1985). Matemática Financeira. São Paulo: Atlas.
Gitman, L. J. (2002). Princípios de Administração Financeira. São Paulo: Pearson.
Hoji, M. (2001). Administração Financeira: Uma Abordagem Quantitativa. São Paulo: Atlas.
Kuhnen, A., & Bauer, E. (2001). Matemática Financeira. São Paulo: Atlas.
Mathias, R., & Gomes, J. (2002). Matemática Financeira. São Paulo: Saraiva.
Neves, A. S. (1982). Matemática Financeira. Rio de Janeiro: Forense Universitária.
Pilão, J. P., & Hummel, F. E. (2004). Matemática Financeira Aplicada. São Paulo: Saraiva.
Puccini, F. J. (1973). Matemática Financeira. São Paulo: Atlas.
Puccini, F. J. (2006). Matemática Financeira. São Paulo: Atlas.
Rezende, M. S. (2003). Matemática Financeira. São Paulo: Saraiva.
Simonsen, M. H., & Ewald, M. (1990). Matemática Financeira. Rio de Janeiro: Forense.
Veras, E. (1991). Matemática Financeira. São Paulo: Atlas.
