USO DO SOFTWARE GEOGEBRA COMO FERRAMENTA PARA APLICABILIDADE DA NÚMERO DE OURO NA EEMTI PROFESSOR CLODOALDO PINTO

USE OF GEOGEBRA SOFTWARE AS A TOOL FOR APPLICABILITY OF THE GOLDEN NUMBER IN EEMTI PROFESSOR CLODOALDO PINTO

REGISTRO DOI: 10.69849/revistaft/cs10202408221805

Nilo Pinheiro Landim; Francisco Diego Moreira Oliveira; Regina Maria Lima Rocha; Osiel Gomes da Silva; Ana Maria Pinheiro; Alan Bruno Lopes Barbosa; Adriano Melo Araujo; Monique Maranbaia dos Santos Souza; Francisco Alexandre Coelho

Resumo

A motivação deste trabalho revela-se na preocupação em discutir assuntos relacionados ao cotidiano e explicá-los de uma forma atraente para que o aluno possa absorver as informações necessárias para o aprendizado do conteúdo da forma mais atraente possível, facilitando assim o seu aprendizado. O objetivo deste trabalho é mostrar a importância da Razão Áurea para o estudo da Geometria e das seqüências numéricas nas escolas de Ensino Médio, entender como os matemáticos fizeram para chegar à razão áurea utilizando conceitos algébricos e geométricos e mostrar situações que usaram ou não do número de ouro, como a questão envolvendo as pirâmides egípcias, a utilização da razão áurea por Leonardo da Vinci, a relação desse número com a seqüência de Fibonacci, a aplicação na botânica e etc. A metodologia utilizada foi a realização de levantamentos bibliográficos em livros e em trabalhos realizados nessa área e aplicação de uma atividade envolvendo o uso do software Geogebra e outra relacionada a sequências com alunos do ensino médio abordando o conteúdo. Os resultados observados foram um pouco de dificuldade no manuseio inicial com o software, porém um alto nível de concentração e empolgação após a transmissão da história da construção do número de ouro e como pode ser observado na natureza.

Palavras-Chaves: Razão Áurea, Geometria, Número de Ouro, GeoGebra

ABSTRACT

The motivation of this work is revealed in concern to discuss issues related to daily life and explain them in an attractive manner so that the student can absorb the information necessary for learning content more appealing as possible, thereby facilitating their learning. The objective of this work is to show the importance of the Golden Ratio to the study of geometry and number sequences in high schools, to understand how mathematicians have made to reach the golden ratio using algebraic and geometric concepts and situations that used to show whether or not the number gold, as the issue involving the Egyptian pyramids, the use of the golden ratio by Leonardo da Vinci, the relationship of this number to the Fibonacci sequence, the application in botany and so on. The methodology was used to conduct literature surveys on books and works done in this area and applying an activity involving the use of GeoGebra software and other related sequences with high school students addressing the content. Results were a little difficult in the initial handling with the software, but a high level of concentration and excitement after the transmission of the history of building the number of gold and as can be observed in nature.

Keys-Words: Golden Ratio, Geometric, Number Gold, GeoGebra

1. INTRODUÇÃO

A Matemática é uma ciência que se relaciona com as demais áreas de estudos, como: humanas e exatas. A Matemática está presente em áreas que muitas pessoas desconhecem, não por culpa delas, mas por falta de informação. Ela está presente no nosso cotidiano, nas artes, na natureza, na história antiga, entre outros.

É muito comum ouvirmos dos alunos ao selecionarmos assuntos da matemática do ensino fundamental ou médio, perguntas como: “Professor, onde vou utilizar isso na minha vida?”, “Qual a importância disso para meu futuro?”, “Professor, isso é aplicado em algum lugar?”. Foram perguntas como essas que motivaram a realização deste trabalho, tratando de um assunto que dificilmente é lecionado nas escolas de ensino médio, mas que tem uma grande aplicação em várias áreas de ensino, que é a Razão Áurea.

A Razão Áurea, que também é conhecido por, Número de Ouro ou Número Áureo ou Proporção Divina é uma constante irracional com o valor 1,6180339…, esta constante é representada pelo símbolo Φ (Phi). Esta constante também recebe outras definições como: Seção Áurea, Razão Áurea, Razão de Ouro, Divina Proporção, Proporção em Extrema Razão, Divisão de Extrema Razão. Todas essas expressões possuem o mesmo significado, mas dependendo do matemático ou filósofo ou qualquer pessoa que venha a abordar esse assunto, pode utilizar uma expressão diferente.

Alguns estudos indicam que a Razão Áurea vem sendo aplicado há muito tempo, principalmente na área das Artes, onde este número representa uma proporção muito utilizada em esculturas, pinturas e na arquitetura. Estudos mostram que alguns artistas, entre eles destacam-se Lê Corbusier, mais conhecido como o Modulor, e Leonardo da Vinci, utilizaram dessa proporção para realizar seus trabalhos.

Com base nas referências estudadas, este trabalho tem como objetivo geral:

Mostrar a importância da Razão Áurea para o estudo da Geometria nas escolas de Ensino Médio.

Este trabalho tem como objetivos específicos:

Pesquisar os mais importantes aspectos que se relacionam à Razão Áurea.
Entender como os Matemáticos fizeram para chegar à Razão Áurea, utilizando principalmente conceitos geométricos.
Indicar situações que possam utilizar a Razão Áurea no ensino da Matemática.
Mostrar as mais importantes propriedades relacionadas ao Número de Ouro.

Com este trabalho, temos a pretensão de estimular o estudo de assuntos que vêm sendo discutidos por grandes matemáticos , inclusive antes de Cristo.

Na história da Razão Áurea, iremos mostrar as Pirâmides de Quéops e Quéfren e mostrar relatos sobre a dúvida se elas foram ou não construídas baseado no Número de Ouro.
Além das Pirâmides, existe outra grande construção que possui relação das medidas relacionadas ao Número de Ouro, que é o Tempo de Parthenon, construído por Fídeas em Atenas, na Grécia.
Mostraremos que se pode encontrar o Número de Ouro em situações nunca imaginadas, como em medições no corpo humano, na botânica, na reprodução de animais, na arquitetura, entre outros.
A importantíssima sequência de Fibonacci tem importante relação de seus termos com a Razão Áurea.

2. FUNDAMENTAÇÃO TEÓRICA OU REVISÃO DA LITERATURA

2.1 – Motivações para o tema Razão Áurea

Para a realização desse trabalho, buscamos um tema que não é muito comentado nas escolas de Ensino Médio. Esse tema com certeza dá margem a uma pergunta: “Por que esse tema?” Afinal, existem temas mais fáceis para serem trabalhados do que a Razão Áurea.

Esse assunto foi o escolhido por apresentar uma grande aplicação em outras áreas, ou seja, possui uma grande variedade interdisciplinar, além de toda sua beleza e perfeição, não à toa é considerado um símbolo de harmonia.

Como esse tema é pouco ou não é trabalhado nas escolas, os alunos à primeira vista irão ter dificuldade. Nos PCN (1998) onde trata sobre influência da História da matemática no currículo escolar, é defendido que o professor tem que conhecer a dificuldade de como esse assunto foi descoberto e produzido na época para melhor compreender as dificuldades que o aluno terá para entender o assunto, pois o professor analisando e observando todo o trabalho que tiveram os grandes matemáticos para desenvolver esse tema, fica mais sensibilizado com as dificuldades apresentadas pelo aluno.

Consideramos esse assunto bastante rico, pois além de trabalhar um pouco da História da Matemática e claro a Razão Áurea, acaba por trabalhar também assuntos como:

Razão e Proporção
Noções de Geometria
Equação do 2º grau
Seqüências Numéricas
Aproximação de Números

2.2 – Definição de razão Áurea

Veremos mais adiante que a Razão Áurea representa um símbolo de harmonia e beleza para alguns matemáticos, filósofos e pintores. Veremos também que essa Razão Áurea pode estar presente em várias áreas, como: Botânica, reprodução dos animais, medidas do corpo humano, construções antigas, quadros e etc.

Mas podemos fazer algumas perguntas, como:

“O que é a Razão Áurea?”
“Quanto vale a Razão Áurea?”
“Como fazer para encontrá-la?”

2.2.1 – Definição Geométrica:

Se quiséssemos dividir um segmento AB em duas partes, teríamos uma infinidade de maneiras de o fazer. Existe, no entanto, uma para a qual o matemático alemão Zeizing, formulou, em 1855, o seguinte principio, relativamente a esta divisão:

“Para que um todo dividido em duas partes desiguais pareça belo do ponto de vista da forma, deve apresentar entre a parte menor e a maior a mesma relação entre esta e o todo.“

O grande matemático Euclides, também definiu geometricamente o conceito de Razão Áurea, no famoso livro intitulado por “Elementos”, onde consta:

“Para que um segmento seja dividido em Seção Áurea, a razão entre o segmento e a parte maior deve ser igual a razão entre a parte maior e a parte menor”

A definição geométrica de Razão Áurea é que seja um segmento AB, dizemos que esse segmento está dividido pela Razão Áurea, quando colocamos sobre este segmento um ponto C entre os pontos A e B, sendo AC > BC, de tal forma que AC dividido por BC seja igual a AB dividido por AC, de acordo com a figura abaixo:

2.2.2 – Definição Algébrica:

Portanto, o valor algébrico do Número de Ouro (Φ) é 1,6180339887… Vale lembrar que alguns autores, ao invés de considerar a Razão Áurea como sendo x/y, consideram y/x, nesse caso o valor da razão será o inverso do valor encontrado, que será 0,6180339887…

2.3 – Propriedades do Número de Ouro

Existem duas propriedades interessantes que dizem respeito ao Número de Ouro, que é o seu quadrado e o seu inverso. Ao digitarmos em uma calculadora o Número de Ouro 1,6180339887… e apertarmos o botão do seu quadrado [Φ²], veremos que o resultado será 2,6180339887…, observando melhor, percebemos que o quadrado do Número de Ouro, possui exatamente os mesmos números depois da vírgula do Número de Ouro, e na parte inteira é adicionado apenas uma unidade, ou seja, podemos concluir que a Razão Áurea possui a propriedade de encontrar o seu quadrado apenas somando 1. Fazendo o mesmo raciocínio para o inverso de Número de Ouro, também encontraremos uma propriedade interessante, ao digitarmos o Número de Ouro na calculadora, e calcularmos o seu inverso [1/Φ] encontraremos o seguinte resultado 0,6180339887…, que novamente após a vírgula possui os mesmos números do Número de Ouro, e na parte inteira é subtraída apenas uma unidade, ou seja, para encontrarmos o inverso do Número de Ouro, basta subtrairmos uma unidade do Número de Ouro. Então, podemos escrever essas duas propriedades, como sendo:

1ª) Φ ² = Φ + 1

2ª) 1/ Φ = Φ – 1

Em 1997, foi publicado um poema de Paul S. Bruckman, no periódico The Fibonacci Quarterly, com o nome de “Constantemente Médio”, onde ele se refere ao Número de Ouro como “Razão Média”. Esse poema relata justamente essas duas propriedades citadas anteriormente. A primeira estrofe desse poema é:

A média áurea é algo absurdo,
Não é um irracional comum.
Se você o inverte (isso é divertido!),
Você a obtém de novo, reduzida de um.
Mas se pela unidade for somado,
Acredite, isso dá seu quadrado.

2.4 – Pentágono regular e o Triângulo Áureo

Um Pentágono é chamado de regular quando possui os cinco lados e ângulos iguais. Para sabermos o valor de cada ângulo interno de um pentágono regular, é necessário que saibamos primeiro o valor da soma dos ângulos internos, onde pode ser encontrado através da fórmula 180. (n – 2), onde n é o número de lados. Como o pentágono tem cinco lados iguais, então para n = 5, teremos que a soma dos ângulos internos será 540 graus. Portanto o valor de cada ângulo interno do pentágono será 540/5 = 108 graus. Seja um pentágono regular ABCDE e nele traçamos as duas diagonais partindo de A, formando assim três triângulos isósceles. Os dois primeiros isósceles são os triângulos ADE e ABC, pois os dois lados iguais desses triângulos são os lados do pentágono e o outro triângulo isósceles é o ACD, pois os lados iguais desse triângulo são as duas diagonais do pentágono. Sabemos que em um triângulo isósceles os ângulos da base são iguais, então nós dois triângulos ADE e ABC os ângulos da base irão medir 36 graus, pois é justamente a metade de 180 – 108. Sendo assim o triângulo ACD irá possuir os ângulos da base medindo 72 graus e o outro medindo 36 graus. Observe o passo a passo desse raciocínio na figura abaixo.

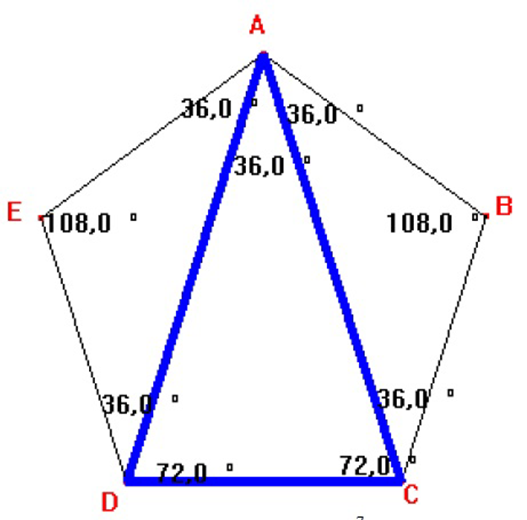
Figura 2 – Pentágono ABCDE

Considerando agora somente o triângulo isósceles ACD e traçando a bissetriz interna do ângulo D desse triângulo, onde essa bissetriz vai interceptar o lado AC no ponto F.

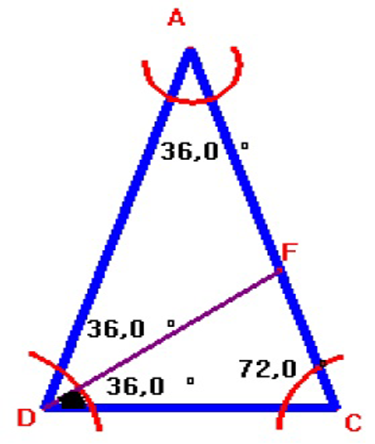
Figura 3 – Triângulo Isósceles ACD

Observe que o triângulo CDF também é isósceles, pois como DF é bissetriz, então o ângulo D interno desse triângulo mede 36 graus e como o ângulo interno C desse triângulo mede 72 graus, logo o ângulo interno F desse triângulo também medirá 72 graus, pois a soma dos ângulos internos de um triângulos tem que medir 180 graus. Então, o triângulo CDF também é isósceles, com os lados iguais sendo CD e DF.

Observando agora os triângulos ACD e CDF, notamos que eles possuem os três ângulos iguais, pois o ângulo C é comum aos dois triângulos, o ângulo D interno a ao triângulo CDF é igual ao ângulo A interno a ACD, logo os ângulos então concluímos que esses dois triângulos são semelhantes.

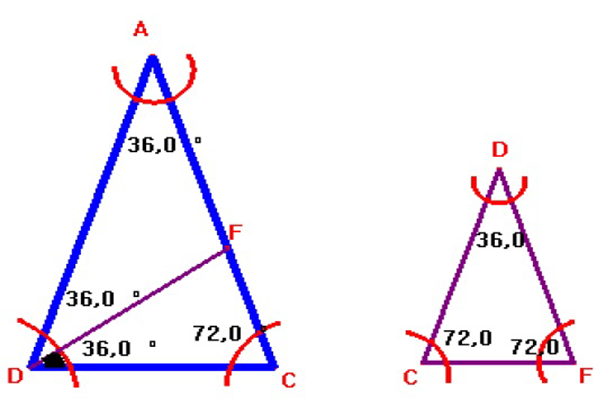
Figura 4 – Triângulos Isósceles ACD e CDF

Como esses dois triângulos são semelhantes, então podemos atribuir a relação de semelhança:

Se observarmos a relação [3], ela significa que o ponto F divide a linha AC pela Razão Áurea, pois esta relação [3] nada mais é do que a definição euclidiana da Razão Áurea no lado AC. Portanto o triângulo ADC é chamado de Triângulo Áureo.

Uma grande influência do Pentágono regular na História da Matemática, é com relação aos Pitagóricos, pois o Pentagrama (estrela de cinco pontas) formada a partir da conexão de todos os vértices do pentágono com as diagonais, representa irmandade.

Vimos que o Pentagrama é formado pelas diagonais do pentágono regular, que também forma outro pentágono menor no seu interior, e continuando o raciocínio, as diagonais desse pentágono menor, formam em seu interior outro pentagrama e outro pentágono menor ainda (Figura 5). Essa progressão prossegue ao infinito.

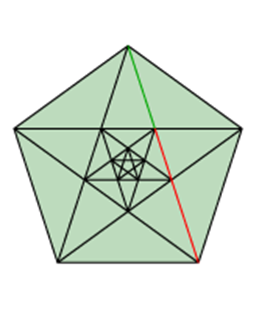
Figura 5 – Formação do Pentagrama

Mas qual a relação dessa progressão de pentágonos e pentagramas com o número de ouro? A razão entre o lado do pentágono maior com o do pentágono imediatamente menor é justamente o Número de Ouro, e essa razão se conserva para toda a sequência.

2.5 – Retângulo de Ouro

Podemos definir um retângulo como um paralelogramo, onde seus lados formam ângulos retos entre si, então ele possui dois lados paralelos entre si verticalmente e dois lados paralelos horizontalmente. Mas o que vem a ser um Retângulo de Ouro ou Retângulo Áureo? Um retângulo é chamado de Áureo, quando a razão entre o lado maior e o lado menor é justamente o Φ, ou seja, 1,6180…

Mas como fazer para construir um retângulo que pode ser considerado como Áureo a partir de um segmento qualquer AB? Observe os passos abaixo.

1º Passo:

Com a medida do segmento AB determinado, construa um quadrado ABCD de lado medindo AB.

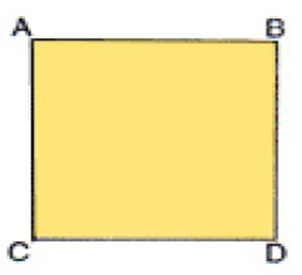
Figura 6 – Quadrado ABCD

2º Passo:

Marcar os pontos E e F, nos lados AB e CD respectivamente, onde E e F sejam os pontos médios desses segmentos, formando o segmento tracejado EF.

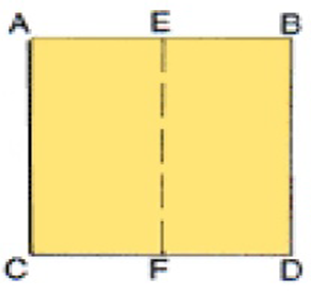
Figura 7 – Quadrado ABCD com os pontos médios E e F

3º Passo:

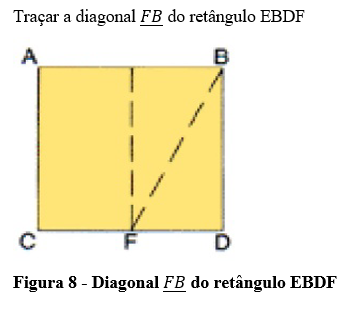
4º Passo:

Prolongando o lado CD e usando um compasso com centro em B, traçar o arco com raio BF, onde esse arco encontre o prolongamento do lado CD, esse ponto de encontro chamará de G.

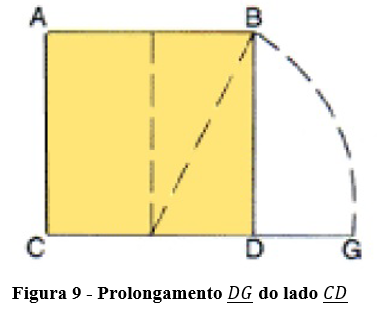
5º Passo:

Forme o retângulo BDGH junto ao quadrado ABCD, formando o retângulo ACGH. Esse último retângulo, é um Retângulo Áureo.

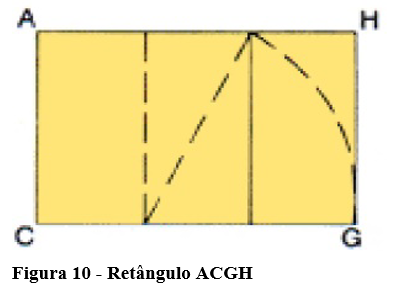
Mas porque esse retângulo pode ser considerado um Retângulo Áureo? Chamando o lado do quadrado ABCD de x, e como o ângulo D é ângulo interno de um quadrado, então ele vale 90º, daí posso afirmar que o triângulo FBD é retângulo. Usando o Teorema de Pitágoras, podemos concluir que o segmento BF mede:

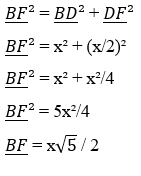
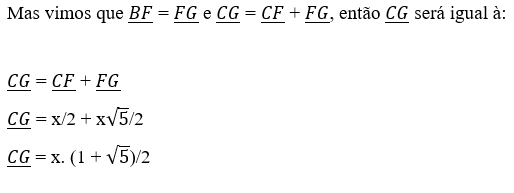
Foi visto que a definição de Retângulo Áureo é quando a razão entre o lado maior e o lado menor do retângulo, é justamente o Número de Ouro. Então, calculando a medida dessa razão no retângulo ACGH, teremos:

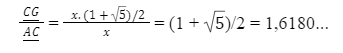
Então, está justificado que o Retângulo ACGH é um Retângulo de Ouro

2.6 – Espiral de Ouro

Existem na natureza várias evidências que se encontra formas de espirais em movimentos ocasionados por animais, no crescimento das plantas, em alguns objetos. Mas existe uma espiral em particular que chamou a atenção de Jacques Bernoulli, que é conhecida como Espiral Logarítmica, pois ela possui uma propriedade conhecida como auto-similaridade, onde nessa espiral, à medida que aumentamos seu raio no sentido horário, a curva não altera seu formato. Entusiasmado com essa propriedade, Jaques escreveu que a Espiral Logarítmica:

“pode ser usada como um símbolo tanto de vigor e constância na adversidade quanto do corpo humano, o qual, após todas as mudanças, até mesmo após a morte, será restaurado ao seu exato e perfeito ser”

Mas por que essa Espiral Logarítmica é chamada de Espiral de Ouro? Na verdade, a Espiral Logarítmica e o Número de Ouro estão relacionados entre si, pois essa Espiral é encontrada tanto no Retângulo de Ouro, como no Triângulo de Ouro.

Vimos que o retângulo é chamado de Áureo, quando a razão entre o seu lado maior e o menor é justamente a Razão Áurea. No interior desse retângulo, forma-se um quadrado utilizando o lado menor do retângulo como sendo o lado do quadrado, forma-se também um retângulo ao lado do quadrado com as mesmas características do retângulo áureo. Repetindo o mesmo processo indefinidamente, nesse novo retângulo menor formado obteremos a chamada Série de Retângulos Áureos, conforme a figura abaixo.

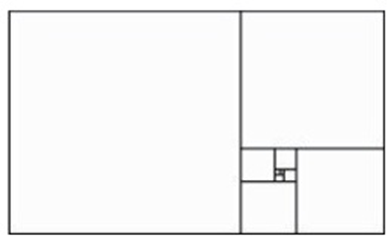
Figura 11 – Série de retângulos áureos

Considerando os quadrados formados dentro de retângulo áureo inicial, e unindo os arcos dentro desses quadrados, formamos a Espiral Logarítmica, também conhecida como Espiral de Ouro. Observe a figura abaixo:

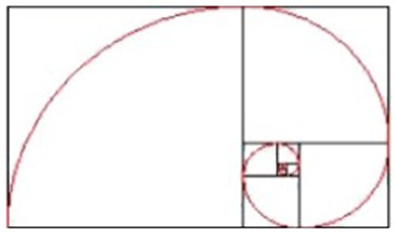
Figura 12 – Espiral de Ouro dentro da Série de Retângulos

Vimos que para um triângulo ser considerado um Triângulo Áureo é necessário primeiro que ele seja isósceles e que a razão entre um de seus lados iguais e sua base, seja a Razão Áurea. Vimos que a demonstração desse triângulo áureo vem da utilização da bissetriz do ângulo da base, onde formará outro triângulo menor semelhante ao triângulo inicial, ou seja, esse triângulo menor também será áureo. Repetindo o processo indefinidamente, encontraremos a chamada Série de Triângulos Áureos, conforme a figura abaixo:

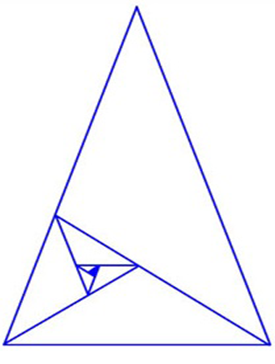
Figura 13 – Série de Triângulos Áureos

A Espiral de ouro pode ser encontrada nesta Série de Triângulo, unindo os vértices deste triângulo com uma curva contínua, de acordo com a figura abaixo:

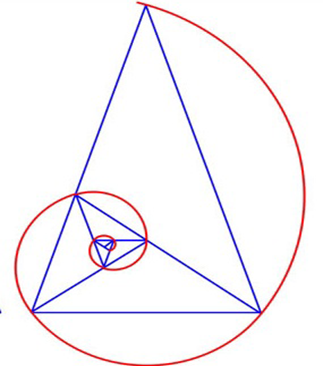
2.7 – Relação entre o Número de Ouro e Fibonacci.

Leonardo Fibonacci nasceu na década de 1170, filho de um homem de negócios e funcionário do governo chamado Guglielmo. O apelido Fibonacci foi provavelmente introduzido pelo historiador de matemática Guillaume Libri, em 1938, embora alguns pesquisadores atribuem o primeiro uso do nome Fibonacci a matemáticos italianos do fim do século XVIII.

Mas qual a relação entre Fibonacci e o Número de Ouro? Fibonacci foi o responsável por responder um problema famoso na área da matemática, o problema está no Capítulo 12 do Liber Abaci, e diz o seguinte:

“Um homem pôs um par de coelhos num lugar cercado por todos os lados por um muro. Quantos pares de coelhos podem ser gerados a partir desse par em um ano se, supostamente, todo mês cada par dá à luz um novo par, que é fértil a partir do segundo mês.”

No primeiro mês temos apenas o par de coelhos inicial. No segundo mês, como o par de coelhos ainda não é fértil, então continuou apenas com um par de coelhos. No terceiro mês, o par de coelhos dá a luz a outro par de coelhos, então teremos dois pares de coelhos. No quarto mês o primeiro par de coelhos dá a luz a outro par, mas o segundo par de coelhos ainda não é fértil, totalizando três pares de coelhos neste mês. No quinto mês, o primeiro casal de coelhos gera outro casal, o segundo casal também dá a luz a outro casal de coelhos, mas o terceiro casal ainda não é fértil, totalizando então cinco pares de coelhos. No sexto mês, o primeiro casal gera o sexto casal de coelhos, o segundo casal gera o sétimo casal de coelhos, o terceiro casal, agora fértil, gera o oitavo casal de coelhos e o quarto e quinto casais ainda não são férteis. Então, no sexto mês, temos exatamente oito pares de coelhos. Sendo assim temos a seguinte sequência até o momento 1, 1, 2, 3, 5, 8 … onde cada número representa a quantidade de coelhos que existem no determinado mês.

Observe a figura abaixo para visualizar melhor.

Figura 14 – Reprodução dos Coelhos

Verificando a sequência dada, percebe-se que a partir do terceiro termo, um termo qualquer é sempre a soma dos dois termos imediatamente anteriores a ele. Daí surge à famosa Seqüência de Fibonacci, onde a seqüência é definida recursivamente, onde podemos definir o f_n como o n-ésimo termo da seqüência, sendo f₁ = 1 e f₂ = 1, então f_n = f_{n – 1}+ f_{n – 2}, para n > 2. Aplicando essa fórmula recursiva, temos então a sequência, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … Então, como cada mês da sequência representa os números de par de coelhos existentes, podemos concluir que após 12 meses, teremos exatamente 144 pares de coelhos.

O matemático Kepler foi muito importante no estudo da Razão Áurea. Em 1608, ele escreveu uma carta para um professor em Leipzing, onde percebemos que ele havia descoberto a relação entre o Número de Ouro e os Números de Fibonacci. Kepler escreveu:

“[…]É arranjada de tal maneira que os dois termos menores de uma série progressiva constituem juntos o terceiro, e destes, os últimos dois, quando somados, resultam no termo imediatamente subseqüente, e assim por diante, até o infinito, enquanto a mesma proporção continua intacta…quanto mais avançarmos a partir do primeiro número, mais perfeito fica o exemplo. Sejam os menores números 1 e 1…some-os, e a soma será 2; some esse com o último dos uns, resultando 3. Some 2 a isso, e tenha 5. Some 3, e tenha 8; 5 e 8, 13; 8 e 13, 21. Assim como 5 está para 8, 8 está para 13, aproximadamente, e 8 está para 13, assim como 13 está para 21, aproximadamente.”

Se considerarmos a sequência definida pela razão entre um termo de Fibonacci e o seu antecessor, iremos perceber que essa sequência converge para o Número de Ouro. Considera-se u_n como essa seqüência, então u_n = f_{n + 1} / f_n. Então, u₁ = 1/1 = 1; u₂ = 2/1 = 2; u₃ = 3/2 = 1,5; u₄ = 5/3 = 1,666… ; u₅ = 8/5 = 1,6 ; u₆ = 13/8 = 1,625 ; u₇ = 21/13 = 1,6153 ; convergindo realmente para o Número de Ouro, como foi dito antes.

Podemos ilustrar isso através do gráfico abaixo, onde o eixo vertical seria o índice u_n e o eixo horizontal seria o termo de da sequência de Fibonacci.

Figura 16 – Gráfico que indica a convergência para o Número de Ouro

Outro caso que aparece no Número de Ouro na Natureza é na árvore genealógica do zangão, o macho da abelha. Para efeito de informação, os ovos da abelha operária que não são fertilizados se tornam zangões, já os que são fertilizados pelos zangões se tornam abelhas (fêmeas). Portanto, um zangão não possui “pai”, apenas “mãe”. Já a abelha possui “pai” e “mãe”. Observe a figura abaixo que diz respeito a árvore genealógica do zangão.

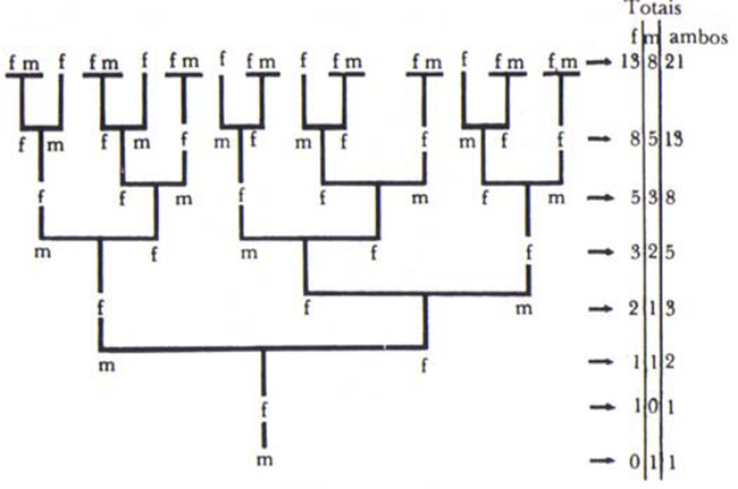
Figura 17 – Reprodução das Abelhas

Observe que, um zangão tem uma mãe, dois avós (pais de sua mãe), três bisavós (dois pais da avó mais a mãe do avô), cinco trisavós (dois para cada bisavó e um para seu bisavô) e assim sucessivamente.

Nas três colunas da direita da figura acima, que diz respeito respectivamente à quantidade de fêmeas, machos e os dois juntos, é possível perceber que a sequência dos números diz respeito à Seqüência de Fibonacci.

Após observarmos os dois fenômenos da reprodução dos coelhos e a árvore genealógica de um zangão, a sequência de Fibonacci também pode ser encontrada no campo da Física, sendo mais específico na óptica dos raios de luz. Suponhamos uma situação em que se sobreponham duas placas de vidros com índices de refração diferentes. Ao colocarmos essas placas na exposição da luz, esta pode passar pela placa sem sofrer nenhuma reflexão, pode sofrer uma reflexão, duas reflexões, três reflexões, quatro reflexões e assim sucessivamente. A sequência de Fibonacci vai aparecer nesse caso, quando formos contar o número de raios que emergiram desse sistema. Na figura abaixo, no caso de nenhuma reflexão, observe que somente existirá um raio emergido. No caso de sofrer uma reflexão interna, temos duas possibilidades de raios de luz emergentes. Na próxima parte, no caso de duas reflexões internas, teremos três possibilidades de raios emergidos. Continuando o raciocínio, na parte de três reflexões internas, teremos cinco raios emergidos.

Figura 18 – Número de reflexões dos espelhos

Observe que a seqüência dos números de raios emergidos desde o caso em que não tem nenhuma reflexão forma uma seqüência de Fibonacci (1, 2, 3, 5, 8, 13, …) de acordo com a tabela abaixo:

Figura 19 – Relação entre o número de reflexões com os raios emergidos

3. METODOLOGIA

Como foi relatado no início deste trabalho, o tema Razão Áurea dificilmente é trabalhado no Ensino Médio e em alguns casos é trabalhado no ensino superior, inclusive alguns graduados em Matemática nunca estudaram algo sobre este número na graduação. Alguns assuntos que podem ser trabalhados com os alunos do Ensino Médio com este número são Proporções, Equações do 2º grau, Seqüências Numéricas e Geometria, com o auxílio do Laboratório

Foi escolhido trabalhar uma atividade com os alunos na área da geometria com a utilização do Software GeoGebra, tanto para diferenciar das aulas “tradicionais” como para proporcionar uma melhor visualização das figuras geométricas por parte dos alunos.

De início, irei abordar um pouco sobre a Razão áurea, trabalhando a parte teórica, como definição e aplicações deste número em várias outras áreas. Levando para a parte prática, irei fazer um passo a passo da construção do Retângulo de Ouro e do Triângulo de Ouro através das ferramentas do GeoGebra.

3.1 – Construção do Retângulo Áureo no GeoGebra.

Observação: Lembrando que Retângulo Áureo é todo retângulo que possui uma importante propriedade, onde a razão entre o lado maior e o lado menor resulta no Número Áureo.

1º Passo: Construir um Quadrado ABCD

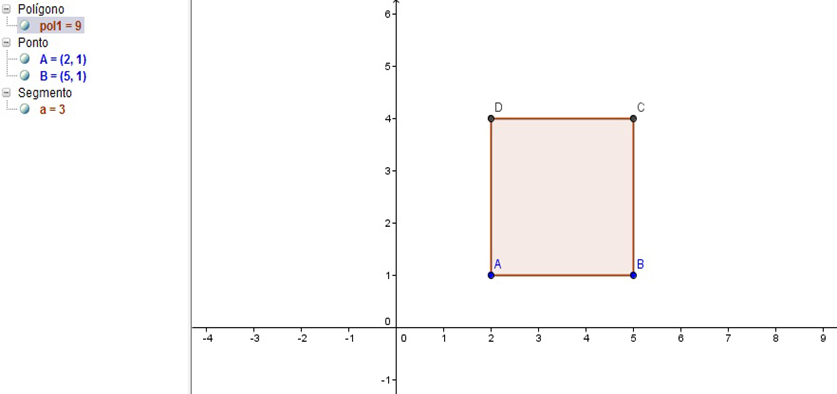
Figura 20 – Quadrado ABCD no GeoGebra

2º Passo: Marque os Pontos E e F no quadrado, onde esses pontos serão o Ponto Médio de AB e CD

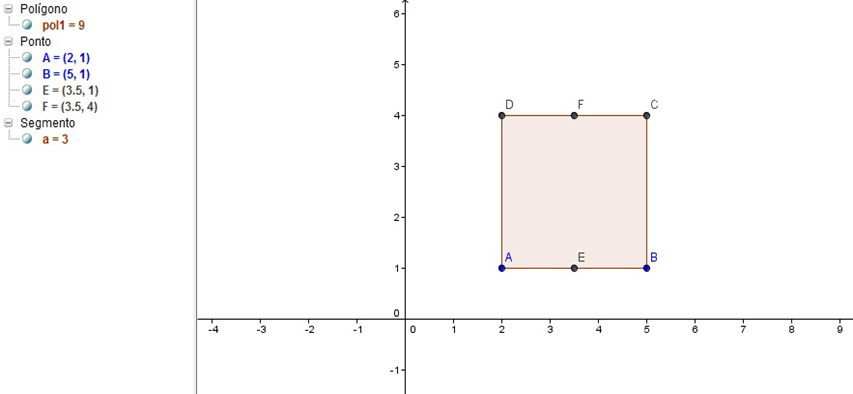
Figura 21 – Quadrado ABCD com os Pontos Médios E e F no GeoGebra

3º Passo: Ligar os pontos C e F encontrando o segmento CE

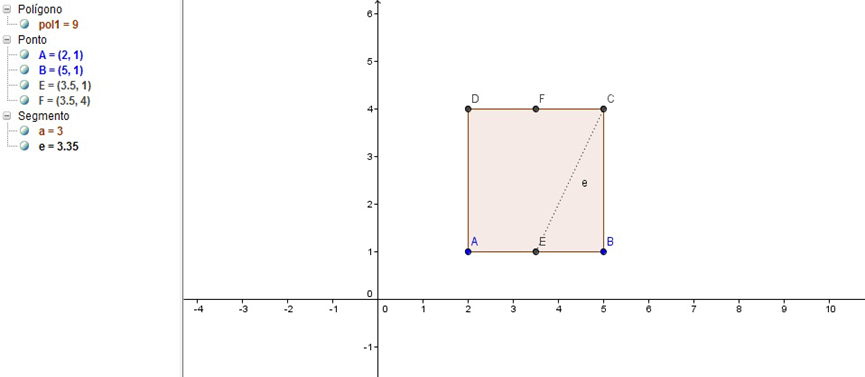
Figura 22 – Construção do Segmento CE no GeoGebra

4º Passo: Traçar a circunferência de centro em E e raio CE

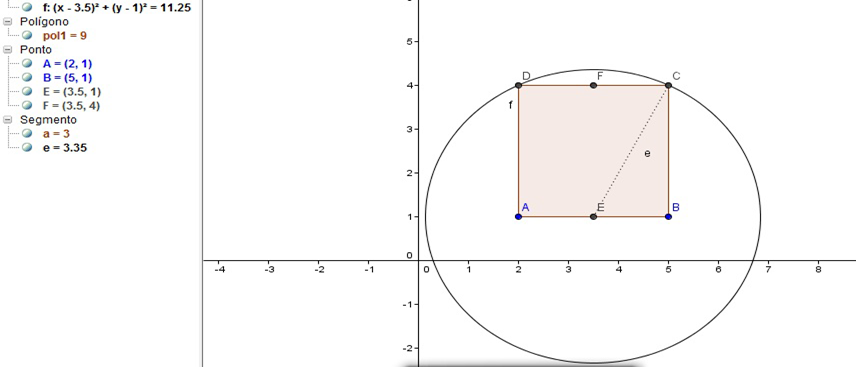
Figura 23 – Circunferência de Centro E no GeoGebra

5º Passo: Prolongue o lado AB até encontrar a circunferência, encontrando o Ponto G

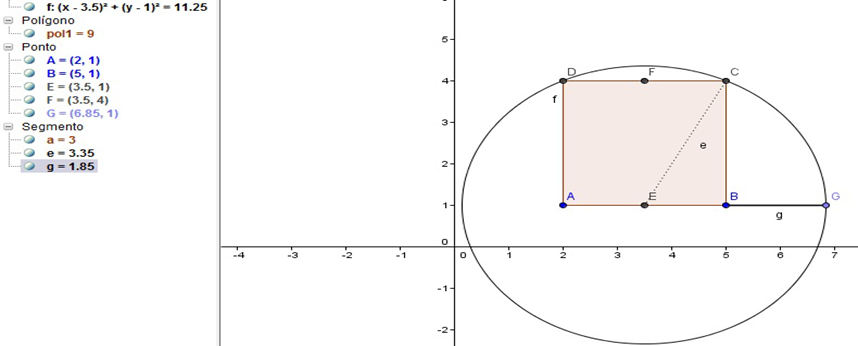
Figura 24 – Prolongamento do lado AB, no GeoGebra

6º Passo: Sendo BC e BG os lados de um retângulo, desenhe o retângulo BCGH.

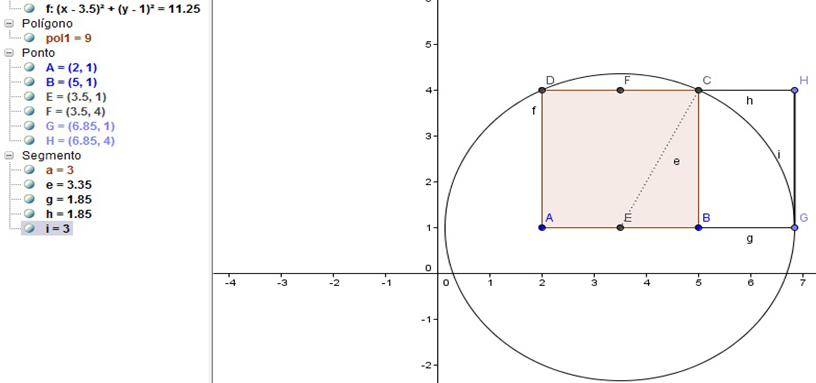
Figura 25 – Formando o Retângulo BCGH, no GeoGebra

7º Passo: Observar que o retângulo ADGH é um Retângulo Áureo, pois:

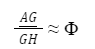
3.2 – Construção do Triângulo Áureo no GeoGebra.

Observação: Lembrando que o Triângulo Áureo é todo triângulo Isósceles que possui os ângulos da base medindo 72 graus e outro ângulo medindo 36 graus e possui a importante propriedade de que a razão entre um dos lados iguais e o lado da base, resulta no Número Áureo.

1º Passo: Traçar um segmento de reta AB.

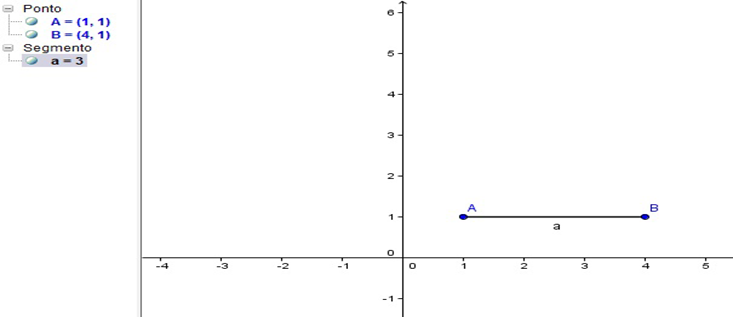
Figura 26 – Segmento AB, no GeoGebra.

2º Passo: Traçar a mediatriz do segmento de reta AB.

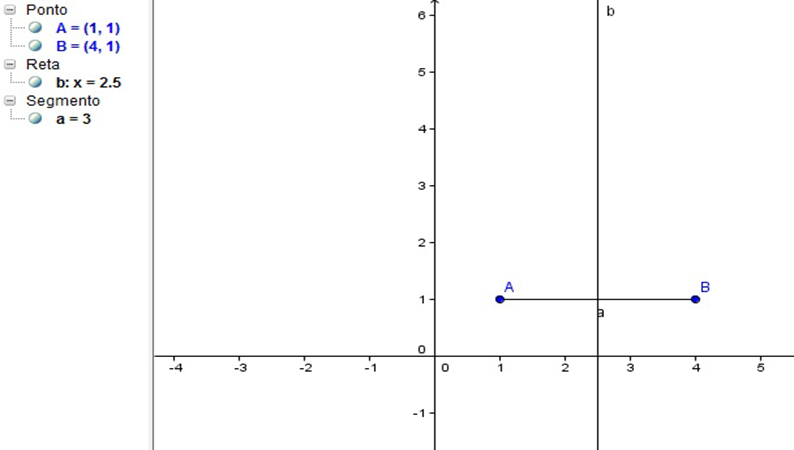
Figura 27 – Mediatriz do segmento AB, no GeoGebra.

3º Passo: Marcar os dois ângulos de 72 graus no segmento de reta AB conforme a figura abaixo.

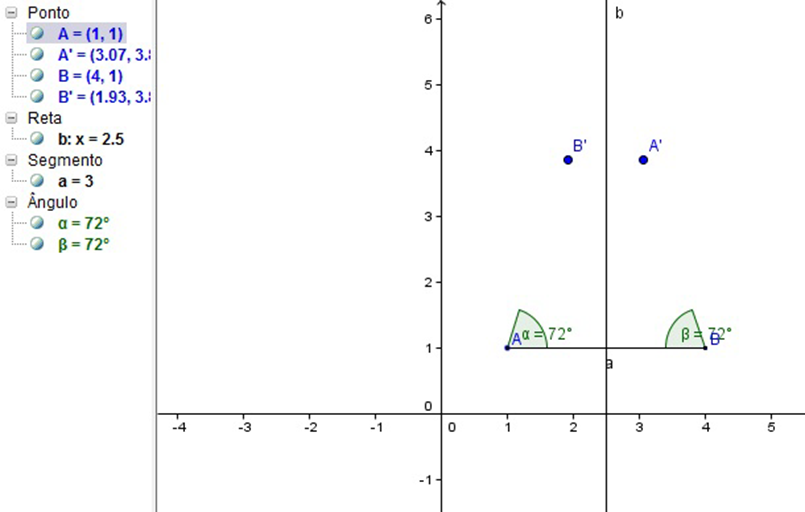
Figura 28 – Construção dos ângulos de 72°, no GeoGebra

4º Passo: Traçar o segmento de reta partindo de A e passando por B’ até encontrar a mediatriz e traçar o segmento de reta partindo de B e passando por A’ até encontrar a mediatriz, o ponto de encontro desses dois segmentos com a mediatriz será o ponto C, formando o triângulo isósceles ABC.

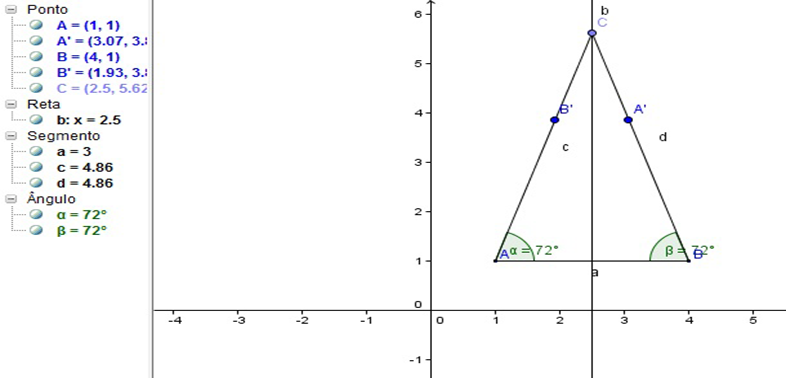
Figura 29 – Construção do Triângulo Isósceles ABC

5º Passo: Observar que o Triângulo ABC é um Triângulo Áureo, pois:

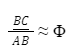
6º Passo: Como o triângulo ABC é Áureo, então ao traçarmos a bissetriz do ângulo interno A e marcando o ponto D como a interseção da bissetriz com o lado BC. Trace os segmentos de retas CD e BD. Observar que:

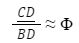
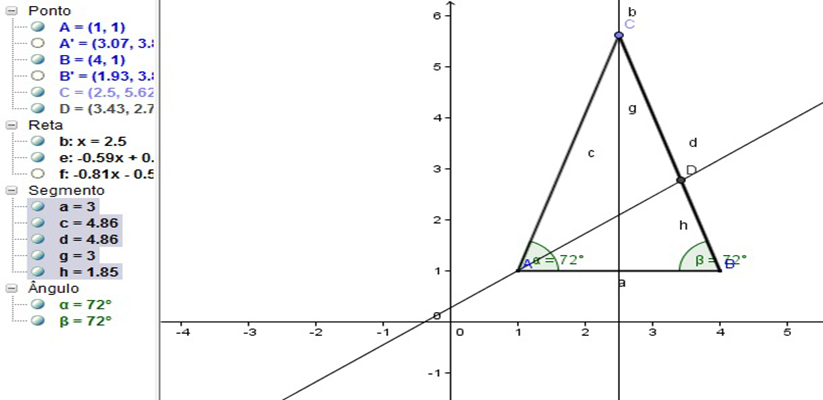
Figura 30 – Verificar que o Triângulo ABC é Áureo.

4. RESULTADOS E DISCUSSÕES OU ANÁLISE DOS DADOS

As atividades propostas foram aplicadas nas quatro turmas do 1º ano da EEMTI (Escola de Ensino Médio em Tempo Integral) Professor Clodoaldo Pinto, em Maracanaú-CE. Tais atividades foram realizadas em um dos três Laboratórios Escolares de Informática (LEI) que a escola possui, com o apoio da equipe de professores que trabalha dando suporte aos LEIs.

Para constatar o fato de que os alunos desta escola dão mais atenção às aulas quando se utiliza TICs como ferramenta no ensino, seja qual for a disciplina, foi feita uma pesquisa de opinião com todos os alunos do 1º ano do ensino médio. Dele foram obtidos os seguintes resultados: O aluno pode opinar de quatro formas distintas, “Concordo Totalmente”, “Concordo Parcialmente”, “Discordo Parcialmente” e “Discordo Totalmente”, as duas primeiras serão chamadas de “Faixa do Concordo” onde a opinião está mais para favorável do que desfavorável, e as duas últimas serão chamadas de “Faixa do Discordo” onde as opiniões estão mais para desfavorável do que para favorável. Um total de 108 alunos responderam a pesquisa com a pergunta “O uso das TICs em sala torna as aulas mais interessantes”, com os resultados expostos na tabela abaixo:

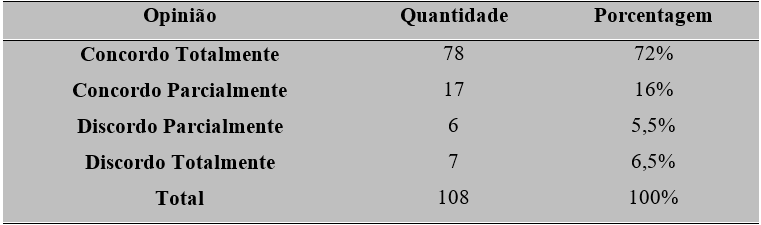
5. CONCLUSÃO/CONSIDERAÇÕES FINAIS

O Número de Ouro é uma constante onde raramente se estuda algo relacionado a ela no Ensino Médio e inclusive em algumas Universidades, pouco se estuda sobre ela nos cursos de graduação em matemática ou cursos afins. Este é um tema bom para se trabalhar com os alunos no Ensino Médio, mas na forma de Laboratório de Matemática.

Após a abordagem teórica que apresentamos aos alunos, reparamos que eles gostaram da parte relacionada a aplicações do Número de Ouro nas diversas áreas (Enigma das Pirâmides, Templo de Partenon, Botânica, Corpo Humano, Artes e etc.) e principalmente da Seqüência de Fibonacci, onde mostramos alguns problemas relacionados a essa seqüência, inclusive colocando como atividade para eles resolverem antes de citar sobre a seqüência.

Vale ressaltar a importância de se fazer uma pesquisa a fundo sobre o tema, pois em alguns artigos ou livros possui informações que não são corretas relacionada ao Número de Ouro, ocorre o que chamamos de malabarismo numéricos, onde alguns resultados são forçados a darem o que o pesquisador deseja, é o que ocorre na questão das Pirâmides, no Templo de Partenon, no quadro da Mona Lisa e no crescimento da concha dos Náutilus.

A parte que identificamos uma maior dificuldade da parte deles, como já esperávamos, foi a parte da demonstração do valor do Número de Ouro, principalmente na parte relacionada a Razão e Proporção, pois eles tiveram bastante dificuldade de visualizar as proporções.

Considero o uso do Software GeoGebra como uma ótima alternativa para atrair a atenção dos alunos e também como uma forma de modificar o estilo de aula. É normal eles terem um pouco de dificuldade para manusear o programa, pois é o primeiro contato deles com esse Software, mas de modo geral considero positiva a experiência desse programa.

Trabalhos como esses são interessantes para mostrar outras atribuições da matemática, diferente daquela tradicional conhecida pelos alunos, onde de certa forma acaba se tornando uma “mesmice” para a maioria deles, ocasionando uma grande rejeição pela disciplina. Por isso é muito importante a divulgação dos Laboratórios de matemática na utilização de aulas como essas.

REFERÊNCIAS

HUNTLEY, H. E. A Divina Proporção: um ensaio sobre a beleza na matemática. Tradução: Luís Carlos Ascêncio Nunes. – Brasília: Editora da UNB, 1985.

BOYER, C. B. História da Matemática. Tradução: Elza Gomide. São Paulo. Edgard Blucher, 1974.

LÍVIO, Mário. Razão Áurea: a história de Fi, um número surpreendente. Tradução: Marco Shinobu Matsumura. – 6. ed. – Rio de Janeiro: Record, 2011.

ÁVILA, Geraldo. Retângulo Áureo, divisão áurea e Seqüência de Fibonacci. Revista do Professor de Matemática. – São Paulo, v. 6, p. 9-14, 1985.

AZEVEDO, A. Seqüências de Fibonacci. Revista do Professor de Matemática. – São Paulo, v. 45, p. 44-47, 2001.

BIEMBENGUT, Maria Salett. Número de Ouro e secção áurea: Considerações e sugestões para a sala de aula. Blumenau/SC: Ed. da FURB, 1996.

OLIVEIRA, E.; FERREIRA, T. E. O Número de Ouro e suas manifestações na Natureza e na Arte. Revista Complexus. – Instituto Superior de Engenharia Arquitetura e Design – Ceunsp, Salto-SP, Ano. 1, n_ 2, p. 64-81, Janeiro/2024.

AZEVEDO, Natália de Carvalho. O Número de Ouro e Construções. Universidade Federal de Goiás. Disponível em: <http://bit.profmat-sbm.org.br/xmlui/bitstream/handle/123456789/538/2011_00439_NATALIA_DE_CARVALHO_DE_AZEVEDO.pdf?sequence=1> Acessado em 20/03/2024

CARVALHO, Lucas Santos. Número Áureo e o Ensino Básico. Universidade Estadual de Santa Cruz. Disponível em: <http://bit.profmat-sbm.org.br/xmlui/bitstream/handle/123456789/266/2011_00114_LUCAS_SANTOS_DE_CARVALHO.pdf?sequence=1> Acessado em 18/03/2024

KFOURI, Viviane de Oliveira. O Número de Ouro. Universidade Federal de Goiás. Disponível em: <http://bit.profmat-sbm.org.br/xmlui/bitstream/handle/123456789/550/2011_00454_VIVIANE_DE_OLIVEIRA_KFOURI.pdf?sequence=1> Acessado em 10/03/2024