REGISTRO DOI: 10.5281/zenodo.8061045
Kátia Regina Barboza da Silva¹
Resumo: Este artigo, tem como objetivo mostrar a aplicabilidade das razões trigonométricas no cotidiano em uma turma de primeiro ano do ensino médio através de recursos didáticos produzidos a partir do uso do material concreto. verificando se com essa prática haverá melhora no desempenho dos discentes com relação ao conteúdo abordado. Trata-se de uma investigação descritiva de enfoque qualitativo em uma escola do ensino médio de tempo integral. Este estudo se justifica pela dificuldade que os alunos possuem em compreender e entender os conceitos matemáticos sobre razões trigonométricas. Foram abordados os conceitos matemáticos através da história da trigonometria, as leis de fundamentação do estudo da trigonometria, a importância do uso do material concreto no ensino das razões trigonométricas, as dificuldades encontras no ensino das razões trigonométricas e a aplicabilidade das razões trigonométricas no cotidiano. A pesquisa constatou que a dificuldade na aprendizagem do conteúdo em estudo deve-se à falta de conhecimentos matemáticos e à dificuldade na contextualização e interpretação dos problemas. E no final observou-se pela reação dos alunos, a importância de um tratamento diferenciado ao conteúdo de trigonometria no triângulo retângulo, e o quanto essa metodologia contribuiu para a aprendizagem dos educandos.
Palavras- chave: Razões trigonométricas; Material concreto; Quadrante.
INTRODUÇÃO
A presente pesquisa visa mostrar uma proposta de ensino com o uso do material concreto no ensino das razões trigonométricas no triângulo retângulo para uma turma de primeiro ano do Ensino Médio. Valendo-se da história da matemática e dos conhecimentos concernentes à trigonometria e do material concreto no processo de ensino e aprendizagem da matemática.
A opção pelo uso do material concreto no ensino das razões trigonométricas se deu devido à metodologia tradicional usado por alguns docentes em sala de aula que não permite aos alunos tempo necessário para que eles compreendam plenamente os conceitos básicos de matemática. Percebe-se ainda que muitos alunos, independentemente da série escolar apresentam dificuldades relacionadas à aprendizagem da trigonometria.
Segundo Pestalozzi (1746-1827) acreditava que uma educação seria considerada genuinamente educativa se a sua ação pedagógica enfatizasse as atividades realizadas pelos alunos, como por exemplo, a manipulação de objetos concretos. Para Piaget (1973) estudou os estágios de desenvolvimento cognitivo de crianças, o que, segundo ele, ocorre através de ações que são executadas em resposta ao ambiente através da manipulação de objetos.
Com o intuito de verificar se com essa prática de ensino houve uma melhora no desempenho dos alunos no conteúdo abordado. A pesquisa foi aplicada em uma turma de primeiro ano do ensino médio, na Escola Estadual de Tempo Integral Governador Melo e Póvoas, na cidade de Manaus, Amazonas, compreendendo alunos na faixa etária de 14 a 17 anos em diferentes níveis de aprendizagem.
Ao trabalhar com os discentes do Ensino Médio, verificou-se as dificuldades de alguns alunos em compreender o emprego das razões trigonométricas no cotidiano e na resolução dos problemas propostos como exercícios de fixação. A falta de interesse deles em relação aos conteúdos de matemática sugere que o professor utilize outros recursos além do livro didático, quadro e pincel.
Nesse contexto, o uso do material concreto (trena, fita métrica, régua, calculadora e o quadrante) pode ser um grande aliado no processo de formação do conhecimento permitindo melhor interação entre professor e aluno. As atividades experimentais realizadas com a utilização dos materiais concretos permitem auxiliar os alunos a transformarem os conhecimentos matemáticos adquiridos com a prática em conhecimentos matemáticos abstratos.
Os parâmetros Curriculares Nacionais (2000, p.58) destacam os benefícios do emprego de materiais concretos pelos professores como um recurso metodológico alternativo, que pode tornar bastante expressivo o processo de ensino-aprendizagem da matemática.
Dessa forma, realizou-se uma investigação descritiva de enfoque qualitativo, no qual foi aplicada atividade prática com o uso do material concreto em sala de aula, contextualização de problemas e observação participativa. Onde os objetivos são ampliar os conhecimentos matemáticos sobre razões trigonométricas por meio da história da matemática. Utilizar o material concreto na elaboração de atividades práticas que auxiliem no processo de ensino e aprendizagem da trigonometria.
Cujo intuito é trazer à compreensão as relações métricas no triângulo retângulo incluindo-se, naturalmente, o teorema de Pitágoras (catetos e hipotenusa) a construção das relações, seno, cosseno e tangente assim como os ângulos notáveis (30º, 45º e 60º) e a tabela das razões trigonométricas. No sentido de promover uma associação dos saberes concernentes ao conhecimento trigonométrico trabalhados em sala de aula de modo que o aluno perceba que o conhecimento matemático é uma construção presente no cotidiano.
Buscando diminuir as dificuldades no ensino, foi proposta uma atividade que envolvesse os alunos com o conteúdo de razões trigonométricas, utilizando como ponto de partida o uso do material concreto. Permitindo a interação entre o aluno e o conhecimento no processo do ensino e aprendizado da matemática, por meio de uma atividade prática utilizando o material concreto (o quadrante) em sala de aula.
A pesquisa foi desenvolvida pelo professor titular do componente de matemática que acompanhou o processo de elaboração e desenvolvimento das atividades no sentido de promover uma associação de conhecimentos trigonométricos trabalhados em sala de aula com situações do cotidiano.
Constatou-se a necessidade de uma intervenção por meio de uma atividade prática diferenciada que motivasse o aluno, a participar e interagir durante as aulas. Detectaram-se também problemas de aprendizagem no conteúdo de razões trigonométricas no triângulo retângulo.
Como a trigonometria é considerada um dos conteúdos mais difíceis da matemática pelos alunos, o que contribui para dificultar o processo de aprendizagem por eles. Então foi proposta uma atividade como o uso do material concreto no ensino das razões trigonométricas como ferramenta de apoio do professor no processo de ensino e aprendizagem aplicado ao cotidiano do aluno.
A historia da Matemática como uma ferramenta de auxilio no ensino e aprendizagem da trigonometria.
história da trigonometria pode ser usada pelo professor como um recurso pedagogico na aquisição de conhecimentos científicos e no auxilio do ensino e aprendizagem da trigonometria. “A historia da matematica é um elemento fundamental para perceber como teorias e práticas matemáticas foram criadas, desenvolvidas e utilizadas num contexto especifico de sua época.” D’ambrosio (2012, p. 27).
Por meio da história da matemática o professor tem a oportunidade de mostrar aos estudantes como a matemática contribuiu para o desenvolvimento de muitas civilizações, levantar questionamentos sobre certos conteúdos estudados em sala de aula. Ancorados nas ideias de D’Ambrosio (2012) conhecer os pontos mais relevantes da matematica de ontem ajudará a entender mais facilmente a matematica de hoje.
Para Mendes (2009) a história da matemática pode ser uma grande aliada no processo de ensino e aprendizagem desde que as aulas e as atividades sejam preparadas dentro de contextos históricos necessários explicando os porquês para muitas indagações.
Nesse sentido o estudo da trigonometria integrada à história da matemática pose ser benéfica possibilitando bons resultados no ensino e aprendizagem da trigonometria. No entanto para que esse objetivo seja alcançado o professor deve elaborar suas atividades de forma dinâmicas, práticas, experimentais e contextualizadas. Dessa forma contribuindo para a aprendizagem de conceitos matemáticos relativos à trigonometria.
Um breve resumo da evolução histórica da trigonometria nas antigas civilizações
As civilizações chamadas de Babilônias, eram civilizações antigas que habitavam a Mesopotâmia 4000 anos A.C, eram civilizações muito desenvolvidas como os Caldeus, Assírios, Fenícios, Acadianos e os Sumérios que nessa época já possuíam uma escrita cuneiforme que é possivelmente anterior à hieroglífica egípcia. A civilização Babilônica possuía um grande interesse pela astronomia que estavam relacionadas com a religião, o calendário de plantio e astronomia. As contribuições dos Babilônios na matemática são admiráveis no domínio da álgebra e da aritmética.
Para EVES (2004) A história mostra que os babilônios foram os primeiros a elaborar conceitos de matemática trigonométrica esse estudo se deu a partir de cálculos de razões entre números e lados de um triângulo descrito na tábua de “Plimpton 322”.
Outra grande civilização que contribuiu para o estudo da trigonometria foi a egípcia se desenvolveu no vale do rio Nilo por volta dos 4000 a.C., nesse período os antigos egípcios utilizavam a aritmética para resolver problemas do cotidiano ligadas à agricultura e a engenharia. Essas práticas permitiram o desenvolvimento da matemática egípcia na produção do calendário egípcio, em 4241 a.C. que é considerado o mais antigo evento datado no período pré-dinástico. Aproximadamente em 3000 a.C. inicia-se o desenvolvimento da engenharia permitindo a construção de monumentos grandiosos como a pirâmide de Queops, que exibe muita precisão matemática.
No Egito antigo a trigonometria é descrita no papiro de Rhind ou papiro Ahes, que descreve seqt de um ângulo que de acordo com Boyer (2012), o significado da palavra seqt corresponde ao termo usado atualmente pelos arquitetos para indicar a inclinação de uma parede. Presume-se que esse conceito foi utilizado para manter certa inclinação nas construções das pirâmides. Em concordância com Boyer (2012), é possível concluir que seqt de uma pirâmide seria o equivalente à cotangente de um ângulo. Essas ideias estavam anunciando a chegada, séculos depois, das funções tangentes e cotangente que surgiram de modestas necessidades de medição de alturas e distâncias.
Contribuindo para o estudo da trigonometria podemos destacar a civilização chinesa que possui indícios de sua existência a cerca de 7000 a 8000 anos a.C indicados pelas ruínas de culturas que se desenvolveram ao longo dos rios Iang-tse e amarelo, registros arqueológicos datam escritos de 4000 a.C.
Na china aproximadamente 1200 a.C. foi encontrado uma trigonometria primitiva onde evidências mostram como da trigonometria relacionados aos triângulos retângulos e das relações trigonométricas eram frequentemente usados para medir distâncias, comprimentos e profundidades, não havendo registro das ferramentas utilizadas para realização dessas atividades e nem das medidas utilizadas. Há indícios que por volta do ano 152 a.C. na china o conhecimento matemático foi escrito em uma coleção de livros denominada “A matemática em nove livros” modificada no século I d.C. onde os chineses já o utilizavam o número π=3,1547 e no século III d.C. faziam a aplicação do teorema de Pitágoras.
Podemos destacar ainda a civilização Indiana que em meados do século IV d.C. passou a se tornar o novo centro cultural da Europa Ocidental com a queda do Império Romano e as invasões bárbaros Germânicos.
De acordo com Boyer (2012). Os hindus introduziram um equivalente da função seno na trigonometria com a finalidade de substituir a tabela grega de cordas. As tabelas mais antigas da função seno que foram preservadas são as do Siddhãntas e do Arybhatiya. Onde são dados os senos de 90° para vinte e quatro intervalos iguais de 3(3/4)° cada um.
A matemática Indiana é descrita como uma matemática intuitiva, embora os hindus tenham emprestados parte de seus conhecimentos dos gregos e a outros povos eles adaptavam tais conhecimentos ao seu próprio estilo peculiar adotando e desenvolvendo somente os aspectos que lhes agradavam.
O desenvolvimento da matemática deve-se muito aos hindus como a outros povos e a transmissão desse conhecimento se deu também através do povo árabe. A expansão do islã proporcionou o desenvolvimento da matemática a partir do ano 622 com a Hégira, nome dado a fuga do profeta Maomé para Medina. O nascimento da trigonometria reside na astronomia, ciência mais estudada pelos islâmicos, devido aos horários exatos de suas orações e rituais.
Nesse período, houve um avanço da matemática para o estudo da astronomia, os árabes adotaram a função seno, herdados da geometria indiana, em vez do tratado de cordas de um arco usadas na trigonometria grega. Desenvolveram a trigonometria esférica e a álgebra permitindo cálculos mais precisos nos cálculos astronômicos e que se sobressaíram na matemática.
Enfim destacamos a grande civilização grega que floresceu na região sul da península balcânica, ao redor do Mar Egeu e o Mar Adriático. A matemática trigonométrica na Grécia cobriu um intervalo de tempo indo de pelo menos 600 a.C e 600 d.C., com os gregos encontramos um estudo trigonométrico sistemático de relações entre ângulos num círculo e comprimentos de cordas.
Para Boyer (2012), ressalta que durante o período entre Hipócrates e Erástones, período este que compreende 250 anos aproximadamente, os gregos estudaram as relações entre retas e círculos aplicando esse conhecimento em vários problemas relacionados a astronomia, porém esse estudo não resultou em uma trigonometria sistemática.
Então pode-se estabelecer que o desenvolvimento da trigonometria na Grécia se deu graças ao estudo da astronomia que talvez tenha sido a primeira ciência a incorporar o estudo de ângulos como uma aplicação da matemática.
Um breve resumo do contexto histórico do uso de materiais concretos no ensino da matemática.
O uso do material concreto ao longo da história da matemática tem sido aplicado para explicar situações cotidianas do homem e para auxiliar em atividades matemáticas. Na antiguidade o homem primitivo utilizava o material concreto como pedaços de madeiras onde fazia riscos pedras empilhadas ou nó em cordas para contar suas ovelhas, objetos para contar outros objetos.
Um dos primeiros materiais concretos criados pelo homem foi o esquadro usado pelos egípcios na construção das pirâmides, em seguida vieram à régua e o compasso usado em construções geométricas. Aproximadamente 190 a.C. na Mesopotâmia e nos países asiáticos surgiu o ábaco utilizado para trabalhar cálculos aritméticos. Em seguida foi criado o Astrolábio, a Dioptra, o quadrante todos usados na agrimensura ou no estudo da astronomia.
Arquimedes em meados dos anos 250 a.C. em uma carta escrita a Eratóstenes, relata o modo pelo qual fazia suas descobertas matemáticas e confirmou a importância das imagens e dos objetos no processo de construção de novos saberes, (LORENZATO, 2012 p.5)
Segundo Lorenzato (2012) no último século muitos educadores e pensadores famosos, ressaltaram a importância do uso do material concreto como facilitador da aprendizagem:
- Comenius por volta do ano de 1650 escreveu que o ensino deveria partir do concreto para o abstrato, sugeria o uso de objetos do cotidiano ou suas representações em sala de aula;
- Locke (1632-1704) falava da falta das práticas experimentais para alcançar o conhecimento;
- Rousseau (1712-1778) recomendou as experiências sobre os objetivos visando à aprendizagem;
- Pestalozzi (1746-1827) e Froebel (1782-1852) por volta de 1800 reconheceram que o ensino deveria começar pelo concreto;
- Hebert em 1800 defendeu que a aprendizagem começa pelo campo sensorial;
- Dewey (1859-1952) em 1900 reafirmava o pensamento de Comenius afirmando as práticas experimentais como fator básico para a construção do conhecimento;
- Poincaré recomendava o uso de imagens vivas para clarear as verdades matemáticas.
O autor ressalta a importância dos pensadores e educadores em relação ao uso do material concreto no processo de ensino e aprendizagem. Lorenzato (2012) ainda destaca alguns pensadores mais recentes:
- Montessori (1870-1952) deixou como herança inúmeros exemplos de materiais didáticos e atividades de ensino que valorizam a aprendizagem através dos sentidos;
- Piaget disse que o conhecimento se dá pela ação refletida sobre o objeto;
- Vygotsky e Bruner, afirmaram que as experiências no mundo real constituem o caminho para a criança construir seu raciocínio;
- Claparéde (1872-1940) defendia a inclusão de brinquedos e brincadeiras na sala de aula;
- Freinet recomendava o uso de cantinhos temáticos.
Pestalozzi (1746-1827) destacou o uso dos materiais manipuláveis, ao defender que a educação deveria começar pela percepção de objetos concretos.
No Brasil na década 1920 deu-se o início a utilização de recursos didáticos nas aulas de matemática, esse período foi denominado de empírico-ativista uma nova tendência no ensino da matemática. Com destaque a Júlio César de Mello e Souza o Malba Tahan e Manoel Jairo Bezerra que contribuíram para a divulgação do material didático como apoio às aulas de matemática. Todos os pensadores e educadores citados defendia o uso do material didático como papel fundamental na aprendizagem nesse período no Brasil foi possível a produção de novos materiais para o ensino da matemática.
Nesse período autores como Dienes (1916-2014) e Bruner (1960-1986) (apoiados nas ideias de Piaget) trouxeram suas próprias contribuições para matemática. Dienes afirma que o conhecimento matemático é adquirido em etapas, primeiro o professor deve propiciar um meio artificial para promover a aprendizagem de um conceito matemático, incentivou o uso de jogos e materiais didáticos.
Bruner propôs um modelo de ensino baseado na interação do aluno com o meio ambiente. Segundo Bruner a criança representa o mundo através da relação entre a experiência e a ação, da manipulação e do tocar, a criança nesse estágio consegue formular hipóteses e fazer deduções.
Fundamentação do uso do material concreto no ensino da matemática
Segundo Reys (1982) a partir da comparação de várias teorias da aprendizagem identifica alguns aspectos que fundamentam o uso de materiais concretos no ensino e aprendizagem da matemática:
- A formação de conceito é a essência para aprender matemática;
- A aprendizagem é baseada na experiência;
- A aprendizagem sensorial é a base de toda a experiência, portanto é o imo da aprendizagem;
- A aprendizagem é um processo de crescimento natural do indivíduo;
- A aprendizagem é caracterizada por diferentes estágios de desenvolvimento;
- A aprendizagem é intensificada com a motivação;
- A aprendizagem procede do concreto para o abstrato;
- A aprendizagem requer participação ativa do aluno;
- A formulação de abstrações matemáticas é um processo longo.
A partir da década de 1990 foram introduzidos no ensino da matemática diversos recursos didáticos para o ensino da matemática como a calculadora e o computador. Segundo Godiño (1998) a calculadora e o computador são considerados materiais concretos, pois trabalha a percepção visual e auditiva e podem ser denominados de material concretos gráfico-textual-verbal.
Para conceituar material concreto muitos educadores e autores utilizam diversos temos e definições; ferramenta de aprendizagem, instrumento de aprendizagem, objeto de aprendizagem, material didático ou materiais manipuláveis.
De acordo com Vale (2002) Material didático são todos os materiais utilizados durante o processo de ensino e aprendizagem. Segundo esta autora os materiais didáticos podem ser divididos em materiais, didáticos, pictoriais e simbólicos:
- Materiais concretos permitem a manipulação direta com o estudante, permitem representar uma ideia matemática através de objetos a três dimensões.
- Materiais pictoriais permitem observações audiovisuais, permitem uma representação de ideias matemáticas entre o concreto e o simbólico usados em livros de textos.
- Materiais simbólicos permitem que os alunos ouçam, leiam e escrevam com papel e lápis, representam uma ideia matemática por meios de numerais e sinais e indicam uma operação ou uma relação matemática.
Segundo (LORENZATO, 2012, p.18) “material didático é qualquer instrumento útil ao processo de ensino-aprendizagem”. Dessa forma um material didático pode ser uma régua, uma calculadora, um papelão, uma caixa, um livro, entre outros, referindo-se ao “material didático” como material manipulável concreto. Lorenzato (2012) classifica os materiais concretos em:
a)Materiais que não podem ser modificados enquanto sua forma;
b)Materiais que permitem interação;
c)Materiais dinâmicos que permitem transformações.
Metodologia
O quadrante é um instrumento de medição que data meados do século XV, usado pelos antigos navegadores que usavam os astros para se orientarem em suas viagens. Provavelmente nessa época eram construídos de madeira e latão. O quadrante tem como objetivo medir ângulos, calcular distâncias e alturas com base nas relações trigonométricas, esses cálculos envolviam as posições dos astros no céu. Na navegação o quadrante era utilizado para determinar o ponto de partida e o lugar onde a embarcação se encontrava, esses cálculos baseavam-se na altura do sol durante o dia e a noite na estrela polar.
O quadrante é formado por um quarto do círculo graduado de 0º a 90º graus, com duas peças perfuradas alinhadas que funcionam como uma espécie de mira.
No vértice há um pequeno peso na ponta de um fio, cujo fio está amarado a esse vértice. Para medir o ângulo, basta apontar a mira do quadrante, até ver o ponto desejado. O fio pendurado indica a escala de 0º a 90º a medida desejada como mostra a figura abaixo.
Atividade prática com o Quadrante

O quadrante (escolar) é um material concreto cuja finalidade é medir distâncias e aturas de objetos.
Para a construção do quadrante foram utilizados os seguintes materiais:
- Um fio de barbante com um peso na ponta
- Base de papelão
- Hastes de madeira
- Pequeno pedaço de madeira com um furo
- Cola pra isopor
- Papelão
- Um prego de 1” (polegada)
O quadrante

Pensando sempre em confeccionar materiais de baixo custo e no aproveitamento de materiais recicláveis o quadrante foi construído da seguinte forma:
Primeiro passo foi imprimir um quarto do transferidor no formato pôster 2×1 que foi recortado e colado e uma base de papelão.
Segundo passo foi colar duas hastes de madeira nas bordas do quadrante, em seguida com a ajuda de uma furadeira foi feito dois pequenos furos em dois pedaços de hastes de madeira e colados em uma das bordas.
O fio de barbante é preso no prego de uma polegada.
Para realização da atividade prática com o quadrante foram necessárias 2 aulas com duração com 60 minutos cada.
Esta atividade teve como objetivo calcular distâncias e alturas de um objeto em situações-problemas que envolvem conhecimentos de razões trigonométricas aplicados ao cotidiano. A atividade iniciou-se com uma aula introdutória onde foi abordada a história do quadrante e sua utilização prática pelos antigos construtores e navegadores.
O quadrante como proposta de ensino

Primeiro passo: um aluno com ajuda de uma trena foi medido a distância do muro até um segundo aluno que nesse momento mirava até topo do muro para que fizesse a leitura do ângulo no quadrante.
Segundo passo foi efetuar os cálculos com os dados obtidos através da experiência prática com o quadrante e com os dados referentes ao cálculo das alturas realizadas na atividade 2. Pretende-se que os estudantes encontrem o ângulo de observação dado as distâncias do muro determinadas para cada dupla, logo após a leitura do ângulo com o quadrante o aluno foi instruído a fazer um desenho representando suas ações. Analisando qual das razões trigonométricas (seno, cosseno e tangente) usaria para resolver a situação problema.
Análise dos resultados
Antes das atividades práticas com situações-problemas envolvendo as razões trigonométricas e o uso do material concreto (o quadrante), foi abordado o contexto histórico das razões trigonométricas, e a origem do quadrante usado na prática experimental.
Nessa ordem de preocupação foi revisado conteúdo de trigonometria no triângulo retângulo, visto que os alunos apresentaram dificuldades em identificar o nome dos lados do triângulo retângulo.
Foram revisados também Teorema de Pitágoras, ângulos e seus elementos, tipos de ângulos, como medir um ângulo utilizando um transferidor, identificação dos eixos que representam as razões trigonométricas seno, cosseno e tangente. Em relação às quais os estudantes também apresentavam dificuldades.
Além das dificuldades relacionadas à falta de conhecimentos trigonométricos por parte dos estudantes, a pesquisadora deparou-se com a falta de material disponível na escola para a reprodução das atividades a serem usadas na aplicação das práticas experimentais pelos estudantes.
A escola dispõe de um fotocopiadora, porém seu uso é restrito a secretaria da escola com um número copias mensal. Nesse caso quando o professor se propõe a ministrar uma aula diferenciada faz uso dos seus próprios recursos.
Segundo o PCNEM (2000, p.1) diz que [..] “é necessário investigar a maneira como o aluno aprende determinado conteúdo, analisar as dificuldades, consultar quais são suas necessidades e sintonizar o conteúdo com a prática.
Seguindo as recomendações do PCNEM foi elaborada atividade práticas envolvendo o uso do material concreto no ensino das razões trigonométricas no triângulo retângulo, seguindo as ideias de Dienes (1916-2014) que enfatiza que o professor deve promover condições que proporcionem a aprendizagem de um conceito matemático.
Os dados coletados durante a aplicação são a seguir, analisados. Participaram dos instrumentos de pesquisa 36 alunos, divididas em duplas, em sala de aula, cada dupla recebeu uma numeração de 1 a 16 como identificação, as atividades foram realizadas em cinco aulas de 60 minutos cada. Todos os alunos participantes deste estudo frequentam o primeiro ano do ensino médio.
A atividade prática foi proposta utilizando o material concreto denominado de quadrante com a finalidade de medir distâncias inacessíveis como recomenda os Parâmetros Curriculares Nacionais – PCN+
“O que deve ser assegurado são as aplicações da trigonometria na resolução de problemas que envolvem medições, em especial o cálculo de distância inacessíveis [..] com ênfase na primeira volta do círculo trigonométrico e à perspectiva histórica das aplicações das relações trigonométricas” (PCN +, 2002, p. 122).
A proposta da atividade é permitir que os estudantes utilizassem outros recursos didáticos para medir alturas de arvores, prédios o muro da escola entre outros. O uso do quadrante como recurso didático permitiu a aplicação dos conceitos matemáticos em situações reais partindo da teoria para prática.
Segundo Vale (2002) os materiais concretos são ajudas significativas para aprendizagem em qualquer estágio de desenvolvimento. “Onde os conceitos matemáticos devem ser aprendidos com apoio em modelos concretos e simbólicos”. VALE (2002, p. 14).
Nessa atividade a proposta é calcular a altura da parede da sala de aula utilizando o quadrante como recurso didático. Lorenzato (2012) refere-se ao material didático como material concreto.
Resolução da atividade da dupla 06
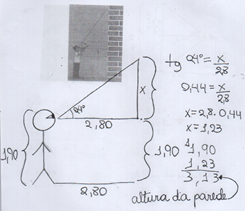
Nessa atividade verificou-se que das 16 duplas participantes da pesquisa 04 duplas chegaram num resultado incorreto. Foi possível verificar que os estudantes, não tiveram dificuldades na identificação das razões trigonométricas a ser usado no cálculo da atividade e conseguiram encontrar o valor da parede da sala de aula.
Resolução da atividade da dupla 10.
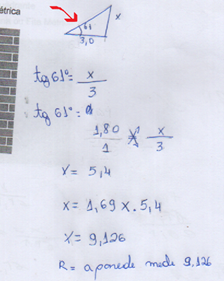
Nessa atividadequatro duplas chegaram à solução incorreta, é possível observar na figura 34 que os cálculos estão certos, porém o erro na atividade aconteceu na leitura do ângulo no quadrante, dessa forma objetivo da atividade foi alcançado.
Verificou-se por meio da observação participativa que ao trabalhar com os materiais concretos, os alunos demonstraram um maior interesse em participar das aulas, das atividades e pelo conteúdo de razões trigonométricas no triangulo retângulo. Através das atividades realizadas com o material concreto (o quadrante), possibilitou que os alunos fossem capazes de distinguir e identificar as razões trigonométricas de forma correta e aplicá-las na resolução de situações- problemas. Bem como fazer medições de ângulos com ajudas do material concreto e medir distâncias com a trena, permitindo dessa forma que os alunos adquirissem o conhecimento de noção de espaço, no qual também apresentavam dificuldades.
No início das atividades, os alunos se mostravam meios distantes, pois observou-se que muitos alunos não tinham conhecimentos básicos de trigonometria e não sabiam identificar uma razão trigonométrica.
Verificou-se que os alunos aprovaram a atividade utilizando o material concreto (o quadrante) no ensino das razões trigonométricas, que ocorreu de maneira significativa, favorecendo a construção de conhecimentos dos conceitos trigonométricos.
Com efeito, nas atividades propostas, considera-se que houve aprendizagem por parte dos alunos, pois eles conseguiram estabelecer relações entre os conceitos matemáticos abstratos contidos nos livros e aplicá-los na resolução de situação-problema e na atividade prática com o material concreto.
Observou-se que todos os alunos conseguiram resolver os problemas propostos, algumas duplas de forma rápida e outras requereram um tempo maior para realizar as atividades propostas, buscando mais informações a respeito dos conceitos trigonométricos. Houve muita interação entre as duplas participantes, questionamentos e criatividade na resolução do problema proposto com o material concreto.
Por conseguinte, o desenvolvimento da pesquisa foi satisfatório, pois no final da atividade prática, todos os alunos conseguiram identificar corretamente os lados do triângulo. Distinguir a diferença entre cateto oposto e cateto adjacente, fazer a leitura correta dos ângulos, identificar as razões trigonométricas e aplicá-las de maneira correta na resolução dos problemas. Fazer a leitura dos ângulos na tabela trigonométrica e entender como funciona a sua estrutura e como são calculados os valores de cada ângulo correspondente a seno, cosseno e tangente.
Dessa forma, os resultados positivos obtidos com a atividade proposta com o material concreto (o quadrante) mostram que, a metodologia utilizada conseguiu promover autonomia dos alunos, proporcionando meios para questionamento sobre conceitos trigonométricos trabalhados em sala de aula.
Consequentemente ao desenvolver a atividade experimental com a utilização do material concreto, verificou-se que houve um aprendizado de forma significativa em relação ao conteúdo proposto na pesquisa. O sucesso dessa aprendizagem deu-se devido ao planejamento elaborado antes da atividade proposta, escolha adequada do material concreto utilizado, a participação e o envolvimento dos alunos na resolução dos problemas propostos nas das atividades experimentais e a interação entre a professora e seus alunos.
CONCLUSÃO
Nessa pesquisa foi mostrado o uso do material concreto como proposta de ensino e aprendizagem das razões trigonométricas no triângulo retângulo, a partir de situações problemas aplicados ao cotidiano.
Para responder as questões, utilizou-se a experiência de ensino em dois momentos. No primeiro, identificou-se os conhecimentos teóricos matemáticos mais relevantes sobre o tema razões trigonométricas através da história da matemática, no segundo utilizou-se o material concreto como recurso didático no ensino das razões trigonométricas, bem como sua aplicabilidade no cotidiano.
A atividade proposta com o uso do material concreto permitiu interagir a matemática com a astronomia, engenharia e arquitetura, tornando as aulas mais práticas e criativas, mostrando que o homem sempre esteve em busca de soluções para situações-problemas do cotidiano, e a matemática é o recurso utilizado pelo homem para chegar às soluções.
A atividade foi fundamentada nos conhecimentos prévios obtidos através da aula expositiva e dialogada. Tendo com referencial as teorias de Dienes e Bruner (apoiados nas ideias de Piaget). Promovendo resultados positivos no processo de ensino e aprendizagem da trigonometria, onde o estudante é levado a formular e verificar hipóteses, formar conceitos e desenvolver sua criatividade. Na sequência foi utilizado o quadrante na atividade prática. A utilização desse material foi essencial para compreensão de conceitos e significados das razões trigonométricas no triangulo retângulo.
A partir dos dados coletados por meio da observação participativa, foi possível verificar que, após a aplicação das atividades práticas com o material concreto que as dificuldades apresentadas pelos estudantes não estavam relacionadas diretamente ao conteúdo razões trigonométricas no triângulo retângulo. Uma vez que os estudantes conseguiram identificar os conceitos trigonométricos em determinada situação, porém alguns estudantes não foram capazes de aplicá-los adequadamente em uma situação-problema.
A proposta de medir distâncias e alturas inacessíveis por meio das razões trigonométricas utilizando o material concreto em situações-problemas possibilitou que o ensino da trigonometria aplicado numa situação relacionada à realidade local do estudante, pode promover resultados positivos no processo de ensino e aprendizagem das razões trigonométricas no triângulo retângulo.
Os resultados das medidas obtidos através da aplicação da atividade contextualizada utilizando o quadrante ficou bem próxima às medidas reais.
Entende-se que o aprendizado da matemática por meio da experimentação, da manipulação e da observação permite ao estudante construir mentalmente representações abstratas dos conceitos matemáticos, então os materiais concretos servem com facilitador nesse processo de ensino e aprendizagem.
Da análise dos resultados permitem concluir que nem todos os estudantes evoluíram da mesma maneira, os resultados também apontam para diferentes e complexos fatores que interferem na aprendizagem, como a desmotivação, o desinteresse nas aulas de matemática, a infrequência dos estudantes, a falta de compreensão de denominados conteúdos e a falta de conceitos trigonométricos nas series anteriores. Observou-se também que alguns alunos demonstraram aptidão mais acentuada para resolução de situações-problemas.
A atividade prática aplicada em sala de aula com o material concreto possibilitou uma aprendizagem significativa, possibilitando que o ensino da trigonometria acontecesse de forma dinâmica e motivadora, levando o estudante a fazer questionamentos e discussões sobre a aplicação das razões trigonométricas no cotidiano.
Dessa forma considera-se que o objetivo dessa pesquisa foi alcançado e que a prática desenvolvida possa servir como sugestão de trabalho a outros discentes. Observou-se também que o interesse dos estudantes em realizar e desenvolver a atividade indica uma avaliação positiva da experiência.
REFERÊNCIAS
BOYER, Carl B. História da matemática. Trad. De Elza Gomide, Ed. Edgard Blucher Ltda, São Paulo, 2012.
BRASIL. Parâmetros Curriculares Nacionais. Ciências da Natureza e Matemática e suas Tecnologias. Brasília: MEC, 2000.
BRASIL, Orientações Educacionais Complementares aos Parâmetros Curriculares Nacionais (PCN+). Ciências da Natureza e Matemática e suas Tecnologias. Brasília: MEC, 2006.
Ciências da Natureza, Matemática e suas Tecnologias/Secretaria de Educação Básica. – Brasília: Ministério da Educação, Secretaria de Educação Básica, 2006. 135 p. (Orientações Curriculares para o Ensino Médio, volume 2).
D’AMBRÓSIO, U. (2018). Educação Matemática: da Teoria à prática.
DIENES, zoltam Paul. As seis etapas do processo de aprendizagem em matemática. Trad. Maria Pia Brito de Macedo Charlier e René François Joseph Charlier e René François. São Paulo: EPU, Brasília: INL, 197 5f.
EVES, Howard. Introdução a história da matemática. Campinas, SP: Editora Unicamp, 2004.
FIORENTINI, D.; MIORIM, M. A. Uma reflexão sobre o uso dos materiais concretos e jogos MP ensino da matemática. BOLEMA, n.7, p. 5-10, 1990
FIORENTINI, D. Alguns modos de ver e conceber o ensino da matemática no Brasil. Zettike 2009.
HERNANDEZ SAMPIERI, Roberto, Metodologia da Pesquisa. 5ª Ed.- Porto Alegre: Penso, 2013.
LORENZATO, Sérgio. Laboratório de Ensino de Matemática na Formação de Professores.Campinas, SP: Autores Associados, 2006. (Coleção Formação de Professores).
MOREIRA, Antônio Flávio Barbosa; SILVA, Tomaz Tadeu. (Org.). Currículo, cultura e sociedade. 2. ed. São Paulo: Cortez, 1997.
MONTESSORI, Maria. Pedagogia Científica: Trad. Aury Azélio Brunetti. São Paulo: Flamboyant, 1965.
MOTA, T. B.; JUCÁ, R. S.; PINHEIRO, C.A.M. Uma análise de erros nas relações trigonométricas no triângulo retângulo. In: XI Encontro Nacional De Educação.
PIAGET, Jeam. Seis estudos de psicologia. 24. Ed. Trad. Maria Alice Magalhães D’Amorim e Paulo Sergio Lima Silva. Rio de Janeiro: forense Universitaria, 2006.
VALE, Isabel. Materiais Manipuláveis. Viana do Castelo: ESE, 2002.
VYGOTSKY, L. S. Pensamento e linguagem. São Paulo: Livraria Martins Fontes, 1989
1Mestre em Ciências da Educação pela Universidad Del Sol – UNADES-PY e Especialista em Metodologia do Ensino da Matemática pela Universidade Estadual do amazonas-UEA. E-mail:
