REGISTRO DOI: 10.5281/zenodo.10439723
Diego Soares Monteiro da Silva
Resumo:
Neste artigo apresentamos uma heurística que permite alinhavar, por meio dos métodos de continuação, diversas soluções de um sistema não linear F(〖x)=b〗_, para isso, escrevemos tal sistema na forma vetorial e consideramos como hipóteses que a função F é própria e diferenciável definida entre espaços de dimensão finita . O estudo de caso de exemplos em dimensão dois, nos permite descrever geometricamente e apresentar um algoritmo, que pode ser aplicado para cálculo de pré-imagens de funções mais gerais, inclusive para problemas discretizados em altas dimensões. A pesquisa de natureza exploratória-investigativa representação uma extensão do algoritmo da saturação.
Palavras–Chave: sistemas não lineares, métodos de continuação, saturação, fibras unidimensionais.
Abstract:
In this article we present a heuristic that allows us to put together, through continuation methods, several solutions of a non-linear system F(〖x)=b〗_. To do this, we write such a system in vector form and consider as hypotheses that the function F is proper and differentiable defined between finite-dimensional spaces. The case study of examples in dimension two allows us to geometrically describe and present an algorithm, which can be applied to calculate pre-images of more general functions, including for discretized problems in high dimensions. Exploratory-investigative research represents an extension of the saturation algorithm.
Keywords: nonlinear systems, continuation methods, saturation, one-dimensional fibers.
Introdução
Neste artigo, apresentamos uma heurística que permite alinhavar diversas soluções de alguns sistemas não lineares específicos. Sejam X = Y = R^2, dado b ∈Y, estamos interessados em calcular as pré-imagens x ∈X, tal que F(〖x)=b〗_com F sendo uma função diferenciável e própria.
Definimos o processo de alinhavar soluções, como uma construção de uma curva contínua unidimensional no domínio a partir dos métodos clássicos de continuação.
Para construção de tal heurística nos valemos de informações geométricas obtidas a partir de alguns estudos de casos com o auxílio de um programa que inverte funções do plano no plano, o 2×2 (acessível na página de Humberto Bortolossi, UFF: http://www.imuff.mat.br/puc-rio/2×2). Mais especificamente, neste programa o conjunto crítico-uma união de curvas- pode ser discretizado, e a análise, classificação das singularidades (dobras e cúspides) pode ser empregada (MALTA,I. et al, 1993). Para funções próprias definidas em domínio e imagem de dimensões maiores que dois, a mesma técnica utilizada no 2×2 se torna impraticável, assim neste trabalho, propomos um caminho simples e alternativo que permite a busca de soluções para funções próprias com domínio e imagem em dimensões maiores que dois.
Evidências numéricas e teóricas, indicam que mesmo para dimensões maiores que dois as singularidades genéricas – dobras- se fazem presentes. Com base nisto, Kaminski (2016) propõe um algoritmo que usa a técnica de inversão por continuação explorando a análise numérica na vizinhança de dobras e que impõe condições de compatibilidade entre arcos no domínio para obter outras pré-imagens a partir de uma já conhecida, chamaremos tal algoritmo de saturação e o descreveremos nas primeira seção do artigo.
A partir de um estudo de caso em que a representação geométrica do conjunto crítico e sua imagem descritas por placas pelo programa 2×2 são conhecidas e a partir da revisão teórica sobre a saturação, apresentamos o estado da arte deste trabalho: um algoritmo que alinhava diversas pré-imagens por meio da construção de uma curva no domínio, denominada fibra. A heurística é construída através de uma combinação entre compatibilidade de arcos e o método da saturação.
A construção de tal heurística é similar à apresentada por Cal Neto e Tomei (2012) para o estudo de equações diferenciais elípticas semilineares, isto é, problemas em dimensão infinita, entretanto, a abordagem apresentada no presente trabalho dá origem a um algoritmo que não está associado a decomposição de Lyapunov-Schimidt.
Por fim, apresentamos o método numérico utilizado no processo de alinhamento das pré-imagens, bem como as mudanças em relação ao que foi apresentado em Kaminski(2016). Os métodos utilizados, apesar de aparentemente parecerem simples de implementação computacional, por exemplo, Newton, continuação, bissecção, requerem cuidados por questões de custo computacional e estabilidade. Estratégias de passos são utilizadas, e também um método híbrido- para cálculo de um ponto crítico em um intervalo- que desempenha tão bem quanto bissecção, porém podendo apresentar velocidade de execução próxima ao dos métodos mais instáveis como o das secantes.
A pesquisa apresentada é de natureza quantitativa e de caráter investigativo-experimental. Ademais, converge para a linha de pesquisa de perfil não dedutivo que cresce nos últimos anos na matemática aplicada, que é a matemática experimental, como podemos destacar no trecho a seguir.
“Um ponto de partida natural, portanto, em uma pesquisa de métodos não dedutivos em matemática, é olhar para o surgimento de um gênero conhecido como “matemática experimental”. O últimos 15 anos ou mais, vimos o aparecimento de periódicos (por exemplo, The Journal of Experimental Mathematics), institutos (por exemplo, do Instituto de Matemática Experimental da Universidade de Essen), colóquios (por exemplo, o Experimental Mathematics Colloquium em Rutgers University) e livros (por exemplo, Borwein e Bailey 2003 e 2004) dedicado a este tema. Estes últimos autores também argumentam, em Borwein e Bailey (2015), pela importância da experiência matemática dentro da prática matemática de forma mais geral, enquanto Sorensen (2016) fornece uma visão histórica e sociológica mais ampla análise da matemática experimental”. (BAKER, ALAN,2020)
Aporte teórico
Seja F: X=R^n → Y=R^n uma função diferenciável, um ponto p ∈X é dito regular se a matriz jacobiana DF(p) é inversível, isto é, det(DF(p))≠0, caso contrário é dito ponto crítico. Um ponto na imagem de F é definido como valor crítico se existe pelo uma sua pré-imagem que é ponto crítico de F. Um ponto em Y que não é valor crítico é definido como valor regular. Denotaremos por C, o conjunto dos pontos críticos de F e por F(C) sua imagem. O conjunto I=F^(-1) (F(C)), chamaremos da flor de F.
Uma função F é própria, se dado um compacto K ⊂Y , temos que F^(-1) (K) é compacto em X. Em dimensão finita isto é equivalente a dizer que F leva infinito para infinito.
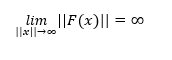
Ademais, se F é própria e diferenciável, todo ponto b ∈Y\F(C), que está na mesma componente conexa tem o mesmo número de pré-imagens, em outras palavras, o número de pré-imagens é constante em cada componente conexa.
Um ponto crítico p* de F é dito ser uma dobra- singularidade de Morin de ordem 1- se existem difeomorfismos locais ψ e ϕ na vizinhança de p* e F(p), respectivamente tal que próximo a origem do plano o mapa ϕ ◦ F ◦ ψ assume a forma normal:
(x_1,x_2,…,x_(n-1),y) → (x_1,x_2,…,x_(n-1),y^2 )
Geometricamente, podemos ter a seguinte interpretação: existem pontos s_1 e s_2, na vizinhança de uma dobra p com det(DF(s_1)) > 0 e det(DF(s_2)) < 0, tal que F(s_1)=F(s_2), como podemos ver na figura 1.1.
Figura 1.1: Vizinhança de uma dobra à esquerda e sua imagem à direita.
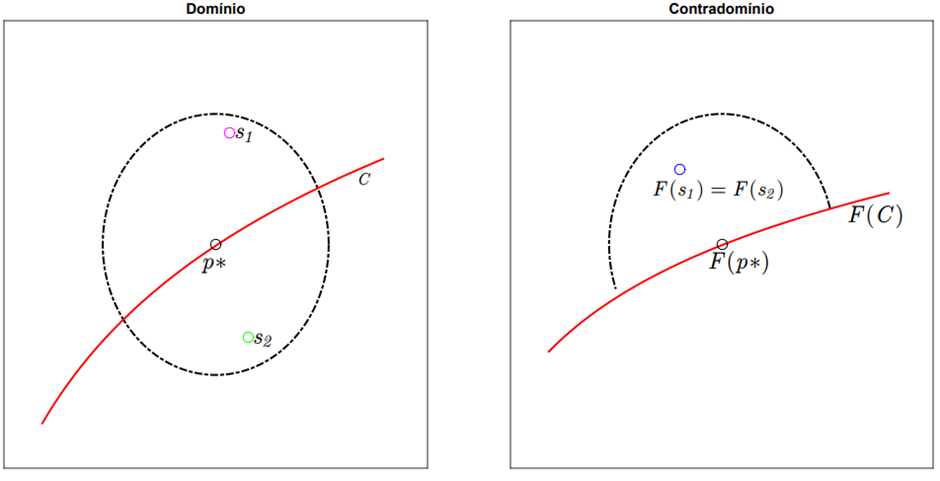
Os segmentos de reta no contradomínio que passam por F(p) e F(s_1)=F(s_2) apresentam uma região com duas pré-imagens e a outra com nenhuma. Além disso, as duas pré-imagens se tangenciam e a direção de tangência é dada pelo núcleo da matriz jacobiana de F em p . Tal proposição pode ser demonstrada diretamente, para forma normal da dobra próximo a 0, uma vez que os difeomorfismos preservam as propriedades de interesse. Assim, para a forma normal o Nuc(DF(p))=Span{(0, 0, …, 1)} e os segmentos de reta que passam pela origem, no contradomínio, são da forma 〖t(v〗1,v_2,…,v_n). As pré-imagens destes são as curvas 〖α(t)=(tv〗_1,tv_2,…,tv(n-1),±√(tv_n )), as quais ficam bem definidas, somente, quando √(tv_n )≥ 0 e que são verticais na origem (KAMINSKI,O., 2016).
Numericamente, exploramos uma caracterização mais direta para uma dobra que é a seguinte: um ponto p é uma dobra se;
- grad(DF(p*))≠ 0,
- K =Nuc(DF(p*)) tem dimensão 1,
- a reta tangente ao conjunto crítico em p* e K não coincidem.
A saturação por um estudo de caso
O algoritmo desenvolvido por Kaminski(2016) para resolver F(〖x)=b〗_, tem como elemento básico a inversão de F -por algum método de continuação (ALLGOWER, E. L.; GEORG, K.,1991) -ao longo de um segmento β ∈Y. Suponha que o segmento tenha uma extremidade em F(x_i), na qual uma pré-imagem x_i é conhecida- chamaremos x_i de condição inicial.
O segmento β=[F(x_i),g]={(1-t)F(x_i)+tb,t ∈[0,1]} pode ser parametrizado por F(x_i)+tw_i, com w_i=b-F(x_i). Representaremos as pré-imagens de b por p_i . Por β_i , indicaremos o segmento a ser invertido e γ_i o respectivo arco determinado pela inversão de β_i. Em certos casos usaremos a notação γ_i e γ˜_i para indicar que os caminhos são levados por F a um mesmo segmento β_i. Os caminhos que são levados a um mesmo segmento β_i serão representados pela mesma cor.
O comportamento de uma função numa vizinhança de um ponto regular pode ser obtido pelo teorema da função inversa. Mas e próximo a um ponto crítico? A classificação e o estudo detalhado das singularidades para n>2 se torna impraticável, mas ainda assim, as singularidades genéricas -dobras- se fazem presentes de forma abundante e a saturação explora este fato.
Para descrevermos a saturação, vamos considerar o seguinte modelo do plano no plano:
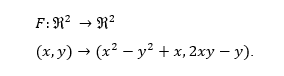
As curvas em vermelho, nas figuras a seguir, representam o conjunto crítico C={(x,y) ∈R^2; 4x^2+4y^2=1} e sua imagem F(C). A função F é sobrejetiva (tem grau não-nulo) (MALTA,I. et al, 1993,1996), pontos na placa ilimitada da imagem de R^2\F(C) apresentam 2 pré-imagens, isso pode ser visto uma vez que F em notação complexa é dada por F ̂(z)=z^2+▁z. Pontos na placa limitada apresentam 4 pré-imagens. Sem perda de generalidade, escolhemos a seguir, um ponto b na placa limitada, pois nos permite exemplificar de maneira mais detalhada as etapas da saturação.
O primeiro passo do algoritmo consiste em determinar pelo menos uma pré-imagem p_1 de b através de um método clássico de continuação. Ao iniciarmos o processo com uma com uma condição inicial x_0, temos que a inversão de β_1 nos leva a um arco γ_1 constituído somente por pontos regulares, veja o arco preto na figura 1.2. Em seguida, sorteamos (lançamos) uma nova condição inicial x_1 e de posse de uma pré-imagem já conhecida, neste caso p_1, tentamos realizar a inversão do segmento β_2, considerando como partida p_1, caso não encontremos o conjunto crítico na inversão de β_2, chegaremos a um ponto 〖x_1≠x_1〗^- o que nos fornece o indício de que existe uma outra pré-imagem p_2 que está na mesma componente conexa de x_1, logo inverta β_2 partindo da condição x_1 – ou chegaremos ao próprio x_1, portanto como a função é própria e o arco é formado apenas por pontos regulares não ganharíamos uma nova pré-imagem ao inverter β_2 partindo da condição x_1. Vejamos as situações descritas nas figuras 1.2 e 1.3
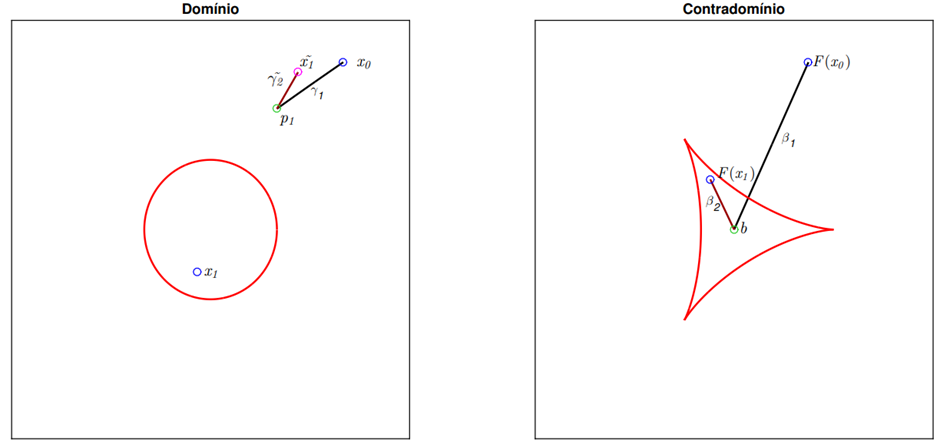
Figura 1.2: Sorteio de uma condição inicial x_1 e busca por novas pré-imagens a partir de uma já conhecida, neste caso, p_1.
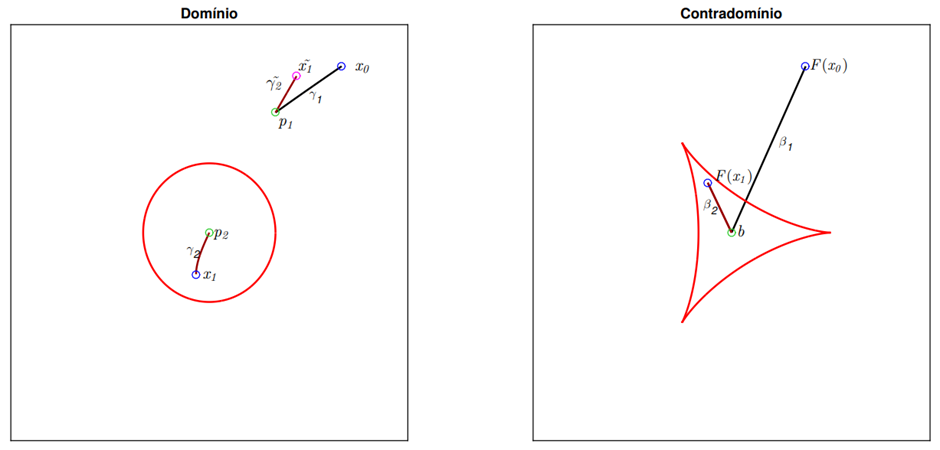
Figura 1.3: Como 〖〖x^~〗^ 〗_1≠x_1, temos indício de que exista uma pré-imagem p_2 na mesma componente conexa de x_1. Inverta β_2 com semente〖 x〗_1 .
Na situação descrita acima, consideramos um caso em que ao lançarmos uma nova condição inicial x_1 e analisarmos a compatibilidade com a pré-imagem p_1 obtivemos arcos 〖〖γ_2〗^ 〗^ e 〖γ_2〗^~ formado apenas por pontos regulares, entretanto poderíamos ter uma situação em que o processo de inversão por continuação é interrompido ao encontrarmos o conjunto crítico. Na tese de Kaminski (2016) é apresentada uma forma de estender o processo de inversão além do conjunto crítico, neste caso, a saturação tenta explorar a propriedade de dobra já descrita.
Inserimos uma nova condição inicial x_2. Conhecemos, agora, duas pré-imagens p_1 e p_2, podemos interpretar, aqui, que temos uma escolha a fazer entre as duas pré-imagens e isso nos levaria a arcos distintos no domínio, ou podemos pensar na formação de uma árvore ao analisarmos a compatibilidade de cada uma dessas pré-imagens com x_2. Por objetividade, faremos uma escolha pela pré-imagem p_2. Ao tentarmos inverter o segmento β_4 com condição inicial x_2, veja figura 1.4, chegamos a s_1 um ponto próximo a um ponto crítico p_1* , o qual interrompe o processo de continuação, até este momento temos bem definido o arco γ_3 e o segmento β_3. A singularidade p_1* é uma dobra, portanto é de se esperar que exista uma cópia de γ_3 em relação a p_1* , tal cópia é γ_3˜ e nos leva a uma nova pré-imagem p_3, como mostra figura 1.5. Ainda assim, falta invertermos o segmento β_4 considerando a condição inicial x_2, mas nesse caso chegamos a uma solução já conhecida p_1, porém poderia ser uma pré-imagem inédita, veja a curva verde na figura 1.7
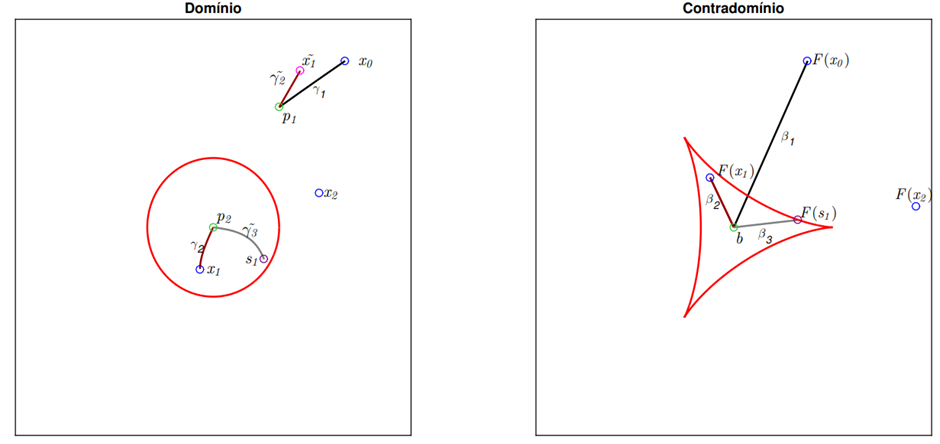
Figura 1.4: Inserção da condição inicial x_2. A inversão do segmento F(x_2) até b partindo de p_2 é interrompida ao encontrarmos o conjunto crítico.
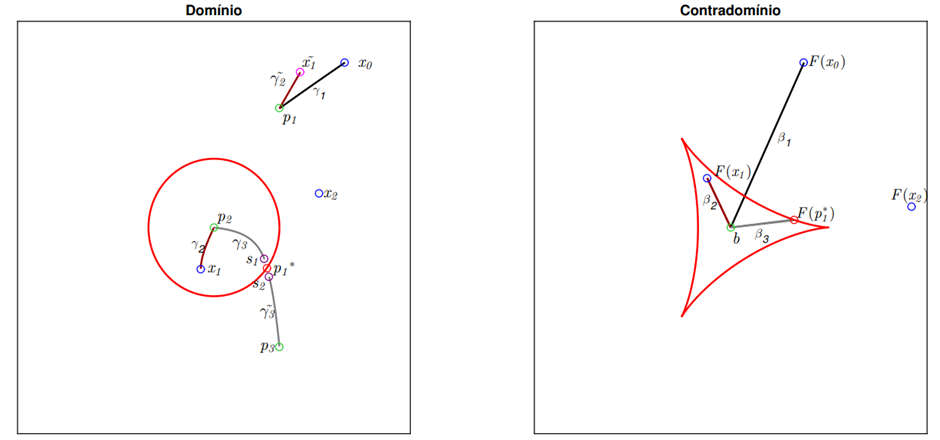
Figura 1.5: Inversão de β_3 com condição inicial s_2.
Na etapa descrita acima, conhecemos o ponto s_1, o mesmo pertence a curva γ_3 e está na vizinhança de um ponto crítico p_1* , que a princípio não sabemos qual é. A fim de obtermos uma aproximação para tal singularidade e um ponto s_2 na outra componente conexa de R^2\C calculamos o uma aproximação para o “quase núcleo” em s_1 dado por K=Nuc(DF(s_1)). Sobre a reta s_1+mK, com m ∈R, procuramos por um ponto na vizinhança de s_1 tal que det(DF(s_1+mK)) ≈ 0, o qual nos fornece uma aproximação para a singularidade, e um salto s_2 próximo a esta, onde det(DF(s_1))det(DF(s_2)) < 0. Na figura 1.6, temos uma ampliação da figura 1.5 em torno de p_1*. A imagem de s_2 pode não pertencer ao segmento, ao qual estamos invertendo, mas podemos conectar por um pequeno caminho 〖F(s〗_2) a este segmento com condição inicial s_2 e seguir com a inversão do segmento de reta no sentido oposto.
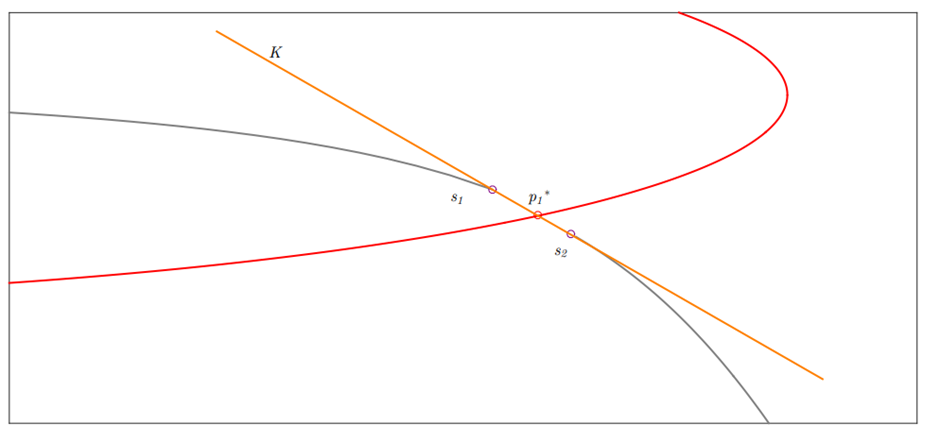
Figura 1.6: Cálculo aproximado de p_1* e s_2 conhecendo s_1.
Por fim, apresentamos na figura 1.7 as 4 soluções obtidas com a saturação. A seguir, iremos descrever uma forma de alinhavar algumas soluções, o que nos permite obter as 4 pré-imagens a partir da inversão de uma curva especial. O fato de que na primeira etapa precisamos determinar uma pré-imagem, para estabelecermos as ideias supracitadas pode não ser direta, sendo necessário às vezes lançarmos diversas condições iniciais até encontrarmos uma solução por continuação. Uma forma de contornar isso é que ao encontrarmos o conjunto crítico podemos dar um “salto” e com a nova condição inicial em outra componente conexa seguirmos com o processo de inversão, isto é, estendermos além do conjunto crítico como foi apresentado.
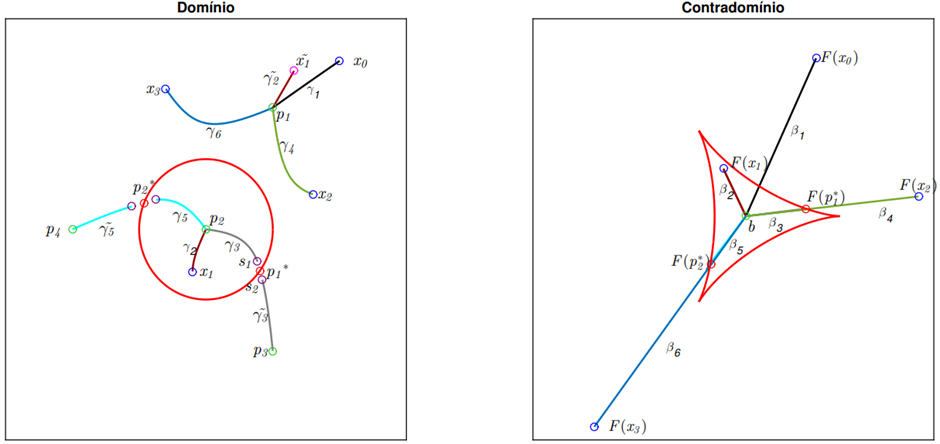
Figura 1.7: As 4 pré-imagens p_1, p_2, p_3 e p_4 de b.
Fibras unidimensionais
Uma dificuldade presente no algoritmo descrito acima é a necessidade de lançarmos ou sortearmos uma condição inicial em cada etapa, com o objetivo de automatizarmos tal processo realizamos a seguinte pergunta: será que existe alguma curva especial a ser invertida, na qual conseguimos alinhavar diversas pré-imagens a partir da inserção de uma condição inicial? De maneira geral, trabalharemos com F própria e diferenciável e nesse caso, a resposta é sim. O comportamento descrito pela inversão de uma reta vertical r (b ∈r) indo de “+∞” para “−∞”, a partir de uma condição inicial x_0 suficientemente longe da origem (“+∞”), é uma curva no domínio, que chamaremos de fibra e que em muitos casos, possui múltiplas soluções de F(x)=b.
Para uma melhor descrição, vamos considerar o mesmo exemplo estudado na saturação e inverter ainda um ponto b na placa limitada de R^2\F(C). Além do conjunto crítico em vermelho e sua imagem, vamos desenhar a flor I (em cinza-tracejada), a qual nos fornece uma ideia do comportamento global de F.
Utilizamos a combinatória descrita por arcos de C e F no domínio, com os arcos de F(C) no contradomínio, que nos permite verificar a compatibilidade do caminho a ser construído no domínio (a fibra) a partir da inversão sobre a “reta vertical” r. Apesar de realizarmos a apresentação levando em consideração uma comparação entre arcos (domínio e contradomínio) a heurística apresentada dá origem a um algoritmo que independe de conhecer a flor associada ao sistema não linear.
Vamos começar invertendo sobre r a partir de F(x_0) com condição inicial x_0. Trespassamos os arcos AC, no domínio e imagem sem dificuldades, encontramos uma primeira pré-imagem p_1 de b e seguimos por continuação até chegarmos bem próximo ao ponto crítico p_1* , veja a figura 1.8 onde a inversão de β_(1 )⊂r descreve a curva γ_1 . Vale ressaltar, que apesar de passarmos por um valor crítico F(p_2)a primeiro momento, a pré-imagem deste encontra-se na flor e não no conjunto crítico, portanto o processo de inversão só é interrompido quando chegamos a F(p_1) ∈ AB , o qual é imagem do ponto crítico p_1* ∈ AB.
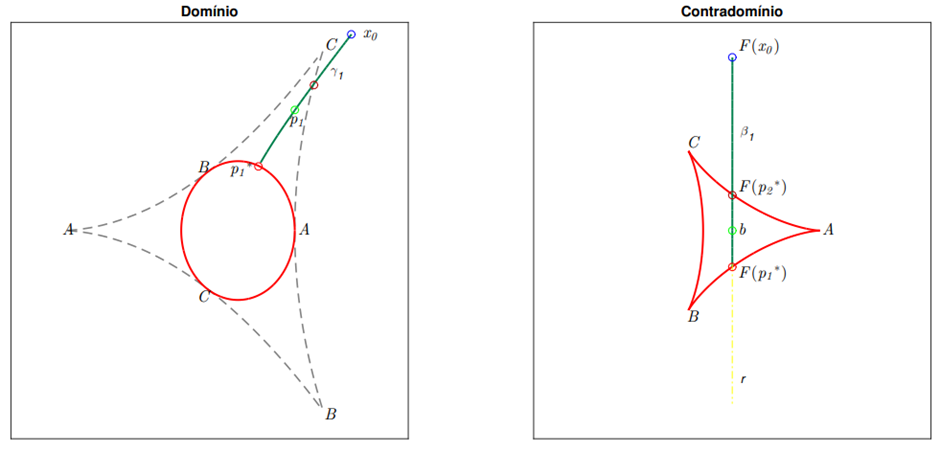
Figura 1.8: Invertendo β_(1 )⊂r com condição inicial x_0 suficientemente grande.
Ao chegarmos a uma vizinhança do ponto crítico p_1* , que é um ponto de dobra, adotaremos a mesma postura já explicitada na saturação. Assim, invertemos o segmento β_2=▁(F(p_1)F(p_2)) , o qual desenha a curva γ_2 ambos em laranja na figura 1.9, obtemos nessa etapa uma nova pré-imagem p_2. Numericamente, sabemos que na vizinhança de p_1* existem pontos s_1 e s_2 que estão em componentes conexas distintas de e tornam tal inversão possível, exatamente como apresentado na figura 1.6, não os colocamos na figura 1.9 apenas por questões visuais. Na etapa descrita, partimos de um ponto no arco AB até um ponto no arco AC tanto no domínio, quanto no contradomínio. Novamente, chegamos a uma singularidade p_2* ∈AC e estendemos a inversão além do conjunto crítico, ao invertermos o segmento β_3 (em azul) determinamos mais uma pré-imagem p_3 e a inversão segue em direção a “−∞” trespassando o arco AB, como pode ser visto na figura 1.10.
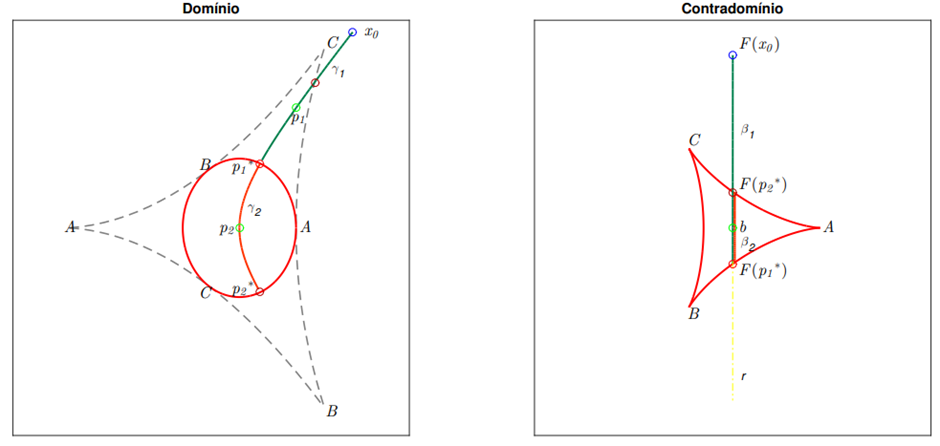
Figura 1.9: Estendendo a inversão além do conjunto crítico. Passamos pelo ponto crítico p_1* mudamos o sentido de inversão na imagem.
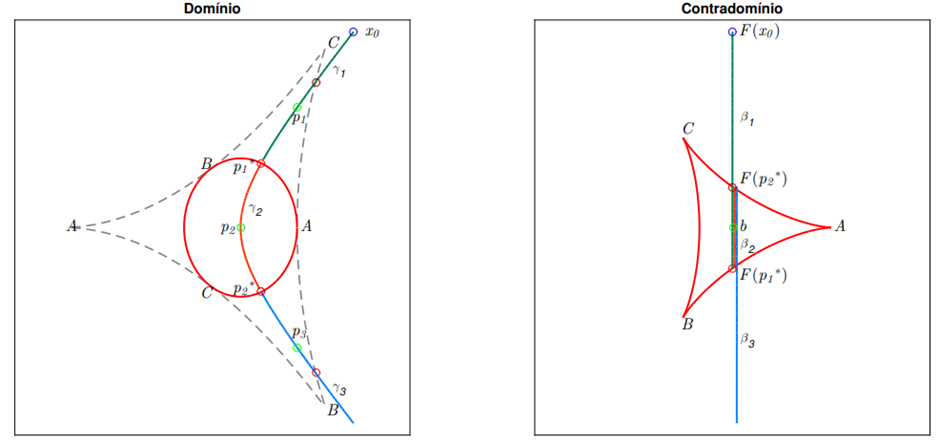
Figura 1.10: Invertendo β3 em direção a −∞.
Sabemos que ainda falta encontrarmos uma pré-imagem. A função F em infinito -notação complexa- se comporta como z→ z^2 (MALTA,I. et al, 1993, 1996), portanto o ponto F(x_0) possui uma pré-imagem 〖x_0〗^~ na placa ilimitada no domínio, que é diferente de x_0. Para calcularmos tal pré-imagem, podemos considerar uma bola com centro na origem no contradomínio, de modo que a mesma comece e termine em F(x_0). A partir da inversão desta bola com condição inicial x_0 chegamos a uma condição inicial 〖x_0〗^~, com a qual podemos inverter β(4 )⊂r (em roxo na figura 1.11) e obtermos a pré-imagem p_4, destacamos que a curva γ_4 é constituída somente por pontos regulares, não havendo interrupção no processo de inversão.
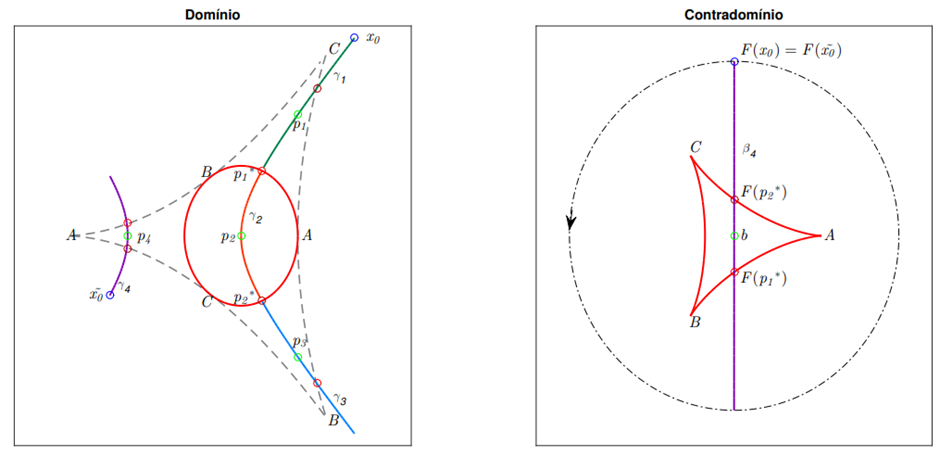
Figura 1.11: O comportamento de F em infinito nos fornece boas condições iniciais para o alinhavamento. As 4 pré-imagens p_1, p_2, p_3 e p_4 de b.
Fluxograma
O algoritmo para construção de fibras unidimensionais pode ser melhor resumido através de um fluxograma, para isso, utilizamos uma notação similar a presente em Kaminski(2016):
– Blocos com “a → b condição inicial= d” representam o uso do inversor de segmentos no sentido de a para b com condição inicial= d ;
– Os caminhos com “C” e “NC” indicam se a inversão parou ou não no conjunto crítico, respectivamente;
– Todo ponto crítico p_i* encontrado é armazenado, assim como os pontos em suas vizinhanças em diferentes componentes conexas;
– Pré-imagens de b só são armazenadas se forem inéditas.
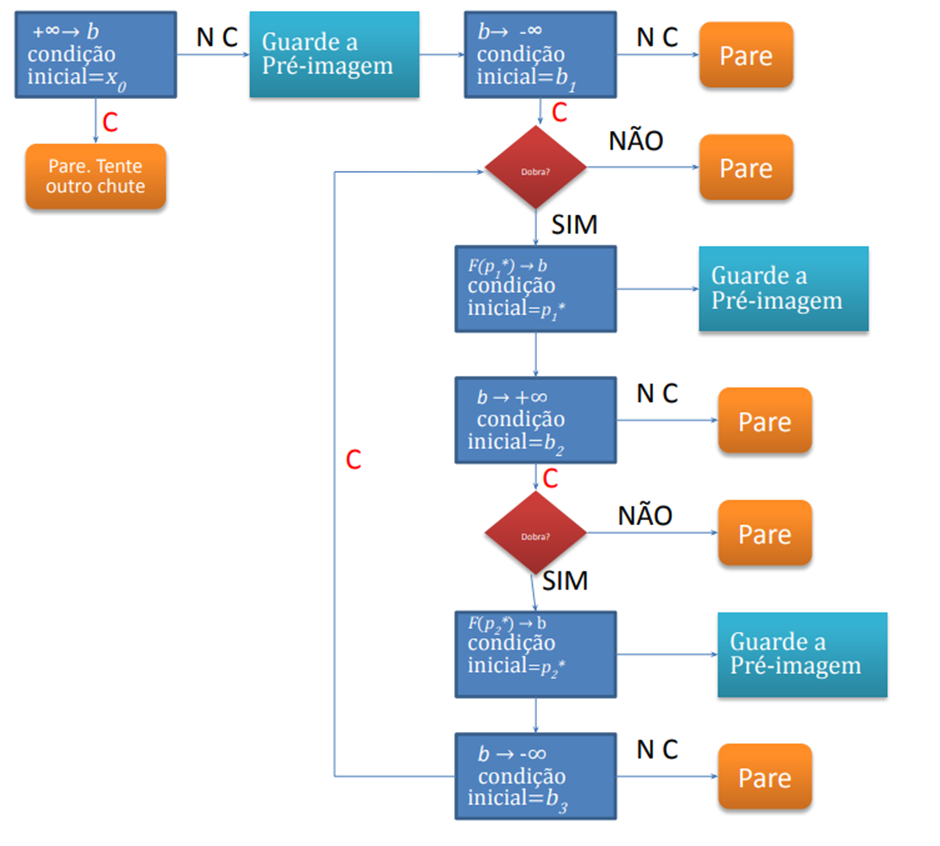
Figura 1.12: Fluxograma para o estudo de caso e construção das fibras unidimensionais.
Ressaltamos que apesar do fluxograma acima colocar como condições iniciais os pontos críticos (dobras), numericamente, devemos utilizar pontos em suas vizinhanças que estejam em componentes conexas distintas da apresentada na etapa anterior.
Estratégias numéricas
Uma forma de realizar a inversão de um segmento βi é discretizar o mesmo em relação a t, o chamado parâmetro de continuação e resolver em cada passo um sistema não-linear. O método aplicado por Kaminski(2016), conhecido na literatura como “Embedding Algoritm” (ALLGOWER, E. L.; GEORG, K.,1991), considera a solução convergida x_i em um passo t_j como a condição inicial para obter a solução no passo t(j+1). Para δt=t_(j+1)-t_j suficientemente pequeno é de se esperar que x_i esteja no raio de convergência do método utilizado para resolver o sistema, por exemplo pelo método de Newton. Entretanto, a necessidade de δt pequeno demanda um grande esforço computacional (ALLGOWER, E. L.; GEORG, K.,1991), a fim de diminuir tal efeito, buscaremos nos mover ao longo de β com os maiores passos possíveis .
Consideremos uma sequência de pontos igualmente espaçados t_i=i/n_ref , com 0 ≤ i ≤ n_ref e n_ref indicando o refinamento (número de pontos com i≠ 1) ao longo da combinação convexa, que descreve a homotopia. Começamos com n_ref = 1, se o método de Newton não convergir em um certo número de iterações fornecido pelo usuário, dobramos n_ref e recomeçamos o processo, de tal forma que as sequências geradas apresentem cada vez mais pontos na combinação convexa. Estabelecemos um valor limite para n_ref , por exemplo 210
Além da estratégia de passo adotada no método de continuação, precisamos também controlar o passo no método de Newton. Em suma, para resolvermosF(x)=b, o método de Newton consiste em um método iterativo onde passamos de uma solução aproximada x_i, para uma outra, supostamente, melhor em〖 x〗(i+1). Podemos descrever o processo iterativo por:
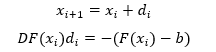
Para o caso em que DF(x_i) é não singular o passo d_i está bem definido, mas vale ressaltar que quando a matriz jacobiana é quase singular, a mesma pode nos levar a grandes incrementos d_i . Assim, se desejamos estudar pontos em uma vizinhança de um ponto crítico, torna-se necessário que tenhamos controle sobre d_i , de forma geral o passo é comumente normalizado. Assim, se ||d_i|| > ϵ||x_i||, atualizamos d_i = ϵ||x_i||d_i/ ||d_i|| , sendo ϵ um parâmetro fornecido pelo usuário. Para calcularmos DF(x_i), aproximamos as derivadas por quocientes de Newton.
Na figura 1.6, apresentamos uma situação em que o processo de inversão era interrompido em s_1 por nos aproximarmos de um ponto crítico p_1* . Numericamente, acompanhamos o sinal do determinante da jacobiana nas iterações de Newton, quando existe uma mudança de sinal, o processo é interrompido e devolve dois pontos s_1 e 〖s_2〗^~ em componentes conexas distintas “separadas” pelo conjunto crítico. Verificamos se 〖s_2〗^~ está próximo à reta r^~:s_1+mK com K=Nuc(DF(s_1)) e m ∈R, se sim conectamos 〖s_2〗^~ a r^~ chegando a um ponto 〖s_2〗^ e temos um intervalo 〖〖 [s〗_1,〖s_2〗^ 〗^ ], no qual uma aproximação do ponto crítico p_1* pertence. Aplicamos um método híbrido para calcular o zero do det(DF((1−q)〖 s〗_1+q〖 s〗_1)) com q ∈ [0, 1]. Conhecido na literatura como método de Brent, o mesmo combina bisseção, secante e interpolação quadrática inversa, o que nos permitiu aumentar a velocidade de convergência ao comparar com Kaminski (2016). Caso 〖s_2〗^~ esteja “longe” de r^~, o que não é de se esperar, uma vez que adotamos estratégias de passos, ainda assim, tentamos buscar um intervalo sobre a reta r^~, que nos permita calcular p_1* e obter 〖s_2〗^, para estendermos o processo de inversão. Por fim, mencionamos que o quase núcleo K é determinado através da decomposição SVD, por meio do uso de funções próprias do Matlab.
Considerações finais
O trabalho teve como objetivo apresentar um caminho possível para soluções de sistemas não lineares para uma classe de funções. A construção das fibras unidimensionais se torna um processo realístico para dimensões maiores que dois, uma vez que não depende da construção do conjunto crítico e sim da identificação de alguns pontos críticos.
A partir de um estudo de caso e por meio de uma compatibilidade de arcos a partir da geometria global da função, construímos uma extensão mais eficiente do que o método da saturação, uma vez que não depende do lançamento ou sorteio de diversas condições iniciais e sim da inversão de uma curva especial. Finalizamos o trabalho apresentando estratégias de passo para o método de continuação empregado por Kaminski(2016) e uma forma mais eficiente de obtermos aproximações de um ponto crítico, que foi o método de Brent.
Referências
ALLGOWER, E. L.; GEORG, K. Numerical continuation methods: an introduction. Springer-Verlag, New York, 1991.
BAKER, A., “Métodos Não Dedutivos em Matemática”, The Stanford Encyclopedia of Philosophy (edição de verão de 2020), Edward N. Zalta (ed. ), Disponível on-line em https://plato.stanford.edu/archives/sum2020/entries/mathematics-nondeceptive/.
CAL NETO, J. T. ; TOMEI, C. Numerical analysis of semilinear elliptic equations with finite spectral interaction. Journal of Mathematical Analysis and Applications, 395(1):63–77, 2012
KAMINSKI, O. Análise Numérica de Operadores Elípticos Semi–Lineares com Interação Espectral Finita, Tese, PUC–Rio, Rio de Janeiro, 2016.
MALTA, I. ; SALDANHA, N. C. ; TOMEI, C. Geometria e Análise Numérica de Funções do Plano no Plano. 19º Colóquio Brasileiro de Matemática, Impa, Rio de Janeiro, 1993
MALTA, I. ; SALDANHA, N. C. ; TOMEI, C. The numerical inversion of functions from the plane to the plane. Mathematics of Computation, 65(216):1531–1552, 1996.
Doutor em Matemática pela PUC-Rio
