REGISTRO DOI:10.5281/zenodo.10938750
Johnny Luís Mércuri
Abimael dos Santos Rodrigues
Bruna Karla Pereira de Souza Castro
Claudenice Teixeira Magalhães
Hammhwygem Tadach Araujo de Oliveira
Raimundo Laudemir dos Santos
RESUMO
O presente artigo tem por finalidade apresentar o método de interpolação de Lagrange, apresentando os conceitos e como obter o polinômio interpolador ao assumir n+1 pontos, mostrar na prática como gerar um polinômio de grau 2 assumindo 3 pontos conhecidos. E por fim, apresentar os resultados obtidos por BALZ e FENGLER, que utilizaram o método de interpolação de Lagrange a fim de analisar a resistência do concreto ao se aplicar uma compressão simples.
Palavra -chave: Interpolação de Lagrange, polinômio, método de interpolação
ABSTRACT
This article aims to present the Lagrange interpolation method, introducing its concepts and how to obtain the interpolating polynomial by assuming n+1 points. It demonstrates practically how to generate a polynomial of degree 2 by assuming 3 known points. Finally, it presents the results obtained by BALZ e FENGLER, who used the Lagrange interpolation method to analyze the resistance of concrete when subjected to simple compression.
Keyword: Lagrange interpolation, polynomial, interpolation method
1. INTRODUÇÃO
Em 1795 o matemático e físico Joseph Lagrange, publicou o método que levou seu nome, método interpolador de Lagrange, que basicamente consiste em estimar valores intermediários entre um conjunto discreto de pontos conhecidos por meio de um polinômio.
A aplicabilidade de tal método se estende a várias áreas, por exemplo, na computação gráfica renderizando curvas suaves, na modelagem matemática criando modelos com base em dados discretos e na engenharia ao gerar modelos para estimar o comportamento físico com base em dados experimentais.
Visto a gama de aplicações em diversas áreas do conhecimento, o presente artigo tem por objetivo apresentar o que é o método de interpolação de Lagrange, como obtê-lo ao assumir alguns valores e apresentar os resultados obtidos em um projeto de pesquisa desenvolvido na UNIJUI (Universidade Regional do Nordeste do Estado do Rio Grande do Sul), elaborado pelas alunas Andréia Balz e Sarah Blauth Fengler do curso de engenharia civil em 2016.
2. METODOLOGIA
O artigo baseou-se no estudo bibliográfico, usando como referência principal o livro publicado por RIGGIERO e LOPES em 2005, que tem como título “Cálculo Numérico: Aspectos teóricos e computacionais”.
Para gerar o gráfico do polinômio de grau 2, utilizou-se o software livre GeoGebra.
3. DESENVOLVIMENTO
Segundo (RUGGIERO; LOPES, 2005) interpolar uma função f(x) consiste em aproximar essa função por uma outra função g(x), escolhida entre uma classe de funções definida a priori e que satisfaça algumas propriedades. A função g(x) é então usada em substituição á função f(x). Logo, interpolar uma função é encontrar uma outra função que possa ser utilizada para representar a função buscada.
Ruggiero e Lopes (2005), apontam que a necessidade de se efetuar esta substituição surge em várias situações, por exemplo:
- Quando são conhecidos somente os valores numéricos de uma função para um conjunto de pontos e é necessário calcular o valor da função em um ponto não tabela.
- Quando uma função em estudo tem uma expressão tal que às operações como diferenciação e a integração são difíceis de serem realizadas.
Assim, Ruggiero e Lopes enfatizam que o método de interpolação se torna aplicável na obtenção de valores numéricos não conhecidos, visto que existem situações em que é inviável calcular todos os valores numéricos de uma função. Logo, ao se buscar esses valores não conhecidos, em um determinado intervalo, pode-se aplicar o método de interpolação e assim, obter valores que são razoavelmente aceitáveis.
Segundo (RUGGIERO; LOPES, pg.212, 2005), para se obter um polinômio interpolador, deve-se considerar (n+1) pontos distintos, assumiu-se x0, x1, … , xn, sendo esses os nós da interpolação, e os valores de f(x) nos respectivos pontos,
tendo assim as respectivas imagens f(x0), f(x1), … , f(xn).
Como interpolar uma determinada função f(x) é obter uma outra função, chamada g(x), que se aproxime da f(x) para todo xn do domínio, tem-se então o sistema a seguir.
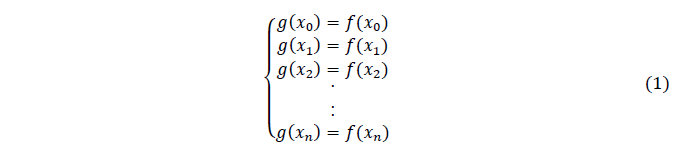
Uma concepção gráfica sobre o que é determinar um polinômio g(x) que possa ser utilizado para substituir a f(x) é apresentada a seguir, assumindo valores conhecidos x0, x1, x2, x3, x4, x5 e suas respectivas imagens f(x0), f(x1), f(x2), f(x3), f(x4), f(x5), onde g(x) é um polinômio de grau 4, como afirma (RUGGIERO; LOPES, 2005).
Figura 1 – Polinômio interpolador g(x)

Fonte: Imagem retirada do site: https://sites.google.com/site/calnumerico2016/lista-4/introducao
Assim, assumindo a priori que se conhece n+1 pontos, por meio desses valores aplicando o método de interpolação, obtém-se uma g(x) de grau n que pode ser utilizada para obter valores no intervalo [x0, xn].
3.1. O MÉTODO DE INTERPOLAÇÃO DE LAGRANGE
Sejam x0, x1, … , xn, (n+1) pontos distintos conhecidos pertencentes a uma função f e suas respectivas imagens. Tomando um polinômio pn(x) de grau menor ou igual a n para interpolar f nesses pontos, segundo (RUGGIERO; LOPES, pg.216, 2005) tem-se que pn(x) é expresso da seguinte forma.
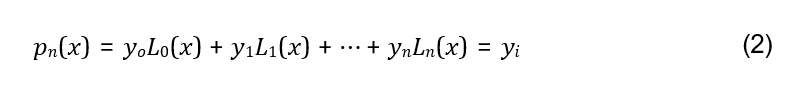
Onde os polinômios Lk(x) são de grau n. Para cada i, tem-se que a condição pn(xi) = yi seja satisfeita, tendo assim:
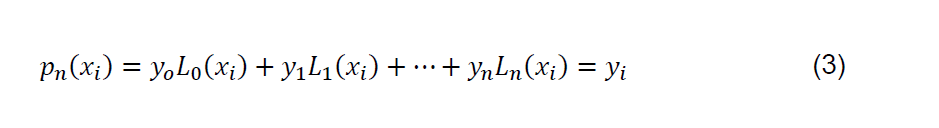
Por Ruggiero e Lopes (2005), a forma de satisfazer essa condição é impor:
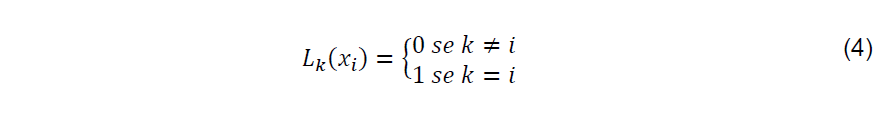
Tendo assim, Lk(x) da seguinte forma segundo (RUGGIERO; LOPES, 2005):
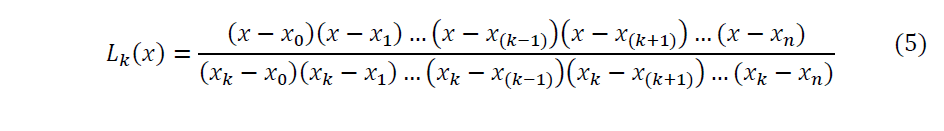
Portanto a forma de Lagrange para polinômio interpolador de acordo com (RUGGIERO; LOPES, pg.217, 2005):

3.2. APLICANDO LAGRANGE PARA UM POLINÔMIO DE GRAU 2
Assumindo os seguintes valores conhecidos, x0 = −1, x1 = 0 e x2 = 2 e suas respectivas imagens f(x0) = 4, f(x1) = 1 e f(x2) = −1. Buscou-se aplica o método de interpolação de Lagrange a fim de gerar o polinômio interpolador que passe pelos três pontos dados.
Como são 3 pontos conhecidos, o polinômio gerado será de grau 2, como aponta (RUGGIERO; LOPES, 2005), aplicando a expressão (3) para i = 0,1 e 2 tem- se o polinômio desejado a seguir.
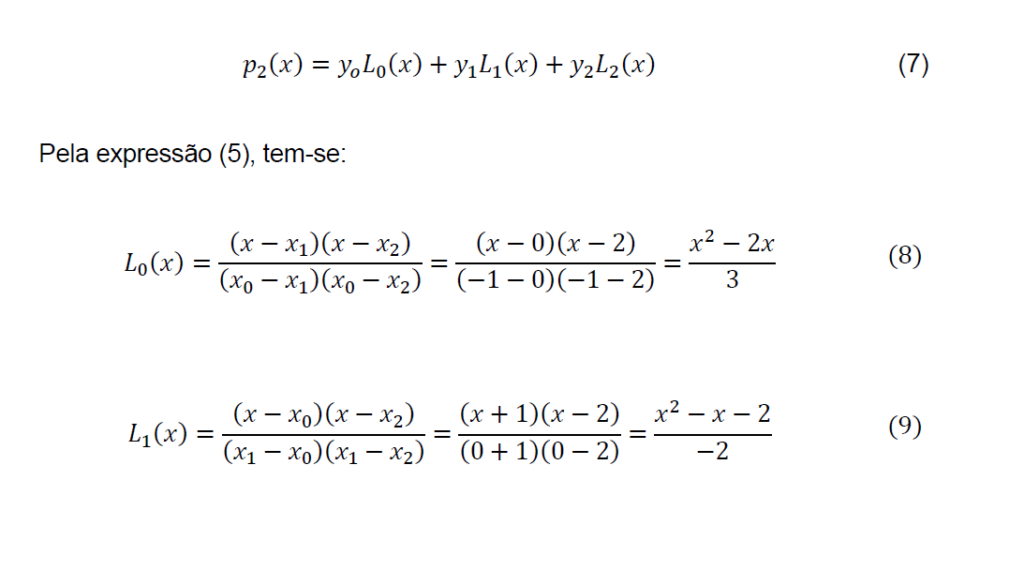

Substituindo o obtido em (8), (9) e (10) em (7), obtém-se a expressão a seguir:

Portanto, o polinômio interpolador obtido com base nos três valores apresentados é:
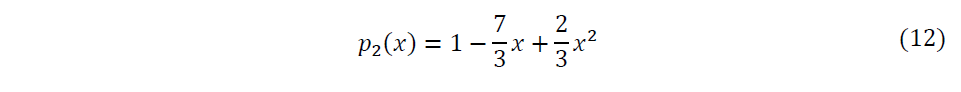
O gráfico do polinômio (12) obtido, após aplicar o método do polinômio interpolador é apresentado a seguir.
Figura 2 – Polinômio de grau 2 gerado
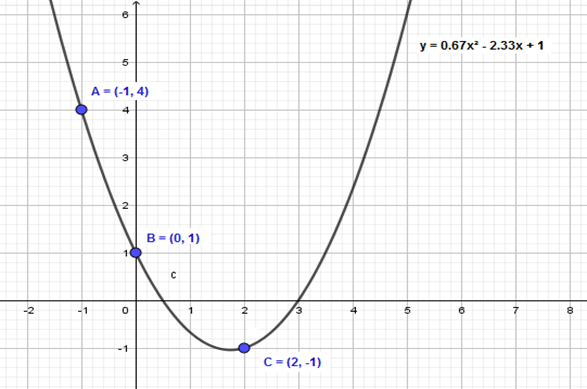
Fonte: Criado pelo autor usando o software livre GeoGebra
4. UMA APLICAÇÃO DO MÉTODO NA ENGENHARIA
Visto a gama de aplicações para o método de interpolação de Lagrange, apresentou-se a seguir os resultados obtidos em um projeto de pesquisa desenvolvido na UNIJUI (Universidade Regional do Nordeste do Estado do Rio Grande do Sul), elaborado pelas alunas Andréia Balz e Sarah Blauth Fengler do curso de engenharia civil.
O trabalho desenvolvido por BALZ e FENGLER, tem por objetivo analisar dados do ensaio de resistência à compressão simples do concreto apresentados no trabalho de conclusão de curso de Maíra Splendor Sganderla, desenvolvido no ano de 2015 e obter um polinômio para descrever os resultados obtidos.
Para isso, BALZ e FENGLER utilizaram o método de Lagrange para obter curvas que melhor condiziam com o ensaio à resistência à compressão do concreto com agregado graúdo reciclado, obtendo assim uma curva confiável, mas, que varia conforme o número de intervalos, sendo cada vez mais precisa conforme se aumenta o número de dados adicionados, visto que a adição de valores no método de interpolação torna o modelo gerado mais preciso, com aponta (RUGGIERO; LOPES, 2005).
Na análise dos dados, BALZ e FENGLER apontam que utilizaram o ensaio de resistência a compressão simples de três diferentes trações do concreto, sendo elas:
Traço 1: Concreto com uma dosagem padrão, sem a adição de agregado miúdo reciclado.
Traço 2: Concreto parcialmente substituído 20% de agregado miúdo natural por agregado miúdo reciclado.
Traço 3: Concreto parcialmente substituído 40% de agregado miúdo natural por agregado miúdo reciclado.
Onde obtiveram os resultados:
Tabela 1– Resultados apresentados por BALZ e FENGLER em 2016
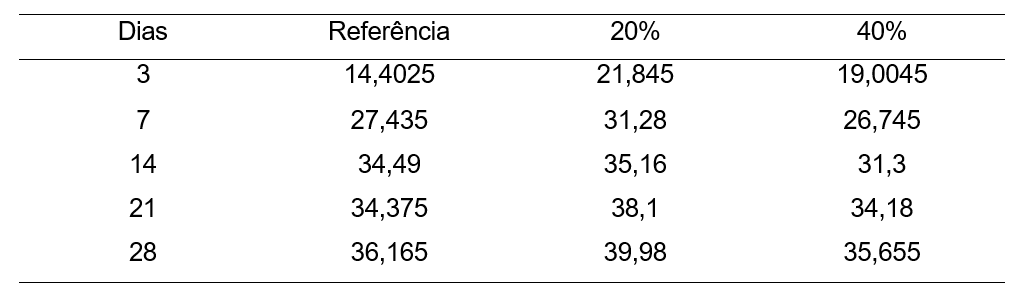
Fonte: Relatório técnico científico Balz, A; Fengler, S. B. Aplicação de Interpolação por Lagrangecom Agregado Miúdo Reciclado
Usando o software Matlab (Matrix Laboratory), Balz e Fengler obtiveram as seguintes curvas usando o método de interpolação de Lagrange.
Figura 3 – Modelo gerado por BALZ e FENGLER (Traço1)
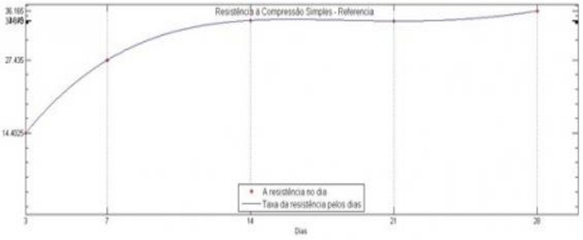
Fonte: Relatório técnico científico Balz, A; Fengler, S. B. Aplicação de Interpolação por Lagrange em Concreto com Agregado Miúdo Reciclado
Figura 4 – Modelo gerado por BALZ e FENGLER (Traço 2)
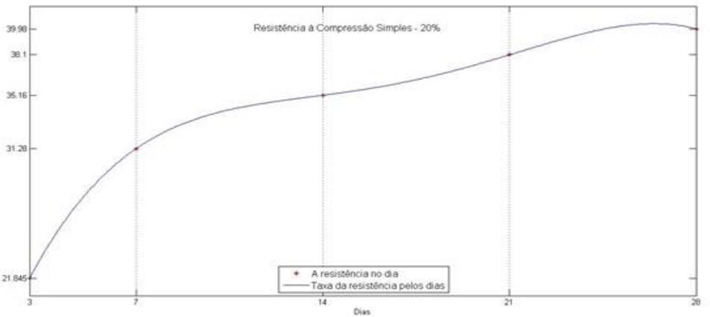
Fonte: Relatório técnico científico Balz, A; Fengler, S. B. Aplicação de Interpolação por Lagrange em Concreto com Agregado Miúdo Reciclado
Figura 5 – Modelo gerado por BALZ e FENGLER (Traço 3)

Fonte: Relatório técnico científico Balz, A; Fengler, S. B. Aplicação de Interpolação por Lagrange em Concreto com Agregado Miúdo Reciclado
Segundo BALZ e FENGLER (2016), nos ensaios de 20% e de 40% de agregado miúdo reciclado, pode-se perceber uma continuação de crescimento notável na resistência a partir dos 21 dias, mostrando o efeito consequente dos benefícios da adição deste componente. Logo, os autores conseguem concluir que a utilização de areia reciclada melhora a resistência à compressão, mas com um certo limite.
5. CONCLUSÃO
O método de interpolação de Lagrange é uma feramente bastante útil para obter valores desejados de uma determinada função, onde não se conhece todos esses valores. Para tal, deve se conhecer alguns valores e assim aplicar o método de interpolação para obter um polinômio interpolador e obter uma função próxima a função original desejada. Para gerar o modelo, dados n + 1 pontos o polinômio
interpolador resultante será de grau n.
Pode-se verificar que na engenharia o método de interpolação pode ser aplicado para analisar a resistência da compreensão no concreto, analisando a sua resistência ao variar a adição de agregado miúdo reciclado, onde essa resistência variando conforme a porcentagem desse agregado varia na mistura do concreto.
REFERÊNCIAS
Ruggiero, M. A. G; Lopes, V. L. R. Cálculo Numérico Aspectos Teóricos e Computacionais. IMECC— UNICAMP. 2°. ed. Editora: Pearson, Ano: 2005.
Balz, A; Fengler, S. B. Aplicação de Interpolação por Lagrange em Concreto com Agregado Miúdo Reciclado. UNIJUI — Salão do Conhecimento, Ano: 2016.
