ARTIFICIAL NEURAL NETWORKS AS AN ASSISTANT TOOL IN THE MANAGEMENT OF RHEUMATIC DISEASES
REGISTRO DOI: 10.69849/revistaft/cs10202411240642
Alexandre de Oliveira Tinoco Patricio
Bruno Zanelli Saraiva
Maezio Pereira da Silva
Resumo
As redes neurais artificiais (RNAs) começaram a ser estudadas por volta de 1940, porém com as limitações da época não era possível ter um conhecimento muito aprofundado e nem realizar tantos testes. Com os avanços tecnológicos e o crescimento das possibilidades, houve um aumento de interesse nesta área que vem se mostrando uma aliada em todas as áreas do conhecimento. Neste trabalho será mostrado uma série de pesquisas do uso das redes neurais no manejo das doenças reumatológicas, sendo possível observar o quanto elas evoluíram desde seu início e como podem auxiliar na área da saúde, tendo por um dos objetivos apresentar tanto as melhorias que podem ser obtidas quanto às limitações e os desafios para aplicação das RNAs. Foi realizada uma revisão da literatura para entender como a inteligência artificial pode auxiliar no tratamento destas doenças, e foi observado um avanço na medicina personalizada e tomadas de decisões mais precisas, possibilitando um tratamento individual e mais assertivo para cada paciente.
Palavras-chave: redes neurais artificiais, inteligência artificial, reumatologia.
1. Introdução
As doenças reumáticas estão classificadas pela 10ª revisão do Código Internacional de Doenças (CID-10) com a denominação “Doenças do Sistema Osteomuscular e do Tecido Conjuntivo” (SOCIEDADE BRASILEIRA DE REUMATOLOGIA, 2023). Bonetti, Souza e Resmini (2020) analisaram o perfil epidemiológico de pacientes atendidos no ambulatório de reumatologia das clínicas integradas de uma Universidade do Extremo Sul Catarinense no período de julho de 2016 até julho 2018 através de um estudo retrospectivo, descritivo, com coleta de dados secundários e de natureza quantitativa. Foram analisados 218 prontuários referentes às primeiras consultas do ambulatório de reumatologia. Os dados demográficos demonstraram maior prevalência do sexo feminino (83,5%), com média de idade de 55,9 anos e ensino fundamental incompleto (59,6%). As queixas principais que motivaram o agendamento de consulta foram artralgia/mialgia em 71,1% dos casos, seguido de dor axial em 18,8%; 18,3% para acompanhamento doença reumatológica já diagnosticada; queixas de artrite em 2,3% dos casos e 1,8% dos motivos eram em relação à alteração de exames laboratoriais. Nos pacientes previamente diagnosticados com doenças reumatológicas autoimunes, a maioria possuía Artrite Reumatoide (52,6%), seguido por 21,1% com Lúpus Eritematoso Sistêmico (LES).
Tabela 1. Resumo da epidemiologia das principais doenças reumáticas.
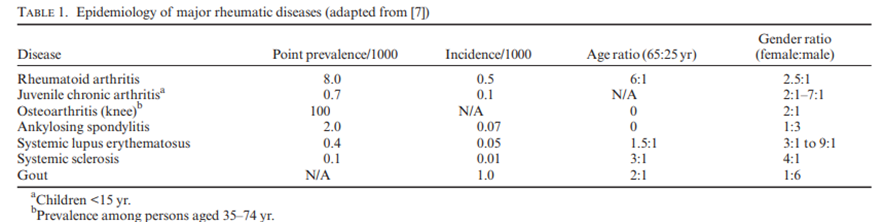
Fonte: O. Sangha (2000).
As doenças reumáticas estão divididas didaticamente em 6 grupos: artropatias, doenças sistêmicas do tecido conjuntivo, dorsopatias, transtornos dos tecidos moles, osteopatia, condropatias e outros transtornos do sistema osteomuscular e do tecido conjuntivo. Um aspecto relevante das doenças reumáticas sistêmicas é que a maioria não tem um teste patognomônico, isto é, sinal cuja presença é própria de uma única doença, e, portanto, o diagnóstico é um desafio e depende de um conjunto de manifestações clínicas, exames laboratoriais ou de imagem (SOCIEDADE BRASILEIRA DE REUMATOLOGIA, 2023).
Tecnologias emergentes como as redes neurais artificiais (RNAs) estão impactando significativamente a prática da reumatologia, ao oferecerem ferramentas avançadas para o manejo de doenças reumáticas. Demonstrando grande eficácia na avaliação da progressão e remissão de doenças (CHANDWAR & MISRA, 2024), as RNAs proporcionam um monitoramento mais preciso e individualizado dos pacientes. Além disso, sua integração em sistemas de diagnóstico por imagem melhora a capacidade dos profissionais de saúde em diagnosticar condições reumatológicas com maior precisão e agilidade. Essas inovações não apenas aprimoram o tratamento, mas também possibilitam novas abordagens diagnósticas e terapêuticas, beneficiando a qualidade dos cuidados oferecidos aos pacientes.
Popularmente conhecida como Inteligência Artificial (IA), as RNAs são sistemas computacionais inspirados na estrutura e no funcionamento do cérebro humano, projetados para reconhecer padrões, aprender com dados e tomar decisões de forma autônoma. Uma RNA de bom desempenho assume valores baixos em sua função perda, isto é, a diferença entre as previsões feitas por um modelo e os valores reais dos dados de treinamento. Para minimizá-la, utilizam-se técnicas como o gradient descent e suas variações (SGD e mini-batch), o algoritmo Adam, e métodos de regularização, como L1 e L2, que previnem overfitting. Outras abordagens incluem early stopping, que interrompe o treinamento para evitar perda de generalização, e dropout, cuja função é desativar aleatoriamente neurônios durante o treinamento para melhorar a robustez do modelo. Com o avanço da IA, essas redes têm desempenhado um papel cada vez mais significativo na sociedade, impactando diversas áreas como saúde, finanças, educação e entretenimento.
Diante do exposto, o presente trabalho objetiva elucidar o papel das RNAs como ferramenta auxiliar a especialidade médica da reumatologia.
2. Objetivos gerais
Revisar as principais bibliografias existentes sobre o uso de machine learning na especialidade médica da reumatologia
2.1 Objetivos específicos
- Analisar e revisar o estado da arte do uso de Redes Neurais Artificiais (RNAs) na reumatologia, com foco em sua aplicação no diagnóstico e no acompanhamento de doenças reumáticas.
- Identificar os principais desafios e limitações técnicas para a implementação de RNAs na prática clínica reumatológica.
- Investigar os impactos potenciais das RNAs no suporte à decisão médica, com ênfase em personalização e precisão do tratamento.
- Avaliar a aplicabilidade das RNAs em diferentes tipos de imagens médicas, como radiografias e ressonâncias magnéticas, para a detecção precoce e monitoramento de progressão de doenças reumáticas.
3. Fundamentação teórica ou revisão da literatura
Essa seção tem como objetivo elucidar os conceitos fundamentais sobre redes neurais artificiais e como ela vem sendo aplicada na reumatologia.
3.1 Redes neurais artificiais: uma breve história
O surgimento das RNAs deu-se com o modelo matemático do neurônio biológico proposto por Warren McCulloch e Walter Pitts em 1943. O modelo, denominado neurônio MCP (McCulloch-Pitts), é descrito por um conjunto de n entradas, as quais são multiplicadas por um determinado peso e, em seguida, os resultados são somados e comparados a um limiar. No ano de 1958 foi proposto um modelo de topologia de rede chamada MLP (Percéptrons de Múltiplas Camadas) criado por Frank Rosenblatt possibilitando um aumento de trabalhos nesta área, porém foi apresentada deficiencias e limitações neste modelo por Minsky e Papert, o que causou desinteresse na área que só voltou a ter interesse em 1982 através do trabalho de Hopfield (FLECK, 2016)
3.2 Tipos de redes neurais
As redes neurais podem ser definidas em 2 tipos segundo a forma de aprendizagem (MACEDO, 2021):
a) Aprendizado supervisionado: a RNA recebe uma saída desejada em relação ao padrão de entrada fornecido pelo supervisor tornando possível comparar a saída da RNA com a desejada e minimizar o erro de forma gradual.
b) Aprendizado não supervisionado: não tendo supervisor no processo de aprendizagem a RNA deve comparar as entradas buscando correlação ou redundância.
3.3 Tipos de função de ativação
As funções de ativação desempenham um papel crucial no treinamento de redes neurais, fornecendo a não linearidade essencial para que o modelo aprenda representações complexas. As funções de ativação mais comumente utilizadas podem ser divididas em duas categorias principais: funções lineares por partes e funções localmente quadráticas (RASAMOELINA; ADJAILIA & SINCAK, 2020).
Tabela 2. Propriedades das funções de ativação cruciais para o aprendizado

Fonte: Rasamoelina, Adjailia e Sincak (2020)
Os diferentes tipos de funções de ativação serão apresentados a seguir conforme descrito por Rasamoelina, Adjailia e Sincak (2020). As funções descritas pelos autores estão sumarizadas pela tabela abaixo.
Tabela 3. Sumário das funções de ativação

Fonte: Rasamoelina, Adjailia e Sincak (2020)
3.4 Funções de ativação lineares por partes
As funções de ativação lineares por partes é uma função composta de um número limitado de segmentos lineares definidos sobre um número igual de intervalos, usualmente de tamanhos iguais.
Exemplo de função de ativação linear por partes:
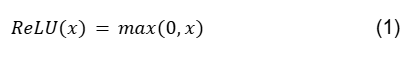
A principal característica desses tipos de funções de ativação é a ausência de curvatura em cada intervalo definido por seu ponto de inflexão, ou seja, possuem uma derivada de primeira ordem constante.
3.5 Funções de ativação localmente quadráticas
Qualquer função de ativação suave e não linear com derivada segunda diferente de zero é localmente quadrática.
Exemplos de função de ativação localmente quadrática:
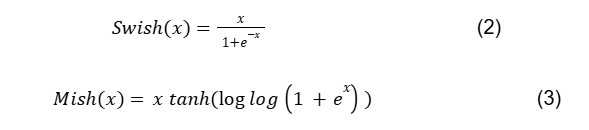
Uma função linear por partes que possui uma derivada segunda diferente de zero em pelo menos um intervalo também é uma função localmente quadrática.
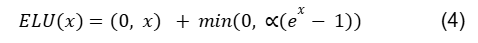
Esse comportamento torna a aproximação da função quadrática eficiente por qualquer rede neural que utilize esses tipos de ativação.
3.6 Função de ativação: sigmoide
A função de ativação sigmoide traduz o intervalo de entrada de (-8; +8) para o intervalo em [0; 1]. É não linear por natureza e possui uma derivada suave, conforme mostrado na figura 1.
Figura 1. Gráfico da função sigmoide e sua derivada
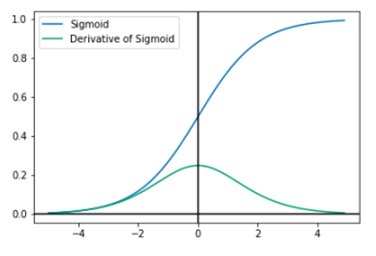
Fonte: Rasamoelina, Adjailia e Sincak (2020)
Devido ao intervalo de saída da sigmoide [0;1], a saída de cada unidade também é comprimida, causando o desaparecimento do gradiente, especialmente em uma rede profunda. Esse comportamento torna a rede muito difícil de otimizar e, após certo ponto, a função de ativação Sigmoide ou Logística é definida da seguinte forma:

O panorama de saída da função sigmoide é mostrado pela figura 2.
Figura 2. Panorama de saída da função sigmoide

Fonte: Rasamoelina, Adjailia e Sincak (2020)
3.7 Função de ativação: tangente hiperbólica
A função Tangente Hiperbólica possui uma estrutura muito similar à função Sigmoide. No entanto, ela comprime o valor de entrada no intervalo de [-1, +1]. A principal vantagem em relação à função sigmoide é que sua derivada é mais acentuada, como mostrado na figura 3, o que significa que pode obter mais valor.
Figura 3. Gráfico da função tangente hiperbólica e sua derivada

Fonte: Rasamoelina, Adjailia e Sincak (2020)
Apesar de ter um gradiente mais acentuado e devido ao seu valor de saída limitado, o gradiente tende a desaparecer com essa função, que pode ser definida por:
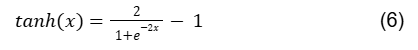
O panorama de saída da função Tangente Hiperbólica é mostrado na figura 4.
Figura 4. Panorama de saída da função tangente hiperbólica

Fonte: Rasamoelina, Adjailia e Sincak (2020)
3.8 Função de ativação: Rectified Linear Unit (ReLU)
A ReLU é a função de ativação mais utilizada entre praticantes e pesquisadores de deep learning. O sucesso da ReLU se baseia em seu desempenho superior em treinamento em comparação com outras funções de ativação, como a sigmoide logística e a tangente hiperbólica.
A função ReLU (Unidades Lineares Retificadas) é definida da seguinte forma:
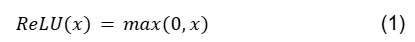
A ReLU é linear (identidade) para todos os valores positivos e zero para todos os valores negativos. No entanto, os valores de saída variam de 0 até o infinito. Uma das vantagens de usar a ReLU é sua simplicidade. Ela é capaz de gerar um valor zero verdadeiro, permitindo que a ativação das camadas ocultas em redes neurais contenha um ou mais valores zero verdadeiros, aumentando a esparsidade representacional da rede. A ReLU geralmente não é recomendada em Redes Neurais Recorrentes, pois elas podem ter saídas muito grandes e, portanto, são mais propensas a explodir do que funções de ativação com valores limitados.
A principal desvantagem da ReLU é que todos os valores negativos são transformados em zero. Esse problema é chamado de “dying ReLU” (ReLU morta). É um caso especial do problema do gradiente que desaparece. Assim, uma vez que o neurônio fica negativo, é improvável que ele se recupere. O panorama de saída da função ReLU é mostrado na figura 5, e a figura 6 mostra o gráfico da ReLU e sua derivada.
Figura 5. Panorama de saída da função ReLU
Fonte: Rasamoelina, Adjailia e Sincak (2020)
Figura 6. Gráfico da função tangente hiperbólica e sua derivada
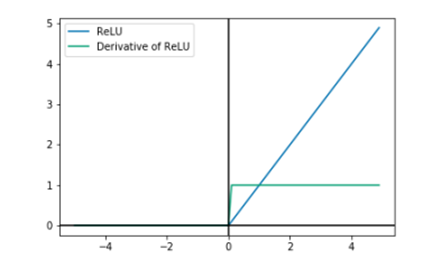
Fonte: Rasamoelina, Adjailia e Sincak (2020)
3.9 Função de ativação: Exponential Linear Unit
A ELU foi proposta pela primeira vez como uma melhoria em relação à ReLU. Foi demonstrado que ela leva a resultados de classificação superiores em comparação com a ReLU tradicional. Para x ≥ 0, segue a mesma regra da ReLU, e para x < 0, aumenta exponencialmente. Como mostrado na figura 7, a ELU se torna suavemente lenta até que sua saída seja igual a −1.
Figura 7. Gráfico da função ELU e sua derivada
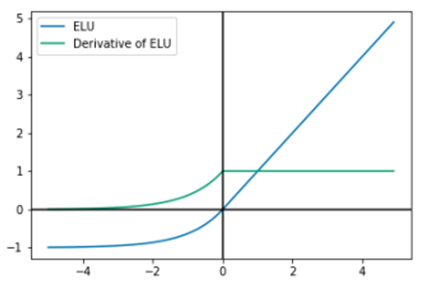
Fonte: Rasamoelina, Adjailia e Sincak (2020)
A principal melhoria da ELU em relação à ReLU é que ela é capaz de gerar valores negativos.
A função de ativação ELU é expressa por:
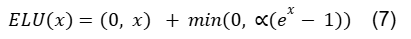
3.10 Método de otimização
Algoritmos de otimização são técnicas fundamentais no campo da ciência da computação e matemática aplicada, projetados para encontrar a melhor solução possível para um problema específico, dentro de um conjunto de restrições e condições. Otimização refere-se à tarefa de minimizar ou maximizar uma função f(x) alterando x. Geralmente, formulamos a maioria dos problemas de otimização em termos de minimizar f(x). A maximização pode ser realizada por meio de um algoritmo de minimização, minimizando −f(x). A função que queremos minimizar ou maximizar é chamada de função objetivo ou critério. Quando estamos minimizando, também podemos chamá-la de função de custo, função de perda. Frequentemente, denotamos o valor que minimiza ou maximiza uma função com um superscrito ∗. Por exemplo, podemos dizer x* = arg min f(x). (GOODFELLOW, BENGIO & COURVILLE, 2016). Esses algoritmos buscam melhorar o desempenho de sistemas e processos, maximizando ou minimizando funções objetivas, como custo, tempo ou eficiência. Dentre os algortimos de otimização, destacam-se:
3.11 Descida do gradiente
O método de descida do gradiente será apresentado a seguir conforme descrito por Goodfellow, I., Bengio, Y., & Courville, A. (2016).
A figura 8 mostra como o algoritmo de descida do gradiente utilizando as derivadas de uma função pode ser usado para seguir a função ladeira abaixo até um mínimo.
Figura 8. Descida do gradiente
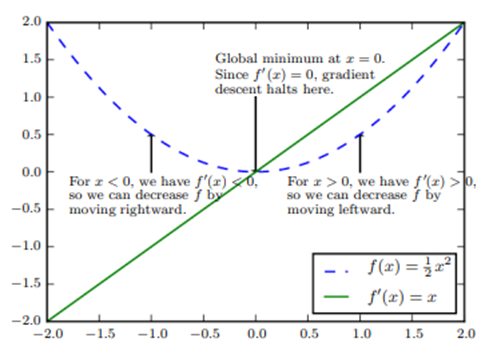
Fonte: Goodfellow, I., Bengio, Y., & Courville, A. (2016).
Suponha que temos uma função y=f(x), onde tanto x quanto y são números reais. A derivada dessa função é denotada como f'(x) ou ∂y∂x. A derivada f'(x) fornece a inclinação de f(x) no ponto x. Em outras palavras, ela especifica como escalonar uma pequena mudança na entrada para obter a mudança correspondente na saída: f(x+ϵ)≈f(x)+ϵf'(x).
A derivada é, portanto, útil para minimizar uma função porque nos informa como alterar x para fazer uma pequena melhoria em y. Por exemplo, sabemos que f(x-ϵsign(f'(x))) é menor que f(x) para valores pequenos o suficiente de . Podemos, assim, reduzir f(x) movendo x.
em pequenos passos na direção oposta ao sinal da derivada. Esta técnica é chamada de descida do gradiente. Sua importância reside na capacidade de ajustar iterativamente os parâmetros de um modelo para minimizar a função de custo, permitindo que o modelo aprenda padrões e faça previsões mais precisas. A técnica é amplamente utilizada em aprendizado de máquina e redes neurais profundas, além de ser aplicada em diversos campos como economia, física e engenharia para otimizar processos e resolver problemas complexos.
Quando f'(x) = 0, a derivada não fornece informações sobre em que direção se mover. Pontos onde f'(x) = 0 são conhecidos como pontos críticos ou pontos estacionários. Um ponto crítico é um ponto com inclinação zero. Tal ponto pode ser um mínimo local, que é mais baixo do que os pontos vizinhos; um máximo local, que é mais alto do que os pontos vizinhos; ou um ponto de sela, que tem vizinhos tanto mais altos quanto mais baixos do que o próprio ponto conforme a figura 9.
Figura 9. Exemplos de cada um dos três tipos de pontos críticos em 1-D.
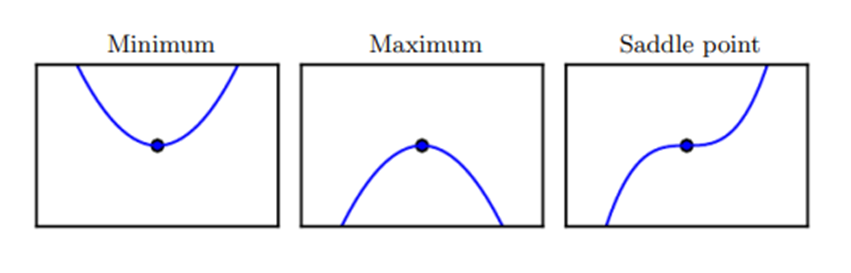
Fonte: Goodfellow, I., Bengio, Y., & Courville, A. (2016).
Um ponto que obtém o valor absoluto mais baixo de f(x) é um mínimo global. Pode haver um único mínimo global ou múltiplos mínimos globais de uma função. Também é possível que existam mínimos locais que não são globalmente ótimos. No contexto do aprendizado profundo, otimizamos funções que podem ter muitos mínimos locais não ótimos e muitos pontos de sela rodeados por regiões muito planas. Tudo isso torna a otimização muito difícil, especialmente quando a entrada da função é multidimensional. Portanto, geralmente buscamos encontrar um valor de f(x) que seja muito baixo, mas não necessariamente mínimo em um sentido formal.
Figura 10. Mínimos locais ou platôs presentes.
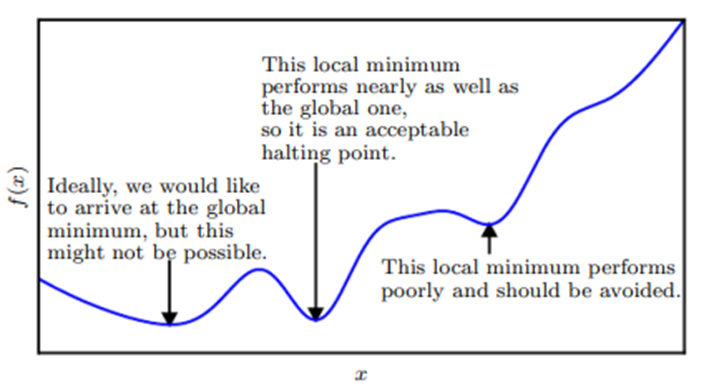
Fonte: Goodfellow, I., Bengio, Y., & Courville, A. (2016).
Frequentemente minimizamos funções que têm múltiplas entradas: f: Rn→ R. Para que o conceito de “minimização” faça sentido, ainda deve haver apenas uma saída (escalar).
Para funções com múltiplas entradas, devemos utilizar o conceito de derivadas parciais. A derivada parcial ∂xifx mede como f muda à medida que apenas a variável xi aumenta no ponto x. O gradiente generaliza a noção de derivada para o caso em que a derivada é em relação a um vetor: o gradiente de f é o vetor que contém as derivadas parciais denotado por xf(x). O elemento i do gradiente é a derivada parcial de f em relação a xi. Em múltiplas dimensões, pontos críticos são pontos onde cada elemento do gradiente é igual a zero.
A derivada direcional na direção u (um vetor unitário) é a inclinação da função f na direção u. Em outras palavras, a derivada direcional é a derivada da função f(x + au) em relação a a, avaliada em a = 0. Usando a regra da cadeia, podemos ver que ∂/∂af(x + au) avalia para uT∇x f (x) quando a = 0.
Para minimizar f, é preciso encontrar a direção na qual f diminui rapidamente. Podemos fazer isso usando a derivada direcional:
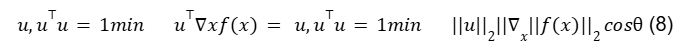
Onde é o ângulo entre u e o gradiente. Substituindo em llull2 = 1 e ignorando fatores que não dependem de u, isso se simplifica para minu cos 0. Isso é minimizado quando u aponta na direção oposta ao gradiente. Em outras palavras, o gradiente aponta diretamente para cima, e o gradiente negativo aponta diretamente para baixo. Podemos diminuir f movendo na direção do gradiente negativo. Isso é conhecido como o método da descida mais acentuada ou descida do gradiente.
A descida mais acentuada propõe um novo ponto:

Onde E é a taxa de aprendizado, um escalar positivo que determina o tamanho do passo. Podemos escolher E de várias maneiras diferentes. Uma abordagem comum é definir E como uma constante pequena. Às vezes, podemos resolver para o tamanho do passo que faz com que a derivada direcional se torne zero. Outra abordagem é avaliar f(x – Exf(x)) para vários valores de E e escolher aquele que resulta no menor valor da função objetivo. Essa última estratégia é chamada de busca em linha.
O método da descida mais acentuada converge quando cada elemento do gradiente é zero (ou, na prática, muito próximo de zero). Em alguns casos, podemos evitar a execução desse algoritmo interativo e pular diretamente para o ponto crítico resolvendo a equação xf(x) = 0 para x.
Embora o descenso do gradiente seja limitado à otimização em espaços contínuos, o conceito geral de fazer repetidamente um pequeno movimento (que é aproximadamente o melhor pequeno movimento) em direção a melhores configurações pode ser generalizado para espaços discretos. Subir uma função objetivo de parâmetros discretos é chamado de escalada de colina.
3.12 Diferenciação automática e o algoritmo back-propagation
De maneira geral, o campo da diferenciação automática preocupa-se com a forma de calcular derivadas de maneira algorítmica. Uma das abordagens para diferenciação automática é o algoritmo de retropropagação (GOODFELLOW, BENGIO & COURVILLE, 2016):
O algoritmo de retropropagação é muito simples. Para calcular o gradiente de um escalar z em relação a um de seus predecessores x no gráfico, começamos observando que o gradiente em relação a z é dado por ∂z∂z=1. Podemos então calcular o gradiente em relação a cada pai de z no gráfico multiplicando o gradiente atual pelo Jacobiano da operação que produziu z. Continuamos multiplicando pelos Jacobianos enquanto percorremos o gráfico para trás até chegarmos a x. Para qualquer nó que possa ser alcançado ao retroceder de z através de dois ou mais caminhos, simplesmente somamos os gradientes que chegam de diferentes caminhos a esse nó (GOODFELLOW, BENGIO & COURVILLE, 2016).
O algoritmo de retropropagação é uma aplicação direta da programação dinâmica. Ele contém duas fases principais, conhecidas como as fases direta e reversa, respectivamente.
Na fase direta, as entradas de uma instância de treinamento são alimentadas na rede neural. Isso resulta em uma cascata direta de cálculos através das camadas, usando o conjunto atual de pesos. A saída prevista final pode ser comparada com a da instância de treinamento e a derivada da função de perda em relação à saída é calculada. A derivada dessa perda agora precisa ser calculada em relação aos pesos em todas as camadas na fase reversa.
O principal objetivo da fase reversa é aprender o gradiente da função de perda em relação aos diferentes pesos, utilizando a regra da cadeia do cálculo diferencial. Esses gradientes são usados para atualizar os pesos. Como esses gradientes são aprendidos na direção reversa, começando do nó de saída, esse processo de aprendizado é conhecido como fase reversa.
A fase direta é necessária para calcular os valores de saída e as derivadas locais em vários nós, e a fase reversa é necessária para acumular os produtos desses valores locais ao longo de todos os caminhos do nó até a saída (AGGARWAL, 2018).
O esquemático de um algoritmo de retropropagação é ilustrado pela figura 11.
Figura 11. Algoritmo de retropropagação.
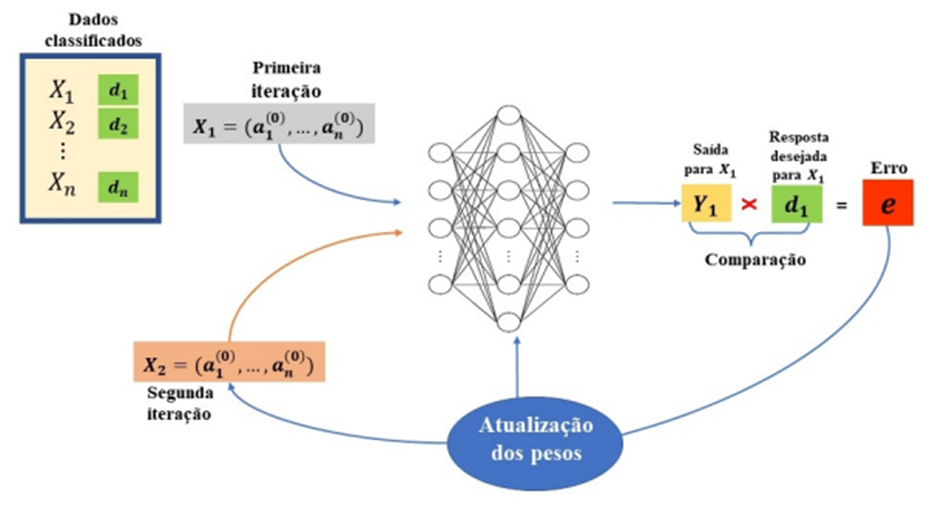
Fonte: Silva (2022).
3.13 Função perda
O treinamento de uma rede neural consiste em minimizar as funções perda, que são os erros ou problemas que podem ocorrer no processo de aprendizagem. Desta forma otimizando este treinamento para que ele ocorra de uma forma mais rápida e eficaz (VALLE, 2021). Quanto menor a perda de uma função, mais precisa ela se torna. (MICROSOFT, 2019)
3.14 Limitações
As RNAs apresentam algumas limitações como redes que utilizam o método backpropagation que são conhecidas como “caixas pretas”, pois não apresentam justificativas para suas respostas. O tempo de treinamento nas redes que utilizam backpropagation é lento na maioria das vezes, isto dificulta a escolha de uma arquitetura ideal de RNA para cumprir exatamente o propósito determinado de modo que seja grande o suficiente para atender a quantidade de informações desejadas, mas em uma medida ideal para que tenha um rápido aprendizado (ANDRE, 2024) (FLECK,2016).
4. Metodologia
Foi utilizado uma revisão da literatura a fim de responder como a inteligência artificial pode ser usada como ferramenta auxiliar no tratamento de doenças reumáticas. A estratégia de busca baseou-se na síntese quantitativa de artigos sobre o tema em bases de dados revisadas por pares, aplicando-se operadores booleanos nos descritores de pesquisa e ferramentas de filtragem. O presente trabalho foi realizado de acordo com as recomendações do Statement Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA).
4.1 Estratégias de busca
A pesquisa foi conduzida em setembro de 2024 nas bases de dados PubMed e Oxford Academic. Foi utilizado os seguintes descritores “Artificial neural networks”, “Artificial Intelligence” e “Rheumatology”, onde foram aplicados operadores booleanos para formar os tesauros ilustrados na figura 12.
Figura 12. Tesauros utilizados na busca dos dados

Fonte: o autor (2024)
4.2 Triagem
Após a busca, as referências de cada banco de dados foram exportadas para o programa Mendeley® (https://www.mendeley.com/), com o objetivo de identificar todos os artigos duplicados, promover uma maior confiabilidade na seleção e avançar para a etapa de elegibilidade dos artigos.
4.3 Critérios de elegibilidade e de exclusão
Critérios de exclusão/filtragem: estudos fora do período de 2019 a 2024, exceto por estudos incluídos em versões prévias deste artigo. Estudos em línguas diferentes da portuguesa ou inglesa. Estudos com metodologia inadequada ou não descrita com clareza. Não adequação ao tema. Estudos com amostras muito pequenas para resultados confiáveis ou com poder estatístico insuficiente para detectar o efeito desejado. Dados incompletos, inconsistentes ou com alto risco de viés.
4.4 Resultados e discussões ou análise dos dados
Durante o processo de seleção dos artigos, após a exclusão inicial dos que não se enquadram no escopo desta revisão, a análise prosseguiu com a leitura dos títulos e resumos dos artigos remanescentes. Os artigos que atenderam aos critérios de inclusão e não violaram os critérios de exclusão foram então lidos na íntegra.
4.5 Resultados
A presente seção está a discutir os resultados obtidos a partir das pesquisas identificadas pela metodologia.
4.6 Resumo da pesquisa
Ao utilizar as estratégias de busca, um total de 1296 publicações foram identificadas. Após eliminar 2 trabalhos duplicados, 305 trabalhos fora do período estabelecido, 4 trabalhos em línguas diferentes daquelas duas admitidas e 787 trabalhos que não se enquadram no formato de revisão ou pesquisa, 198 obras foram selecionadas para análise por título e resumo. Após a leitura dos títulos e resumos desses artigos, 180 estudos foram excluídos, de acordo com os critérios de seleção estabelecidos, e 18 artigos foram selecionados para leitura completa. Após a leitura, 5 publicações foram excluídas. Finalmente, 13 artigos completos incluídos na análise qualitativa. Todo o processo de seleção de artigos é descrito na figura 13, que mostra os diagramas de fluxo PRISMA para inclusão.
Figura 13. fluxograma PRISMA©
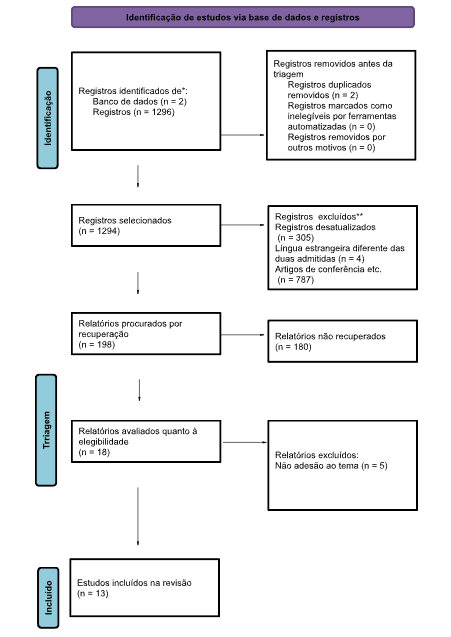
Fonte: o autor (2024)
5. O que a IA, de fato, significa para a reumatologia?
A maioria dos profissionais de saúde e pacientes está ciente do verificador de sintomas no Google. Ao simplesmente inserir um conjunto de sintomas em um mecanismo de busca, as pessoas podem receber uma variedade de diagnósticos potenciais e obter uma compreensão preliminar do seu problema (CHINNADURAI et al., 2023). A capacidade de uma máquina aprender culmina em aplicações diversas.
A figura 14 elucida os potenciais usos da IA em reumatologia.
Figura 14. Aplicações potenciais da Inteligência Artificial na reumatologia

Fonte: Chandwar & Misra (2024)
Além disso, modelos de linguagem como GPT-4 e LLaMA têm grande potencial na reumatologia, auxiliando na atualização de profissionais com as pesquisas mais recentes, criando materiais educativos personalizados para pacientes e automatizando tarefas administrativas. Além disso, com ajuste e validação adequados, podem ser usados em ferramentas de apoio à decisão, ajudando no diagnóstico e tratamento de doenças reumáticas complexas (VENERITO et al., 2023).
5.1 IA na pesquisa reumatológica
Madrid-García et al. (2023) investigaram clínica e tecnicamente o escopo das doenças reumáticas e musculoesqueléticas que empregam técnicas de IA na pesquisa. Os autores descobriram que a maioria dos dados que envolvem o uso de IA na reumatologia estão focados nas doenças de osteoartrite, artrite reumatoide e lúpus eritematoso sistêmico, das quais se extraem as seguintes hipóteses:
- A artrite reumatoide é a doença autoimune sistêmica mais prevalente entre as doenças reumáticas inflamatórias musculoesqueléticas, enquanto a prevalência da osteoartrite é notável, sendo uma das principais causas de incapacidade.
- Como as imagens médicas podem ser usadas para diagnosticar e quantificar o estado e a progressão de uma doença, especialmente na osteoartrite, a visão computacional e os algoritmos de DL podem ter atraído pesquisadores, com especial interesse nessas técnicas.
Além disso, a PCA, a redução de dimensionalidade e o Lasso, técnicas de seleção de variáveis, parecem ser altamente populares. Por outro lado, as técnicas de mineração de dados possibilitaram o estudo e a caracterização de doenças raras de uma maneira diferente, obtendo informações valiosas e revelando novos padrões que provavelmente não teriam sido descobertos de outra forma. Por exemplo, técnicas de aprendizado não supervisionado, e mais concretamente a clusterização, foram decisivas na caracterização de subgrupos de doenças. Além disso, alguns grupos de pesquisa reconheceram o potencial dessas técnicas e as adotaram como ferramentas relevantes para extração de conhecimento ao estudar a patologia de doenças específicas (MADRID-GARCÍA et al., 2023).
A IA pode analisar estruturas químicas de antibióticos para prever sensibilidade e resistência, permitindo a escolha das melhores combinações com estabilidade e menor resistência. Isso reduz tempo e custo no desenvolvimento de antibióticos e também acelera a medicina de precisão e terapias direcionadas. Na reumatologia, a IA pode agrupar pacientes com dados de genômica, proteômica e metabolômica para otimizar tratamentos, testar a eficácia e segurança de medicamentos em modelos virtuais e favorecer o desenvolvimento de anticorpos monoclonais, promovendo avanços em medicina personalizada (CHINNADURAI et al., 2023).
Por fim, Chandwar & Misra (2024), apontam potenciais usos da inteligência artificial na otimização da conduta de pesquisa, planejamento, escrita de protocolos e manuscritos médicos, trabalhos administrativos, aconselhamento de pacientes e educação médica.
5.2 IA no processamento de imagens
O aprendizado de máquina, especialmente com redes neurais convolucionais, tem melhorado significativamente a interpretação de imagens na radiologia musculoesquelética (HUGLE et al., 2020). A radiografia é o padrão-ouro para a avaliação de danos estruturais nas articulações (JIANG et al., 2021). Para analisar imagens com maior eficácia e eficiência, considerável esforço tem sido dedicado ao desenvolvimento de métodos de IA para realizar processamento de imagens. Somente recentemente, no entanto, esses métodos automatizados alcançaram uma precisão que iguala ou até supera o desempenho humano em áreas específicas, como na classificação de lesões cutâneas e na detecção de retinopatia diabética (STOEL, 2020). A figura 15 ilustra a detecção baseada em deep learning da vascularização pulmonar arterial e venosa. (A) Secção transversal sagital de um pulmão direito em uma tomografia computadorizada (TC) de tórax; (B) detecção de todas as linhas centrais dos vasos pulmonares; (C) classificação em artérias (vermelho) e veias (azul) por deep learning.
Figura 15. Aplicações potenciais da Inteligência Artificial na reumatologia: classificação de artérias e veias de TC por DL
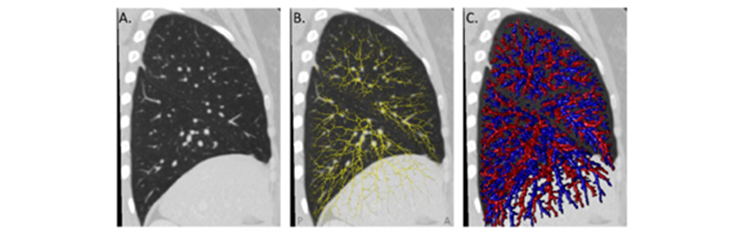
Fonte: Stoel (2020)
A análise de imagens por IA cai sobre o Deep Learning (CHANDWAR & MISRA, 2024). Estudos recentes demonstraram que o uso de redes neurais convolucionais (CNNs) para analisar imagens adquiridas por smartphones foi eficaz na detecção de artrite ativa nas articulações das mãos de pacientes com artrite reumatoide (AR), com acurácia variando entre 62% e 84%, dependendo da articulação. Além disso, a análise de dados de marcha através de câmeras infravermelhas, também com CNNs, mostrou uma AUC superior a 70% para diagnosticar anormalidades de marcha. A ultrassonografia de articulações inflamadas, realizada por robôs, foi considerada tão eficaz quanto a feita por humanos, sendo bem aceita pelos pacientes. O aprendizado profundo também tem sido aplicado na geração de imagens sintéticas de tomografia computadorizada (CT) a partir de dados de ressonância magnética (MRI), melhorando a precisão no diagnóstico de erosões e anquilose em espondiloartropatia, com precisão comparável às imagens de CT reais. Essas técnicas também foram exploradas para detectar anormalidades em grandes vasos em pacientes com vasculite, ajudando a distinguir essa condição da aterosclerose (CHANDWAR & MISRA, 2024).
A interpretação automática pode ajudar os médicos na prática clínica, facilitando a detecção de lesões e áreas de interesse, como em mapas de calor apresentados na figura 16 (HUGLE et al., 2020).
Figura 16. Mapa de calor de uma radiografia de mão indicando regiões de alta atenção para OA.
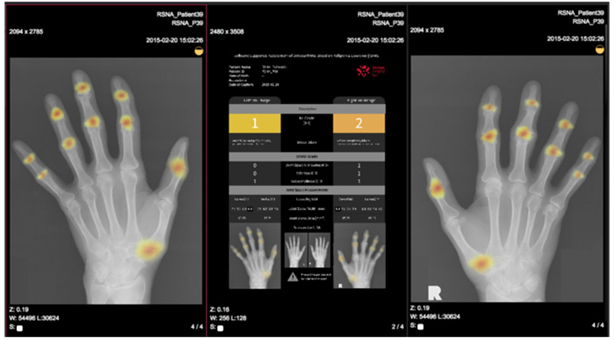
Fonte: Hugle et al. (2020)
Isso é particularmente útil para avaliações quantitativas, que seriam demoradas e caras se feitas manualmente. O aprendizado de máquina oferece uma forma mais rápida, prática e confiável de realizar essas avaliações, com destaque para sua aplicação em distúrbios reumatológicos (HUGLE et al., 2020).
5.3 IA e microscopia
O aprendizado profundo facilita a análise rápida de modalidades de imagem experimental de alto conteúdo, incluindo a microscopia multiplexada. Essa refere-se ao uso de dados de imagem em que a distribuição espacial de múltiplos marcadores biológicos, como proteínas de superfície celular, é capturada por meio de análise de imunohistoquímica ou imunofluorescência. Anteriormente, esse tipo de dado era analisado manualmente ou utilizado apenas para apresentar exemplos representativos de fenômenos biológicos. As redes neurais convolucionais profundas (DCNNs) têm sido particularmente úteis para automatizar a segmentação e classificação de regiões, estruturas e células em tecidos (DURKEE et al., 2021).
Uma aplicação fundamental do aprendizado de máquina na microscopia de tecidos é a automação da identificação de estruturas e células individuais em imagens. A segmentação celular é realizada por meio do treinamento interativo de algoritmos de visualização computacional baseados em IA (DURKEE et al., 2021).
Figura 17. Algoritmos de visão computacional supervisionados por IA são treinados usando dados de referência manual para alcançar segmentações celulares precisas em um domínio específico de imagens (à esquerda). Um algoritmo treinado pode então ser usado para extrair automaticamente características quantitativas de dados de microscopia, respondendo a questões relacionadas à clínica e à biologia (à direita).
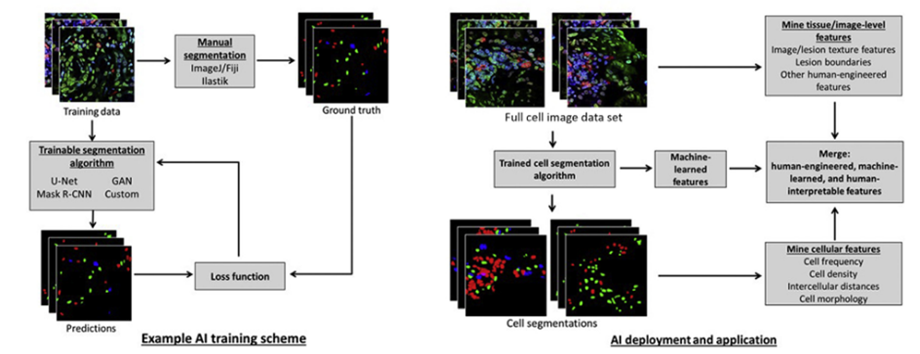
Fonte: Durkee et al (2021)
Esses modelos treinados podem então ser usados para prever a segmentação celular em novos dados, permitindo a mineração em larga escala de descritores quantitativos da patologia tecidual. A automação da classificação de imagens e detecção de células facilita a análise em grande escala, especialmente na microscopia multiplexada. Ferramentas de código aberto tornam essas tecnologias mais acessíveis. A extração de características por meio de aprendizado de máquina pode fornecer novos insights sobre ambientes celulares relacionados a doenças. Contudo, a aplicação de métodos de aprendizado de máquina requer atenção a considerações experimentais para garantir a geração de conjuntos de dados robustos e significativos (DURKEE et al., 2021).
5.4 IA e ressonância magnética
A IA demonstra um considerável potencial no uso de ressonância magnética (MRI) na reumatologia, com possíveis aplicações no diagnóstico, classificação e manejo de doenças. Ao utilizar o poder dos algoritmos de IA para analisar dados complexos de imagens, como os de MRI, os clínicos podem tomar decisões mais informadas e oferecer planos de tratamento personalizados para pacientes com doenças reumáticas (ADAMS et al., 2023). Ademais, ao olharmos para o futuro, a aplicação de IA em ressonância magnética (MRI) na reumatologia demonstra potencial, mas há espaço para avanços. Algoritmos de IA aprimorados, como aprendizado profundo e por reforço, podem aumentar a precisão da análise de MRI, identificando sinais sutis de doenças reumáticas. A integração de dados de MRI com informações genéticas e clínicas pode aprimorar o diagnóstico e tratamento. Análises longitudinais de MRI oferecem insights sobre a progressão da doença, permitindo monitoramento mais preciso e intervenções oportunas (ADAMS et al., 2023).
5.5 Aprendizado de máquina, aprendizado profundo e reumatologia
Modelos preditivos de aprendizado de máquina podem dizer o curso de doenças reumáticas como a remissão ou progressão das mesmas (CHANDWAR & MISRA, 2024). O aprendizado profundo é uma técnica importante e promissora na medicina, especialmente na reumatologia, com potencial para melhorar a eficiência clínica e gerar novos conhecimentos, como na análise de dados não estruturados (textos e imagens) (MCMASTER et al., 2020). Aprendizado de máquina também se faz presente na análise de dados ômicos (genômica, transcriptômica e proteômica), que fundamentalmente envolve de centenas a milhares de dados. A análise transcriptômica de sangue total de pacientes com síndrome de Sjögren, utilizando aprendizado de máquina, ajudou a identificar potenciais biomarcadores da doença, bem como a identificar novos alvos terapêuticos em potencial, utilizando docking molecular. A análise de dados de metabolômica do soro de pacientes com gota, utilizando aprendizado de máquina, foi capaz de identificar metabólitos que poderiam prever crises de gota (CHANDWAR & MISRA, 2024).
Avanços na biologia molecular, juntamente com o aprendizado de máquina usando o AlphaFold, um modelo baseado em redes neurais artificiais, ajudaram a prever com precisão a estrutura tridimensional de proteínas a partir de sequências de aminoácidos. Isso tem o potencial de auxiliar no desenvolvimento de novos alvos terapêuticos ou na reorientação de alvos terapêuticos existentes, com base em uma melhor compreensão da patogênese. De forma semelhante, outro modelo de aprendizado de máquina, o AlphaMissense, foi capaz de caracterizar se mutações genéticas tinham ou não significância patogênica (CHANDWAR & MISRA, 2024).
5.6 IAs funcionalizadas a doenças específicas
Medicina de precisão e inteligência artificial estão intimamente ligadas, especialmente quando as redes neurais são funcionalizadas ao tratamento de uma doença específica. Na artrite reumatoide a RNA pode ser utilizada para a predição de riscos, diagnóstico, atividade da doença/progressão por imagens, resposta terapêutica e comorbidades (SHI et al., 2024).
Gilvaz e Reginato (2023) discutem o impacto da inteligência artificial (IA) no manejo da artrite reumatoide (AR), uma doença autoimune complexa e comum. Com o aumento dos registros digitais de saúde e dados de diagnóstico, a IA, especialmente com aprendizado de máquina (ML) e aprendizado profundo, permite novas abordagens para melhorar o diagnóstico, monitorar a progressão e prever a resposta a tratamentos na AR. Modelos de ML e redes neurais convolucionais têm mostrado alta precisão na identificação de pacientes com AR, classificação de subtipos de doenças e monitoramento de flares (exacerbações) por meio de dados de atividade. No tratamento, a IA auxilia na escolha de terapias personalizadas e na previsão de respostas, contribuindo para uma medicina mais eficaz. No entanto, desafios como acesso limitado a dados, complexidade interpretativa dos modelos e regulamentação restrita ainda impedem a adoção ampla de IA na reumatologia. Ceccarelli et al. (20) explora o potencial do aprendizado de máquina (ML) no manejo do Lúpus Eritematoso Sistêmico (LES), uma doença autoimune com manifestações clínicas e imunológicas complexas. O uso de modelos de ML pode melhorar diagnósticos, prever manifestações específicas (como nefrite lúpica) e facilitar tratamentos personalizados, especialmente em áreas de maior risco de lesão crônica e complicações, como envolvimento renal e neurológico. Além disso, os modelos podem estratificar pacientes com base na atividade da doença e nos perfis imunológicos, ajudando a personalizar as intervenções médicas e prever respostas terapêuticas. Contudo, são destacadas limitações, como a necessidade de validações internas e externas, para que esses modelos sejam aplicados na prática clínica de forma confiável e replicável
5.7 IA na educação médica e do paciente
A IA pode mudar a forma como a educação médica é transmitida, acessada e aplicada. Integrar a IA pode ajudar a analisar os padrões de aprendizado de um indivíduo e adaptar o conteúdo conforme seu tempo e necessidades. A IA pode avaliar os pontos fortes e fracos do profissional para criar módulos de aprendizado que imitem cenários da vida real. Além disso, o currículo médico pode precisar de uma reformulação para incluir a IA e facilitar que os estudantes lidem com essa nova ferramenta com confiança (CHINNADURAI et al., 2023). Ferramentas de IA generativa como ChatGPT 4 também podem fornecer informações educacionais aos pacientes em poucos minutos. A capacidade de personalizar informações dependendo da doença do paciente, de seu nível educacional e de seu contexto geográfico faz com que a IA se destaque em relação ao mecanismo de busca tradicional do Google. Isso ajudaria os clínicos a redigir respostas para as perguntas dos pacientes, permitindo uma gestão mais eficaz do tempo com melhor consistência (CHINNADURAI et al., 2023).
5.8 Detecção e estratificação da doença
O aprendizado de máquina está sendo cada vez mais aplicado aos prontuários eletrônicos de saúde em várias áreas médicas, pois eles contêm grandes e heterogêneos conjuntos de dados que podem ser usados para treinar métodos de detecção ou classificação de doenças com técnicas de aprendizado supervisionado. Até o momento, muitas abordagens de detecção de doenças em reumatologia têm utilizado SVMs ou random forests para realizar classificação (HUGLE et al., 2020).
5.9 Predição quanto a progressão da doença
Dado que o desenvolvimento de uma doença a longo prazo pode ser influenciado por muitos fatores imprevistos, a previsão da progressão da doença é muito mais complexa do que a detecção da doença. No entanto, o aprendizado de máquina pode ser usado para desenvolver modelos de previsão de doenças, que são de grande interesse para a escolha de tratamentos ou intervalos de consulta (HUGLE et al., 2020).
6. Conclusão
O uso de Redes Neurais Artificiais (RNAs) em doenças reumáticas representa um avanço significativo na medicina personalizada e na tomada de decisões clínicas mais precisas. As RNAs têm o potencial de melhorar o diagnóstico, monitorar a progressão da doença e prever a resposta ao tratamento, possibilitando um cuidado mais individualizado para os pacientes. Apesar das inúmeras oportunidades, há desafios a serem superados, como o acesso a conjuntos de dados robustos, a complexidade dos modelos e a necessidade de validação clínica antes de sua adoção generalizada. Conclui-se que, com um desenvolvimento contínuo e a resolução de desafios técnicos, as RNAs poderão se tornar uma ferramenta crucial para o aprimoramento da prática clínica em reumatologia, impactando positivamente tanto os profissionais de saúde quanto os pacientes.
REFERÊNCIAS
SOCIEDADE BRASILEIRA DE REUMATOLOGIA. *Livro da Sociedade Brasileira de Reumatologia*. 3. ed. São Paulo: Editora Manole, 2023.
O. Sangha, Epidemiology of rheumatic diseases, Rheumatology, Volume 39, Issue suppl_2, December 2000, Pages 3–12, https://doi.org/10.1093/rheumatology/39.suppl_2.3.
Rasamoelina, A. D., Adjailia, F., & Sincak, P. (2020). A Review of Activation Function for Artificial Neural Network. 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI). doi:10.1109/sami48414.2020.9108717
BONETTI, DÉBORA F.; DE SOUZA, LUCAS; RESMINI, MARCUS B.; Avaliação do perfil epidemiológico de pacientes atendidos no ambulatório de reumatologia das clínicas integradas de uma universidade. Revista Saúde (Sta. Maria). 2020; 46 (1).
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press. ISBN: 978-0262035613.
AGGARWAL, Charu C. Neural Networks and Deep Learning: A Textbook. [S.l.]: Springer, 2018.
SILVA, José Jorge de Souza. O algoritmo de retropropagação. 2022. Trabalho de Conclusão de Curso.
Chandwar K, Prasanna Misra D. What does artificial intelligence mean in rheumatology? Arch Rheumatol. 2024 Feb 12;39(1):1-9. doi: 10.46497/ArchRheumatol.2024.10664. PMID: 38774703; PMCID: PMC11104749.
Madrid-García A, Merino-Barbancho B, Rodríguez-González A, Fernández-Gutiérrez B, Rodríguez-Rodríguez L, Menasalvas-Ruiz E. Understanding the role and adoption of artificial intelligence techniques in rheumatology research: An in-depth review of the literature. Semin Arthritis Rheum. 2023 Aug;61:152213. doi: 10.1016/j.semarthrit.2023.152213. Epub 2023 May 30. PMID: 37315379.
Adams LC, Bressem KK, Ziegeler K, Vahldiek JL, Poddubnyy D. Artificial intelligence to analyze magnetic resonance imaging in rheumatology. Joint Bone Spine. 2024 May;91(3):105651. doi: 10.1016/j.jbspin.2023.105651. Epub 2023 Oct 4. PMID: 37797827.
Stoel B. Use of artificial intelligence in imaging in rheumatology – current status and future perspectives. RMD Open. 2020 Jan;6(1):e001063. doi: 10.1136/rmdopen-2019-001063. PMID: 31958283; PMCID: PMC6999690.
Shi Y, Zhou M, Chang C, Jiang P, Wei K, Zhao J, Shan Y, Zheng Y, Zhao F, Lv X, Guo S, Wang F and He D (2024) Advancing precision rheumatology: applications of machine learning for rheumatoid arthritis management. Front. Immunol. 15:1409555. doi: 10.3389/fimmu.2024.1409555
Venerito V, Bilgin E, Iannone F, Kiraz S. AI am a rheumatologist: a practical primer to large language models for rheumatologists. Rheumatology (Oxford). 2023 Oct 3;62(10):3256-3260. doi: 10.1093/rheumatology/kead291. PMID: 37307079; PMCID: PMC10547503.
Durkee MS, Abraham R, Clark MR, Giger ML. Artificial Intelligence and Cellular Segmentation in Tissue Microscopy Images. Am J Pathol. 2021 Oct;191(10):1693-1701. doi: 10.1016/j.ajpath.2021.05.022. Epub 2021 Jun 12. PMID: 34129842; PMCID: PMC8485056.
FLECK, Leandro et al. Redes neurais artificiais: Princípios básicos. Revista Eletrônica Científica Inovação e Tecnologia, v. 1, n. 13, p. 47-57, 2016.
MACEDO, F.S. Estratégia de otimização de processos com o uso de redes neurais artificiais.Dissertação (Pós-Graduação em Engenharia Química) -Universidade Federal Fluminense,2021.
ANDRE. MLP: Multilayer Perceptron. Instituto de Ciências Matemáticas e de Computação (ICMC), 2000. Disponível em: https://sites.icmc.usp.br/andre/research/neural/MLP.htm. Acesso em: 5 nov. 2024.
VALLE, Leonardo de. Redes neurais artificiais. 2021. Disponível em: https://www.ime.unicamp.br/~valle/Teaching/MS571/Aula%2015%20–%20Redes%20Neurais%20Artificiais.pdf. Acesso em: 5 nov. 2024.
MICROSOFT. Artificially Intelligent: How Do Neural Networks Learn? MSDN Magazine, abril de 2019. Disponível em: https://learn.microsoft.com/pt-br/archive/msdn-magazine/2019/april/artificially-intelligent-how-do-neural-networks-learn. Acesso em: 05 nov. 2024.
Chinnadurai S, Mahadevan S, Navaneethakrishnan B, Mamadapur M. Decoding Applications of Artificial Intelligence in Rheumatology. Cureus. 2023 Sep 28;15(9):e46164. doi: 10.7759/cureus.46164. PMID: 37905264; PMCID: PMC10613315.
Hügle M, Omoumi P, van Laar JM, Boedecker J, Hügle T. Applied machine learning and artificial intelligence in rheumatology. Rheumatol Adv Pract. 2020 Feb 19;4(1):rkaa005. doi: 10.1093/rap/rkaa005. PMID: 32296743; PMCID: PMC7151725.
McMaster C, Bird A, Liew DFL, Buchanan RR, Owen CE, Chapman WW, Pires DEV. Artificial Intelligence and Deep Learning for Rheumatologists. Arthritis Rheumatol. 2022 Dec;74(12):1893-1905. doi: 10.1002/art.42296. Epub 2022 Oct 26. PMID: 35857865; PMCID: PMC10092842.
Jiang M, Li Y, Jiang C, Zhao L, Zhang X, Lipsky PE. Machine Learning in Rheumatic Diseases. Clin Rev Allergy Immunol. 2021 Feb;60(1):96-110. doi: 10.1007/s12016-020-08805-6. PMID: 32681407.
Gilvaz VJ, Reginato AM. Artificial intelligence in rheumatoid arthritis: potential applications and future implications. Front Med (Lausanne). 2023 Nov 16;10:1280312. doi: 10.3389/fmed.2023.1280312. PMID: 38034534; PMCID: PMC10687464.
Ceccarelli F, Natalucci F, Picciariello L, Ciancarella C, Dolcini G, Gattamelata A, Alessandri C, Conti F. Application of Machine Learning Models in Systemic Lupus Erythematosus. Int J Mol Sci. 2023 Feb 24;24(5):4514. doi: 10.3390/ijms24054514. PMID: 36901945; PMCID: PMC10003088.
