PREDICTION OF STOCK CLOSING PRICES USING LSTM NEURAL NETWORKS
REGISTRO DOI: 10.5281/zenodo.10182843
Diego Maximo Albuquerque1
Gabriel Hiemisch Ribeiro Cordeiro2
Herbert Feliciano Beserra3
Mateus Borba Cavalcanti dos Santos4
Paulo Sérgio Silva de Oliveira5
Victor Leme Beltran6
Orientadores: Geise Dioneia de Albuquerque Saunier7
Nelson Augusto Oliveira de Aguiar8
RESUMO
Este artigo tem como objetivo investigar o uso de ‘Long Short Term Memory’ (LSTM) para prever o preço de fechamento de uma ação do mercado financeiro. Devido a sua memória e a sua repetição de execução, as LSTMs são uma classe de redes neurais adequadas para lidar com dados sequenciais, como séries temporais de preços de ações. Este estudo busca avaliar o desempenho dessas redes no contexto de predição de preços de ações e então entender sua eficácia. Para atingir esse objetivo, utilizou-se técnicas de aprendizado de máquina com foco nas LSTMs e implementou-se o experimento usando bibliotecas de Python, como por exemplo o Pytorch e Onnx.
Palavras-chave: Inteligência artificial. Mercado financeiro. Redes neurais.
- INTRODUÇÃO
No cenário atual de avanços tecnológicos e da globalização, as bolsas de valores tornaram-se espaços cruciais para a economia mundial. O fluxo dinâmico de transações e a imprevisibilidade inerente ao mercado acionário têm desafiado investidores e analistas na busca por estratégias mais precisas de previsão.
Para a análise de valores de ativos financeiros, existem diversos métodos propostos, desde simulações de Monte-Carlo, método de Black-Scholes, regressões lineares, até o uso de redes neurais recorrentes. Para o presente estudo, são utilizadas redes neurais recorrentes do tipo LSTM (Long Short Term Memory) em combinação com camadas fully connected para a predição de valores de fechamento futuro de ações, dado um breve histórico de precificação destas ações (MACUKOW, 2016) (HOCHREITER, SCHMIDHUBER, 1997).
Pretende-se com este artigo, analisar o desempenho de LSTM’s, na análise de ações americanas, em termos de seu custo computacional e assertividade.
- FUNDAMENTAÇÃO TEÓRICA
O uso de Redes Neurais para previsão de ações em um período de curto prazo vem se provando eficaz, mas ao mesmo tempo incerta por conta da aleatoriedade e ruído dos dados (MACUKOW, 2016) (Malkiel, 1970). No que tange o conceito de Redes Neurais e seus diversos tipos com a finalidade de predição de preço de ações em um curto prazo, tem sido feitos estudos que, utilizam diferentes técnicas como, por exemplo, ANN (Artificial Neural Networks), como CNN (Convolutional Neural Networks), Multilayer perceptron, RNN (Recurrent Neural Networks) e LSTM (Long Short Term Memory) (LOSHCHILOV, HUTTER, 2019) ( SHEN, SHANFIQ, 2020) (KIM, HAN, 2000). Além do uso de redes neurais, regressões baseadas em outros métodos de Machine Learning, como SVM, também têm sido utilizadas e com resultados melhores do que os obtidos por meio de multi layer perceptron em alguns cenários (HOCHREITER, SCHMIDHUBER, 1997) (Ince, 2008). Em geral, os trabalhos recentes estudam diferentes métodos de extração e extensão de features afim de tornar os métodos existentes mais precisos, dando luz à modelos híbridos como, por exemplo, a utilização de uma combinação entre CNN e LSTM na qual a CNN realiza uma extração automática de features baseadas em dados quantitativos enquanto a LSTM preserva a série temporal das features para um retorno dos lucros (GOOGLE, 2023). Outro exemplo de extensão de features é o modelo baseado em LSTM proposto em, que enriquece os dados por meio do uso de análise de sentimento em redes sociais (STEWART, 2023) (VARGAS, 2022).
A Arquitetura LSTM
O modelo desenvolvido se utiliza de dois tipos de camadas de redes neurais, sendo LSTM’s e camadas totalmente conectadas de neurônios. A escolha de LSTM’s se deve ao fato de se trabalhar com uma sequência de valores em uma série temporal os quais devem ser lembrados e considerados de acordo com um certo nível de relevância para a inferência. Uma alternativa seria o uso de RNN’s, porém dada a possibilidade de problemas de gradiente devido à profundidade da rede proposta e a complexidade do problema, LSTM’s se apresenta como uma alternativa mais viável, apesar do maior custo computacional (HOCHREITER, SCHMIDHUBER, 1997).
Neurônios do tipo LSTM são compostos por chaveamentos internos, sendo eles porta de esquecimento, porta de entrada e de saída. O processo de aprendizado é ilustrado na Figura 1.
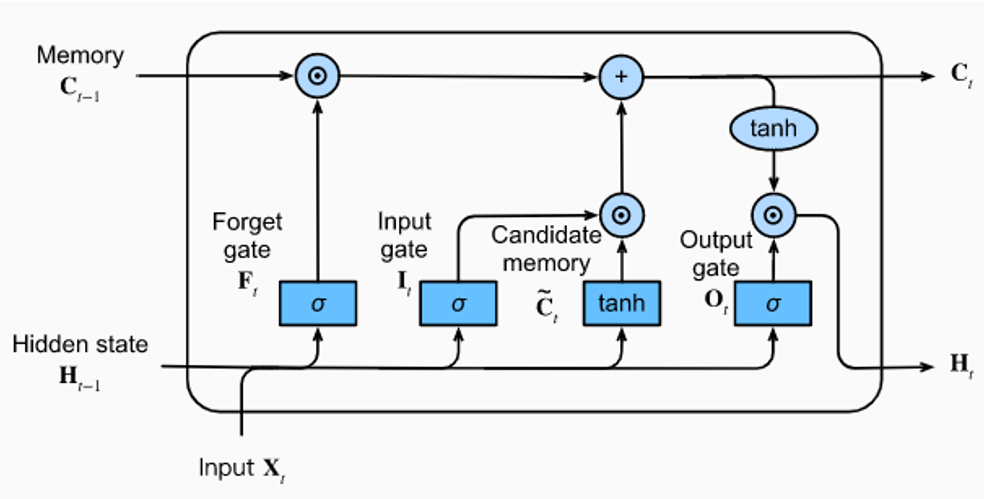
Figura 1 – LSTM (Long Short Term Memory). Adaptado de (DIVE INTO DEEP LEARNING, 2023)
A base da LSTM é a célula de memória, que é um estado que se faz presente por todas as operações no fluxo, tendo somente alguns pontos de interação lineares por meio das portas de esquecimento, de saída e de entrada. As portas, em geral, são basicamente compostas por uma função de ativação, seguido de uma operação pontual com a memória (HOCHREITER, SCHMIDHUBER, 1997).
O primeiro passo em um forward pass em uma LSTM é decidir quais informações serão dispensadas da memória. Isto é definido pela
porta de esquecimento, que é definida por uma ativação sigmoidal, seguida de um produto com a memória, sendo formalmente definida como:
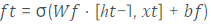
equaçãoAdaptado1 de (HOCHREITER,SCHMIDHUBER, 1997)
O próximo passo é decidir quais novas informações serão adicionadas à célula de memória. Este passo é composto por duas partes, sendo a primeira uma ativação sigmoidal, que é combinada com um vetor de candidatos que poderá ser adicionado à memória. A representação formal matemática pode ser verificada na equação 2 e equação 3.
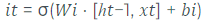
equação. Adaptado2 de (HOCHREITER,SCHMIDHUBER, 1997)
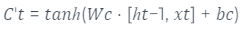
equaçãoAdaptado3 de (HOCHREITER,SCHMIDHUBER, 1997)
Feito isto, será realizada a atualização da célula de memória que é descrita pela equação 4.
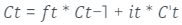
equaçãoAdaptado4 de (HOCHREITER,SCHMIDHUBER, 1997)
Por fim, é gerado a saída final da célula por meio da porta de saída. Esta por sua vez é definida por meio de uma sigmoidal que decide quais partes do estado da célula estará sendo enviado para saída e uma ativação tanh que é aplicada nos valores da célula de memória. Com ambos os valores, ou seja, a saída da sigmóide e da tanh, realiza-se a multiplicação destes e se obtém a saída final. Isto é definido pelas equações 5 e 6.
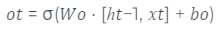
equação 5Adaptado de (HOCHREITER,SCHMIDHUBER, 1997)

equação 6Adaptado de (HOCHREITER,SCHMIDHUBER, 1997)
Pode-se observar que LSTM’s são uma proposta bastante interessante para a aplicação em questão, pois são capazes de reter memória de dados relevantes e ao mesmo tempo descartar dados que são considerados irrelevantes de sua memória por meio do chaveamento, tendo portanto uma capacidade para contextualização de dados em uma série temporal e até mesmo uma capacidade de discernir sobre os dados mais e menos importantes em um dado contexto.
Para criação do modelo utilizamos tecnologias como aprendizado supervisionado uma variante do aprendizado de máquina que nos possibilitou analisar historicamente as bases de dados, descobrir padrões e reduzir os riscos. Foi utilizado a linguagem Python por sua popularidade, facilidade de uso e principalmente por suas bibliotecas como, Pandas que auxilia a manipular os dados e processá-los, Pytorch para criação, treinamento e testes de redes neurais, Scikit-learn (sklearn) por facilitar no desenvolvimento nos fornecendo funções e algoritmos reutilizáveis de sua API, Numpy por ser uma biblioteca com desempenho alto para processamento e análise de dados e CUDA que possibilitou cálculos e processamento dos dados paralelamente utilizando os núcleos da GPU por meio de aceleração de hardware.
- O MODELO
A rede neural criada para o estudo é composta por 8 camadas de LSTM com input de um vetor unidimensional de 25 valores, correspondendo aos valores de fechamento da ação em análise nos prévios 25 dias; seguidos de uma camada de 64 neurônios completamente conectadas, à uma outra camada de 64, que por sua vez se conectam à uma de 32, e esta que então se conecta à um único neurônio de saída da rede, que retorna um valor de 0 à 1 correspondente ao valor normalizado previsto para a ação. A Figura 3 demonstra a estrutura da Rede Neural.

Figura 3 – Rede Neural utilizada.
- TREINAMENTO
Para o treinamento da rede foi utilizado uma base histórica de 30 papéis de diferentes empresas do mercado de ações americano, com dados diários de valores de fechamento dessas ações pelo período de 10 anos. No total foram aproximadamente 68 mil registros únicos, os quais foram separados 90% para treinamento e 10% para teste.
Os dados recebem um tratamento de normalização, a fim de colocar todas as entradas em uma mesma escala de 0 à 1, conforme um minMaxScaler do scikitlearn e após isto, as sequências de 25 registros foram randomizadas para evitar overfit durante o treinamento ou algum comportamento anômalo devido às sequências utilizadas no treinamento.
Como função de Loss do modelo foi utilizado a MSE (Mean Squared Error), que é uma medida quadrática de o quanto o modelo erra em suas predições em relação ao valor real e para otimizador de taxa de aprendizado foi utilizado AdamW (LOSHCHILOV, HUTTER, 2019) (STEWART, 2023) (GOOGLE, 2023). O treinamento foi composto por 100 épocas em batches de 1000 registros com uma learning rate inicial de 0.001.
A Loss do modelo ao longo do treinamento é como descrita na figura 4, atingindo o valor de 0,000276 ao fim do treinamento, sendo devido à suavização do gráfico abaixo representado com o valor de 0,000142.
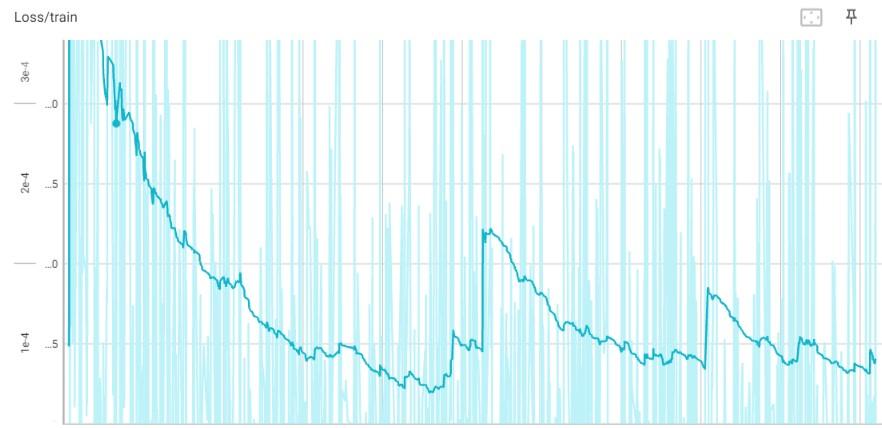
Figura 4: Gráfico de loss ao longo do tempo.
Durante a etapa de teste , a Loss ficou ao final com o valor de 0,000259, porém, devido à suavização do gráfico para melhor visualização, o valor representado é de 0,000182, conforme pode ser visualizado na Figura 5.
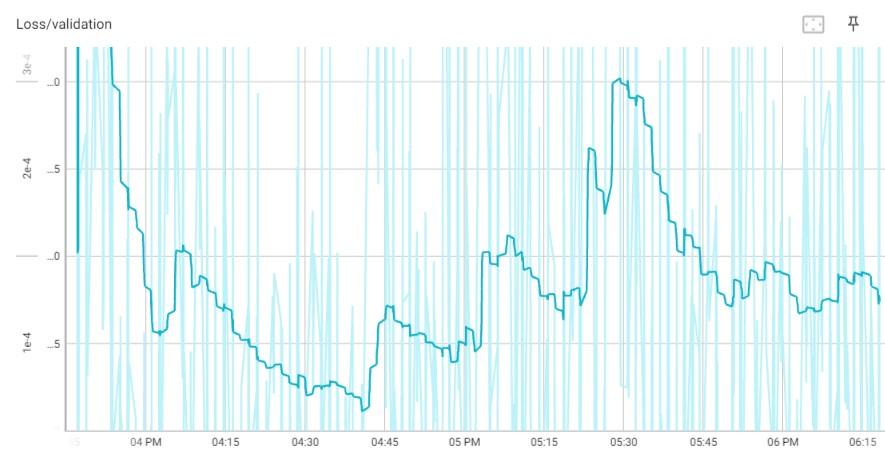
Figura 5: Gráfico de loss ao longo do tempo.
Vale ressaltar que para a medida de Loss em um modelo, quanto mais próximo de 0 o valor, melhor. Logo, no caso do modelo em questão, a métrica de Loss se apresenta promissora, pois está muito próxima do valor ideal de 0 e com uma diferença pequena entre a Loss de teste e de treino, indicando que não houve um overfit do modelo para o set de treino, ou seja, este detém um bom grau de generalização.
- VALIDAÇÃO DE RESULTADOS
Para a aferição do desempenho do modelo, foram calculadas as métricas de MAE, RMSE e R² (SCHNEIDER, XHAFA, 2022) (CHRISTIE, NEIL, 2022) (NEVIL, 2023). Sendo calculadas, para diversos cenários, tanto onde o modelo já havia visualizado os dados, como em cenários onde os dados nunca antes haviam sido vistos pelo modelo.
Durante a avaliação do modelo, para um cenário de sequências temporais independentes, ou seja, múltiplos casos de inferência onde os insumos não são relacionados entre diferentes inferências na batch, mas que já haviam sido visualizados durante o treinamento foi obtido as seguintes métricas:
Tabela 1 – Cálculo de métricas
Métricas Valor MAE 0.00653 RMSE 0.00921 R² 0.99834
Como referência, as métricas de MAE e RMSE são diferentes modos de medir o nível de erro do valor predito pelo modelo em relação ao valor real. Portanto, para o caso destas métricas, quanto mais próximo de 0, melhor o resultado obtido pelo modelo.
A métrica de R² no entanto é o que se denomina por coeficiente de determinação, está por sua vez é uma métrica capaz de determinar o quão bem correlacionado são os valores, sendo para o caso do modelo, o quão próximos e correlatos são os valores preditos e os valores reais das ações. Esta métrica diferentemente das anteriores utilizadas, têm como valor ideal, 1, indicando perfeita correlação entre os valores preditos e valores reais da ação, enquanto 0, indica que não há qualquer correlação entre os valores preditos e os reais.
Durante a avaliação de uma sequência temporal com dados reais de ações, em um período de 8 anos, para uma ação nunca antes vista, as métricas obtidas foram as seguintes:
Tabela 2 – Cálculo de métricas
Métricas Valor MAE 0.02635 RMSE 0.03753 R² 0.99574
Além da validação por métricas, foi realizado o estudo de comparação entre o desempenho de ganhos financeiros do modelo contra um caso randômico que presume a venda e compra de ações de maneira consecutiva, sem qualquer discernimento. A validação de ganhos financeiros será composta por uma comparação entre o quão mais seguro se torna o investimento se for baseado no modelo, comparado ao randômico, bem como o nível de lucro obtido nas transações.
Para estabelecer-se uma métrica de segurança, é utilizado a seguinte equação:
equação 7
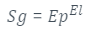
Onde “sg” seria a métrica de segurança, El, o número de eventos de lucro dado o período temporal e Ep, o número de eventos de prejuízo no mesmo período analisado. Deste modo, é possível medir o quão mais provável é que se obtenha lucro em relação ao caso randômico.
Para o cálculo de lucro obtido pelo uso do modelo, se respeitará a lógica que, caso o valor futuro previsto seja inferior ao presente, não é realizada a compra da ação. Caso o valor seja superior ao do presente dia, a compra é efetuada e no dia seguinte, se presume que a ação seja vendida e se é calculado o faturamento obtido, seja lucro ou prejuízo e somado ao montante final. Ao final do processamento da série temporal, é obtido o lucro ou prejuízo para o caso de uso do modelo.
Com a finalidade de metrificar o comportamento do modelo em cenários reais, são utilizados três cenários diferentes. O primeiro cenário se trata de um de alta do preço da ação, ou seja, será analisado um período onde a ação em uma perspectiva geral, tende a subir. Como referência, será utilizada a ação da Electronic Arts (EA). Para este primeiro cenário foram obtidos os seguintes valores:
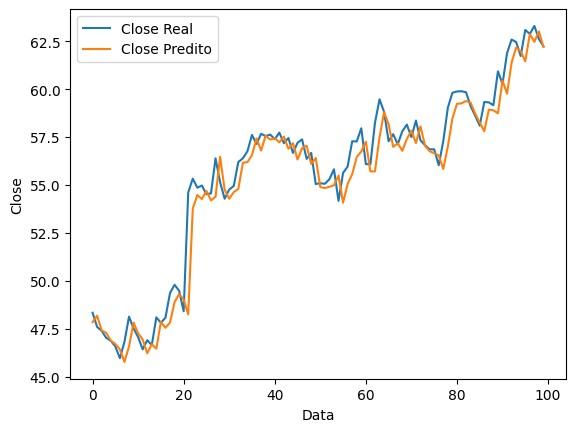
Figura 6: Gráfico do close real x close previsto ao longo do tempo, em um cenário de alta.
Tabela 3 – Cálculo de métricas
Métricas Cenário com modelo Cenário randômico Sg 1,1 1,0 Eventos totais 99 99 Eventos de Lucro 34 50 Eventos dePrejuízo 31 49 Faturamento FinalTotal USD 11,36 USD 13,91 Investimento Total USD 63,29 USD 63,29 Proporção deRetorno 17% 21% Acurácia 82,8% 50,5%
Como primeira métrica, temos o coeficiente de segurança, em seguida temos a quantidade de eventos totais, ou seja, o número total de dias analisados; posteriormente, temos eventos de lucro, ou seja, o número de operações de venda o qual obtivemos lucro no período analisado; eventos de prejuízo, que é o número de vendas nas quais tivemos prejuízo; o faturamento final total, que é quanto se teve de lucro ou prejuízo ao final do período; o investimento total, que caracteriza quanto foi gasto efetivamente ou seja, o quanto foi gasto como investimento inicial, somado dos valores necessários para prosseguir com a estratégia; em seguida temos a proporção de retorno, que é quanto de lucro obtivemos em relação ao investimento inicial e por fim a acurácia, que é a proporção de classificações de eventos de alta ou baixa para compra realizados corretamente, em relação ao total.
Para este caso de alta fica evidente que com o auxílio do modelo, temos uma sutil melhora no coeficiente de segurança e uma pequena melhoria.
Para este segundo cenário, foi avaliado um período de queda da ação, ou seja, onde a tendência geral da curva de valor de fechamento da ação é negativa.
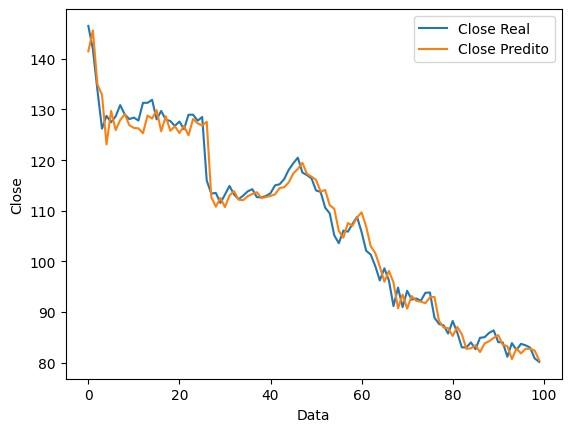
Figura 7: Gráfico do close real x close previsto ao longo do tempo, em um cenário de baixa.
Tabela 4 – Cálculo de métricas para os cenários com modelo e randômico.
Métricas Cenário com modelo Cenário randômico Sg 1 0,76 Eventos totais 99 99 Eventos de Lucro 24 43 Eventos dePrejuízo 24 56 Faturamento FinalTotal USD -10,08 USD -66,13 Investimento Total USD 146,49 USD 146,49 Proporção deRetorno -6% -45% Acurácia 70,7% 43,43%
Observa-se uma mais expressiva vantagem do uso do modelo neste cenário não favorável de mercado. O modelo apresenta um coeficiente de segurança muito mais elevado e, ao final do período, apresenta um prejuízo consideravelmente menor em relação ao caso randômico.
Para o terceiro e último cenário analisado, têm-se o que podemos chamar de cenário caótico, ou seja, um em que o valor da ação varia com alta volatilidade, mas que ao final do período se apresenta com valor semelhante ao do inicial.
Figura 8: Gráfico do close real x close previsto ao longo do tempo, em um cenário caótico.
Tabela 5 – Cálculo de métricas para os cenários com modelo e randômico.
Métricas Cenário com modelo Cenário randômico Sg 1,5 1,3 Eventos totais 99 99 Eventos de Lucro 18 57 Eventos dePrejuízo 12 42 Faturamento FinalTotal USD 3,56 USD 3,18 Total investido USD 143,19 USD 148,97 Proporção deRetorno +2,4% + 2,1% Acurácia 57,57% 57,57%
No cenário caótico há uma visível queda de desempenho do modelo em relação ao caso randômico, principalmente no que se refere à quantidade de eventos de lucro. Este apesar de gerar lucro próximo ao cenário randômico, detém uma leve vantagem em lucro final, coeficiente de segurança e se equipara em acurácia.
Por fim, têm-se uma média do desempenho do modelo para os cenários, para gerar uma linha de comparação geral dado o conjunto como um todo.
Tabela 6 – Cálculo de métricas para os cenários com modelo e randômico.
Métricas Cenário com modelo Cenário randômico Sg 1,20 1,02 Eventos totais 297 297 Eventos de Lucro 76 150 Eventos dePrejuízo 67 147 Faturamento FinalTotal USD 4,84 USD -49,95 Total investido USD 352,97 USD 306,78 Proporção deRetorno Médio +4,46% – 20,33% Acurácia Média 70,35% 50,5%
Com os resultados do conjunto pode-se observar que o modelo é ligeiramente melhor que o cenário randômico, principalmente no quesito de faturamento final, tendo também um desempenho significativamente melhor no que se refere à acurácia média e proporção de retorno médio.
- CONCLUSÃO
Conclui-se que se comparado ao caso de decisão randômica, o modelo se apresenta mais seguro e consideravelmente mais robusto para lidar com mercado em baixa. Apesar disso, o modelo se apresenta sensível à ações voláteis, tendo um melhor desempenho em cenários em que há uma tendência mais clara de baixa e tendo um desempenho pior que o randômico em termos de lucro para cenários de alta.
É, portanto, possível concluir que com o uso de redes neurais baseadas em arquiteturas com LSTMs, como a estudada, não é capaz de prever eficientemente valores das ações no mercado de ações, tendo um desempenho similar ao cenário randômico, sendo significativamente melhor somente em cenários mais específicos. Apesar da capacidade de previsão limitada, é possível se colocar a possibilidade de utilizar o resultado do modelo, como uma variável à mais em um modelo robusto de trading como por exemplo uma solução automatizada, baseada em reinforcement learning, que por meio de um tipo de transfer learning, obtido por meio do uso da saída do modelo proposto como uma feature a ser considerada na sua decisão, realiza decisões de compra e venda de ações.
- REFERÊNCIAS
CHRISTIE, D.; NEIL, S. P. Comprehensive Renewable. Volume 8, 2022, Pages 149-175.
Disponível em:
<https://www.sciencedirect.com/topics/engineering/root-mean-squared-error>.Acesso em: 1 de novembro de 2023.
DIVE INTO DEEP LEARNING. Long Short-Term Memory. Disponível em:
<https://d2l.ai/chapter_recurrent-modern/lstm.html>. Acesso em 13 de novembro de 2023.
GOOGLE. Descending into ML: Training and Loss | Machine Learning Crash Course.
Disponível em:
<https://developers.google.com/machine-learning/crash-course/descending-into-ml/training-a nd-loss>. Acesso em: 12 novembro de 2023.
HOCHREITER, S.; SCHMIDHUBER, J. Long Short-Term Memory. Neural Computation, v.
9, n. 8, p. 1735–1780, 1997. Disponível em:
<https://www.researchgate.net/publication/13853244_Long_Short-term_Memory>. Acesso em 12 de novembro de 2023
INCE, H.; TRAFALIS, T.B. Short term forecasting with support vector machines and application to stock price prediction. Int J Gen Syst. 2008.
KIM, K.; HAN, I. Genetic algorithms approach to feature discretization in artificial neural networks for the prediction of stock price index. 2000.
LOSHCHILOV, I.; HUTTER, F. Decoupled Weight Decay Regularization. 2019. Disponível em: <https://arxiv.org/abs/1711.05101v3>. Acesso em: 1 de novembro de 2023.
MACUKOW, B. Neural Networks – State of Art, Brief History, Basic Models and Architecture. Computer Information Systems and Industrial Management, v. 9842, n.
1611-3349, p. 3–14, 6 set. 2016. Disponível em:
<https://www.researchgate.net/publication/307908595_Neural_Networks_-_State_of_Art_Bri ef_History_Basic_Models_and_Architecture>. Acesso em: 12 novembro de 2023.
MALKIEL, B.G.; FAMA, E.F. Efficient capital markets: a review of theory and empirical work. J Finance. 1970.
NEVIL, S. How the Coefficient of Determination Works. Disponível em:
<https://www.investopedia.com/terms/c/coefficient-of-determination.asp>. Acesso em: 1 de novembro de 2023.
SCHNEIDER, P.; XHAFA, F. Anomaly Detection and Complex Event Processing over IoT
Data Streams. 2022, Pages 49-66. Disponível em:
<https://www.sciencedirect.com/topics/engineering/mean-absolute-error>. Acesso em: 1 de novembro de 2023.
SHEN, J.; SAHFIQ, M.O. Short-term stock market price trend prediction using a comprehensive deep learning system. J Big Data 7, 66 (2020).
STEWART, K. Mean Squared Error (MSE) | Definition, Formula, Interpretation, & Facts | Britannica. Disponível em: <https://www.britannica.com/science/mean-squared-error>.
Acesso em: 1 de novembro de 2023.
VARGAS, G.; SILVESTRE, L.; RIGO JÚNIOR, L.; ROCHA, H. B3 Stock Price Prediction
Using LSTM Neural Networks and Sentiment Analysis. IEEE Latin America Transactions, [S. l.], v. 20, n. 7, p. 1067–1074, 2022. Disponível em: https://latamt.ieeer9.org/index.php/transactions/article/view/6236. Acesso em: 12 novembro de 2023.
1 Discente do Curso Superior de Engenharia da Computação do Instituto São Judas Tadeu Campus Paulista e-mail: d.maximoalbuquerque@gmail.com
2 Discente do Curso Superior de Engenharia da Computação do Instituto São Judas Tadeu Campus Paulista e-mail: gabriel.h.r.cordeiro@gmail.com
3 Discente do Curso Superior de Engenharia da Computação do Instituto São Judas Tadeu Campus Paulista e-mail: Herbert.beserra@gmail.com
4 Discente do Curso Superior de Engenharia da Computação do Instituto São Judas Tadeu Campus Paulista e-mail: santosmateus2001@gmail.com
5Discente do Curso Superior de Engenharia da Computação do Instituto São Judas Tadeu Campus Mooca e-mail: oliveirapaulo.estudos@gmail.com
6 Discente do Curso Superior de Engenharia da Computação do Instituto São Judas Tadeu Campus Paulista e-mail: victor.l.beltran@gmail.com
7 Desenvolvedora de Software da VILT, Bacharel em Engenharia de Software e-mail: geisesaunier3939@gmail.com.
8 Docente da Universidade São Judas Tadeu, Mestre em Engenharia Elétrica – Inteligência Artificial Aplicado a Automação. Doutor em Ciência. e-mail: prof.nelsonaguiar@gmail.com.
