THE USE OF GEOTECHNOLOGIES AS TOOLS FOR TEACHING MATHEMATICS: A PROPOSAL OF UNIVERSITY EXTENSION
REGISTRO DOI: 10.5281/zenodo.7941657
Luiz Carlos Teixeira Coelho Filho1
Resumo
O presente trabalho visa a apresentar à comunidade acadêmica e à comunidade de professores em geral uma possibilidade de engajamento dos alunos no processo de aprendizagem de conceitos matemáticos através da utilização de tecnologias de geoinformação facilmente disponíveis em dispositivos de informática como celulares ou tablets. O desenvolvimento do trabalho parte de breve levantamento, a partir de pesquisas acadêmicas, das principais dificuldades apontadas no ensino da Matemática. Em seguida, apresenta a utilização de tecnologias de geoinformação (como mapas online e aplicativos de geolocalização) como oportunidades para explorar conhecimentos matemáticos previstos na Base Nacional Comum Curricular. Por fim, descreve possibilidades de interação desse processo com o aprendizado de disciplinas não-necessariamente correlatas à Matemática, mas que se utilizam do ferramental de mapas e sistemas de informação geográfica. O trabalho em pauta apresenta, ainda, resultados de experimento conduzido no âmbito de projeto de extensão universitária, demonstrando sua pertinência como forma de comunicação universidade-sociedade, interligando programas universitários que trabalhem com geotecnologias com atividades escolares de Ensino Fundamental e Médio.
Palavras-chave: geoinformação, matemática, ensino, aprendizagem, multidisciplinaridade
Abstract
This article aims to present to the academic community and to the teaching community in general a possibility of engaging students in the process of learning mathematical concepts through the usage of geoinformation technologies easily available on electronic devices such as cell phones or tablets. The development of this research starts with a brief survey (based on academic research) of the main difficulties related to teaching Math. After it, it presents how geoinformation technologies (such as online maps and geolocation apps) as opportunities for students to explore mathematical abilities stipulated by the National Joint Curriculum. Finally, the article describes how these activities can be integrated with learning subjects not necessarily related to Mathematics, but which share the same usage of maps and geographic information systems. The present work also portrays the results of an experiment conducted within the scope of a university extension project, thus showing its importance as a form of university-society communication, linking university programs that work with geotechnologies with elementary and high school activities.
Keywords: geoinformation, mathematics, teaching, knowledge, multidisciplinarity
1. INTRODUÇÃO
Recentes estatísticas citadas pela mídia apontam para resultados consistentemente ruins no tocante ao desempenho dos alunos brasileiros. O aprendizado de Matemática é, corriqueiramente, um dos mais deficitários. Segundo dados do SAEB (FAJARDO et al, 2018), avaliação bianual utilizada pelo governo federal para medir a aprendizagem dos alunos ao fim de cada etapa de ensino (5º e 9º anos do ensino fundamental e 3º ano do ensino médio), os resultados são desencorajadores. Cerca de 33% dos alunos do 5º ano, 63% dos alunos do 9º ano e 72% dos alunos do 3º ano do Ensino Médio apresentam resultados insuficientes quanto à proficiência em Matemática, segundo avaliações oriundas da Prova Brasil e do Índice de Desenvolvimento da Educação Básica (IDEB).
Tal problemática levanta o constante problema que se apresenta, em geral, aos docentes de Matemática. Como apresentar os conteúdos exigidos pela Base Nacional Comum Curricular (BNCC) de forma que os alunos os compreendam, assimilem e saibam empregá-los na resolução de problemas? A resposta, apresentada por muitos pesquisadores da área, invariavelmente perpassa por trazer para a realidade e a vida dos alunos a experiência do ensino-aprendizagem, permitindo que sejam sujeitos ativos nesse processo, enxergando a importância do entendimento da disciplina e a aplicabilidade da mesma no seu dia a dia.
O presente trabalho busca apresentar o uso de geotecnologias no ensino da Matemática, muitas das quais hoje são acessíveis ao clique de um smartphone, como ferramentas de geolocalização, rotas e mapas online. Além de estarem gratuitamente disponíveis aos professores e permitirem o trabalho com conceitos básicos de diferentes anos da BNCC, têm o caráter multidisciplinar e possibilitam a integração de conteúdos transversais a outras disciplinas.
2. ESTRATÉGIAS PARA O USO DE GEOTECNOLOGIAS NO ENSINO DE MATEMÁTICA
O uso de mapas foi historicamente confinado à Geografia e a algumas outras poucas ciências humanas. Entretanto, um dos maiores desafios dos profissionais dessas áreas do conhecimento, em sala de aula é prover aos alunos o ferramental de aprendizagem que os possibilite compreender os fenômenos relacionados ao espaço geográfico. Tais fenômenos não ocorrem ex nihilo: possuem coordenadas, áreas, distâncias… E a partir dos mesmos, uma série de conteúdos matemáticos também pode ser igualmente trabalhada.
Segundo TIRITAN (2013), a Cartografia é a “espacialização dos fenômenos em forma de símbolos e imagens que facilitam a localização e a leitura da informação, mas também uma forma de codificação e representação do espaço e dos fenômenos ocorridos nele.” A Cartografia permite aos alunos ler a informação geoespacial e entender como se desdobram os fenômenos no espaço através de sua codificação em elementos gráficos, presentes no mapa. Não é possível, contudo, ter uma plena noção da realidade representada em mapas sem que haja o conhecimento básico das operações matemáticas e geométricas envolvidas na sua construção.
As novas tecnologias de comunicação e informação permitiram avançar no tocante à disponibilização de recursos cartográficos online. BASTOS JUNIOR (2014) refere-se à geoinformação como informação geograficamente referenciada, mediante o uso da tecnologia. Os recursos de geoinformação podem ser compartilhados a partir de mapas digitais, muitos dos quais podem ser facilmente disponibilizados via Internet, de forma gratuita.
Provavelmente, o recurso mais conhecido e de amplo acesso é o Google Maps, ou sua versão em aplicativo Google Earth. Ambas as ferramentas apresentam um globo interativo e virtual que pode ser aproximado até o nível da cartografia cadastral (cartografia com edificações para fins urbanos). A figura 1 apresenta algumas capturas de tela que demonstram os principais conteúdos que podem ser trabalhados com essa aplicação. A ferramenta permite o cálculo de rotas e distâncias, a partir das quais é possível trabalhar conceitos como escala, velocidades de meios de transportes (ao verificar a diferença de rotas em cada modal: automóvel, transporte público, etc.), perímetros e áreas. Também possui uma bússola indicando o norte geográfico, a partir do qual podem ser trabalhados rumos e azimutes, baseados em ângulos trigonométricos. Permite também a análise do mosaico de imagem de satélite. Numa atividade interativa, alunos podem inclusive usar tais aplicativos em tablet ou celular, marcando pontos e percorrendo rotas, realizando a orientação pelos pontos cardeais e calculando escalas sob a supervisão do professor.
Esse tipo de ferramenta não foi concebido prioritariamente para o uso em sala de aula, mas contém vários elementos cartográficos necessários ao desenvolvimento do aluno enquanto cidadão. Numa era em que celulares e tablets são ubíquos e aplicativos de geolocalização estão disponíveis gratuitamente, é interessante considerá-los no desenvolvimento de atividades em sala de aula também.
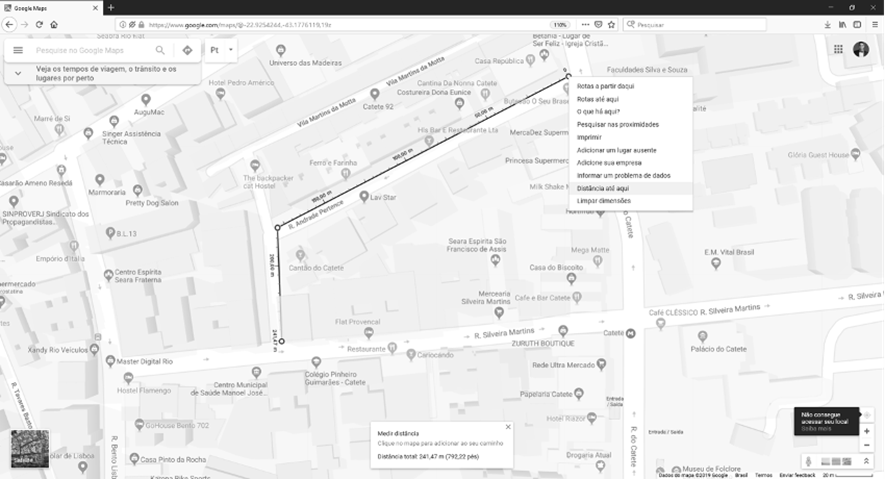
Figura 3 – Acima: tela do Google Maps mostrando a cartografia cadastral, bem como a possibilidade de medição de distâncias e rotas.
Turner (2018) apresenta uma série de conteúdos que podem ser trabalhados numa aula de Matemática, no contexto norte americano do Ensino Fundamental (3º a 5º anos):
“Inicie com a introdução da ferramenta Google Maps e navegação de algumas viagens para as quais os alunos escolhem as localizações de início e fim das rotas. Exiba para eles informações de milhagem, direções, tempo de duração, conversões entre sistemas de medidas, etc. Exponha em itens o que os estudantes completarão para essa lição em particular. Por exemplo: Hoje buscaremos a resposta para a questão ‘qual é a distância’
a) Precisamos de uma localização inicial, por favor, alguém pode identificar um local para o começo da atividade?
b) Agora necessitamos identificar quatro destinos.
c) Usemos Google Maps e math Journals para criar uma tabela de distâncias desde a localização inicial.
d) Vamos então ordenar as distâncias da mais longe até a mais perto (ou vice-versa).
e) Escreva no seu caderno duas formas de utilização dessa informação numa situação de vida real.
Outro exemplo: Hoje buscaremos a resposta do tempo de duração de uma viagem pela estrada.
a) Vamos usar o Google Maps para descobrir a quantidade de tempo que leva na viagem de uma localização para outra.
b) Usando os dados do Google Maps, o que faríamos se começássemos a jornada em ________, e quanto tempo levaria?
c) Se precisamos chegar em tal lugar às _________ horas, precisamos partir antes de que horário?
d) Cada um agora pode criar seu planejamento de viagem no caderno, a partir das informações colhidas no Google Maps.”
Tal abordagem pode ser replicada em outros aplicativos que registram distâncias, tempo e fazem medidas, como Bing Maps, Waze e Google Earth. Os conteúdos podem ser mais incrementados para anos posteriores, ao trabalhar conteúdos como escala, razão e proporção, área, perímetro e formas geométricas planas. Os alunos podem ser desafiados a buscar nos aplicativos suas próprias localizações, entender a partir da matemática a distância de suas residências a outros pontos relevantes e calcular a área do imóvel onde vivem, por exemplo.
As aplicações citadas apresentam uma dentre múltiplas possibilidades de conteúdos matemáticos abordados dentro do contexto de mapas digitais e sistemas de informação geográfica, mas não esgotam o assunto. Tais produtos cartográficos podem ser entendidos matematicamente como formas de visualizar números e geometria. Em sala de aula, educadores podem exaustivamente trabalhar conceitos de geometria e cálculos matemáticos em variedades e graus diversos de profundidade com seus alunos.
Na Educação Infantil, o conteúdo de geoinformação pode ser trabalhado no entendimento de orientação, relações e formas espaciais. No Ensino Fundamental, descritores como cálculo de áreas, perímetros, distâncias, razão e proporção (no entendimento de escala) são facilmente verificáveis em aplicativos de geoinformação. Para anos mais avançados, no final do Ensino Fundamental e no Ensino Médio, outros conteúdos podem ser abordados, como estatísticas, cálculo de áreas e volumes de formas complexas e densidades geográficas por área e volume. Todos esses conteúdos são eminentemente multidisciplinares, e não se relacionam somente com o ensino de Geografia. Por exemplo, ao trabalhar o conceito de distâncias e percursos, são utilizados elementos desenvolvidos também no ensino de Física, no Ensino Médio.
Ao explorar os diversos conceitos matemáticos da cartografia, espacialmente e graficamente, os alunos são convidados a relacionar o uso da Matemática com a realidade ao seu redor, visualizada em mapas e imagens de satélite. Isso desmistifica a Matemática como ferramenta útil e acessível a todos, reduzindo o perigo da mato fobia e permitindo a aprendizagem de diversos tópicos paralelos, como biodiversidade, fenômenos históricos, acidentes naturais, meio ambiente, ordenamento do território, matrizes energéticas, aproveitamento da água e da energia e tantas outras questões que perpassam os bancos escolares e são aplicadas na realidade profissional das pessoas e na experiência de vida como um todo.
O tratamento matemático da cartografia digital interativa permite ao professor trabalhar uma série de conteúdos da BNCC, como contagem e operações com números, localização e descrição de objetos e pessoas no espaço, relações geométricas e espaciais bi e tridimensionais, unidades de grandeza e medidas, probabilidade, estatística, representação gráfica e por tabelas. Grosso modo, tais assuntos sobrepõem unidades temáticas presentes nas BNCC para o Ensino Fundamental – 1º Segmento (Unidades Temáticas Números, Álgebra, Geometria, Grandezas e Medidas e Probabilidade e Estatística) e Ensino Fundamental – 2º Segmento (Unidades Temáticas Números, Álgebra, Geometria, Grandezas e Medidas e Probabilidade e Estatística). Já no tocante ao Ensino Médio, a possibilidade de multidisciplinaridade e sobreposição de dados permite não somente tratar de temas atinentes às unidades temáticas, mas também dentro das competências específicas listadas nas BNCC. O grau de aprofundamento depende muitas vezes do nível escolar e contextual da turma, e o professor pode recursivamente voltar à ferramenta de geoinformação para voltar a trabalhar a mesma unidade temática – desta vez num nível de aprofundamento diferente.
Essa abordagem escalonada e multidisciplinar dos mapas digitais educacionais também apresenta uma possibilidade de aplicação matemática a partir de paradigmas recomendados pela literatura da área, como: ser matematicamente importante dentro e fora da sala de aula, tratar dos conceitos propostos de forma interativa e a partir das experiências cotidianas dos alunos, e recursivamente rememorar conceitos de anos anteriores, combinados com novos conteúdos. Qualquer tipo de informação que possa ser especializada num sistema de informação geográfica se encaixa nesses critérios, já que uma ampla gama de conceitos matemáticos pode ser visualizada e aplicada usando esses sistemas.
A partir de tais propostas, BARRETT (2015) propõe uma série de exercícios lúdicos que incrementam as ferramentas básicas estabelecidas por Turner. Utilizando marcações nos mapas de diversas localidades ao redor do mundo, associadas a códigos distintos, o professor propõe problemas que os alunos podem realizar enquanto navegam e descobrem o traçado urbano de cidades famosas.
Barrett propôs, dessa forma, uma série de atividades ao redor do mundo, com títulos como “medidas em Madri, formas em Paris, manipulação de dados em Nottingham, adições em Adelaide, matemática em Edimburgo e matemática em Bradford”.
Por exemplo, na figura 2, vemos um problema marcado no mapa como relativo à temática de sexto ano, a partir do qual, os alunos são convidados a localizar cinco piscinas ao redor daquele ponto, medi-las e responder qual é a mais larga, qual é a mais comprida, o somatório da distância percorrida ao se nadar em cada uma delas, bem como o somatório de percursos a pé entre elas.

Figura 2 – Exercício de medidas em Madri, proposto para o currículo de 6º ano (fonte: Barrett, 2015)
Um conteúdo completamente diferente é tratado na figura 3, segundo o qual os alunos são convidados a contar quantas pessoas estão em cada quadra de tênis, ordenar segundo listas crescentes e decrescentes, calcular média e mediana. O conteúdo está adaptado para o currículo de 5º ano no sistema educacional britânico.
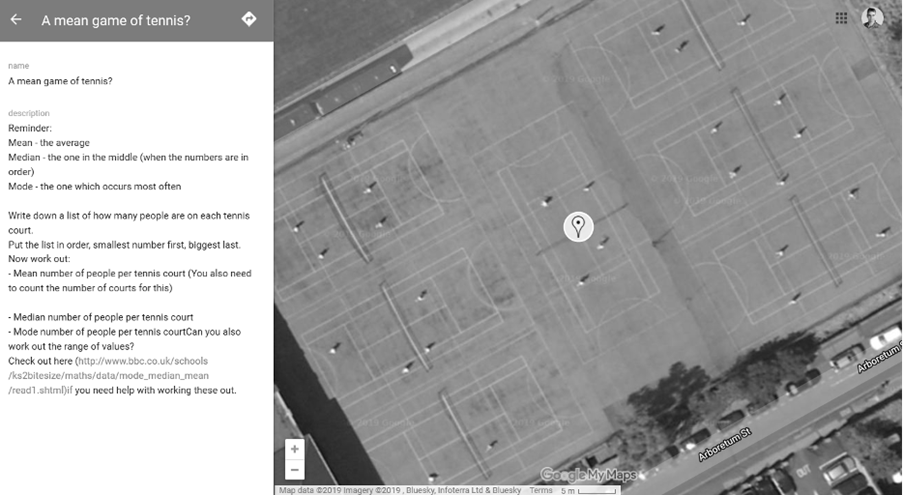
Figura 3 – Exercício estatístico em Nottingham, proposto para o currículo de 5º ano (fonte: Barrett, 2015)
A iniciativa de Barrett (2015) é louvável, mas não necessariamente necessita ser individual de cada professor. À medida que municipalidades e órgãos públicos desenvolvem portais de informação geográfica, seria importante que a educação matemática fosse contemplada dentro dos conteúdos voltados para estudantes dos ensinos Fundamental e Médio.
Por exemplo, o Armazenzinho (Figura 4) é uma ferramenta desenvolvida pelo Instituto Pereira Passos, da Prefeitura do Rio de Janeiro, a fim de apoiar o ensino de Geografia, História e Ciências mediante mapas dinâmicos da cidade. Possui diversos aplicativos que compreendem tabelas, réguas do tempo, mapas dinâmicos de temas como divisão política, meio-ambiente e transportes, glossários e um atlas escolar interativo. Os conteúdos dele poderiam ser ampliados de modo a também contemplar atividades diretamente relacionadas ao ensino de Matemática, bem como interdisciplinares que compreendam o ensino de Matemática.
Ferramentas educativas online, já desenvolvidas por diversos portais educacionais e apoiadas, também, no uso de mapas, podem ser incrementadas a partir da adição de temas também relacionados à Matemática, conforme os apresentados anteriormente.
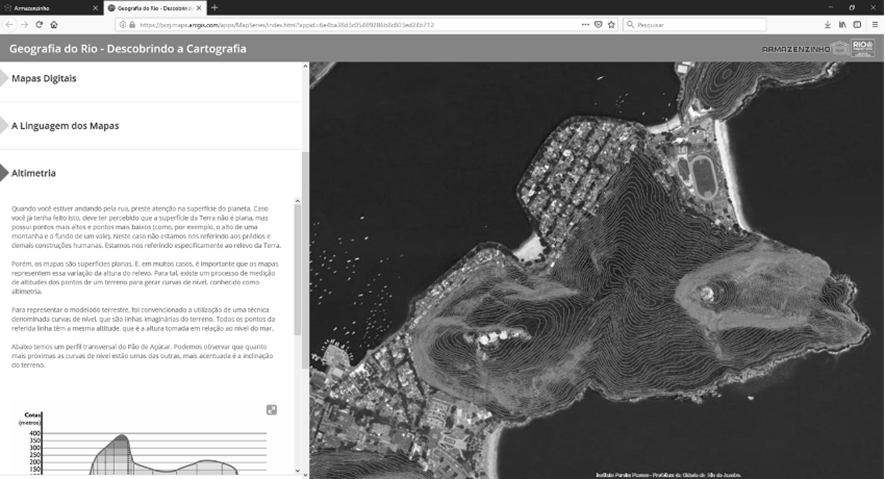
Figura 4 – Armazenzinho (fonte: Instituto Pereira Passos)
4. ESTUDO DE CASO: EMANCIPA EDUCAÇÃO POPULAR
Como professor de caráter voluntário de matemática (reforço e preparatórios para ENEM e Vestibular UERJ), do projeto Emancipa Educação Popular (projeto de extensão da Universidade Federal do Rio de Janeiro), foi possível aplicar proposta de integração de ferramentas de geoprocessamento no ensino da geometria, como estudo de caso para a melhor compreensão das formas geométricas e seus relacionamentos de áreas e perímetros. A proposta adveio, principalmente, da tipologia de problema que surge nas principais avaliações e vestibulares, comumente focado em situações concretas, como a geometria de lotes e edificações.
Aos alunos, foram apresentadas diversas possibilidades de medição de feições geográficas usando as ferramentas gratuitas disponibilizadas pelo Instituto Pereira Passos, na plataforma Data.Rio. Os trabalhos envolviam medições de perímetros e áreas de figuras simples e complexas, presentes nas próprias feições geográficas da cidade, e propondo aos alunos estratégias para enxergarem feições geométricas no tecido urbano.
Dentre as muitas experimentações abordadas, são destacadas neste artigo duas: a circunferência e o cálculo aproximado de e a medição de áreas de quadriláteros.
No primeiro caso, alunos foram convidados, em seus celulares e em tablets disponibilizados de forma voluntária, a buscarem feições de formato circular na cartografia da cidade. Em seguida, os alunos foram orientados a medir, de forma aproximada, o perímetro (circunferência) e o diâmetro dessas feições. As figuras 5 e 6 demonstram essa medição, feita para a Praça da Cruz Vermelha, no Centro do Rio.
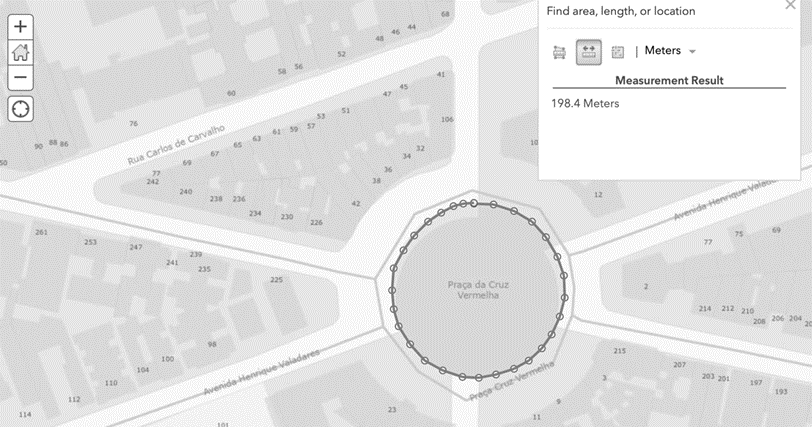
Figura 5 – Medição aproximada da circunferência da Praça da Cruz Vermelha, feita no aplicativo do Data.Rio, evidenciando 198,4 m.
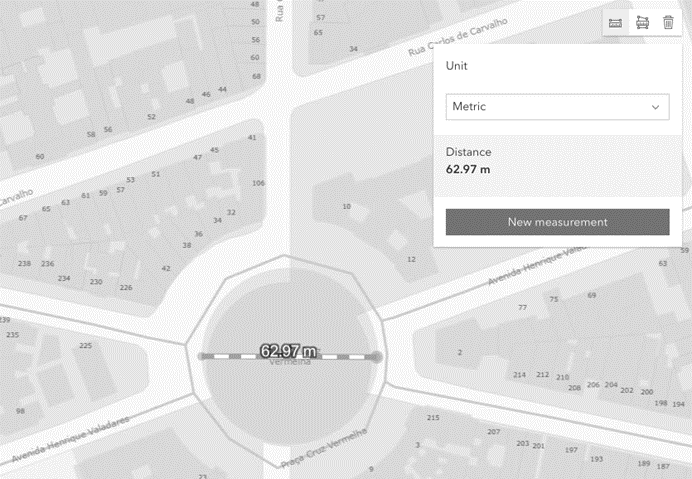
Figura 6 – Medição aproximada do diâmetro da Praça da Cruz Vermelha, feita no aplicativo do Data.Rio, evidenciando 62,97 m.
A partir das medidas feitas, os alunos foram convidados a estimar o valor de e depois obtê-lo com o uso de calculadora. Para esse caso, em particular, a estimativa buscou arredondar os valores para números mais amigáveis. Nesse caso, trabalhou-se com a circunferência igual a 200m e o diâmetro igual a 60m. Essa divisão dá uma dízima periódica bastante conhecida: 3,333… permitindo também trabalhar o tópico de operações aritméticas, números racionais e irracionais. Já a divisão por calculadora, com os valores obtidos na medição, deu, aproximadamente: 3,15 – valor muito mais próximo do real valor de (3,1416…).
O passo seguinte, descrito na figura 7, foi estimar a área pela multiplicação de
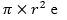
e pela ferramenta de medição disponível no portal de geoinformação. Utilizando o diâmetro medido anteriormente (62,97 m), a área do círculo seria equivalente a
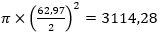
m2. Na medição feita na tela do computador, o valor encontrado por esse aluno foi de 3169,7 m2.
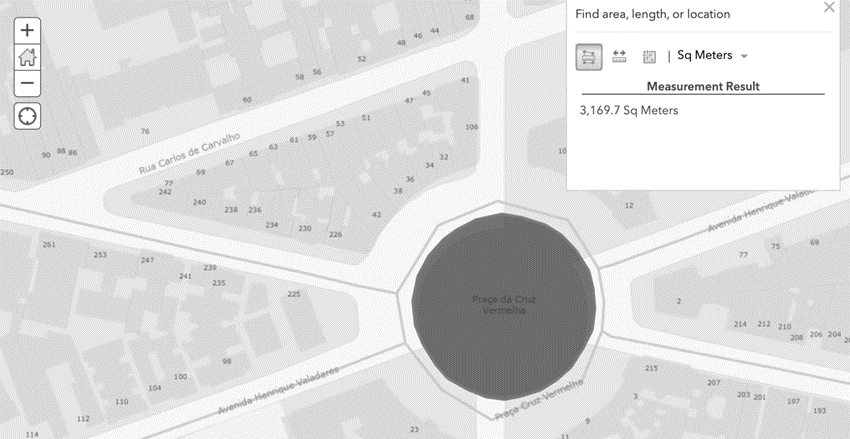
Figura 7 – Medição aproximada da área da Praça da Cruz Vermelha, feita no aplicativo do Data.Rio, evidenciando 3169,7 m2.
Outro grupo trabalhou o tópico “áreas de quadriláteros”. A partir das medições de largura e comprimento de quadras, buscaram chegar a resultados aproximados de áreas, confrontando-os com a área medida no portal de geoinformação. No caso descrito pelas figuras 8, 9 e 10, a área calculada através da multiplicação comprimento largura deu 6561,27 m2, um pouco diferente da medição pela ferramenta (6381 m2), possivelmente por não se tratar de um retângulo perfeito.
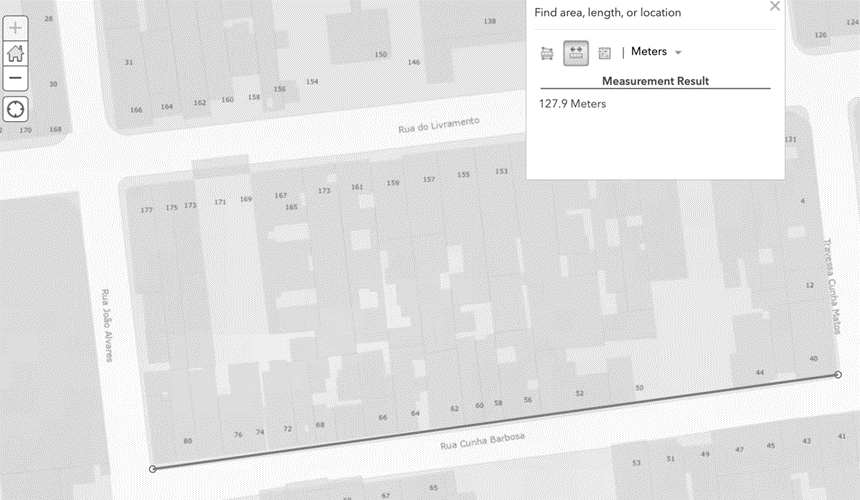
Figura 8 – Medição aproximada de comprimento de quadra quase-retangular, feita no aplicativo do Data.Rio, evidenciando 127,9 m
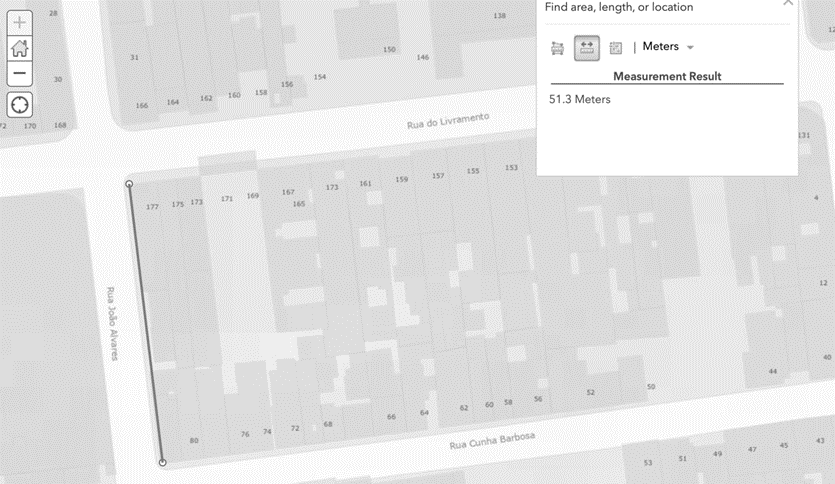
Figura 9 – Medição aproximada de largura de quadra quase-retangular, feita no aplicativo do Data.Rio, evidenciando 51,3 m

Figura 10 – Medição aproximada de área de quadra quase-retangular, feita no aplicativo do Data.Rio, evidenciando 6381 m2
Cada aluno (ou grupo de alunos) trabalhou com feições de sua livre escolha, buscando navegar pelo mapa para encontrar, no arranjo de quadras e logradouros, objetos geométricos para medir. O trabalho evoluiu também para áreas complexas, nas quais alunos precisavam pensar criativamente quanto à adição e subtração de figuras geométricas simples. Um exemplo que pôde ser verificado in loco (visto que as aulas do Emancipa ocorrem na Igreja Metodista de Vila Isabel) foi a Praça Barão de Drummond, no mesmo bairro. Como calcular a área da face sul da praça? Diversas propostas foram apresentadas, sobretudo aquelas que buscavam a medição de algum tipo de quadrilátero, seguida da subtração da área de um semicírculo (figura 14).
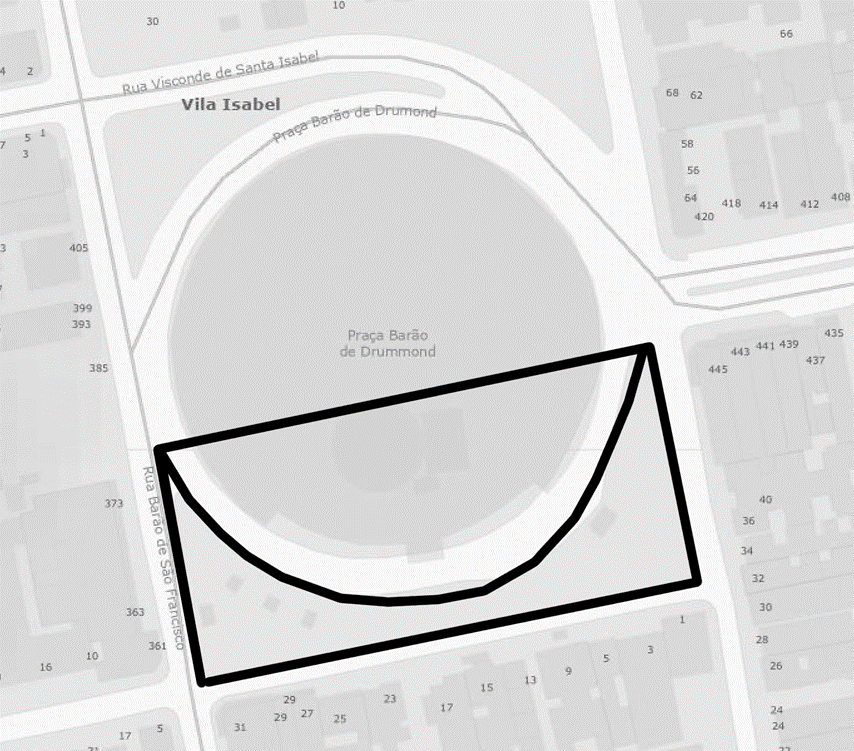
Figura 11 – Como medir a parte sul da Praça Barão de Drummond? Uma aproximação seria subtrair de um retângulo uma área ligeiramente menor que um semicírculo.
5. CONSIDERAÇÕES FINAIS
O ensino de Matemática, na realidade brasileira, ainda tem várias lacunas a serem preenchidas. A mato fobia é uma realidade presente entre muitos estudantes da atualidade. A contextualização do ensino de Matemática, bem como o tratamento recorrente de temas básicos, à medida que novos conteúdos são apresentados, são necessidades prementes.
Como forma de maior interação e aproveitamento em sala de aula, muitos educadores propõem exercícios adaptados à realidade dos alunos, empregando novas tecnologias e oportunidades de interação, permitindo ao professor agir como mediador na aquisição de novos conhecimentos por parte dos alunos, e aos alunos aprenderem entre si.
Nesse sentido, este trabalho apresenta uma oportunidade de uso de geotecnologias facilmente disponibilizadas via web, como exercício gratuito, interativo e disciplinar que facilita a aquisição de conhecimentos também no campo da Matemática. Esse tipo de atividade pode ser realizado como projeto de extensão universitária, integrando cursos de arquitetura, planejamento urbano e geociências com a realidade escolar de alunos de Ensino Fundamental e Médio. Num cenário em que a extensão passou a ser vislumbrada como eixo fundamental da Universidade, propostas inovadoras no campo da didática escolar, que sirvam como atividades de extensão, são mais que bem-vindas.
Desse modo, o trabalho apresentado é proposto como uma forma de difundir o ensino de Matemática de forma contextualizada, multidisciplinar e transversal às temáticas do dia a dia na vida de estudantes e educadores.
REFERÊNCIAS
BARRETT, Tom. Maths Maps. 2015. Disponível em: http://edte.ch/blog/maths-maps/. Acesso em: 20 maio 2019.
BERTANHA, Priscilla. Didática Geral. 1 ed. Batatais: Claretiano, 2005.
CLEMENTE, César, GONÇALVES, Juliana Brassolatti e SANTOS, Miriam Aparecida de Negreiros Pereira dos. Metodologia do ensino da Matemática. Batatais: Claretiano, 2014.
FREIRE, Paulo. Aprendendo com a própria história. Rio de Janeiro: Paz e Terra, 1994.
FREIRE, Paulo e HORTON, Myles. O caminho se faz caminhando: conversas sobre educação e mudança social. 4 ed. Petrópolis: Vozes, 2003.
GONÇALVES, Cecília de Morais. Dificuldades do ensino e aprendizagem da matemática na educação fundamental a baixa utilização da tecnologia deinformação e comunicação pelos docentes das séries iniciais. (Monografia) Especialização em Ensino e Tecnologia. Universidade Tecnológica Federal do Paraná, 2015.
KRASTANOV, Stefan Vasilev e CORRÊA, Rubens Arantes. Fundamentos históricos e filosóficos da educação. Batatais: Claretiano, 2013.
MACHADO, Ivete Alves. Algumas dificuldades do ensino da Matemática na 7ª Série do Ensino Fundamental. (Monografia) Curso de Matemática/Universidade Católica de Brasília, 2005.
MINISTÉRIO DA EDUCAÇÃO. Base Nacional Comum Curricular. 2017.
OAKWOOD, Liam. Teaching Math with GIS. GIS Lounge, Califórnia, EUA, 5 jul. 2017. Disponível em: https://www.gislounge.com/teaching-math-gis/. Acesso em: 22 maio 2019.
OLIVEIRA, Eliete Alves de Castro e OLIVEIRA, Maria de Fátima Alves de. Dificuldades apresentadas por alunos do Ensino Fundamental na disciplina de Matemática. Revista Práxis, ano III, nº 5 – janeiro 2011.
OLIVEIRA, Vinícius Augusto de, PAIVA, Eleide de Andrade, MELO, Luciane Magda. Ensino de Matemática: análise das dificuldades apresentadas pelos alunos ingressantes – Campus Patos de Minas. Instituto Federal de Educação, Ciência e Tecnologia do Triângulo Mineiro, 2015.
PACHECO, Marina Buzin e ANDREIS, Greice da Silva Lorenzzetti. Causas das dificuldades de aprendizagem em Matemática: percepção de professores e estudantes do 3º ano do Ensino Médio Revista Principia, n. 38, 2018.
PESTANA, Simone Freire Paes. Afinal, o que é Educação Integral? Revista Contemporânea de Educação, vol. 9, n. 17, janeiro/junho de 2014.
PREFEITURA DO RIO DE JANEIRO. Atlas Escolar 2018. Disponível em http://apps.data.rio. Acesso em: 22 maio 2019.
PREFEITURA DO RIO DE JANEIRO. Armazenzinho. Disponível em http://apps.data.rio. Acesso em: 22 maio 2019.
RESENDE, Giovani e MESQUITA, Maria da Glória. Principais dificuldades percebidas no processo ensino-aprendizagem de matemática em escolas do município de Divinópolis, MG. Educação Matemática em Pesquisa. v.15, n.1, pp. 199-222, 2013.
SANTOS, Jamison Luiz Barros Santos, SANTOS, Gracineide Barros e ARAGÃO, Ildema Gomes. Possibilidades e Limitações: as dificuldades existentes no processo de ensino-aprendizagem da Matemática. InfoEscola. 2015. Disponível em: https://www.infoescola.com/pedagogia/possibilidades-e-limitacoes-as-dificuldades-existentes-no-processo-de-ensino-aprendizagem-da-matematica. Acesso em: 22 maio 2019.
SANTOS, Josiel Almeida, FRANÇA, Kleber Vieira e SANTOS, Lúcia S. B. dos. Dificuldades na Aprendizagem de Matemática. (Monografia) Licenciatura em Matemática. Centro Universitário Adventista de São Paulo, 2007.
SILVA, Meiriane Vieira da. As dificuldades de aprendizagem da Matemática e sua relação com a matofobia. (Monografia) Especialização em Fundamentos da Educação: Práticas Pedagógicas Interdisciplinares. Universidade Federal da Paraíba, 2014.
SILVA, Raquel Silveira da, MARTINEZ, Márcia Lorena Saurin. Dificuldades na Matemática básica: o processo de ensino-aprendizagem para a vida. XIII EDUCERE, IV SIRSSE, VI SIPD – Cátedra UNESCO (Anais), 2017.
SILVA, V. A. Relação com o saber na aprendizagem matemática: uma contribuição para a reflexão didática sobre as práticas educativas. Revista Brasileira de Educação, v.13, n.37, jan./abr. 2008.
TIRITAN, Carolina Doranti. Cartografia. Batatais: Claretiano, 2013.
TURNER, Lea Ann. Using Google Maps to teach Math. Technology Applications Teacher Network, 2018.
Use Google Maps to teach Math. 2015. Disponível em: https://www.lessonplanet.com/teachers/use-google-maps-to-teach-math. Acesso em: 22 maio 2019.
FAJARDO, Vanessa e FOREQUE, Flavia. 7 de cada 10 alunos do ensino médio têm nível insuficiente em português e matemática, diz MEC. G1. 2018. Disponível em: https://g1.globo.com/educacao/noticia/2018/08/30/7-de-cada-10-alunos-do-ensino-medio-tem-nivel-insuficiente-em-portugues-e-matematica-diz-mec.ghtml. Acesso em: 22 maio 2019.
1Engenheiro Cartógrafo (IME), Licenciado em Matemática e Geografia (Claretiano), Mestre em Informática (UFAM), Doutor em Planejamento Urbano e Regional (UFRJ) Universidade do Estado do Rio de Janeiro – Professor Adjunto – Instituto Municipal de Urbanismo Pereira Passos – Pesquisador – Universidade do Estado do Rio de Janeiro, Faculdade de Engenharia, Departamento de Engenharia Cartográfica
luiz.coelho@eng.uerj.br
https://orcid.org/0000-0002-4466-9772
http://lattes.cnpq.br/6920722851435707
