REGISTRO DOI: 10.5281/zenodo.8136720
Raphael Henrique Lobato de Assumpcão¹
Leonardo Monteiro Trotta²
RESUMO
A álgebra linear é uma das áreas mais importantes da matemática, por estar presente em diversas profissões e no cotidiano das pessoas. O ensino e aprendizagem da álgebra linear nos cursos das ciências exatas, tem sido bastante desafiador, devido toda a abstração necessária para a compreensão dos conceitos. Dessa forma, é necessário o profissional da educação repensar constantemente em estratégias para inovar a sua didática, para assim, buscar promover uma aprendizagem significativa e dinâmica. Assim, este trabalho propõe utilizar o software GeoGebra como estratégia de promoção desta dinâmica, e assim, gerar uma aprendizagem significativa. Este artigo apresenta uma análise experimental do software numa aplicação de resolução e visualização gráfica de sistemas lineares. Ao fim, mostramos que houve uma aprovação significativa dos professores, em relação ao uso do software como recurso pedagógico no ensino da álgebra linear. Esperamos mostrar como esta pesquisa ajudará os estudantes a compreenderem e visualizarem melhor alguns conceitos trabalhados em sala de aula, além de deixar o conteúdo mais interessante.
Palavras-chave: Aprendizagem significativa. Álgebra Linear. Geogebra.
ABSTRACT
Linear algebra is one of the most important areas of mathematics, as it is present in many professions and in people’s daily lives. The teaching and learning of linear algebra in exact sciences courses has been quite challenging, due to all the abstraction needed to understand the concepts. In this way, education professionals have to think of strategies to innovate their didactics, in order to promote meaningful and dynamic learning. Thus, this work proposes to use the GeoGebra software as a strategy to promote dynamic didactics, and thus generate meaningful learning. This article presents an experimental analysis of the GeoGebra software in an application for solving and graphical visualization of linear systems. Therefore, there was a significant approval from teachers regarding the use of geogebra software as a pedagogical resource in the teaching of linear algebra, as it will help students to better understand and visualize some concepts worked in the classroom, in addition to making the content more pleasant and interesting.
Keywords: Meaningful learning. Linear algebra. Geogebra.
1 INTRODUÇÃO
É muito comum o professor de matemática se encontrar na situação no qual a turma não demonstra interesse no assunto, apresenta dificuldade e não está disposta a seguir as orientações recebidas. Dessarte, o professor tem que pensar em estratégias para aprimorar e inovar a sua metodologia de ensino, promovendo uma aula mais dinâmica e atrativa.
Muitos alunos surgem com o seguinte argumento: “Por que aprender sobre algo que nunca vou utilizar na vida?”. Esse argumento é difícil de ser confrontado, ainda que quase todas as teorias da matemática sejam habitualmente utilizadas no cotidiano. No ensino médio, principalmente, são apresentadas teorias que, para o senso comum, seriam direcionadas para profissões específicas e situações essencialmente técnicas (CÓSER FILHO, 2008).
Todos ainda reconhecem o papel das instituições de ensino no desenvolvimento intelectual, social e afetivo do cidadão. Por extensão, na contemporaneidade do século XXI, há mudanças contínuas, com avanços nas Tecnologias Digitais de Informação e Comunicação (TDIC), que provocam mudanças no processo de ensino-aprendizagem, numa tentativa de crescimento, maturidade e o desenvolvimento com as pessoas num mundo globalizado. Nesse processo, o professor assume um papel ainda mais desafiador na aprendizagem, buscando utilizar de ferramentas pedagógicas que venham a contribuir com a construção de conhecimento do aluno.
Em relação ao ensino da matemática, existem diversos recursos que podem auxiliar a aprendizagem dos conteúdos, como os recursos disponíveis na internet, softwares, jogos educativos, entre outros. Partimos da consideração que grande maioria dos alunos do Ensino Médio possuem dificuldade em matemática, como afirma a mestranda do Programa de Pós-graduação em Gestão e Avaliação da Educação pública, Tatiane Gonçalves Moraes. A autora aponta: “Os alunos estão saindo do Ensino Médio com o mesmo conhecimento matemático dos estudantes do Ensino Fundamental” (MORAES; FERREIRA, 2017).
Entendemos que o objetivo de todos os professores é promover o ensino de qualidade para os alunos, através de uma boa didática e prática pedagógica, conquistando o interesse e atenção dos estudantes. Para isso, é importante que o docente inove nas suas estratégias pedagógicas para promover uma aprendizagem mais eficaz.
Segundo a teoria de Ausubel, a aprendizagem é muito mais significativa à medida que um novo conhecimento é incorporado ao aluno, a partir de um conhecimento já existente na sua estrutura cognitiva (PELIZZARI et al., 2002), ou seja, há uma estrutura de conhecimento que vai sendo construída de maneira espiralar diante de um novo desafio. Ao contrário, se a aprendizagem se define como mecânica, no qual a memorização é considerada a única forma de aprender, o caminho metodológico não funciona na trajetória da construção de conhecimento e pode fazer com que os alunos percam o interesse pelo conteúdo a ser ensinado.
Assim, este trabalho abordará a importância do professor em inovar na sua didática, utilizando as TDICs para promover uma aprendizagem significativa, mais especificamente, na álgebra linear, visto que é uma área da matemática que está presente em inúmeras profissões, como, Ciência da Computação, Engenharias no geral, Geologia; e onde os estudantes possuem dificuldades de entendimento, por conter teorias que envolvam muitos conceitos e cálculos. Além do mais, a álgebra linear também introduz uma linguagem e um raciocínio bastante complexo, no qual o aluno que a estuda pela primeira vez, pode de fato apresentar bastante dificuldade.
Dessa forma, essas dificuldades contribuem diretamente para a problemática desta pesquisa, juntamente com o distanciamento e a abordagem formal e técnica adotada pelos professores, gerando um sentimento de frustração nos alunos, causado pela sensação de pouco envolvimento com o componente. Assim, colocamos o seguinte problema: Como explorar as potencialidades das tecnologias no ensino da matemática, para promover uma aprendizagem mais dinâmica e significativa no processo de ensino e aprendizagem da álgebra linear?
Apesar das dificuldades de aprendizagem da álgebra linear, tanto no ensino médio, quanto no superior, percebe-se que há um número reduzido de pesquisas em educação matemática que explique a principal causa dessas dificuldades e que apresentem alternativas para o ensino dessa disciplina, visando amenizar tais problemas (KRIPKA et al., 2018).
Um fato que também nos chama a atenção é o crescimento exponencial da tecnologia e o seu uso nas salas de aula, os quais têm influenciado os estudantes nas formas de agir, pensar e conviver. Este é um caminho que pode facilitar a mediação do professor na construção de conhecimento. Assim, nossa hipótese dar-se-á por meio das TDICs serem uma boa alternativa que fortaleça o conhecimento dos alunos e consiga gerar uma maior interação entre o professor e aluno, para assim, promover uma maior proximidade e, consequentemente, facilitar o processo de ensino e aprendizagem.
Desta forma, esta pesquisa propõe especificamente o ensino da álgebra linear, por meio das Tecnologias Digitais de Informação e Comunicação (TDICs), com a intenção de promover uma aprendizagem significativa por meio do software Geogebra, podendo ser este um excelente aliado durante o processo de ensino e aprendizagem. Entendemos que desta forma podemos gerar mais interesse no aluno, pelo fato dele se sentir mais estimulado e curioso em aprender, já que a proposta é partir das suas relações de usuário de tecnologia e de vincular os conhecimentos da álgebra linear com suas situações do cotidiano.
2 AVALIAÇÃO DA APLICABILIDADE EM SALA DE AULA
A utilização de recursos tecnológicos digitais no contexto escolar é uma linha de trabalho que precisa ser fortalecida, pois existe uma distância significativa entre o avanço tecnológico na produção de softwares educacionais gratuitos e a compreensão e utilização desses recursos nas aulas pelos docentes.
Primeiramente, vale destacar que diversos docentes não estão devidamente preparados para utilizar as TDIC na sala de aula, uma vez que não possuem os conhecimentos e habilidades necessárias para integrar a tecnologia na sua prática pedagógica. O segundo fator que pode ser evidenciado é a importância ainda exagerada do livro escolar tradicional, em detrimento de outras possibilidades educacionais. Nele, a álgebra linear é apresentada simplesmente como um conjunto de definições, propriedades, nomes e fórmulas, colocadas exclusivamente no papel, desconectada a aplicações de natureza histórica, coerente, concretas e/ou cotidianas.
A proposta de utilização de um software matemático no processo de ensino e aprendizagem de álgebra pode contribuir em muitos fatores, principalmente em termos de visualização gráfica, além de permitir que a natureza geométrica inerente à álgebra linear seja ampliada e não reduzida à abordagem algébrica tradicional. A capacidade de visualização pode ser desenvolvida, desde que o aluno disponha de material didático de apoio, baseado em elementos concretos representativos do objeto geométrico em estudo.
Nos cursos de graduação, pensando no processo de ensino e aprendizagem da disciplina de álgebra linear, o conteúdo de sistemas lineares costuma ser inserido de forma clássica, sem a inserção de outros recursos, exceto lousa e giz. Não é que essa abordagem seja insatisfatória, porém, ao revisar os conteúdos e as possibilidades de abordagem nessa disciplina, percebe-se que o dinamismo gerado pelo software GeoGebra pode esclarecer muitas dúvidas e auxiliar os alunos a compreender os objetos de forma mais simples e dinâmica.
Assim, a maior parte das atividades do recurso digital construído consiste em visualizar os sistemas lineares e sua representação gráfica. Outrossim, permite a construção e manipulação de objetos visualmente por meio de comandos de programação. O intuito é que o estudante entenda de fato as definições da álgebra linear.
Para melhor embasamento da presente pesquisa, foi realizada uma entrevista com professores de matemática de nível fundamental, médio e superior, em relação à metodologia adotada por eles em sala de aula. A entrevista teve como objetivo analisar se os profissionais da educação conhecem e/ou aplicam métodos de aprendizagem significativos e dinâmicos em sala de aula e se os resultados obtidos são realmente satisfatórios, em relação ao processo de ensino e aprendizagem.
O apêndice 1³ ilustra a opinião dos professores sobre a aprendizagem significativa, no qual constataram que já utilizam essa abordagem em sala de aula e concordaram que o emprego das tecnologias como forma de enriquecer o processo de ensino e aprendizagem pode ajudar os estudantes no processo de aprendizagem de conteúdo. No entanto, foi possível observar que houve uma maior relutância em relação ao contexto histórico dos alunos, isto é, na grande maioria dos casos, eles não são tão habituados com o método de ensino que aborda o uso de tecnologias, principalmente se os estudantes vieram da rede pública de ensino4. Além disso, os profissionais da educação entrevistados relataram que, apesar de concordar com a proposta metodológica, seria necessário pôr em prática para analisar se os resultados obtidos realmente seriam satisfatórios.
3 CAMINHOS METODOLÓGICOS
A proposta da utilização de softwares matemáticos no processo de ensino e aprendizagem da álgebra linear, pode contribuir em diversos fatores, principalmente relacionados a visualização de gráficos. Os alunos podem adquirir habilidades de visualizar e interpretar os gráficos à medida que se forneçam materiais de apoio didáticos baseados em elementos representativos do objeto em estudo.
De acordo com Nascimento (2012), no ensino fundamental e, principalmente, no ensino médio, os estudantes devem trabalhar com modelos sólidos e com materiais visuais. O autor ainda afirma que, em diversas situações, o aluno se sente mais confortável com o uso de tecnologias do que o próprio docente, pois nos últimos anos os adolescentes e jovens fazem o uso dessa tecnologia com mais frequência.
Assim, softwares educativos representam grandes possibilidades de simulação, já que proporcionam situações virtuais que possibilitam grande proximidade com a realidade, além de possibilitar a geração de um ambiente colaborativo. Este artigo apresenta agora uma análise experimental do software GeoGebra numa aplicação de resolução e visualização gráfica da função do primeiro grau, abordando ainda conceitos básicos do plano cartesiano, como o quadrante.
4 APLICAÇÃO DA ÁLGEBRA LINEAR NO SOFTWARE GEOGEBRA
O GeoGebra é um software de matemática para todos os níveis que reúne geometría, álgebra, planilha de cálculos, gráficos, probabilidade, estatística e cálculos numéricos. Esse software se tornou um líder na área dos softwares de matemática dinâmica, por apoiar o ensino em ciência, tecnologia, engenharia e matemática (GEOGEBRA, 2021).
O GeoGebra foi desenvolvido através de uma tese de doutorado de Markus Hohenwarter em 2001, na Universidade de Salzburgo, para ser uma ferramenta utilizada durante as aulas de matemática, no entanto, hoje em dia, conta com a colaboração de inúmeros pesquisadores e cientistas e está em constante crescimento.(DE SANTANA et al, 2019).
Sua interface, composta por janelas, traz muitas contribuições para o processo de aprendizagem da matemática, como ilustra a Figura 1. As operações básicas do software são apresentadas no Quadro 1
Figura 1 – Software GeoGebra.
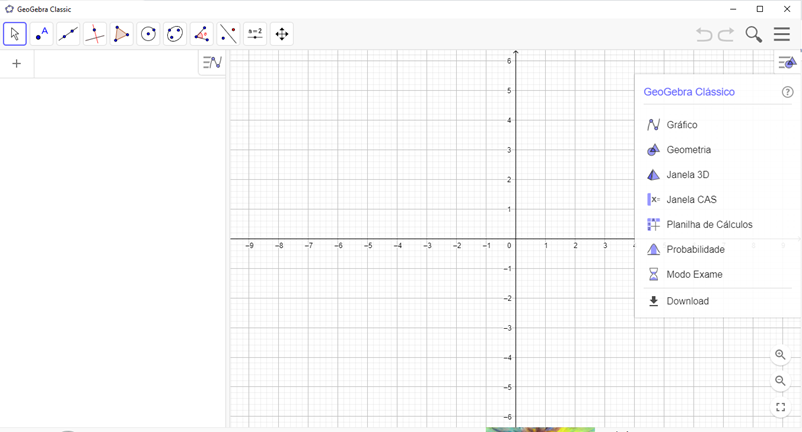
Quadro 1 – Operações do GeoGebra.
Operação Símbolo Exemplo Adição + 8+9 Subtração – 8-9 Divisão / 8/9 Multiplicação * 8*9 Potenciação ^ 8^9 Módulo abs() abs(-8) Raiz Quadrada sqrt() sqrt(4) Raiz ^(m/n) 8^(1/3) = ³√8 Fatorial ! 8! Número Primo ÉPrimo() Éprimo (3), resposta: True
Éprimo (8), resposta: FalseMínimo Múltiplo Comum MMC (,) MMC (8,9) Máximo Divisor Comum MDC (,) MDC (8,9)
Para aplicação de algumas das definições já vistas, apresenta uma demonstração de alguns exemplos, nos quais pode ser relacionado a aplicabilidade e conciliação do campo teórico com o cotidiano e ilustrativo com o uso do software.
Exemplo 1: Aula – Localização no plano
Função do 1º grau João deseja ver sua namorada Maria que mora a 10 quilômetros, mas deseja fazer o trajeto de táxi e deseja saber a estimativa, considerando, que o preço de partida é de R$5,90 e por cada km rodado é de R$2,90, qual valor a ser pago no trajeto desconsiderando fatores não apresentados no enunciado
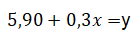
A Figura 2 mostra a resolução do sistema do através do GeoGebra. Observe na Figura 2 que o eixo vertical, y, representa a unidade monetária da moeda(dinheiro) horizontal, x, representa o deslocamento do automóvel.
Assim, para se obter a estimativa de uma corrida de táxi, levando em consideração somente o deslocamento como variável, é possível prever seu valor ao realizar a interseção de duas retas. A primeira, no caso em tela demonstrado na cor verde, representa a reta da função do primeiro grau ou afim:
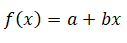
Ressalta-se que a referida reta possui uma inclinação ascendente para o lado direito do plano cartesiano5, representando que
A segunda, de cor vermelha, será traçada sobre o eixo horizontal, x, representando o deslocamento do veículo.
A reta de cor verde corresponde à progressão do valor da corrida, sendo determinado o valor preciso da corrida de acordo da interseção da reta azul que especifica a quilometragem da corrida. Este ponto de interseção é exatamente a desenvoltura da cobrança de uma corrida de táxi tendo como única variável a quilometragem.
Inicia-se a proposta da abordagem didática com a entrada do passageiro no taxi, ou seja, o mesmo não percorreu nenhum quilômetro, tendo x=0, logo, tem-se y como valor de R$5,90(cinco reais e noventa centavos), vejamos:
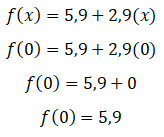
Figura 2: Ilustração inicial do Exemplo1: x=0.
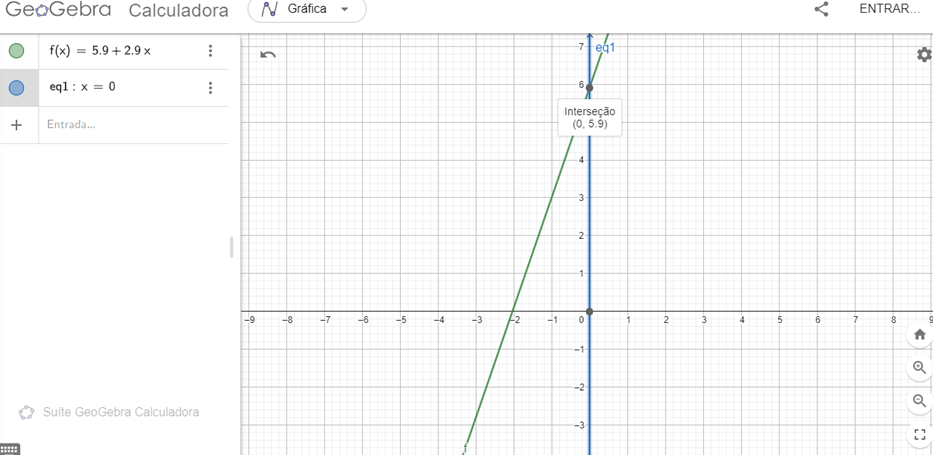
Importante destacar que o geogebra possui como plano de fundo ao plano cartesiano possui linhas finas, singelas, em ambos os eixos, assemelhando-se a uma folha milimetrada que facilita a percepção do aluno no espaço ao correlacionar o ponto de interseção das retas e assim ter uma projeção no eixo “x”
Outrossim é a possibilidade da explicação através da ilustração, sobre os quadrantes, no caso em tela estar-se-á trabalhando no primeiro quadrante pois “x” e “y” estará sempre empregado valores positivos. Prosseguindo para a resolução do problema proposto, substitui-se o valor de “X”, para 9(nove), obtendo-se o valor da corrida, “y”, como 32, vejamos:
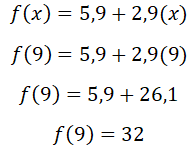
Figura 3: Ilustração do Exemplo1: x=9.
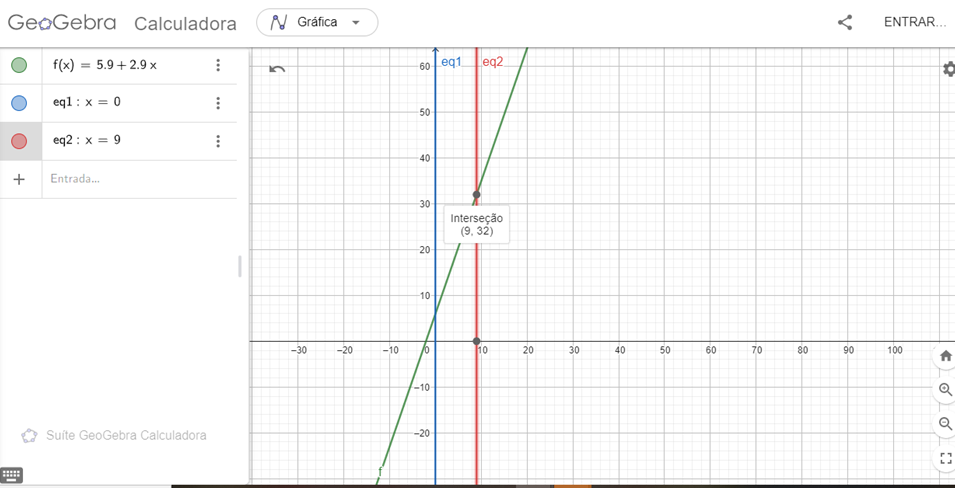
Diante das ilustrações apresentadas será possível apresentar, a representação das coordenadas (x, y), bem como o conceito de variável independente, x, e variável dependente, “y”, demonstrando que esta sofrerá variação em detrimento do valor especificado por aquela, ou seja, quem norteará a localização do espaço será a coordenada “x”, que incidirá de forma substitutiva na equação a fim de se obter um determinado valor.
Em seguida, o professor com maior interação com a turma poderá explorar a variação do deslocamento(quilometragem) do taxi(“x”), pedindo sugestão da turma, nesse aspecto fazendo quantas operações quiserem sem a necessidade de apagar lousa, que deixa rastro.
Observe que é possível deixar registrado os valores atribuídos a “x”, quando se atribui o valor de zero o software atribuiu a nomenclatura a equação de “eq1” e identificou a reta na cor azul, na segunda equação como “eq2” e cor vermelha, possibilitando visualmente identificar a localização no espaço em função da variável independente “x”, a obtenção do valor da coordenada dependente “y”, possibilitando infinitas possibilidades de exploração do software, dependendo das inúmeros variáveis que afligem o ambiente educacional, assim, caso o professor deseja explorar ainda o software e aprofundar nos seus ensinamentos poderá propor por exemplo a continuação da situação problema com fatos ainda dentro do cotidiano, ao sugerir o questionamento:
Exemplo 2 – Comparação entre as localizações
João e Maria desejam ir ao teatro que fica a 5 quilômetros da casa de Maria, o que sai mais barato João pegar um táxi e ir até a casa de Maria e depois pegar um outro para ir ao teatro ou irem no mesmo táxi?
Embora haja maneiras diferentes de abordar esta resolução, por motivo didático e por não haver a pretensão de exaurir o tema, mas de apresentar sugestões, serão apresentadas duas variações adaptativas do exemplo citado seguida cada uma da sua empregabilidade no Geogebra. Sabendo que Maria mora a 9 quilômetros de João e o teatro está a 5 quilômetros da casa dela, far-se-á a somatória das distâncias a fim de se obter o distanciamento total a ser percorrido pelo táxi, assim, tem-se x = 9 + 5 = 14, substituição na equação:
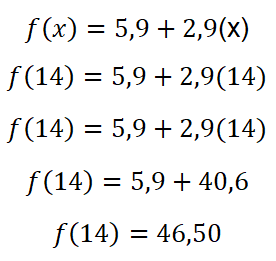
Para a elucidação desta equação o Geogebra, fora identificada como “eq1” e reta na cor verde, tendo as coordenadas identificadas (14, 46,5).
Figura 4: Ilustração do Exemplo 2: x=14.
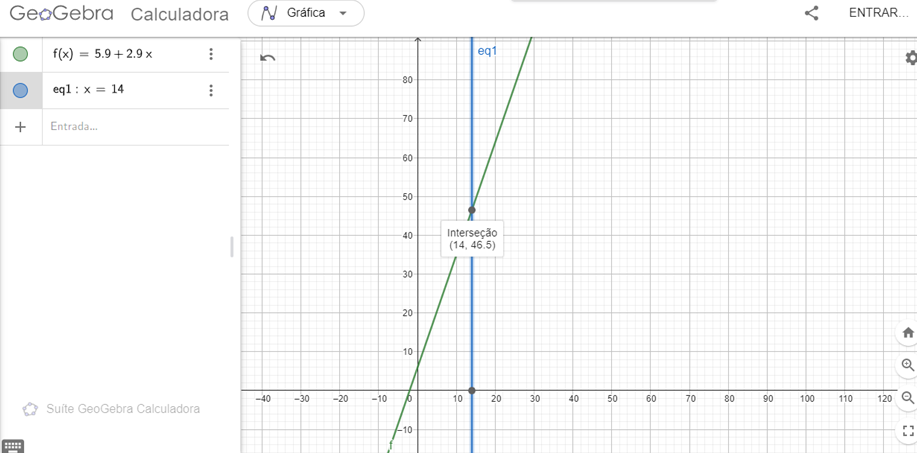
Na segunda hipótese, a fim de realizar uma desmistificação da apresentação da equação, tradicionalmente apresentada pelo f(x), representando desta vez, de forma sugestiva como g(x), a fim de apresentar uma forma didaticamente simplificada, será multiplicado o valor da partida por 2(dois), representando a quantidade de vezes iniciou a corrida, visto que a distância permanece a mesma de 14(quatorze) quilômetros, tendo assim a seguinte expressão:
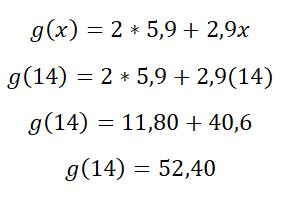
Figura 5: Ilustração do Exemplo 2: dobrando o valor da partida e x=14.
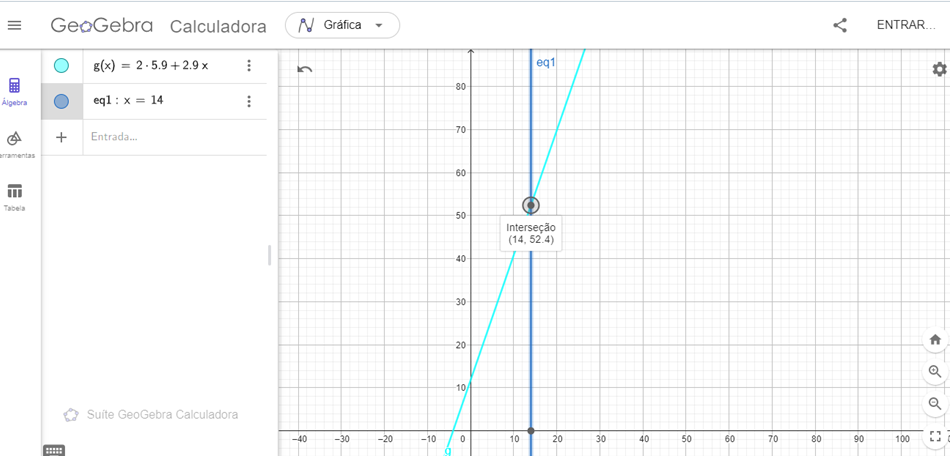
Para a elucidação desta equação o Geogebra, fora identificada como “eq1” e reta na cor verde, tendo as coordenadas identificadas (14, 46,5). O Geogebra permite trabalhar e apresentar a aplicabilidade de mais de uma equação, sobre uma mesma coordenada, como se observa:
Figura 6 : Ilustração do Exemplo 2: sobreposição de equações sobre uma mesma coordenada – g(x).
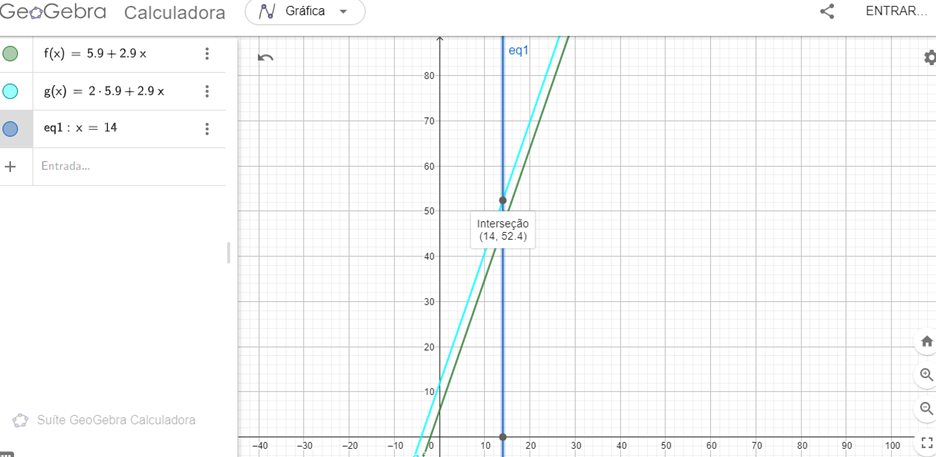
Desta forma, caracteriza a importância da empregabilidade do Geogebra, como instrumento de ensino, diferenciando do ensino tradicional ao possibilitar a demonstração gráfica, mais limpa, fluida, alterável e adaptável a cada empregabilidade desejada, inclusive armazenando registros, para comparações e sobreposições, o que muita das vezes fica comprometido com a empregabilidade similar na lousa, além de tornar mais didático, interativo e célere o processo de ensino, pelo fato do próprio software realizar de forma automática a exposição visual, possibilitando o professor utilizar melhor o tempo em sala de aula. Acrescentamos que são possibilidades a serem trabalhadas em sala pelo professor, as competências descritas na BNCC para o campo matemático. Acreditamos que competências como argumentação, comunicação e pensamento crítico podem ser amplamente trabalhadas a partir do uso do software, partindo de metodologias ativas como a problematização e aprendizagem colaborativa que podem provocar uma participação mais ativa do estudante que provocado pelo professor, otimiza seus questionamentos matemáticos, fugindo ao estereótipo de passividade e fuga para com o componente, o que já foi apresentado na introdução deste artigo.
5 CONCLUSÃO
Este trabalho foi desenvolvido para abordar a aprendizagem significativa como estratégia para inovar o processo de ensino e aprendizagem da álgebra linear, por meio do uso didático das Tecnologias Digitais de Informação e Comunicação (TDICs) e com a proposta de trazer o software geogebra para aprimorar o conhecimento dos estudantes, para assim, propor uma abordagem interativa e significativa, que o aluno possa vincular os novos conhecimentos, com outros preexistentes na sua estrutura cognitiva.
A pergunta norteadora deste trabalho foi: “Como explorar as potencialidades das tecnologias no ensino da matemática, para promover uma aprendizagem mais dinâmica e significativa no processo de ensino e aprendizagem da álgebra linear?”.
Conforme as percepções identificadas, a questão defendida é que o uso das TDICs favorecem a didática do professor e enriquecem a aprendizagem do aluno. Dessa forma, foi proposto o software Geogebra como uma forma de inovar no processo de ensino e aprendizagem, saindo daquele ensino tradicional, no qual o professor apenas expõe o conteúdo e o aluno o recebe. Assim, o estudante irá compreender melhor os conceitos matemáticos, comparando os resultados obtidos por meio dos cálculos realizados e do software, bem como irá observar e compreender os gráficos esboçados pelo software.
Além disso, haverá uma interação maior entre o aluno e o professor, por meio da ampliação da prática pedagógica do docente, que proporcionará novas experiências e conceitos, relacionando conhecimentos de informática, com os pedagógicos. Salienta-se que a integração da informática com o ensino, faz com que o professor se aproprie de uma nova postura que seja capaz de gerir situações que envolvam o Geogebra em sala de aula.
Vale ressaltar que o professor não deve apenas dominar a tecnologia do Geogebra. É necessária uma proposta pedagógica bem definida que seja capaz de proporcionar experiencias aos estudantes e que contribuam no processo de aprendizagem.
Para melhor entendimento da proposta desta pesquisa, também foi abordado alguns conceitos da álgebra linear, bem como o passo a passo da resolução de questões que podem ser realizadas manualmente e por meio do software geogebra, para que o aluno consiga entender as duas maneiras da resolução de exercícios. Portanto, ao adotar e incentivar o uso de tecnologias na sala de aula, o professor proporcionará ao estudante uma forma mais simples e segura de tornar o ensino mais atraente e dinâmico, além de criar possibilidades de ilustrar graficamente de forma concreta as soluções, visto que são, muitas das vezes, analisadas de maneira abstrata.
³Trazemos aqui, apenas a título de ilustração, um pequeno apanhado das opiniões coletadas.
4Há aqui a abertura de um outro debate que veio à tona com a pandemia de Covid-19 que é a ausência ou precarização tecnológica por parte das escolas públicas e pela própria família brasileira de maneira geral.
5O Plano cartesiano foi idealizado por René Descartes. Consiste num objeto matemático plano representado por duas retas perpendiculares numeradas possuindo apenas um ponto em comum, 0(zero), obtido no angulo de 90°(noventa graus), identificado como origem, ponto de partida. Sendo usualmente utilizado para localização no plano.
REFERENCIAS
CÓSER FILHO, Marcelo Salvador. Aprendizagem de Matemática financeira no Ensino Médio: uma proposta de trabalho a partir de planilhas eletrônicas. Dissertação (Mestrado em ensino de matemática). Universidade Federal do Rio Grande do Sul. Porto Alegre, 2008.
DE SANTANA, Fabiana Tristão et al. Inovação no processo de ensino e aprendizagem de álgebra linear usando o software geogebra. Brazilian Journal of Development, v. 5, n. 9, p. 15095-15105, 2019.
GEOGEBRA. O que é Geogebra? 2022. Disponível em: https://www.geogebra.org/about?lang=pt-PT. Acesso em: 01 ago 2022.
KRIPKA, Rosana Maria Luvezute et al. Uso de tecnologias digitais no ensino e na aprendizagem de álgebra linear na perspectiva das teorias da aprendizagem significativa e dos registros de representação semiótica. Tese (doutorado) – Programa de pós-graduação em educação em ciências e matemática. Pontifícia Universidade Católica do Rio Grande do Sul. Porto Alegre, 2018.
MORAES, Tatiane Gonçalves; FERREIRA, Rosângela Veiga Júlio. Pesquisa identifica dificuldades de aprendizado de matemática entre os alunos do ensino médio. UFJF. 2017. Disponível em: < https://www2.ufjf.br/noticias/2017/03/08/pesquisa-identifica-dificuldades-de-aprendizado-de-matematica-entre-alunos-do-ensino-medio/>. Acesso em: 09 jul. 2022.
NASCIMENTO, Eimard GA do. Avaliação do uso do software GeoGebra no ensino de geometria: reflexão da prática na escola. XII Encontro de Pós-Graduação e Pesquisa da Unifor, ISSN, v. 8457, p. 2012, 2012.
PELIZZARI, Adriana et al. Teoria da aprendizagem significativa segundo Ausubel. revista PEC, v. 2, n. 1, p. 37-42, 2002.
RAFAEL, Thayná Fernandes; SOUZA, Bianca Maria Inês. Informática na matemática: o uso do excel no ensino-aprendizagem da matemática financeira do 3ºano do ensino médio. Matemática-Tubarão, 2018.
¹Mestrando em Novas Tecnologias Digitais na Educação no Centro Universitário Carioca/Unicarioca. E-mail: rhlobato@gmail.com
²Doutor em ciência da literatura e professor no curso de Novas Tecnologias Digitais na Educação no Centro Universitário Carioca/Unicarioca.
