GEOGEBRA SOFTWARE AS A TOOL FOR TEACHING ANALYTICAL GEOMETRY AT EEMTI LICEU VILA VELHA
REGISTRO DOI: 10.69849/revistaft/ni10202408111720
Francisco Diego Moreira Oliveira; Regina Maria Lima Rocha; Osiel Gomes da Silva; Nilo Pinheiro Landim; Ana Maria Pinheiro; Alan Bruno Lopes Barbosa; Adriano Melo Araujo
RESUMO
O presente trabalho tem como objetivo apresentar uma metodologia diferenciada de ensino da geometria analítica no ensino médio com o auxilio do software GeoGebra. Para isso é apresentado uma sequência de atividades desenvolvidas pelos autores em que são propostas construções que envolvem os conteúdos básicos da geometria analítica. O trabalho também apresenta um estudo histórico da geometria analítica e sua importância na atualidade. Também é feito um estudo da importância e as contribuições que as Tecnologias da Informação e Comunicação (TICs) podem fazer para o ensino da matemática, bem como as orientações provenientes dos Parâmetros Curriculares Nacionais (PCNs) que incentivam a utilização das TICs. Para um melhor desenvolvimento do trabalho é realizado um aprofundado estudo do software GeoGebra. Logo após as atividades propostas, é apresentado um estudo de caso realizado com uma turma do terceiro ano do ensino médio na EEMTI (Escola de Ensino Médio Em Tempo Integral) Liceu Vila Velha no ano de 2014, neste estudo são analisados tanto os resultados qualitativos como também a opinião dos alunos sobre o uso das TICs em sala de aula e mais especificamente do GeoGebra como ferramenta para o ensino da geometria analítica. Por fim, são feitas considerações e conclusões positivas com relação a realização do trabalho e também considerações sobre as dificuldades encontradas e as perspectivas para suas aplicabilidades futuras.
Palavras-chave: Geometria Analítica, Ensino, GeoGebra, TICs.
ABSTRACT
This paper aims to present a methodology differentiates teaching of analytic geometry in high school with the help of GeoGebra software. For this sequence of activities developed by the authors that are proposed constructions involving the basic contents of analytic geometry is presented . The paper also presents a historical study of analytic geometry and its importance today. Also made a study of the importance and contribution that Information and Communication Technologies ( ICT ) can make to the teaching of mathematics as well as the guidelines from the National Curricular Parameters ( PCN ) that encourage the use of ICTs . For better development of the work a thorough study of GeoGebra software is performed . Shortly after the proposed activities , a case study conducted with a group of third year of high school at EEMTI(High School) Vila Velha, this study analyzes both the qualitative results as well as the students’ opinion on the use of ICTs in the room is shown classroom and more specifically the GeoGebra as a tool for the teaching of analytic geometry . Finally, consideration and positive conclusions are made regarding the completion of the work and also considerations on the difficulties encountered and the prospects for its future applicability.
Keywords: Analytic Geometry , Education , GeoGebra , ICT
INTRODUÇÃO
Um dos grandes desafios para o professor de matemática do ensino médio, atualmente, é conseguir fazer com que o aluno se interesse por assuntos cada vez mais complexos. De acordo com Markarian (1998), o objetivo da matemática se torna, de certa forma, imperceptível, visto que as abstrações contidas nas primeiras noções estudadas no ensino de matemática constituem um processo de difícil assimilação, erros cometidos nesta etapa podem causar traumas futuros desmotivando o aluno para o estudo da matemática. Um dos conteúdos que apresentam essa dificuldade é a Geometria Analítica Plana, normalmente ministrada no terceiro ano do ensino médio, que exige uma variedade de competências por parte do aluno.
Também é perceptível que, com o avanço tecnológico e nossa dependência diária das novas Tecnologias da informação e comunicação, existe uma necessidade de trazer tais tecnologias para dentro da sala de aula, para que assim o próprio sistema de ensino não se torne defasado.
Pensando nisso, esse trabalho foi desenvolvido com o objetivo de torna o ensino e aprendizado da matemática algo menos complexo, que esteja mais próximo da realidade do aluno, do seu dia a dia, utilizando as Tecnologias da Informação e Comunicação (TICs) como ferramenta.
O uso das TICs já é amplamente reconhecido como algo benéfico para o ensino. Na matemática esse reconhecimento vem através da grande quantidade de softwares desenvolvidos como o objetivo de auxiliar o professor a expor e dinamizar os conteúdos relativos à matemática.
Um dos softwares que possui maior reconhecimento por parte dos professores de que é uma excelente ferramenta para o ensino da matemática é o GeoGebra, por sua diferenciação dos outros softwares ao juntar em um mesmo ambiente virtual a geometria e a álgebra. A partir destas observações foi desenvolvido neste trabalho uma sequência de atividades práticas para sala de aula em que o software GeoGebra é utilizado como ferramenta para o ensino da geometria analítica plana, dando maior enfoque nos conteúdos relativos a ponto, reta e circunferência.
O trabalho foi desenvolvido em x topicos, no primeiro é feito uma abordagem histórica da geometria analítica, quais seus principais estudiosos e desenvolvedores e também uma abordagem de qual a sua importância atualmente. No segundo tópico é feito um estudo da importância do uso das TICs na sala de aula, dando um enfoque no estudo e ensino da geometria analítica e também nas orientações que os Parâmetros Curriculares Nacionais (PCNs) dão em relação à utilização das TICs e o ensino da matemática. No terceiro capítulo é feita uma apresentação bem do software GeoGebra. No quarto tópico é apresentada uma sequência de cinco atividades, desenvolvidas pelos autores, que são sugeridas como uma forma de tornar as aulas de geometria analítica mais interessantes, dinâmicas e com um maior rendimento por parte dos alunos. No quinto tópico é apresentado um estudo de caso, realizado na EEMTI Liceu Vila Velha na cidade de Fortaleza-CE no ano de 2014. Em tal estudo, as atividades propostas no quarto tópico são aplicadas a uma turma de terceiro ano de ensino médio para uma análise qualitativa dos resultados obtidos. A análise levou em conta o aumento do rendimento e interesse dos alunos pela geometria analítica, e também a opinião destes alunos com relação ao uso das TICs em sala de aula, mais especificamente, o uso do GeoGebra para o ensino de geometria analítica. No sexto e último tópico são feitas considerações finais sobre o trabalho, a sua aplicabilidade, as dificuldades encontradas e as expectativas dos autores com relação à contribuição que o trabalho pode trazer para ajudar os colegas docentes no desafio que é ensinar matemática.
1. GEOMETRIA ANALÍTICA PLANA: DA SUA CRIAÇÃO AOS DIAS DE HOJE.
A Geometria Analítica é normalmente abordada no 3º ano do ensino médio, seu enfoque é quase que exclusivamente na Geometria Analítica Plana, com ênfase nos conteúdos Ponto, Reta e Circunferência.
Como se trata de um conteúdo com várias aplicações em nosso cotidiano, a maioria dos livros didáticos faz uma abordagem mais prática, tentando relacioná-la ao dia-a-dia do aluno e buscam ao máximo propor atividades que possam tornar o seu aprendizado mais dinâmico. Muitos destes livros já trazem sugestões de atividades com a utilização de softwares de geometria dinâmica. Um bom exemplo vem dos livros da coleção “Matemática Completa” de Giovanni & Bonjorno, livro didático bastante utilizado e reconhecido como um dos melhores da Matemática do ensino médio, que em suas versões mais atuais já trás sugestões de atividades com o uso das TICs.
De acordo com Guedes (2013) em pleno século XXI muitos professores ainda tem dificuldade de lidar com o uso da informática enquanto que os alunos já nasceram nessa “Era Digital” e acham as aulas com esses recursos bem mais interessantes.
A principal motivação deste trabalho é trazer o enfoque de como o ensino e aprendizado da Geometria Analítica pode se tornar interessante com o uso de ferramentas que tragam mais dinâmicas às aulas e coloque os alunos em posição de protagonistas neste processo.
Objetivando dá um maior foco ao estudo da geometria analítica plana vamos fazer um resumo do histórico de seu desenvolvimento, aplicações e a importância do estudo de seus conteúdos para a humanidade nos dias de hoje. Eves (2004 p.382) ressalta como foi grandiosa a criação da Geometria Analítica:
Poucas experiências escolares podem ser mais emocionantes para o aluno do curso colegial avançado ou início de faculdade do que uma introdução a esse novo e poderoso método de enfrentar problemas geométricos. A essência da idéia, quando aplicada ao plano, lembre-se, consiste em estabelecer uma correspondência entre pontos do plano e pares ordenados de números reais, viabilizando assim uma correspondência entre curvas do plano e equações em duas variáveis, de maneira tal que para cada curva do plano está associada uma equação bem definida f (x, y) = 0 e para cada equação dessas está associada uma curva (ou conjunto de pontos) bem definida do plano. Estabelece-se, além disso, uma correspondência entre as propriedades algébricas e analíticas da equação f (x, y) = 0 e as propriedades da curva associada. Transfere-se assim, de maneira inteligente, a tarefa de provar um teorema em geometria para a de provar um teorema correspondente em álgebra e análise.
Percebe-se com o que foi exposto acima a importância do estudo da geometria analítica ao despertar o interesse dos estudantes visto a revolução que ela traz para o estudo da geometria.
1.1 Geometria Analítica nos dias atuais
A importância do estudo da Geometria Analítica nos dias atuais se dá pela sua principal característica, o fato de transformar problemas envolvendo figuras geométricas em problemas com equações. Essa característica, além de facilitar o entendimento humano, tornou muito mais fácil a sua aplicação em sistemas de informática, afinal, para um computador não é problema fazer cálculos, basta lhe programar com os algoritmos corretos. De acordo com Brasil (2007, p. 121):
O aluno deve perceber que um mesmo problema pode então ser abordado com diferentes instrumentos matemáticos de acordo com suas características. Por exemplo, a construção de uma reta que passa por um ponto dado e seja paralela a uma reta dada pode ser obtida de diferentes maneiras. Se o ponto e a reta estão desenhados em papel, a solução pode ser feita por meio de uma construção geométrica, usando-se instrumentos. No entanto, se o ponto e a reta são dados por suas coordenadas e equações, o mesmo problema possui uma solução algébrica, mas que pode ser representada graficamente.
É notório o fato de que como o foco principal do ensino médio é a preparação do aluno para o mercado de trabalho e para o ensino superior, então será necessário os conhecimentos básicos de Geometria Analítica. Mesmo que o aluno não tenha como objetivo as áreas que envolvam ciências exatas, o estudo da Geometria Analítica lhe proporciona uma melhor leitura de mundo.
Várias atividades de nosso dia-a-dia utilizam conhecimentos da Geometria Analítica, como, por exemplo, os aparelhos de GPS amplamente usados para navegação em terra, no ar ou no mar, utilizam conhecimentos básicos de localização de pontos representados por coordenadas. Os diversos gráficos de funções utilizadas pelos cientistas de hoje são melhor representados e estudados em um plano cartesiano. A engenharia civil e seus softwares de computador se baseiam no sistema cartesiano para criação de projetos. Em consonância com a álgebra linear a geometria analítica é utilizada para a programação de computadores desde sistemas simples de banco de dados aos mais complexos jogos eletrônicos.
Percebemos claramente o quanto a geometria analítica está presente em nosso cotidiano e como ela nos ajuda a entender melhor o mundo em que vivemos.
2. O ENSINO DA MATEMÁTICA E AS TECNOLOGIAS DA INFORMAÇÃO E COMUNICAÇÃO (TICs)
Entende-se por Tecnologia todo meio utilizado para facilitar a vida humana em seus vários momentos, por Informação a difusão dos conhecimentos passados, presentes e futuros, e por Comunicação o Meio pelo qual a informação é difundida. Desta forma pode-se dizer que as TICs fazem parte e são fundamentais no cotidiano e assim estão cada vez mais presentes na sala de aula. Uma prova disso é a utilização, por parte dos docentes, de computadores, projetores de imagem, TVs, DVDs e a internet, maior ferramenta de comunicação e informação, no ambiente educacional. Segundo Andrade (1996, p.23):
O Brasil iniciou a busca de um caminho para informatizar a educação em 1971, quando pela primeira vez se discutiu o uso de computadores no ensino de Física. Em 1973, algumas experiências começaram a ser desenvolvidas em outras universidades, usando computadores de grande porte como recurso auxiliar do professor para ensino e avaliação em Química (Universidade Federal do Rio de Janeiro – UFRJ) e desenvolvimento de software educativo na Universidade do Rio Grande do Sul – UFGS.
Ressaltamos o fato de que as atuais gerações têm como principal característica o fato de serem “Nativos Digitais”, isto é, pessoas que nasceram e tem contato precoce com as TICs tais como a Internet, compartilhamento de arquivos, telefones móveis, tablets e smartphones.
De acordo com Calil (2011) aulas tradicionais, onde o professor expõe o conteúdo de forma unilateral, propõe listas intermináveis de exercícios e aplica avaliações descontextualizadas, não despertam mais o interesse do aluno de hoje. O uso das TICs acaba sendo inevitável para dar esse diferencial nas aulas.
Assim, não há como negar a necessidade e o desafio que é atrelar as TICs aos métodos de ensino e aprendizagem, justamente pelo fato de elas atraírem mais a atenção e o interesse dos discentes.
2.1 Ensino e Aprendizagem da Matemática
A Matemática, historicamente, é descrita como uma disciplina complexa, de difícil aprendizado e também desafiador para os docentes e discentes. A frase “Eu odeio matemática” é bem comum por parte dos discentes e já praticamente estigmatizaram essa disciplina. Por outro lado, existe um grande reconhecimento da mesma como essencial no sistema de ensino, seja para desenvolver a capacidade de raciocínio-lógico do discente ou até mesmo para melhores chances de emprego no mercado de trabalho.
No ensino médio, o desafio para o ensino da Matemática é ainda maior, pois como os conteúdos são mais complexos, a não contextualização destes conteúdos acaba por prejudicar e muito o seu aprendizado, fazendo com que o aluno perca o interesse pelo mesmo e profira outra frase muito conhecida pelos professores de ensino médio: “Para que serve isso?”. A contextualização com o cotidiano do aluno, e a interdisciplinaridade, favorecem e muito o ensino da matemática, de acordo com Brasil (2007, p. 108):
Aprender Matemática de uma forma contextualizada, integrada e relacionada a outros conhecimentos traz em si o desenvolvimento de competências e habilidades que são essencialmente formadoras, à medida que instrumentalizam e estruturam o pensamento do aluno, capacitando-o para compreender e interpretar situações, para se apropriar de linguagens específicas, argumentar, analisar e avaliar tirar conclusões próprias, tomar decisões, generalizar e para muitas outras ações necessárias à sua formação.
As TICs por sua vez, facilitam o processo de contextualização dos conteúdos estudados no ensino médio.
3 O SOFTWARE GEOGEBRA
GeoGebra é um software de geometria dinâmica desenvolvido e lançado em 2001 por Markus Hohenwarter da Universidade de Salzburg para educação matemática nas escolas. Além da interface da geometria dinâmica, o GeoGebra se destaca por permitir a inserção de coordenadas e fórmulas algébricas possibilitando assim uma interação entre a figura geométrica e sua representação algébrica. Por isso o nome, “Geo” de geometria e “Gebra” de Álgebra.
Além disso, existem duas outras características que tornam o GeoGebra tão popular:
I – Sua distribuição é livre e regida pelos termos da GNU General Public License (GPL). Segundo Sabino e Kon (2009, p. 4) a GNU baseia-se em 4 liberdades:
1. Você tem a liberdade de executar o programa, para qualquer propósito.
2. Você tem a liberdade de modificar o programa para adaptá-lo às suas necessidades (para tornar essa liberdade efetiva na prática, você precisa ter acesso ao código fonte, já que fazer alterações em um programa sem ter o código fonte é muito difícil).
3. Você tem a liberdade de redistribuir cópias gratuitamente ou mediante pagamento.
4. Você tem a liberdade de distribuir versões modificadas do programa para que a comunidade possa se beneficiar de suas melhorias.
Em termos gerais, isso permite que qualquer pessoa, do leigo ao profissional em Tecnologia da Informação (TI) possa ter acesso, aperfeiçoar e distribuir o software.
II – O software é escrito em linguagem de programação Java, uma das linguagens computacionais mais populares do mundo, o que permite que ele seja disponibilizado em várias plataformas operacionais tais como Windows, Linux, Mac e, mais recentemente, na plataforma Android abrangendo seu uso para dispositivos de informática mais versáteis como tablets e smartphones.
Existem várias formas de se adquirir o GeoGebra. A principal, e mais indicada, é pelo site do próprio software, www.geogebra.org, pois neste endereço sempre está disponível a versão mais recente do software que atualmente é a versão 4.4. Na figura 2 temos a página inicial do site do GeoGebra.
Figura 2: Página Virtual do GeoGebra
3.1 Conhecendo o GeoGebra
De acordo com Araújo e Nóbriga (2010) o maior diferencial do software GeoGebra para os outros programas de geometria dinâmica é a possibilidade de interação e manipulação, seja através do mouse ou do Campo de Entrada, das funções e objetos que estejam na Janela de visualização ou na Janela de Álgebra.
Na figura 3, temos um exemplo de uma construção feita no GeoGebra e é posto em destaque suas principais ferramentas.
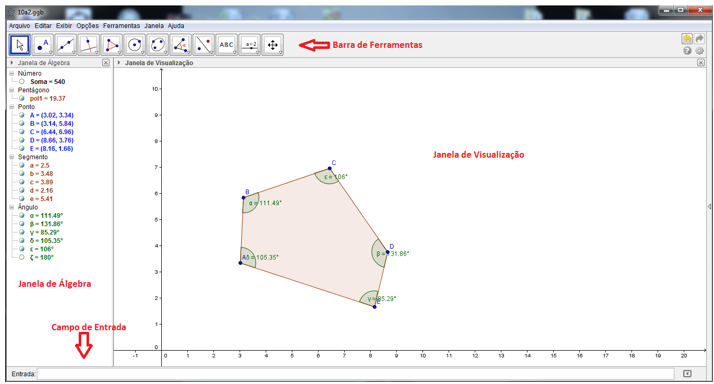
Figura 3: Exemplo de uma construção feita no GeoGebra versão 4.2
Como podemos observar acima, o GeoGebra possui doze conjuntos de ferramentas em sua Barra de Ferramentas que podem ser utilizadas em diversas construções geométricas e manipulações algébricas.
4 ATIVIDADES PRÁTICAS DE GEOMETRIA ANALÍTICA COM O USO DO GEOGEBRA
As atividades abaixo foram elaboradas com o objetivo de trabalhar os conceitos básicos desta etapa de ensino, bem como as características e as principais propriedades dos elementos matemáticos ponto, reta e circunferência. Sem deixar de lado o protagonismo estudantil onde o aluno é instigado a procurar respostas a partir das construções feitas.
Cada atividade é composta por uma ou mais construções, passo-a-passo, de forma que a medida que as construções vão ficando mais complexas certos passos vão ficando menos detalhados para que assim o estudante tenha a oportunidade de por em prática o que foi aprendido nos passos anteriores. A seguir, serão mostradas as atividades com o uso do GeoGebra.
Atividade 01 – Conhecendo o Software GeoGebra
Objetivo: Apresentar aos alunos o Software Geogebra e suas ferramentas básicas, fazendo com que eles pratiquem um pouco e comecem a se habituar com o ambiente de Geometria Dinâmica do Geogebra.
Nesta atividade serão trabalhados alguns elementos geométricos fundamentais tais como:
1) Ponto no plano cartesiano;
2) Segmento de reta;
3) Reta no plano cartesiano;
4) Retas Paralelas;
5) Construção de um polígono convexo;
6) Características de um Paralelogramo;
7) Ângulo Interno de um polígono;
8) Ângulo Externo de um polígono.
Como o leitor perceberá, os passos nessa atividade são bem mais detalhados visto a falta de familiaridade com o software GeoGebra.
1º Passo- Digite no campo de Entrada “A = (1,1)” e tecle Enter;
2º Passo- Digite no campo de Entrada “B = (6,1)” e tecle Enter;
3º Passo- Digite no campo de Entrada “C = (3,4)” e tecle Enter;

Pergunta 01:
Quais objetos apareceram na Janela de Álgebra? O que eles representam?
________________________________________________________________________________________________________________

8º Passo – Novamente, clique sobre a opção “Segmento definido por dois pontos” e clique sobre os pontos B e D e depois sobre os pontos C e D.
Pergunta 02:
Que figura foi formada? Quais propriedades garantem esse fato?
_______________________________________________________________________________________________________________

10º Passo – Clique duas vezes sobre o ponto A e mude suas coordenadas para (-1,-1).
Pergunta 03:
Qual forma geométrica é formada pelos pontos ABCD? O que garante esse fato?
________________________________________________________________________________________________________________
11º Passo- Por fim, tecle Esc. Clique e segure sobre o ponto A e arraste-o para qualquer canto da Janela de Visualização.
Pergunta 04:
O tipo de figura geométrica mudou? Por quê?
________________________________________________________________________________________________________________
Após o 10º passo é esperado o resultado exibida na figura 5.
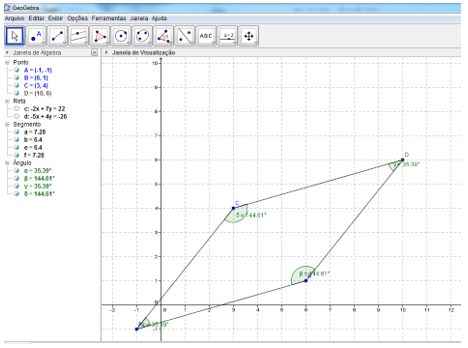
Figura 5: Atividade 1 ao final do 10º passo.
Atividade 02: O conceito de ponto, ponto médio de um segmento de reta e a distância entre um ponto e uma reta.
Objetivo: Entender o conceito de ponto médio, perceber que ele é, por construção, um objeto dependente dos pontos que formam as extremidades do segmento e, por fim, entender a relação entre a distância entre um ponto e uma reta.
Nesta atividade iremos trabalhar:
1) Conceito de Ponto no Plano Cartesiano;
2) Conceito de Ponto Médio de um segmento de reta;
3) Propriedade da equidistância de um ponto que pertence a uma circunferência a seu centro;
4) Lugar Geométrico de um ponto médio onde suas extremidades tem determinadas características.
5) Relação entre o perpendicularismo e a distância entre um ponto e uma reta.
Nesta atividade teremos três construções, a primeira ajudará a entender o conceito e característica do ponto médio de um segmento no plano cartesiano. Na segunda construção instigaremos o aluno a investigar o lugar geométrico de um determinado objeto construído. Na terceira construção, o aluno será levado a analisar a relação entre o perpendicularismo e a distancia entre um ponto e um a reta.
Construção 1:
1º Passo – Insira no campo de entrada o ponto A(2,3) e B(5,6).

Pergunta 1:
Quais as coordenados do ponto C? O que ele representa?
________________________________________________________________________________________________________________
Pergunta 2:

________________________________________________________________________________________________________________

Pergunta 3:
Quais as coordenados do ponto C? Por que as coordenadas mudaram?
________________________________________________________________________________________________________________

Pergunta 4:
Quais as Coordenadas do Ponto C?
(____,____)
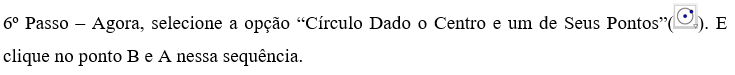
Pergunta 5:
Que figura foi formada e quais suas características?
________________________________________________________________________________________________________________
Pergunta 6:
Qual o lugar geométrico dos pontos médios de A e B onde B = (5,6) e A são todos os ponto com distância 5 do ponto B?
________________________________________________________________________________________________________________
Neste ponto o aluno deverá ser capaz de elaborar uma construção que responda a pergunta, caso isso não aconteça é sugerido que se faça a construção abaixo.
Construção 2:
1º Passo – Selecione o menu Arquivo – Nova Janela.

3º Passo – Agora, tecle Esc e clique duas vezes sobre o ponto A e mude suas coordenadas para (5,6).
4º Passo – Selecione a ferramenta “Novo Ponto” e clique sobre qualquer ponto da circunferência que foi criada.
5º Passo – Selecione a Ferramenta “Ponto Médio ou Centro” na segunda guia. Em seguida, clique sobre o ponto A e depois sobre o ponto B.
7º passo – Agora, tecle Esc e mova o Ponto B sobre a circunferência. Observe o que acontece e, finalmente, determine o Lugar Geométrico pedido na pergunta 6. Na figura 6 vemos o resultado esperado após a construção que foi sugerida anteriormente.
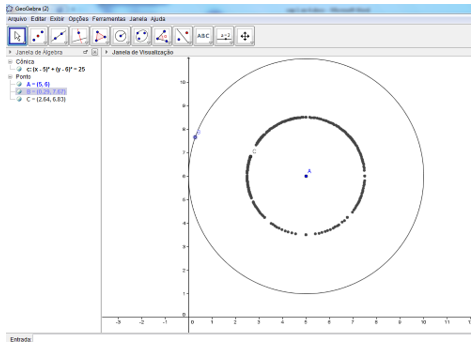
Figura 6: Construção 2, lugar geométrico do ponto médio de pontos equidistantes a um ponto dado.
Construção 3:
1º Passo: Selecione o menu Arquivo – Nova Janela. Insira no Campo de Entrada o seguinte texto “y = 2*x + 1” relativo a equação da reta y = 2x+1.
2º Passo: Insira no Campo de Entrada o ponto A = (5,2).


Pergunta 1:

Pergunta 2:
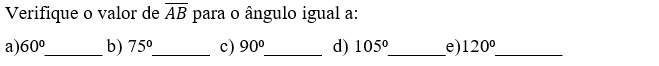

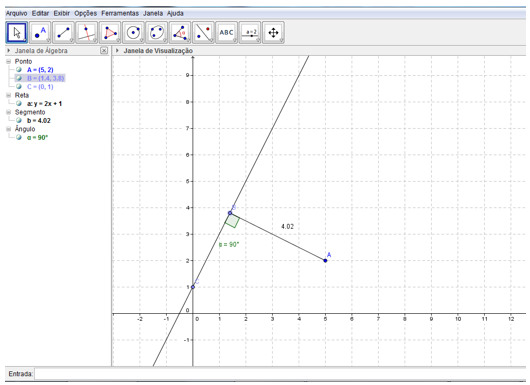
Figura 7: Atividade 2, construção 3 com ângulo reto.
Atividade 03 – Distância Entre Dois Pontos e Baricentro de um Triângulo qualquer.
Objetivo: Deduzir de forma intuitiva as fórmulas para o cálculo da distância entre dos pontos e o baricentro de um triângulo qualquer no plano cartesiano.
Nessa atividade teremos duas construções: a primeira tratará da distância entre dois pontos no plano e a fórmula para calcular tal distância e na segunda construção estudaremos o baricentro de um triângulo no plano cartesiano.
Construção 1:

6º Passo: Por fim, selecione a ferramenta “Distância, Comprimento ou Perímento” na janela 8, e clique sobre os objetos que acabaram de ser criados “j”, “k” e “l”.
Pergunta 1:
Preencha os valores dos comprimentos de (Use apenas duas casas decimais após a vírgula):

Pergunta 2:
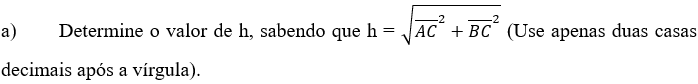
_______________________________________________________________
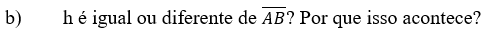
________________________________________________________________________________________________________________
Pergunta 3:
A partir do que foi analizado nas perguntas anteriores, determine a fórmula da distância entre os pontos A=(a,b) e B=(c,d).
________________________________________________________________________________________________________________
Na figura 8 temos o resultado esperado para a construção anterior.
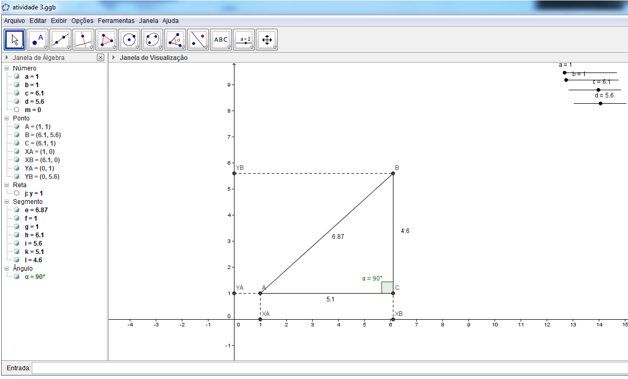
Figura 8: atividade 3, construção 1.
Construção 2:
1º Passo: Com a ferramenta “Novo Ponto” crie três pontos aleatórios na Janela de Visualização.
Pergunta 1:
a) Escreva abaixo as coordenadas dos 3 pontos criados:
A = (_____,_____) B = (_____,_____) C = (_____, _____)
b) Determine o valor da média aritmética das coordenadas x dos três pontos criados._____________
c) Determine o valor da média aritmética das coordenadas y dos três pontos criados._____________

4º Passo: Por fim, com a ferramenta “Novo Ponto” clique sobre a interseção das 3 medianas encontrando assim o baricentro do triângulo representado na costrução pela letra G.
Pergunta 2:
Compare os valores encontrados na Pergunta 1 com as coordenadas do ponto G e desta forma deduza a fórmula para o cálculo do baricentro de um triângulo de coordenadas A=(x1, y1), B=(x2, y2) e C=(x3, y3).
________________________________________________________________________________________________________________
Na figura 9 temos o resultado espera na construção 2.
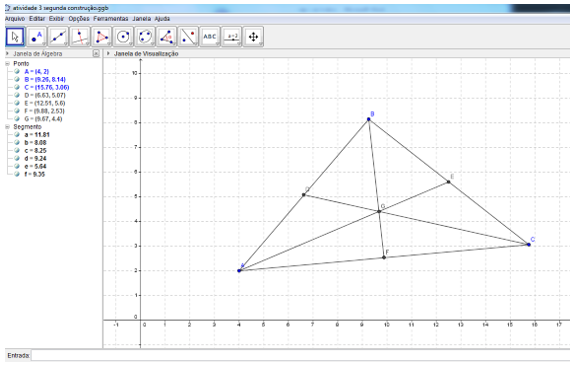
Figura 9: Atividade 3, construção 2.
Atividade 04 – Posição relativa entre retas – construção de retas paralelas e de retas pependiculares.
Objetivo: Entender a relação entre a posição relativa entre duas retas e seus respectivos coeficientes angulares e lineares.
Essa atividade será composta de duas construções, na primeira será trabalhado a relação entre a inclinação e a posição de uma reta e sua equação reduzida, junto com a relação entre os coeficientes angulares de duas retas paralelas. Na segunda, será trabalhado a relação entre os coeficientes angulares de duas retas perpendiculares.
Construção 1:

2º Passo: no “Campo de Entrada” digite “y = a*x + b”. E logo depois crie o ângulo entre o eixo x e a reta “c” que acabou de ser criada.
Pergunta 1:
a) O que acontece se você variar os valores do objeto “a”? Por que isso acontece?
________________________________________________________________________________________________________________
b) O que acontece se você variar os valores do objeto “b”? Por que isso acontece?
________________________________________________________________________________________________________________
c) Em qual das duas situações o valor do ângulo muda? Por quê?
________________________________________________________________________________________________________________
3º Passo: Com a ferramenta “Novo Ponto” crie dois pontos quaisquer na “Janela de Visualização” de forma que tais pontos não pertençam a reta “c”.

5º Passo: Com a ferramenta “Ângulo” crie os ângulos que as novas retas fazem com o eixo x.
Pergunta 2:
a) Qual o valor do ângulo das retas? Por que eles tem esse valor?
________________________________________________________________________________________________________________
b) Modifique os valores do objeto “a”. O que acontece com as retas “d” e “e”? Por que isso acontece?
________________________________________________________________________________________________________________
c) Modifique os valores do objeto “b”. O que acontece com as retas “d” e “e”. Por que isso acontece?
________________________________________________________________________________________________________________
Na figura 10 temos o resultado esperado após o 5º passo da construção 1.
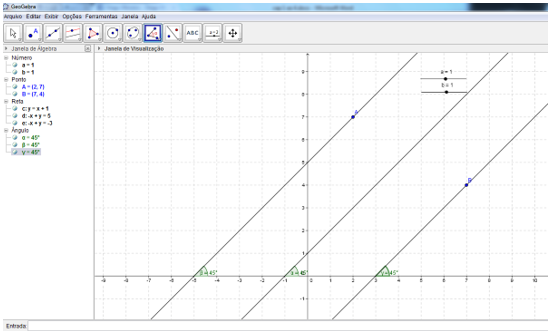
Figura 10: Atividade 4, construção 1 apos o 5º passo.
Construção 2:

Pergunta 1:
Determine:
a) O valor do coeficiente angular de “c”:____
b) O valor do coeficiente angular de “d”:____
c) O valor do produto dos coeficientes angulares de “c” e “d”: _______
d) Confira com seu colega do lado se ambos obtiveram o mesmo resultado no item c. Desta forma, conclua a relação entre os coeficientes angulares de duas retas Perpendiculares.
________________________________________________________________________________________________________________
Pergunta 2:
a) Modifique os valores do objeto “a”. O que acontece com a reta “d”? Por que isso acontece?
________________________________________________________________________________________________________________
b) Modifique os valores do objeto “b”. O que acontece com a reta “d”. Por que isso acontece?
________________________________________________________________________________________________________________
Na figura 11 temos o resultado esperado para a construção 2.
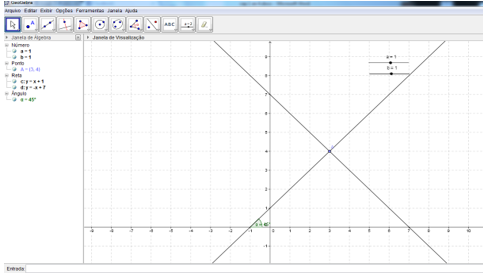
Figura 11: Atividade 4, construção 2.
Atividade 05 – Circunferências e posição relativa entre reta e circunferência.
Objetivo: Construir retas e cincunferências em uma mesma janela de visualização e entender suas caracteristicas de acordo com a posição relativa entre as mesmas.
Nesta atividade teremos três construções, a primeira tratará das caracteristicas de uma circunferência, a segunda e a terceira das posições relativas entre uma circunferência e uma reta. Os passos já são bem menos detalhados para que o estudante possa por em prática suas habilidades com o software GeoGebra adquiridas com o desenvolvimento das atividades anteriores.
Construção 1:
1º Passo: Com a ferramenta “Novo Ponto” crie um ponto em qualquer local da Janela de Visualização.
2º Passo: Com a ferramenta “Segmento com Comprimento Fixo” clique sobre o ponto A e depois determine um valor entre 2 e 10.
3º Passo: Clique com o botão direto do mouse sobre o ponto B e selecione a ferramenta “Habilitar Rastro”.
4º Passo: Selecione a ferramenta “Mover” depois clique segure e arraste o ponto B para várias direções.
Pergunta 1:
a) Que figura geométrica foi formada com o rastro?
________________________________________________
b) Qual a equação geral, a equação reduzida e as característica deste objeto?
________________________________________________________________________________________________________________
Na figura 12 temos o resultado esperado para a construção 1.
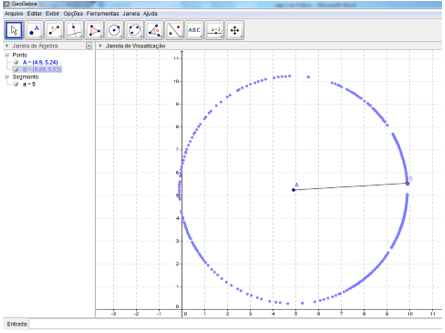
Figura 12: Atividade 5, construção 1.
Construção 2:
1º Passo: Selecione menu Arquivo “Nova Janela”. Com a ferramenta “Círculo dados Centro e Raio” crie na janela de visualização um circunferência de centro em (4,5) e raio 3.
2º Passo: Com a ferramenta “Reta Definida por Dois Pontos” construa a reta que passa pelos pontos (6,0) e (9,3).
3º Passo: Com a ferramenta “Reta Perpendicular” crie a reta perpendicular a reta “a” e que passe pelo ponto A.
4º Passo: Com a Ferramenta “Segmento Definido por Dois Pontos” crie o segmento que começa em A e termina no ponto de interseção entre as duas retas desta construção.
Pergunta 1:
a) Qual a equação geral da reta “a” e da circunferência criada na construção?
________________________________________________________________________________________________________________
b) Qual a distância entre a reta “a” e a circunferência? _________________________________________________________
c) Essa distância é maior, menor ou igual ao raio? Por que isso acontece?
________________________________________________________________________________________________________________
Na figura 13 temos o resultado esperado para a construção 2.
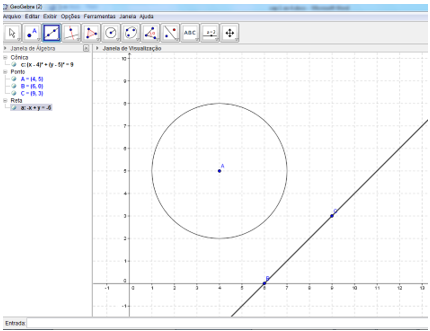
Figura 13: Atividade 5, construção 2.
Construção 3:
1º Passo: Abra uma nova janela e com a ferramenta “Reta Definida Por Dois Pontos” crie a reta que passa pelos pontos (4,0) e (7,2).
2º Passo: Com a Ferramenta “Controle Deslizante” crie um objeto que varie de 1 a 20.
3º Passo: Com a Ferramenta “Círculo Dados Centro e Raio” crie uma circunferência de centro em (5,6) e raio definido pelo objeto “b”.
4º Passo: Com o botão direto do mouse clique sobre o objeto “b” e selecione a opção “Animar”.
Pergunta 1:
a) Para quais valores de “b” a reta é externa a circunferência? _________
b) Para qual valor de “b” a reta é tangente à circunferência? _________
c) Para quais valores de “b” a reta é secante à circunferência?________
d) Se “b” for igual a 7 quais serão os pontos de interseção entre a reta e a circunferência?
Primeiro Ponto (____,____) Segundo Ponto (_____,_____)
Na figura 14 temos o resultado esperado para a construção 3, quando o valor do controle dislizante b é igual a 7.
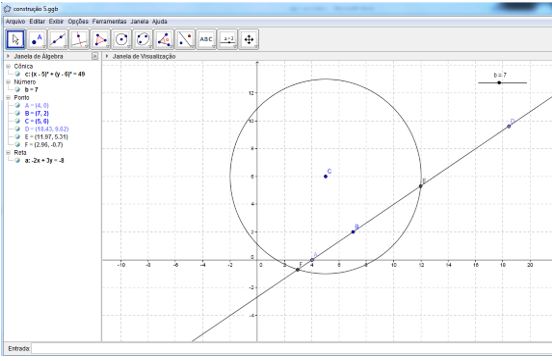
Figura 14: Atividade 5, construção 3.
5. DESENVOLVIMENTO DO TRABALHO E RESULTADOS OBTIDOS
As atividades propostas no capítulo 4 foram aplicadas em uma turma do 3º ano, da EEMTI (Escola de Ensino Médio em Tempo Integral) Liceu Vila Velha, em Fortaleza-CE. Tais atividades foram realizadas em um dos três Laboratórios Escolares de Informática (LEI) que a escola possui, com o apoio da equipe de professores que trabalha dando suporte aos LEIs. O Núcleo Gestor deu total apoio às atividades realizadas, disponibilizando todo o material e tempo necessário.
Para constatar o fato de que os alunos desta escola dão mais atenção às aulas quando se utiliza TICs como ferramenta no ensino, seja qual for a disciplina, foi feita uma pesquisa de opinião com todos os alunos do 3º ano do ensino médio. Dele foram obtidos os seguintes resultados: O questionário é divido em seis afirmações, no qual o aluno pode opinar de quatro formas distintas, “Concordo Totalmente”, “Concordo Parcialmente”, “Discordo Parcialmente” e “Discordo Totalmente”, as duas primeiras serão chamadas de “Faixa do Concordo” onde a opinião está mais para favorável do que desfavorável, e as duas últimas serão chamadas de “Faixa do Discordo” onde as opiniões estão mais para desfavorável do que para favorável.
Um total de 68 alunos responderam, com uma média de idade igual a 17,07 anos e esses alunos fazem parte das turmas que ainda não tiveram contato com o software GeoGebra. Com relação à afirmação 01, “O uso das TICs em sala torna as aulas mais interessantes”, obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 53 78% Concordo Parcialmente 15 22% Discordo Parcialmente 0 0% Discordo Totalmente 0 0% Total 68 100%
Tabela 1: Opinião dos alunos com relação a afirmação 1 do questionário 1.
Percebemos facilmente o interesse despertado pela TICs quando utilizados nas aulas, visto que nenhum aluno chegou a discordar da afirmação, estão todas as opiniões na “Faixa do Concordo”.
Com relação à afirmação 02, “Eu prefiro uma aula “Tradicional” do que uma aula no laboratório de informática”, obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 4 6% Concordo Parcialmente 15 22% Discordo Parcialmente 22 32% Discordo Totalmente 27 40% Total 68 100%
Tabela 2: Opinião dos alunos com relação à afirmação 2 do questionário 1.
Neste caso, entendemos como aula “Tradicional” o tipo de aula onde são usados os recursos básicos, tais como quadro negro e livro didático. Esse conceito foi passado para os alunos e na opinião de 72% deles (Faixa do Discordo) as aulas “Tradicionais” não são mais interessantes do que aulas diferenciadas, tais como as que utilizam o LEI como recurso.
Com relação à afirmação 3, “Eu prefiro aulas com recursos multimídias tais como Datashow” obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 41 60% Concordo Parcialmente 16 24% Discordo Parcialmente 6 9% Discordo Totalmente 5 7% Total 68 100%
Tabela 3: Opinião dos alunos com relação à afirmação 3 do questionário 1.
Neste caso percebemos uma concentração de 84% das opiniões na “Faixa do Concordo”, ou seja, resultado semelhante à afirmação 1, porém neste caso dando um enfoque ao uso do Datashow.
Com relação à afirmação 04, “Consigo aprender melhor os conteúdos quando o professor utiliza TICs, tais como o Laboratório de Informática e recursos multimídia”, obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 39 57% Concordo Parcialmente 23 34% Discordo Parcialmente 5 7% Discordo Totalmente 1 2% Total 68 100%
Tabela 4: Opinião dos alunos com relação à afirmação 4 do questionário 1.
Neste caso, percebemos que além de os alunos consultados acharem as aulas com TICs mais interessantes, eles também consideram aprender melhor os conteúdos. Isso é outra consequência positiva.
Com relação à afirmação 5, “O professor que utiliza TICs parece ter maior domínio de conteúdo do que os que não utilizam”, obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 18 27% Concordo Parcialmente 30 44% Discordo Parcialmente 11 16% Discordo Totalmente 9 13% Total 68 100%
Tabela 5: Opinião dos alunos com relação à afirmação 5 do questionário 1.
A motivação para a inclusão dessa afirmação foi a conclusão de muitos docentes de que, quando estão ministrando os conteúdos, os alunos parecem não estar entendendo, causando no aluno a impressão de que o professor não consegue explicar o conteúdo de forma eficiente. Por isso 71% das opiniões desta afirmação se concentram na “Faixa do Concordo”, pois como as TICs melhoram muitos aspectos didáticos das aulas, o aluno tem uma percepção de que o professor é mais bem preparado e conhece melhor o conteúdo. É importante observa que essa afirmação se trata apenas de uma tentativa de fazer com que o aluno reflita sobre o assunto, visto que na realidade o fato de o professor não usar TICs não significa que ele não possua domínio do conteúdo.
Por fim, temos a afirmação 6, “Considero importante o domínio das TIC’s para conquistar uma vaga no mercado de trabalho.” obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 38 56% Concordo Parcialmente 18 26% Discordo Parcialmente 11 12% Discordo Totalmente 9 6% Total 68 100%
Tabela 6: Opinião dos alunos com relação à afirmação 6 do questionário 1.
Como 82% das opiniões estão na “Faixa do Concordo” esse resultado concretiza o fato de os alunos de ensino médio considerarem que o domínio das TICs é fundamental para uma conquista de uma vaga no mercado de trabalho. Neste ponto reforçamos que um dos principais objetivos do ensino médio brasileiro é preparar o aluno para o mercado de trabalho.
Depois da aplicação e análise dos resultados do questionário 1, foram feitas as aplicações e desenvolvimentos das atividades propostas no tópico 4. A aplicação das atividades aconteceu durante as aulas de matemática. A dinâmica do processo de aplicação foi a seguinte:
Em um primeiro momento o professor expôs o conteúdo de Geometria Analítica Plana, em sala, com o auxílio de um Datashow para projetar apresentações em Slides e alguns exemplos dinâmicos usando o GeoGebra. Normalmente esse procedimento levou uma hora/aula. Em seguida, os alunos eram conduzidos ao laboratório de informática onde com o auxílio de um Datashow e das atividades impressas, elas eram realizadas e, ao mesmo tempo, respondidas as indagações. Para que o processo acontecesse de forma dinâmica e colaborativa os alunos foram postos em duplas, assim, alunos com mais conhecimentos no manuseio do computador ajudavam aos colegas com mais dificuldades, alguns inclusive, se tornaram monitores, destacando-se nas atividades e na colaboração com os colegas. Por fim, os alunos foram orientados a salvar as suas construções em uma pasta que depois foi repassada para o professor, podendo o professor fazer uma avaliação da aplicabilidade destas construções.
Durante a primeira atividade foi utilizado duas aulas, primeiro houve uma apresentação da versão 4.2 do software GeoGebra, foram apresentadas suas características e as suas principais ferramentas, além de como obter e instalar o software. Para praticar os conhecimentos expostos foram realizadas as construções da atividade 01, descrita no capítulo 4. Esse passo foi essencial, pois nenhum aluno conhecia o software GeoGebra, porém algo que foi notável era a facilidade em eles lidarem com o computador.
Uma dificuldade encontrada nessa atividade foi à falta de conhecimentos básicos de matemática, o que fez com que os alunos levassem mais tempo para concluí-las. Com um intervalo de dois dias, foi aplicada a atividade 2, ela levou duas horas/aula para ser concluída e se deu de forma bem proveitosa sem muita dificuldade por parte dos alunos. A atividade 3 foi realizada uma semana depois da atividade 2. Sua realização se deu após o conteúdo relativo à distância entre dois pontos e baricentro de um triângulo ter sido ministrado em sala de aula. Algo notável, e ao mesmo tempo preocupante, foi a dificuldade da maioria dos alunos em responder aos questionamentos da construção 1, pois tais alunos não tinham domínio do “Teorema de Pitágoras”, demonstrando assim uma certa deficiência de aprendizado no ensino fundamental.
A aplicação das atividades 4 e 5 ficaram para o segundo bimestre letivo de 2014, pois os conteúdos trabalhados em tais atividades, só serão ministrados neste bimestre.
Se necessário fosse, seria dado mais um tempo para responder as perguntas das atividades em sala de aula, e alguns alunos que, por um motivo ou outro, tinham faltado à realização de alguma atividade, puderam realizá-la em casa ou em um outro momento em um dos LEIs da escola, as apresentando depois para o professor. As respostas apresentadas nas atividades foram condizentes com que se esperava, mostrando que os objetivos propostos no trabalho foram atingidos.
Durante a elaboração das respostas das perguntas foi permitido que os alunos consultassem o seu livro didático, para que os mesmos se sentissem mais seguros ao elaborar as respostas, visto que o caráter dessas atividades não era avaliativo e sim investigativo.
Para consolidar e chancelar os resultados esperados com a realização das atividades propostas foi aplicada uma segunda pesquisa de opinião com os vinte e seis alunos que participaram da prática das três primeiras atividades do capítulo 4. O questionário da segunda pesquisa de opinião se encontra no apêndice deste trabalho e com ele foram obtidos os resultados que seguem.
Com relação à afirmação 1, “O GeoGebra torna as aulas de Matemática mais interessantes”, temos que:
Opinião Quantidade Porcentagem Concordo Totalmente 20 77% Concordo Parcialmente 4 15% Discordo Parcialmente 2 8% Discordo Totalmente 0 0% Total 26 100%
Tabela 7: Opinião dos alunos com relação à afirmação 1 do questionário 2.
Percebemos que o a opinião dos alunos se concentra em 92% na “Faixa do Concordo” demonstrando assim que o GeoGebra despertou o interesse deste alunos não somente com relação ao software em si, mas também com à aula de matemática.
Na afirmação 2, “Consigo aprender melhor os conteúdos quando o professor utiliza o GeoGebra para expor o conteúdo”, obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 14 54% Concordo Parcialmente 10 38% Discordo Parcialmente 2 8% Discordo Totalmente 0 0% Total 26 100%
Tabela 8: Opinião dos alunos com relação à afirmação 2 do questionário 2.
Ou seja, ao levar o software GeoGebra para expor e dinamizar o conteúdo em sala de aula, isso, na opinião de 92% dos alunos consultados, melhorou o aprendizado.
Com relação à afirmação 3, “Achei importante o uso do GeoGebra para o ensino da Geometria Analítica”, obtemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 18 69% Concordo Parcialmente 8 31% Discordo Parcialmente 0 0% Discordo Totalmente 0 0% Total 26 100%
Tabela 9: Opinião dos alunos com relação à afirmação 3 do questionário 2.
Neste caso é notório que 100% das opiniões estão na “Faixa do Concordo”, ou seja, todos os alunos reconheceram que o software GeoGebra tem grande utilidade nas aulas de Geometria Analítica.
Com relação à afirmação 4, “Consigo aprender melhor quando manipulo e visualizo os pontos, retas e circunferências com a ajuda do GeoGebra”, obtivemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 22 85% Concordo Parcialmente 4 15% Discordo Parcialmente 0 0% Discordo Totalmente 0 0% Total 26 100%
Tabela 10: Opinião dos alunos com relação à afirmação 4 do questionário 2.
Neste caso tivemos outra totalidade na “Faixa do Concordo”, demonstrando assim o reconhecimento por parte dos alunos que as atividades dinâmicas propostas melhoram o aprendizado dos conceitos básicos da Geometria Analítica.
Com relação à afirmação 5, “Tenho interesse em aprender mais sobre o GeoGebra”, obtivemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 16 61% Concordo Parcialmente 8 31% Discordo Parcialmente 2 8% Discordo Totalmente 0 0% Total 26 100%
Tabela 11: Opinião dos alunos com relação à afirmação 5 do questionário 2.
Neste caso tivemos 92% na “Faixa do Concordo”, ou seja, as atividades realizadas acabaram por despertar o interesse dos alunos em aprofundar seus estudos com relação ao software GeoGebra.
Por fim, com relação à afirmação 6, “Fiquei mais interessado em estudar matemática em casa com o uso do GeoGebra”, obtivemos o seguinte resultado:
Opinião Quantidade Porcentagem Concordo Totalmente 10 39% Concordo Parcialmente 12 46% Discordo Parcialmente 4 15% Discordo Totalmente 0 0% Total 26 100%
Tabela 12: Opinião dos alunos com relação à afirmação 6 do questionário 2.
Com um total de 85% das opiniões na “Faixa do Concordo”, percebemos que o GeoGebra incentiva inclusive o autodidatismo, ao estimular o aluno a estudar matemática em casa com o auxílio do software.
Diante desta análise realizada neste tópico estamos prontos para concluir a nossa pesquisa e faremos isso dentro das considerações finais deste trabalho.
6. CONSIDERAÇÕES FINAIS
Após o desenvolvimento do trabalho é possível tecer considerações importantes no que diz respeito aos objetivos propostos, as limitações encontradas, os resultados alcançados e as perspectivas de aplicações deste trabalho.
Em seu objetivo, o trabalho propôs uma metodologia diferenciada de ensino da Geometria Analítica Plana no terceiro ano do ensino médio da EEMTI Liceu Vila Velha, em Fortaleza-CE, com o auxílio do software GeoGebra. Com o desenvolvimento das cinco atividades propostas no tópico 4, percebeu-se o quanto as ferramentas do GeoGebra se aplicam ao ensino da Geometria Analítica.
A sequência de atividades propostas também incentiva o aprendizado contínuo do aluno ao apresentar em seu desenvolvimento inicial passos bem detalhados e, à medida que as atividades vão progredindo, os passos vão ficando menos detalhados forçando o aluno a pôr em prática o que foi aprendido com as atividades anteriores.
Na aplicação da atividade em sala de aula observou-se, através das pesquisas de opinião e dos resultados apresentados ao responderem os questionamentos feitos de forma condizente ao esperado, que de fato a utilização do software GeoGebra contribui para a melhoria do aprendizado da Geometria Analítica.
Com relação às limitações, a que mais pesou de forma negativa foi a defasagem no aprendizado da matemática básica, apresentada pela maioria dos alunos que participaram da pesquisa.
Seja como for, esse trabalho cumprirá seu objetivo a partir do momento em que um colega professor sentir curiosidade, motivar-se, ou até mesmo, propagar o uso das TICs em sala de aula, principalmente no diz respeito ao uso do software GeoGebra nas aulas de Geometria Analítica.
Por fim, pensando em uma perspectiva futurista, o avanço das TICs e o desenvolvimento cada vez mais aprimorado do GeoGebra, permitirão futuras abordagens deste trabalho, tornando-o aberto a novos olhares e ao desenvolvimento de novas metodologias que possam contribuir para o enriquecimento das práticas pedagógicas e melhorar o ensino-aprendizado da matemática.
REFERÊNCIAS
ANDRADE, P. F. A utilização da Informática na escola pública brasileira . Brasília: Secretaria de Educação a Distância, 1996. Disponível em: http://www.proinfo.gov.br. Acesso em: 23 de Novembro de 2012.
ARAÚJO, Luís Cláudio Lopes de; NÓBRIGA, Jorge Cássio Costa. Aprendendo Matemática com o GeoGebra. São Paulo: Editora Exato, 2010.
BRASIL. PCN+ Ensino Médio Orientações Educacionais Complementares aos Parâmetros Curriculares Nacionais. Ciências da Natureza, Matemática e suas Tecnologias, 2007. Disponível em http://portal.mec.gov.br/arquivos/pdf/CienciasNatureza.pdf acesso em 13 de agosto de 2013.
CALIL, Alexandre Marques. Caracterização da Utilização das TICs Pelos Professores de Matemática e Diretrizes para Ampliação do Uso. Juiz de Fora, 2011. Disponível em http://www.ufjf.br/mestradoedumat/files/2011/11/Dissertação_ALESSANDRO_MARQUES_CALIL.pdf. acesso em 04 de março de 2014.
EVES, Howard. Introdução à História da Matemática. São Paulo: Editora UNICAMP, 2004.
GUEDES, Paulo Cesar Camargo. Algumas Aplicações do Software GeoGebra ao Ensino de Geometria Analítica. Dissertação (Mestrado Profissional em Matemática em Rede Nacional) Universidade Federal do Espírito Santo. Vitória, 2013. Disponível em http://bit.profmat-sbm.org.br/xmlui/bitstream/handle/123456789/587/2011_00376_PAULO_CEZAR_CAMARGO_GUEDES.pdf acesso em 27 de fevereiro de 2014.
MARKARIAN, Roberto. A matemática na escola: Alguns problemas e suas causas. Revista do Professor de Matemática v.38 n. 38, p. 23-32, 1998.
SABINO, Vanessa; KON, Fabio. Licenças de Softwares Livres Histórias e Características. São Paulo, 2009. Disponível em http://ccsl.ime.usp.br/files/relatorio-licencas.pdf acesso em 24 de março de 2014.
