GEOGEBRA AS A TOOL FOR TEACHING TRIANGULAR INEQUALITY IN THE 7TH GRADE OF ELEMENTARY SCHOOL
REGISTRO DOI: 10.5281/zenodo.10806048
Israel da Silva Pinto1;
Profa. Dra. Luciana Silva dos Santos Souza2
Resumo
Este trabalho discute a incorporação de tecnologias, especificamente o software GeoGebra, no ensino de matemática em especial da geometria, com foco na desigualdade triangular no 7º ano do ensino fundamental. A pesquisa bibliográfica e a análise de documentos oficiais, como os Parâmetros Curriculares Nacionais (PCN), Base nacional comum curricular (BNCC) e o currículo de Pernambuco, foram realizadas para entender a relevância e a aplicabilidade de tecnologias em especial o GeoGebra no contexto educacional. Além disso, foi realizada uma pesquisa em diversos livros didáticos e artigos no que se refere a forma como abordam o conteúdo da desigualdade triangular, mais precisamente, se ao abordar esse conteúdo, esses materiais apresentam atividades que envolvam a utilização de algum software, especialmente o GeoGebra. Após análises detalhadas, constatou-se que os documentos oficiais defendem a utilização e implementação de softwares educacionais em sala de aula, especialmente no contexto da geometria. No entanto, quando se trata do conteúdo específico da desigualdade triangular, os livros analisados não apresentaram esses recursos como ferramentas de apoio para os professores. Diante dessa lacuna constatou-se a importância de que os professores busquem alternativas além dos materiais didáticos tradicionais. Uma opção viável é explorar as atividades disponíveis no site do GeoGebra, uma ferramenta digital amplamente utilizada na área de matemática. Essas atividades são de fácil acesso e oferecem uma abordagem prática e interativa para o ensino da desigualdade triangular.
Palavras chave: Tecnologias digitais; GeoGebra; Desigualdade triangular; ensino de matemática; anos finais do ensino fundamental.
Abstract
This paper discusses the incorporation of technologies, specifically the GeoGebra software, in the teaching of mathematics, especially geometry, with a focus on triangular inequality in the 7th grade of elementary school. Bibliographic research and analysis of official documents, such as the National Curriculum Parameters (PCN), National Common Curriculum Base (BNCC) and the Pernambuco curriculum, were carried out to understand the relevance and applicability of technologies, especially GeoGebra, in the educational context. In addition, a research was carried out in several textbooks and articles regarding how they approach the content of triangular inequality, more precisely, if when addressing this content, these materials present activities that involve the use of some software, especially GeoGebra. After detailed analyses, it was found that the official documents defend the use and implementation of educational software in the classroom, especially in the context of geometry. However, when it comes to the specific content of triangular inequality, the books analyzed did not present these resources as support tools for teachers. In view of this gap, it was found that it is important for teachers to seek alternatives beyond traditional teaching materials. One viable option is to explore the activities available on the GeoGebra website, a digital tool widely used in the field of mathematics. These activities are easy to access and offer a hands-on, interactive approach to teaching triangular inequality.
Keywords: Digital Technologies; GeoGebra; Triangular Inequality; Mathematics Teaching; Final Years of Elementary School.
1. Introdução
O ensino de matemática, e particularmente da geometria, apresenta desafios significativos, sendo tema de muitos estudos. Talvez esse seja um dos fatores que ocasionou o negligenciamento do ensino dos conteúdos desta unidade temática do currículo na Educação Básica, como afirma Ambrósio (2012): é muito difícil motivar com fatos e situações do mundo atual uma ciência que foi desenvolvida em outros tempos. Ainda segundo Ambrósio (2012): Do ponto de vista de motivação contextualizada, a matemática que se ensina hoje nas escolas é morta. A complexidade dos conceitos e a falta de recursos didáticos são alguns dos obstáculos.
[…] Com o movimento da Matemática Moderna, a partir de 1950, o ensino dessa disciplina passou a enfatizar o simbolismo e a exigir dos alunos maiores abstrações, distanciando a Matemática da vida real. O que se percebe é que o aluno formado por esse currículo aprendeu muito pouco de geometria e não consegue perceber a relação deste conteúdo com sua realidade. (TASHIMA E SILVA, 2017, n.p.)
O organizador curricular do Estado de Pernambuco (Brasil), norteia o ensino de matemática no Ensino Fundamental, ao definir habilidades, conteúdos e objetos de conhecimento. Em se tratando do 7o ano do Ensino Fundamental o ensino da desigualdade triangular (foco desta pesquisa) é sugerido no currículo de Pernambuco (EF07MA24PE3). Para nós, o trabalho com este objeto de saber matemático é essencial, pois é por meio dele que o aluno aprenderá que importância do estudo da desigualdade triangular transcende simplesmente entender um conceito matemático; ela serve como um pilar fundamental para o desenvolvimento de habilidades cognitivas e lógicas essenciais. A desigualdade triangular é uma base sólida que sustenta muitos outros conceitos matemáticos e habilidades práticas.
Em primeiro lugar, compreender a desigualdade triangular é crucial para a geometria, pois estabelece os limites e condições para a formação de triângulos. Triângulos são formas geométricas fundamentais que encontram aplicação em várias áreas, desde a arquitetura até a engenharia civil. Conhecendo as condições necessárias para a formação de um triângulo, os estudantes podem aplicar esse conhecimento na resolução de problemas do mundo real, como calcular áreas de terrenos ou determinar a estabilidade de estruturas.
Além disso, a desigualdade triangular está intimamente ligada a conceitos de medidas de comprimento, como a distância entre dois pontos em um plano. Ao entender como a soma das medidas dos lados de um triângulo afeta sua forma e tamanho, os estudantes podem posteriormente em níveis mais avançados relacionar esse conhecimento com outras áreas da matemática, como a geometria analítica e a trigonometria.
No âmbito das habilidades práticas, a compreensão da desigualdade triangular promove o pensamento crítico e a capacidade de resolver problemas. Os alunos aprendem a analisar situações, identificar padrões e aplicar estratégias de resolução de problemas de forma eficaz. Essas habilidades são transferíveis para diversas situações do cotidiano, desde a tomada de decisões financeiras até a resolução de problemas de engenharia.
Fora da sala de aula, os estudantes do 7º ano podem estabelecer conexões com outros conceitos matemáticos e habilidades através da desigualdade triangular. Por exemplo, ao estudar proporções e razões, os alunos podem explorar como a desigualdade triangular se relaciona com a ideia de proporções entre os lados de um triângulo. Além disso, ao aprender sobre simetria e transformações geométricas, os estudantes podem aplicar a desigualdade triangular para entender como diferentes manipulações afetam a forma e o tamanho dos triângulos.
Assim sendo, a experiência em sala de aula (nos estágios supervisionados e não obrigatórios), no cerne da formação no curso de Licenciatura em Matemática (Universidade de Pernambuco – Campus Garanhuns) revelou que quando se trata do ensino de geometria no 7º ano do ensino fundamental, a desigualdade triangular, tem sido um conteúdo desafiador tanto para a transposição didática quanto em relação às aprendizagens dos estudantes. Essas dificuldades podem ser atribuídas à natureza abstrata dos conceitos geométricos envolvidos, requerendo uma compreensão intuitiva das relações entre os lados de um triângulo, o que pode ser desafiador para alunos nessa fase de desenvolvimento cognitivo.
Portanto, é essencial desenvolver métodos de ensino que tornem esses conceitos mais acessíveis e compreensíveis para os alunos. Logo, essas dificuldades exigem estratégias pedagógicas eficazes para melhorar o ensino e a aprendizagem da geometria. Com isso, a incorporação de tecnologias no ambiente educacional pode ser um dos mecanismos mais eficazes para o combate a essas dificuldades.
Em particular, o uso de softwares educacionais, como o GeoGebra, que é um software de matemática gratuito, no ensino de matemática, mais especificamente da geometria no ensino fundamental, tem demonstrado potencial para transformar a maneira como os conteúdos são ensinados e aprendidos. No entanto, a eficácia dessas tecnologias depende em grande parte da capacidade dos professores de integrá-las de maneira eficaz em suas práticas de ensino.
As tecnologias e seu uso nas aulas de Matemática tem sido tema de muitas pesquisas entre os que fazem Educação Matemática. Entretanto, se pensarmos que as tecnologias, desde os tempos remotos, vêm ditando o comportamento do homem e da sociedade em que vive, sua influência dentro do cenário educacional não está ocorrendo há pouco tempo. (ALMEIDA, 2012, p. 224)
Tais tecnologias permitem que os professores que ensinam matemática, apresentem informações de maneiras inovadoras e envolventes, como vídeos interativos, jogos educacionais e simulações virtuais. Além disso, elas podem facilitar a personalização do ensino, pois proporcionam uma grande diversificação de atividades permitindo que os alunos aprendam no seu próprio ritmo e de acordo com suas preferências de aprendizagem.
O uso das tecnologias na sala de aula vem se tornando uma ferramenta de grande importância, pois consegue auxiliar tanto o professor quanto o aluno na explicação e na compreensão dos conteúdos. Com a tecnologia na aula os alunos sentem-se mais motivados a aprender e a partir disso o docente consegue ensinar de forma mais dinâmica e criativa (SÁ, MACHADO, 2017, p. 1)
Muitas vezes, o curso de licenciatura em matemática oferece poucas oportunidades para que os futuros professores de matemática conheçam e utilizem as tecnologias digitais. Na UPE – Campus Garanhuns por exemplo, a professora orientadora desta pesquisa ofertou no 2º semestre de 2023, um curso de extensão (30h) para que os estudantes do curso de licenciatura em matemática e pedagogia pudessem conhecer a interface do GeoGebra e incorporá-lo nas suas práticas a fim de favorecer o ensino de geometria. Mas, sabemos que tal ação almeja um objetivo mais amplo de fomentar o processo de autoformação dos licenciandos, para que aprendam e utilizem o referido software de geometria dinâmica.
Para Lima e Araújo (2021): O uso da informática como ferramenta pedagógica oferece um aumento na eficácia e na qualidade do ensino. Logo, com as novas tecnologias os professores têm a possibilidade de tornar suas aulas mais dinâmicas, têm possibilitado extrapolar as fronteiras do ensino mais tradicional, tornando as aulas mais atraentes e criando diversas com o intuito de promover as aprendizagens esperadas.
De acordo com os Parâmetros Curriculares Nacionais (PCNs) de Matemática (1998, p. 43) “as tecnologias, em suas diferentes formas e usos, constituem um dos principais agentes de transformação da sociedade, pelas modificações que exercem nos meios de produção e por suas consequências no cotidiano das pessoas”. Já a BNCC (2017, p. 61) diz que: “Há que se considerar, ainda, que a cultura digital tem promovido mudanças sociais significativas nas sociedades contemporâneas. Em decorrência do avanço e da multiplicação das tecnologias de informação e comunicação e do crescente acesso a elas pela maior disponibilidade de computadores, telefones celulares, tablets e afins, os estudantes estão dinamicamente inseridos nessa cultura, não somente como consumidores”. Por sua vez, os alunos tendem a se envolver mais ativamente no processo de aprendizado. Com a tecnologia, eles têm a oportunidade de explorar novos conceitos de maneira interativa e prática, o que pode aumentar a compreensão dos conteúdos abordados. Sendo assim, a utilização de softwares educacionais pode ser um diferencial no ensino, por exemplo, de conteúdos da geometria, que é considerada uma das áreas mais complexas da matemática.
Apesar de a geometria ser um ramo importante da Matemática, por servir principalmente de instrumento para outras áreas do conhecimento, professores do ensino fundamental apontam problemas relacionados tanto ao seu ensino quanto à sua aprendizagem. (ALMOULOUD et al., 2004, p. 94)
Ou seja, o ensino de geometria no ensino fundamental é, de fato, um desafio. Embora a geometria seja um componente crucial da matemática e sirva como uma ferramenta valiosa em várias áreas do conhecimento, existem várias barreiras que podem dificultar seu ensino e aprendizagem. Dessa forma, é essencial identificar e superar esses desafios para aprimorar a maneira como a geometria é ensinada e aprendida no ensino fundamental.
Sendo assim, objetiva-se com este trabalho explorar os benefícios do uso do GeoGebra no ensino da Geometria, com foco específico na desigualdade triangular, visando melhorar tanto o processo de ensino quanto a aprendizagem da matemática no ambiente escolar.
Para isso, os objetivos específicos são: analisar como o GeoGebra transforma a maneira de ensinar e aprender conceitos matemáticos e geométricos no ensino fundamental; avaliar a necessidade de capacitação dos professores para utilizar efetivamente o GeoGebra e tecnologias similares em suas práticas de ensino; examinar a relevância e aplicabilidade do GeoGebra no contexto educacional, embasando-se em pesquisa bibliográfica e análise de documentos oficiais como os Parâmetros Curriculares Nacionais (PCN) e o currículo de Pernambuco, especialmente no 7º ano do ensino fundamental; e analisar como os livros didáticos abordam o conteúdo da desigualdade triangular, propondo atividades alternativas disponíveis no site do GeoGebra como complemento ou substituição às atividades que utilizam materiais concretos ou métodos tradicionais de ensino.
1.1. Educação na era tecnológica: a transição do professor de transmissor para orientador
Para que o uso de tecnologias seja utilizado de maneira eficaz em sala de aula, é necessário que o professor esteja capacitado para seu uso.
O professor não deve mais ser mero transmissor de conteúdo, mas sim, um orientador da aprendizagem, fazendo com que o aluno pense e estimule suas capacidades, crie oportunidades de utilizar os seus talentos, respeitando os diversos modos de aprender, […]. É importante lembrar que o computador é somente uma máquina e para que se torne uma ferramenta didática necessita de um profissional que saiba manusear e tenha uma intenção, pois somente assim o computador deixará de ser um simples objeto, passando a ser uma ferramenta de trabalho, tal modernização já faz parte do cotidiano de muitos alunos e por fazer parte deve ser explorado, principalmente para que o aluno saiba que pode encontrar na informatização não só divertimentos com jogos, mas conhecimento (ABREU, 2011, p. 10).
De acordo com os parâmetros curriculares nacionais (PCNs) de introdução aos parâmetros curriculares nacionais (1997, p. 30): “O professor é visto, então, como facilitador no processo de busca de conhecimento que deve partir do aluno. Cabe ao professor organizar e coordenar as situações de aprendizagem, adaptando suas ações às características individuais dos alunos, para desenvolver suas capacidades e habilidades intelectuais”.
O professor na atualidade não deve apenas ensinar, mas também estimular os alunos a pensar, a desenvolver suas capacidades e a criar oportunidades para utilizar seus talentos. Ele respeita os diversos modos de aprender, e reconhece que cada aluno é único e que diferentes métodos de ensino podem ser mais eficazes para muitos alunos.
Com a intensificação do uso de tecnologias e ao acesso à informação, as novas gerações de estudantes requerem que os professores se adaptem a esta nova realizada e incorporem em sua prática pedagógica novas estratégias de ensino baseadas nas tecnologias educacionais. (PESCAROLO, 2018, n.p.)
A evolução do papel do professor não se limita à sala de aula. As novas tecnologias desempenham um papel cada vez mais importante na educação. Mas é importante lembrar que para que elas se tornem uma ferramenta didática eficaz, é necessário um profissional que saiba manuseá-las com intenção e propósito.
De acordo com os parâmetros curriculares nacionais (PCNs) de introdução aos parâmetros curriculares nacionais (1997, p. 30): “a prática de todo professor, mesmo de forma inconsciente, sempre pressupõe uma concepção de ensino e aprendizagem que determina sua compreensão dos papéis de professor e aluno, da metodologia, da função social da escola e dos conteúdos a serem trabalhados. A discussão dessas questões é importante para que se explicitem os pressupostos pedagógicos que subjazem à atividade de ensino, na busca de coerência entre o que se pensa estar fazendo e o que realmente se faz. Tais práticas se constituem a partir das concepções educativas e metodologias de ensino que permearam a formação educacional e o percurso profissional do professor, aí incluídas suas próprias experiências escolares, suas experiências de vida, a ideologia compartilhada com seu grupo social e as tendências pedagógicas que lhe são contemporâneas”.
1.2. Aprendendo geometria: obstáculos e estratégias no ensino fundamental
Os alunos do ensino fundamental frequentemente enfrentam desafios ao aprender geometria por várias razões. A geometria é uma área que exige muito raciocínio e uma boa visualização, habilidades que podem não ser tão desenvolvidas em crianças nessa faixa etária. Além disso, alguns conceitos podem ser abstratos e difíceis de entender sem a aplicação prática ou sem mecanismos adequados.
Diante todas as mudanças sofridas pelo ensino de matemática e de geometria, especificadamente, com o passar do tempo políticas e parâmetros foram desenvolvidos para que as práticas a serem adotadas fossem em prol de um único objetivo: o desenvolvimento e a aprendizagem dos alunos de uma forma satisfatória e eficaz (GOMES; AGUIAR, 2014).
Ou seja, ao longo do tempo, o ensino de matemática e especificamente da geometria sofreu várias mudanças. Estas mudanças foram impulsionadas por uma variedade de fatores, incluindo avanços tecnológicos, mudanças nas teorias pedagógicas e a necessidade de melhorar a eficácia do ensino.
As políticas e parâmetros desenvolvidos para orientar o ensino de matemática e geometria refletem um esforço para garantir que as práticas adotadas sejam direcionadas para um objetivo comum: o desenvolvimento e a aprendizagem dos alunos de uma maneira satisfatória e eficaz.
Este objetivo é fundamental para a educação. Afinal, o propósito principal da educação é facilitar a aprendizagem e o desenvolvimento dos alunos. Portanto, é essencial que as práticas de ensino sejam projetadas e implementadas com este objetivo em mente. No entanto, alcançar este objetivo não é uma tarefa fácil. Requer que o professor tenha profunda compreensão das necessidades e capacidades dos alunos, e com isso tenha também uma abordagem pedagógica eficaz.
Logo, o ensino de matemática e geometria é um campo em constante evolução. As mudanças que ocorreram ao longo do tempo refletem um esforço para melhorar a qualidade e a eficácia do ensino. No entanto, é importante continuar buscando novas estratégias e abordagens para garantir que o ensino de matemática em especial da geometria continue a evoluir de maneira a atender às necessidades dos alunos de maneira satisfatória e eficaz.
1.3. O software GeoGebra
Segundo o próprio site “GeoGebra é um software dinâmico de matemática para todos os níveis de educação que reúne geometria, álgebra, planilhas, gráficos, estatísticas e cálculos em uma única plataforma. Além disso, o GeoGebra oferece uma plataforma online com mais de 1 milhão de recursos gratuitos criados por nossa comunidade em vários idiomas. Esses recursos podem ser facilmente compartilhados através de nossa plataforma de colaboração GeoGebra Tarefa, onde o progresso dos alunos pode ser monitorado em tempo real.
GeoGebra é uma comunidade de milhões de usuários localizada em quase todos os países. Tornou-se o fornecedor líder de software dinâmico de matemática, apoiando a educação em ciência, tecnologia, engenharia e matemática (STEM) e inovações no ensino e aprendizagem em todo o mundo. O mecanismo matemático da GeoGebra alimenta centenas de sites educacionais em todo o mundo de diferentes maneiras, desde demonstrações simples até sistemas de avaliação on-line completos.
Em 2021, GeoGebra passou a fazer parte da família BYJU com centenas de milhões de estudantes em suas plataformas de aprendizagem. Os aplicativos da GeoGebra, recursos para sala de aula, GeoGebra Classroom e outros recursos continuarão disponíveis ao público gratuitamente. GeoGebra continua a operar como uma unidade independente dentro do grupo BYJU’s sob a liderança dos fundadores e desenvolvedores originais da GeoGebra”. (www.geogebra.org/about, Acesso em 13/01/2024 às 22:04)
No entanto, como com qualquer ferramenta, o sucesso do GeoGebra na sala de aula depende de como ele é usado. Os professores devem receber formação adequada para utilizar eficazmente o GeoGebra e integrá-lo ao currículo de maneira significativa. Além disso, é importante lembrar que a tecnologia deve complementar, e não substituir os recursos já existentes.
Vale ressaltar que o GeoGebra pode ser utilizado não só em computadores e notebooks, mas também em celulares e tablets, o que o torna ainda mais acessível.
Figura 1- Interface inicial do GeoGebra
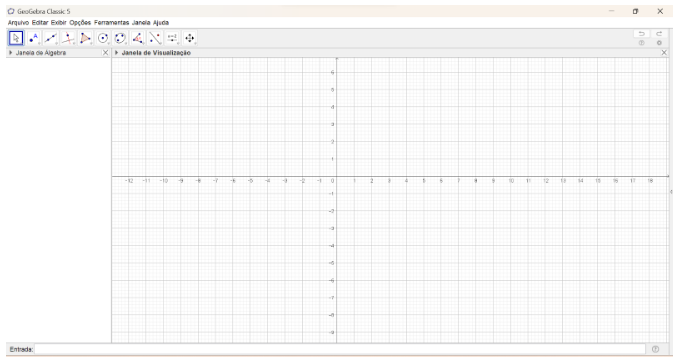
Fonte: Aplicativo do GeoGebra
A imagem acima ilustra a interface inicial do aplicativo GeoGebra, que é repleta de diversas ferramentas matemáticas. Essas ferramentas são projetadas para auxiliar os professores a enriquecer suas aulas com recursos interativos.
1.4. GeoGebra na sala de aula: integrando tecnologia ao ensino
A BNCC (2017, p. 298) diz que: “Desse modo, recursos didáticos como malhas quadriculadas, ábacos, jogos, livros, vídeos, calculadoras, planilhas eletrônicas e softwares de geometria dinâmica têm um papel essencial para a compreensão e utilização das noções matemáticas. ”
Ao analisar o currículo de Pernambuco vemos que a construção de triângulos usando uma régua e um compasso é uma habilidade básica em geometria. Isso envolve desenhar segmentos de linha de comprimentos específicos (usando a régua) e ângulos específicos (usando o compasso), a competência citada diz ainda que softwares de desenho geométrico, como o GeoGebra, também podem ser usados para essa tarefa.
Sabe-se que é importante a utilização de matérias como a régua e o compasso, pois aprender a usar uma régua e um compasso pode ajudar os alunos a desenvolver habilidades práticas que são úteis em muitas áreas, incluindo engenharia e arquitetura. Por outro lado, com um mundo cada vez mais tecnológico e com tecnologias cada vez mais avançadas sendo utilizadas nas mais diversas profissões a utilização de softwares como o GeoGebra precisa ter cada vez mais espaço no cotidiano dos alunos.
1.5. Desigualdade triangular
A desigualdade triangular tem origem na geometria euclidiana e é um dos teoremas mais conhecidos da geometria. Este teorema nos diz que a soma de dois dos lados do triângulo é maior que o terceiro lado do triângulo. Logo, é de suma importância pois se tivermos um segmento maior que a soma dos outros dois segmentos, não podemos formar um triângulo.
Consideremos então um triângulo ABC
Conforme a figura abaixo:
Figura 2- Triângulo ABC
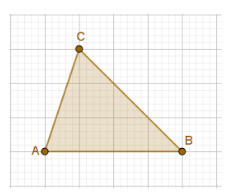
Fonte: Autoria própria, 2024
A desigualdade triangular estabelece que a medida de qualquer lado deve ser sempre inferior à soma das medidas dos outros dois lados.
Ou seja:
{AB<AC+BC AC<AB+BC BC<AB+AC}
De uma perspectiva mais ampla, se as dimensões dos lados de um triângulo forem a, b e c, então é necessariamente:
{|b-c|<a<b+c |a-c| <b<a+c |a-b| <c+a+b}
2. Metodologia
A pesquisa realizada se configura como qualitativa de natureza exploratória. A fim de responder a problemática inicial, elegemos como ferramenta metodológica a análise documental, proposta por Bardin (2011).
Na primeira etapa do percurso metodológico procedemos a revisão bibliográfica cujas análises foram pautadas em resultados de estudos acadêmicos (artigos publicados em periódicos), que abordaram o mesmo tema ou temas correlatos ao conteúdo curricular em foco.
Na segunda etapa, nos debruçamos sobre as orientações contidas nos documentos oficiais (BNCC e o Currículo do Estado de Pernambuco) acerca do ensino da desigualdade triangular. Na terceira etapa procuramos nos textos supracitados elementos relacionados aos métodos, estratégias e/ou recursos utilizados ou sugeridos para o ensino do conteúdo que elegemos. O objetivo desta etapa foi identificar e avaliar diferentes abordagens pedagógicas que poderiam ser aplicadas no ensino da desigualdade triangular.
Na penúltima etapa, pesquisamos atividades específicas disponíveis no site do GeoGebra que são relevantes para o ensino da desigualdade triangular. As atividades encontradas no site do GeoGebra foram analisadas em termos de sua aplicabilidade e eficácia no ensino da desigualdade triangular.
Ao final do percurso metodológico apresentamos as análises e discussões acerca dos achados relacionados à desigualdade triangular com base nos corpos de dados que construímos a partir de cada fonte de informação.
3. Resultados e discussão
A demonstração da desigualdade triangular, embora seja simples, parece não ser evidente para os estudantes do 7º ano do ensino fundamental e, por isso, carece de atenção do professor de matemática quanto às escolhas didáticas (métodos, recursos e estratégias de ensino). Nesse contexto, o livro didático por exemplo desponta como um importante recurso para que professores e estudantes explorem os objetos de saberes matemáticos, dentre os quais a desigualdade triangular. Aliado a este recurso, o GeoGebra apresenta ferramentas que poderão favorecer as aprendizagens acerca do tema, tal como afirmam NASCIMENTO (2012) e GRAVINA e DE OLIVEIRA CONTIERO (2011).
Portanto, é essencial que os professores busquem e diversifiquem os métodos que podem ser utilizados para comprovar esse teorema, com ou sem suporte nos recursos didáticos mais usuais, tais como: régua, compasso, canudos e palitos (indicados nos textos analisados como ferramentas para o trabalhar esse conteúdo de forma empírica ou intuitiva).
Assim sendo, apresentamos no Quadro 1, a seguir a análise da tipologia das atividades encontradas nos livros didáticos4 de matemática e nos artigos científicos selecionados nesta pesquisa. Desse modo, cumpre ressaltar que o nosso propósito consistiu também na identificação das abordagens do conceito da desigualdade triangular nas fontes de dados mencionadas anteriormente. E, no alinhamento destas, com os documentos curriculares.
Tabela 1- Análise de atividades nos livros didáticos e artigos científicos em relação ao conteúdo da desigualdade triangular.
Fonte de Referência na construção de dados da pesquisa Tipos de atividade propostas/sugeridas Atividades com suporte de materiais concretos (lápis, papel, régua ou esquadros e compasso) Atividades com o uso de softwares (GeoGebra, Cabri Gèometre, Geoplan) Atividade apenas com lápis e papel Livro didático de matemática 8 de 10 (80%) 0 de 10 (0%) 2 de 10 (20%) Artigos científicos 2 de 6 (33,3%) 4 de 6 (66,6%) 0 de 6 (0%) BNCC Não há sugestões5 Não há sugestões6 Não há sugestões Documento Curricular de Pernambuco Não há sugestões7 Não há sugestões8 Não há sugestões Site do GeoGebra Não há sugestões ≃ 1609 Não há sugestões
Fonte: Autoria própria, 2024.
Nesta análise os livros didáticos de matemática, relacionados na Tabela 1 (Anexo A), aprovados no Programa Nacional do Livro Didático (2024 – 2025), verificamos que as atividades sugeridas sobre o teorema da desigualdade triangular, estão alicerçadas apenas em atividades que precisam de lápis, papel e em alguns casos materiais como régua, compasso, barbante. Enquanto nos artigos científicos analisados, há uma gama maior de atividades, além da utilização de materiais concretos (régua, esquadros e/ou compasso), também o uso de softwares (GeoGebra, Cabri Gèometre, Geoplan). Nesse sentido, destacamos que as atividades propostas nos livros didáticos e nas proposições didáticas dos autores dos artigos científicos, estão alinhadas com as diretrizes curriculares, pois a BNCC e o currículo de Pernambuco preconizam a utilização de diferentes recursos didáticos, incluindo materiais concretos e softwares, para promover uma aprendizagem mais significativa e acessível aos alunos.
Em alguns LDM analisados, o software GeoGebra e o Cabri Gèometre são sugeridos no manual destinado ao professor de matemática (última sessão do livro – orientações didáticas e pedagógicas). Entretanto, os dados apresentados no Quadro 1 revelam a ausência de atividades pautadas no uso de softwares (sobretudo, que incentivem ou proponham o uso do GeoGebra), na abordagem do conteúdo desigualdade triangular. Tal fato, denota uma escassez de atividades dessa natureza. Ou seja, o incentivo e o direcionamento de atividades envolvendo os softwares mencionados ou com outros recursos tecnológicos na classe de matemática disponíveis é incipiente no LDM.
De acordo com a BNCC e o Currículo de Pernambuco, a integração dessas ferramentas pode enriquecer ainda mais o ensino e favorecer a aprendizagem de conteúdos e objetos de saber geométricos na Educação Básica. Ainda de acordo com a BNCC “[…] os recursos didáticos como […] calculadoras, planilhas eletrônicas e softwares de geometria dinâmica têm um papel essencial para compreensão e utilização das noções matemáticas. (BRASIL, 2018, p. 276)”.
No que tange aos artigos científicos, a pesquisa no google acadêmico e em periódicos aponta que há poucos10 trabalhos contendo atividades sugeridas ao trabalho com a desigualdade triangular (cerca de 11 publicações) nos anos finais do ensino fundamental ou ensino médio. Nos textos analisados, os autores apresentam vivências vinculadas às atividades que têm como base a utilização de softwares, dentre os quais o GeoGebra. Portanto, os referidos textos sugerem aos professores que ensinam matemática a utilização do GeoGebra em sala de aula como potencializadora do ensino e da aprendizagem acerca da desigualdade triangular. Nesse contexto, os estudantes poderão se engajar melhor na construção do conhecimento geométrico, por meio de atividades significativas de exploração, experimentação e investigação nos recursos ofertados pela interface do GeoGebra em contraposição ao ensino mais tradicional.
Os dados nos fizeram pesquisar no site do GeoGebra11 exemplos de atividades relacionadas à desigualdade triangular a fim de oportunizar aos professores de matemática, conhecer o software e as atividades que poderão ser elaboradas, adaptadas e/ou reproduzidas gratuitamente como ferramenta para o ensino e a aprendizagem da desigualdade triangular.
Com isso foi realizado uma pesquisa no site já mencionado, onde foi possível obter diversas atividades sobre o conteúdo, atividades essas que poderiam ser facilmente implementadas pelo professor em sala de aula. Essas atividades podem ser realizadas com recursos digitais, como computadores e celulares. A seguir, apresentaremos algumas dessas atividades encontradas no site do GeoGebra.
Figura 3- Atividade sobre desigualdade triangular proposta no site do GeoGebra
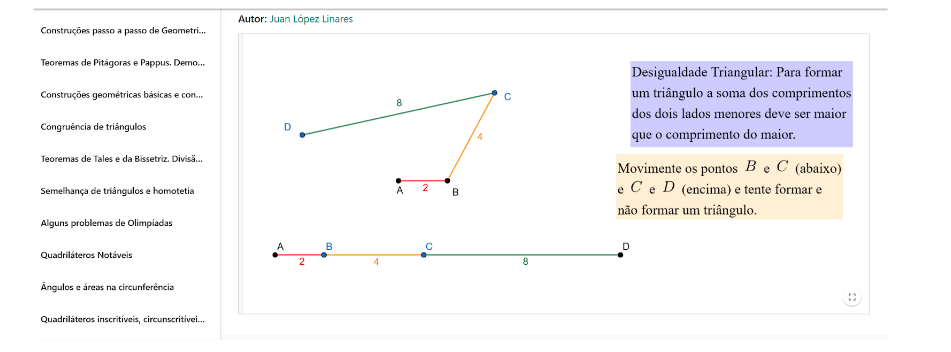
Fonte: Site do GeoGebra12.
Essa atividade consiste em movimentar os pontos a fim do aluno conseguir formar triângulos, caso não consiga então deve modificar o comprimento dos segmentos de reta para que isso seja possível, dessa forma o aluno deve perceber que só será possível formar um triângulo se a soma das medidas de dois de seus lados for maior que a medida do terceiro lado.
Figura 4- Atividade sobre desigualdade triangular proposta no site do GeoGebra.

Fonte: Site do GeoGebra13.
Essa atividade consiste em modificar o comprimento dos pontos B e C movimentando o segmento de reta, dessa forma quando a medida de um dos segmentos for maior do que a soma das medidas dos outros dois segmentos, o triângulo deixará de existir na imagem.
Além das atividades mencionadas, o site apresenta uma variedade de outras tarefas relacionadas ao mesmo conteúdo. Isso demonstra que o GeoGebra é uma ferramenta extremamente útil e pode ser um excelente recurso para auxiliar os professores em suas atividades didáticas.
Figura 5- Atividades sobre desigualdade triangular proposta no site do GeoGebra.
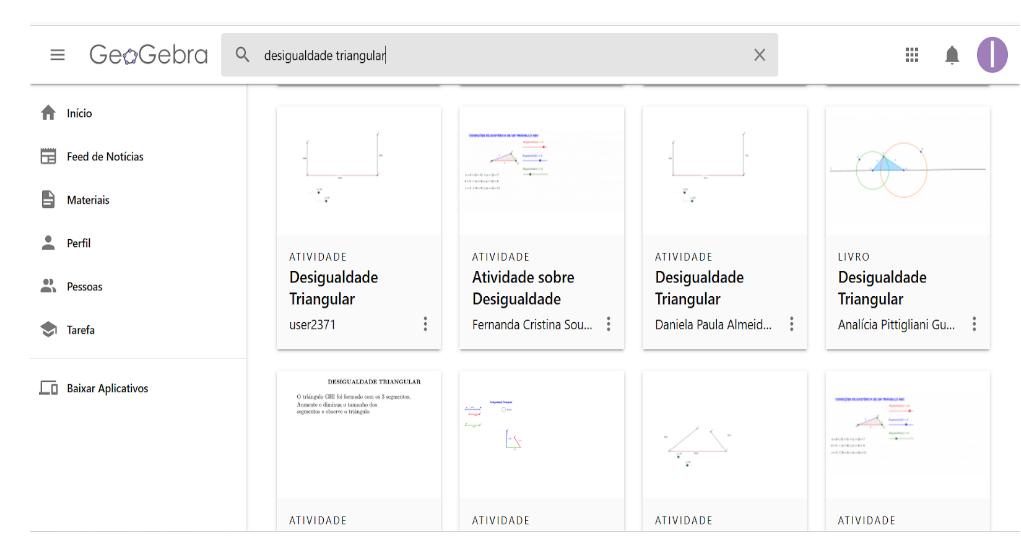
Fonte: Site do GeoGebra14.
Na imagem acima vemos uma variedade de atividades sobre desigualdade triangular criadas por autores cadastradas no site do GeoGebra, todas essas atividades estão disponíveis para serem acessadas, logo o professor tem uma gama de opções de atividades sobre o mesmo conteúdo para serem utilizadas em suas aulas.
Ao utilizar essas atividades em sala de aula, os professores podem personalizar sua abordagem de ensino, escolhendo aquelas que melhor se adequam ao estilo de aprendizagem de seus alunos e aos objetivos educacionais almejados. Além disso, a disponibilidade desses recursos online e gratuitos torna-os acessíveis a uma ampla gama de educadores em todo o mundo, contribuindo para a disseminação do conhecimento e da prática pedagógica eficaz.
Portanto, essa diversidade de atividades sobre desigualdade triangular oferece aos professores uma valiosa oportunidade de enriquecer suas aulas, promovendo uma aprendizagem mais significativa e estimulante para os alunos.
4. Considerações finais
Portanto, com a realização dessa pesquisa, podemos concluir que o uso do GeoGebra em sala de aula para ensinar a desigualdade triangular também promove o desenvolvimento de habilidades digitais entre os alunos. Eles não só aprendem um conceito matemático importante, mas também se familiarizam com uma ferramenta digital que é amplamente utilizada no campo da educação matemática. Desse modo, os alunos podem explorar e entender o conceito de forma interativa e prática, sendo capazes de visualizar e manipular triângulos, reforçando a compreensão de que a soma das medidas de dois lados de um triângulo é sempre maior que a medida do terceiro lado.
A respeito da integração do GeoGebra no currículo de matemática, demonstra ser uma estratégia pedagógica eficaz, facilitando o entendimento dos alunos sobre a desigualdade triangular, mas também os prepara para o mundo digital em constante evolução. Essa constante evolução tecnológica também abre portas para a criação de futuras propostas de pesquisa, explorando novas formas de integração de ferramentas digitais no ensino de matemática.
Estudos futuros poderiam investigar como outras tecnologias emergentes podem ser utilizadas para aprimorar ainda mais a compreensão dos alunos sobre conceitos matemáticos abstratos e sua aplicação prática. Ao acompanhar de perto essas tendências, educadores e pesquisadores podem desenvolver abordagens inovadoras para promover o aprendizado significativo dos estudantes em um mundo cada vez mais digitalizado.
3Construir triângulos, usando régua, compasso e/ou softwares, reconhecer a condição de existência do triângulo quanto à medida dos lados e verificar que a soma das medidas dos ângulos internos de um triângulo é 180°
4Analisamos os seguintes livros de matemática aprovados no Programa Nacional do Livro Didático (PNLD, 2024/2025): Amplitude matemática (BONJORNO, José Roberto Et al.), Teláris essencial (DANTE, Luiz Roberto; VIANA, Fernando), Geração alpha (OLIVEIRA, Carlos N. C de; FUGITA, Felipe), Matemática e realidade (IEZZI, Gelson, DOLCE, Osvaldo, MACHADO, Antonio.), Desafios da matemática (SILVEIRA, Ênio), SuperAÇÃO (TEIXEIRA, Lilian Aparecida), A conquista da matemática (GIOVANNI JÚNIOR, José Ruy.) Jornadas Novos Caminhos (ANDRADE, Thais Marcelle de), Matemática Bianchini (BIANCHINI, Edwaldo), Araribá conecta (GAY, Mara Regina Garcia)
5Na BNCC encontramos uma habilidade onde sugere que o professor use materiais concretos na abordagem do conteúdo, porém não é uma sugestão de atividade e por isso não foi considerada na tabela.
6Na BNCC encontramos textos que defendem a utilização de softwares no ensino da geometria, porém não são sugestões de atividade, por isso não foram considerados na tabela.
7No currículo de Pernambuco encontramos uma habilidade onde sugere que o professor use materiais concretos na abordagem do conteúdo, porém não é uma sugestão de atividade por isso não foi considerada na tabela.
8No currículo de Pernambuco encontramos textos que defendem a utilização de softwares no ensino da geometria, porém não são sugestões de atividade, por isso não foram considerados na tabela.
9O site continha aproximadamente 160 atividades sobre desigualdade triangular, porém a maioria eram repetidas, ou seja, a mesma atividade postada no site por pessoas diferentes.
105 desses artigos não foram considerados nas análises pois a abordagem do conteúdo era mais apropriada para nível superior e não para 7º ano do ensino fundamental.
11https://www.geogebra.org
12https://www.geogebra.org/m/vsfydv2v#material/awvjd7ys
13https://www.geogebra.org/search/desigualdade%20triangular
14https://www.geogebra.org/m/vsfydv2v#material/awvjd7ys
Referências
AMBRÓSIO, U.D. Educação Matemática: Da teoria à prática. 23ºed. Campinas: Papirus, 2012
TASHIMA, Marina Massaco; SILVA, Ana Lúcia da. As lacunas no ensino-aprendizagem de geometria. 2015. 2017.
ALMEIDA, H. R. F. L. de. DAS TECNOLOGIAS ÀS TECNOLOGIAS DIGITAIS E SEU USO NA EDUCAÇÃO MATEMÁTICA. Nuances: Estudos sobre Educação, Presidente Prudente, v. 26, n. 2, p. 224–240, 2016. DOI: 10.14572/nuances.v26i2.2831. Disponível em: https://revista.fct.unesp.br/index.php/Nuances/article/view/2831. Acesso em: 19 jan. 2024.
LOURENÇO DE SÁ, Adriana; COSTA MACHADO, Marília. O USO DO SOFTWARE GEOGEBRA NO ESTUDO DE FUNÇÕES. Anais do Encontro Virtual de Documentação em Software Livre e Congresso Internacional de Linguagem e Tecnologia Online, [S.l.], v. 6, n. 1, jun. 2017. ISSN 2317-0239. Disponível em: <http://www.periodicos.letras.ufmg.br/index.php/anais_linguagem_tecnologia/article/view/12142>. Acesso em: 20 jan. 2024.
LIMA, Marilia Freires de; ARAÚJO, Jefferson Flora Santos de. A utilização das tecnologias de informação e comunicação como recurso didático-pedagógico no processo de ensino e aprendizagem. Revista Educação Pública, v. 21, nº 23, 22 de junho de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/23/a-utilizacao-das-tecnologias-de-informacao-e-comunicacao-como-recurso-didatico-pedagogico-no-processo-de-ensino-aprendizagem
Almouloud SA, Manrique AL, Silva MJF da, Campos TMM. A geometria no ensino fundamental: reflexões sobre uma experiência de formação envolvendo professores e alunos. Rev Bras Educ [Internet]. 2004Sep;(27):94–108. Available from: https://doi.org/10.1590/S1413-24782004000300007
http://basenacionalcomum.mec.gov.br/implementacao/biblioteca-de-apoio/pcn-ensino-fundamental-6-ao-9-ano/
ABREU, Astúrio Cardoso. O Uso de Software na Aprendizagem da Matemática. 2011. 37 f. Monografia (Especialização) — Universidade Federal do Mato Grosso, São Paulo, 2011
http://portal.mec.gov.br/seb/arquivos/pdf/livro01.pdf
PESCAROLO, Henrique Marques. Uma proposta de ensino aprendizagem de trigonometria em triângulos por meio do software Geogebra. 2018. 64 f. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Universidade Tecnológica Federal do Paraná, Cornélio Procópio, 2018.
GOMES, M. C. G.; AGUIAR, D. S. Utilização do laboratório de matemática nas aulas de geometria como facilitador da aprendizagem. In: 5ª Jornada de Iniciação Científica e Extensão, Instituto Federal do Tocantins, 2014.
www.geogebra.org/about, Acesso em 13/01/2024 às 22:04
http://basenacionalcomum.mec.gov.br/
http://www.afogadosdaingazeira.pe.gov.br/selecao-simplificada/CURRICULO-DE-PERNAMBUCO-ENSINO-FUNDAMENTAL.pdf
BONJORNO, José Roberto Et al. Amplitude matemática 7. 1. Ed. São Paulo: Editora do Brasil, 2022.
DANTE, Luiz Roberto, VIANA, Fernando. Teláris essencial 7. 1. Ed. São Paulo: Editora Ática, 2022.
OLIVEIRA, Carlos N. C de, FUGITA, Felipe. Geração Alpha 7. 4. Ed. São Paulo: Editora SM Educação, 2022.
IEZZI, Gelson, DOLCE, Osvaldo, MACHADO, Antonio. Matemática e realidade 7. 10. Ed. São Paulo: Saraiva Educação S.A., 2022.
SILVEIRA, Ênio. Desafios da matemática 7. 1. Ed. São Paulo: Moderna, 2022.
TEIXEIRA, Lilian Aparecida. SuperAÇÃO! 7. 1. Ed. São Paulo: Moderna, 2022.
GIOVANNI JÚNIOR, José Ruy. A conquista da matemática 7. 1. Ed. São Paulo: FTD, 2022.
ANDRADE, Thais Marcelle de. Jornadas: Novos caminhos 7. 1. Ed. São Paulo: Saraiva Educação S.A., 2022.
BIANCHINI, Edwaldo. Matemática Bianchini 7. 10. Ed. São Paulo: Moderna, 2022.
GAY, Mara Regina Garcia. Araribá conecta 7. 1. Ed. São Paulo: Moderna, 2022.
LINARES, Juan López. Jogos com a desigualdade triangular. CQD-Revista Eletrônica Paulista de Matemática, 2022.
LINARES, Juan López; DOS SANTOS, João Paulo Martins; DE JESUS, Alessandro Firmiano. Extremos com desigualdades na Geometria: resolução de cinco problemas propostos para a Olimpíada Internacional de Matemática. CQD-Revista Eletrônica Paulista de Matemática, 2021.
CARMO, José Avelino. A propósito da desigualdade triangular: Relato de uma aula com uma turma do 7º ano. Educação e Matemática, n. 103, p. 36-38, 2009.
DA SILVA GOMES-JÚNIOR, Antônio; OLIVEIRA, Izabela Caren Maffi; LINO, Eliedete Pinheiro. Uso de materiais concretos no ensino da desigualdade triangular. Revista Ensin@ UFMS, v. 1, n. 1, p. 195-204, 2016.
MARQUES, Lucas Rozendo et al. Proposta de atividades envolvendo áreas de triângulos por meio do GeoGebra. 2021.
SILVA, Jonas Weverson Araújo et al. O uso do GeoGebra no estudo de alguns resultados da Geometria Plana e de Funções. Revista do Instituto GeoGebra Internacional de São Paulo, v. 1, n. 1, p. CLXXX-CXCII, 2012.
https://www.geogebra.org/m/vsfydv2v#chapter/623455
ANEXO A – LIVROS DIDÁTICOS DE MATEMÁTICA ANALISADOS (PNLD 2024 – 2025)
Nome da coleção Autoria Editora Edição Amplitude matemática. BONJORNO, José Roberto Et al. Editora do Brasil 1.ed. Teláris essencial. DANTE, Luiz Roberto; VIANA, Fernando. Editora Ática 1.ed. Geração alpha. OLIVEIRA, Carlos N. C de; FUGITA, Felipe. SM Educação 4.ed. Matemática e realidade. IEZZI, Gelson, DOLCE, Osvaldo, MACHADO, Antonio. Saraiva 10.ed. Desafios da matemática. SILVEIRA, Ênio. Editora Moderna 1.ed. SuperAÇÃO. TEIXEIRA, Lilian Aparecida. Editora Moderna 1.ed. A conquista da matemática. GIOVANNI JÚNIOR, José Ruy. FTD 1.ed. Jornadas Novos Caminhos. ANDRADE, Thais Marcelle de. Saraiva 1.ed. Matemática Bianchini. BIANCHINI, Edwaldo. Editora Moderna 10.ed. Araribá conecta. GAY, Mara Regina Garcia. Editora Moderna 1.ed.
Fonte: Autoria própria, 2024
ANEXO B – ARTIGOS CIENTÍFICOS ANALISADOS
Título do artigo Autoria Universidade Ano Link do site/doi Jogos com a desigualdade triangular LINARES, Juan López. UNESP 2022 https://doi.org/10.21167/cqdv22n32022073094 Extremos com desigualdades na Geometria: resolução de cinco problemas propostos para a Olimpíada Internacional de Matemática. LINARES, Juan López. UNESP 2021 https://sistemas.fc.unesp.br/ojs/index.php/revistacqd/article/view/317 A propósito da desigualdade triangular: Relato de uma aula com uma turma do 7º ano. CARMO, José Avelino. APM 2009 https://em.apm.pt/index.php/em/article/view/1786 Uso de materiais concretos no ensino da desigualdade triangular. DA SILVA GOMES-JÚNIOR, Antônio; OLIVEIRA, Izabela Caren Maffi; LINO, Eliedete Pinheiro. UFMS 2016 https://periodicos.ufms.br/index.php/anacptl/article/view/1922 Proposta de atividades envolvendo áreas de triângulos por meio do GeoGebra. MARQUES, Lucas Rozendo et al. UFJ 2021 http://bdtd.ufj.edu.br:8080/handle/tede/62 O uso do GeoGebra no estudo de alguns resultados da Geometria Plana e de Funções. SILVA, Jonas Weverson Araújo et al. PUCSP 2012 https://revistas.pucsp.br/IGISP/article/view/9050
Fonte: Autoria própria, 2024
1Graduando do Curso de Licenciatura em Matemática – UPE – Campus Garanhuns,
Universidade de Pernambuco, Brasil, Email:israel.silva@upe.br;
2Professora adjunta do Curso de Licenciatura em Matemática – UPE – Campus Garanhuns. Universidade de Pernambuco, Brasil, Email: luciana.santos@upe.br
