NÚMEROS PERFEITOS: UMA ABORDAGEM COMPUTACIONAL

REGISTRO DOI: 10.5281/zenodo.12533662

Emerson Charles do Nascimento Marreiros¹
Esrom José Galvão do Nascimento²
Listemácio Alves de Carvalho³
Wallace Sales Cardoso Gomes⁴

RESUMO

A história dos números perfeitos remonta à antiguidade, com os primeiros registros conhecidos datando de cerca de 300 a.C. na Grécia antiga. O matemático grego Euclides foi um dos primeiros a abordar os números perfeitos em seu trabalho “Elementos”, onde ele descreveu a relação entre números perfeitos e números primos. Ao longo dos séculos, matemáticos como Pierre de Fermat e Euler contribuíram para o estudo e compreensão dos números perfeitos. A busca por números perfeitos também esteve ligada ao desenvolvimento da teoria dos números e à descoberta de novas propriedades matemáticas. Atualmente, os números perfeitos continuam a ser um tópico de interesse na matemática pura, e a busca por números perfeitos cada vez maiores permanece como um desafio emocionante para os matemáticos. Nesta nota, expomos uma visão computacional e binária dos números perfeitos, bem como, determinamos analiticamente algoritmos algébricos e computacionais de conversão dos números perfeitos em numeração binária, cuja a estrutura será usada para implementar um modelo matemático em forma de algoritmo computacional, que valida a aplicação do algoritmo e sua funcionalidade através da execução, aplicação e implementação do mesmo utilizando a linguagem de programação Python.

Palavras-chaves: Números Perfeitos, Modelo Matemático, Algoritmo Computacional.

ABSTRACT

The history of perfect numbers dates back to antiquity, with the first known records dating back to around 300 BC in ancient Greece. The Greek mathematician Euclid was one of the first to address perfect numbers in his work “Elements”, where he described the relationship between perfect numbers and prime numbers. Over the centuries, mathematicians such as Pierre de Fermat and Euler have contributed to the study and understanding of perfect numbers. The search for perfect numbers was also linked to the development of number theory and the discovery of new mathematical properties. Today, perfect numbers continue to be a topic of interest in pure mathematics, and the search for ever larger perfect numbers remains an exciting challenge for mathematicians. In this note, we present a computational and binary view of perfect numbers, as well as analytically determine algebraic and computational algorithms for converting perfect numbers into binary numbering, whose structure will be used to implement a mathematical model in the form of a computational algorithm, which validates the application of the algorithm and its functionality through its execution, application and implementation using the Python programming language.

Keywords: Perfect Numbers, Mathematical Model, Computational Algorithm.

INTRODUÇÃO

Números perfeitos é um tema fascinante, pois nos dias atuais tem alguns mistérios para serem solucionados, não sabemos se todos esses números são pares, não sabemos também se são infinitos. Por definição um número perfeito é aquele que é igual à soma de seus divisores próprios positivos, excluindo o próprio número. O exemplo mais conhecido é o 6, que tem divisores próprios 1, 2 e 3, e sua soma 1 + 2 + 3 = 6. Existem também números perfeitos mais complexos, como o 28 e o 496. A busca por números perfeitos tem sido um tópico de interesse ao longo da história da matemática. O método clássico para encontrar os números perfeitos é através do método desenvolvido pelo matemático Euclides, que relaciona números primos e números perfeitos. De acordo com a fórmula de Euclides, temos o seguinte modelo matemático, definido pela expressão algébrica [2^{(p − 1)}] ∙ [2^p − 1], em que “p” é número natural primo, e o resultado dessa multiplicação é o que chamamos de número perfeito. No entanto, não podemos esquecer que essa parcela (2^p − 1) da multiplicação é denominada de números de Mersenne. Determinar manualmente números perfeitos é uma tarefa complexa e demorada, especialmente para números grandes. Atualmente, os números perfeitos conhecidos são todos gerados pelo modelo do matemático Euclides, porém, neste texto apresentamos um modelo matemático diferente da fórmula de Euclides para encontrarmos os números perfeitos, e demostraremos a eficácia desse modelo matemático através do uso e da implementação computacional de um algoritmo que valida esse modelo matemático.

HISTÓRIA DA ARTE

A história dos números perfeitos é antiga, e passa por muitos matemáticos. Começa com a descoberta destes números na época dos pitagóricos (por volta de 540 a. C.), matemáticos que faziam parte da escola criada por Pitágoras, uma irmandade ligada por ritos secretos e cheia de misticismos. Os pitagóricos acreditavam que o número é o conceito fundamental do universo. Eles classificavam os números de diversas formas: números amigos, figurados, triangulares, pentagonais, primos, etc. A forma mais importante é a da primalidade; um número é chamado de número primo se nenhum outro número, além do 1 e dele próprio, pode dividi-lo. Por exemplo, o número 13 é primo pois só é divisível por 1 e por 13. Outra das classificações que mostra características muito interessantes é a da perfeição de um número. Segundo essa classificação, um número é chamado deficiente se a soma de seus divisores (sem contar o próprio número) é menor do que ele mesmo. Sendo assim, o número 8 é deficiente pois seus divisores, 1, 2 e 4, somados dão 7.

Da mesma forma, o número 12 é chamado excessivo ou abundante porque a soma de seus divisores é maior que 12, assim: 1+2+3+4+6 = 16 podemos ver que o resultado da adição é maior que 12. Os mais importantes são aqueles que são exatamente a soma de seus divisores. Por exemplo, o número 6, cujos divisores são 1, 2 e 3 (1+2+3=6). Por conta disso, os pitagóricos diziam que estes números representavam a perfeição e os denominaram números perfeitos. Fazendo essa classificação, os pitagóricos procuravam encontrar propriedades especiais dos números e dar significado a elas, propriedades estas que foram estudadas também por outros matemáticos, e outros povos.

Após os pitagóricos, o próximo matemático a fazer parte da história dos números perfeitos foi Euclides aproximadamente 300 a. C., cujo seu IX livro dos Elementos contém, além da definição de números perfeitos, uma proposição muito particular a respeito desses números:

“Se tantos números quantos se queira começando a partir da unidade forem dispostos continuamente numa proporção duplicada até que a soma de todos resulte num número primo, e se a soma multiplicada pelo último origina algum número, então o produto será um número perfeito”.

O que quer dizer, na linguagem matemática atual, que se um número da forma 2ⁿ-1 é primo, então o número
2^n-1(2ⁿ-1) é um número perfeito. Isso fez com que fosse mais fácil encontrar números perfeitos e foi, de fato, a primeira fórmula para se encontrar tais números. Um exemplo de um número perfeito encontrado usando a fórmula é colocando o número 5 no lugar de n:

2^5-1(2⁵-1) = 2⁴(2⁵-1) = 16(32-1) = 16 × 31 = 496

Os gregos antigos só conheciam os quatro primeiros números perfeitos: 6, 28, 496 e 8.128, calculados a partir da fórmula de Euclides para n = 2, 3, 5 e 7, respectivamente. Por conta disso, um Neo-pitagórico chamado Nicômaco de Gerase (Palestina, aprox. 100 d. C.) fez afirmações baseadas nestes quatro primeiros números. Ele afirmou que se 6 tinha um dígito, 28 tinha dois, 496 tinha três e 8.128 tinha quatro, o próximo número perfeito teria cinco dígitos. Outra afirmação foi que o próximo número perfeito seria gerado a partir do número primo 11, já que os primeiros haviam sido gerados pelos primeiros números primos. Ou ainda, que os números perfeitos alternavam o final entre 6 e 8. Todas essas afirmações foram sendo derrubadas com as descobertas dos próximos números perfeitos. O quinto número perfeito, 33.550.336, foi acrescido à lista no século XV, e com oito dígitos derrubou as duas primeiras afirmações de Nicômaco, pois é gerado a partir do número n = 13 e não n = 11. A última afirmação de Nicômaco foi quebrada quando foi descoberto o sexto número perfeito, 8.589.869.056 que também termina em 6.

Outra propriedade dos números perfeitos é que se um número é perfeito e par, então ele é triangular, o que significa que ele pode ser escrito da forma de uma soma de números em sequência:

6 = 1+2+3
28 = 1+2+3+4+5+6+7
496 = 1+2+3+4+5+…+31
8.128 = 1+2+3+4+5+…+127

A perfeição dos números foi constatada posteriormente quando foi observado que a Lua demora 28 dias para dar uma volta completa sobre a Terra; e também quando Santo Agostinho em seu livro A Cidade de Deus disse:

“O número é perfeito em si mesmo e não porque Deus criou todas as coisas em seis dias. O inverso é mais verdadeiro, Deus criou todas as coisas em seis dias porque este número é perfeito. E continuaria perfeito mesmo que o trabalho de seis dias não existisse”.

Alhazem, por volta de 1.000 d. C., percebeu que a volta da proposição de Euclides era válida para números perfeitos pares, ou seja, se um número era perfeito par então ele era da forma 2^n-1.(2ⁿ-1), mas não conseguiu demonstrar. Realmente, Alhazem estava correto em sua afirmação e Leonhard Euler, um matemático suíço do século XVIII, provou essa afirmativa. Euler foi um dos matemáticos mais produtivos de todos os tempos, se não o mais produtivo, e foi um exemplo, pois mesmo após ficar cego continuou produzindo artigos e trabalhos. Um matemático que deve tê-lo inspirado muito foi Pierre de Fermat, que não tinha a matemática como profissão, mas criou um problema que durou por 358 anos (Último Teorema de Fermat) para ser resolvido. Ele também estudou propriedades dos números perfeitos, inclusive, a partir destes estudos, pode ter criado um teorema que ficou conhecido como Pequeno Teorema de Fermat.

Com a prova de Euler a busca por números perfeitos se resumiu à busca por números primos da forma 2ⁿ-1, mais conhecidos como Primos de Mersenne, nome dado em homenagem a Marin Mersenne, um matemático que estudou esses números. Assim a procura por números perfeitos ficou mais simples.

Para que 2ⁿ-1 seja primo é necessário que n seja primo, mas se n é primo isso não quer dizer que 2ⁿ-1 também o é. Um caso que mostra esse fato é para n = 11, onde 2¹¹-1 = 2.047 não é primo (2047 = 23 × 89). À medida que os números se tornam grandes a dificuldade de ver se eles são primos é muito maior, por exemplo, 2¹⁰⁰⁰ é um número imenso, e para ver se ele é primo ou não precisamos dividi-lo por vários números primos antes dele, que também são muitos, para confirmar que ele realmente não é divisível por nenhum número antes dele. A prova de Euler também não dizia nada sobre números perfeitos ímpares, o que significa que se existe algum número perfeito ímpar ele não será encontrado utilizando essa fórmula. Edouard Lucas, o matemático criador da Torre de Hanoi, também teve papel importante na história dos números perfeitos. Ele provou que todos os números perfeitos pares terminam em 16, ou 28, ou 36, ou 56, ou 76, ou ainda 96. E, além disso, mostrou que o número 2¹²⁷ – 1 é primo e este é o maior número primo de Mersenne encontrado antes da era do computador.

NÚMEROS PRIMOS DE MERSENNE

Com o surgimento dos computadores a busca por números primos de Mersenne e por números perfeitos se potencializou e vários números foram encontrados. Até 1985 já eram conhecidos 30 números de Mersenne e assim, 30 números perfeitos.

NÚMEROS PERFEITOS EM BINÁRIOS

Números binários são uma representação alternativa de números usando apenas dois símbolos, geralmente 0 e 1. No sistema binário, todas as quantidades são representadas com base em dois números, ou seja, zero e um. Por exemplo, o número binário “1010011010” consiste apenas em 0s e 1s, ao contrário dos números decimais, que são formados por 0, 1, 2, 3, 4, etc. O sistema binário é amplamente utilizado em ciências da computação e eletrônica, onde os circuitos digitais operam com base nesse sistema de numeração posicional. A conversão entre números binários e decimais é uma operação comum, e existem calculadoras e ferramentas online disponíveis para facilitar essa conversão, como o conversor binário da Omni. Além disso, a adição e subtração de números binários seguem regras específicas, assim como a representação de números inteiros na base decimal. O sistema binário é fundamental para o funcionamento de computadores e dispositivos eletrônicos.

Outra propriedade sobre números perfeitos descoberta após a chegada do computador foi que todo número perfeito escrito em linguagem binária (linguagem só de zeros e uns) é formado por uma sequência de “n” uns seguidos por n-1 zeros, onde n é o mesmo n da fórmula:

2n-1(2n-1)

Vejamos então os exemplos a seguir:

2(2²-1) = 6 = (110)₂
2²(2³-1) = 28 = (11100)₂
2⁴(2⁵-1) = 496 = (111110000)₂
2⁶(2⁷-1) = 8.128 = (1111111000000)₂
2¹²(2¹³-1) = 33.550.336 = (1111111111111000000000000)₂

Diante da conversão dos números perfeitos em números binários, foi observado que a soma dos conjuntos de bits (zeros ou uns) de cada número perfeito convertidos em binários, há somas que têm como resultados números primos e outros números quadrados perfeitos, como podemos ver nos exemplos abaixo:

6 em binário:

110
2 bits 1
1 bit 0
soma dos bits: 1 + 2 = 3

28 em binário:

11100
3 bits 1
2 bits 0
soma dos bits: 3 + 2 = 5

496 em binário:

111110000
5 bits 1
4 bits 0
soma dos bits: 5 + 4 = 9

8128 em binário:

1111111000000
7 bits 1
6 bits 0
soma dos bits: 7 + 6 = 13

33.550.336 em binário:

1111111111111000000000000
13 bits 1
12 bits 0
soma dos bits: 13 + 12 = 25

8.589.869.056 em binário:

111111111111111110000000000000000
17 bits 1
16 bits 0
soma dos bits: 17 + 16 = 33

137.438.691.328

1111111111111111111000000000000000000
19 bits 1
18 bits 0
soma dos bits: 19 + 18 = 37

2.305.843.008.139.952.128

1111111111111111111111111111111000000000000000000000000000000
31 bits 1
30 bits 0

ALGORITMO DE CONVERSÃO DE DECIMAL PARA BINÁRIO

Apresentamos a seguir, na Figura_1, um algoritmo para converter números decimais em binários utilizando a linguagem de programação Python:

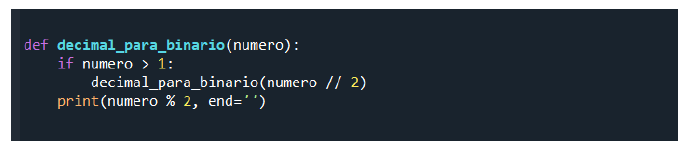
Figura_1

Neste algoritmo, a função “decimal_para_binario” realiza a conversão do número decimal para binário por meio da divisão sucessiva por 2 e coleta dos restos das divisões. O resultado é impresso na ordem correta para formar a representação binária do número.

NÚMEROS PERFEITOS EXISTENTES

Apresentamos o modelo matemático que irá gerar o algoritmo computacional para determinar os números perfeitos, esses números serão encontrados através da fórmula:

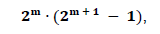
sendo que a expressão matemática entre parênteses, seja um número primo. Para calcular um número perfeito, basta apenas achar o natural “m” tal que (2^m+1– 1) seja um número primo, o que não é uma tarefa fácil. Temos logo a seguir, na Tabela 1, a relação dos nove primeiros números perfeitos, os quais foram calculados aritmeticamente usando modelo matemático aqui apresentado.

Diante das informações contidas na Tabela_1, apresentamos a seguir, na Figura_2, um algoritmo, para determinar números perfeitos através do modelo matemático. Modelo esse que será aplicado nos cálculos computacionais para determinar os números perfeitos contidos na Tabela_1. Assim, vindo a provar a eficácia do modelo computacional para calcular os números perfeitos já existes.

MODELO COMPUTACIONAL PARA DETERMINAR NÚMEROS PERFEITOS A PARTIR DE UM NÚMERO INTEIRO POSITIVO DIGITADO

Esse algoritmo exibe todos os números perfeitos existentes contidos no intervalo número antes do valor digitado, por exemplo, se digitarmos o número inteiro positivo 100 (cem), o algoritmo vai exibir a penas os números perfeitos menores que 100, ou seja, exibirá apenas os números 6 e 28, conforme vemos na tabela_1.

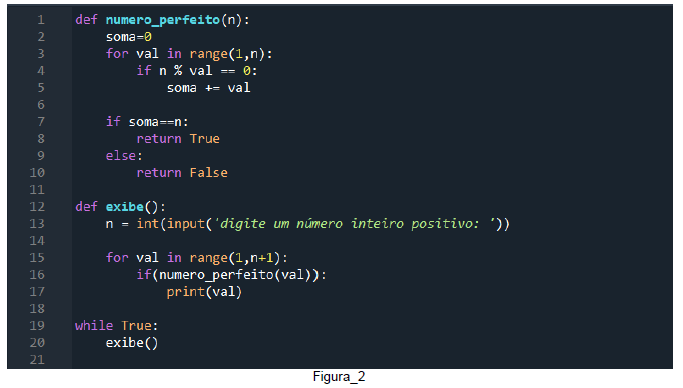
Explicando o modelo computacional:

Na função numero_perfeito( n ), devemos pegar o argumento passado n e fazer o resto da divisão por 1, 2, 3, 4, …, até n. Fazemos isso com a função range(1, n+1), que vai testar de 1 até n. Se der 0 o resto da divisão, é porque esse valor é um divisor de n.

Vamos somar esse valor a uma variável chamada soma, que inicializamos com valor 0, no início da função numero_perfeito().

No final, pegamos o valor contido em soma e comparamos com n.

Se forem iguais, retornamos True (verdadeiro), pois é perfeito.

Se NÃO forem iguais, NÃO É um número perfeito e retornamos False (falso).

Usando esse modelo computacional para exibir números perfeitos menores que o número inteiro positivo digitado, para exibir os números perfeitos a partir de um inteiro positivo n digitado, usaremos a segunda parte do algoritmo do modelo computacional, em que a função exibe(), que inicialmente pede um número inteiro ao usuário, n. O que essa função vai fazer é jogar de 1 até n na função numero_perfeito() e exibir os números que retornarem True, ou seja, que são perfeitos!

Fazemos isso com um simples laço FOR com range(1, n+1) e um IF dentro do laço, para testar o retorno da função numero_perfeito(). Podemos testar o algoritmo do modelo computacional usando como teste os valores contidos na Tabela_1.

CONCLUSÃO

Podemos ver a grande importância que os números perfeitos têm. Além da maior procura por números perfeitos, a procura por números primos de qualquer gênero se tornou importante com o surgimento da criptografia, um estudo de técnicas que transformam informações em códigos legíveis apenas pra quem tem a chave de segurança. Hoje em dia todo o sistema de segurança de dados, seja de bancos ou militares ou até de compras, são baseados em criptografia, e a base da criptografia são os números primos. Existe uma afirmação (Teorema Fundamental da Aritmética) que diz que todo número é primo ou produto de primos, o que significa que um número com 30 milhões de dígitos pode ser escrito de forma única como um produto de números primos. Dessa forma, uma pessoa pode esconder informações em números e só quem sabe quais são os primos que multiplicados dão aquele número é que saberá qual é o código. A vantagem disso é que leva muito tempo para se calcular os fatores primos de um número grande e, quando alguém finalmente descobre o código, esse número já mudou e a descoberta não serve para nada.

Algumas empresas de segurança de dados usam os números primos para criar códigos criptografados, bem como usam também os números perfeitos já descobertos como fonte se seus códigos criptografados, há empresas de nicho que atualmente estão ofertando os seguintes prêmios de US $250.000,00, US $50.000,00, US $100.000,00 e US $150.000,00 para a pessoa ou grupo de pessoas que encontrasse números primos com 10⁶, 10⁷ e 10⁸ dígitos, respectivamente. O objetivo da empresa é proporcionar a descoberta de números primos maiores, pois com números maiores a criptografia se torna mais elaborada e difícil de ser quebrada e assim, a qualidade da proteção de dados fica cada vez melhor.

Em 1996, foi criado o GIMPS (Great Internet Mersenne Prime Search), que é um grupo que procura por números primos de Mersenne. Ele se baseia na procura coletiva por números primos de Mersenne. Um software é instalado no computador de quem faz parte do grupo e este computador ajuda a calcular candidatos a primos de Mersenne. Esse grupo, no dia 6 de abril de 2000, ganhou o prêmio de US$ 50.000,00 por ter encontrado o primeiro primo com 10⁶dígitos. E, em 23 de agosto de 2009, encontraram o primeiro primo de Mersenne com 10⁷dígitos, o que lhes rendeu, em 22 de outubro do mesmo ano, o prêmio de US $ 100.000. A diferença entre a data da descoberta e da concessão do prêmio é devida à confirmação da descoberta do número (constatação de que ele é realmente primo).

Os prêmios de US$ 150.000,00 e US$ 250.000,00 ainda continuam sem um ganhador e a procura por números perfeitos continua. Hoje são conhecidos 47 primos de Mersenne (e 47 números perfeitos) dos quais o maior deles tem 12.978.189 dígitos. O último encontrado até o momento é um pouco menor com 12.837.064, que foi descoberto em 2009 por Odd Magnar Strindmo, na Noruega utilizando o programa do GIMPS, Prime95. De 2009 até hoje não foi encontrado nenhum primo de Mersenne maior que esse. Neste paper mostramos uma visão computacional dos números perfeitos, cujas as implementações algébricas e computacional de algoritmos gerou resultados satisfatórios, bem como mostramos o quão é interessante e importe os números perfeitos, exibimos as premiações ofertadas, assim como, os incentivos financeiros ofertados pelas empresas e investidores interessados em melhor seus códigos criptográficos com o uso de números primos, bem como, com as descobertas dos novos números perfeitos.

BIBLIOGRAFIA

B. Mathews. Theory of numbers (Cambridge, Deighton Bell, 1892 : Part 1 only published).
J. S. Smith. Report on the theory of numbers (Reports of the British Association, 1859-1865: reprinted in vol. i of Smith’s Collected mathematical papers)
Na introduction to the theory of numbers. By: g.h.hardy and e.m.wright.Publication date:1956. Publisher: Oxford at the Clarendon press.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos.São Paulo, edição digital, 2019.
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012.
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020.
DICKSON, L. E. History of the Theory of Numbers: Divisibility and primality. Washington, USA: Carnegie Institution of Washington, 1919.
DUARTE, L. D.; GONÇALVES, H. H.; NÓBREGA, N. P. Tudo é número: uma análise conceitual da ideia de número em Pitágoras. Revista Princípia, João Pessoa, n. 33, p. 99- 107, maio 2017.
ESCOTT, E. B. E. Amicable Numbers. Scripta Math, [S. l.], v. 12, p. 61-72, 1946.
EUCLIDES. Os Elementos. Tradução e introdução de Irineu Bicudo. São Paulo: UNESP, 2009.
HOGENDIJK, J. P. Thabit ibn Qurra and the Pair of Amicable Numbers 17296, 18416. Historia Mathematica, n. 12, p. 269-273, 1985.
KARLSON, P. A Magia dos Números. Porto Alegre: Editora Globo, 1961.
LAERCIO, D. Los diez libros de Diógenes Laercio. Tomo II. Tradução de Josef Ortiz Sanz. Madrid: Imprenta Real, 1972.
NICÔMACO. Introduction to Arithmetic. Translated into English by Martin L. D’Ooge. NY: Macmillam Company, 1926.
O’CONNOR, J. J. ROBERTSON, E. F. Perfect Numbers. 2003. Disponível em <http:// www-history.mcs.st-andrews.ac.uk/HistTopics/Perfect_numbers.html>. Acesso em: 17 fev. 2018.
ORE, O. Number theory and its history. New York, USA: Dover Publications, 1976.
PICKOVER, C. A. The loom of God: tapestries of mathematics and mysticism. New York, USA: Sterling, 2009.
PICUTTI, E. Pour l´histoire des sept premiers nombres parfaits. Historia Mathematica, n.16, p. 123-136, 1989.

¹Mestre em Modelagem Matemática e Computacional pela Universidade Federal da Paraíba – UFPB.
ORCID: https://orcid.org/0009-0006-0374-7056

²Bacharel em Sistemas de Informação pela Faculdade UNINASSAU – Polo Parnaíba – PI.
ORCID: https://orcid.org/0009-0004-2561-3118

³Especialista em Docência do Ensino Superior pela Faculdade Santo Agostinho – Teresina – PI.

⁴Especialista em Metodologia do Ensino de Matemática pela Faculdade entre Rios do Piauí – PI.