INFLUENCE OF TRANSFORMER CORE MATERIAL ON THE GENERATION OF HARMONIC DISTORTIONS IN THE MAGNETIZING CURRENT
REGISTRO DOI:10.5281/zenodo.11181508
Wendell Hosed Saran1
Orientador: Paulo César Álvares Mota2
Resumo
O artigo presente consiste no estudo sobre distorções harmônicas geradas pelo funcionamento de transformadores com núcleo de metal silício, analisando a poluição harmônica causada pela corrente de magnetização e como afetam a qualidade da energia elétrica. A pesquisa foi concebida por meio da representação das características elétricas e magnéticas de um transformador de 15 kVA no programa ATPDraw, a fim de efetuar simulações computacionais sob diferentes condições de alimentação e analisar o comportamento das tensões do primário e secundário. Para tanto, as características magnéticas do material do núcleo foram representadas por meio das curvas de magnetização e histerese de um aço silício comercial comumente utilizado na fabricação de transformadores de distribuição. Adicionalmente, a representação proposta neste estudo conduziu ao comportamento observado na prática da corrente de magnetização. Os resultados obtidos mostraram a importância das propriedades e peculiaridades dos materiais usados no núcleo de transformadores para o aprimoramento destes equipamentos. O trabalho contribuiu para o entendimento da influência das características magnéticas do núcleo na formação da corrente de magnetização, bem com o modelo computacional apropriado para a realização das análises.
Palavras-chave: Transformadores; Qualidade de energia; Corrente de magnetização; Distorção harmônica.
Abstract
This article studies the harmonic distortions generated by the operation of transformers with a silicon metal core, analyzing the harmonic pollution caused by the magnetizing current and how it affects the quality of electrical energy. The research was conceived by representing the electrical and magnetic characteristics of a 15 kVA transformer in the ATPDraw program, to carry out computer simulations under different power supply conditions and analyze the behavior of the primary and secondary voltages. To this end, the magnetic characteristics of the core material were represented using the magnetization and hysteresis curves of a commercial silicon STEEL commonly used in the manufacture of distribution transformers. In addition, the representation proposed in this study led to the behavior of the magnetizing current observed in practice. The results obtained showed the importance of the properties and peculiarities of the materials used in the core of transformers for improving this equipment. The work contributed to an understanding of the influence of the magnetic characteristics of the core on the formation of the magnetizing current, as well as the appropriate computer model for carrying out the analyses.
Keywords: Transformers; Power quality; Magnetizing current; Harmonic distortion.
1. INTRODUÇÃO
Os transformadores são dispositivos capazes de transformar grandezas elétricas como tensão e corrente, graças à não linearidade do material do núcleo MAMEDE FILHO (2013). Dentro deste contexto, esses equipamentos podem se tornar fontes de poluição harmônica quando estão em vazio, pois nesta situação a sua corrente será constituída apenas da parcela de magnetização, a qual possui elevado conteúdo harmônico.
Diante do exposto, a pesquisa buscou analisar as distorções harmônicas produzidas pela corrente de magnetização de um transformador com núcleo de aço silício, a fim de entender o grau de influência desta corrente nos níveis de distorções harmônicas de tensão e, principalmente, na injeção de harmônicas não características no sistema elétrico. Para tanto, foi analisado o espectro harmônico da corrente de magnetização de acordo com o estado de saturação do material magnético do núcleo, o qual está atrelado à tensão aplicada nos enrolamentos primários. Foram investigadas as magnitudes de cada ordem harmônica da corrente, dando uma contribuição para os estudos sobre a geração de distorções harmônicas devido à operação de transformadores na rede. Esses dados foram obtidos por meio de ensaios laboratoriais, sendo utilizado um transformador de 15 kVA para a medição e observação de sua corrente de magnetização sob diferentes condições de alimentação: subtensão, tensão nominal e sobretensão.
Em seguida, o transformador foi representado no programa ATPDraw com base no modelo proposto por FANDI (2003), com o intuito de obter o mesmo comportamento da corrente de magnetização de acordo com as condições de alimentação impostas nos ensaios. A concepção desta representação no ATPDraw envolveu a utilização de informações obtidas no catálogo de um fabricante de aço silício comercial STEEL (2009), para a elaboração de características magnéticas do núcleo. As simulações computacionais conduzidas a partir deste modelo propiciaram uma análise dos fatores que contribuem para a formação de determinadas ordens harmônicas na corrente de magnetização e o grau de impacto desta corrente na distorção harmônica de tensão nos terminais do transformador. Diante do exposto, este artigo apresenta a correlação entre as distorções harmônicas da corrente de magnetização e o material magnético empregado para a fabricação do núcleo de transformadores, bem como o grau de interferência destas correntes nas distorções harmônicas de tensão nos terminais do equipamento.
1.1 Objetivos
Este trabalho tem como objetivo geral demonstrar como o núcleo de um dispositivo não linear (transformador), pode gerar distorções harmônicas que influenciam diretamente na qualidade de energia, detalhando as componentes harmônicas na corrente de magnetização, utilizando ensaios com transformador a fim coletar parâmetros para alimentar uma modelagem computacional com objetivo de evidenciar resultados de um circuito ideal, mantendo-se coerente com um transformador real. No entanto, este modelo será capaz de representar as características de impedância do equipamento, alinhando-se a curva de magnetização e ao laço de histerese, que permitirá analisar diversos transformadores apenas atribuindo alguns de seus parâmetros como resistência de magnetização, indução da bobina e resistência do núcleo.
Para isso, os resultados serão apresentados de uma forma comparativa entre o transformador real e a simulação computacional, por meio de tabelas para uma análise quantitativa, espectros harmônicos de corrente para destacar visualmente as distorções harmônicas presentes, curvas da corrente de magnetização, proporcionando uma visão detalhada do comportamento do núcleo do transformador em relação à curva de magnetização ideal. Visto que é almejável aproximar-se de um desvio pequeno mostrando que o modelo pode ser fidedigno com todos os tópicos estudados. Esta análise comparativa será essencial para validar a eficácia da modelagem computacional proposta para contribuir sobre o desempenho dos transformadores em termos de distorções harmônicas e qualidade de energia.
2 Materiais e métodos
2.1 Transformadores
Os transformadores são dispositivos estáticos de conversão de energia elétrica e operam por meio do princípio do eletromagnetismo, proporcionando a transferência de energia do circuito primário para o secundário sem a necessidade de uma conexão física entre seus enrolamentos. Na figura 1 (a) observa-se o transformador trifásico utilizado neste estudo e em (b) os dados de placa do equipamento.
Figura 1 – (a) vista frontal do transformador – fabricante Waltec; (b) dados de placa do equipamento.

FONTE: Autoria própria, fotos retiradas no Laboratório de Qualidade de Energia da Universidade Federal de Uberlândia.
A análise do princípio de operação dos transformadores pode ser feita a partir do entendimento da dinâmica da corrente que percorre pelo equipamento. Ainda que ele esteja com os seus terminais de saída (secundário) desconectados de qualquer tipo de carga, pode- se observar que, ao aplicar uma tensão alternada nos terminais de entrada (primário), é estabelecida uma corrente nestes enrolamentos denominada por corrente de magnetização. Esta condição de operação é denominada por operação a vazio do transformador e a corrente resultante deverá atender os fenômenos físicos observados nestas circunstâncias:
- Queda de tensão nos enrolamentos devido à parte resistiva, gerando também aquecimento proporcional ao quadrado da corrente – perdas no cobre; (R.I2)
- Potência ativa dissipada no núcleo devido à circulação de correntes induzidas no local – perdas por correntes parasitas ou perdas por Foucault;
- Potência ativa dissipada no núcleo devido à alteração da configuração dos domínios magnéticos durante cada semiciclo da forma de onda da tensão induzida nos enrolamentos – perdas por histerese.
- Parcela da tensão aplicada nos terminais de entrada que não é induzida nos enrolamentos, considerando a parte do fluxo que não é enlaçado pelos enrolamentos primário e secundário – fluxo de dispersão;
- Densidade de fluxo magnético a ser estabelecido no núcleo de acordo com a tensão induzida nos enrolamentos, geometria e material empregado – magnetização do núcleo.
A figura 2 ilustra a corrente de magnetização na sua forma fasorial. Percebe-se que esta corrente é constituída de uma parte real (Îc), proveniente das perdas no cobre e no núcleo, e uma parte imaginária (Îm), proveniente da magnetização do núcleo e indução de tensão nos enrolamentos secundários.
Figura 2 – Diagrama fasorial da corrente de magnetização (a vazio).
FONTE: UMANS, STEPHEN D. (2014, p. 69) – adaptada


Com as relações estabelecidas em (3), é possível determinar os parâmetros referente ao enrolamento secundário de acordo com a tensão aplicada no enrolamento primário, o que possibilita a criação de um único circuito elétrico equivalente considerando apenas a tensão de entrada V1. Os parâmetros do enrolamento secundário estarão “referidos” ao enrolamento primário pela relação de transformação N2/N1.
A figura 6 mostra o circuito elétrico equivalente por fase do transformador, o qual é amplamente adotado e difundido na literatura CHAPMAN (2013). Os valores de R1 e Xl1 são referentes à resistência e indutância de dispersão do enrolamento primário, respectivamente, e R’2 e X’l2 são referentes ao enrolamento secundário, cujos valores estarão referidos à tensão de entrada (primário). O ramo paralelo do circuito equivalente (conhecido por ramo de magnetização) representa o núcleo magnético, em que Rc diz respeito às perdas no núcleo (histerese e correntes parasitas) e Xm à corrente necessária para a magnetização do núcleo. Destaca-se que este circuito visa representar o transformador nas condições nominais de operação e, portanto, os valores de Rc e Xm poderão ser constantes.
Figura 6 – Circuito equivalente de um modelo de transformador real.
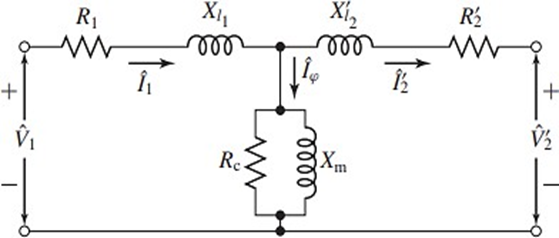
FONTE: CHAPMAN, STEPHEN (2013, p.88).
2.2 Influência do Fenômeno da Histerese na Formação da Corrente de Magnetização em Transformadores
Nos dispositivos de conversão eletromecânica de energia existem dois pilares importantes para seu desempenho: a densidade de fluxo magnético B e a intensidade de campo magnético H, UMANS et al (2014). Com o aumento do fluxo magnético, essas duas grandezas também se alteram e, consequentemente, interferem nas tensões induzidas nos enrolamentos e corrente de magnetização. Nesse sentido, o material do núcleo é fundamental para estabelecer a relação ótima entre tensão induzida x corrente de magnetização, sendo almejado obter uma tensão induzida de valor mais próximo da tensão de entrada e requerer uma corrente de magnetização mínima.
Os materiais magnéticos cristalinos são compostos por diversos grãos que são estruturas atômicas dotadas de polarização interna – domínios. Ao aplicar um fluxo magnético externo, esses domínios começam a se alinhar, proporcionando um meio mais favorável à passagem de fluxo em relação ao ar. Se o fluxo externo continuar aumentando, haverá um instante em que os domínios magnéticos já estarão alinhados com as linhas de fluxo e, por isso, será necessária uma intensidade de campo H muito maior para proporcionar um pequeno incremento de B no material. Esta condição é conhecida por “saturação magnética”, cuja região na curva de saturação do material pode ser identificada na figura 7.
Figura 7 – Curva de magnetização de um material ferromagnético.
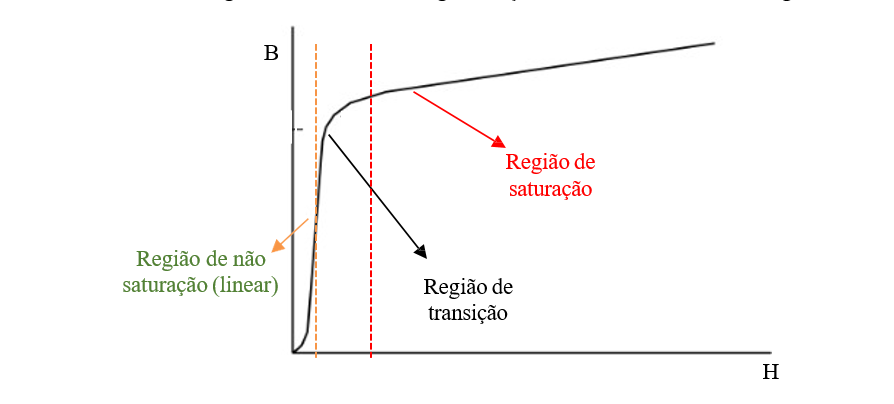
FONTE: DUGAN, ROGER C.et al, (2004, p.196) – adaptada;
Sabendo que o fluxo magnético em transformadores é proporcional à tensão induzida no primário, – equação (3) – é possível estabelecer a relação entre intensidade de campo H e a corrente de magnetização referida ao primário I1 por meio da equação (8).

Em que l é comprimento médio do caminho magnético a ser percorrido pelo fluxo. Portanto, pode-se dizer que a densidade de fluxo B está diretamente ligada à tensão aplicada nos terminais de entrada – V1 – enquanto a intensidade de campo H está diretamente relacionada com a corrente de magnetização I1.
Considerando que a tensão aplicada nos terminais de transformadores é alternada, os domínios magnéticos se movimentarão em uma dada direção para o primeiro semiciclo da tensão e, no outro semiciclo, para o sentido oposto. Essa movimentação dos grãos provoca calor que se dissipa ao longo do material magnético, sendo isso conhecido por Perdas por Histerese. É importante destacar que as Perdas por Histerese também estão relacionadas com a interação entre os grãos e o fluxo aplicado, fazendo com que o material detenha uma componente residual de magnetização e, consequentemente, a energia absorvida durante o primeiro ciclo da magnetização não seja devolvida ao sistema no segundo ciclo. A figura 9 ilustra os semiciclos positivos de laços de histerese obtidos para diferentes níveis de saturação magnética do material, em que as perdas por histerese consistem na área interna total descrita pelo laço de histerese.
Figura 9 – Metades superiores dos laços de histerese para aço silício de grão orientado de 0,3mm.
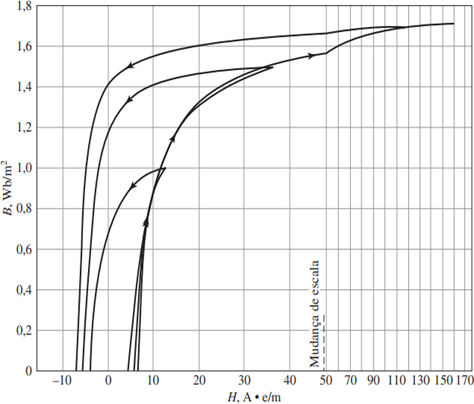
FONTE: UMANS, STEPHEN D. (2014, p. 20) – adaptada.
A figura 10 mostra os gráficos das curvas do fluxo magnético e corrente de magnetização em relação ao tempo, fazendo uma correspondência destas curvas com o laço de histerese do material. Nesta figura é possível constatar que a curva da corrente de excitação (ou corrente de magnetização), diante da saturação magnética provocada pela tensão instantânea induzida nos enrolamentos, possui distorções harmônicas em relação à frequência fundamental (60 Hz), visto o seu formato fortemente não senoidal. Os principais níveis harmônicos que se manifestam são as de ordem ímpar (3, 5, 7, 9 – conforme o tipo de ligação entre os enrolamentos), mas pode haver também as harmônicas não características, que são as componentes de ordem par (2, 4, 6, 8…).
Figura 10 – Comparação entre os gráficos de fluxo magnético, corrente de excitação e laço de histerese.
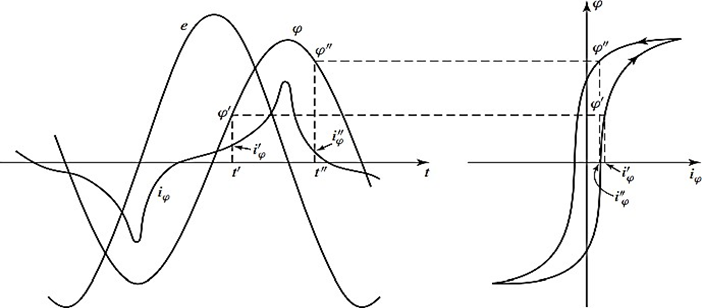
FONTE: UMANS, STEPHEN D. (2014, p. 22) – adaptada.
2.3 Origem de Harmônicas Não Características na Forma de Onda da Corrente de Magnetização em Transformadores Trifásicos
No caso de um transformador trifásico, sua estrutura básica consiste em um núcleo composto por três colunas, onde são enroladas as bobinas primária e secundária de cada fase. Devido à geometria do núcleo e aos caminhos magnéticos estabelecidos para os fluxos gerados pelas correntes de cada fase, ocorrem diferenças nas correntes de excitação de acordo com a coluna onde as bobinas primária e secundária estão situadas: as correntes que percorrem os enrolamentos da coluna central serão de menor magnitude em relação às correntes dos enrolamentos das colunas laterais CHAPMAN (2013). Isso pode ser constatado por meio da análise do circuito magnético ilustrado na Figura 8 (a), a qual retrata o instante em que o fluxo é máximo na coluna central. Neste caso, os caminhos magnéticos encontrados pelo fluxo serão iguais.
Figura 12 – (a) Diagrama esquemático do circuito magnético de um transformador trifásico considerando o fluxo máximo na coluna central; (b) circuito magnético correspondente quando o fluxo é máximo na coluna lateral; (c) correntes de magnetização dos ensaios laboratoriais coletados no equipamento POWER QUALITY AND ENERGY ANALYZER, marca Fluke.
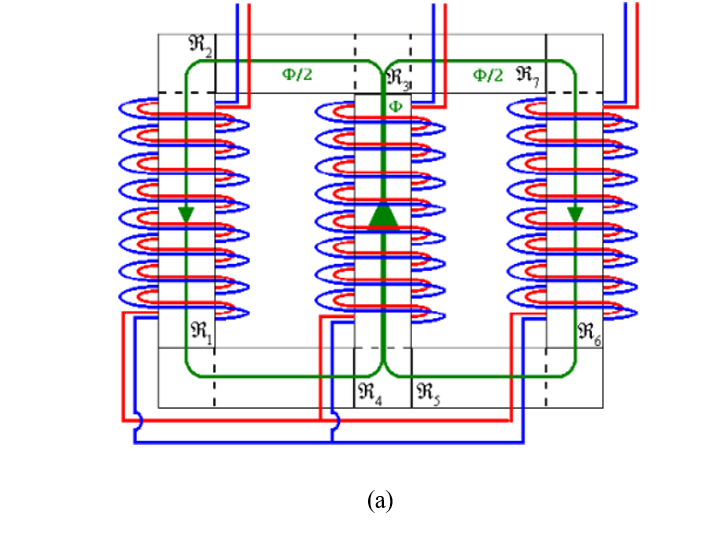
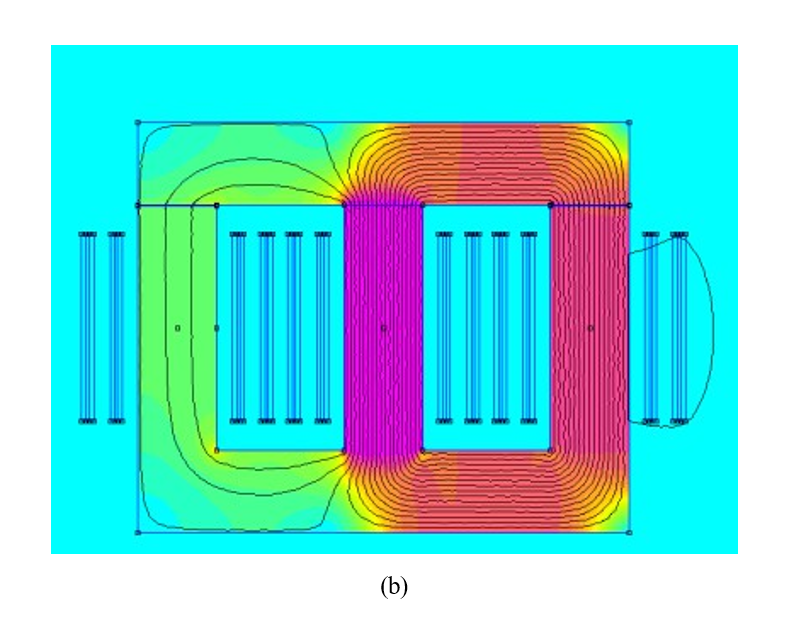
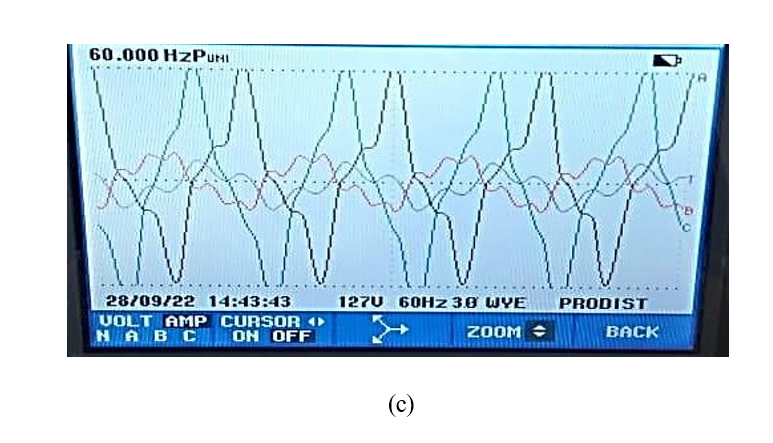
FONTE: (a) CHAVES (2009, 92 p.) – adaptada; (b) CHAVES (2009, 73p.) – adaptada; (c) Autoria própria fotografia do instrumento de medição pertencente ao laboratório da UFU.
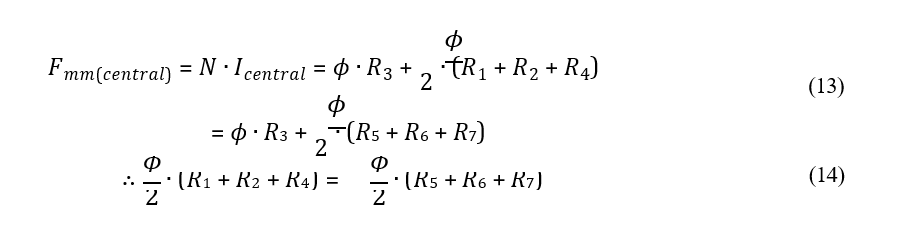



Nota-se que, nessa situação, a relutância magnética resultante a ser vencida pelo fluxo é maior do que na primeira (fluxo máximo na coluna central), o que acarreta maior força magnetomotriz e, consequentemente, maior corrente de excitação nos enrolamentos das colunas laterais. Essa constatação pode ser verificada na Figura 8 (c), em que são apresentadas as correntes de magnetização correspondentes a cada fase do transformador (fase B correspondente à coluna central e fases A e C às colunas laterais). Diante do desequilíbrio de corrente oriundo da geometria do núcleo de um transformador trifásico, sua forma de onda terá harmônicas de ordem par, as quais são denominadas por harmônicas não características pelo fato de que o sistema elétrico é predominantemente equilibrado (mesma magnitude e defasagem angular das tensões e correntes trifásicas).
3. Ensaio laboratorial e modelagem computacional
Tendo como cerne os trabalhos apresentados em CHAVES (2009) e FANDI (2003), a pesquisa foi desenvolvida por meio da execução de duas etapas:
- Etapa 1: realização de ensaio a vazio em um transformador trifásico de 15 kVA no laboratório de Qualidade da Energia Elétrica da Universidade Federal de Uberlândia – UFU, considerando diferentes níveis de tensão de alimentação para a verificação da forma de onda e espectro harmônico da corrente de magnetização; potências ativa, reativa e aparente;
- Etapa 2: desenvolvimento de uma representação computacional do transformador no programa ATPDraw compatível com as observações práticas e, desse modo, contribuir para a realização de estudos de caso do transformador sob diferentes condições impostas pelo sistema elétrico.
Diante do exposto, são apresentados na sequência os ensaios laboratoriais executados e a representação computacional do transformador estudado.
Etapa 1: Realização do Ensaio a Vazio em um Transformador Trifásico de 15 kVA
As figuras 17 (a) e (b) mostram a configuração feita no transformador de 15 kVA para a execução do ensaio a vazio e os instrumentos de medição utilizados. É importante destacar que foi feita a ligação estrela nos enrolamentos primários do transformador, sendo num primeiro momento com neutro não aterrado e no segundo momento com neutro aterrado.
Figura 17 – (a) instrumentos de medição e ligação estrela; (b) transformador conectado ao disjuntor em ligação estrela no primário e sem carga (a vazio) no secundário.

FONTE: Autoria própria, fotos retiradas no Laboratório de Qualidade de Energia da Universidade Federal de Uberlândia.
A figura 18 mostra a fonte de tensão regulável utilizada para a execução do ensaio a vazio. Os instrumentos de medição foram conectados em cada fase para a coleta de dados, antes do disjuntor conectado aos terminais de entrada do transformador – figura 9 (a).
Figura 18 – Fonte regulável de tensão da marca California Instruments.

FONTE: Autoria própria, fotos retiradas no Laboratório de Qualidade de Energia da Universidade Federal de Uberlândia.
A fonte de tensão regulável permitiu a aplicação de diferentes níveis de tensão para a verificação da corrente de excitação de acordo com o nível de saturação magnética do núcleo. Considerando que a tensão nominal era de 127 V, foram considerados dois níveis de tensão abaixo do nominal (80 V e 100 V) e dois níveis acima (150 V e 180 V), além da própria tensão nominal, para a realização das medições. Diante do exposto, os seguintes dados foram coletados:
- Espectro Harmônico de corrente: Análise detalhada das componentes harmônicas presentes na corrente de magnetização e tensão aplicada. A figura 19 mostra um dos registros feitos durante a execução dos ensaios.
Figura 19 – Espectro harmônico da corrente de magnetização.
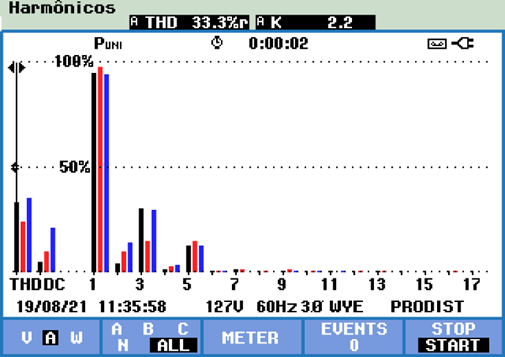
FONTE: Autoria própria – qualímetro da marca Fluke.
- Desequilíbrio entre fases: avaliação do nível de desequilíbrio de tensão, entre as fases do transformador. A figura 20 mostra o nível de desequilíbrio verificado na tensão de 127 V.
Figura 20 – Desequilíbrios de tensão e corrente entre as fases do transformador.

FONTE: Autoria própria – qualímetro da marca Fluke.
- Potências: medição das potências ativa, reativa e aparente do transformador operando a vazio. A figura 21 ilustra as potências medidas do transformador para a tensão de 127 V nos terminais de entrada.
Figura 21 – Potências medidas e fator de potência do transformador de 15 kVA operando a vazio.

FONTE: Autoria própria – qualímetro da marca Fluke.
Etapa 2: Representação Computacional do Transformador no ATPDraw
Análise computacional: criação de modelo para simulação computacional ilustrado na figura 22, utilizando os parâmetros previamente obtidos na etapa experimental, no software Alternative Transient Program (ATPDraw), essa modelagem possibilitou a extração de relatórios, incluindo;
- Distorções harmônicas por ramo de magnetização: utilizando a transformada de Fourier, foram analisadas e registradas as distorções harmônicas específicas associadas a cada ramo de magnetização do transformador.
- Plot das curvas de saturação e laço de histerese: curvas caracterizando a saturação do núcleo e o laço de histerese foram capturadas, oferecendo uma visualização clara das propriedades magnéticas do transformador.
Figura 22 – Captura de tela do software ATPDraw representando o circuito equivalente de um transformador real.
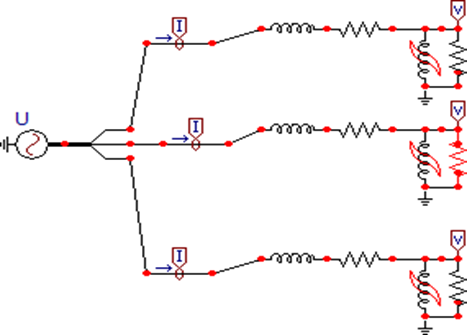
FONTE: autoria própria
A abordagem no ATPDraw proporcionou uma simulação computacional precisa, permitindo aprofundar-se no comportamento do transformador em resposta aos diferentes parâmetros de entrada. Os relatórios extraídos dessas simulações são importantes para comparar e validar os resultados da modelagem computacional com os dados experimentais.
3. Resultados
As tabelas I e II mostram os valores medidos nos ensaios executados, considerando a operação a vazio do transformador de 15 kVA sob os diferentes níveis de tensão.
Tabela I – Medições realizadas no transformador de 15 kVA com neutro da estrela aterrado.
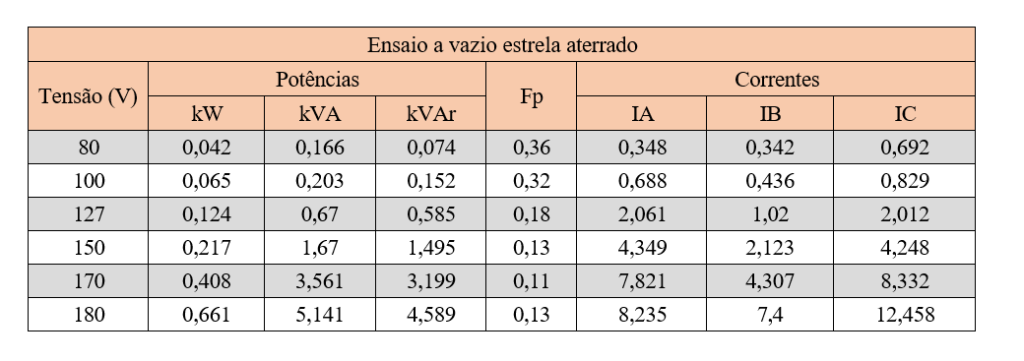
FONTE: Autoria própria.
Tabela II – Medições realizadas no transformador de 15 kVA com neutro da ligação estrela não aterrado.
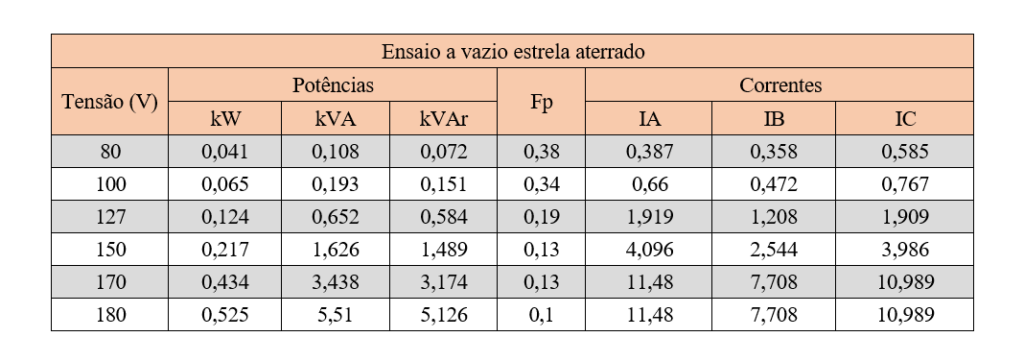
O estudo conduzido neste trabalho destaca a estreita correspondência entre a simulação computacional e o comportamento observado no modelo real do transformador em âmbito da qualidade de energia. Para consolidar essa correlação, foi fundamental a representação da curva de histerese do dispositivo na figura 23 (a), tomando como base o meio laço de histerese do catálogo STEEL (2009), figura 23 (b), onde contribuiu com proporcionalidades e visibilidade para nortear os resultados, pois o material do transformador é de um fabricante distinto.
Figura 23 – (a) Curva de histerese gerada a partir de extrapolação matemática se baseando no catálogo; (b) laço positivo de histerese de chapas de aço com cristais de silício catálogo de referência.
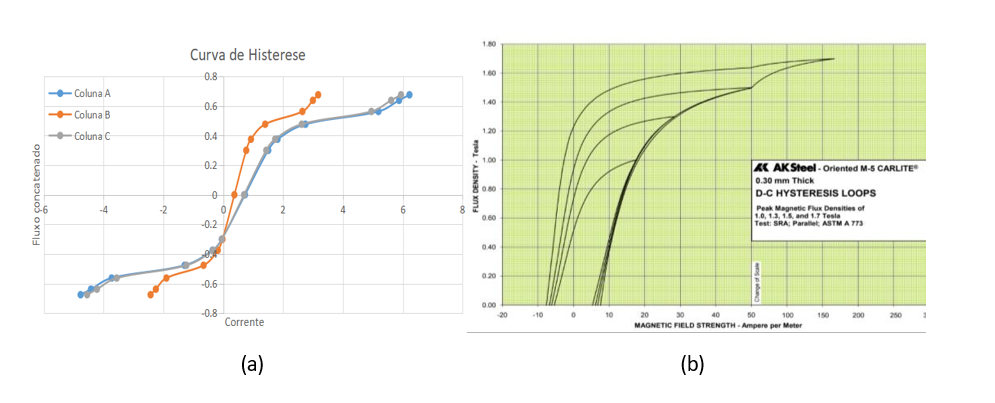
FONTE (a): Autoria própria; (b): Data sheet AK STEEL, PRELIMINARY PRODUCT DATA BULLETIN (2009).
Ao analisarmos a curva, conseguimos captar com maior precisão as nuances das características do transformador e como ele reage em face de diferentes condições de operação. Vale ressaltar o desenvolvimento de um circuito específico (figura 22), para descrever de maneira mais aproximada as propriedades do equipamento, e a curva de histerese foi representada graficamente figura 23 (a), utilizando o software Excel.
Após traçar a curva de histerese por meio de análise gráfica utilizando dados do catálogo do fabricante de um transformador convencional de metal silício STEEL (2009), obtivemos os valores de fluxo concatenado, e os demais parâmetros por cálculos analíticos. Esses dados foram inseridos para cada bobina (A, B e C), do transformador no software ATPDraw, figura 24, onde a janela de Characteristic é mostrada, para garantir o funcionamento adequado, todos os valores foram adicionados na simulação levando em consideração as características do transformador real de 15KVA.
Figura 24 – Parâmetros de corrente e fluxo concatenado aplicados na bobina A do transformador modelado.
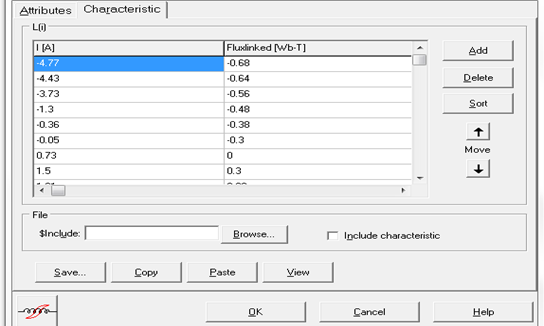
Este processo garante que o circuito seja projetado e operado dentro dos limites adequados, levando em conta as propriedades magnéticas específicas do transformador utilizado.
Posteriormente as curvas de espectros de onda foram comparadas entre simulações, figura 25 (a) e (b), avaliando a frequência fundamental no momento de excitação do equipamento modelado, e no seu estado de saturação com distorções harmônicas, apresentados a seguir.
Figura 25 – (a) Espectro da corrente de magnetização na frequência fundamental na simulação computacional; (b) Espectro da corrente de magnetização em estado de saturação com poluição harmônica total até a 30° ordem.
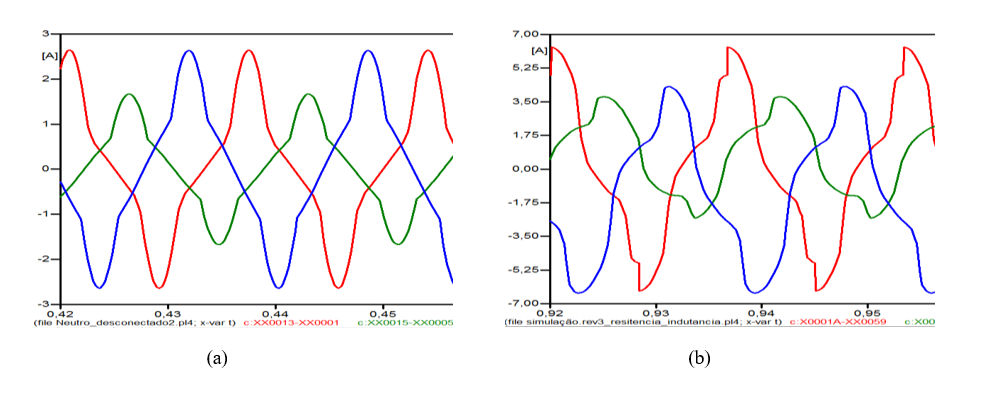
FONTE: Plot’s do software ATPDraw das curvas de corrente de magnetização.
Após executar a simulação, os dados extraídos de distorções harmônicas na corrente eficaz até 30° ordem, correspondentes a cada tensão aplicada nas bobinas, onde foi aplicado a eq. 26 e 27 de qualidade de energia para tabelar os resultados de cada distorção harmônica total por ramo, durante as aplicações de tensão entre 80 e 180 volts como evidenciado posteriormente.

Onde:
DIIh = Distorção de corrente Harmônica individual
DTI = Distorção total de corrente
Ih = Valor eficaz de corrente de ordem n
I1 = Valor eficaz de corrente fundamental
Na tabela III observamos o desvio entre os valores reais de cada cenário entre tensões aplicadas, comparando as grandezas ensaiadas e simulados na ligação estrela aterrada.
Tabela III
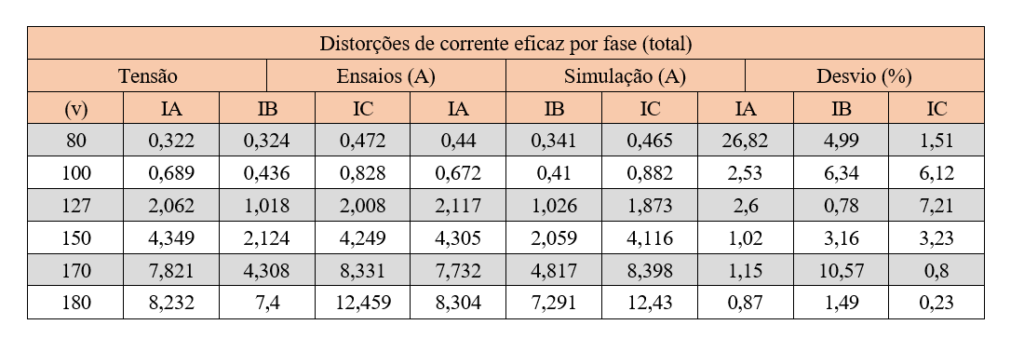
FONTE: Autoria própria.
Os resultados desta pesquisa apresentam aspectos relevantes sobre o tema estudado. No entanto, é fundamental ressaltar que a amostragem apresentada constitui a soma total de distorções harmônicas por enrolamento de acordo com a eq. 26. Para uma compreensão mais completa dos efeitos das harmônicas e suas influências nos diferentes ramos do transformador (A, B e C), será necessário analisar individualmente cada ordem harmônica. Dessa forma, pode-se identificar com mais precisão as características específicas de cada ramo e como as harmônicas afetam seu desempenho.
4. Conclusão
Essa pesquisa teve como objetivo principal responder aos problemas de qualidade de energia com base em um estudo comparativo entre transformadores construídos com aço silício e ligas amorfas, a fim de analisar as vantagens e desvantagens de cada alternativa em relação à geração de componentes harmônicos de corrente de magnetização. No entanto, surgiu o desafio de obter um transformador com núcleo amorfo que tivesse potência, tensões e impedâncias similares ao transformador utilizado, isso impossibilitou a continuidade dos estudos com esse tipo de material.
Apesar dessa barreira, houve uma adaptação aos objetivos e à metodologia da pesquisa, resultando em contribuições para a compreensão do comportamento do transformador, simulações computacionais e distorções harmônicas, com um circuito genérico modelado que pode atender diversos cenários operacionais.
Os estudos indicaram que a corrente de magnetização tem influência pouco significativa nos níveis de distorção harmônica. No entanto, em relação às harmônicas não características
na corrente de magnetização (distorções de ordens pares), pode ocorrer uma extrapolação dos limites admissíveis, sendo necessário levar em consideração características específicas do dispositivo, como tensão, potência nominal, material magnético utilizado no núcleo e distorções harmônicas geradas. Constatou-se que a característica de magnetização proveniente do laço de histerese é um fator relevante para a formação das componentes harmônicas, sendo uma propriedade intrínseca dos materiais magnéticos não lineares empregados no núcleo do equipamento.
Para dar continuidade aos estudos iniciados nesta pesquisa, serão necessários uma investigação aprofundada das características dos materiais magnéticos. Será importante realizar uma pesquisa sobre as ligas amorfas, que são consideradas “vidro metálico” capaz de reduzir substancialmente as perdas por histerese, levando em consideração a produção de distorções harmônicas não características, a fim de utilizar uma estratégia mais eficiente com menor impacto na qualidade.
Referências
MAMEDE FILHO J. Manual de Equipamentos Elétricos. LTC. 4ª edição, 2013.
FANDI, Juliana. Modelagem de Transformador de 3 colunas no ATP. 2003. 250 f. Dissertação De Mestrado (Pós-graduação) – Universidade Federal de Uberlândia, Uberlândia, 2003.
AK STEEL, (USA). PRELIMINARY PRODUCT DATA BULLETIN: Grain Oriented Electrical STEELs. In: PRELIMINARY PRODUCT DATA BULLETIN: ORIENTED ELECTRICAL STEELS. West Chester: [s. n.], 2009. cap. HYSTERESIS LOOPS, p. 1-27.
UMANS, Stephen et al. Máquinas Elétricas: de Fitzgerald e Kingsley. 7ª edição. Tradução: AMGH EDITORA LTDA. -Porto Alegre: AMGH, 2014
CHAPMAN, Stephen J. Fundamentos de Máquinas Elétricas. 5ª edição. Tradução: Anatólio Laschuk. -Porto Alegre: AMGH, 2013.
DUGAN, Roger et al. Electrical Power Systems Quality. 2ª edição, 2004.
CHAVES, Camilla de Sousa. Análise de fenômenos eletromagnéticos em transformadores utilizando o programa computacional FEMM. Orientador: José Roberto Camacho. 2009. 92 p. Trabalho de Conclusão de Curso (Bacharelado em Engenharia Elétrica) – Faculdade de Engenharia Elétrica, Universidade Federal de Uberlândia, Uberlândia, 2009.
CHAVES, Camilla de Sousa et al. Análise da correlação entre as perdas adicionais e os fluxos de dispersão em transformadores sob distintos níveis de saturação magnética. IX WORKSPOT- International workshop on power transformers, equipment, substations and materials, Foz do Iguaçu, 26 nov. 2018.
SARAIVA, Elise. Um estudo das alterações dos parâmetros de transformadores oriundas de
deformações nos enrolamentos: uma contribuição para o diagnóstico de vida útil. Orientador: Geraldo Caixeta Guimarães. 2011. 220 p. Tese (Doutorado em Engenharia Elétrica) – Faculdade de Engenharia Elétrica, Universidade Federal de Uberlândia, Uberlândia, 2011.
SARAIVA, Elise; CHAVES, Marcelo Lynce Ribeiro; HERIVELTO DE SOUZA, Bronzeado. Proposta de metodologia para implementação do ciclo de histerese no modelo de transformadores trifásicos no programa ATP. XVIII SNPTEE – SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA, Curitiba, p. 1-8, 17 out. 2005.
HAYT JR, William H. Eletromagnetismo. 3ª edição. Tradução: Paulo Cesar Pfaltzgraff Ferreira- Rio de Janeiro. LTC- livros técnicos e científicos Editora S.A, 1985.
1Discente do Curso Superior de Engenharia Elétrica do Instituto Federal do Triângulo Mineiro Campus
Patrocínio e-mail: wendell.saran@estudante.iftm.edu.br
2Docente do Curso Superior de Engenharia Elétrica do Instituto Federal do Triângulo Mineiro Campus
Uberlândia. Doutor em Engenharia Elétrica (UFU). e-mail: paulomota@iftm.edu.br
