REGISTRO DOI: 10.69849/revistaft/cs10202501311516
Ana Paula Mendonça de Souza
Rayani Costa da Silva Vaz
Dr. Whasgthon Aguiar de Almeida
RESUMO:
Este artigo aborda o tema da tecnologia na sala de aula, focando no uso do software matemático em uma sala de aula amazônica. O objetivo principal foi analisar os impactos do GeoGebra no desenvolvimento dos alunos nas atividades curriculares e na compreensão dos conceitos matemáticos. Para isso, adotou-se uma metodologia de abordagem qualitativa e quantitativa, utilizando procedimentos de pesquisa-ação. A coleta de dados foi realizada por meio de entrevistas semiestruturadas. A proposta investigativa foi concebida com a intenção de oferecer aos alunos um contato direto com o software e seus benefícios, observando o impacto na aprendizagem através do uso do programa e estimulando o interesse pela matemática. A pesquisa se justifica por evidenciar os benefícios da tecnologia na aprendizagem dos alunos, bem como pela fundamentação teórica relacionada às metodologias ativas e à cultura Maker, que desenvolvem habilidades cognitivas e criativas dos estudantes. Os resultados indicaram que a utilização do software nas aulas de matemática foi positiva. No entanto, alguns alunos enfrentam dificuldades ao utilizar os computadores, pois não sabiam como manuseá-los. A aplicação das novas metodologias mostrou-se muito proveitosa nas aulas de matemática, demonstrando a eficácia das metodologias ativas.
Palavras-chaves: Geogebra. Metodologia Ativa. Matemática. Amazônia.
INTRODUÇÃO
Nas últimas décadas houve uma evolução significativa no mundo, em sua economia, na área social, científica e em especial no conhecimento. O conhecimento é um dom, um potencial que a educação deve desenvolver, quanto melhor a educação, maior o desenvolvimento da inteligência. De acordo com (Bacich; Moran, 2018, p. 221) “vivemos a era da informação, na qual a sociedade é impactada pelo ritmo acelerado das novidades tecnológicas, resultado evidente do acúmulo e evolução do conhecimento científico […]”. Portanto ensinar é provocar atitudes que estimulem a construção do conhecimento científico, e ensinar Matemática é desenvolver o raciocínio lógico, buscando estimular a criatividade e competência de resolver problemas, procurando novas alternativas para melhorar a motivação pela aprendizagem, ajudar a organização, concentração e a atenção dos discentes em sala de aula.
Nesta perspectiva Baldin (2023) apresenta que o uso da tecnologia na sala de aula, colabora com a personalização do aprendizado dos discentes. Tornando o processo educacional mais eficiente e eficaz, pois fornece materiais específicos como algoritmos que identificam as necessidades do aluno. A sala de aula tradicional torna-se um ambiente interativo e dinâmico, com a presença dos computadores e outros recursos midiáticos que estimulam e exploram os conceitos abordados pelo professor.
A metodologia ativa no ensino de matemática tem muito a contribuir, promovendo novos comportamentos em relação ao processo de ensino e aprendizagem, colocando o estudante como protagonista na construção do seu conhecimento. A “Cultura Maker”, os “Os espaços Makers” são formados por computadores e outros equipamentos que buscam a criatividade e imaginação. Nos espaços educacionais tem como objetivo oportunizar os alunos a explorar e inovar novas ideias ao tentar e errar para acertar. Nesse sentido Soares (2021), os estudantes têm a liberdade de explorar as possibilidades do erro. O professor atua como facilitador, promovendo a interação entre os colegas e criando um ambiente colaborativo onde cada aluno possa contribuir com o seu melhor.
Nesse sentido, este artigo pretende compartilhar a trajetória pessoal, como professora e pesquisadora de matemática, em que a aprendizagem das novas maneiras de ensinar e aprender com uso de recursos computacionais trouxe conhecimentos ampliados sobre o que é importante na prática profissional de ensinar, potencializado com recursos tecnológicos para comunicar conteúdos matemáticos.
Neste contexto, o presente artigo tem como objetivo geral analisar os impactos do programa Geogebra no desenvolvimento dos discentes nas atividades curriculares e na relação com os conceitos matemáticos. Desta forma, tem-se à disposição novas tecnologias, especificamente os Softwares matemáticos, que visam oportunizar a motivação e apropriação do conteúdo estudado em sala de aula. No atual contexto escolar, observa-se que é crescente a dependência do uso de computadores, bem como a utilização de Softwares educativos no ensino da matemática.
Tendo em vista que o uso das ferramentas computacionais é imprescindível para o desenvolvimento dos discentes na educação atual. Os mesmos estão tornando-se protagonistas da cultura digital, tendo autonomia direta em novos desenhos multimidiaticos e multimodal das sociedades em rede e cabe às instituições terem o compromisso por esta formação a fim de contribuir para o pleno desenvolvimento e aprendizagem das novas tecnologias. Na disciplina de matemática a utilização de software tem sido bem trabalhada por alguns livros didáticos e torna importante o professor fazer uso desta prática nas suas aulas.
Nesse sentido as Metodologias ativas são arquitetadas em uma abordagem pedagógica a partir de olhar específico no processo de ensino-aprendizagem. Considerando a importância do envolvimento do discente no seu próprio aprendizado, que ele seja participativo, crítico e reflexivo colaborando com o processo de ensino. O docente precisa analisar que tais práticas devem estar associadas às situações reais dos educandos para que possam promover uma aprendizagem mais efetiva e significativa. Segundo Fernandes, et al. (2021): “as MAs são idealizadas a partir de uma concepção pedagógica, e são baseadas em um processo de ensino-aprendizagem participativo, crítico-reflexivo, durante toda a formação do estudante, a partir de situações significativas […]” (p.14-15).
O presente artigo baseou-se em uma pesquisa-ação, utilizando práticas pedagógicas e atividades computacionais, onde foram propostos exercícios relacionados ao conteúdo ministrado. Espera-se que, como resultado do uso do software matemático GeoGebra, ele atue como facilitador no processo de ensino e aprendizagem na área de matemática. Nesse sentido, nossa questão norteadora foi: como o software Geogebra impacta o desenvolvimento dos alunos nas atividades curriculares e a relação com os conceitos matemáticos? Dessa forma espera-se promover uma aprendizagem significativa a partir da utilização do software na disciplina de matemática. O contexto da escola amazônica se distingue por sua localização geográfica, marcada por rios e pequenas cidades situadas às suas margens. Os alunos, muitas vezes, não têm contato diário com a informática de maneira pedagógica, embora estejam familiarizados com a tecnologia por meio de seus smartphones. Nesse sentido, oferecer aos estudantes das águas e florestas um ambiente informatizado na sala de aula reforça e complementa o desenvolvimento tecnológico que eles vivenciam fora da escola.
DESENVOLVIMENTO
A TECNOLOGIA NO CONTEXTO EDUCACIONAL
A Tecnologia ocupa diversos campos da nossa sociedade, é possível perceber a utilização dos computadores com muita frequência como ferramenta de trabalho tanto de professores quanto de alunos. No contexto educacional isto não é diferente, parte do trabalho dos profissionais de educação são realizados com a utilização da tecnologia. As tecnologias digitais de informação e comunicação (TDIC), são utilizadas em vários espaços derrubando fronteiras, estamos cada vez mais conectados e informados. O dinamismo da informática e seu potencial de interação são algumas das características que tem chamado à atenção dos pesquisadores de educação nas questões que tange o poder de despertar nos estudantes uma motivação a mais para a aprendizagem, o que pode auxiliar bastante nas práticas em sala de aula. É muito interessante como a tecnologia atrai as pessoas com seus jogos, internet, aplicativos e outras ferramentas. No contexto da sala de aula isso não é diferente, a maioria dos estudantes tem demonstrado entusiasmo por estarem no laboratório de informática, seja para brincar ou mesmo fazer pesquisas. O educador deve desenvolver a capacidade de saber lidar com essas ferramentas que contribuem para o ensino aprendizagem dos estudantes. De acordo com (Cardoso, 2019) a utilização de softwares educacionais tem se mostrado uma ferramenta muito importante para o ensino-aprendizagem da matemática, especialmente no ensino da álgebra e da geometria. (p.46)
Neste sentido Pires (2018, p. 9) destaca que:
O uso desse software é justificado pelo crescente acesso a informática que deve ser visto como um direito, tanto nas escolas públicas como particulares. Os alunos devem ter acesso a uma educação que inclua a alfabetização tecnológica, que deve ser entendida como o aprender em uma nova mídia, e não simplesmente um curso de informática.
O computador pode ser um grande aliado do desenvolvimento cognitivo dos alunos, principalmente por possibilitar adaptação a diferentes ritmos de aprendizagem. O computador possui uma habilidade importante a do feedback imediato, o erro se torna muito simples de ser eliminado, e há uma facilidade de construção e reconstrução das atividades, a capacidade de mudança imediata. Um aspecto muito importante é o fato da mudança da rotina da sala de aula a partir de qualquer proposta metodológica como por exemplo o uso de jogos, material concreto e o computador como auxiliar dos alunos e do professor como ferramenta de ensino. O professor deve estar em constante aprendizado, analisando criticamente as propostas de curriculum e experimentando novas propostas de ensino. Nas palavras de Almeida e Cabral (2020, p. 360) os ambientes informatizados, […], contribuem para enriquecer as experiências e possibilitam a realização de um trabalho abrangente que promove a pesquisa e a investigação, […] intrínsecos à construção do conhecimento que resulta em experiência formativa, criativa e inovadora.
A mente é um instrumento de trabalho muito importante, que deve ser cultivado diariamente. Precisa estar em constante atualização e acompanhando o desenvolvimento das ciências e tecnologias. Tendo em vista que os alunos devem utilizar diferentes fontes de informação e recursos tecnológicos para adquirir e construir conhecimentos. (Oliveira, 2021, p. 15) […]. Assim, percebe-se que o componente de Matemática, com o uso da tecnologia, será mais compreendido pelos alunos. Isso significa que cabe ao professor encontrar a melhor forma de contribuir com a sua aula e principalmente com a aprendizagem dos alunos.
Segundo a BNCC (2018, p.528-529)
Diante dessas considerações, a área de Matemática e suas Tecnologias tem a responsabilidade de aproveitar todo o potencial já constituído por esses estudantes no Ensino Fundamental, para promover ações que ampliem o letramento matemático iniciado na etapa anterior. Isso significa que novos conhecimentos específicos devem estimular processos mais elaborados de reflexão e de abstração, que deem sustentação a modos de pensar que permitam aos estudantes formular e resolver problemas em diversos contextos com mais autonomia e recursos matemáticos.
Dessa maneira, faz-se necessário que o professor esteja atento e procure aspectos positivos nos aplicativos, com a finalidade que se constituam um facilitador para uma aprendizagem significativa, dentro dos objetivos estabelecidos. Os softwares educacionais são construídos para ser usado especificamente no âmbito educacional e seguem uma concepção educacional, os softwares podem se constituir em uma importante ferramenta pedagógica para o processo de ensino-aprendizagem.
SOFTWARE MATEMÁTICO GEOGEBRA
A informática desponta no contexto educacional como uma ferramenta que pode contribuir significativamente para o processo ensino-aprendizagem, incrementando ou mesmo modificando as metodologias que já estão estabelecidas no cotidiano escolar. Isso pode ser um fato positivo, pois exige novas reflexões e novas posturas frente à educação como um todo. Nesta perspectiva, a busca do conhecimento deixa de ser somente tarefa do professor passando a ser de todos os envolvidos, onde cada um dentro de suas habilidades desempenha papeis importantes, tanto os professores, quanto os alunos. Neste sentido, o professor não domina o computador ou software, mas sim o torna auxiliador na construção e desenvolvimento do conhecimento adquirido sobre o conteúdo e sobre como o computador pode se integrar ao ensino. Conforme BNCC (2017, p. 61): “É importante que a instituição escolar preserve seu compromisso de estimular a reflexão e a análise aprofundada e contribua para o desenvolvimento, no estudante, de uma atitude crítica em relação ao conteúdo e à multiplicidade de ofertas midiáticas e digitais”.
E neste sentido que o uso dos softwares no contexto da sala de aula podem-se tornar uma ferramenta enriquecedora tanto para o estudante quanto para o educador. Com os softwares os assuntos de matemática tomam um brilho especial, os erros muitas vezes são tão fáceis de serem eliminados, imagens se movimentam e principalmente as dimensões podem ser percebidas facilmente. É lógico que nem sempre é possível trabalhar os softwares, uma vez que em nossa região as nossas escolas se encontram em uma realidade muito diferente das escolas das outras regiões, que tem contato quase que diário. No entanto, se o educador tem possibilidades de mostrar estas ferramentas para os estudantes, deve fazê-lo e incentivá-lo a manusear, para que possam desenvolver seus conhecimentos nessa área, uma vez que alguns deles apresentam limitações no domínio do computador. A este propósito, Almeida e Cabral (2020) afirmam que:
A principal característica desses softwares é a possibilidade de representações dos objetos matemáticos serem modificadas, mantendo-se suas propriedades inalteradas. Esses programas apresentam a característica de serem de manipulação direta, ou seja, o usuário age diretamente sobre a representação dos objetos que estão na tela. Uma das abordagens que o professor pode trabalhar com tal instrumento é a de exploração de conjecturas que poderão ser verificadas com auxílio das ferramentas disponíveis. (p. 361)
Para (Oliveira, 2021, p.10) “o trabalho com tecnologia na sala de aula vem sendo bastante discutido nos dias atuais”. Os professores estão cada vez mais se aperfeiçoando e trazendo novos recursos para suas aulas, principalmente nas aulas de Matemática, a qual necessita de uma grande atenção. A utilização da informática educativa possibilita um entendimento mais profundo acerca dos campos conceituais até uma abertura para análise de possíveis erros que possam ser analisados e corrigidos pelos softwares. Neste sentido, usar os softwares na resolução de problemas, ou mesmo na validação de conteúdos já ensinados pode tornar-se uma boa contribuição para a aprendizagem dos alunos, ou mesmo instruindo os alunos ao uso dos softwares de Matemática. Pode se tornar muito vantajoso o uso dos softwares no contexto da sala de aula, tendo em vista que o professor deve avaliar o momento exato para inseri-lo, seja no momento da aplicação do conteúdo, ou posteriormente quando os alunos já tiverem adquirido os conceitos do conteúdo.
O Geogebra é um software livre, a distribuição se alinha nos termos da General Public License (GNU) e é escrito em linguagem Java, o que possibilita estar disponível em várias plataformas. Possui a (junção das palavras geometria e álgebra), o mesmo é um aplicativo de matemática dinâmica que mistura conceitos de geometria e álgebra em uma única interface. Conforme (Junior, Estevam, 2022, p.4) “um dos softwares que tem se destacado nesse cenário é o GeoGebra, por se tratar de um software livre, cujo foco não incide apenas na geometria, mas também na álgebra, probabilidade, estatística, […]”.
Ele foi desenvolvido por Markus Hohenwarter da Universidade de Salzburg para educação matemática nas escolas. Pode ser obtido facilmente em sites de busca ou no endereço (www.geogebra.at). O objetivo desse trabalho é introduzir as noções básicas do programa e utilizá-lo no estudo de certos conteúdos matemáticos como polígonos, funções reais, e em especial no estudo das cônicas. São inúmeras as aplicações das cônicas no cotidiano.
Pode ser utilizado facilmente como uma importante ferramenta para despertar o interesse pela busca do conhecimento Matemático, principalmente dos alunos do Ensino Fundamental e Ensino Médio. Possibilita trabalhar de forma dinâmica em todos os níveis da educação básica permitindo a abordagem de diversos conteúdos especialmente os relacionados ao estudo da geometria e função e outros conteúdos matemáticos. É capaz de interpretar e realizar as atividades com situações reais, dinâmicas e interativas no software educativo. (Nascimento et. al, 2017). Assim o estudante consegue com identificar o conteúdo mediante a visualização na tela do computador
METODOLOGIAS ATIVAS, CONTRIBUIÇÕES À APRENDIZAGEM
As metodologias ativas são arquitetadas em uma abordagem pedagógica a partir de um olhar específico no processo de ensino-aprendizagem. Considerando a importância do envolvimento do discente no seu próprio aprendizado, que ele seja participativo, crítico e reflexivo colaborando com o processo de ensino. Metodologias ativas para proporcionar uma educação transformadora, capaz de modificar as aulas em experiências mais envolventes e significativas. Em um mundo cada vez mais digital, os alunos têm expectativas diferentes em relação ao aprendizado e ao desenvolvimento, comparadas às gerações anteriores. As metodologias ativas são fundamentais para atender essas novas demandas e garantir que a educação seja relevante e eficaz para os estudantes da era digital. (Almeida, 2018).
Nesse sentido, proporcionar um ambiente reflexivo e prático para os estudantes garante uma educação dinâmica, promovendo a reflexão sobre o conteúdo estudado “as metodologias ativas para uma educação inovadora apontam as particularidades do professor como orientador, possibilitando as aulas em experiências de aprendizagem extraordinárias”. (Souza; Almeida, 2024, p. 29). Assim, no contexto educacional atual essas metodologias são desenvolvidas para possibilitar uma experiência de ensino que atenda os anseios dos estudantes contemporâneos. Diante do exposto (Daros, 2018) expõe “as metodologias ativas de aprendizagem desenvolvem-se nesse contexto, com alternativa necessária a essa finalidade”. (p.13).
A aprendizagem deve ser um processo contínuo e dinâmico, onde professores e estudantes estão sempre curiosos e abertos a novas descobertas. É importante manter uma relação de debates e questionamentos para aprofundar a compreensão do conteúdo abordado. Atividades que envolvam a criação de novos projetos e experimentos são essenciais para que os alunos coloquem em prática o que foi aprendido. Com todos esses processos, é possível criar um ambiente de sala de aula que favoreça a troca de experiências, a consolidação do conhecimento e a melhoria das práticas educativas. (Moran, 2018).
Ao empregar nesses métodos, o ensino e a aprendizagem se ampliam para áreas de conhecimento mais desenvolvidas e atingem níveis de profundidade maiores, proporcionando uma educação mais rica e envolvente. Uma aprendizagem ativa, com os alunos engajados na participação, nos debates, projetos e experimentos. Porém essa participação implica a reflexão acerca do que estão assimilando, isso deve ser um processo contínuo de análise e avaliação das próprias experiências de aprendizagem para compreender conteúdos, desenvolver competências e reconhecer a importância do que está sendo discutido. Para (Moran, 2018) a palavra ativa na educação precisa “sempre estar associada à aprendizagem reflexiva, para tornar visível os processos, os conhecimentos e as competências do que estamos aprendendo com cada atividade”. (p.3).
No contexto atual é importante implementar metodologias pedagógicas que se preocupam não apenas com a transmissão de conteúdo. Uma práxis educativa progressista integrando teoria e prática, capacitando o estudante em uma formação de sujeito crítico e inovador para conceber e encontrar soluções. Bem como uma aprendizagem colaborativa para que os discentes desenvolvam habilidades sociais, troca de ideias com seus pares aplicando os conhecimentos adquiridos para resolver questões práticas e desafios do mundo real. (Daros, 2018)
As metodologias ativas podem desenvolver um aprendizado completo, preparando os alunos não apenas academicamente. Mais que tenham a capacidade de lidar com os problemas reais do cotidiano, liderando e resolvendo tais situações focando na ação prática a partir dos conteúdos aprendidos, “métodos ou metodologias ativas são identificadas como qualquer atividade onde os estudantes ficam envolvidos em fazer algo e pensar no que estão fazendo”. (Cortelazzo et. al, 2018, p. 107).
O ensino por experimentação envolve testar hipóteses e assimilar conhecimentos através de descobertas que incentivam a curiosidade. Essa abordagem permite que os alunos verifiquem o que foi aprendido utilizando o computador como ferramenta. A tecnologia colabora e amplia as possibilidades de aprender. “No contexto digital temos a aprendizagem por experimentação, por design e a aprendizagem maker são expressões atuais de aprendizagem ativa, personalizada, compartilhada”. (Moran, 2018, p.3).
Particularmente, ao utilizar metodologias ativas, o ensino se torna mais dinâmico e centrado no aluno, promovendo um aprendizado significativo e preparando-os para situações reais. “As metodologias ativas baseiam-se em formas de desenvolver o processo de aprender, utilizando experiências reais ou simuladas, visando resolver os desafios da prática social ou profissional em diferentes contextos”. (Daros, 2018, p. 13). É colocar o estudante em contato com experiências voltadas para os conteúdos ministrados, é importante relacionar teoria e prática na sala de aula. “Empregamos a palavra “experiência” com a mesma riqueza de sentido. E, a isto, assim como à vida em sua mera significação fisiológica, se aplica o princípio da continuidade por obra da renovação” (Dewey, 1979, p.2).
Dessa forma, atender às necessidades dos estudantes e tratá-los como sujeitos críticos e participativos no seu próprio processo de construção escolar demonstra respeito por suas particularidades enquanto seres humanos. (Soares, 2021). A educação tradicional com apenas transmissão de conteúdos, aos poucos tem perdido espaço para educação ativa promovendo o protagonismo dos alunos. Nesse sentido a cultura Maker com a utilização do laboratório de informática pode relacionar teoria e prática dos conteúdos de matemática. De acordo com (Neto et. al, 2014 p.107) “nos últimos anos, a cultura maker tem emergido como uma abordagem inovadora e promissora para o ensino e aprendizagem em diversas áreas do conhecimento”.
Além disso, na disciplina de matemática, sempre que possível, relacionar os conteúdos com a prática deixa os alunos mais engajados e torna o ensino mais concreto. Os laboratórios de informática são aliados essenciais, permitindo que toda a teoria seja visualizada com imagens coloridas e em diferentes dimensões. “[…] a Matemática é uma disciplina que é muito beneficiada pela experiência laboratorial, por trazer uma maior proximidade do aluno com os conteúdos apresentados”. (Ribeiro et. al, 2023, p.2). A cultura Maker é baseada no faça você mesmo, encorajando e tornando os discentes protagonistas de sua aprendizagem. Ela incentiva a criatividade, o pensamento crítico e a resolução de problemas. (Neto et. al, 2014). Assim o software GeoGebra pode ser empregado para explorar e visualizar conceitos matemáticos complexos, tornando o aprendizado mais interativo e visual.
Além disso, a Cultura Maker é um movimento que se insere nas metodologias ativas, permitindo que os estudantes vivenciem a teoria na prática. Isso ocorre através da resolução de problemas e da construção de suas próprias criações, utilizando ferramentas computacionais, sejam elas digitais ou físicas. Dessa forma, os alunos podem visualizar possíveis dúvidas e solucioná-las de maneira prática e inovadora. (Souza, 2021). E a matemática é uma área fértil para que os docentes possam usufruir destes métodos para auxiliar suas práticas. (Neto et. al, 2014). Certamente, professores e alunos podem se beneficiar do uso de espaços com computadores nas escolas. Proporcionar aos estudantes contato com computadores e smartphones que exibem gráficos, planilhas e outras formas matemáticas enriquece a experiência de aprendizagem. Segundo (Ribeiro et.al, 2023) “a Matemática é uma disciplina que é muito beneficiada pela experiência laboratorial, por trazer uma maior proximidade do aluno com os conteúdos apresentados”. (p.2).
Decerto, com a junção da cultura Maker, softwares matemáticos contribuem para uma educação ativa que possibilita aos educandos estarem inseridos na era digital, ao integrar toda a habilidade que possuem com os computadores.
ASPECTOS METODOLÓGICOS DA PESQUISA
O presente projeto consistiu em um processo de pesquisa mista com a abordagem da Pesquisa Qualitativa e Quantitativa. Segundo (Sampieri et al, 2013) “o enfoque misto da pesquisa, que envolve um processo de coleta, análise e vínculo de dados quantitativos e qualitativos em um mesmo estudo de pesquisas para responder uma formulação do problema”. (p. 549). Bem como a Pesquisa mista traz perspectiva mais ampla e profunda dos dados, indagações mais dinâmicas com maior solidez e rigor. Melhor exploração e aproveitamento dos dados ricos e criativos.
A pesquisa baseou-se em um procedimento de pesquisa-ação, conforme Vieira (2009, p.1) “tem a finalidade de implementar mudanças em uma comunidade. O pesquisador é o agente, […], o processo envolve a colaboração do pesquisador com os participantes da pesquisa. […]”, a pesquisa ação é uma forma de compreender como a mudança de atitudes ou de práticas pode beneficiar a própria comunidade. Para coleta de dados foi aplicado um questionário que segundo Lakatos e Marconi (2002, p.98) “é um instrumento de coleta de dados constituído por uma série ordenada de perguntas, que devem ser respondidas por escrito e sem a presença do entrevistador.”. Ao final, foi solicitado que os alunos respondessem um questionário de pesquisa, com o intuito de verificar os conhecimentos geométricos adquiridos e avaliar a atividade. Para o questionário foram construídas 7(sete) perguntas classificadas em aberto e fechadas e com justificativas. As perguntas foram baseadas na execução do software, um diagnóstico sobre o programa computacional geogebra após sua execução no laboratório de informática.
O conteúdo abordado foi a “soma dos ângulos internos de um triângulo”, ministrado na sala de aula através de exercícios contextualizados. Em seguida foram aplicados exercícios no laboratório de informática relacionados ao tema. O projeto foi desenvolvido nos dias 19 e 20 de outubro, no turno matutino com a turma do 8ᵒano 01 da Escola Estadual Professora Nazira Litaiff Moriz na cidade de Tefé no Amazonas.
O trabalho foi desenvolvido com 31 alunos matriculados, no dia 19 de outubro trabalhamos com 12 estudantes, pois esse foi o número máximo que o laboratório de informática podia acomodar, com dois alunos por computador. No dia 20, aproveitando os dois períodos de aula, trabalhamos com 19 estudantes: 12 no primeiro horário e 7 no segundo. No primeiro momento, apresentamos o programa GeoGebra, seguido pelo conteúdo sobre polígonos, a soma dos ângulos internos de um triângulo e a construção de figuras planas.
No programa Computacional Geogebra, é possível utilizar uma planilha que, entre outras funções, serve para realizar cálculos com as medidas de figuras construídas no próprio programa.
Procedimentos para acessar algumas ferramentas do programa.
➢ Planilha.
No menu Exibir, desmarque a opção Eixos e marque a opção Planilha – Figura 1.
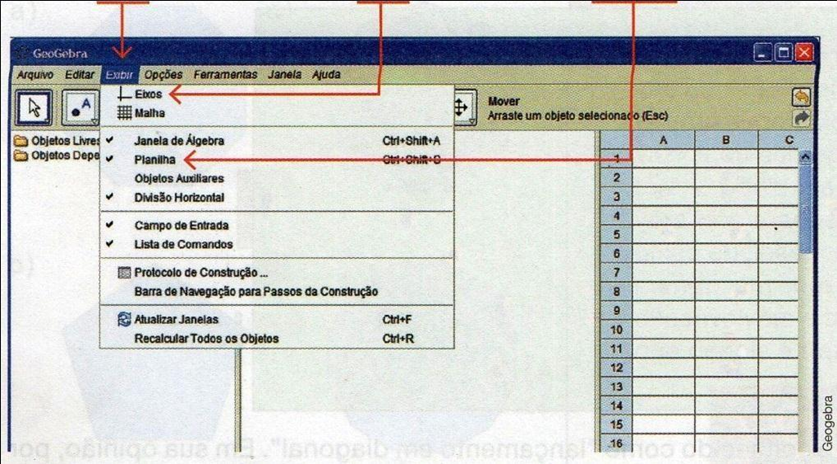
Figura 1: Ilustração de acesso a planilha.
- Construção de polígonos
Selecione a ferramenta Polígono no botão e, em seguida, desenhe um triângulo. Para isso, marque os pontos A, B, C na área de trabalho e, para finalizar, clique no ponto A – Figura 2.
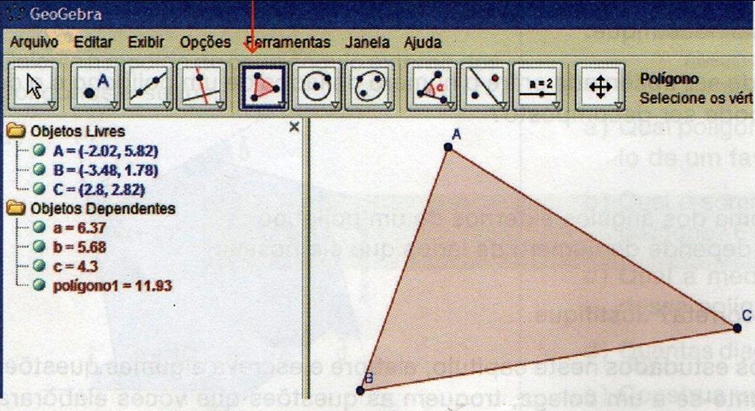
Figura 2: Ilustração demonstrativa da construção de um polígono (triângulo).
Construção de ângulo
Com a ferramenta Ângulo, meça e renomeie os três ângulos internos do triângulo, para isso clique no botão . Colocar o ponto no sentido horário no ângulo “BAC”. Repita esse procedimento para os ângulos “CBA” e “ACB” – Figura 3.
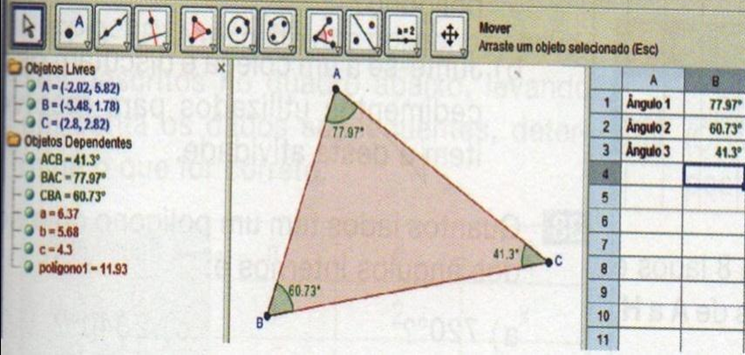
Figura 3: Ilustração da construção de ângulo
✓ Uso da planilha cálculo do ângulo interno. Soma dos ângulos internos de um triângulo.
- Clique nas células A1, A2 e A3, digite Ângulo 1, Ângulo 2 e Ângulo 3, respectivamente.
- Nas células B1, B2 e B3, digite: Ângulo (B, A, C), Ângulo (A, C, B) e Ângulo (C, B, A), respectivamente.
1. Soma de ângulo de um triângulo
Na célula A5, digite “Soma” e, na célula B5, digite a fórmula “= B1+B2+B3”. Observe que a soma será igual 180ᵒ.
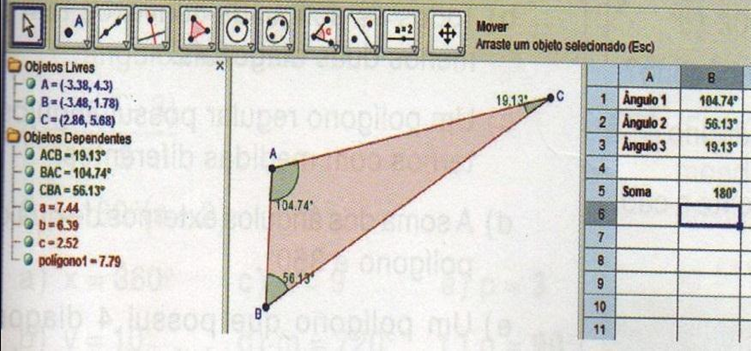
Figura 4: Ilustração da soma dos ângulos internos de um triângulo.
Aplicação de Questionário
Após a abordagem do programa foi repassado aos alunos um questionário com algumas questões sobre o programa e algumas temáticas, para observar se os objetivos propostos foram alcançados. O questionário abordava alguns tópicos, como: se gostavam da disciplina de matemática; se haviam gostado ou sentido dificuldades na utilização do software Geogebra; o que achavam da utilização em sala de aula de programas e jogos de informática. E por fim, uma questão sobre a percepção dos próprios alunos a respeito de seu desenvolvimento, ou seja, se os alunos se desenvolveram melhor no programa computacional ou nos exercícios escritos.
RESULTADOS E DISCUSSÕES
A prática com o uso do programa Geogebra se mostrou bastante promissora na aprendizagem dos alunos. Foi possível perceber que a aceitação do programa foi boa. Os alunos interagiram com o programa à medida que este foi sendo apresentado a eles. O Gráfico 1 mostra que a nova metodologia foi muito bem avaliada pelos alunos. “Acredita-se que associar o ensino da Geometria com softwares educacionais, no caso, o Geogebra, e atividades de natureza exploratório-investigativa, onde os alunos têm a oportunidade de testar os conhecimentos teóricos na prática através das manipulações, observações e discussões, […]”. (Nascimento et. al, 2017, p.4). O uso do GeoGebra parece ser uma abordagem eficaz e promissora no ensino da Geometria, proporcionando uma experiência de aprendizado interativa e engajadora para os alunos.
Gráfico 1: Aceitação do software Geogebra.
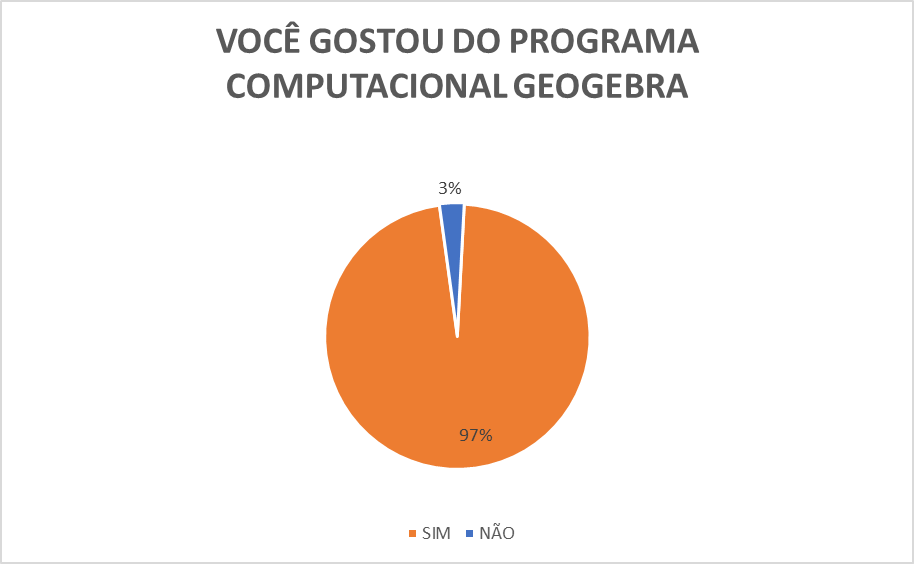
FONTE: SOUZA, 2024
Quanto às dificuldades, foi possível perceber que foram poucas. Os alunos que mais apresentaram dificuldades foram aqueles que quase nunca manuseiam computador. A principal dificuldade não foi a respeito do programa e sim no fato de os alunos não saberem utilizar computador e suas ferramentas, em alguns momentos houve a necessidade de ensinar a digitar e explicar alguns nomes técnicos das ferramentas do computador. “Os ambientes informatizados, na área da educação, contribuem para enriquecer as experiências e possibilitam a realização de um trabalho abrangente que promove a pesquisa e a investigação, aspectos intrínsecos à construção do conhecimento […]”. (Cabral; Almeida, 2020, p. 3). Uma minoria foi excelente no uso do programa, e para nossa grata surpresa, foram os alunos com maior afinidade com a Matemática, além daqueles que têm contato diário com o computador. O Gráfico 2 demonstra que a maioria conseguiu manusear bem o software de Matemática.
Gráfico 2: Dificuldade com o Geogebra.

FONTE: SOUZA, 2024
Podemos observar no Gráfico 3 que a maior parte alunos acharam o método computacional melhor, isto demonstra que novas práticas na sala de aula são importantes, tanto na questão da aprendizagem quanto na mudança de rotina. “A tecnologia deve ser usada de modo a permitir, ao aluno, ter acesso à propriedade ou a particularidades de um conceito; ou ainda a atividades matemáticas diferentes daquelas habitualmente tratadas no ambiente de papel e lápis”. (Junior, Estevam, 2022, p.5-6). Alguns alunos expuseram que conseguiram entender melhor o assunto. Mas isto só se tornou possível porque a parte teórica já havia sido trabalhada, então eles puderam perceber os conceitos na tela do computador. No entanto, alguns alunos mostraram preferência pelo método tradicional, quadro branco e pincel, alegando que aprendem melhor ou porque não dominam o computador, o que gerou um desconforto.
Gráfico 3: Aceitação do método computacional.
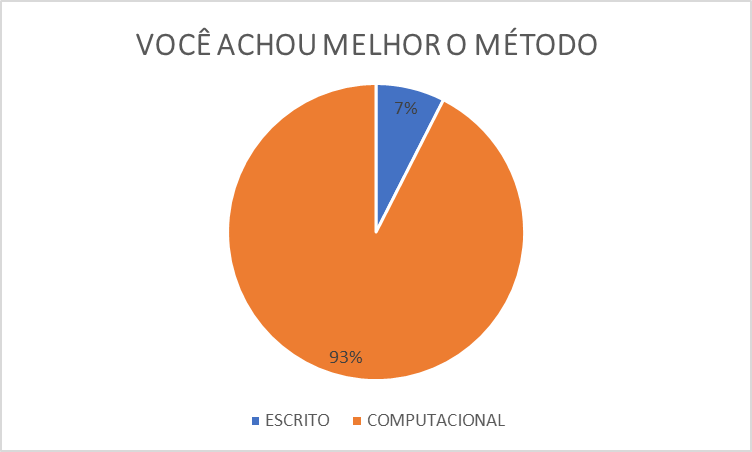
FONTE: SOUZA, 2024
Nesta turma foi observado que o contato com o computador nas aulas de matemática é muito pouco, no Gráfico 4. “A existência do computador desafia os professores de Matemática a propor tarefas que aproveitem o potencial desses recursos e apoiem novas formas de aprendizagem”. (Junior, Estevam, 2022, p.6)
No questionamento, alguns alunos disseram que sim, isto foi possível porque em outro momento alguns alunos desta turma já haviam sido escolhidos para participar de um trabalho que abordava o uso da tecnologia na sala de aula, e puderam trabalhar com o jogo “labirinto da matemática”.
Gráfico 4: Contato com um programa matemático.
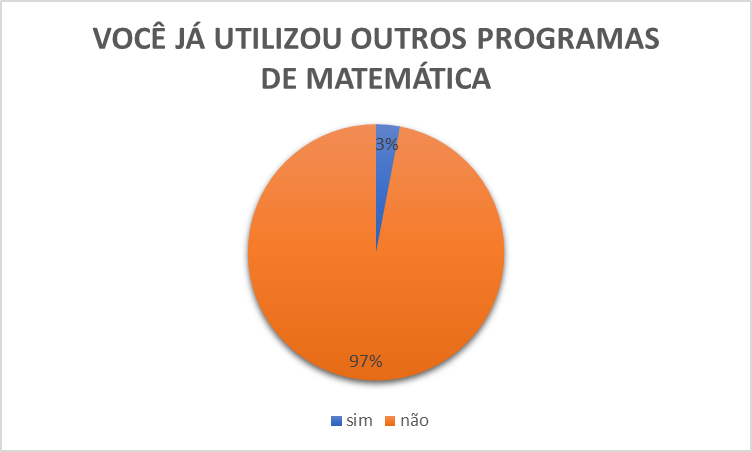
FONTE: SOUZA, 2024.
Ainda sobre os questionamentos foi possível coletar dados importantes, como o fato de os alunos gostarem da disciplina de matemática, de quererem aprender. Em alguns relatos foi dito que “Eu penso que a aula vai ser divertida e que eu vou aprender muito mais”
Ou ainda “Eu penso nossa vai começar a aula de matemática legal”. Em uma abordagem interativa e prática, as aulas são mais envolventes, motivando os estudantes a participar ativamente e, consequentemente, facilitando a aprendizagem. “Acredita-se que associar o ensino da Geometria com softwares educacionais, no caso, o Geogebra, e atividades de natureza exploratório-investigativa, […] despertar o interesse dos alunos pelas aulas, o que, naturalmente, tende a favorecer a aprendizagem”. (Nascimento et. al, 2017, p.4).
Diante do entusiasmo demonstrado pelo aluno e o uso de metodologias ativas e ferramentas digitais na educação evidencia como a inovação no ensino pode transformar a percepção e o envolvimento dos estudantes, tornando as aulas mais atrativas e eficazes.
Alguns alunos pensam nas dificuldades que vem a cada tempo de aula de matemática, nos problemas que vão resolver, mas dizem que no final estão aprendendo. “São atividades que tiram o estudante da posição passiva de apenas “recebedores” de informação, para uma posição mais ativa de “construtores” de sua própria aprendizagem”. (Cortelazzo et. al, 2018, p. 107). Eles percebem que as atividades propostas os tiram da posição passiva e os colocam em uma posição ativa do próprio conhecimento.

Quanto à utilização dos softwares na sala de aula, foi muito bem aceito pelos alunos. Estes interagiram com o programa Geogebra, fizeram perguntas e pude perceber o quanto é importante uma nova metodologia, visando os objetivos o programa, ele modificou a sala de aula, os alunos ficaram muito receptivos ao assunto de Polígonos, soma dos ângulos internos de um triângulo. “[…] a tecnologia está possibilitando que educadores do mundo inteiro se motivem a repensar qual o papel da escola, uma vez que acumular conteúdo já não faz sentido”. (Soares, 2021, p. 55)
Ao empregar a cultura Maker, foi possível proporcionar aos alunos se tornarem protagonistas, ativos nas soluções dos exercícios propostos com a utilização dos computadores, democratizando o acesso aos recursos e estimulando a cultura do fazer. “As metodologias ativas permitem que os alunos busquem o conhecimento, desenvolvendo a capacidade de pesquisar, sintetizar, refutar, recriar, produzir a partir dos conhecimentos adquiridos e colaborar, tornando a experiência educativa mais instigante”. (Soares, 2021, p. 142). Dessa forma os alunos tornam-se em sujeitos ativos e críticos, capazes de construir seu próprio conhecimento e colaborar de forma eficaz.
Quando utilizamos o software GeoGebra, os alunos vivenciaram a integração entre teoria e prática. Ao construírem desenhos na tela do computador, perceberam a importância da teoria para fornecer embasamento às atividades práticas. Demonstraram grande interesse pelo software e pelo laboratório de informática, ficando animados nas aulas práticas e expressando o desejo por mais aulas com essa abordagem. “O uso de um recurso didático nas aulas leva os alunos a aprenderem o conteúdo de uma forma dinâmica e pensativa e não de uma forma já pronta e acabada, pois o recurso dispõe da capacidade de pensar do aluno, […]”. (Oliveira, 2021, p.8). A conexão entre a prática com o GeoGebra e a teoria mostra como a integração de ferramentas tecnológicas pode transformar o ambiente de aprendizagem, tornando-o mais envolvente e eficaz.
Figura 5 – Visualização da construção da figura plana “triângulo”, exercício realizado pela aluna.
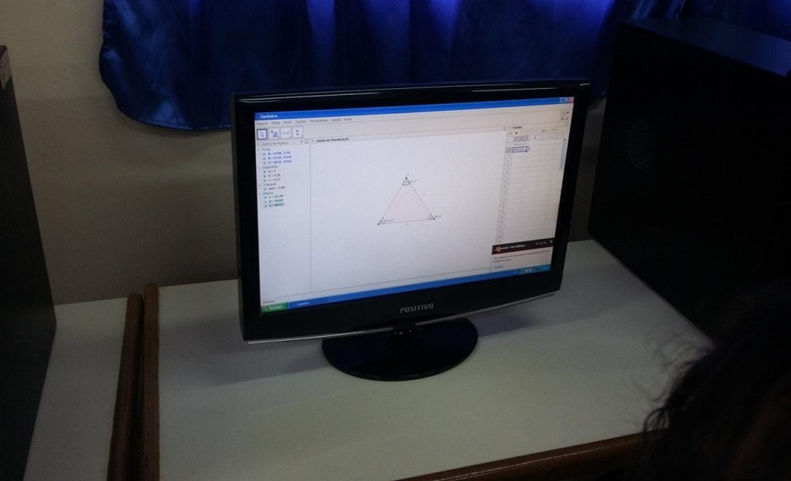
FONTE: SOUZA, 2024
O programa computacional é mais uma nova oportunidade de aprender Matemática. De tornar fácil o conteúdo que muitas vezes pode ser difícil de aprender na teoria. “As representações gráficas associadas a novas formas de exploração e visualização de conteúdos, em especial na Matemática, colaboram na construção de ambientes tecnológicos que podem ampliar as possibilidades de abordagens no ensino […]”. (Souza, 2018, p.26)
De transformar aulas teóricas em aulas práticas, de resolver sempre uma conta de matemática. Para alguns o computador é melhor do que do escrever, e por fim aprender a utilizar o computador. “O uso da tecnologia na sala de aula faz com que o aluno se sinta motivado a aprender de maneira dinâmica e que traga resultados positivos”. (Oliveira, 2021, p.8).
As metodologias ativas transformam o aprendizado em um processo mais envolvente e significativo, colocando os alunos no centro e focando na aplicação prática do conhecimento. Em uma escola amazônica, um ambiente diferenciado permitiu aos estudantes explorar novas abordagens na disciplina de matemática. “Metodologias ativas de aprendizagem são mecanismos didáticos que colocam o aluno direta e ativamente no centro do processo de aquisição do conhecimento, pois concentram o ensino e aprendizagem no fazer para aprofundar o saber”. (Neves, 2018, p.13)
Os alunos colaboram entre si na realização das atividades, tirando dúvidas e ajudando na construção dos projetos. A tela do computador, interativa e colorida, permitia ampliar e reduzir os desenhos, refazer em caso de erros ou até mesmo deletar e reconstruir do zero. Essa dinâmica facilitou o aprendizado e promoveu um ambiente de cooperação e experimentação. “O software educativo proporciona aos alunos uma melhor visualização do conteúdo abordado levando o mesmo a pensar e refletir sobre o que está sendo trabalhado naquele momento em sala de aula”. (Oliveira, 2021, p.8).
Nas figuras (2 e 3) mostram os alunos manuseando os computadores, utilizando o programa Geogebra.

FONTE: SOUZA, 2024
CONSIDERAÇÕES FINAIS
De acordo com a BNCC (2017) cabe às instituições de ensino propiciar uma qualidade de ensino a esses estudantes com autonomia e criticidade para competirem na sociedade, proporcionando os meios tecnológicos e as fontes de informações necessárias para buscarem por seus objetivos em uma margem de igualdade.
O uso dos meios tecnológicos provocou uma dinâmica na sala de aula. Fazer com esses alunos tenham um contato com os computadores, tornou o conhecimento mais interessante do ponto de vista metodológico. Torna-se importante utilizar outros processos de ensino para direcionar e estimular os alunos na construção do conhecimento e de um pensamento lógico-matemático de forma significativa. Os recursos tecnológicos em sala de aula oferecem uma grande contribuição para a aprendizagem, além de valorizar o professor que poderá ensinar com mais segurança estará mais próximo da realidade extraclasse do aluno, que dia a dia tem contato com a televisão, computador e internet. Dessa forma, a integração de novas mídias, a calculadora e até mesmo o computador não são mais novidades nas aulas, e sim um recurso que contribuem para a criação de novas estratégias de ensino, aprendizagem e desenvolvimento.
O Software Geogebra foi utilizado como ferramenta auxiliadora do professor, contribuindo na aprendizagem dos alunos. Na escola de aplicação os alunos interagiram muito bem, certo que com algumas dificuldades mais conseguiram executar a atividade proposta, isso ajudou a despertar em cada um interesse pelo programa. Desta forma o computador e o software funcionam como aliado do professor possibilitando assim o interesse dos alunos para o conhecimento matemático. Com a metodologia ativa, o estudante tem a chance de aprender de maneira envolvente e divertida, e o educador deixa de ser o foco do processo de ensino, dando lugar ao próprio aluno.
Conclui-se que o software GeoGebra pode ser um recurso favorável ao desenvolvimento dos alunos em sala de aula, especialmente em matemática, proporcionando oportunidades de reflexão e resolução de problemas. Além disso, a utilização da metodologia ativa e da cultura Maker permite aos professores adotarem novas práticas didáticas, contribuindo para a melhoria da aprendizagem dos alunos.
REFERÊNCIAS BIBLIOGRÁFICAS
ALMEIDA, Maria Elizabeth Bianconcini de. Apresentação. In. BACICH, Lilian; MORAN, José. Metodologias ativas para uma educação inovadora. Porto Alegre: Penso, 2018. p.10-13.
BALDIN, Yuriko. Yamamoto. Da Matemática Experimental à ferramenta didática: o papel do GeoGebra na formação de professores da educação básica. Revista Do Instituto GeoGebra Internacional De São Paulo, 12(2), 194–220. 2023. Disponível em: https://doi.org/10.23925/2237-9657.2023.v12i2p194-220. Acesso: 16 de agosto de 2024.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2018.
BACICH, Lilian; MORAN, José. Metodologias ativas para uma educação inovadora. Porto Alegre: Penso, 2018.
CABRAL, Clara Alice Ferreira; ALMEIDA, Talita Carvalho Silva de. Semelhança de Triângulos e GeoGebra: uma alternativa de ensino por meio de representações dinâmicas. Revista Sergipana de Matemática e Educação Matemática, v. 5, n. 1, p. 358–375-358–375, 2020.
CARDOSO, Tatiane Alves et al. A Utilização do Software GeoGebra no Ensino e Aprendizagem da Matemática. Ideias e Inovação-Lato Sensu, v. 5, n. 1, p. 45-45, 2019.
CORTELAZZO, Angelo Luiz; FIALA, Diana Andreia de Souza; JUNIOR, Dilermando Piva; PANISSON, Luciane; JUNQUEIRA, Maria Rafaela; RODRIGUES, Bruno. Metodologias ativas e personalizadas de aprendizagem. Rio de Janeiro: Alta Books, 2018.
DAROS, Thuinie. Prefácio. In. CAMARGO, Fausto; DAROS, Thuinie. A sala de aula inovadora: estratégias pedagógicas para fomentar o aprendizado ativo. Porto Alegre: Penso, 2018.
DEWEY, John. Democracia e educação: introdução à filosofia da educação / 4.ed. São Paulo: Nacional, 1979.
FERNADES, Geraldo W. Rocha; MARIANO, Halanda de Matos; SCHETINO, Luana Pereira Leite; ALLAIN, Luciana Resende. Metodologias e Estratégias Ativas: um encontro com o Ensino de Ciências. São Paulo, Editora Livraria da Física: 2021
JUNIOR, João Carlos Alves Pereira; ESTEVAM, Everton José Goldoni. Aspectos potenciais do software GeoGebra para o ensino e a aprendizagem de Matemática: um olhar a partir de dissertações. Alexandria: Revista de Educação em Ciência e Tecnologia, v. 15, n. 2, p. 3-32, 2022.
MORAN, José. Metodologias ativas para uma aprendizagem mais profunda. In. BACICH, Lilian; MORAN, José. Metodologias ativas para uma educação inovadora. Porto Alegre: Penso, 2018. p. 1-25.
NASCIMENTO, Dandara Lorrayne do; SÁ, Daiana Luiza de; VIEIRA, Thayná Pereira; BRAZ, Lúcia Helena Costa. Minicurso: Construções De Triângulos Através Do Software Geogebra. ForScience, v. 5, n. 3, 2017.
NETO, João Ribeiro; MAIAC, Lucas Emanuel de Oliveira; MENEZES, Daniel Brandão; VASCONCELOS, Francisco Herbert Lima. A Cultura Maker como Metodologia Ativa de Ensino: Contribuições, Desafios e Perspectivas na Educação. Revista de Ensino, Educação e Ciências Humanas, v. 25, n. 1, p. 107-115, 2024.
NEVES, Vander José das. Introdução. In. NEVES, Vander José das; MERCANTI, Luiz Bittencourt; LIMA, Maria Tereza. Metodologias ativas: perspectivas teóricas e práticas no ensino superior. São Paulo: Pontes Editora, 2018. p.13-14.
OLIVEIRA, Edvaldo Ramalho de. O uso da tecnologia no ensino da matemática contribuições do software GeoGebra no ensino da função do 1º grau. 2021. 24f. Dissertação de Mestrado (Especialização em Ensino de Ciências e Matemática) – Instituto Federal da Paraíba, Patos, 2021.
PIRES, Karl Marlow. Relações métricas no triângulo retângulo com GeoGebra. 46f. Dissertação (mestrado profissional) – Universidade Estadual Paulista “Júlio de Mesquita Filho”, Instituto de Biociências, Letras e Ciências: São José do Rio Preto, 2018.
RIBEIRO, D. M. A. A; PINHO, E.N.G; VIANNA, F. R. I; VIANA, J. P. C. Matemática e Cultura Maker. In: Congresso de Ensino Pesquisa e Extensão-CONEPE. 2023.
SAMPIERI, Roberto Hernández; COLLADO, Carlos Fernández; LUCIO, María del Pilar Baptista. Metodologia de pesquisa. Porto Alegre: Penso, 2013.
SOARES, Cristine. Metodologias ativas: uma nova experiência de aprendizagem. São Paulo: Cortez, 2021.
SOUZA, Ana Paula Mendonça de; ALMEIDA, Whasgthon Aguiar de. Processos Formativos no ensino de matemática a partir de metodologias ativas. In. MACHADO, Rita de Cassia Fraga. I Encontro de mestrandos do programa de pós-graduação em educação da UEA. As Pensadoras, 2024. p. 26-32
SOUZA, Laís dos Santos et al. A cultura maker na educação: perspectivas para o ensino e a aprendizagem de matemática. TCC (Graduação – Licenciatura em Matemática) – Instituto de Federal de Educação, Campus Valparaíso de Goiás, 2021. 67f
VIEIRA, Sônia. Como elaborar questionário. São Paulo: Atlas, 2009.
