Hardenability estimation by finite elements method
REGISTRO DOI: 10.5281/zenodo.10184099
Guilherme Xavier1
Lavinia Santana2
Alexandre Iartelli3
Resumo: O objetivo deste projeto é viabilizar uma análise prévia, através do método de elementos finitos, para estimativa da microestrutura do aço 1045 após sua submissão ao tratamento térmico de têmpera. A têmpera é um tratamento térmico que visa aumento de dureza de determinados materiais através da transformação cristalina por meio de resfriamento rápido em fluído. O Método dos Elementos Finitos é um método numérico comumente utilizado e recomendado para análise de modelos físicos submetidos a condições de contorno. As condições de contorno são definidas pelo problema, suas considerações e hipóteses simplificadoras.
Para essa análise, o ensaio Jominy foi simulado, as condições de contorno aplicadas foram tomadas com base na norma ASTM A255-02. Após essa análise as curvas de resfriamento foram plotadas no diagrama TTT do aço carbono 1045 e a curva de dureza comparada com a curva encontrada na literatura. Comparada às da literatura, a curva deste trabalho demonstra comportamento em condições similares às esperadas em ensaio realizado na prática, o que validou este estudo como uma maneira de obter resultados prévios de ensaios Jominy, podendo, assim, evitar custo, tempo e demais recursos.
Palavras-chave: Elementos, Finitos, Têmpera, Ensaio, Jominy.
Abstract: Finite Elements is a numerical method commonly used and recommended for the analysis of physical models subjected to boundary conditions determined by the designer. Tempering is a heat treatment that aims to increase the hardness and strength of materials through fluid cooling and the objective of this project was to enable a prior analysis, through the finite element method, of the results obtained in the material structure after the tempering treatment. For this analysis, a Jominy test model was developed, the boundary conditions of the test were applied and the result of them analyzed thermally, after this analysis the cooling curves were plotted on the TTT diagram of carbon steel 1045 and compared with the values found in literature. Compared to the values in the literature, the curves showed behavior under conditions similar to those expected in tests carried out in practice, which validates the finite element method as a way to obtain previous results from Jominy tests, thus avoiding cost, time and other resources spent on trials where the expected results would not be found.
Keywords: Finite, Elements, Quenching, Jominy, Tests.
1. Introdução
Para os diversos tipos de tratamentos térmicos presentes na indústria, a forma mais comum de se analisar a dureza resultante nos materiais testados é após seu tratamento, por meio de análises laboratoriais. O trabalho de conclusão de curso aqui apresentado, porém, envida esforços no entendimento do uso de modelagem numérica para a estimativa da microestrutura de peças submetidas a tratamentos térmicos, com propósito de se obter uma metodologia que permite uma redução de custos.
O estudo aqui proposto, que será devidamente detalhado nos capítulos que se seguem, consiste na modelagem do ensaio Jominy de um corpo de prova feito em aço-carbono 1045, onde utilizou-se o método dos elementos finitos (MEF) para estimativa das curvas de resfriamento obtidas a partir de análises térmicas, tendo como base comparativa as pesquisas acadêmicas indicadas no item 3.1 Ensaio Jominy e 4.2 Metodologias, em que se
permitiu avaliar a consistência das análises, e, por fim, a influência dos procedimentos nas características físicas do material em função das curvas de resfriamento.
1.1 Justificativa
A estimativa da temperabilidade de uma determinada peça, que será submetida à têmpera, por meio de análises numéricas pode resultar numa economia considerável de recursos. Este fato justifica que pesquisas, como a que se apresenta neste trabalho, sejam direcionadas para a determinação de uma metodologia que permita a consistência de tais modelos.
1.2 Objetivos (Geral e específicos)
O objetivo geral desse trabalho é estudar a utilização do método de elementos finitos na estimativa de se determinar a temperabilidade de um corpo de prova submetido ao ensaio Jominy. Para cumprir o objetivo geral, foram definidos os dois objetivos específicos apresentados abaixo:
- Realização de simulações, pelo método dos elementos finitos, do ensaio Jominy;
- Levantamento das curvas de resfriamento em pontos dispersos ao longo do corpo de prova.
2. Revisão Bibliográfica
2.1 Ensaio Jominy
Walter Jominy, formado pela Universidade de Michigan, trabalhando na Chrysler em 1930, desenvolveu um teste que se tornou amplamente adotado para avaliar a temperabilidade dos aços e que na atualidade é conhecido como Ensaio Jominy. Foi padronizado pela Sociedade Americana de Testes e Materiais em 1942, sob a norma ASTM A 255-07 (NUNURA, 2009, p. 52). O ensaio de temperabilidade consiste em aquecer um corpo de prova padronizado, conforme Figura 1. O corpo de prova é aquecido em um forno até a temperatura de austenitização, a norma ASTM A 255-07 padroniza a temperatura de austenitização de acordo com o percentual de carbono. Em seguida, o corpo de prova é resfriado por 10 minutos em um aparato padronizado para realização do ensaio Jominy. O tempo máximo de transferência do corpo de prova do forno para o equipamento de resfriamento é de 5 segundos.
Figura 1 – Corpo de prova
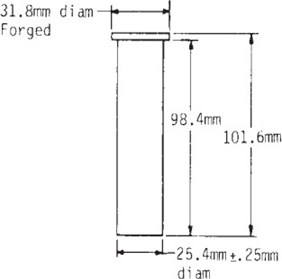
Fonte: ASTM A 255-07
O equipamento para a realização do ensaio Jominy também é especificado pela norma ASTM A 255-07. A distância entre o jato de água e o corpo de prova deve ser de 12,7 mm e a temperatura da água deve estar na faixa de 5 a 30°C. O diâmetro do tubo de saída da água para o resfriamento é de 12,7 mm. A altura do jato de água deve ser de 63,5 mm. A Figura 2 exemplifica o dispositivo do ensaio.
Figura 2 – Dipositivo Jominy
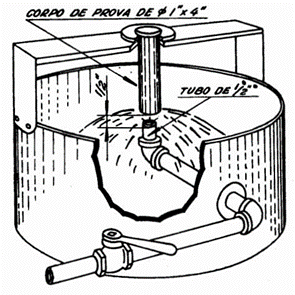
Fonte: ASTM A 255-07
O equipamento para a realização do ensaio Jominy também é especificado pela norma ASTM A 255-07. A distância entre o jato de água e o corpo de prova deve ser de 12,7 mm e a temperatura da água deve estar na faixa de 5 a 30°C. O diâmetro do tubo de saída da água para o resfriamento é de 12,7 mm. A altura do jato de água deve ser de 63,5 mm. A Figura 2 exemplifica o dispositivo do ensaio.
Figura 3 – Curva Jominy
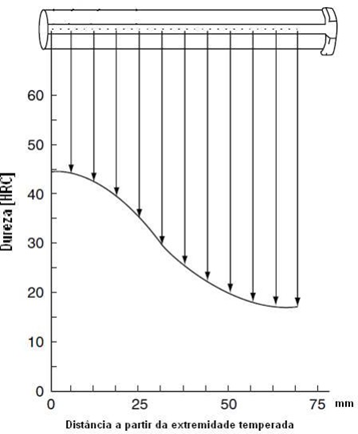
A transferência de calor durante o ensaio Jominy ocorre no regime transiente, devido ao resfriamento brusco, a temperatura no interior do corpo de prova varia conforme o tempo. Os mecanismos de transferência de calor que estão associados ao ensaio são convecção forçada, condução e radiação. O coeficiente de transferência de calor por convecção forçada para o ensaio Jominy foi estimado por HIGUERA et al. (2007) durante a modelagem do ensaio Jominy via elementos finitos em 15000 W/m²K (NUNURA, 2009).
2.2 Tratamentos Térmicos
Componentes metálicos são utilizados amplamente em diversos setores industriais. Esses componentes são fabricados principalmente com ligas à base de ferro, alumínio, cobre e níquel e se enquadram em aplicações específicas em função das propriedades necessárias para atingir o desempenho previsto do componente em serviço.
As ligas à base de ferro são, sem dúvida, as de maior importância e aplicação industrial, seja no número e variedade de componentes fabricados, seja na
quantidade produzida anualmente nas usinas siderúrgicas. Essas ligas possuem o carbono como elemento de liga principal, e o sistema Fe-C permite a obtenção de microestruturas variadas em condições de equilíbrio ou de não equilíbrio. O sistema Fe-C possui teores nominais de carbono que variam de 0,05% até 6,67%. Industrialmente, os produtos siderúrgicos são classificados de acordo com o teor de carbono na forma em duas grandes famílias: os aços, com teor de carbono entre 0,05% até 2,20%, que caracteristicamente podem ser trabalhados por deformação a quente e a frio para obtenção das mais variadas formas e dimensões. Os aços são as ligas do sistema Fe-C com aplicações abrangentes em segmentos industriais como: construção civil, automotivo, aeronáutico e aeroespacial, petróleo e gás, químico, farmacêutico, biomédico, entre outros. Essa variedade de aplicações se deve à possibilidade de se obter diferentes microestruturas após ciclos térmicos específicos de aquecimento e resfriamento, ou seja, após os tratamentos térmicos. A adição de elementos de liga como manganês, cromo, molibdênio, vanádio, tungstênio etc. amplia as possibilidades de se combinar as propriedades mecânicas, químicas e físicas nas ligas à base de ferro (PINEDO, 2021, p. 4).
Ainda de acordo com Pinedo, as principais famílias de aços utilizados comercialmente são:
- Aços-carbono;
- Aços para construção mecânica ou para beneficiamento;
- Aços inoxidáveis;
- Aços ferramenta.
Nos capítulos abaixo, são apresentados dois dos principais tratamentos térmicos responsáveis por essas diferentes microestruturas que permitem essa grande variedade de aplicações. Com foco e maior nível de detalhes sobre a têmpera, uma vez que nesse estudo comparativo, uma das propriedades analisadas é a temperabilidade dos aços.
2.2.1 Têmpera e revenimento
A têmpera e o revenimento são tratamentos combinados, de forma que, uma vez que a peça tenha sido temperada, ela deve obrigatoriamente sofrer o tratamento de revenimento. Isso ocorre porque a têmpera é o meio pelo qual se obtém o máximo endurecimento de um aço, para a composição química especificada. Entretanto, esse endurecimento máximo, que promove a elevação nas propriedades de resistência mecânica, conduz a um mínimo na resistência a fratura, tenacidade. Componentes industriais confeccionados em aço devem, obrigatoriamente, combinar resistência mecânica ao carregamento e resistência a fratura da melhor maneira possível para a sua composição e aplicação.
Esse equilíbrio entre resistência, dureza, e resistência a fratura, tenacidade, é conseguido pelo tratamento de revenimento, que deve ser realizado imediatamente após a têmpera. O revenimento é responsável por aliviar as tensões associadas à transformação martensítica por meio da precipitação progressiva de carbonetos com o aumento da temperatura, diminuindo por consequência a supersaturação e a tetragonalidade da martensita até a sua completa recristalização.
Por outro lado, é o revenimento que permite obter uma gama de durezas de serviço mais ampla que a dureza dos aços no estado recozido ou no temperado, os extremos da menor e da maior dureza, respectivamente. Com o revenimento, a dureza pode ser selecionada em função da aplicação. Por exemplo, o aço SAE 4140 no estado recozido apresenta uma dureza próxima de 20 HRC e no estado temperado, próxima de 56 HRC. Somente com a combinação da têmpera com o revenimento é possível obter para o aço SAE 4140 durezas de serviço entre 26 HRC e 40 HRC, adequadas para uma grande variedade de componentes que necessitam combinar propriedades mecânicas como de tração, compressão, fadiga, torção, cisalhamento e resistência a fratura. Para isso, é necessário determinar, para cada tipo de aço, a sua curva de revenimento, ou seja, a variação da dureza para temperaturas progressivas entre 100 °C e 700 °C (PINEDO, 2021, p. 24).
A têmpera visa alcançar o maior valor de dureza possível para um aço tratado e esse valor é diretamente relacionado às propriedades químicas, de temperabilidade e do método utilizado no tratamento.
Na prática industrial existem diferentes fornos para o aquecimento de peças destinadas à têmpera. Os mais utilizados são os fornos do tipo câmara, banhos de sal e sob vácuo. Em termos gerais, a seleção do tipo de forno de aquecimento depende: da temperatura de austenitização, do requisito de integridade superficial, da integridade de forma e dimensão e da sequência necessária no resfriamento. Atualmente, os tratamentos térmicos mais empregados para aços-carbono e média liga são fornos tipo câmara e banho de sal. Para aços de alta liga a preferência é por tratamentos em forno a vácuo. A têmpera está relacionada fundamentalmente ao meio de resfriamento utilizado e sua adequação à composição química do aço em processo. O esquema do ciclo térmico da têmpera é apresentado na Figura 4. Uma vez que o aço seja austenitizado, diferentes meios e métodos podem ser utilizados no resfriamento para a têmpera, cada qual com uma característica e velocidade de resfriamento. Na Figura 4 o meio com resfriamento mais rápido é a água, seguido de óleo e ar. É apresentado também o resfriamento por “martêmpera” e “têmpera interrompida”, que são práticas utilizadas para controlar a transformação martensítica em aços de alta liga, de forma a obter uma microestrutura homogênea na seção transversal, evitar geração de tensões de origem térmica do resfriamento e associadas à expansão da transformação martensítica e, desta forma, buscar a máxima estabilidade dimensional com mínima possibilidade de geração de trincas (PINEDO, 2021, p. 24).
Figura 4 – Ciclo de têmpera em diferentes meios de resfriamento
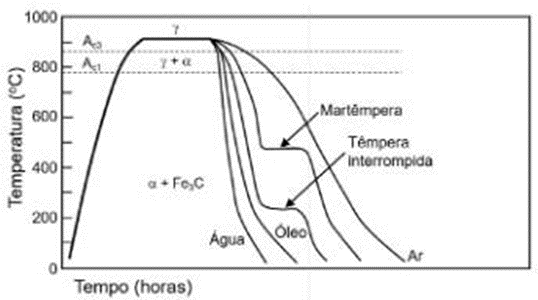
Fonte: PINEDO (2021)
A etapa de resfriamento é fundamental na têmpera, de forma que a seleção do meio de têmpera deve fornecer uma velocidade de resfriamento, em °C/min, sempre superior à velocidade crítica de têmpera. Ou seja, a velocidade de resfriamento deve estar adequada à temperabilidade do aço em tratamento. Em vista disso, é importante entender a característica de resfriamento dos meios mais utilizados: o líquido e o gasoso. Quando a têmpera é realizada em meio líquido, o processo de resfriamento consiste em três etapas: formação de uma cobertura de vapor, evaporação e convecção. Cada uma dessas etapas extrai calor com uma velocidade diferente, como mostrado na Figura 5. Nos estágios iniciais, a elevada temperatura da peça causa intensa vaporização do líquido e gera a cobertura de vapor que praticamente isola a peça do líquido refrigerante, fazendo com que a extração de calor seja baixa. Com a diminuição da temperatura da peça ocorre apenas a evaporação do líquido e a velocidade de resfriamento aumenta significativamente até que ocorra apenas o processo de convecção nos estágios finais do resfriamento com menor velocidade. O controle dessas etapas pela correta seleção do meio líquido refrigerante, por exemplo a água, óleo ou um polímero, é fundamental para a transformação martensítica, na geração das tensões residuais e para a estabilidade dimensional e de forma (PINEDO, 2021, p. 25).
Figura 5 – Estágios de resfriamento na têmpera em meio líquido
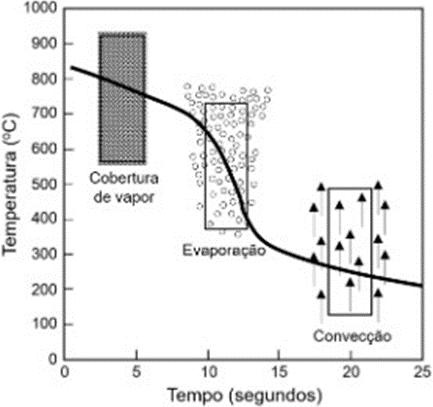
Fonte: PINEDO (2021)
A Figura 6 mostra a comparação entre o resfriamento em meio de têmpera líquido e gasoso. A Figura 6 (a) mostra que no resfriamento de um cilindro em meio líquido, óleo ou água, ocorrem três etapas principais, cada qual com uma característica de extração de calor: (i) na primeira etapa, logo ao introduzir a peça no meio, ocorre a formação de um filme gasoso decorrente da intensa vaporização do líquido causada pela elevada temperatura da peça recém-saída da austenitização. Esse filme de vapor isola a peça do meio e promove um baixo coeficiente de transferência de calor (α em W/m2K); (ii) uma vez que a peça continue o resfriamento, a formação do filme é interrompida e ocorre apenas a formação de bolhas de vapor, com a máxima intensidade de extração de calor; e (iii) com a contínua extração de calor da peça, ocorre apenas a convecção e a velocidade de extração de calor diminui gradativamente. Essa sequência de eventos causa um perfil de temperatura heterogêneo ao longo do comprimento da peça e pode gerar dois problemas importantes na peça: (i) em aços de baixa temperabilidade, a transformação martensítica pode não ocorrer por completo ao longo do comprimento e da seção transversal com uma têmpera não homogênea; e (ii) os gradientes de temperatura geram contração térmica e expansão de transformações de fase diferentes, causando uma variação dimensional maior na região mais fria e com isso distorção do cilindro temperada. A Figura 6 (b) mostra que no resfriamento em meio gasoso a característica é diferente. O fluxo gasoso em alta pressão envolve toda a superfície da peça, o que gera uma frente de extração de calor plana com a mesma intensidade ao longo do comprimento. Com isso, o perfil de temperatura no resfriamento varia da superfície para o núcleo, através da seção transversal, e não ao longo comprimento. Em consequência disso, a variação dimensional decorrente da variação de temperatura e da transformação martensítica ocorre de forma mais homogênea, o que resulta em menor distorção (PINEDO, 2021, p. 25).
Figura 6 – Representação esquemática da troca de calor durante o resfriamento em meio líquido, óleo e água (a) e com fluxo de gás (b)
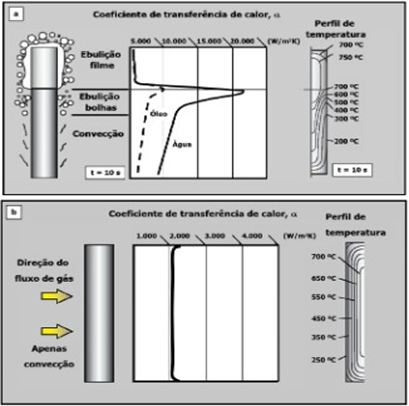
Fonte – PINEDO (2021)
Os meios de resfriamento na têmpera têm, portanto, características diferentes de extração de calor que devem ser consideradas em um amplo espectro de variáveis. A Figura 7 apresenta as curvas de resfriamento para a água, óleo e nitrogênio (injetado a 86 m/s) no resfriamento de amostra de aço para rolamento do tipo SAE 52100 (1%C-1,5%Cr) (3). Observa-se claramente a maior severidade da água comparada ao óleo e do óleo comparado ao fluxo gasoso de nitrogênio. A escolha do meio de têmpera ideal dependerá da temperabilidade do aço a ser tratado, da dimensão da seção transversal da peça e da complexidade geométrica, para que a velocidade de resfriamento seja suficientemente elevada para garantir a máxima formação da martensita através da seção transversal, mas não rápida demais para favorecer a ocorrência de trinca, fratura e/ou distorção (PINEDO, 2021, p. 25).
Figura 7 – Curvas de resfriamento contínuo em diferentes meios para aço tipo SAE 52100 para cilindros com diâmetro de 20 mm e comprimento de 60 mm
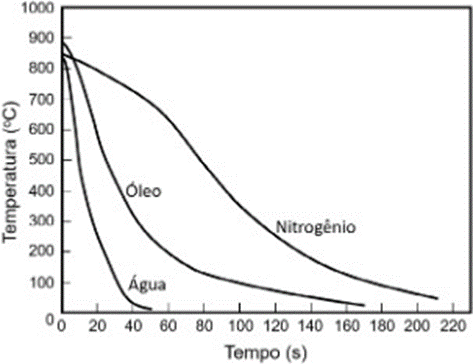
Fonte: PINEDO (2021)
As taxas de resfriamento com gás variam de acordo com a pressão de injeção. A Figura 8 mostra o aumento da velocidade de resfriamento na injeção de nitrogênio em diferentes pressões de 1 a 5 bar. A evolução da tecnologia nos fornos a vácuo permite, atualmente, o uso de pressões de injeção de até 20 bar, possibilitando a têmpera de uma ampla faixa de aços, desde os aços para construção mecânica, como SAE 4140 e 4340, de menor temperabilidade, até os aços de alta liga, como os aços ferramentas e inoxidáveis martensíticos, de temperabilidade elevada. A
eficiência na troca de calor pode ser elevada com a injeção de outros gases, como argônio, hélio e hidrogênio. A Figura 9 mostra as velocidades de resfriamento desses diferentes gases (PINEDO, 2021, p. 25).
Figura 8 – Curvas de resfriamento para uma barra de aço rápido tipo AISI M2 com diâmetro de 25 mm e comprimento de 48 mm em gás nitrogênio em diferentes pressões de injeção
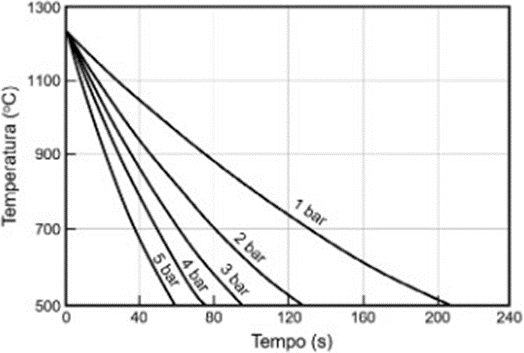
Fonte: PINEDO (2021)
Figura 9 – Curvas de resfriamento para diferentes gases na têmpera
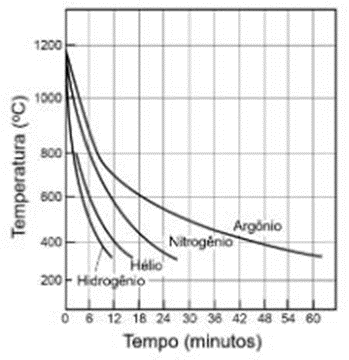
Fonte: PINEDO (2021)
A eficiência do resfriamento também depende do sistema construtivo do forno a vácuo. O gás deve circular na câmara de forma a atingir todas as peças o mais homogeneamente possível. A Figura 10 exemplifica um sistema com saídas distribuídas diametralmente pela câmara do forno – setas brancas –, o que permite uma injeção completa e homogênea por toda a seção da câmara. Neste sistema o gás é injetado frio, atinge as peças para resfriamento, se aquece e retorna quente ao sistema de refrigeração, para então retornar frio e dar sequência ao resfriamento (PINEDO, 2021, p. 26).
Figura 10 – Forno a vácuo com a indicação das saídas de nitrogênio – setas brancas – e do sistema de circulação e resfriamento de gás
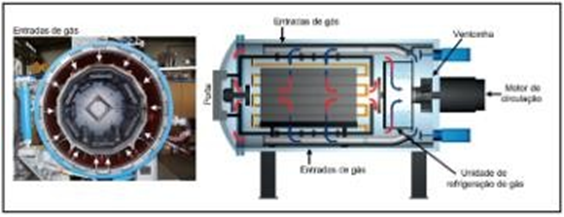
Fonte: PINEDO (2021)
Para meios de têmpera líquidos, além da garantia da transformação martensítica para a maior profundidade de seção transversal possível, também é importante:
- Proporcionar a velocidade de resfriamento apropriada em todo o intervalo de temperatura utilizado, em particular para temperaturas abaixo de Ms, em que a velocidade deve ser suficientemente lenta para prevenir a distorção;
- Manter a estabilidade durante o tempo de uso em serviço, ou seja, os meios devem ser resistentes a decomposição térmica e a oxidação;
- Impedir a interação do meio com a superfície das peças, com a atmosfera ou com o tanque de resfriamento;
- Os resíduos de líquido de têmpera devem ser facilmente removíveis da superfície das peças tratadas pelos métodos de lavagem disponíveis.
- Adequar os meios aos requisitos de toxicidade, inflamabilidade, legislação ambiental, de saúde e de segurança no trabalho;
- Ter um custo otimizado por unidade de produção.
Existem vários fatores que colaboram para a variação dimensional e de forma no tratamento térmico de têmpera e revenimento. Apesar de esses fatores agirem de forma isolada, eles estão relacionados entre si e atuam simultaneamente. Os principais fatores são o térmico e o das transformações de fase. O fator térmico está relacionado à variação da temperatura no aquecimento, etapa de expansão, e resfriamento, etapa de contração, e a sua homogeneidade na seção transversal. Isto porque, durante o aquecimento, a temperatura entre a superfície e o núcleo é diferente. Esse gradiente de temperatura aumenta com o aumento da seção transversal da peça. Desta forma, a expansão da superfície mais aquecida é restrita pela região do núcleo mais frio e com menor plasticidade, gerando tensões que promovem a deformação da externa com maior plasticidade. A taxa de aquecimento, o uso de patamares intermediários de pré-aquecimento e a seção transversal da peça são parâmetros de controle importantes para minimizar a distorção. O fator transformação de fase está relacionado à transformação alotrópica da ferrita em austenita no aquecimento, que causa uma contração, até o patamar de austenitização, e à transformação martensítica no resfriamento para a têmpera, que gera uma expansão.
A Figura 11 exemplifica as etapas envolvidas na variação dimensional que uma peça sofre quando submetida ao tratamento térmico de têmpera. Em primeiro lugar, a variação dimensional é decorrente da variação da temperatura (T), ou seja, expansão (+) no aquecimento e contração (-) no resfriamento. Conjuntamente, ou não, está associada a variação dimensional relacionada às transformações de fase (TF) no aquecimento e no resfriamento. Assim, no aquecimento para a austenitização, até a temperatura Ac1, ponto 1, ocorre apenas a expansão pelo aumento da temperatura. Acima de Ac1 ocorre o início da transformação alotrópica da ferrita (CCC) em austenita (CFC), e essa mudança de reticulado cristalino resulta em uma contração, que se associa à contínua expansão associada ao aumento da temperatura. Entre os pontos 1 e 2 a peça sofre simultaneamente expansão e contração. No resfriamento rápido da têmpera, entre os pontos 3 e 4, a austenita não transformada sofre contração do resfriamento até atingir a temperatura de início de transformação martensítica MS, ponto 4. A transformação martensítica promove uma expansão de forma que entre o início MS e o final da transformação em MF, ponto 5, ocorrem simultaneamente a contração da austenita não transformada e a expansão da martensita (α’) recém-transformada. Abaixo da temperatura MF, com a transformação martensítica completa, ocorre apenas a contração final, com o resfriamento progressivo até a temperatura ambiente (PINEDO, 2021, p. 26).
Figura 11 – Representação esquemática do ciclo térmico da têmpera com as expansões (+) e contrações (-) associadas à variação da temperatura (T) e às transformações de fase (TF)
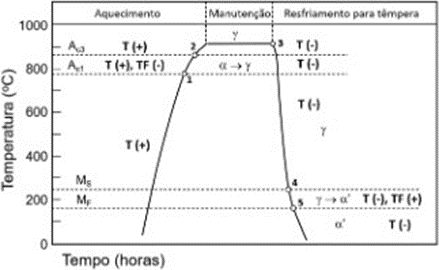
Fonte: PINEDO (2021)
Além dos fatores térmicos e de transformação de fase relacionados anteriormente, existem diversos outros fatores que estão presentes e que interferem na estabilidade dimensional e de forma de uma peça na têmpera. Os principais são:
- Composição química do aço, teor de carbono e elementos de liga;
- Temperabilidade do aço;
- Homogeneidade de composição química na seção transversal, grau de microssegregação;
- Tensões residuais existentes antes do tratamento térmico;
- Correta escolha da temperatura e tempo de austenitização;
- Seleção do meio de têmpera adequado à temperabilidade do aço e à massa da peça;
- Montagem da carga na câmara de tratamento térmico;
- Relação dimensional entre comprimento, largura e espessura;
- Complexidade geométrica da peça.
(PINEDO, 2021, p. 26)
2.3 Temperabilidade dos aços
A temperabilidade de um aço consiste na capacidade de endurecimento da peça metálica ao ponto de atingir uma estrutura martensita, ou seja, a temperabilidade do aço tem como finalidade de ajustar a propriedade mecânica do material modificando através das microestruturas do aço, sendo assim, fazendo com que haja uma maior resistência mecânica. Aponta-se que, para haver uma estrutura martensita, precisa-se passar por uma série de etapas até atingir o ponto final da estrutura desejada e para isso, é feita a têmpera do aço, analisada através de ensaios utilizando corpo de prova, o revenimento, recozimento, entre outras etapas.
2.4 Método numérico de elementos finitos
O Método dos Elementos Finitos (MEF) é um método numérico para resolução de equações diferenciais parciais cuja aplicação se dá em várias áreas, sendo uma delas a engenharia, na qual é utilizado para resolução de problemas de análise de tensões e deformações, transferência de calor, escoamento de fluidos e eletromagnetismo.
Milhões de engenheiros e cientistas em todo o mundo usam o MEF para prever o comportamento estrutural, mecânico, térmico, elétrico e químico de sistemas, tanto na etapa de projeto quanto na análise de desempenho.
Uma vez que os diferentes fenômenos da engenharia são descritos por equações diferenciais parciais e os métodos analíticos de resolução dessas equações atendem apenas a problemas e geometrias simples, isto é, para problemas e geometrias mais complexas a resolução analítica é praticamente impossível. Em resposta a essa demanda, surge então o MEF, como ferramenta para auxiliar o
engenheiro a entender e resolver os diversos problemas de diversas áreas da engenharia (FISH, 2009, p. 1).
São várias as aplicações do MEF na engenharia, como, por exemplo, no cálculo do escoamento de fluidos em tubulações ou aeronaves, tensões e deformações em estruturas metálicas, resfriamento ou aquecimento em componentes eletrônicos e solidificação e conformação de processos de fabricação. De fato, o surgimento do Método dos Elementos Finitos revolucionou o campo da engenharia e proporcionou avanços significativos que impactam diretamente a vidas das pessoas.
O MEF foi desenvolvido primeiramente na indústria aeroespacial nos anos 1950 e, em decorrência do desenvolvimento científico na década anterior, cuja primeira menção ao método foi no artigo de Courant, em 1943, no qual cita a interpolação polinomial por partes sobre sub-regiões triangulares para modelar problemas de torção (CHANDRUPATLA, 2014).
Posteriormente, em 1956, M. J. Turner, R. W. Clough, H. C. Martin e L. J. Topp publicaram um artigo sobre a formulação da matriz de rigidez dos elementos, intitulado “Análise de rigidez e deflexão de estruturas complexas”. Um dos autores do artigo, Ray Clough, publicou alguns anos depois outro artigo, em que utilizou pela primeira vez o termo “elementos finitos”, sendo, portanto, um dos pioneiros na aplicação do MEF em problemas em mecânica estrutural. Clough foi professor na Universidade da Califórnia – Berkeley e seu trabalho na área de elementos finitos influenciou muitos pesquisadores a seguirem com os estudos nessa área, devido a isso, Berkeley se tornou um renomado centro de pesquisa em elementos finitos.
Em 1965 a NASA desenvolveu o primeiro software de elementos finitos, o NASTRAN, que fazia análise de tensões em duas e três dimensões em vigas e elementos de casca. Nesta mesma época, John Swanson desenvolveu para a Westinghouse um software para a análise de tensões em reatores nucleares. Alguns anos depois, em 1969, Swanson lançou o ANSYS, capaz de fazer análises lineares e não lineares. Em 1978 foi desenvolvido pela companhia HKS o software ABAQUS. A companhia HKS foi comprada pela Dessault Systems em 2005. O NASTRAN, ANSYS e ABAQUS são softwares de cálculo que utilizam o MEF, que é amplamente usado nos diversos setores da indústria em todo o mundo (FISH, 2009). O método consiste em dividir-se a geometria em vários elementos que são conectados por nós, que, por sua vez, possuem um número definido de graus de liberdade (GDL), conforme Figura 12. Este conjunto de elementos e nós constitui o que se chama de malha. Desta forma, a malha representa o domínio contínuo, de forma discretizada, do problema, que em sua forma contínua possui um número infinito de GDL. Esse processo é chamado de discretização do sistema contínuo. Portanto, o problema passa de um número infinito de GDL para um problema com número finito de GDL, cuja solução pode ser determinada (ESSS, 2022).
Figura 12 – Nós e Elementos
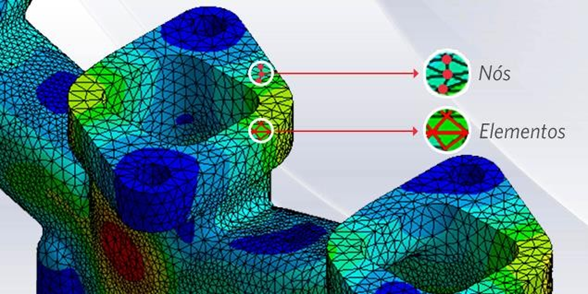
Fonte: ESSS (2022)
2.5 Transferência de calor
Uma definição simples, mas geral, fornece uma resposta satisfatória para a pergunta: O que é transferência de calor? Transferência de calor (ou calor) é energia térmica em trânsito devido a uma diferença de temperatura no espaço. (INCROPERA, 2008, p.14).
Logo a transferência de calor existe no momento em que dois corpos (podendo ser esses corpos um sólido ou um líquido) possuam diferença de temperatura, pois haverá, necessariamente o fenômeno da energia em trânsito de um para o outro, obrigatoriamente do corpo com mais energia térmica para o corpo com menor energia térmica.
São três as principais formas de transferência de calor conhecidas pelo homem: a condução, a convecção e a radiação, exemplificadas na Figura 13.
Figura 13 – Modos de transferência de calor: condução, convecção e radiação

2.5.1 Condução
A condução térmica, também chamada de difusão térmica, é um tipo de propagação de calor que acontece num meio material decorrente das agitações das moléculas. Com o aumento da temperatura de um corpo sólido (seja por aquecimento ou contato com outro), a energia cinética também aumenta (GOUVEIA, 2011, p.01). Como demonstrado na Figura 14.
Figura 14 – Associação da transferência de calor por condução à difusão de energia devido à atividade molecular
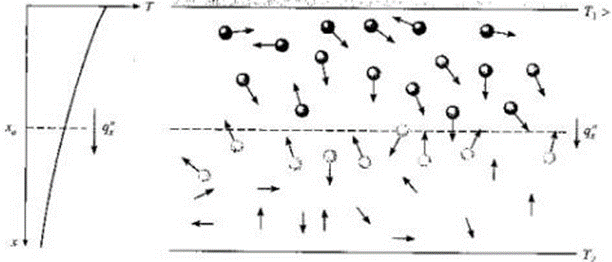
Fonte: INCROPERA (2008)
Como dito anteriormente, temperaturas mais elevadas estão associadas a energias moleculares mais altas, e quando ocorrem as colisões (que ocorrem a todo momento), acontece uma transferência de energia entre elas, das com maior energia molecular para as com menor energia molecular. Então a troca de calor por condução deve acontecer na direção da diminuição de temperatura, sendo ainda assim na ausência das colisões como mostrado na Figura 14. Contudo, as moléculas vindas das partes superiores se diferem por serem as que possuem maior temperatura se colidindo com as moléculas vindas da parte inferior que, por sua vez, são as moléculas que possuem menor temperatura, fazendo com que ocorra a diminuição do gradiente de temperaturas em busca de um equilíbrio térmico natural. Dada como menção de Incropera, “(…) uma transferência liquida de energia pelo movimento molecular aleatório como uma difusão de energia”.
É possível então quantificar um processo de transferência de calor usando, assim, a lei de Fourier, que torna possível calcular a quantidade de energia sendo transferida por unidade de tempo, resultando então na equação de fluxo térmico, nas condições de estado estacionário mostrado na Figura 15 (INCROPERA 2008, p.15):

Figura 15 – Transferência de calor unidimensional por condução (difusão de energia)
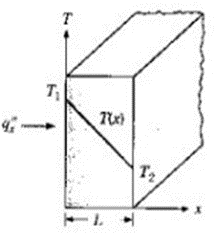
Fonte: INCROPERA (2008)
2.5.2 Convecção
A convecção térmica é uma das formas de propagação do calor que ocorre nos líquidos e gases. Ela recebe esse nome pois a transmissão do calor acontece por meio das correntes de convecção circulares que se formam por conta da diferença de densidade entre os fluidos. Note que a densidade muda quando a temperatura varia (GOUVEIA, 2011, p. 1). O modo de transferência de calor por convecção, se dá por dois tipos de mecanismos, o já citado anteriormente “difusão” presente na condução, e devido ao movimento global, ou macroscópico do fluido. Que é definido pela movimentação de uma grande quantidade de moléculas como um agregado. Ocorrendo com o contato de um fluido em movimento á uma superfície, e uma consequência desta interação é o surgimento de uma região no fluido onde a velocidade varia de zero (y = 0), e um valor finito (u_∞), em relação ao fluido em escoamento, essa região formada é denominada com “camada limite hidrodinâmica”. E se as temperaturas de fluido e superfície forem distintas existirá um local no fluido em que a temperatura terá uma variação de T_s associada a y = 0, até T_∞ associada ao local afastado da superfície (“Camada limite térmica”). Que pode ser maior, menor ou até igual daquela através da qual a velocidade varia, e caso T_s>T_∞ a transferência de calor ocorrerá da superfície para o fluido. Como demonstrado na Figura 16 (INCROPERA, 2008).
Figura 16 – Desenvolvimento da camada limite na transferência de calor por convecção
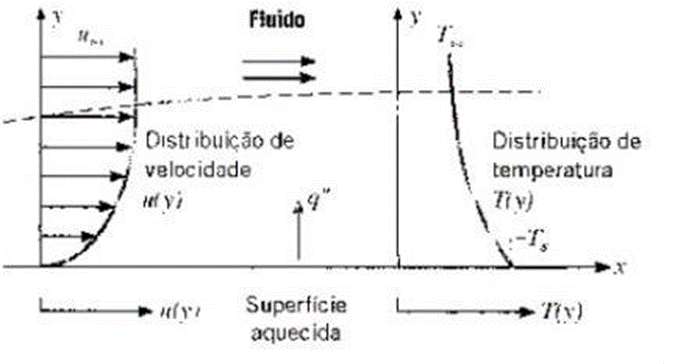
Fonte: INCROPERA (2008)
Existindo assim, 4 tipos diferentes de processos de transferência de calor por convecção, ilustrados na Figura 17 (INCROPERA, 2008).
Figura 17 – Processos de convecção forçada (a), convecção natural (b), ebulição (c) e condensação (d)
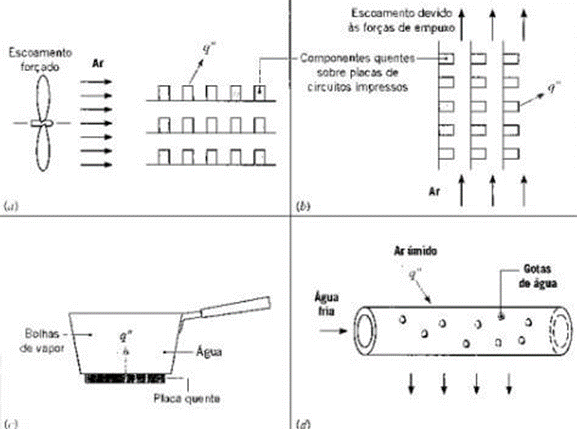
Fonte: INCROPERA (2008)
Porém, a despeito da diferença desses processos de transferência de energia que é dada pela convecção, a equação adequada para a taxa de troca de calor tem a forma de (INCROPERA, 2008):

2.5.3 Radiação
A irradiação (ou radiação) térmica é uma das formas de propagação do calor que ocorre por meio de ondas eletromagnéticas, chamadas de ondas de calor (GOUVEIA, 2011, p. 1). Diferentemente da condução e da convecção, que necessariamente dependem de um meio físico para a realização da troca de calor, a radiação não precisa de tal meio. Na verdade, a transferência de temperatura por radiação é mais eficiente em meio ao vaco.
Na radiação, a energia é transportada dentro de um campo de radiação por ondas eletromagnéticas, e essa radiação que é emitida pela superfície vem da energia térmica delimitada pela superfície e a taxa de energia liberada por unidade de área (W/m²). Famosamente conhecida como “poder emissivo”, determinada pela lei de Stefan- Boltzmann.

Obtendo, assim, a seguinte equação:

3. Materiais e Métodos (ou Metodologia se corresponde)
Este capítulo descreve os materiais e os métodos que foram utilizados para a realização da análise utilizando o Método dos Elementos Finitos e a estimativa de temperabilidade.
3.1. Materiais
Os materiais utilizados na realização deste trabalho foram:
- Computador de Mesa com processador AMD FX-8320E Eight-Core Processor 3.20 GHz e memória 16.0 GB;
- Ansys Mechanical 2021 R2.
3.2. Metodologias
Para a realização da análise térmica, foram feitas as seguintes considerações:
- Para a modelagem do ensaio Jominy no Ansys, foi considerada uma transferência de calor unidirecional, isto é, a transferência ocorre ao longo do comprimento do corpo de prova;
- Transferência de calor por convecção forçada na extremidade inferior do corpo de prova;Transferência de calor por condução no interior do corpo de prova;
- Desconsiderou-se a troca térmica por radiação nas laterais do corpo de prova;
- Desconsiderou-se a troca térmica por convecção natural nas laterais do corpo de prova;
- Coeficiente de transferência de calor por convecção foi considerado constante;
- O material do corpo de prova é o aço carbono ABNT 1045.
As considerações foram feitas com base no trabalho de NUNURA (2009), que estuda os fatores que podem afetar a temperabilidade de um aço. Nesse estudo, NUNURA (2009) correlaciona as taxas de resfriamento obtidas através de ensaio experimental com simulação em aplicativo computacional para simulação das curvas de resfriamento do ensaio Jominy. Além disse, conforme citado no tópico do Ensaio Jominy, HIGUERA et al. (2007), realizou um estudo em que, estimou o coeficiente de convecção em 15000 W/m²K através da modelagem do ensaio Jominy via elementos finitos. Para a realização do estudo de temperabilidade através da simulação numérica, foi modelado o corpo de prova Jominy de acordo com a norma ASTM A255-02. Na Figura 18 o respectivo modelo e suas dimensões em milímetros estão apresentadas. Foram feitas marcações no modelo, que correspondem aos pontos onde serão extraídas as curvas de resfriamento para estimativa da dureza. A distância entre os pontos é de 3,2 mm, essa é a distância recomendada pela norma ASTM A255-02, para a medição da dureza após a realização da etapa de resfriamento.
Figura 18 – Modelo utilizado em simulação
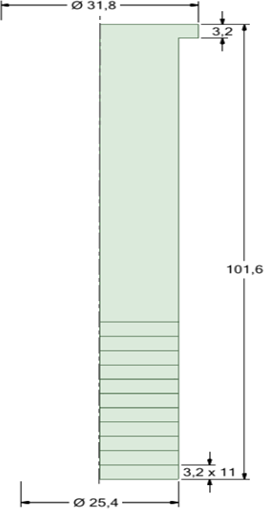
A Tabela 1 apresenta as propriedades térmicas do material, necessárias para a realização da simulação numérica.
Tabela 1 – Propriedades térmicas do aço 1045
Propriedade Valor Temperatura de Austenitização (Ti) 850°C Coeficiente de Condução Térmica (h) 60,5 W/m.K Densidade Aço 1045 (ρ) 7854 kg/m³ Calor Específico Aço 1045 (Cp) 434 J/kg.K Temperatura da Água (T∞) 20° C Coeficiente de Convecção Térmica (k) 15000 W/m².K
Fonte: ABNT
Após modelagem do corpo de prova, foi realizada a análise térmica, onde foi simulada a etapa de resfriamento do ensaio Jominy. Devido ao fato da temperatura do corpo de prova variar ao longo do tempo, foi realizada uma análise térmica transiente com modelo axissimétrico. Como o corpo de prova possui simetria ao longo de seu eixo axial e o fenômeno de transferência de calor para este caso ocorre também simetricamente, a representação axissimétrica pode ser utilizada, devido a isso, o tempo da análise e o custo computacional foram reduzidos.
A temperatura de austenitização para o aço ao carbono 1045, conforme Tabela X, é de 845°C com tolerância de ±5°C, segundo a norma ASTM A255-02. Para o estudo de temperabilidade foi adotada a temperatura de austenitização de 850°C e o tempo de duração do resfriamento do corpo de prova é de 10 minutos. A Figura 19 mostra o modelo do corpo de prova.
Figura 19 – Corpo de prova estudado

Após a realização da análise térmica as curvas de resfriamento dos 10 pontos são extraídas do software e essas curvas de resfriamento são transportadas para o diagrama TTT do aço carbono 1045 com escala a de dureza Rockwell, onde serão analisadas as durezas correspondentes de cada um dos 10 pontos. Os dados obtidos em cada ponto foram plotados com o auxílio do Microsoft Office Excel para geração da curva de temperabilidade.
4. Resultados e Discussão
A Figura 20 mostra as curvas de resfriamento do corpo de prova Jominy extraídas da simulação por Elementos Finitos.
Figura 20 – Curvas de resfriamento encontradas
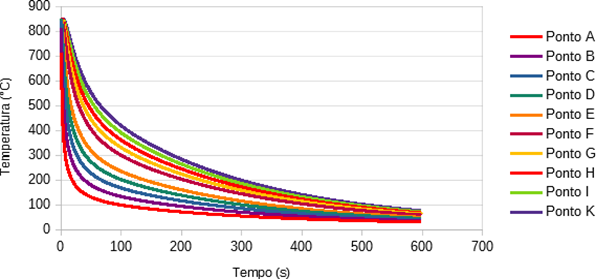
As curvas obtidas através da simulação do resfriamento, foram sobrepostas sobre o diagrama TTT do aço 1045, dessa forma, é possível estimar a dureza de cada um dos 10 pontos selecionados do corpo de prova. Os 10 pontos selecionados são apresentados na
Figura 19 no capítulo anterior. Na Figura 21 estão apresentadas as curvas sobre o diagrama TTT.
Figura 21 – Curvas de resfriamento representadas no diagrama TTT
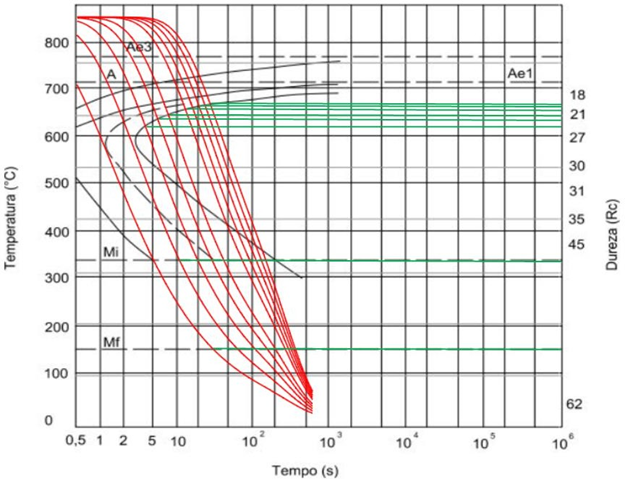
A Tabela 2 apresenta os valores das durezas estimadas dos respectivos pontos do corpo de prova.
Tabela 2 – Valores encontrados em corpo de prova
Ponto Distância x 1/16” Dureza (HRC) A 2 56 B 4 33 C 6 25 D 8 23 E 10 21 F 12 20,5 G 14 20,3 H 16 20,1 I 18 20 J 20 19
Com a estimativa das durezas pode -se fazer as comparações entre os dados existentes na literatura e os obtidos na simulação. A norma ASTM A255-02 menciona que os valores abaixo de 20 HRC sejam descartados, porém, neste estudo os valores abaixo de 20 HRC foram utilizados apenas para critério de análise. O comparativo pode ser visualizado na Figura 22.
Figura 22 – Comparação de curva de temperabilidade encontrada na literatura e na simulação
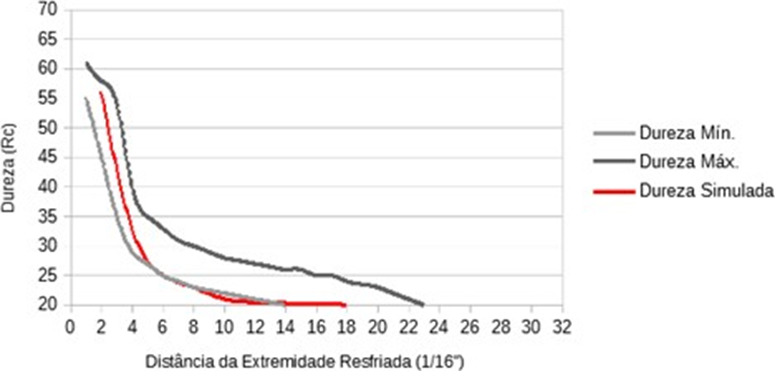
Nota-se, de acordo com a curva simulada, que o aço obteve maior temperabilidade da extremidade inferior e caiu consideravelmente ao longo do corpo de prova como esperado, visto que, a extremidade inferior é a região de maior contato com a água no momento do resfriamento, sendo resfriada rapidamente e por isso apresenta a maior dureza.
5. Considerações Finais/Conclusões
Os resultados apresentados demonstraram que as curvas levantadas através das análises térmicas através do MEF do ensaio Jominy para o corpo de prova feito em aço carbono 1045, se encontram dentro dos limites máximos e mínimos descritos na literatura levantada neste trabalho, o que demonstra que esta metodologia pode ser utilizada para a estimativa de temperabilidade, conforme o estudo previamente apresentado.
É sugerido que a aplicação do MEF aqui apresentada, seja explorada com maior profundidade, para a possibilidade de uma maior generalização de seu uso. Sugere-se ainda que, em trabalhos futuros, sejam utilizadas novas geometrias complexas e/ou outros materiais para discussão, além disso, a validação dos estudos com base em curvas experimentais trarão resultados mais fidedignos que permitirão sua aplicação na vida prática da engenharia.
6. Referências Bibliográficas
ASTM. 07, Stantard Test Methods for Determining Hardenability of Steel. PA, United States: ASTM A 255, 2007.
CHANDRUPATLA, T. R; BELEGUNDU, A. D. Elementos Finitos. 4ª edição. São Paulo: Pearson Education do Brasil, 2014.
CHIAVERINI, V. Aços e Ferros Fundidos. São Paulo: Associação Brasileira de Metalurgia e Materiais ABM, 2005.
ESSS. O Que é Método dos Elementos Finitos. Disponível em:
<https://www.esss.co/blog/metodo-dos-elementos-finitos-o-que-e/>. Acesso em: 16 set. 2022.
FILHO, A. A. Elementos Finitos – A Base da Tecnologia CAE. 6ª edição. São Paulo: Editora Érica, 2013.
FISH, J.; BELYTSCHKO, T. Um Primeiro Curso em Elementos Finitos. 1ª edição. Rio de Janeiro: LTC – Livros Técnicos e Científicos Editora S.A., 2009.
GOUVEIA, R. Condução Térmica. Disponível em:
<https://www.todamateria.com.br/conducao-termica>. Acesso em: 16 set. 2022.
HIGUERA, O.; TRISTANCHO, J.; FLORES, L. Simulación Térmica em Cosmosworks de um acero sometido a um ensayo de templabilidad Jominy. Volume 8. Colômbia: Scientia et Technica, 2007.
INCROPERA, F. P. Fundamentos de transferência de calor e de massa. 6ª edição. Rio de Janeiro: LTC – Livros Técnicos e Científicos Editora S.A., 2008.
NUNURA, C. R. Correlação Numérico – Experimental da microestrutura, taxa de resfriamento e características mecânicas do aço ABNT – 1045. Rio Grande do Sul: Dissertação (Mestrado em Engenharia) UFRGS – Universidade Federal do Rio Grande do Sul, 2009.
PINEDO, C. E. Tratamentos térmicos e superficiais dos aços. 1ª edição. São Paulo: Blücher, 2021. VANDER, V. G. F. Atlas of Time-Temperature Diagrams for Irons e Steels. PA, United States: ASM International, 2007.
FILIAÇÃO
