THE IMPLICATIONS OF UNDERSTANDING MATHEMATICS IN TEACHING PRACTICE
REGISTRO DOI: 10.69849/revistaft/ch10202504301618
Mariana Mendonça da Silva1
Tamires Oliveira Paixão2
Resumo
O presente artigo tem como finalidade trazer a análise crítica e reflexiva sobre as implicações da forma como vemos e entendemos a Matemática na prática de ensino. No Brasil, várias metodologias de ensino foram e são utilizadas nas salas de aula, cada uma com suas particularidades. Nesse sentindo, a cosmovisão do professor influencia na sua prática docente, de forma que esta nem sempre é a única e melhor maneira apreendida pelos alunos. A partir da leitura e reflexão dos textos de Duval, Fiorenti e Pierce, buscamos ressaltar a importância das diferentes simbólicas matemáticas com a finalidade de contribuir na formação ampla do ensino da Matemática.
Palavras-chave: Implicações; Matemática; Ensino.
Abstract
The purpose of this article is to bring a critical and reflective analysis on the implications of how we see and understand Mathematics in teaching practice. In Brazil, several teaching methodologies have been and are used in classrooms, each with its own particularities. In this sense, the teacher’s worldview influences his teaching practice, so this is not always the only and best way learned by students. From the reading and reflection of the texts by Duval, Fiorenti and Pierce, we seek to emphasize the importance of different mathematical symbols in order to contribute to the broad formation of the teaching of Mathematics.
Keywords: Implications; Mathematics; Teaching.
A origem da matemática
A matemática de hoje surgiu por volta de 3500 a.C. Os primeiros sinais da matemática na história surgiram da necessidade de solucionar problemas e desafios do cotidiano, das relações sociais e com a natureza. Como medir a quantidade de alimentos em uma negociação? Como medir a distância exata para capturar um animal? Essas questões, dentre tantas outras, foram fundamentais para o desenvolvimento da Matemática e para que ela fosse se tornando cada vez mais complexa de acordo com os problemas encontrados com o passar do tempo.
A Matemática da Roma Antiga, por exemplo, até hoje é uma das mais utilizadas em nossa sociedade, principalmente nas escolas, como representação de séculos e datas, em alguns relógios e em indicações de capítulos de livros. Outra grande contribuição utilizada nos dias de hoje é a Matemática da Grécia Antiga, com os diversos sistemas de numeração, o alfabeto grego e os registros dos pensadores Tales de Mileto e Pitágoras.
Imagem 1: Matemática Roma Antiga
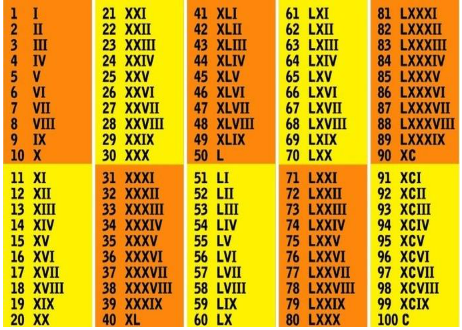
Fonte: https://www.todamateria.com.br/historia-da-matematica/.
Imagem 2: Matemática Grega

Fonte: https://estudandomatematicasite.wordpress.com/2016/04/13/a-matematica-dos-antigos-gregos/.
As inúmeras formas de concepção da Matemática variam entre as culturas, de acordo com a forma que vemos e simbolizamos os números, com o papel da Matemática na nossa sociedade e a forma como a ensinamos. Todas essas vertentes possuem propósitos pessoais. A classificação da Matemática é uma lógica que só existe com relação entre o próprio sujeito.
Os objetos matemáticos
Os objetos matemáticos são conceitos e ideias, não são objetos palpáveis. O grande problema no processo de ensino aprendizagem, principalmente o da matemática, é a confusão dos objetos e suas representações. Na matemática, o desafio é maior porque nós que ensinamos não temos acesso as ideias, ou seja, aos pensamentos dos alunos. Estamos dentro de um mundo de ideias e conceitos, e nesses conceitos não há como termos acesso sem sua representação. Ao falar a matemática estamos ensinando as representações e seus tratamentos. Por exemplo, o desenho de uma bola não é um círculo, é apenas sua representação. Devemos ter muito cuidado com a ideia que esse objeto representa no processo de ensino e aprendizagem para não gerarmos confusão neste processo.
As representações semióticas de um objeto matemático são necessárias no processo ensino-aprendizado da matemática, é fundamental neste processo, porém devemos ter uma práxis docente que faça sentido e que esteja de acordo com o desenvolvimento do indivíduo, pois tanto a falta quanto o excesso de estímulos de representações podem levar a confusão. Apenas uma representação não favorece a compreensão do conceito trabalhado. A imagem do conceito depende das diversas representações semióticas que fazemos do objeto.
Em uma aula de matemática buscamos compreender um conceito q não é palpável, estamos trabalhando no sentido da ideia. Somente com os símbolos, desenhos ou equações conseguimos atuar sob os objetos. Então, isto é uma atividade extremamente semiótica, sendo um exercício de linguagem basicamente. O sentido e significado sob o objeto se encontram em vários níveis de representações. Representamos o objeto e sua concretude para a apreensão dos conceitos, podendo ser em jogos ou outras maneiras necessárias para que se construa sentidos, porém, sempre ampliando estas perspectivas além de somente um objeto. Nesta perspectiva, apresentamos além do objeto, os desenhos, esquemas, gráficos, figuras dentre outros.
A linguagem falada também é uma forma de representação, no discurso e diálogo temos a forma mais natural da linguagem. A linguagem verbal, associada na representação simbólica, são influentemente potencializadoras no processo de ensino- aprendizado. A partir da metáfora de quadros por exemplos, podemos ver vários ângulos de uma mesma imagem, representações dos objetos matemáticos precisam de uma representatividade por multifaces. Um dos grandes problemas é a limitação do regramento. Estas limitações presentes nas regras de determinados sistemas por muitas vezes se tornam um empecilho no processo de ensino aprendizagem da matemática, porém, a partir do momento que temos em vista essa questão, podemos usar nossa linguagem oral como uma ferramenta para potencializar e ilustrar estas regras de uma forma mais acessível.
Quando refletimos mais afundo e nos encontramos com os pensamentos de Duval, compreendemos que há um paradoxo cognitivo. Ele é atravessado por uma relação entre semiose e noesis.
O paradoxo cognitivo do pensamento matemático e as dificuldades que resultam para sua aprendizagem se dá pelo fato de que não há noesis sem semiose enquanto houver vontade de ensinar matemática, como se a semiose fosse uma operação desprezível em relação a noesis.
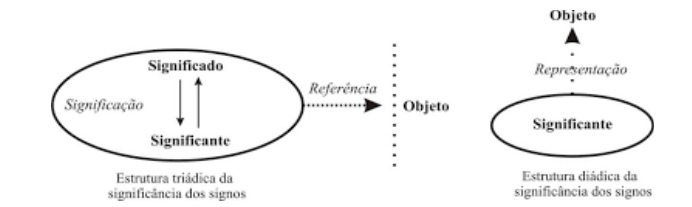
Fonte: periodicos.ufsc.br.
De um lado temos a apreensão de um conceito somente a partir de sua representação, mas de outro lado temos esta representação de algo a partir de uma pré-compreensão de algo que não temos acesso. Como Platão afirmava sobre as representações aqui e sua matéria real no mundo das ideias também nos deparou com esse paradoxo, que é difícil de ser transferido em palavras.
Isto pode ser considerado, portanto, um paradoxo cognitivo do pensamento matemático: de um lado, a apreensão dos objetos matemáticos não pode ser mais do que uma apreensão conceitual e, de outro, é somente por meio de representações semióticas que a atividade sobre objetos matemáticos se torna possível. (Duval, 2012. p. 268)
Devemos nos atentar ao fato de que por muitas vezes temos como dado a conexão entre a ideia e suas propriedades e representações, porém devemos pensar que para o aluno, muitas vezes, isto ainda não foi construído. A partir da representação, temos um processo de articulação dentro da semiose, entre o que há no externo e no interno, a relação direta entre pensamento e linguagem é algo natural, não há separação entre semiose e noesi.
A representação em si não diz para ao outro exatamente aquilo que você pensa, porém, as regras na linguagem matemática tendem a levar estas concepções diretamente ao ponto especifico.
Há uma palavra às vezes importante e marginal em matemática, é a palavra “representação”. Ela é, na maioria das vezes, empregada sob a forma verbal “representar”. Uma escrita, uma notação, um símbolo representam um objeto matemático: um número, uma função, um vetor… (Duval, 2012. P.01)
A distinção entre o objeto e seu símbolo é algo que merece atenção, principalmente quando estamos na sala de aula com o papel de ensinar, pois a partir do momento em que não há conexão com os mesmo, a confusão pode se tornar um empecilho, contribuindo aquela ideia que costumamos ter acerca da matemática, aquele mito e medo que temos desta disciplina, principalmente nos segmentos escolares. Os objetos matemáticos não devem ser confundidos com a representação que se faz dele, portanto uma linha reta, um círculo ou um traço são uma representação e não o objeto em si.
Há um paradigma enorme em torno do ensino e aprendizagem da matemática, pois a confusão entre o objeto e suas representações:
As representações semióticas são produções constituídas pelo emprego de signos pertencentes a um sistema de representações que tem inconvenientes próprios de significação e de funcionamento. Uma figura geométrica, um enunciado em língua natural, uma fórmula algébrica, um gráfico são representações semióticas que exibem sistemas semióticos diferentes. (Duval, 2012. p.269).
As representações semióticas são essenciais na formação mental, “no desenvolvimento das representações mentais: estas dependem de uma interiorização de representações semióticas, do mesmo modo que as representações mentais são uma interiorização daquilo que é percebido” (VYGOTSKY, 1962; PIAGET 1968).
As tendências concebidas no ensino da Matemática
Com o entendimento da abstração da matemática, sendo esta uma existência que não existe, os professores, a partir de suas perspectivas entendidas sobre essa questão, coloca em sua prática docente tendências e modalidades próprias de ensino. A matemática na sua forma tradicional passou por diversas modificações metodológicas na busca do que era melhor para a educação e propósitos de cada época. Atualmente, as mais utilizadas nas escolas são: Construtivista, Etnomatemática e Tecnicista.
Tendência Construtivista: a educação construtivista segue os princípios de Jean Piaget, onde o conhecimento é ativamente construído pelo aluno e não adquirido de forma bancária. O aluno é visto como único e singular e os trabalhos em grupo são incentivados e muito valorizados. Piaget afirma que a ideia da matemática é constituída no cotidiano, na observação, experimentação e relação dos objetos, onde se constrói o pensamento lógico. Nesse sentido, o papel do professor seria de instigar os alunos e criar situações problemas para eles, de forma ativa, sejam estimulados e assim consigam interpretar essas situações de forma significativa. A construção de uma base sólida desse conhecimento matemático é de suma importância no processo dinâmico do “fazer matemático”, onde através da experiência e dos entendimentos das estruturas mentais, por tentativas e erros, o conhecimento matemático é construído. A construção do processo evolutivo das estruturas cognitivas inicia-se dos primeiros esquemas de natureza lógico-matemática até a constituição do pensamento abstrato.
Tendência Etnomatemática: surgindo também como forma de se diferenciar dos ensinos tradicionais, essa tendência tem como objetivo trabalhar o ensino de acordo com as culturas, sendo a matemática também uma construção política e histórica. No Brasil, possuindo múltiplas culturas, ainda hoje existem metodologias de ensino que tentam padronizar o ensino da matemática e a etnomatemática tem na sua finalidade a valorização do cotidiano dos alunos e suas particularidades. O fazer matemático dessa tendência deve ser algo vivo e que lide com situações reais do tempo atual. Existem diversos segmentos sociais e econômicos que utilizam o conhecimento matemático, o saber popular, mas não são valorizados, como pedreiros, indígenas e carpinteiros. Estudar e entender essas diferenças, utilizadas no cotidiano, é também importante. Os problemas da realidade inseridos em diversos grupos culturais devem trabalhados em sala de aula.
Paulo Freire, em seus textos afirma que assim como a matemática é abstrata na comunicação também existe um abstrato. A fala dos professores como sendo a única aceitável e dominante faz com que exista um grande distanciamento entre o conceito e o concreto. Quando não se conhece a realidade e leitura do aluno, as dificuldades de aprendizagem se tornam latentes. Muitos não participam de debates e propostas por medo de errar. A educação dialógica, nessa tendência, é importante para a práxis matemática. O educador deve ter uma preocupação com a linguagem e metodologia utilizada, de acordo com as necessidades culturais e particulares dos alunos.
“A leitura do mundo precede a leitura da palavra, daí que a posterior leitura desta não possa prescindir da continuidade da leitura daquele.” (Freire, 1989).
Tendência Tecnicista: diferentemente das duas modalidades anteriormente citadas, essa modalidade de ensino é marcada pela repetição de métodos e fórmulas que levam à memorização. O foco não é no aluno e nas suas experiências mas sim na projeção de resultados que este pode alcançar através de métodos e regras. Professor e aluno não mantém uma relação de diálogo, eles são apenas componentes do sistema escolar. Entende-se que se é possível controlar a técnica é possível também dominar o resultado. É a ideia de uma receita pronta. Essa tendência é similar ao modelo de sociedade que vivemos hoje, onde não importa como chegamos a um determinado ponto, importa apenas se ele está correto. Os cursos preparatórios para o ENEM (Exame Nacional de Ensino Médio) podem ser citados como exemplo. Além de conteúdos, técnicas são passadas para que os alunos sabiam otimizar o tempo, tenham maior rendimento e consequentemente um melhor resultado. Na maioria das vezes não é importante que ele entenda todo o processo mas sim que saiba como chegar ao resultado esperado.
O Kumon é outro exemplo são instituições de ensino fora do horário escolar onde utilizam por meio de atividades repetitivas em apostilas e folhas. Outras formas de aprendizagem não são incentivadas, como jogos e experimentações. “Desenvolve a capacidade básica de estudos, que será requisitada na escola, nos vestibulares e na vida profissional. Na Matemática, o objetivo é desenvolver a capacidade de cálculos.” (KUMON, 2020).
Conforme imagem abaixo, as operações matemáticas não possuem relações com o cotidiano ou com situações problemas. As operações são dadas apenas com o intuito de se chegar ao resultado desejado.
Imagem de exercício matemático do curso Kumon.

Fonte: https://www.kumon.com.br/cursos/curso-de-matematica.
A grande problemática dessa metodologia de ensino é que a limitação de representações semióticas pode ser prejudicial à aprendizagem do aluno. Outra questão é que nada é totalmente controlável. Muitas pessoas quando perguntadas do que lembram sobre o que aprenderam na escola dizem não se lembrar. Isso se dá porque de fato não aprenderam, apenas sabiam como dar uma resposta em determinada situação problema.
Vale ressaltar que essa tendência pedagógica foi introduzida no Brasil entre as décadas de 60 e 70, período da ditadura militar no país, onde era necessário ter mão-de-obra para o mercado de trabalho. A escola não era valorizada, o professor não era valorizado e nem o aluno era valorizado.
Enquanto futuros educadores faz-se necessário refletirmos e nos questionarmos acerca de qual realidade queremos passar para nossos alunos. Apesar de ter sido uma tendência muito forte nos anos 60 e 70, essas ideias perduram até hoje em nossa sociedade e os ideais capitalistas seguem estando em primeiro plano no que se refere ao campo da educação. Forma-se para o mercado de trabalho.
A grande problemática não é o ensino de forma técnica. Às vezes o aluno consegue compreender bem quando faz diversos exercícios mas é necessário mostrarmos o todo desse processo até chegar ao cálculo que ele efetua e no porque ser do jeito que é. Não se pode ter essa como única ferramenta de ensino. A partir disso, os caminhos para facilitação da apreensão do conteúdo se tornarão maiores e a qualidade do ensino poderá ser amplificada.
Considerações finais
A partir das análises feitas no presente artigo, fica expresso a importância e influência do professor de matemática no processo de ensino e aprendizagem do aluno. Na aula de matemática, na maioria das vezes o professor não consegue ter convicção de que o conteúdo apresentado foi de fato compreendido pois nem mesmo os alunos possuem essa certeza. A construção de ideias equivocadas passa a se fazer comum, dificultando para os professores identificarem isso e gerando, consequentemente, uma grande bola de neve na cabeça dos educandos.
A multiplicidade de caminhos para a aprendizagem na maioria das vezes é um grande facilitador nessa disciplina. Um sistema de rodízio nas aulas com músicas, jogos, leituras, exercícios e com experiências fora da sala de aula fazendo com que a partir do momento que o aluno experiência ele mesmo começa a desmistificar a matemática. Essa sensibilidade do professor é muito importante.
Quando pensamos em matemática, tendemos a pensar na mesma somente a partir do modo como a aprendemos na escola, onde por muitas vezes, vivemos o aprendizado da matemática sob um mito mítico, onde a mesma é difícil de mais para ser solucionada e entendida. Porém, ao entendermos que vivemos com base nestas crenças de que a matemática é algo como um Deus, temos a possibilidade de nos desvincularmos destas superstições, e encararmos o estudo da matemática de forma crítica.
Se analisarmos o modo como uma aula e matemática funciona, percebemos que há muitos fatores implícitos naquele meio. No discurso do professor ou nos símbolos impressos na lousa, há o encontro de duas linguagens que não dialogam, por mais que sejam a mesma linguagem em si, os contextos e realidades diferentes impedem que o professor e aluno dialoguem. É uma situação complexa, onde por muitas vezes o professor não percebe que sua linguagem não chega aos alunos de forma clara, talvez o modo como ele conduz a matemática gera no aluno ainda mais esta percepção de um monstro matemático, o qual ele não é capaz de enfrentar. Romulo Lins (2004), através de suas reflexões como professor de matemática, afirma que um dos possíveis problemas desse mito que envolve a mesma, ocorre porque a matemática presente nas escolas existe somente dentro da escola, diferente de outras disciplinas como o português, onde o vemos, falamos e lemos, por muitas vezes em momentos prazerosos, já a matemática que vivenciamos dentro da sala de aula, somente com o professor, acentua o afastamento ou a aceitação da matemática de forma significativa.
Existem muitas linguagens, culturas, contextos e histórias, onde se criam abismos, em especial na aula de matemática, formando assim inúmeros obstáculos no processo de ensino e aprendizagem. A linguagem utilizada para representar a matemática é um ponto fundamental a se refletir. “Aprender é uma experiência pessoal, mas ela ocorre em contextos sociais repletos de relações interpessoais” (LENNON, p.03). A comunicação entre os participantes em um ambiente de aprendizagem afeta todo o processo de entendimento. Na ação educativa, usar o diálogo através da linguagem no processo de comunicação e informação, contribui em uma forma de comunicação de qualidade. Ter diálogo e ser mediador do conhecimento, encaminhar o pensamento a partir da lógica, possibilita caminhos positivos no processo de aprendizagem.
Segundo Galileu (1564-1642), a Matemática é o alfabeto com o qual Deus escreveu o Universo, mesmo após séculos de evolução, ainda persistimos nesta crença. Sabemos que o sujeito aprende por processos de produção de significados, na educação matemática, a linguagem é o meio pelo qual o aluno e professor criarão pontes de saberes para o processo de ensino e aprendizagem, portanto, a criação de um espaço dialógico e a manutenção do mesmo, pode possibilitar um estranhamento positivo no ensino da matemática, criando-se ferramentas para a extinção da crença sobre o “monstro” da matemática.
Referências bibliográficas
Araújo, I. L. Do signo ao discurso: Introdução à filosofia da linguagem. São Paulo: Parábola editorial, 2004.
DUVAL, Raymond. Registros de representação semiótica e funcionamento cognitivo do pensamento.
FIORENTINI, Dario. Alguns modo de ver e conceber o ensino da matemática no Brasil.
FREIRE, P. A importância do ato de ler. 23 ed. São Paulo: Autores Associados: Cortez, 1989.
FREIRE, Paulo. Pedagogia da Autonomia: saberes necessários à prática educativa. 1996.
LINS, Romulo Campos. Matemática, Monstros, Significados e Educação Matemática. 2004.
MARCHON, Fabio Lennon. Linguagem & Linguagens Matemáticas.
https://www.kumon.com.br/cursos/curso-de-matematica, Acesso em 20/11/2020.
https://monografias.brasilescola.uol.com.br/matematica/historia-matematica.htm, Acesso em 20/11/2020.
http://periodicos.ufsc.br; Acesso em 21/11/2020.
https://estudandomatematicasite.wordpress.com/2016/04/13/a-matematica-dos-antigos-gregos/. Acesso em 21/11/2020.
https://www.todamateria.com.br/historia-da-matematica/Acesso em 21/11/2020.
1Linguagem Matemática. Niterói, RJ: UFF, 2020 Universidade Federal Fluminense, Curso: Pedagogia,
E-mails: mariana_mendonca@id.uff.br
2Linguagem Matemática. Niterói, RJ: UFF, 2020 Universidade Federal Fluminense, Curso: Pedagogia,
E-mails: tamires_paixao@id.uff.br
