MATHEMATICS IN THE UNIVERSE OF GAMES. “THE USE OF GAMES IN THE TEACHING OF THE FUNDAMENTAL OPERATIONS OF YOUTH AND ADULT EDUCATION (EJA) CLASSES AT THE DEOCLECIANO ALVES MOREIRA STATE SCHOOL”
REGISTRO DOI: 10.5281/zenodo.11212091
Roberto Ranieri Soares de Andrade;
Antonia Milene de Lima Ribeiro.
RESUMO
Este trabalho tem como objetivo a investigação da contribuição dos jogos de cartas a favor do ensino das operações fundamentais de matemática. Sua produção foi desenvolvida sob a forma de pesquisa na Escola Estadual Prof. Deocleciano Alves Moreira, instituição escolar da rede pública no município de Conceição do Araguaia – PA com a turma da 3ª Etapa da EJA, com 29 alunos devidamente matriculados no ano letivo de 2012. A base de pesquisa, desta obra esta fixada na elaboração de 02 questionários como pré-teste, para apuração da situação real dos conhecimentos dos alunos, assim, deu-se continuidade na pesquisa com o desenvolvimento de um jogo matemático envolvendo as operações fundamentais, que foram aplicadas gradativamente como forma acumulativa, partindo desde a soma até a subtração, passando pela multiplicação e finalizando com a divisão, tudo isto com o auxilio do jogo de cartas, seguida de um novo questionário como um pós-teste para comparação dos resultados do projeto e constatou-se que os alunos obtiveram um bom desempenho.
Palavras-chave: Operações Fundamentais. Uso de Jogos. Ensino EJA.
ABSTRACT
This work aims to investigate the contribution of the card games the benefit teaching of basic math operations. Its production was developed the form of research in the State School Prof. Deocleciano Alves Moreira, from public educational institution in the town of Conceição do Araguaia – PA with the class of Leg 3 of the EJA, with 29 students properly registered in academic year 2012. The base of research, this work in the preparation this set of 02 questionnaires as pre-test to ascertaining the real situation of knowledge of students, so was continued research with development of a math game involving the fundamental operations that were gradually implemented as cumulatively, starting from the subtraction the sum up, through multiplication and ending with the division, all this with the help of the card game, followed a new questionnaire as a posttest for comparison of results of the project and it was observed that students obtained a good performance.
Keywords: Fundamental Operations. The use of the Games. Teaching EJA.
INTRODUÇÃO
As dificuldades apresentadas no processo de ensino-aprendizagem pelos alunos do programa de Educação para Jovens e Adultos (EJA) da Escola Estadual de Ensino Fundamental e Médio Prof. Deocleciano Alves Moreira no Município de Conceição do Araguaia – PA foi o principal motivo da pesquisa bibliográfica, com a intenção de propor uma metodologia com foco na utilização de jogos como um processo desenvolvedor de conhecimentos lógicos; cognitivos; atitudes sociais como o relacionamento e trabalho em equipe e principalmente, despertar a curiosidade de aprender de forma diferenciada, com competências que facilitem o desenvolvimento do aluno diante das reais situações do seu cotidiano e principalmente sobre o conteúdo de operações fundamentais da matemática, como no exemplo:
a) 2 + 5 = 7; b) 7 – 5 = 2; c) 2 x 3 = 6; d) 6 ÷ 3 = 2.
São estas pequenas dificuldades encontradas nos alunos das turmas do EJA, que foram observadas durante o módulo de Prática para o Ensino da Matemática I (Prática I) em 2011, que geram possíveis bloqueios no aprendizado de vários alunos.
Estas mesmas dificuldades também foram observadas no ano adjacente pelo atual educador responsável pelo ensino de matemática na EJA da escola, Prof. Carlos de Jesus Costa (Prof. Carlos) que ao admirar os esforços para tentar solucionar tais problemas, solicitou e acompanhou o desenvolvimento do processo da aplicação deste Projeto em 2012.
Vale resaltar sobre a utilização de jogos como grandes ferramentas na construção de conhecimentos, e que o manuseio incorreto, pode comprometer o ensino. Entretanto, o uso do lúdico na educação é se ajustado à medida em que ocorre o desenvolvimento de conhecimentos do aluno, junto ao seu comportamento social.
Assim afirma Kishimoto:
Brincando […] as crianças aprendem […] a cooperar com os companheiros […], a obedecer às regras do jogo […], a respeitar os direitos dos outros […], a acatar a autoridade […], a assumir responsabilidades, a aceitar penalidades que lhe são impostas […], a dar oportunidades aos demais […], enfim, a viver em sociedade. (Kishimoto apud S.Vasconcellos, 1993).
Deste modo, este trabalho foi produzido por meio de leituras pedagógicas que se referem a jogos matemáticos e aplicados aos alunos da terceira etapa de 5ª a 6ª Séries do programa da EJA, com objetivos de investigar quais os principais problemas que prejudicam o processo de ensino aprendizagem das operações fundamentais, apresentando uma proposta de ensino através da modelagem com o jogo “21 matemático e as 4 Operações”. E principalmente, a reconstrução de conhecimentos básicos da matemática com os alunos para dar continuidade no processo de ensino. Destarte, toda esta metodologia está voltada para o ensino das operações fundamentais da matemática, onde tais conhecimentos são de suma importância para o processo de aprendizado tanto nesta disciplina, como também na vida social do aluno.
2. O LÚDICO E SUA IMPORTÂNCIA NO PROCESSO ENSINO/APRENDIZAGEM
2.1 Uma breve história sobre os primeiros passos da EJA no Brasil..
Diversos autores acreditam que a educação de adultos no Brasil teve inicio por volta de 1549, período em que a antiga Grécia apresentava os primeiros passos pedagógicos. Nesta época, a educação era feita pelos Padres Jesuítas a fim de catequizar e ensinar os povos indígenas, tornado a aparecer com maiores traços no início do desenvolvimento político e econômico por volta de 1930, onde era preciso “mão de obra cada vez mais alfabetizadas” para o cumprimento de ordens e manuseio de máquinas, (S. LOPES; Sousa, 2005, p. 1).
Em 1934, criou-se o Plano Nacional da Educação (PNE), visando o ensino de adultos como obrigação do Estado. Mas somente na década de 40, que surgiram os primeiros programas nacionais e políticas pedagógicas em apoio à educação de adultos no Brasil.
As influências de Paulo Freire para a conscientização da população, alertando sobre a importância da educação na década de 60 contribuiu fortemente nas iniciativas formadas por grupos voltados a políticas de educação do País. Foi a partir daí que começaram a surgir várias propostas com base nos saberes de Freire, até meados da década de 90, com o surgimento das Leis de Diretrizes e Bases da Educação Nacional (LDB), garantindo que a educação de jovens e adultos seja posta em prática, com financiamentos arrecadados pelo Fundo de Manutenção e Desenvolvimento da Educação Básica e de Valorização dos Profissionais da Educação (FUNDEB).
2.2. O que é a EJA?
A Educação de Jovens e Adultos (EJA) tem como objetivo além de educacionais, o compromisso com a inclusão e igualdades sociais entre os povos de diversas culturas, etnias e credos, com idades avançadas em relação à série escolar, que não tiveram oportunidade de frequentar uma escola ou continuar os estudos por vários motivos relativos à sua região. Como afirma a Lei de Diretrizes e Bases da Educação Nacional (LDB):
A educação de jovens e adultos será destinada àqueles que não tiveram acesso ou continuidade de estudos no ensino fundamental e médio na idade própria. (Art. 37, Lei nº 9.394/96, LDB).
Desta forma, pode-se perceber o quanto é importante a educação para o Governo brasileiro, que incrementou uma resolução que apoia o ensino de jovens e adultos na constituição com base nos princípios do Art. 03 da LDB que prevê:
[…] igualdade de condições […]; liberdade de aprender, ensinar, pesquisar e divulgar a cultura, o pensamento, a arte e o saber, […] pluralismo de ideias e de concepções pedagógicas; […] respeito à liberdade e a tolerância; […] gratuidade de ensino público […] gestão democrática do ensino público; […] garantia de padrão de qualidade; […] valorização da experiência extraescolar […] vinculação entre a educação escolar, o trabalho e as práticas sociais. (Art. 03; lei nº 9.394/96, LDB).
A lei proporciona em nosso quadro educacional uma forma de reduzir o índice de analfabetismo e aumentar o nível de escolaridade da população brasileira, especialmente daqueles que não tiveram oportunidades de ensino adequado em sua idade certa, e que almejam um futuro de prosperidade.
2.3. O lúdico na educação.
A palavra “lúdico” origina-se do latim ludus, que literalmente significa “brincadeira”. Corbalán descreve como “uma experiência com bom êxito do sentido de algo que traz felicidade aos alunos.” (CORBALÁN apud SANT’ANNA; NASCIMENTO, 2011). Seu uso na educação tornou-se imprescindível quando se percebeu que este facilitaria o aprendizado. Platão concebeu a premissa de quem meninos e meninas deveriam iniciar seus estudos juntos, através de jogos. Outros escritores e pensadores também tinham este pensamento, por exemplo, Rousseau; Pestalozzi; Dewey; Vygostsky; Piaget; Montessori; François Rabelais, este dizia que todas as crianças deveriam através de atividades lúdicas, aprender desde o gosto pela leitura até aritmética.
Vygostsky afirma que a o homem, com interferência direta ou indiretamente de outros, se desenvolve a partir do aprendizado. Sendo que a utilização de jogos cria nos educandos o que chama de Zona de Desenvolvimento Proximal (ZDP), o que estimula a aprender coisas mais complexas, e ensina também a separar objetos e seu significado. Essa Zona de Desenvolvimento Proximal (ZDP) é o caminho percorrido até obter-se um amadurecimento real, o que ele chama de desenvolvimento real, que é a capacidade de completar tarefas autônomas.
A partir da década de 30 que o Brasil passou a investir na economia interna e na produção industrial, o que fez com que houvesse necessidade de mão de obra especializada. Sant’anna e Nascimento (2011, p. 8) consideram sobre as várias técnicas e metodologias para o ensino da matemática:
À época foram publicadas várias técnicas e métodos para o ensino da matemática, de acordo com pesquisas e estudos realizados por matemáticos e especialistas desse movimento, os quais defendiam que a resolução de problemas, ao contrário do mecanicismo, ajudava os alunos a compreenderem os conteúdos matemáticos, devendo então ser aplicados antes dos conteúdos.
Ou seja, havia a defesa da criação de modelos de ensino para a matemática, que em vez do professor levar para sala de aula somente teorias, passaria a utilizar-se das situações vividas pelos alunos para incorporar a nova metodologia no ensino da matemática. O ensino da matemática que antes era tradicional e mecanicista tornou-se audacioso e revolucionário, que passou a atender o desenvolvimento e tornou-se também agente de transformação social.
2.4 O surgimento da Proposta.
A proposta deste trabalho é a verificação da contribuição dos jogos de cartas a favor do ensino das operações fundamentais de matemática. Sua produção foi desenvolvida sob forma de pesquisa na Escola Estadual Prof. Deocleciano Alves Moreira (Escola Deocleciano), instituição escolar da rede pública sitiada no município de Conceição do Araguaia – PA com a turma da 3ª Etapa da EJA, que tem 29 alunos devidamente matriculados no ano letivo de 2012.
Surgindo após a participação dos estágios programados como requisito para formação no Curso de Licenciatura em Matemática no segundo semestre do ano de 2011, que ocorreu na escola já mencionada nas turmas da EJA. Após a formação da equipe de estágio, composto por discentes do curso de licenciatura Érika Laurene, Larice Borges e Roberto Ranieri, foi decidido ficar com as turmas da 3ª Etapa equivalentes à 5ª e 6ª Séries do ensino fundamental. Ao adentrar em sala para iniciar ao período de observação requerido no cronograma, percebeu-se as dificuldades que os alunos tinham em compreender pequenas operações fundamentais que o Professor Carlos de Jesus Costa (Prof. Carlos) escrevia no quadro. Gerando uma grande intriga entre os estagiários, que ao discutirem sobre esta observação, chegaram a uma pergunta: “O que causa a defasagem dos alunos em relação à matemática?”.
A partir dessa dúvida decidiu-se pela presente pesquisa. Foi criado um questionário com 04 questões (vide Apêndice A) e aplicado em sala para investigar o que poderia ser a provável causa do problema. Os resultados mostraram que dos 16 alunos que frequentam a sala de aula, 62,5% responderam que não gostam de matemática, demonstrado nas representações gráficas abaixo:
Tabela 1: Parcial de alunos que frequentam as aulas e relação de vocação pela matemática.
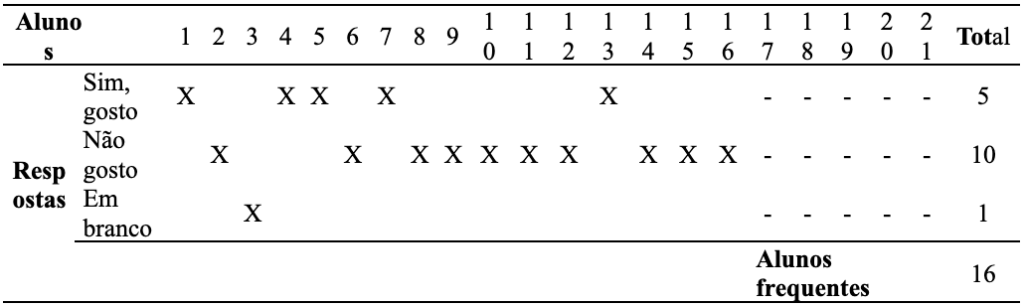
Tabela 2: Amostra da Quantidade e Percentual em relação à vocação pela matemática, com base na Tabela 1.
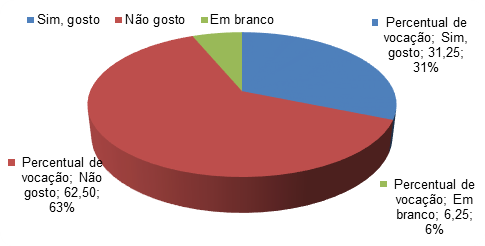
Faixa Etária Quantidade Percentual Sim, gosto 5 31,25 Não gosto 10 62,50 Em branco 1 6,25 Total 16 100,0
Gráfico 1: Percentual em relação à vocação na turma do EJA em 2011.
O que mais impressiona nos resultados analisados, é a frequência das respostas semelhantes no que se refere aos professores dos anos anteriores, não gostarem de lecionar para os alunos, com 75% das respostas, e 25% argumentaram que o professor deveria explicar mais sobre operações fundamentais, segundo os resultados na (Figura 2) a seguir:
Tabela 3: Quantidade e Percentual em relação às argumentações dos alunos em 2011.
Respostas Quantidade Percentual Os professores não gostam de dar aula. 12 75,0 Os professores devem ensinar mais as operações. 4 25,0 Deixaram em branco 0 0,0 Total 16 100,0 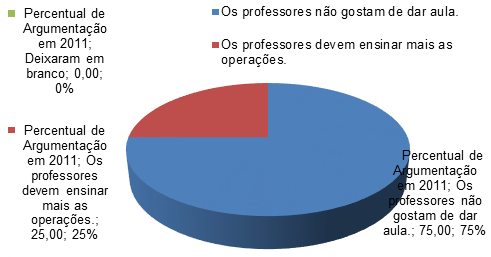
É importante ressaltar que todas as respostas coletadas durante a pesquisa, apesar da peculiaridade dos alunos, estavam todas relacionadas, apontando um possível abandono do docente.
Após analise das amostras e comparação com as observações feitas durante o estágio, chegou-se a um senso comum de que o professor por influência de diversos fatores que variam desde a falta de metodologias a longas jornadas de serviço contribui para um péssimo processo de ensino e até mesmo promove descaso com a educação, fazendo com que os alunos percebam um real desinteresse do professor ao ensina-los.
Segundo N. Duarte (1995, p. 07), este fato esta relacionado principalmente quando se trata do professor em relação ao ensino de matemática para adultos, quando diz:
O ensino de matemática para alfabetizandos adultos tem sido uma área quase que totalmente abandonada. Aqueles que trabalham com educação de adultos têm, em geral, um receio em relação à matemática e, em sua maioria, consideram o ensino para adultos um problema secundário.
Com este pensamento decidiu-se que nos horários vagos seriam dadas aulas de reforço para os alunos, e como consequência, foi desenvolvida uma metodologia com base nos jogos de cartas para ensino das operações fundamentais da matemática, onde pelo pouco tempo que destinado à aplicação, não foi suficiente para aplicação total do projeto. Mas pelos bons resultados obtidos, o Prof. Carlos satisfeito com efeitos iniciais do projeto, propôs no ano seguinte a reaplicação com a nova turma do ano de 2012.
2.4.1 Projeto: Jogos para o Ensino da Matemática.
Com base na didática para o ensino da matemática, e aplicações de jogos didáticos publicados em vários órgãos educacionais, encontraram-se diferentes propostas para desenvolvimentos com base na educação em geral, mas apenas uma dessas tendências fez refletir, analisar, e reformular uma estratégia de aplicação que mais adequou à resolução do problema dentro de sala de aula.
O referido projeto tem como base os jogos educacionais para ensino da matemática, em especial os jogos de cartas, com ênfase no jogo conhecido como “21 matemático” encontrado em vários sites de órgãos educacionais na Internet, porém muito limitado utilizando apenas a soma, ou soma e subtração. Sendo pouco proveitoso na aplicação, uma vez que os objetivos envolvem as competências de ensinar as operações fundamentais, raciocínio lógico e capacidade de agir perante os sistemas socioculturais vividos por cada educando.
2.4.2. O jogo: 21 Matemático e as 4 operações.
O jogo “21 Matemático e as 4 operações”, utiliza cartas de baralho e de fácil acesso, com regras simples e claras (vide Apêndice B), com objetivos de alcançar 21 pontos (base de onde foi retirado o nome do jogo), além de ser muito divertido, em mãos de um bom educador poderá virar uma ferramenta extremamente útil no ensino da matemática.
Embora o processo de ensino das operações seja feita de forma que a cada conteúdo apresentado ao educando, estes serão somado aos seus conhecimentos e armazenados em seu sistema cognitivo.
Para Falcão (2000, p. 20) a aprendizagem.
Sendo pessoal, é gradual. Aprende-se aos poucos, e cada um dentro de seu ritmo próprio. […].
É fácil admitir que o conteúdo hoje aprendido dependa do conteúdo aprendido anteriormente. […]. Daí muitos autores afirmarem ser a aprendizagem um processo cumulativo, em que cada nova aquisição se adiciona ao repertório já adquirido.
Portanto, este jogo proporciona ao professor trabalhar por etapas objetivas e com grande entusiasmo daqueles que os jogam. Apresentando uma forma diferenciada e agradável de ensinar e aprender matemática, pois ao longo da pesquisa mostrou-se como o jogo pode envolver e transformar os próprios educandos em grandes multiplicadores de conhecimento, quando estes informaram que convidaram amigos e parentes para praticar do novo jogo que aprenderam na escola. (relatados feitos pelos próprios alunos). E de certa forma, meio que ludicamente estariam repassando os conhecimentos aprendidos em sala de aula.
Como citado anteriormente, todo este processo foi aplicado durante os horários vagos da turma, tendo em mente que a maior parte dos discentes tinha suas obrigações trabalhistas/domésticos durante o dia e finais de semana ocupados com familiares, o que dificultou o comparecimento de todos os alunos. Vale resaltar que todo o processo foi aplicado com a turma da EJA no período noturno que este por sua vez é onde se encontra o maior índice de desistência influenciado por vários fatores sociais ou psicológicos do educando.
3. METODOLOGIA
3.1. Reconhecimento da turma:
Esta é a fase do projeto considerado com de suma importância. É ela que possibilita uma visão parcial de como se encontra a turma e seus conhecimentos aprendidos nas series anteriores. Inicialmente foram realizadas coletas de dados com 02 questionários como pré-teste, prevendo o reconhecimento total das habilidades dos alunos e suas principais dificuldades com o conteúdo aqui abordado.
3.1.1 O primeiro pré-teste.
O primeiro questionário (vide Apêndice C), contendo 08 questões de conteúdos objetivos e algumas discursivas, teve a função de conhecerem-se os alunos, suas dificuldades e visão que tem da própria sala de aula e do professor. Na primeira questão pode-se observar que dos 29 alunos matriculados, apenas 86,2% (25 alunos) compareceram as aulas como mostra a tabela a seguir:
Tabela 4: Quantidade de alunos frequentes em 2012, com relação com a Faixa etária.

Intrigados com a ausência dos alunos foi perguntado o que estaria acontecendo aos demais que não puderam comparecer as aulas, pois era começo de ano letivo, e não se fazia ideia de quais motivos levaram a ausência destes. Motivos que aos poucos foram aparecendo respostas e hipóteses conformando a todos.
Analisando os dados da tabela acima, percebe-se que a maior parte dos educandos tinha em média idade menor ou igual há 21 anos, com 68,0% da turma, e que 12,0% tenham idades acima de 30 anos, veja representação gráfica abaixo:
Tabela 5: Amostra da Quantidade e Percentual em relação à faixa etária retirada da Tabela 4.
Faixa Etária Quantidade Percentual Até 21 17 68,0 22 a 30 5 20,0 Acima de 30 3 12,0 Total 25 100,0 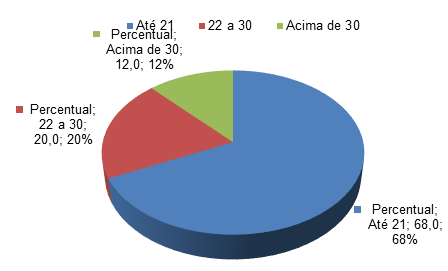
Como se pode vê, a variação de educandos no ensino da EJA é formada por jovens que estão entrando na fase adulta, e os poucos adultos que frequentam:
Podemos dizer que, “estão aqui para buscar formação e melhoria de vida, para conseguir um emprego melhor e até mesmo servir de exemplo para seus filhos”. (Sr. Antonio, aluno 3 Etapa EJA, 2012). Frase citada por um aluno, que merece muito respeito e admiração pelo exemplo e ilustre idade.
3.1.2. O segundo pré-teste
O segundo questionário foi aplicado com 16 questões (vide Apêndice D) sendo algumas pequenas operações fundamentais com compatibilidade à etapa da EJA estudada, onde 04 questões envolvendo soma simples, 04 de subtração, 04 de multiplicação e 04 de divisão. Os resultados são impressionantes, onde a quantidade de acerto foi muito baixa, as expectativas eram que questões simples do questionário apresenta-se uma turma equivocada perante as respostas do teste anterior, porém este veio apenas confirmar que os alunos ali presentes realmente precisavam de um apoio para continuar confiantes no processo de ensino. Nesta fase, o objetivo era confirmar quais conhecimentos os educandos já haviam adquirido com as series anteriores. De acordo com a tabela a seguir:
Tabela 6: Gabarito do 2º questionário, com as respostas dos alunos.
Na tabela acima é fácil perceber que os alunos apresentam grandes dificuldades em relação às operações fundamentais da matemática, principalmente à subtração, multiplicação e divisão com maiores números de erros, que quando somados alcança a margem de 65,5% do resultado, os outros 34,5% que representa os acertos da turma, estão distribuídos por toda a tabela, correspondente aos 138 acertos. A figura abaixo apresenta uma melhor compreensão:
Tabela 7: Visualização Percentual com base na Tabela 6.
Respostas Quantidade Percentual Acertos 138 34,5 Erros 262 65,5 Total 400 100,0 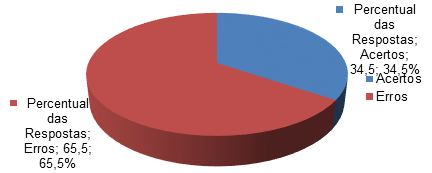
Embora os gráficos apresentem dados pouco favoráveis ao ensino, pode-se perceber na Tabela 6 que a adição é a que contém o maior número dos acertos, um total de 64 questões, por outro lado a divisão esta em alta com 84 questões erradas que estão bem representadas na tabela abaixo:
Tabela 8: Visão geral da situação de acertos e erros.
Operações Respostas Acertos Percentual Erros Percentual Adição 64 46,4 36 13,7 Subtração 40 29,0 60 22,9 Multiplicação 18 13,0 82 31,3 Divisão 16 11,6 84 32,1 Total 138 100,0 262 100,0 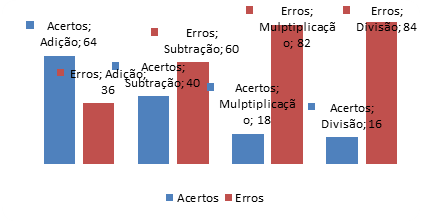
Após todas as analises feitas, o arquivamento dos resultados é muito importante para à comparação da fase seguinte, que mostrará se todas as medidas tomadas no processo de ensino estão sendo eficaz.
3.2. Metodologia de Aplicação.
Para que se tenha um bom rendimento desta fase, é necessário que os conteúdos sejam orientados de forma detalhada, com paciência e muita disposição, pois como já dito, nem todo mundo aprende com a mesma velocidade e facilidade, cada um tem seu ritmo, e quaisquer deslize do professor, poderá afetar bruscamente o aprendizado.
Primeiramente foram revisados com os alunos os conteúdos de adição, com a utilização da tradicional tabuada, exposição no quadro, representações com as cartas do baralho desenhadas no quadro para uma pequena introdução do jogo e com exercícios contextualizados com o cotidiano da turma. Veja o exemplo:
a) “Em uma pescaria, João pescou 7 peixes, enquanto seu amigo Marcos conseguiu pescar apenas 4. Quantos peixes João e Marcos pescaram juntos?”.
Trabalhar questões contextualizadas com os alunos reforça o aprendizado dando-lhes a chance de observar, e compreender onde a matemática é utilizada na maioria das vezes no cotidiano. Com o exemplo acima foi desenvolvida uma resolução utilizando a tabuada, seguida de acompanhamento no quadro com os desenhos das cartas e participação direta dos alunos. Muitos dos alunos já estavam acostumados a resolver estes tipos de problemas, o que facilito na ajuda dos demais educandos que ainda sentiam dificuldades com a soma.
Após todo preparo feito com a revisão e o apoio das cartas, foi apresentado aos discentes às regras do jogo de cartas conhecido como 21, cujas regras igualam as do projeto, porém aplicado de modo bem simples, utilizando apenas a soma como opção de alcançar os pontos desejados e a retirada das cartas conhecidas como Valetes (J), Damas (Q) e Reis (K), que serão utilizadas nas outras operações. Vale resaltar que um jogo de cartas comuns contém 52 cartas e com a retirada citada acima utilizaremos apenas 40 cartas nesta fase, lembrando que a carta representada pela letra (A), chama-se “As” e equivale ao numeral 1.
3.2.1 Iniciando a adição com as cartas do jogo.
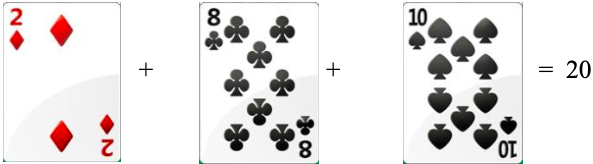
Separados 4 alunos, em volta de uma mesa, e pedindo-se para que os outros acompanhassem de perto os movimentos e instruções das regras, foi dado inicio a uma partida de apresentação do jogo orientado cuidadosamente para que não aconteça equívocos. Na regra geral todos os participantes da mesa deveriam iniciar com 3 cartas cada um, feito este processo, foi pedido para que um dos jogadores apresentasse as cartas que tinha em mãos. O mesmo apresentou as seguintes cartas:

Pediu-se que os alunos fizessem as somas utilizando os valores das cartas. Alguns ainda não tinham total habilidade para somar mentalmente, Estes utilizaram papel e lápis para realizar a soma, uma vez que só tinham aprendido a somar colocando as parcelas em alinhamento no papel, e assim visualizar de como fazer a soma. O resultado apresentado por eles deu o total de 20 pontos como esperado, o mesmo foi feito no quadro das seguintes formas:
E na forma como os educandos aprenderam, em formação de parcelas:
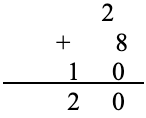
Logo em seguida foi solicitado para o segundo jogador mostra suas cartas, e assim o fez.
As cartas eram as seguintes:

Automaticamente os alunos começaram a fazer suas somas e responderam que havia 16 pontos, porém alguns não obtiveram o mesmo resultado. Foi sugerido para que os mesmo explicassem no quadro como chegara a esta conclusão, e os mesmos perceberam onde haviam errado e fizeram as correções.
Como o jogador tinha apenas 16 pontos, sugeriu-se que o mesmo poderia adquirir mais uma carta que estava ao centro da mesa, local onde são deixadas todas as cartas do jogo, que não foram entregues no início aos jogadores. Então o jogar decidiu e tomou mais uma carta pra si, obtendo uma carta maior do que a esperada.
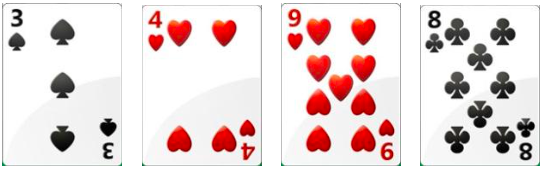
Imediatamente os alunos foram fazer a soma, chegaram ao total de 24 pontos, indicando que o jogador “estourou” o limite de pontos do jogo. Repetiu-se todo o processo com o 3º e 4º jogadores, até obter os resultados 19 e17 pontos respectivamente, dando ao 1º jogador a vitória. Formaram-se, então várias equipes espalhadas pela sala, os que já dominavam melhor o jogo e a operação de adição foram recrutados para ajudar a compartilhar seus conhecimentos entre as varias partidas consequentes.
Repetindo esse processo por mais 2 encontros com a turma, até que os mesmo encontrarem por si, o prazer de aprender brincando, houve um relato de um educando que disse ter passado o final de semana jogando junto com a família e amigos. Este fato deve ser comparado como exercício prático da educação, ajudando o aluno a fixar melhor os conteúdos, além disso, transformando o aluno em um pequeno multiplicador de conhecimento.
Durante estes passos notou-se que alguns alunos que antes precisavam anotar os cálculos no papel, já demonstravam habilidades para fazer os cálculos mentalmente, apesar de ser em poucas frequências, mais este fato corresponde a uma grande evolução nos conhecimentos adquiridos pelos educandos.
3.2.2. Introduzindo a subtração ao jogo.
O processo de ensino da subtração seguiu com a mesma metodologia utilizada da soma, mas com pequena modificação na parte de aplicação prática usando a adição e subtração para efetuação dos cálculos.
Feitas as devidas revisões de subtração com os alunos, utilizou-se aulas expositivas no quadro, com uso da tabuada, desenhos das cartas do jogo para melhor visualização e compreensão de como ocorrerá à subtração no jogo. Verificando o aprendizado dos alunos em relação à subtração, deu-se inicio a primeira aula pratica com a utilização das cartas. As regras permaneceram as mesmas, a soma feita automaticamente à medida que as cartas são retiradas, e a subtração ganha um novo aliado, a carta que representa o “Valetes” (J) agora passa a equivaler ao sinal da subtração, nesta carta foram marcadas com caneta “pilot” permanente próximo a letra J o símbolo ( – ), como mostra a figura abaixo:
Figura 5: Ilustração de marcações feitas nas cartas “Valetes” (J) com o símbolo de subtração.
Assim os alunos tiveram melhor memorização sobre a função dos valetes. Para intensificar e ficar mais frequente os cálculos com o uso da subtração, foram acrescentados ao conjunto de cartas, mais 15 cartas de valetes, passou-se a utilizar nesta fase o total de 55 cartas.
3.2.2.1. Subtraindo com as cartas.
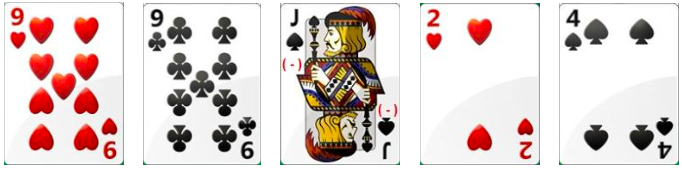
Novamente foram separados 4 alunos em volta da mesa, pedindo-se para que os demais acompanhem os passos e regras. Dadas as 3 cartas aos alunos da mesa, Solicitou-se que a primeira pessoa mostrasse suas cartas e fizesse os cálculos. Este tinha em mãos a carta (2, 9, J). Ficando então sem opção de resposta, sugeriu-se que o mesmo anotasse em um caderno as opções de cálculos que poderiam ser feitos, exemplificadas abaixo:
(9 J 2), equivalente a (9 – 2) = 7(9 2 J), equivalente a (9 + 2 –) = 11 –
Analisando as opções acima, se percebeu que deveriam buscar mais cartas para si, adquirindo outra carta 9, que em seguida reformulou as posições das fórmulas para as seguintes posições:
(9 9 J 2) = 16, equivalente a (9 + 9 – 2) = 16(9 9 2 J) = 20 –, equivalente a (9 + 9 + 2 –) = 20 –(9 J 9 2) = 2, equivalente a (9 – 9 + 2) = 2
Decidido a parar com a segunda opção (20-), foi mencionado que o cálculo estaria incompleto e que o mesmo deveria completá-la. Tomou mais uma carta com o valor 4 que rapidamente reagrupou as opções com a nova carta.
(9 9 J 2 4) = 20, equivalente a (9 + 9 – 2 + 4)= 20(9 9 2 J 4) = 16, equivalente a (9 + 9 + 2 – 4)= 16 (9 J 9 2 4) = 2, equivalente a (9 – 9 + 2 + 4) = 2
Preferindo não arriscar mais na sorte, foi decidido que iria parar com a primeira opção, ilustrada na figura abaixo:
Dando continuidade, foi feito o mesmo procedimento de raciocínio com os cálculos do jogo, onde o 2º e 3º jogadores apresentaram os resultados de:
(1+10+7+7-6=19) e (8+10-6+8+2=22) respectivamente.
As imagens abaixo mostram as organizações feitas pelos próprios alunos sem a intervenção do orientador:


Ocorreu um fato curioso com o 4º jogador, porém já esperado, o mesmo obteve as cartas (3, J, J) em mãos.“O que faremos neste caso?”. Mencionaram os alunos precipitadamente. Orientou-se que as mesmas fossem arranjadas de modo a encaixar-se nas opções de cálculos que estavam por vir, com a aquisição de novas cartas.
À medida que as cartas eram obtidas, a turma ajudava ao jogador a configurar as cartas na melhor posição, por fim surgiu uma configuração surpreendente, para a alegria e comemoração de toda a turma, Como na figura abaixo:

Com esta sequência o 4º jogador vence a partida com um total de 21 pontos. Observe o raciocínio da turma com o seguinte calculo:
(9, 6, 5, 4, 3, J, 2, J,4) = 21, equivalente a (9+6+5+4+3-2-4) = 21
A participação dos alunos que antes eram apenas espectadores foi de grande importância para decidir esta partida, e principalmente para mostrar o quanto os alunos se deixam envolver com aulas práticas e diferenciadas.
Dividiram-se em grupos pela sala e estes passos foram repetidos durante 3 encontros consequentes, foram passados vários exercícios de fixação de resolução em casa. No encontro seguinte deu-se inicio nas operações de multiplicação, e era necessário que ao final desta fase, todos já tivessem domínio da adição e subtração.
3.2.3. Incrementando a Multiplicação nos jogo.
Por ser uma operação em que poucos alunos ao iniciarem, conseguiram visualizar a multiplicação como uma sequência de somatórias, por exemplo:
4 x4=16 ou 4+4+4+4=16.
É importante lembrar que nesta fase o raciocínio desenvolvido anteriormente não deveria ser modificado.
Para dar início ao processo de aprendizagem dos alunos, foi utilizado na revisão, a tabuada como ponto de apoio, exercícios demonstrativos básicos de operações contextualizadas em forma de problemas, desenhos ilustrativos das cartas no quadro e bastantes exercícios de fixação. Este procedimento durou 4 encontros, até que os alunos perderam o receio que tinham sobre a multiplicação e se sentiram convictos em responder as operações.
Repetindo as técnicas utilizadas durante a soma e subtração, a multiplicação foi separada por duas etapas para garantir a eficácia do ensino de multiplicações, a fim de prepara-los para a nova fase.
a) Somente multiplicação com a nova carta Damas (Q).
Nesta etapa as regras são as seguintes: ficou proibida a utilização da soma e da subtração, retiraram-se todas as cartas Valetes do escrínio, tomando apenas as 40 cartas numeradas. Os alunos deveriam conseguir os 21 pontos ou mais próximo possível, utilizando apenas a multiplicação. Foram expostos desenhos ao quadro ensinando como agir com as cartas adquiridas. As figuras 10 e 11 representam uma parte do que foi demonstrado no quadro:

Explicação:
Têm-se as seguintes cartas (2, 5, 2), e pelas regras da multiplicação já estudadas, a ordem dos fatores não altera o resultado. Obtendo-se o produto dos fatores (2 x 5 x 2) a quantia é de 20 pontos.
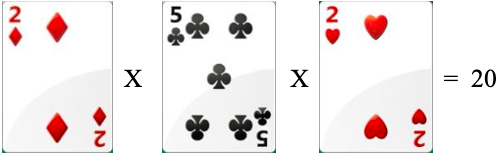
Exemplos como este foram apresentados à turma com intuito de ensinar o processo de multiplicação com as cartas. Seguidos de apresentação da nova carta “Damas” (Q), que recebeu marcações com caneta permanente o símbolo da multiplicação (x), como na imagem abaixo:
Figura 12: Marcação do símbolo de multiplicação nas cartas “Damas” (Q).
Orientou-se que a partir daquele momento em diante, a utilização da carta acima seria o meio de multiplicar os valores das outras cartas e que seriam necessários 4 alunos para fazer a primeira aplicação prática com o jogo, e que precisariam que todos da sala observassem as instruções feitas aos colegas. Sobre as regras, continuaram as mesmas, todos os cálculos seriam feitos somente com a multiplicação, e que as Damas serviriam para orientá-los na visualização das operações.
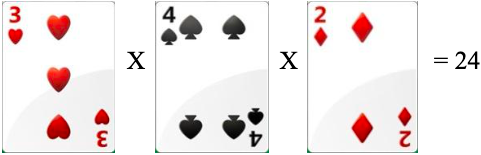
Os passos da aplicação com a soma e a subtração serviram de exemplos para os alunos, que nesta altura já sabiam o que fazer, e começaram a jogar. O primeiro jogador exibindo suas cartas formulou a operação:
(3 x 4 x 2) = 24.
O segundo jogador recebeu as cartas (8, Q, A). Este tomou para si outra carta (5) formulando a seguinte operação, e abaixo a demonstração pela imagem:
(8, Q, A, 5), equivalente a (8 x 1 x 5) = 40

O 3º e 4º jogadores procederam de maneira semelhante aos dois primeiros, obtendo valores acima do esperado respectivamente 192 e 448, não havendo vencedor. As medidas aqui tomadas, na realidade não eram para obter os 21 pontos, e sim exercitar a multiplicação com o uso das cartas. Prevendo o procedimento para o próximo passo.
Assim deu-se continuidade com a divisão da sala em várias equipes para exercitar o que haviam aprendido. Neste exato momento, percebe-se a euforia dos alunos para iniciar o passo seguinte, que se deu o mais breve possível.
b) União da soma, subtração e multiplicação no jogo:
Este passo tem como metodologia a utilização de todas as cartas trabalhadas anteriormente e com o uso das operações de adição, subtração e multiplicação. As regras foram orientadas a turma, em que a soma era feita automaticamente, a subtração com o auxilio dos Valetes (J) e a multiplicação com o uso das Damas (Q). Seguindo o procedimento da fase anterior, convocaram-se 4 educandos para aplicação das novas medidas.
Distribuídas as três cartas aos alunos participantes da demonstração, foi solicitado que o primeiro jogador apresentasse suas cartas, composta por: (10, 5, 3), que pelo presente instante será calculado utilizando a adição.
(10, 5, 3), equivalente a (10 + 5 + 3) = 18
Decidido obter mais uma carta, acrescentou ao seu jogo uma Dama (Q), que em poucos segundo reformulou seu jogo para (10, 5, 3, Q), tornando a buscar mais uma carta, que por sorte consegui um Valete(J). Orientou-se que o mesmo deveria reformula as posições das cartas para obtenção do menor ponto possível. Que com ajuda dos alunos que observavam chegaram a seguinte formação:
5, J, 3, Q, 10, equivalente a 5 – 3×10 = 20
O cálculo acima é um equivoco que deve ser desconsiderado no momento, pois observando a configuração da formula, obtêm-se:
(5 – 3×10) =- 25
Portanto, o que valida o cálculo do aluno, é como este apresenta as cartas sobre a mesa, Como a formação feita na figura abaixo:

Analisando a Figura 15, a disposição das cartas apresenta uma formação semelhante a uma pequena operação matemática:
[(5,J,3), Q, 10], equivalente a [(5 – 3)x10] = 20
Desta forma, ficou provado que a sequência lógica apresentada pelo educando estava correta, e que sem perceberem, estavam dando os primeiros passos para aulas futuras, evolvendo operações da matemática e futuramente álgebra. Este procedimento foi explicado aos alunos com a intenção de introduzir a relação de operações e suas propriedades, mas sem aprofundamentos para não atrasar o cronograma, pois em alguns dias os mesmos estariam entrando em semana de avaliação com os professores.
Os procedimentos com os demais jogadores foram os mesmo, e cada um chegou a uma formação valida mediante comprovação. Tendo como formação:
- O 2º jogador, (7, J, 3, 8, 9, J, 2) = 19,equivalente a (7-3+8+9-2) = 19;
- O 3º jogador com, (10, Q, 4) = 40, equivalente a (10×4) = 40;
- O 4º jogador dispondo das cartas, (5, Q, 6, Q, 10) = 300, equivalente a (5x6x10) = 300.
Dando a vitória ao primeiro jogador. Os passos citados acima foram reconstruídos por mais dois encontros, iniciando-se logo em seguida as operações com divisão.
3.2.4. Primeiros passos para divisão
A revisão dos conteúdos antes de adentrar-se a aplicação, é de suma importância para um bom desempenho dos alunos. Na divisão deve-se demonstrar que esta operação é inversa a multiplicação, utilizando exemplos que comprovem este fator. Como por exemplo:
81÷9 = 9 9 x 9 = 81
Este tratamento especial com os alunos deu melhor resultado na assimilação quanto às duas operações, facilitando o processo de ensino. Assim sucedeu-se a revisão feita nesta fase, com a utilização da tabuada, exposições ao quadro, desenhos das cartas para introdução ao jogo e questões contextualizadas. E durante todos os encontros, foi apresentado exercícios de fixação como tarefas para casa.
O progresso de aplicação com o jogo ocorreu com a seleção de 4 alunos, para o primeiro exemplo de introdução as cartas, por ser um conteúdo em que os discursos deverão ser bem elaborados, e qualquer equivoco afetará na concepção de informações dentro do ensino, e que o restante dos alunos observassem as orientações. Assim como na multiplicação, foram orientados por duas etapas:
a) Somente cálculos com divisão
Figura 16: Marcações feitas nas cartas Reis (K) com o símbolo de divisão.
Neste passo, removeram-se as cartas Valetes e Damas, apresentando uma nova carta conhecida como “Reis” (K), que receberam marcações com caneta permanente o símbolo da divisão (÷), como na figura acima, que em seguida foram adicionadas mais 15 cartas ao conjunto formando o total de 55 cartas. As regras adotadas permitiriam que os cálculos fossem feitos em forma de sucessivas divisões, sem o uso das demais operações, estimulando os alunos a exercitarem um pouco mais a divisão, com mudanças na pontuação, onde o campeão deveria ter o menor valor da rodada, e estes receberiam apenas 2 cartas iniciais.
Inicia-se a partida solicitando ao primeiro jogador, que exponha suas cartas à mesa. Tendo as seguintes cartas (9,3), solicitou-se que os observadores deveriam junto a ele, calcular as divisões. Em pouco tempo apresentaram a resposta, veja o exemplo e a figura abaixo:
(9÷3) = 3
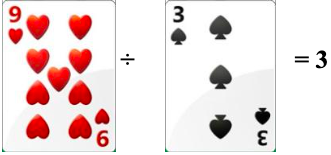
O segundo jogador, que havia retirado as cartas (10, K), percebendo que suas cartas estavam incompletas, obrigou-o a adquirir uma nova carta, orientou-se que os observadores deveriam lhe ajudar, e após a aquisição da carta (2), efetuaram a divisão abaixo:
(10, K, 2=5), equivalente a (10÷2) = 5

Diante das cartas (8, 5), apresentadas pelo terceiro jogador, deixou todos com duvidas, pois até o momento não havia sido trabalhado divisão com números decimais. Foi orientado que se esperava um resultado em números inteiros, e que a divisão das referidas cartas apresentariam um número não exato, contendo “resto” e que não seria necessária até o momento a resolução, pois este conteúdo estaria por vir em seu currículo escolar.
Apresentou-se no quadro a resolução da divisão acima, onde:
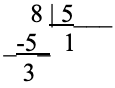
Com a resposta acima, todos decidiram que o jogador tomasse pra si novas cartas, este recolheu três cartas (K, 4, 5), os mesmos foram locados de tal modo deixando o grupo conformado. A figura abaixo mostra o posicionamento das cartas e sua resolução de cálculo.
8, 4,K,5,5=2, equivalente a 8÷45÷5=2

Solicitou-se ao quarto jogador para expor suas cartas, iniciando com (6, K). A turma logo o fez pegar mais uma carta para dar continuidade no jogo, vibrando de alegria por ter apanhado outra carta (6), a turma toda comemora a vitória inesperada do ilustre Sr. Antonio, antes citado pela bela frase argumentada.
Vale resaltar que durante todo o processo, tanto de ensino quanto de aplicação, a turma estava sempre ansiosa, e percebia-se a alegria de aprender e ter conquistado novos conhecimentos, que com toda certeza fará a diferença em suas vidas. Este método tornou a se repetir durante 4 encontros, seguidos de exercícios de fixação.
b) Usando as 4 operações matemática.
Este sem duvidas é o passo mais esperado por todos os participantes, desde alunos, orientadores e professores que acreditaram na evolução dos educandos. Por mais complexo que pareça a utilização das operações em um único jogo, fica bem claro que isto é mera impressão, pois na concepção dos alunos recém-orientados com um trabalho de muito esforço e dedicação, fez destes capazes de resolver questões matemática, dantes inalcançáveis.
Os parâmetros adotados nesta etapa têm como apoio as regras do jogo (vide Apêndice B), e as estratégias criadas por cada aluno para resolverem os cálculos necessários pra levá-los à vitória. Assim, deu-se inicio com as formações de varias equipes separadas pela sala, cada grupo tinha seu escrínio de cartas para não atrapalhar a equipe ao lado, e juntos desenvolveram em várias partidas o trabalho em equipe, onde os colegas da mesa ajudam o parceiro com dificuldades, sempre os orientando de que só valeria cálculos utilizando todas as operações presentes na rodada.
Observou-se uma equipe, para explicar como fariam para chegar aos 21 pontos. Pedindo-lhes para que um da equipe exibisse suas cartas, que ao fazer tinha em mãos: (5, J, 8), sugeriu-se que o mesmo fizesse a operação que achava necessário, e encontrou o valor de (8 – 5) = 3 pontos, direcionando a mão ao centro da mesa para obter outra carta. O jovem adquiriu mais uma carta (8), reformulando suas cartas obteve:
(8 + 8 – 5) = 11 pontos
O que fez com que continuasse a buscar mais cartas colhendo uma Dama (Q), que representa a multiplicação, parou para pensar um pouco, decidindo buscar mais uma carta. Com a nova carta de valor (2), calculou a seguinte expressão:
[(8×2) + (8-5)] =19
Decidindo a parar com apenas as cartas que estavam em mãos, dando oportunidade ao próximo jogador.
Analisando o raciocínio do aluno, o mesmo demonstra total controle e confiança para manusear o jogo e calcular as sequências criadas, Solicitou-se que o mesmo representa se ao quadro como desenvolveu as sentenças.

Figura 20: Ilustração de desenhos feitos pelo aluno no quadro.

Desenhando no quadro observado na figura acima, o jovem exemplificou a disposição das cartas, seguido da operação utilizada para chegar aos 19 pontos. Este desenvolvimento sucedeu-se pelo restante da equipe, seguidos da liberação dos demais grupos para prática de todo conhecimento adquirido, sempre resaltando que o objetivo era a aprendizagem.
3.3. Resultados da Aplicação.
Com a aplicação do mesmo questionário utilizado no reconhecimento da turma (vide Apêndice D), coletaram-se os dados que dão base a conclusão deste sobre o desenvolvimento do aprendizado dos alunos.
Os dados da Tabela 9 e 10 apresenta a evolução dos conhecimentos adquiridos pelos discentes, seguido do gráfico para facilitar a interpretação.
Tabela 9: Gabarito com as respostas dos alunos em Teste Final.
Tabela 10: Estimativas de acertos e Percentual em relação ao primeiro teste.
Teste Questões Acertos Percentual Erros Percentual Teste inicial 400 138 34,50 262 65,50 Teste Final 400 377 94,25 23 5,75 Variação 239 59,75 239 59,75 
De acordo com os dados, nota-se que o índice de acertos em geral, teve um aumento considerável em relação ao teste aplicado na fase de reconhecimento, isto representa um progresso de 34,5% para 94,25% de questões corretas.
Na tabela e gráfico seguintes constatou-se rendimento exuberante de experiência dos educandos após aplicação do projeto, especialmente nas operações de multiplicação e divisão, sendo a divisão a que continha o índice mais alto de erros, caindo de 84 para 12 questões incorretas.
Tabela 11: Demonstrativo da variação de acertos na divisão.
Teste Questões Acertos Erros Teste inicial 100 16 84 Teste Final 100 88 12 Variação 72 -72 
4. CONSIDERAÇÕES FINAIS
Diante de tais resultados, constata-se que houve melhor desempenho da turma, o que faz crer que a metodologia utilizada tem efeitos diretos na aprendizagem, e que a conduta das informações de modo geral, deve ser levada com seriedade. O grau de compromisso do professor é o que faz a diferença e eficácia dos resultados. Mas é importante trabalhar a curiosidade dos alunos, para que os mesmos estejam sempre atentos às orientações, estimulando-os e levando sempre ao alcance dos objetivos propostos.
O lúdico na educação atual vem como uma grande ferramenta de apoio ao professor que deseja inovar na sala de aula, com metodologias diferenciadas, atraentes, quanto agradáveis no aprendizado, sendo um suporte de aplicação para a enorme gama de conteúdos, não só de matemática, mas sim no que se refere à educação em geral, seja esta para jovens e adultos como na educação infantil.
REFERÊNCIAS
BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1997.
______. Ministério da Educação. Leis de Diretrizes e Bases da Educação Nacional. 5. ed. e-book, 2010. Disponível em: <http://bd.camara.gov.br/bd/bitstream/handle/bdcamara/2762/ldb_5e
d.pdf>. Acesso em: 30 nov. 2012
______. MEC. Diretrizes Curriculares para EJA. Parecer 11/2000 – CNE/MEC. Disponível em:<http://portal.mec.gov.br/secad/arquivos/pdf/eja/legislacao/parecer_11_2000.pdf>. Acesso em: 30 nov. 2012.
______. Ministério da Educação. Plano Nacional de Educação. PL 8.035/dezembro de 2010. Disponível em: <http://bd.camara.gov.br/bd/bitstream/handle/bdcamara/5826/projeto_pne_2011_2020.pdf?sequence=1>. Acesso em: 30 nov. 2012.
CORBALÁN, F. Juegos matemáticos para secundaria y bachillerato. Madrid: Sintesis.1994. In: SANT’ANNA, Alexandre; NASCIMENTO, Paulo Roberto de. A história do lúdico na educação. REVEMAT, Florianópolis, v. 6, n. 2, p.19-36 2011. Disponível em: <https://www.google.com.br/url?sa=t&rct=j&q=&esrc=s&source=web&cd=5&cad=rja&ved=0CFoQFjAE&url=http%3A%2F%2Fwww.periodicos.ufsc.br%2Findex.php%2Frevemat%2Farticle%2Fdownload%2F1981-1322.2011v6n2p19%2F21784&ei=Ppb0UOf7MYTg8ASSsYDICQ&usg=AFQjCNGoeXPFDdeV9GCKIiFpaZYuWLleTA&sig2=jTETgBj_PeqxHgNLBZdNIA&bvm=bv.1357700187,d.eWU>. Acesso em: 14 jan. 2013.
DUARTE, Newton. O ensino da matemática na educação de adultos. 7. ed. São Paulo: Cortez,1995.
FALCÃO, Gérson Marinho. Psicologia da aprendizagem – Série Educação, 10. ed. 2. imp. São Paulo: Ática, 2000.
KISCHIMOTO, T. M. Jogos tradicionais Infantil: O jogo, A Criança e a Educação. Petrópolis: Vozes, 1993.In: VASCONCELLOS, Sheila, Uma Breve História do Lúdico na Educação. História na Cozinha, Art., jan. 2011. Disponível em: <http://ogastronomo.files.wordpress.com/ 2011/01/artigo-lc3badico-na-educac3a7c3a3o.pdf >. Acesso em: 18 mai. 2012
LOPES, Selva Paraguassu; SOUSA, Luzia Silva. EJA: uma educação possível ou mera utopia?. Art. mar. 2005. Disponível em: <http://www.cereja.org.br/pdf/revista _v/revista_selvaplopes.pdf>. Acesso em: 17 dez. 2012.
SANT’ANNA, Alexandre; NASCIMENTO, Paulo Roberto de. A história do lúdico na educação. REVEMAT, v. 6, n. 2, p.19-36 Florianópolis, 2011.
VYGOTSKYI, L. S. A formação social da mente. 6. ed. São Paulo: Martins Fontes, 1998.
