MUSICAL FUN AS A STRATEGY FOR THE ASSIMILATION OF THE RULES FOR NOTABLE PRODUCTS IN THE 8TH GRADE
REGISTRO DOI: 10.5281/zenodo.8136100
Francisco das Chagas Vieira¹
Maria Luciana Carneiro de Araújo²
Francisco Wesley Araújo³
Ana Paula Olivindo Rocha4
Márcio José Alves da Silva5
Micael Pereira da Cruz6
Josué Amaral Gomes7
RESUMO
A Matemática é encarada por muitos alunos como uma disciplina complicada devido à forma mecânica que se trabalha alguns conteúdos. Por conta desse contexto, surge a preocupação com a desmotivação e a não assimilação de algumas regras, como a dos produtos notáveis, vistas no Ensino Fundamental II. Na tentativa de fazer com que essas fórmulas sejam aprendidas com rapidez e facilidade, desenvolveu-se um trabalho usando a estratégia do uso de música e o manuseio de material concreto com a turma do o 8º ano do Colégio Tenente Ângelo de Siqueira Passos. Com essa atividade, percebeu-se que é necessário quebrar tabus na maneira tradicional de se trabalhar a Matemática para que haja um maior entendimento dos conteúdos por parte dos alunos e que o uso do lúdico musical se enquadra perfeitamente dentro deste contexto além de oferecer um maior dinamismo às aulas. No caso dos produtos notáveis, a música, que ajuda a fixar suas regras, é encarada como um jogo que associa a melodia com a fórmula e com o concreto quando se usa o dimensional geométrico como recurso prático. Além disso, criar situação problema dentro do contexto atual do aluno só vai enriquecer o processo ensino-aprendizagem. Dessa forma, aproximando a Matemática do que é espontâneo, como sugere a pedagogia da Etnomatemática de D’Ambrósio, o aluno se vê estimulado e apto ao que se propõe.
PALAVRAS-CHAVE: Lúdico. Musical. Regras. Produtos Notáveis. Matemática.
ABSTRACT
Mathematics is viewed by many students as a complicated discipline due to the mechanical form that some content works. Because of this context, there is concern about the lack of motivation and the non-assimilation of some rules, such as the remarkable products, seen in Elementary Education II. In an attempt to get these formulas learned quickly and easily, a work was developed using the strategy of using music and the handling of concrete material with the group of the 8th year of Senteira Passos College. With this activity, it was noticed that it is necessary to break taboos in the traditional way of working in Mathematics so that there is a greater understanding of the contents by the students and that the use of musical entertainment fits perfectly within this context besides offering a greater dynamism to class. In the case of notable products, music, which helps to establish its rules, is seen as a game that associates the melody with the formula and with the concrete when using the geometric dimensional as a practical resource. In addition, creating problem situation within the current context of the student will only enrich the teaching-learning process. Thus, by bringing the Mathematics closer to what is spontaneous, as the pedagogy of D’Ambrósio’s Ethnomathematics suggests, the student finds himself stimulated and apt to what he proposes.
KEYWORDS: Playful. Musical. Rules. Notable products. Mathematics.
1. INTRODUÇÃO
A palavra ludicidade tem sua origem no latim “ludus” que quer dizer “jogo”. Porém, jogar em si não é o único objetivo que se propõe. O jogo aqui vem a ser um meio e não um fim e a música, que não deixa de ser também uma espécie de jogo, vêm a ser, neste caso, uma aliada da matemática na fixação de regras e fórmulas.
Diante da complexidade que parece ser o ensino de Matemática, o jogo vem se encaixar como um recurso facilitador da aprendizagem de seus conteúdos e até de outras disciplinas. Quem aprende brincando fixa melhor o conteúdo, pois o jogo transmite felicidade e acaba sendo um desafio que qualquer um, criança e até adulto gosta de vencer ou conquistar.
Trabalhar com jogos é uma estratégia inovadora que está tendo boa aceitação e repercussão no campo da educação, porém, ainda há professores que sentem dificuldades em fazer este trabalho, talvez pela própria formação que tiveram, ainda nos moldes tradicionais.
É preciso ser flexível e reconhecer que se vive novos tempos e, portanto, não se pode descartar esta chance de fazer com que a Matemática deixe de ser uma disciplina elitista, repressora, para ser um objeto de prazer, em que o automatismo dê vez ao dinamismo.
Prender a atenção dos alunos para a Matemática não é fácil, hoje em dia, principalmente quando essas aulas são marcadas por uma abstração muito forte. Aulas desconectadas de fatos reais e concretos deixam o aluno mais disperso, ocioso e desinteressado. Os alunos gostam e preferem aulas diferentes. A metodologia rotineira, sala de aula com professores escrevendo e o aluno copiando está ultrapassada e não desperta no aluno nenhum estímulo nem interesse de prestar atenção e aprender o que o professor está ensinando.
D’Ambrósio, o Pai da Etnomatemática, vê essa realidade mórbida passível de mudança. Segundo ele,
Os professores precisam aproximar a disciplina do que é espontâneo, deixar a criança à vontade, propor jogos, distribuir balas, objetos, para que o aluno se sinta bem. A criança adquire habilidades para a matemática em casa, no meio em que vive. Cada um tem um modo próprio de aplicá-lo. Só que na escola dizem que a matemática não se faz do jeito de casa. Rechaçam esse conhecimento que o aluno traz e isso cria conflitos (2005, P.99).
De fato, o profissional da educação que não valoriza a “bagagem” discente e só aceita o que é culto, está cometendo um grande erro, tornando-a restrita e frustrando a expectativa de muitos alunos.
D’Ambrósio afirma também que “… há outros pilares da sociedade que estão sendo colocados de lado, como as relações humanas que estão ofuscadas pela busca por uma melhor matemática”. Sendo assim, a Matemática também precisa fazer um resgate de valores, dentro de um contexto interativo com outras disciplinas.
Este trabalho partiu, inicialmente, de um estudo bibliográfico mais aprofundado ao que se refere o lúdico e sua aplicabilidade no ensino da matemática. Para esse apanhado foi utilizado como embasamento teórico autores como: D’Ambrósio, Moura, Kishimoto, Ducourneau, Dante.
O objetivo foi analisar o uso do lúdico musical como forma de melhorar o entendimento e a assimilação do conteúdo de produtos notáveis pelos alunos do 8º ano único da escola Colégio Tenente Ângelo de Siqueira Passos, localizada à Rua Francisco Caldas da Silveira, nº 180, na cidade de Viçosa do Ceará.
Para o desenvolvimento deste trabalho recorreu-se à atividade lúdica por esta ser considerada por muitos estudiosos uma ferramenta eficiente no processo ensino aprendizagem e uma grande aliada da matemática. Jogos, músicas, situações problema interessantes, em clima contextualizado, são instrumentos que favorecem a aprendizagem matemática de forma lógica, rápida e assertiva. Através do lúdico, a criança se vê, portanto, estimulada no que deve aprender.
2. REFERENCIAL TEÓRICO
2.1. Matemática abstrata ou espontânea
O conhecimento, hoje, passa por uma evolução marcante. A educação também vive momentos que alertam para novas posturas quanto ao processo ensino aprendizagem. E, a Matemática, sendo a ciência exata que é, não deve ser trabalhada de forma mecânica e abstrata.
Aragão considera que:
A matemática é uma ciência muito complexa por ser exata. A ciência exata requer atenção especial e disciplina na sua aplicação, o que faz com que muitos alunos apresentem certa dificuldade no momento da sua aprendizagem e execução.
Estudos comprovam que a grande maioria dos alunos, principalmente no inicio dos estudos do ensino fundamental, não entendem a matemática com facilidade e demoram um certo tempo para compreender a importância que a aprendizagem da disciplina representa na vida cotidiana. (2009, p. 3)
Isso, de fato, verifica-se. E quando o professor não assume uma verdadeira postura de educador, através de metodologias inovadoras, acaba contribuindo com uma situação frustrante em que o aluno, sentindo-se desmotivado, não apresenta bons rendimentos escolares, torna-se faltoso e até evadindo do ambiente escolar.
D’Ambrósio, citado na Revista na Escola – Diário do Grande ABC (31/10/2003) diz que “o ensino de matemática assumiu a postura de se encaminhar para o abstrato e se libertar do espontâneo” e acrescenta que “é necessário um grande esforço dos educadores modernos para que a matemática deixe de parecer tão complexa e elitista”.
Matos, citado por Tahan (1966, p. 21) “incube ao professor, criar em suas aulas, um ambiente estimulador e sadio de compreensão, onde atividades interessantes sejam capazes de despertar nos alunos uma maior atenção”.
Complementando estas ideias, D’Ambrósio (2003, p. 19), diz que “O ensino de matemática não deve ser hermético nem elitista. Deve levar em consideração a realidade sócia cultural do aluno, o ambiente em que ele vive e o conhecimento que ele traz de casa”, pois segundo ele (D’Ambrósio), “Quando o aluno chega à escola ele traz experiências de casa, traz o conhecimento de jogos, de brincadeiras, pois já viveu sete anos produtivos e criativos”. E concluindo sua ideia, o autor considera que “… o natural seria a matemática ser tratada como um conhecimento presente em todas as coisas do cotidiano das pessoas”.
Com essas ideias, defendidas aqui, precisa-se pensar, urgentemente, em novas estratégias de ensino que torne o estudo de matemática prazeroso e frutífero. Não basta seguir o livro didático; é preciso dar significado aos conteúdos, associando-os à vivência do aluno, através de metodologias dinâmicas.
Piaget, (citado em Wikipédia – Educação Matemática – fev, 2008) outro pensador, dentro de uma postura construtivista, acredita também que: “A metodologia de resolução de problemas em educação matemática visa tirar o aluno de sua tradicional postura passiva em sala de aula, para uma postura ativa e interessada e desconstruir a noção de que a matemática é algo pronto e acabado”. Sua visão revela que, a matemática, mesmo sendo uma ciência exata, contém uma infinidade de situações problemas que devem ser associadas a fatos e temas do dia-a-dia, que tornam o aprendizado significativo.
2.2. Jogos: quando e por que usá-los?
Para Antunes (1998, p. 30), “A utilização dos jogos devem ser somente quando a programação possibilitar, e somente quando se constituírem em um auxílio eficiente, ao alcance de um objeto dentro dessa programação”.
Nesse caso, o jogo deve ser encarado como um desafio que requer planejamento com objetivos bem traçados para não se constituir em apenas passa tempo, mas num verdadeiro suporte pedagógico. Não basta jogar durante as aulas de matemática. É preciso ver se o ambiente realmente é favorável e se o jogo contempla de fato o que se quer trabalhar.
Para, Kishimoto:
O jogo, na educação matemática, passa a ter o caráter de material de ensino quando considerado promotor de aprendizagem. A criança colocada diante de situações lúdicas aprende a estrutura lógica da brincadeira e, desse modo, aprende também a estrutura da matemática presente. O jogo deve estar carregado de conteúdo cultural e assim o seu uso requer certo planejamento que considere os elementos sociais em que se insere (1994, p. 80).
Segundo Lara (2003, p. 23), “utilizaremos jogos no ensino da Matemática com a pretensão de resgatar a vontade de aprender e conhecer mais sobre essa disciplina, eliminando sua áurea de “bicho-papão”. Com essa proposta, a autora acredita que até o ambiente de sala de aula sofra mudanças, mudando a rotina de todos os dias, levando o/a aluno/a a ter um envolvimento maior com as atividades propostas.
Já Antunes (2002, p. 155-156) afirma que “É fundamental enfatizarmos a importância do professor literalmente “trazer a rua e a vida” para a sala de aula, fazendo com que seus alunos percebam os fundamentos da matéria que ensina na aplicação da realidade”. Neste caso, o papel do professor é contextualizar os conteúdos para tornar a sala de aula um ambiente propício ao desenvolvimento integral do aluno, despertando não só o caráter cognitivo, mas também o emocional e o social, o econômico etc.
Na visão de Borin (1996, p. 9), “Outro motivo para a introdução de jogos nas aulas de matemática é a possibilidade de diminuir bloqueios apresentados por muitos de nossos alunos que temem a matemática e sentem-se incapacitados para aprendê-la”.
Verifica-se, portanto, de acordo com esses contextos, que os jogos são de fato importantes porque abrangem não só o caráter lúdico, mas ajudam o aluno a se relacionar melhor com os seus colegas e a memorizar certas técnicas que facilitam a aprendizagem.
Os PCNs também enfatizam que:
- No ensino da Matemática destacam-se dois aspectos básicos: um consiste em relacionar observações do mundo real com representações (esquemas, tabelas, figuras); outro consiste em relacionar essas representações com princípios e conceitos matemáticos.
- A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.
- Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática.
Diante do que os PCNs colocam, percebe-se que a Matemática não é complexa; é lógica e por isso requer uma prática que propicie, por meio de brincadeiras, músicas, jogos um ambiente favorável à aprendizagem.
2.3. Como memorizar as regras dos produtos notáveis?
Segundo Campagner (2009, p. 35), “alguns produtos algébricos (com incógnitas, tipo a.b, x.y) aparecem com freqüência nos cálculos. Em vez de fazer a multiplicação gradativa e lenta de polinômios a cada vez que essas operações aparecem, vale a pena memorizar suas fórmulas”. Trata-se dos produtos notáveis: Quadrado da soma de dois termos: (a + b)2 = a2 + 2ab + b2 que também pode ser representado da seguinte maneira: (a + b)2 = (a + b) (a + b) e de acordo com a regra de multiplicação de polinômios:

Quadrado da diferença de dois termos: (a – b)2 = a2 – 2ab + b2 ou (a – b)2 = (a – b)(a – b) ou novamente segundo a regra:

Produto da soma pela diferença de dois termos: (a + b)(a – b) = a2 – b2 ou se preferir é só usar a multiplicação:

Os produtos notáveis também podem ser incrementados no estudo das equações de 2º grau, vista com mais detalhes no 9º ano.
Imagine a equação: x2 – 6x + 9 = 0. Ela pode resolvida com o auxílio da fórmula de Bhaskara:
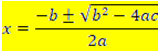
ou pela transformação do trinômio num produto notável – o quadrado da diferença de dois termos, como se vê: x2 – 6x + 9 = (x – 3)2. Logo: (x – 3)2 = 0 ou (x – 3)(x – 3) = 0
Essa forma de encarar a resolução de uma equação do 2º grau dá nesse estudo um caráter prático, levando muitos dos alunos a ter uma melhor compreensão.
2.3.1. Memorizando com música:
Como não é fácil memorizar fórmula nenhuma ou regra, a música pode ser usada como recurso de facilitação.
Ongaro (2006, p. 29) afirma que “A música torna-se uma fonte para transformar o ato de aprender em atitude prazerosa no cotidiano do professor e do aluno”.
Ducourneau (1984, p. 47), diz que “No contexto escolar a música tem a finalidade de ampliar e facilitar a aprendizagem do educando, pois ensina o indivíduo a ouvir e a escutar de maneira ativa e refletida”.
(MURPHEY, 1990, p. 48) considera que “O fenômeno “A música ficou na minha cabeça” também parece reforçar a ideia de que as canções funcionam em nossa memória a curto e em longo prazo”. De fato, quando a música é interessante se canta mesmo sem querer.
Já para Fernandes (2004, p. 6), “trabalhar com música na Educação é um fazer artístico. Os ganhos que a prática musical proporciona, seja pela expressão das emoções, pela sociabilidade, pela disciplina, pelo desenvolvimento do raciocínio, são valiosíssimos, e para a vida toda” e para a professora Míria Therezinha Kolling, diz Fernandes (2004), “A música é uma força geradora de vida, uma energia que envolve o nosso ser inteiro, atuando de forma poderosa sobre o nosso corpo, mente e coração”.
Dar vida aos ensinamentos é o que se quer. E, se é possível fixar os conteúdos através do lúdico musical, então, unir a arte do cantar à assimilação e memorização das regras é uma metodologia que deve ser empregada sempre que possível.
2.3.2. Produtos notáveis: uma visão geométrica
Dante (2003, p. 165-168) sugere o estudo dos produtos notáveis tomando por base a explicação geométrica quando:
a) o quadrado da soma de dois termos (Fig.1) representa a área total do quadrado.a
b) o quadrado da diferença de dois termos (Fig.2) representa a área apenas do quadrado hachurado.
c) o produto da soma pela diferença de dois termos (Fig.3) representa a área da região hachurada.
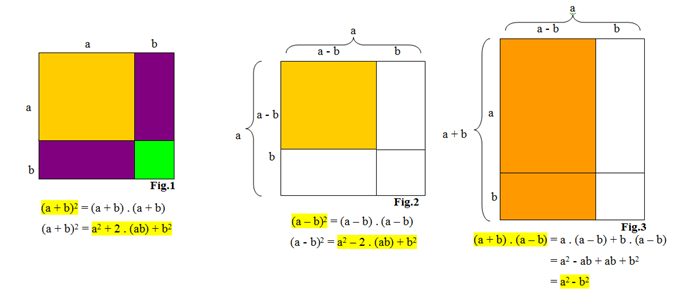
Assim, fica mais fácil compreender a origem e o porquê de cada regra. Dessa forma, associando a Álgebra com a Geometria as regras ficam mais claras e fáceis de serem fixadas na memória. Imagina-se poder associar tudo isso à música que torna o ambiente de estudo mais alegre.
3. METODOLOGIA
3.1. Tipo de pesquisa
Este estudo é uma pesquisa de caráter bibliográfico e de campo, fruto de um trabalho de conclusão de curso (TCC), do curso de Especialização em Gestão Escolar, promovido pela CFEB (Coordenadoria Estadual de Formação de Executivos Escolares) que atua em parceria com a Universidade Estadual Vale do Acaraú – UVA, no ano de 2017. Para a análise dos dados adotou-se uma abordagem qualitativa e quantitativa, uma vez que esta permitiu uma maior compreensão dos conjuntos de informação levantados na pesquisa. Nele lançou-se mão de obras e autores como D’Ambrósio, Borim, Moura, Kishimoto, Lara, Ducourneau, Dante, que mostram o lúdico como uma alternativa de se trabalhar uma matemática de forma mais prazerosa.
3.2. Procedimento
O desenvolvimento desde trabalho teve início com a proposta feita pela disciplina Introdução à Pesquisa Educacional, ministrada pela Professora Maria Joyce Maia Costa Carneiro, quando um fenômeno (a dificuldade de memorizar regras da Matemática) foi detectado na turma do 8º ano do Colégio Tenente Ângelo de Siqueira Passos. Em seguida, desenvolveu-se um estudo bibliográfico e uma pesquisa com a turma citada que julgava como difícil a assimilação e memorização das regras dos produtos notáveis.
Com a autorização do núcleo gestor e aceitação da turma, aplicou-se um questionário misto, através do qual se evidenciou a problemática. Buscando um maior entendimento do conteúdo por parte dos alunos, propôs-se uma metodologia inovadora através da produção de material concreto (figuras geométricas) e associação de áudio às regras que definem cada tipo de produto notável.
Essa foi uma experiência muito válida, pois se pôde comprovar de fato o que os teóricos dizem sobre a eficiência do lúdico na aprendizagem. A mística de que a Matemática é uma ciência difícil fica desfeita, assim.
3.3. Amostra
Participaram dessa pesquisa de 19 alunos do 8º ano tarde do Colégio Tenente Ângelo de Siqueira Passos, que tiveram participação ativa na resolução de questionário e no trabalho de experiência. No começo, mostraram-se receosos de participar das musiquinhas com as regras dos produtos, mas, após ouvirem bem, o próprio ritmo animado incentivou a participação de todos. Cantando, a classe se viu em uma dinâmica que só facilitou a compreensão das regrinhas de resolução do quadrado da soma de dois termos, quadrado da diferença de dois termos e produto da soma pela diferença de dois termos.
3.4. Instrumento
Para desenvolvimento da pesquisa foram aplicados questionários mistos, através dos quais se quantificou, pontuou e analisou as dificuldades e anseios dos alunos do 8º ano do CTASP. Também se utilizou as músicas (som, cd) e cartolinas na construção de figuras geométricas como suporte do estudo dos produtos notáveis, durante a experiência.
3.5. Análise de dados
Os dados foram coletados na própria escola durante uma aula de Matemática, contando com a colaboração da direção e dos alunos. Dezenove (19) alunos do 8º ano tarde responderam ao questionário que contou com a seguinte investigação:
- Você gosta da disciplina Matemática? Por quê? Onze (11) alunos (58%) responderam SIM e 8 (42%) disseram NÃO. Os que disseram gostar, consideraram a matemática uma disciplina exata, interessante, fácil, que trabalha o raciocínio lógico, que as regras não apresentam muitas exceções e, principalmente, que é uma disciplina importante para a vida. Já os que disseram não ter afinidade com a disciplina, afirmaram não gostar de cálculos por conta de muitas regras e porque exige muita concentração que, segundo um deles “esquenta a cabeça”.
- Você sente alguma dificuldade para aprender Matemática? Justifique. Quinze (15) alunos (79%) responderam SIM e 4 (21%) disseram NÃO. Quem disse ter dificuldades pontuou que a junção de números e letras (álgebra), a grande quantidade de regras, a rapidez com que os conteúdos são apresentados e a dificuldade de memorizar fórmulas dificultam seu aprendizado. Por outro lado os que disseram não ter dificuldades justificaram que a Matemática é uma disciplina lógica e que basta atenção e treino na resolução das atividades para aprender.
- O que lhe ajudaria a aprender com mais facilidade os conteúdos de matemática? Sugeriram que jogos favoritos dos alunos, músicas, a repetição das aulas, o reforço escolar no contra turno, aulas práticas, um método dinâmico de transmissão dos conteúdos que envolvesse mais os alunos, videoaulas, enfim, uma aula diferente, pode facilitar os seus aprendizados.
- Você sentiu dificuldade em memorizar algumas fórmulas matemáticas como as dos produtos notáveis? Treze (13) alunos (68,5%) responderam SIM e 6 (31,5%) disseram NÃO. A maioria disse ter dificuldade em memorizar fórmulas matemáticas.
- Você acha que o assunto produtos notáveis tem alguma aplicação em outros conteúdos do ensino de Matemática? Quais, por exemplo? Todos concordaram que produtos notáveis tem aplicação em outros conteúdos, como fatoração, frações e equações algébricas e equações de 2º grau.
- Em sua opinião, aulas diversificadas com a utilização de músicas ou jogos matemáticos, proporcionariam uma melhor compreensão dos assuntos que estão dificultando a sua aprendizagem? Comente. 100% aprovam ideia de aulas diversificadas. Nos comentários, enumeram as seguintes vantagens: 1-Promovem uma maior interação entre os alunos e o professor; 2-Aproximam os conteúdos da realidade; 3-Abrem a mente; 4-As aulas ficam divertidas; 5-Os jogos deixam as aulas mais fáceis; 6-A música nos acalma; 7-Jogos e músicas ajudam a memorizar as fórmulas; 8-Facilitam a compreensão; 9-O aprendizado se torna prazeroso; 10-Quebram a mesmice, evitando a repetição desnecessária; 11-As aulas ficam animadas e produtivas; 12-Chamam a atenção; 13-Ajudam o aluno a criar uma maior afeição com a matéria; 14-As aulas ficam desestressantes e bem legais.
Como se pode ver, através do questionário, a maioria dos alunos reconhece o valor da Matemática, apesar das dificuldades ainda enfrentadas.
Pelas questões 3 e 6, principalmente, eles anseiam por aulas mais dinâmicas e envolventes. No caso dos produtos notáveis também fica provado que o emprego de áudios e material concreto favorece a memorização das regras.
Quando o aluno diz que sente dificuldades mas está tentando aprender, dá sinal de que o conteúdo poderia ser trabalhado de outra forma, quem sabe, através de jogos, dinâmicas, músicas etc. para que essas dificuldades não venham afetar a assimilação de outros conteúdos.
4. CONCLUSÃO
O trabalho que se desenvolveu foi importante principalmente no que se refere à confirmação das propostas defendidas pelos autores D’Ambrósio, Moura, Kishimoto, Ongaro, Ducourrneau, Dante, dentre outros. Neles, encontrou-se o suporte que fez com que se enxergasse a didática dentro de uma perspectiva mais contextualizada, valorizando o aluno em seu meio e com suas experiências de vida. O trabalho de campo também serviu para se comprovar os objetivos propostos, suscitados pela problemática observada inicialmente (a dificuldade dos alunos em memorizar regras e fórmulas matemáticas).
A realidade vivenciada dentro da sala de aula, em alguns casos, infelizmente, ainda é algo distante do que se almeja. Muitos dos alunos encontram-se desmotivados, sem saber ou sem querer resolver atividades escolares e sem uma perspectiva de futuro. Muitas vezes, ouve-se dizer ou percebe-se que são apáticos ou indisciplinados. Investigar todas essas realidades não é tarefa fácil, pois as dificuldades têm explicação que vão além da forma mecanicista como os conteúdos são trabalhados. É notório perceber que aspectos emocionais de ordem socioeconômicas ou familiares de alguns também contribuem para seus fracassos. Pois uma sociedade marcada pelo consumismo e o descartável faz com que as famílias se dissociem, rendendo à escola uma sobrecarga de obrigações no que diz respeito à educação dos alunos.
Porém, todo este contexto não deve servir de desânimo à classe docente. É preciso se encarar a realidade com esperança e achar que a educação ainda é a meio mais eficiente que pode salvar uma sociedade marcada por muitas cicatrizes e desajustes.
Dinamizando as salas de aula com jogos, músicas, questões interessantes, promovendo a interdisciplinaridade e a transdisciplinaridade, como sugere Edgar Morim, na Teoria da Complexidade Humana, pode-se resgatar o gosto pelo saber dos estudantes. Trazendo o lar e a sociedade para dentro da escola, vivenciando sobremaneira uma realidade mais próxima do concreto, pode-se fazer com que o aluno se sinta motivado não só com o estudo da Matemática, mas com qualquer outra disciplina.
Afinal, a Matemática não é uma disciplina pronta, acabada. É exata, mas é vasta. Pode parecer difícil, mas mexe com o raciocínio, aguçando, inclusive, a compreensão de outras matérias. Cabe ao professor fazer dela um campo lógico, trabalhando-a de forma lúdica, espontânea, procurando dar significado a cada assunto, contextualizando, ultrapassando os muros que a fecham e internalizando as questões do mundo.
No caso do tema investigado, a facilitação do aprendizado das regras dos produtos notáveis, a partir do emprego de uma metodologia dinâmica com o uso do lúdico musical e manuseio de material concreto, ficam evidentes que a Matemática não é uma disciplina só para os superdotados. Todos podem aprender se o professor quebrar os paradigmas dos moldes tradicionais. Cantar com eles e descobrir a origem de cada regra, através do cálculo das áreas, tornam, com certeza, a aula prazerosa e o aluno estimulado.
REFERÊNCIAS BIBLIOGRÁFICAS
ARAGÃO, Charles Lopes Freitas. Estudante do Curso Superior de Tecnologia em Gestão de Pequenas e Médias Empresas. Universidade Tiradentes 2007. Matemática Lúdica no Ensino Fundamental. Disponível em:http://www.webartigos.com/articles/27888/1/MATEMATICA-LUDICA-NO-ENSINO-FUNDAMENTAL/pagina1.html.
ALMEIDA, A. Ludicidade como Instrumento Pedagógico. Disponível em: <www.cdof.com.br>.
ALMEIDA, Paulo Nunes. Educação Lúdica: Técnicas e Jogos Pedagógicos. 9ª ed: Loiola, São Paulo, 1998.
ANTUNES, Celso. Jogos para estimulação das múltiplas inteligências. Petrópolis: Vozes, 1998.
_______ Novas maneiras de ensinar – Novas maneiras de aprender. Rio de Janeiro: Artmed, 2002.
BORIN, J. Jogos e resolução de problemas: uma estratégia para as aulas de matemática. São Paulo – SP: IME-SSP, 1996.
Brasil. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais : matemática / Secretaria de Educação Fundamental. – Brasília: MEC/SEF, 1997. 142p.
CAMPAGNER, Carlos Alberto Campagner – Engenheiro mecânico, com mestrado em mecânica, professor de pós-graduação e consultor de informática. Pedagogia & Comunicação. P. 3. Disponível em: <educacao.uol.com.br/matematica/ult1692u35.jhtm >
D’AMBRÓSIO, Ubiratan. Sociedade, cultura, matemática e seu ensino. Revista Educação e Pesquisa. São Paulo, v. 31 p. 99. 2005.
______Etnomatemática. Diário na Escola (Diário do Grande ABC). 2003. Disponível em: <ihbner@diarionaescola.com.br>.
DANTE, Luiz Roberto. Tudo é Matemática. São Paulo: 2003, Ed. Ática, p. 165-168.
DUCOURNEAU, Gérald. Introdução à musicoterapia. São Paulo: Manole, 1984.
FERNANDES, Valéria da Silva Roque. A importância da Música na Escola . (2004, p. 24 -35) . Disponível em: ww.escolapaulofreire.com.br/…/valeria/importancia_musica.htm
GROENWALD, C. L. O.; TIM, U. T. Utilizando curiosidades e jogos matemáticos em sala de aula. Disponível em: <htp://www.somatematica.com.br>. Acesso em: fev./2002.
KISHIMOTO, Tizuko Morchida. O jogo e a educação infantil. São Paulo, Pioneira, 1994.
______Jogos, brinquedos, brincadeiras e educação. 4. ed. São Paulo: Cortez, 2000
LARA, Isabel Cristina Machado de. Jogando com a Matemática.- 1 ed – São Paulo: Rêspel, 2003.
MOURA, Manuel Orisvaldo de. A séria busca jogo: do lúdico na matemática. In: A educação Matemática em Revista, no 3, 1994.
______O jogo na educação matemática. In: Idéias. O jogo e construção do conhecimento na pré-escola. São Paulo, FDE, n. 10, p. 45-53, 1991.
MURPHEY, T. & ALBER,J.L. 1985. A pop song register: the motherese of adolescence as affective foreigner talk, with, TESOL Quarterly 19 (4)793-795. Disponível em:www.profala.com/arteducesp124.htm>
ONGARO, Carina de Faveri. . Acadêmicas do 2º ano do curso de Pedagogia (2006) UNIMEO/CTESOP.A importância da música na aprendizagem.
PIAGET, Jean. O Juízo Moral da Criança. São Paulo, Summuns, 1994. (Tradução: Elzon Lenardon).
RODRIGUES, Jeniffer de Oliveira – Acadêmica do 1º ano do curso de matemática – UNIMEO – CETESOP/2008. Jogos Matemáticos como um recurso didático www.unimeo.com.br/…/jogos+matematicos+um+recurso+didatico.pdf
TAHAN, M. A arte de ser um perfeito mau professor. Rio de Janeiro – RJ: VECCHITA, 1996.
TIMM, U. T. Utilizando curiosidades e jogos matemáticos em sala de aula. Disponível em: <http//paginas.terra.com.br/educação/calculu/Artigos/Professores/utilizando jogos.htm>
WIKIPEDIA – Educação Matemática. Disponível em: <“https://lookup-api.apple.com/pt.wikipedia.org/w/index.php?title=Educação_matemática&oldid=50461098“> Acesso em 18/11/2017-9:00 h
¹Graduado em Matemática pela Universidade Estadual Vale do Acaraú. UVA. E-Mail: fcvieirafilho@gmail.com
²Graduanda em Matemática-PARFOR/Universidade Estadual Vale do Acaraú. UVA. E-Mail: lucianacarneiro2008@gmail.com
³Graduando em Matemática-PARFOR/Universidade Estadual Vale do Acaraú. UVA. E-Mail: Wa605027@gmail.com
4Graduada em Pedagogia pela Faculdade Entre Rios do Piauí- FAERPI. Graduanda em Matemática-PARFOR/Universidade Estadual Vale do Acaraú. UVA. E-Mail: paula.olyy@gmail.com
5Graduado em Sistemas de Informação pela Faculdade FIED. E-Mail: marcio18alvesprof@gmail.com
6Graduando em Matemática-PARFOR/Universidade Estadual Vale do Acaraú. UVA. E-Mail: micaellpereira262@gmail.com
7Graduando em Matemática-PARFOR/Universidade Estadual Vale do Acaraú. UVA. E-Mail: irmaojosue20@gmail.com
