ALGORITMO GENÉTICO COMPACTO BASEADO EM TIPOS ABSTRATOS DE DADOS NA MINERAÇÃO DE DADOS NOS SINAIS DE ELETROCARDIOGRAMA

REGISTRO DOI: 10.69849/revistaft/pa10202507152104

---

Andrilene Maciel¹
Roberta Vieira²

---

Resumo

O processo de mineração de dados em sinais biomédicos de eletrocardiograma usando algoritmos genéticos compactos por tipo abstrato de dados (CGAADT), implementado em MATLAB na arquitetura GPU/CUDA, pode ser considerado um processo não trivial na análise e identificação de desempenho nos operadores genéticos em CPUs convencionais. Os resultados mostram que o algoritmo genético compacto (CGAADT) melhora o desempenho do algoritmo GAADT desenvolvido em CPU, o que viabiliza o uso em sistemas em tempo real no diagnóstico de arritmias quando implementado em arquitetura de alto desempenho, visando melhorar os sistemas de saúde oferecidos aos pacientes com problemas de doenças cardiovasculares.

Palavras-chave: Algoritmo Genético, Mineração de Dados, Graphics Processing Unit (GPU), Compute Unified Device Architecture (CUDA).

1. Introdução

O processo de extrair conhecimento a partir de grandes volumes de dados, chamado Knowledge Discovery in Databases (KDD), pode ser considerado um processo de extração de informações relevantes em grandes bancos de dados e que sejam não- triviais, implícitos, previamente desconhecidos e potencialmente úteis, e tem como principal objetivo a construção de hipóteses para auxiliar processos de tomada de decisão (FAYYAD,1996). A transformação, manipulação dos dados em conhecimento permite utilizar técnicas sofisticadas que propiciem a automação do comportamento inteligente a partir da inteligência artificial, a qual envolve técnicas necessárias para a compreensão da linguagem, percepção, raciocínio, aprendizagem e resolução de problemas, buscando a criação de teorias e modelos com capacidade cognitiva e a implementação de sistemas computacionais baseados nestes modelos focando as técnicas do KDD (FAYYAD,1996).

Segundo Rencher (2002), A mineração de dados ou data mining provém da análise inteligente e automática de dados para descobrir padrões ou regularidades em grandes conjuntos de dados, através de técnicas que envolvem métodos matemáticos, algoritmos baseados em conceitos biológicos, processos linguísticos e heurísticas, os quais fazem parte do processo do KDD responsável pela busca de conhecimentos em banco de dados (ZANTINGUER, 1996), (DINIZ,2000), (HAIR,2005),(CALDERON, 2019).

A multidisciplinaridade da mineração de dados pode ser considerada inevitável devido à integração de diversas áreas de conhecimento no processo de análise, abordando áreas de pesquisas que envolvem estatística, matemática e computação, as quais são disciplinas fundamentais para a realização do processo de mineração de dados. Algumas limitações podem ser identificadas quando se refere à escolha do melhor método de mineração de dados, uma vez que existe uma grande dificuldade dos especialistas na identificação do melhor método minerador. Geralmente, os especialistas buscam adotar o método mais adequado para a resolução do problema específico.

O processo de mineração de dados pode ser dividido em componentes capazes de favorecer a identificação mais adequada dos algoritmos de mineração a serem levados em consideração algumas informações relevantes nos modelos de classificação, regressão, associação, na análise de sequência, sumarização e visualização dos dados, entre outros.

Extrair conhecimento relevante a partir do processamento do algoritmo genético compacto baseado por tipos abstratos de dados (CGAADT) pode ser considerado um processo não trivial, devido à complexidade do algoritmo e aos ruídos encontrados nos sinais de Eletrocardiograma (ECG), que trazem características específicas de doenças cardiovasculares.

O CGAADT desenvolvido por Maciel (MACIEL,2015) foi devidamente instanciado do algoritmo genético baseado por tipo abstrato de dados (GAADT) desenvolvido por Vieira (VIEIRA,2003). Algumas limitações do algoritmo GAADT poderão ser vistas com maiores detalhes em Vieira (VIEIRA,2003), destacam-se aquelas que se tornam impactantes para o desempenho do algoritmo GAADT:

• Como o cálculo da adaptação média pode ser eventualmente feito sobre uma população de grande tamanho, a convergência do GAADT pode se dar de modo lento e, em decorrência, a obtenção dos resultados satisfatórios do problema em questão pode demorar bastante. Isso acarreta a necessidade de, posteriormente, fazer-se um estudo sobre os processos de aceleração dos mesmos. Várias são as ideias a serem utilizadas, como, por exemplo, a adaptação média obtida através de um processo de amostragem adequada, a cada passo, da população funcionalmente aplicada pelo algoritmo (VIEIRA,2003).
• A complexibilidade do algoritmo GAADT quando seu esforço computacional e a sua natureza funcional, isto é, seu aspecto quanto ao programa, sua complexidade estrutural (laços, alinhamentos, sua lógica etc) (VIEIRA,2003).

O algoritmo CGAADT desenvolvido por Maciel (MACIEL,2015) tem como objetivo melhorar a limitação do algoritmo GAADT pelo estudo do esforço computacional. Durante a fase da instanciação do algoritmo, observou-se que havia a necessidade de desenvolver uma base de dados específica, que pudesse medir o esforço computacional dos algoritmos genéticos CGAADT (MACIEL,2015), GAADT (VIEIRA,2003) e HOLLAND (HOLLAND,1975). A implementação dessa base de dados baseada nos sinais de ECG se tornou um avanço no processo de melhorias realizadas pelo algoritmo CGAADT na instanciação do algoritmo genético GAADT.

Este artigo apresenta a instanciação do algoritmo genético compacto baseado em tipos abstratos de dados na análise do esforço computacional dos algoritmos Holland, GAADT e CGAADT, com o objetivo de extrair conhecimento e informações úteis e relevantes realizando a mineração de dados, utilizando um modelo estatístico baseado na regressão logística, para aceleração do algoritmo genético baseado em tipos abstratos de dados a partir de uma arquitetura de alto desempenho.

2.  O Sistema de Monitoramento dos Sinais de Eletrocardiograma

A extração do ECG é um método não invasivo, de baixo custo, rápido e eficiente para fornecer recursos importantes para análise e diagnóstico de doenças cardíacas. Eles apresentam uma sucessão de ondas que correspondem a esses ciclos cardíacos.

A primeira atividade elétrica de cada ciclo cardíaco é registrada pelo sinal de ECG e pela onda P, que representa a ativação dos átrios. Em seguida, é registrada uma linha isoelétrica denominada segmento PR, que é acoplada à onda P, configurando o intervalo PR. Logo após, o complexo QRS pode consistir de uma fase (monofásica), duas fases (bifásica) ou três fases (trifásica) da onda, que corresponde à ativação ventricular.

Novamente, registra um segmento da linha isoelétrica ST, a fim de constituir o intervalo entre a ativação ventricular e o início da repolarização ventricular. Por fim, inscreve-se a onda T, correspondente à representação eletrocardiográfica da despolarização ventricular, seguida da onda U. Finalmente, se torna importante definir o intervalo QT, compreendendo o tempo entre o início da despolarização e repolarização ventricular (MOFFA,2010),(ALHAMEED,2019), (SANCHES,2010).

É importante notar que a atividade mecânica do coração é precedida por um estímulo elétrico responsável pela ativação miocárdica. A estimulação elétrica origina-se no nó sinusal, considerado um marcapasso mais rápido e dominante, se despolarizando espontaneamente (MOFFA,2010). Assim, o eletrocardiograma opera sobre um conjunto de variações no potencial elétrico resultante da atividade cardíaca (Figura 1).

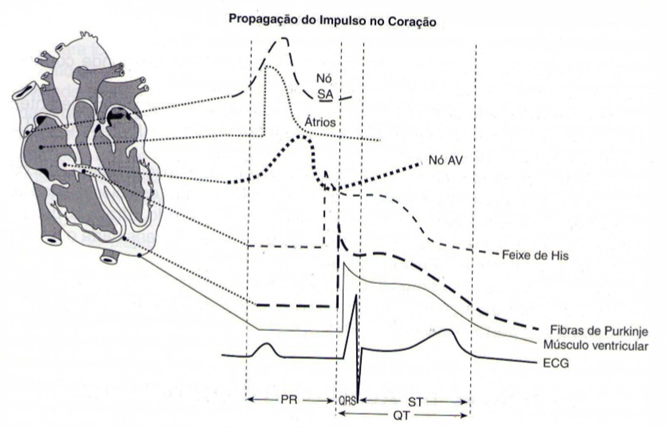
Figura 1. Potenciais curvas de ação das diferentes estruturas cardíacas e a correspondente gênese do ECG(MOFFA,2010).

Os sistemas de monitoração dos sinais de ECG são responsáveis pela identificação das ondas, as quais são analisadas por um médico para um possível diagnóstico de arritmia, sugerindo tratamentos e medicamentos de acordo com a condição clínica do paciente. Para o funcionamento adequado do sistema, é essencial que ele seja capaz de demonstrar morfologias de onda de ECG de qualidade, desde o processamento e limpeza de sinal.

A análise de um eletrocardiograma está diretamente relacionada à qualidade da coleta do sinal de ECG, capaz de extrair as características relevantes das ondas que compõem o sinal (amplitude, duração, ângulos e forma de ondas) (OLIVEIRA,2011).

Com os dados obtidos a partir do sinal de ECG é realizado um estudo que tem como objetivo encontrar arritmias, e, em seguida, permitir um diagnóstico relacionado às alterações estruturais e funcionais do coração em sistemas em tempo real.

A identificação dessas doenças é realizada, em geral, por exames de eletrocardiograma, que registram a funcionalidade do coração ao longo do tempo, pelo desenho de ondas consecutivas (MOFFA,2010). Muitas doenças do coração poderão ser identificadas durante a execução do exame periódico de ECG.

No entanto, ruídos poderão ser visualizados durante a coleta desses sinais e podem esconder características importantes, típicas de doenças cardiovasculares descritas na morfologia do sinal cardiológico, dentre as quais, destacam-se as arritmias, que representa qualquer alteração na regularidade, frequência, local de origem, anormalidade do impulso, de modo a modificar a sequência normal da despolarização dos átrios e do ventrículo, alterações da condução do estímulo elétrico (MOFFA,2010).

O diagnóstico das arritmias cardíacas pode ser difícil de se identificar mesmo com auxílio do eletrocardiograma e de outros métodos de investigação clínica (OLIVEIRA,2011). Os principais pontos para o problema de arritmia cardíaca, está relacionada à identificação das ondas que formam o sinal de eletrocardiograma (ECG): onda P, seguimento PR, complexo QRS, seguimento ST e onda U (OLIVEIRA,2011). O processo de detecção de onda de um eletrocardiograma tem algumas dificuldades, devido as oscilações no sinal, ausência de uniformidade na morfologia das ondas e o surgimento de ruídos durante a extração do sinal de ECG (MOFFA,2010), (MENDIS,2025).

A eficácia do sistema de detecção, extração e visualização das características morfológicas dos sinais de ECG de forma automática, pode ser considerado um processo de grande importância para salvar vidas, e influencia diretamente no diagnóstico precoce das doenças cardiológicas, responsáveis pela maioria das mortes súbitas existentes em todo mundo (OLIVEIRA,2011), (MENDIS,2025). Se o desempenho do sistema de detecção de arritmias for considerado ineficiente, isso pode tornar o sistema de arritmias impraticáveis, devido ao tempo de processamento para extração de características do ECG.

A análise de um eletrocardiograma, está diretamente relacionado à qualidade da coleta do sinal de ECG, capazes de extrair as características relevantes das ondas que compõem o sinal (amplitude, duração, ângulos e forma de ondas) (OLIVEIRA,2011). Com os dados obtidos a partir do sinal é realizado um estudo, que tem como objetivo encontrar arritmias, em seguida, permitir um diagnóstico relacionado nas alterações estruturais e funcionais do coração.

Este artigo apresenta uma aplicação de alto desempenho para aceleração de algoritmos genéticos baseada em tipos de dados abstratos na plataforma GPU / CUDA, visando apresentar uma especificação de uma versão compacta de algoritmo genético baseada em tipos de dados abstratos (CGAADT), na descoberta de conhecimento em bases de dados geradas a partir de amostras de sinais de ECG proveniente da base de dados de arritmia do MIT-BIH (PHYSIONET,2025). Além disso, os resultados obtidos durante processamento dos algoritmos Holland, GAADT e CGAADT demonstra a complexidade do esforço computacional desses algoritmos em gerar dados úteis e relevantes durante o processo de mineração de dados a partir da base de dados do MIT- BIH (PHYSIONET,2025), utilizando o modelo de regressão logística com o método de análise na interpretação dos dados(FAYYAD,1996).

3. Especificação do Algoritmo Genético Compacto Baseado por Tipos Abstratos de Dados (CGAADT)

A modelagem do GAADT em Vieira (VIEIRA,2003) apresenta as definições básicas do algoritmo genético baseado em tipos de dados abstratos, com a representação dos tipos básicos: base, gene, e cromossomos. A arquitetura GAADT e o processo de formação dos alfabetos (base, gene e cromossomo), representam 70% do tempo de processamento do algoritmo quando executado em CPUs convencionais. Na nova versão compacta do CGAADT (MACIEL,2015), a representação do cromossomo é dividida em dois níveis:

• A base é tipo abstrato (B) representada pelo B_Host, executado diretamente na Unidade Central de Processamento ou Central de Processing Unit (CPU);
• Os tipos de cromossomos e genes são executados na Arquitetura de Dispositivo de Computação Unificada ou Compute Unified Device Architecture (CUDA) e no Graphics Processing Unit ou Unidade de Processamento Gráfico(GPU) .

A aplicação do CGAADT requer uma definição de elementos específicos em um ambiente que apresenta o problema em foco (VIEIRA,2003).

3.1 Tipos básicos

3.1.1. Definição (Bases) – O tipo de base para a construção do filtro adaptativo instanciado pelo CGAADT para o processamento de sinais cardiológicos é o conjunto B_{PontosOndasHost} formados pelos períodos do ECG para cada derivação executada na CPU (MACIEL,2015).

O conjunto B_{NomesOndasHost} e o conjunto B_Hostλ contendo as derivações inócuas B_Hostλ.

Bhost=BPontosOndasHost ∪ BNomesOndasHost ∪ BHostλ

O termo B_Hostλ é formado pelos fenômenos elétricos registrados pelos sinais de eletrocardiograma (ECG), pelas deflexões que formam uma determinada derivação e os períodos que representam o final da despolarização ventricular e o início da repolarização.

O termo B_{NomesOndaHost} é o conjunto {Onda_P, Onda_Q, Onda_R, Onda_S, Onda_T, Onda_U}, o qual contém todas as ondas, segmentos e complexos de ondas, que poderão ser detectados no exame de ECG, constantes na base de dados MIT-Databases (PHYSIONET,2025). A identificação e a nomenclatura das ondas que compõem o sinal do ECG, obedecem ao modelo padrão de Willen Einthoven (SANCHES,2010).

Os elementos é o conjunto B_{PontosOndasHost} são ordenados pares X = (x, y), onde X ∈ ℕ × ℝ que conterão valores dos quais será possível extrair as propriedades morfológicas das ondas do ECG no host (amplitude, intervalos e duração) (MACIEL,2015).

O conjunto B_hostλ é formado pelo elemento λ, que representa as ondas, cuja morfologia está dentro do padrão normalidade (MACIEL,2015).

As características (genes) relevantes na GPU para o problema tratado neste artigo são g_D = {Onda_P, Onda_Q, Onda_R, Onda_S, Onda_T, Onda_U}, que fazem parte de uma mesma derivação registrada pelo ECG, e D representa o gene no device (GPU) (MACIEL,2015).

O conjunto que representa essas ondas é o G_DElementos, o qual é formado pela junção dos conjuntos da base (B_host). Os elementos do conjunto G_DElementos contém valores necessários para extrair as propriedades morfológicas dos elementos do ECG (amplitude, duração e intervalos) usadas no processo de detecção (MACIEL,2015).

A estrutura adotada para todos os elementos do conjunto G_DElementos é o elemento_i = (nome, (x^– , y ^–), (x_p, y_p), (x⁺, y⁺) onde i ∈ # (símbolo don´t care que pode ser substituído por qualquer símbolo de alfabeto) adotado para o cromossomo), onde: nome ∈ BNomesOndasHost e    (x−,y),(xp,yp),(x+,y+) ∈ BPontosOndasHost (MACIEL,2015).

Por exemplo, se um gene na GPU representasse o complexo QRS mostrado na figura 3 (onde o ponto S é o ponto inicial da onda, M é o máximo e F o final). O gene resultante representado por g_D=(Complexo_QRS,(x_s,y_s),(x_m,y_m),(x_f ,y_f)) (MACIEL,2015).

A interpretação adotada para os elementos elemento_i é : nome é o elemento; x^– é o menor valor do elemento da coordenada x a onda; x_p é o valor da coordenada x para o pico do elemento; x⁺ é o valor mais alto da coordenada x para o elemento; y^– é o valor da coordenada y para o elemento durante x^–; y_p é o valor da coordenada y para o “elemento” durante x⁺ . Quando em um ECG não for registrada uma dada onda durante um período, o parâmetro nome dessa onda recebe o valor λ (MACIEL,2015).

Definição 3.1.2. (Gene) – O tipo abstrato gene G_D é um conjunto de todos os elementos G_D = <b_h1, b_h2, b_h3, b_h4> ∈ G_D na GPU, representados por h (host), formados pelos elementos do tipo abstrato base B_Host, conforme descrito no item 3.1, e que satisfaz ao conjunto AFGD (Axioma de Formação de Genes no Device) (MACIEL,2015).

Os axiomas do conjunto AGFD estabelecem que:

• A base bh1 ∈ BNomesOndasHost;
• As bases bh2, bh3, bh4 ∈ BPontosOndasHost;
• Para todo gene g_D = <b_h1, b_h2, b_h3, b_h4> ∈ G_d = [b_kij]_mxn;
• Para todo gene g_D = <b_h1, b_h2, b_h3, b_h4> ∈ G_d = [b_kij]_mxn, de tamanho (16×12), a qual representa   melhor a formação de genes e cromossomos na grade, em que i e j representam respectivamente a linha e coluna que o elemento ocupa em B_{nomesOndasHost} (MACIEL,2015).

• O par ordenado b_h2, deve ser um ponto cuja ocorrência seja um período de tempo inferior ou igual ao par ordenado b_h3 no ECG, ou seja, afgd1 = ∀g_D = <b_h1, b_h2, b_h3, b_h4> ∈ G_{D, x –} ≤ x_p(MACIEL,2015).
• Para todo gene g_D = <b_h1, b_h2, b_h3, b_h4>, o par ordenado b_h3 deve ser um ponto, cuja a ocorrência seja um período de tempo inferior ou igual ao do par ordenado b_h4 no ECG, ou seja, afgd2 = ∀g_D = <b_h1, b_h2, b_h3, b_h4> ∈ G_D, x_p ≤ x ⁺ (MACIEL,2015).
• O Conjunto inócuo G_Dλ é formado pela base g_Dλ = <b_h1, b_h2, b_h3, b_h4> , tal que: O b_h1 = λ.

Os elementos deste conjunto é representado por g_Dλ = [gene_D0, …, gene_Dn], em que n ≥ 0∈ {0, …, 191} de threads por bloco (MACIEL,2015).

Definição 3.1.3. (Cromossomo) – O tipo abstrato cromossomo C_D é o conjunto de todos os genes construídos conforme as definições estabelecidas pelo AFCD (Axioma de Formação de Cromossomo no Device)

Assim, o conjunto ACFD é especificado como:

• Os elementos devem ocorrer em sequências de ondas P, QRS, T e U, representadas por C_DPeríodo (MACIEL,2015).
• A não ocorrência de um elemento no bloco será caracterizada pela substituição do gene destinado ao elemento no bloco ausente, pelo gene inócuo (g_Dλ) (MACIEL,2015).
• Os Intervalos de ocorrência das ondas não interceptam, ou seja, x⁺ elemento p ≤ x^– elementoQRS e x⁺ elemento^QRS ≤ x^–elemento^T ≤ x⁺ elemento^U (MACIEL,2015).
• Para todo gene g_D = <b_h1, b_h2, b_h3, b_h4> ∈ G_D = [b_kij]_mxn, de tamanho (16×12), a qual representa melhor a formação de genes e cromossomos na grade, em que i e j representam respectivamente a linha e a coluna que o elemento ocupa em B_{NomesOndasHost} (MACIEL,2015).
• Para um dado período não podem existir elementos no bloco (bk) do mesmo, ou seja afcD1 = ∀C_D1 ∈ C_D (∀ (g_D1i, g_D2i, nome^gD1i ≠ nome^gD2i))), onde nome é uma função que retorna o valor  da  base  do gene que  armazena o  nome do elemento  (b_h1) (MACIEL,2015).
• Cada bk , pertence ao conjunto de derivações do ECG, representados por D₁(DI), D₂(II), D₃(III), aVR, aVL, AVF, V₁, V₂, v₃, v₄, v₅, v₆ (doze derivações), a grade de blocos da GPU.
• O conjunto C_D forma um plano unidimensional (figura 2) ∀C_D ∈ G_d (MACIEL,2015).
• O conjunto de SM (streaming multiprocessor) , representado por SM = {s_m0, …, s_mn} onde n ≥ 0∈{0, .., 3}, formam um C_D de tamanho 2¹¹ × 16, para que não ocorra a explosão exponencial da população em encontrar o resultado mais adaptado durante o processo de convergência (MACIEL,2015).
• Cada sm, terá no máximo 32 threads que formam 6 wraps (W), representam unidades de escalonamento necessárias para melhorar o processamento das operações genéticas. O cálculo para definir a quantidade de wraps é resultante da seguinte expressão:

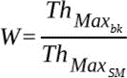
Onde W representa a quantidade de wraps, Th _{Max bk}  (quantidade máxima de threads no bloco) e Th _{Max SM} (quantidade máxima de threads por sms).

• O conjunto cromossomo inócuo denotado por C_Dλ é formado por todos os conjuntos de genes inócuos que satisfazem as restrições no AFCD (Axiomas de Formação de Cromossomos no Device)(MACIEL,2015).

C_D = {g_D1, g_D2, …, g_Dn}, em que n ≥ 0 ∈ ℕ

A população é definida pelo algoritmo genético compacto baseado em tipos de dados abstratos desenvolvido em CUDA, o qual realiza o particionamento da população no processamento de fluxos (SM). O sistema foi desenvolvido representando a seguinte configuração: uma placa aceleradora da NVIDIA, GeForce MX 250 e uma máquina host, usando uma CPU Intel (R) Core TM i7 10^th Gen 1,80 GHz 16GB RAM, MATLAB R2025a (NVIDIA,1999), (OPENCL,2009), (GAO,2019). A caracterização do problema para limpar o sinal de ECG e a aceleração do algoritmo CGAADT na plataforma de alto desempenho será descrita a seguir:

Definição 3.1.4. (População) – O tipo abstrato P_DFRAG é o conjunto de todos os cromossomos construídos de acordo com a definição 3.1.3, que é P_DFRAG ≥ 2¹⁵ do tamanho da população mais adaptada (MACIEL,2015).

3.2  Operadores Genéticos

A especificação dos tipos de dados abstratos: base, gene, cromossomo e população, preservou as exigências contidas na definição de CGAADT. A especificação das funções e relações necessárias para o cálculo da função CGAADT deverá atender a todas as pré-condições de sua definição original.

As definições de funções e relações são apresentadas, cujas especificações para o problema são mais concretas do que a definição original, ficando subtendido que as funções e relações que não forem redefinidas nesta seção preservarão sua definição original pelo GAADT (VIEIRA,2003).

Dado um elemento ”elemento_o” do ECG do paciente, e os limites padrões de altura e largura para este elemento no device, a função comparaElemento retorna VERDADE se o elemento estiver dentro do intervalo para a altura e a largura fornecidos para arritmias e flutter atrial, fibrilação atrial e demais irregularidades encontradas no ECG (arritmias), caso contrário, ela retorna FALSO (MACIEL,2015).

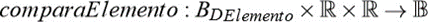
O grau de adaptação do cromossomo para a detecção dos elementos deve considerar se a altura e largura das ondas (P, T, Q, R, S, U) estão representadas no gene fornecido, para cada elemento do cromossomo, deverá atender a esta verificação e deve ser somado mais um ao seu grau de adaptação. Logo, para calcular o grau de adaptação dos cromossomos, é preciso primeiro definir uma função para retornar os padrões das ondas(MACIEL,2015).

Dado um cromossomo C_D = {g_D1, g_D2, g_Dn} e um formato de padrão do elemento a, a função padrão retorna o valor 1 se uma das propriedades para g_D atende às propriedades métricas cadastradas para a onda a, e zero caso contrário(MACIEL,2015).

Definição 3.2.2. (Padrão) – A ocorrência ou não de um dado período de ECG é fornecida pela função padrão_D do seguinte tipo:

Definição 3.2.3. (Grau): O grau de adaptação de um gene é uma função grau do seguinte tipo:

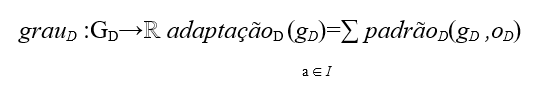
Onde I contêm o nome de todas as ondas cadastradas no sistema(MACIEL,2015).

O peso atribuído ao gene g_Di de um cromossomo é igual a j+1, onde j é o número de ondas cujas características atendem aos padrões. Por exemplo, caso um cromossomo tenha sido formado por genes que atendem às especificações das ondas P, T, complexo QRS e U, então a função grau_D irá retornar o valor 1 para cada gene deste cromossomo, e a adaptação total do cromossomo será igual a 3 (MACIEL,2015).

A especificação do CGAADT para a detecção das ondas trabalha com os operadores genéticos de cruzamento e mutação entre cromossomos adjacentes, ou seja, cromossomos que sejam vizinhos no espaço temporal (MACIEL,2015).

O cruzamento ocorre quando é encontrado um cromossomo que possui pelo menos um gene inócuo. Neste caso, é gerado um novo cromossomo com o gene inócuo sendo substituído por um gene do cromossomo vizinho (MACIEL,2015).

O critério de parada adotado pela função CGAADT são os números máximos de iterações desejadas e o valor da adaptação média da população atual definido por P_corte (conjunto de cromossomos abaixo da média), sendo assim, considerada satisfatória para o resultado do problema em análise (MACIEL,2015).

Estes critérios também fazem parte do conjunto de requisitos do conjunto de problemas R_qD. Para representar o cromossomo mais adequado, foram realizados vários experimentos com valores de 25 a 125 iterações, até que o valor do cromossomo mais adaptado não fosse modificado durante as vinte iterações seguidas (MACIEL,2015).

Desta forma, concluímos que, ao chegar à iteração 100, a população apresentava o cromossomo mais adaptado o problema (MACIEL,2015).

3.4. Arquitetura CGAADT

O algoritmo CGAADT, instanciado pelo GAADT, ambos algoritmos trabalham sobre um ambiente que pode ser modificado de acordo com o problema a ser abordado e como as populações de cromossomos que irão evoluir.

No GAADT, o ambiente A é formado por 8-tuplas< P,IP,R_q, AFG,AFC,T_x,∑, P₀ >, conforme visto em Vieira (VIEIRA,2003), neste ambiente não existe a preocupação com memória e todo o processo é executado na CPU.

No ambiente CGAADT exposto na arquitetura (Figura 2) e maiores detalhes da arquitetura poderá ser visto em Maciel (MACIEL,2015), um algoritmo genético opera sobre populações de cromossomos que evoluem na grade de blocos GPU (device) de acordo com as características do ambiente A. Este ambiente é apresentado por 13-tuplas, [P_DFRAG, IP_DFRAG, R_qD, M_m, G_D, AGFD, AGFD, T_xD, SMs, ∑, P_DFRAG0, P_DFRAGt, P_Rec] onde:

1. P_DFRAG é a população em GPU (device);
2. IP (P_DFRAG) é o conjunto de potência de P_DFRAG;
3. R_qD é o conjunto dos requisitos (características expressas através de fórmulas numa linguagem de primeira ordem) do problema que influência a genealogia da população PDFRAG ;
4. M_m é o conjunto de memórias {M_k,M_G,M_PDFRAG} , onde M_k é a memória de transferência de dados para o kernel, M_G é a memória global na GPU e M_PDFRAG é a memória de transferência da população P_DFRAG para a população inicial P_{DFRAG 0} no host ;
5. G_d representa a grade de blocos de threads na GPU (device);
6. AFGD é o conjunto de axiomas de formação dos genes nos cromossomos da população P_DFRAG na GPU ;
7. AFCD é o conjunto de axiomas de formação dos cromossomos na população P_DFRAG na GPU;
8. T_xD é o conjunto de pares de cromossomos (x,y) , onde x é um cromossomo C_D construído a partir do cromossomo y , pela ação da operação de cruzamento ou mutação, registrando desta forma a genealogia dos cromossomos pertencentes às populações geradas pelo CGAADT durante a sua execução ;
9. SM representa paralelização dos cromossomos nos multiprocessadores streaming para escalonamento das operações do AG;
10. Sigma é o conjunto de operadores genealógicos que atuam sobre a população PDFRAG ;
11. P_DFRAG0 é uma subpopulação pertencente a IP(P_DFRAG0) , chamada de população inicial, com no mínimo um cromossomo .
12. P_DFRAGt é a população mais adaptada ;
13. P_Rec   representa a população reconstruída no formato de ondas de ECG, a qual representa a saída do sistema .

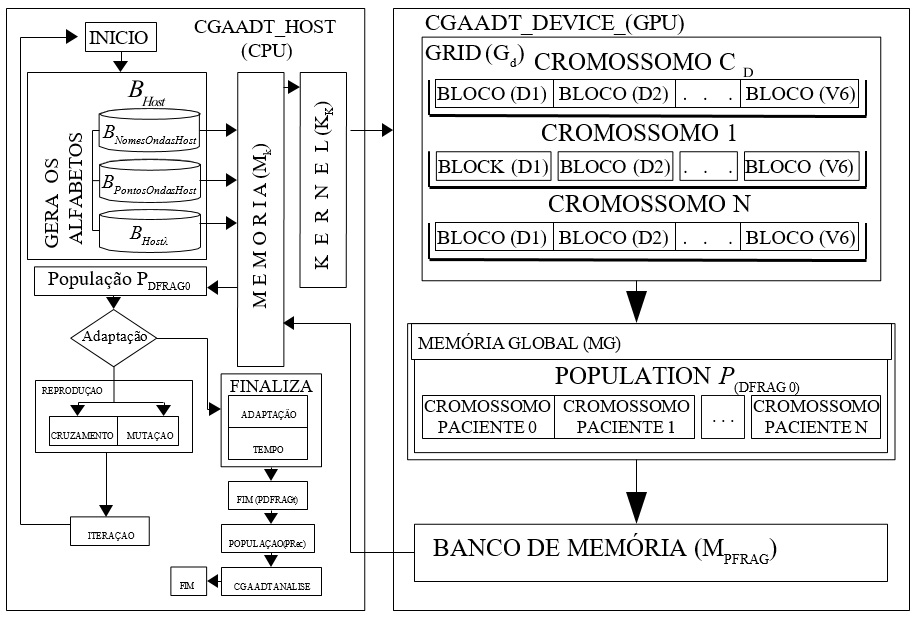
Figura 2 – Arquitetura do CGAADT(MACIEL,2015).

O algoritmo CGAADT é inicializado a partir da criação de alfabetos: gene, base e cromossomo. A função CGAADT-HOST recebe uma base denominada B_Host. Esta base B_Host é formada por outras três bases elementares, as quais formam a morfologia básica do sinal de ECG, destacam-se: B_{NomesOndasHost} ○ B_{PontosOndasHost} ○ B_Hostλ, as quais são transferidas para a memória M_k, tem como objetivo determinar o perfil da área de dados no kernel (K_k), em que e cada thread deverá atuar na GPU, a partir da função CGAADT-DEVICE (MACIEL,2015).

Ao disparar o kernel K_k, a função CGAADT-DEVICE inicializa a paralelização da base de dados, a partir de G_d , que representa a grade de blocos na GPU. Neste momento, as bases B_{nomeOndasHost} ○ B_{pontosOndasHost} ○ B_Hostλ , são transformadas em genes g_D , as quais representam uma sequência de sub-blocos de threads formados pelos elementos de B_Host pertencentes ao conjunto AFGD . Em seguida, os genes g_D são agrupados em conjuntos para formar os cromossomos C_D na GPU, os quais obedecem às condições estabelecidas pelo AFCD .

Estes cromossomos C_D são agrupados em conjuntos na G_d (grade de blocos), para formar uma população e esta representação irá garantir a imparcialidade na avaliação dos cromossomos que compõem a população P_DFRAG , a qual é transferida para a memória global M_G . Cada cromossomo C_D , representa um paciente conforme as características representadas nas bases de dados, constante na tabela 1.

Considerando que, cada paciente é representado pelo cromossomo c_PACIENTE0 são atribuídas as 12(dozes) derivações do ECG. O conjunto de cromossomos definidos na população é limitado a quantidade de pacientes existentes na base de dados. Estes cromossomos C_D formam a população inicial P_DFRAG0 , serão transferidos para o banco de memória M_PFRAG ,para a memória M_k (MACIEL,2015).

O algoritmo CGAADT inicializa sua implementação da seguinte forma:

Inicializa a função grau de adaptação do gene representado pela função do tipo:

grau_D: G_D → ℝ adaptação_D (g_D) = ∑ padrão_D (g_D, o_D) na GPU (MACIEL,2015).

1. Inicializa     a função de adaptação adaptação_D ← 0. Para todo os genes do cromossomo, seleciona os genes dominantes, a partir da função como domi: G × G → G. O gene dominante é uma função dominante do tipo:

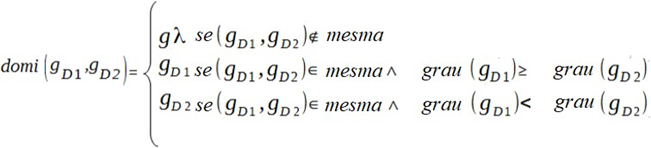
3. Inicializa a função domi(g_D1 ,g_D2), conforme definição de Vieira (VIEIRA,2003), representada na figura 10, na CPU e adaptado no novo modelo em GPU visto na figura

2. Considerando dois genes g_D1 e g_D2 que se referem a uma mesma característica, ou seja, se grau_D (g_D1)≥grau_D (g_D2) , retorne g_D1 , caso contrário g_D2 (MACIEL,2015).

4. Inicializa a função de cruzamento, para todos os pares possíveis com os cromossomos C_D na população P_DFRAG , a partir dos cromossomos mais adaptados. Em seguida, o algoritmo seleciona os genes dominantes, formando todos os cromossomos possíveis com estes genes dominantes e inclua-o na população para realizar o cruzamento (MACIEL,2015).

5. Inicializa a função de mutação, para todo os cromossomos constantes na população menos adaptada. Desta forma, o algoritmo realiza as trocas de até 50% dos seus genes, que resulte em um cromossomo C_adaptação mais adaptado do que cromossomo original C_D (MACIEL,2015).

O algoritmo CGAADT recebe a população P_DFRAG0 e ler o ambiente A com objetivo de submetê-la à simulação de um processo evolutivo, e devolve uma população P_DFRAGt , a qual será reconstruída por P_Rec na CPU, após finalização do processo evolutivo, conforme figura 2. A priori inicializa o cálculo da adaptação do cromossomo C_D da população atual P_DFRAG0 (MACIEL,2015).

O algoritmo CGAADT, seleciona o cromossomo mais adaptado C_Adaptação1 , caso o cromossomo mais adaptado seja C_Adaptação2←C_Adaptação1 , enquanto o processo de adapt_D(C_Adaptação2)≥Adapt_D(C_Adaptação1) , o algoritmo seleciona uma população de cromossomos adaptados. Em seguida o CGAADT, realiza a operação de cruzamento na população de cromossomos mais adaptados (MACIEL,2015).

A população de cromossomos não adaptados, serão selecionados para execução do operador de mutação. Neste caso, os cromossomos C_Adaptação1←C_Adaptação2 , o algoritmo realiza novo cálculo de adaptação do cromossomo e seleciona C_Adaptação2 . Desta forma, o algoritmo CGAADT realiza nova leitura ao ambiente A , para formar nova população PDFRAG=PDFRAGCRUZAMENTO ○ PDFRAGMUTAÇÃO ○ PDFRAGt (MACIEL,2015).

Esta nova população é adicionada ao ambiente A , para finalização do algoritmo CGAADT. Os cromossomos da população P_PDFRAGt são os cromossomos das populações P_{PDFRAG 0} ,P_{PDFRAG 1} , … ,P_PDFRAGt−1 , que melhor satisfazem os requisitos do problema R_qD

. Diz-se então que a população P_PDFRAGt evoluiu da população P_PDFRAG0 . A preservação e morte dos cromossomos da população atual P_PDFRAGt trabalhada pelo CGAADT é orientada por um predicado unário denominado de P_corte (MACIEL,2015).

O predicado pertence ao conjunto de requisitos do problema R_qD na GPU, que atua em conjunto com os SMs sobre os cromossomos de P_PDFRAGt . Os cromossomos que satisfazem o predicado Pcorte irão fazer parte da população P_PDFRAGt+1 , enquanto os outros cromossomos da população P_PDFRAGt irão morrer. Os cromossomos mortos podem ser recuperados através da taxonomia T_xD dos cromossomos da população atual para evitar que eles apareçam novamente nas próximas iterações da função CGAADT (MACIEL,2015).

Esta restrição atende ao entendimento do processo de evolução darwinista, que não contempla a possibilidade de uma espécie extinta voltar a aparecer num outro momento futuro. A função CGAADTANÁLISE, recebe a população P_PDFRAGt e encaminha para o operador P_Rec para reconstrução da população no formato original de dados, que representa os resultados de processamento do algoritmo que envolvem as operações genéticas de seleção, cruzamento, mutação, reprodução, inserção de descendentes na população e as ondas de arritmias, fibrilação atrial e flutter (MACIEL,2015).

4. Infraestrutura de Hardware e Software na implementação do GAADT e CGAADT em GPU/CUDA

Os algoritmos GAADT e CGAADT precisaram de uma infraestrutura mínima para sua implementação, execução e configuração, destacam-se:

4.1 Implementação do GAADT em CPU(Central Process Unit)

–Processador Intel(R), Core TM i7 10^th Gen , CPU 1.80 GHZ, 16GB de RAM;

–Sistema Operacional 64 bits, Windows 11;

–Software Matlab R2025a.

4.2. Implementação do CGAADT em GPU (Graphics Processing Unit)

– Placa de GPU/CUDA GeForce MX 250, NVIDIA.

–Software Matlab R2025a (JODAH,2025), (GAO,2019).

5. Modelo de Regressão na Mineração de Dados no Algoritmo Genético Compacto por Tipo Abstrato de Dados

Os modelos de regressão logística têm aplicabilidade em diversos problemas de análise de dados, nos quais descreve uma relação entre uma dada variável de saída e uma ou mais variáveis explicativas. Quando a variável de saída é discreta, podendo ter dois ou mais valores possíveis, a técnica de regressão logística tem-se tornando um método padrão para essas análises(FAYYAD,1996).

No caso de valores discretos, o que se faz inicialmente é uma transformação de variável, isto é, em vez de trabalhar-se com um modelo linear para representar a probabilidade de sucesso, a escala de probabilidade é primeiro transformada do intervalo [0,1] para [-∞, ∞] (FAYYAD,1996).

A transformação logística (logit) da probabilidade de sucesso p é log[p/(1-p)], que é representada como logit(p). Note que p/(1-p) é a chance de sucesso e, então, a transformação logística de p é o p, no intervalo[0,1], representam os valores de logit (p) no intervalo [-∞, ∞]. A função logit(p) é uma curva em S (sigmóide)(FAYYAD,1996).

A simulação realizada com os algoritmos GAADT e HOLLAND tem como objetivo realizar um estudo do esforço computacional durante o processo de limpeza do sinal de ECG, na execução desses algoritmos a partir do processo de mineração de dados usando CGAADT. O processo de limpeza do sinal de ECG não será aqui tratado, maiores detalhes poderão serem vistos em Maciel (MACIEL,2015). O GAADT foi reformulado para gerir dados durante a execução do algoritmo a partir do modelo de regressão logística, maiores detalhes podem ser vistos no item 6.1.

6.1. As Principais Tarefas do KDD

O processo de descoberta de conhecimento em bases de dados envolve uma sequência de tarefas pré-estabelecidas (Figura 3) de forma interativa para a transformação das informações em conhecimento (FAYYAD,1996) e (HAIR,2005). A figura 3 apresenta as principais tarefas do KDD, as quais serão descritas a seguir:

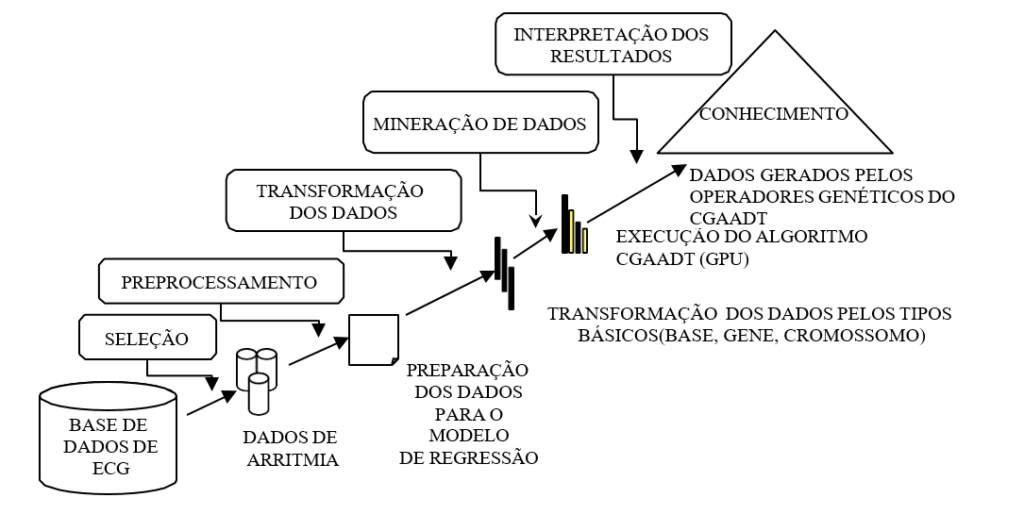
Figura 3. Principais tarefas do processo do KDD adaptado. Fonte: HAIR,2005.

Na fase de execução do algoritmo CGAADT na arquitetura GPU/CUDA, ocorre a seleção interna e automática da base de dados de acordo com os sinais de ECG e o algoritmo seleciona os dados de arritmia cardíaca.

Na fase de pré-processamento dos dados, a base de dados gerada tem origem a partir das 12 derivações/leads do ECG, classificadas pelos leads DI, DII, DIII, AVR, AVL, AVF, V₁, V₂, V₃, V₄, V₅ e V₆, sendo preparados os dados para serem termos integrantes do modelo de regressão logística.

Na fase da transformação dos dados, os operadores genéticos de seleção, cruzamento, mutação, reprodução e inserção de descendentes na população selecionam os leads para tratar a base de dados de acordo com o modelo de regressão logística, que poderá ser consultado em detalhes em Valença (FAYYAD,1996).

Na fase de Data Mining, o algoritmo minerador a ser utilizado é o CGAADT. Neste ambiente, serão calculados o esforço computacional dos operadores genéticos de seleção, cruzamento, mutação, reprodução, inserção de descendentes na população, considerando a execução do algoritmo CGAADT na grade G_D no dispositivo da

GPU/CUDA (MACIEL,2015). Além do cálculo do esforço computacional dos operadores genéticos, também são calculados o modelo de regressão logística linear e a distribuição de probabilidade dos algoritmos GAADT, HOLLAND e CGAADT, Odds Ratio desses algoritmos, o ganho computacional da execução do CGAADT em função dos demais algoritmos citados anteriormente, o percentual do esforço computacional do algoritmo de acordo com o processamento das 12 derivações do ECG e integrando-os aos operadores genéticos do algoritmo CGAADT. Na última fase de interpretação dos resultados, serão analisados os dados gerados pelos operadores genéticos do CGAADT durante a execução do algoritmo, para que se possa realizar a integração do conhecimento gerado pela base de dados do CGAADT. Maiores detalhes poderão ser vistos em Maciel (MACIEL,2015).

6.  Resultados

A base de dados é composta pelo conjunto de dados de 10 (dez) pacientes portadores de obesidade, gastrite, hipertensão e infarto do miocárdio. Cada paciente possui 10.000 (dez mil) números de exemplo de dados, sendo executado no algoritmo CGAADT e GAADT de forma paralela. Os sinais de eletrocardiograma usados nos experimentos são compostos de 12 (doze) derivações do ECG, divididos nas derivações unipolares e bipolares, identificadas pelos leads: DI, DII, DIII, Avr, Avf, Avl, V₁, V₂, V₃, V₄, V₅, V₆.

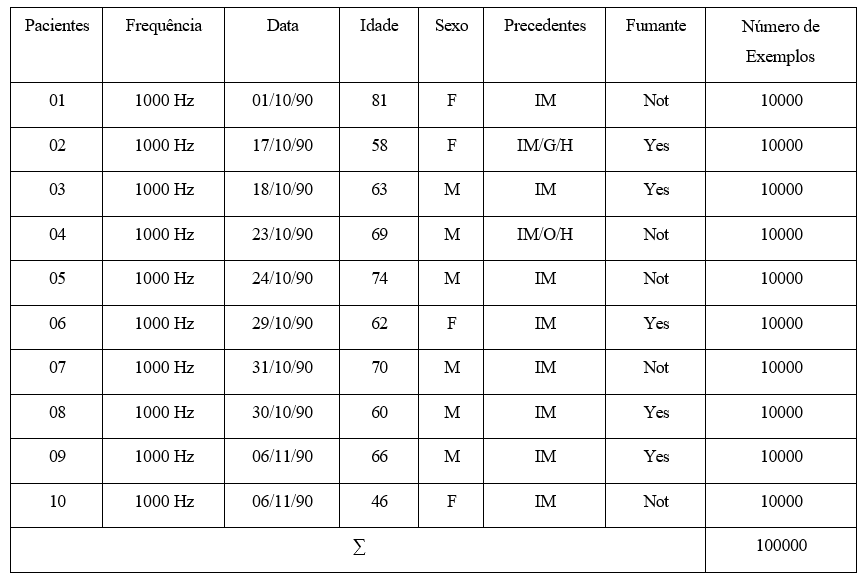
Tabela 1. Características base de dados ECG adaptada. Legenda : (F) Feminino, (M) Masculino, (IM) Infarto do Miocárdio, (G) Gastrite, (H) Hipertensão, (O) Obesidade e (N.E) Número de Exemplos de dados adaptados (MACIEL,2015).

Os dados de entrada, são representados pelos sinais de ECG, contendo as 12(doze) derivações. Em seguida, o algoritmo CGAADT inicia o processo de formação das unidades elementares para gerar os alfabetos, que permite o algoritmo realize a formação do material genético em plataformas distintas, a partir da criação das bases na CPU e dos genes e cromossomos na GPU, para que o material genético seja fragmentado e processado paralelamente. Este processo, cria uma nova população, a qual é transferida para a memória da CPU, com objetivo de inicializar do processo evolutivo.

Caso o processo evolutivo não seja atendido, o algoritmo inicia novo processamento, caso contrário, o CGAADT envia as saídas de dados. O primeiro output de dados é representado pela população atual, submetida ao processo de reconstrução, representada população reconstruída para que seja exibido o sinal de ECG.

A segunda output está relacionada ao arquivo de log que armazena o tempo de processamento das operações genéticas (seleção, cruzamento, mutação, reprodução e inserção de descendentes na população). As saídas do CGAADT são enviadas para a função de análise (GAADT-ANÁLISE), para realizar o processo de análise de dados, a partir do modelo de regressão logística para a coleta de resultados (MACIEL,2015).

Durante a execução do algoritmo CGAADT, cada indivíduo é representado pelo paciente constante na tabela 1, o material genético é manipulado individualmente a partir da seleção dos leads/derivações DI, DII, DIII, Avr, Avf, Avl, V₁, V₂, V₃, V₄, V₅, V₆.

A cada operação genética de seleção, cruzamento, mutação, reprodução e inserção de descendentes na população, essas operações são executadas em paralelo. Por exemplo, o PACIENTE 01, obtém os sinais compostos pelas 12 (doze) derivações do ECG, o conjunto dessas derivações é executado em paralelo de acordo com as operações genéticas, permite uma análise detalhada do comportamento das operações genéticas de acordo com as derivações existentes no sinal do ECG (Figura 4).

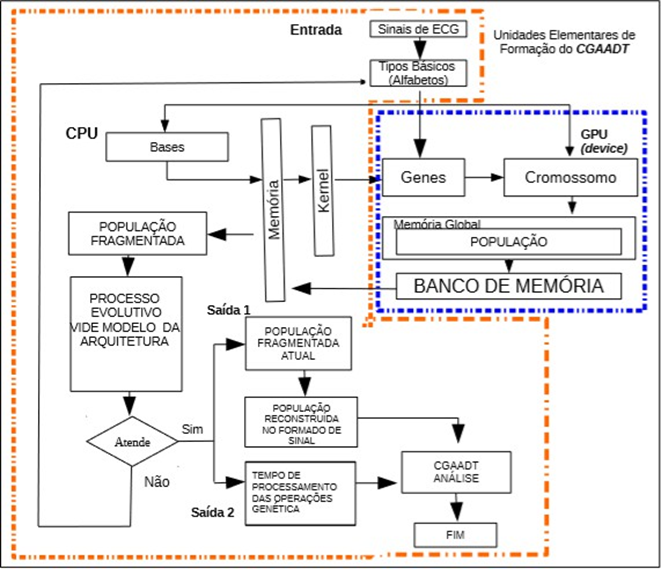
Figura 4 – Fluxo de Dados do CGAADT . Fonte: MACIEL,2015.

O processo de filtragem no CGAADT é realizado a partir do operador genético de cruzamento que representa a diferença entre B_Host e a população reconstruída P_Rec . A medida de desempenho para avaliação do processo de filtragem no algoritmo CGAADT será representada pelo erro médio quadrático e2=[B_Host−P_Rec ]² (MACIEL,2015).

Onde: e2 : erro médio quadrático (EQM), B_Host : resposta do sistema contendo o sinal original de dados no host e P_Rec como resposta do filtro adaptativo CGAADT pela operação de cruzamento, maiores detalhes poderão ser vistos em Maciel (MACIEL,2015).

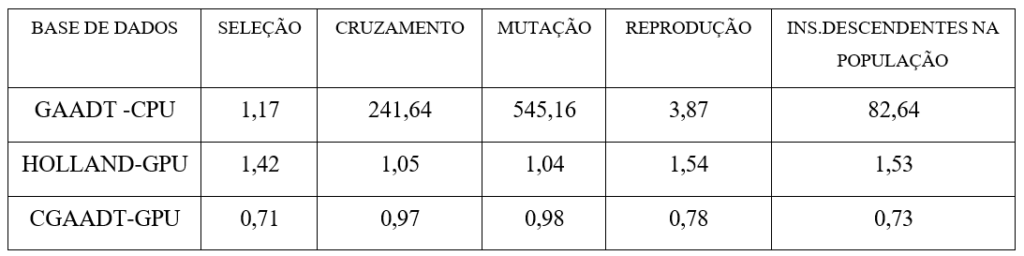
Tabela 2. Percentual Médio do Tempo de Processamento (gargalos dos algoritmos) dos Operadores Genéticos de Seleção, Cruzamento, Mutação, Reprodução e Inserção de Descendentes na População .

De acordo com a tabela 2, demonstra-se os gargalos dos algoritmos HOLLAND, GAADT e CGAADT, considerando o percentual médio no tempo de processamento desses algoritmos.

No trabalho de Vieira (VIEIRA,2003), não foi possível identificar os gargalos do algoritmo destinado ao esforço computacional das operações genéticas. Os dados descritos na tabela 2 demonstram os gargalos do algoritmo GAADT executado em CPU, destinado a 241,64% (seleção), 545,16% (mutação) e 82,64% (inserção de descendentes na população), durante o tempo de processamento dos sinais de ECG na CPU.

A maioria dos algoritmos que implementam o algoritmo genético de Holland, na maioria dos casos, são implementados em CPU devido à praticidade do modelo. Considerando estas limitações, este artigo tem como objetivo realizar um comparativo preciso entre as operações genéticas do algoritmo Holland, sendo necessário desenvolver uma versão específica implementada na arquitetura GPU/CUDA para a realização desse comparativo.

A implementação em GPU/CUDA do algoritmo de Holland demonstra melhorias de 240,59% (Cruzamento), 544,12% (Mutação), 81,11% (Inserção de Descendentes na População), mais vantajoso em relação ao GAADT implementado em CPU. Portanto, observa-se que em algumas situações, o algoritmo de Holland obteve desvantagem de 0,25% (Seleção) em relação ao algoritmo GAADT executado em CPU e obteve melhorias de 2,33% (Reprodução) em relação ao GAADT em CPU.

Considerando a estratificação dos termos abstratos (gene, base e cromossomos), exposta nas figuras 2 e 4, a nova instanciação do algoritmo GAADT pelo CGAADT demonstra melhorias no tempo de processamento do algoritmo de 0,71% (Seleção), 0,97% (Cruzamento), 0,98% (Mutação), 0,78% (Reprodução) e 0,73% (Inserção de Descendentes na População), sendo executado melhorado o tempo de processamento desses operadores genéticos de 2,41% em relação a todos os gargalos encontrados nos operadores genéticos implementados no algoritmo Holland em GPU/CUDA.

Tabela 3. Percentual do Esforço Médio Consolidado do CGAADT (GPU) X GAADT(CPU).

Considerando o percentual do esforço médio com valores consolidados dos algoritmos CGAADT implementado em GPU/CUDA e GAADT desenvolvido em CPU (tabela 3). Conclui-se que os maiores esforços computacionais do algoritmo GAADT, considerando a média aritmética desses valores, representam 98,11% dedicados ao processamento do algoritmo, com isso, o GAADT se torna lento quando comparado ao algoritmo de Holland.

Os resultados obtidos na tabela 3 são considerados os valores médios consolidados entre os operadores genéticos de cruzamento, mutação e inserção de descendentes na população, os quais possuem as maiores demandas de processamento dos sinais de ECG.

Tabela 4. Percentual do Esforço Médio Consolidado do CGAADT (GPU) X HOLLAND(GPU)

Considerando o percentual do esforço médio com valores consolidados baseados na média aritmética desses valores dos algoritmos CGAADT implementado em GPU/CUDA e HOLLAND desenvolvido em GPU (tabela 4). Conclui-se que os maiores esforços computacionais do algoritmo HOLLAND representam 53,82% dedicados processamento do algoritmo em todas as operações genéticas, com isso, o CGAADT se torna ágil quando comparado ao algoritmo de Holland desenvolvido em GPU.

7.  Conclusão

Algumas considerações sobre o desempenho do esforço computacional sobre o algoritmo GAADT devem ser levadas em consideração sobre os resultados encontrados. Em algumas situações, constantes dos operadores genéticos de cruzamento, mutação, reprodução e inserção de descendentes na população. O algoritmo GAADT obteve maior tempo de processamento em relação ao algoritmo genético de Holland implementado em GPU. Considerando a complexidade do algoritmo GAADT de acordo com a modelagem do problema a ser adotado, a semântica, as questões lógicas, os intervalos das funções necessárias para a sua convergência. O algoritmo GAADT, na sua estruturação, pode ser implementado para qualquer tipo de problema e o esforço computacional do algoritmo poderá ser modificado de acordo com o problema a ser adotado.

O algoritmo de Holland implementado em GPU é considerado um algoritmo simples para sua implementação e não pode ser aplicado para todos os problemas. Além disso, a arquitetura GPU/CUDA permite melhorias no desempenho do algoritmo, o que se torna favorável para a sua implementação em CUDA.

Em todas as simulações realizadas, a nova instanciação do GAADT se tornou vantajosa, obtendo melhorias no esforço consolidado do algoritmo de 11,14 % (Seleção), 99,10 % (Cruzamento), 99,6 % (Mutação), 48,7 % (Reprodução) e 90,04 % (Inserção de Descendentes na População), quando comparado com a versão original do GAADT em CPU, sendo executado em arquiteturas distintas. Quando os algoritmos CGAADT e HOLLAND são implementados na mesma arquitetura, esses percentuais ganhos são reduzidos para 1,4% (Cruzamento), 1,12% (Mutação), 9,02% (Reprodução), 15,12% (Inserção de Descendentes na População), com exceção dos 17,43% representados pela operação genética de seleção. Nesta fase, do algoritmo CGAADT, uma parte desse processamento é executada na CPU para a geração dos alfabetos, com isso o ganho médio consolidado baseado na média aritmética desses valores de processamento executado em GPU se torna proporcional àquele executado com o algoritmo GAADT em sua versão original em CPU.

A nova instanciação do algoritmo GAADT pelo CGAADT permite a estratificação dos termos abstratos (gene, base, cromossomo) serem adaptados ao problema a ser adotado, melhorar o desempenho do algoritmo GAADT, permite obter agilidade no processo de análises dos sinais de ECG na busca rápida do diagnóstico de doenças cardiovasculares.

REFERÊNCIAS

ALHAMEED R, at all. Real-time signal processing of data from an ECG. IEEE, Wrexham, UK, 2019.

CUNHA, P. C. N. Modelo de eletrocardiógrafo portátil de baixo consumo. Dissertação de Mestrado em Modelagem Computacional de Conhecimento, Universidade Federal de Alagoas, 2012.

CALDERON A.B.M. ECG Times Series Data Mining Cardiovascular Disease Risk Assessment. Master Thesis. Universidad Politécnica de Madrid, 2016.Disponível em http://oa.upm.es/43314/1/TFM_ALLAN_MENDEZ_CALDERON.pdf. Último Acesso: 10/06/2019.

DINIZ C.A.R, LOUZADA F. Data Mining : Uma Introdução. ABE – Associação Brasileira de Estatística, São Carlos, 2000.

GAO X. . Diagnosing Abnormal Electrocardiogram (ECG) via Deep Learning. IntechOpen, 2019. Disponível em https://www.intechopen.com/online-first/diagnosing- abnormal-electrocardiogram-ecg-via-deep-learning. Último Acesso: 15/06/2025.DOI: 10.5772/intechopen.85509 .

FAYYAD U. at all. Advances In Knowledge Discovery and Data Mining. AAI Press/ The MIT Press., 1996.

HAIR F. JOSEPH J. Análise Multivariada de Dados, 5ª Ed. Bookman, Porto Alegre, 2005.

HOLLAND, J.H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. MIT Press., 1975.

JEFFREY, D.; RAJARAMAN A. Mining of Massive Datasets. Stanford University Press, 2014

JODAH A. MATLAB. R2025a. Self Organizing Map Kohonen Neural Network – Tollbox. Version 1.0.0.0. URL: https://ch.mathworks.com/matlabcentral/fileexchange/46481-self- organizing-map-kohonen-neural-network,2025.

MACIEL A. Um filtro adaptativo de alto desempenho instaciado do algoritmo GAADT para o processamento de sinais de eletrocardiograma, Tese de Doutorado do Centro de Informática da Universidade Federal de Pernambuco, 2015.

MENDIS, S. Global Status Report: on non communicable diseases. WHO Library Cataloguing,     2014.   URL:

https://iris.who.int/bitstream/handle/10665/148114/9789241564854_eng.pdf?ua=1. Último Acesso: 02/05/2025.

MOFFA, P.; SANCHES, P.; Eletrocardiograma: Uma abordagem didática. 1ª edição, Roca, São Paulo, p. 356 ,2010.

NVIDIA CUDA C Programming Guide, Version 4.2,1999.

OpenCL Programming Guide for the CUDA Architecture, V 2.3, 2009.

OLIVEIRA, W. J.; PEDROSA L. C. Doenças do Coração: Diagnóstico e Tratamento. 1ª edição, Revinter, São Paulo, p. 536, 2011.

PHYSIONET, MIT-BIH Arrhythmia Databases. Disponível em: <http://www.physionet.org/physiobank/database/mitdb>. Último Acesso em: 02 de maio de 2025.

SAITO K. at. all.Sistemas Inteligentes em Controle e Automação de Processos. Ciência Moderna, Rio de Janeiro, 2004.

SANCHES, P., MOFFA P. Eletrocardiograma: Uma abordagem didática. 1ª edição, Rocca, 356 p, São Paulo, 2010.

RENCHER A.C. Methods of Multivariate Analysis, Second Edition. Wiley Interscience, Canada, 2002.

VIEIRA, R.V.V. Um Algoritmo Genético Baseado em Tipos Abstratos de Dados e sua especificação em Z, Tese de Doutorado, Universidade Federal de Pernambuco, 2003.

ZANTINGE D., PIETER A. Data Mining. England, 1996.

---

¹ Universidade Federal Rural de Pernambuco, Rua Dom Manuel de Medeiros, s/n – Dois Irmãos, Recife – CEP: 52.171-900,Brasil. e-mail: andrilene.maciel@ufrpe.br

² Instituto de Computação, Universidade Federal de Alagoas -UFAL, Maceió, Alagoas , CEP: 54740-000- Brasil, e-mail: rvvl@ic.ufal.br.