REGISTRO DOI: 10.69849/revistaft/th102412261613
ELISABETE CRISTINA DA SILVA PIRES
Introdução
Praticamente em quase todas as ações humanas o ato de planejar se faz presente, seja tão somente para a organização ou até mesmo a orientação do que será realizado. Dessa forma, observando o planejamento sobre a ótica do trabalho docente, tem-se que o mesmo exerce um papel de fundamental importância para que os objetivos inicialmente traçados em relação ao processo de ensino-aprendizagem sejam alcançados. Assim, de acordo com (FREITAS et al, 2011, p. 111): “Com o planejamento, esperamos prever ações e condições; racionalizar tempo e meios; fugir do improviso e da rotina; assegurar a unidade, coerência, continuidade e sentido ao trabalho docente.” De fato, nessa perspectiva pensar o trabalho docente em meio a ausência de planejamento, pode vir a comprometer de forma substancial que os objetivos inicialmente traçados com relação ao processo de ensino aprendizagem sejam realmente alcançados, traduzidos por meio de um cotidiano em sala de aula mecânico e desinteressante para os alunos.
Nesse contexto, acredita-se que um dos procedimentos utilizados pela maioria dos professores para construção e prática do planejamento escolar nas aulas de Matemática perpassa pela seleção do material que será utilizado nas aulas, material esse que será escolhido de acordo com os objetivos a serem alcançados pelo professor em relação ao processo de ensino-aprendizagem dessa disciplina. Assim, observa-se que uma das formas de realizar as ações para um efetivo planejamento didático está na escolha das atividades que serão propostas aos alunos, e uma das formas de selecionar tais atividades está na observação, bem como na reflexão sobre os níveis de demandas cognitivas exigidas a partir de cada atividade proposta pelo professor de Matemática.
Dessa forma, considerando a importância do conhecimento e da observação dos diversos níveis de demandas cognitivas e como a observação desses níveis poderá auxiliar em um planejamento eficaz para as aulas de Matemática, faremos nesse relato de experiência primeiramente uma breve revisão teórica a fim de compreender o conceito dos diferentes níveis de demandas cognitivas, bem como a relação desses níveis com as escolhas de tarefas Matemáticas, considerando a análise de diversos autores sobre esse assunto. Em seguida será exposta a experiência vivenciada ao se fazer o estudo e análise dos diferentes níveis de Demandas Cognitivas em uma das disciplinas do curso de Mestrado Profissional em Matemática – Profmat, na disciplina: “Tópicos de Matemática”, ministrada pela professora Ana Paula Perovano, na Universidade Estadual do Sudoeste da Bahia – Uesb, campus de Vitória da Conquista. Ao final, será apresentada, como forma de ilustração, a análise sobre os diferentes níveis de Demandas Cognitivas bem como a observação de tais níveis em três atividades retiradas do Livro que fazem parte do acervo de livros do PNLD ( 2021 ), cujo título é Matemática – Multiversos – Estatística e Probabilidade da editora FTD.
Revisão Teórica
Segundo os autores Groenwald et al (2019), baseados nos estudos de Llinares e Penalva (2001), os professores devem estar atentos aos níveis de exigências cognitivas que serão necessários em cada situação de aprendizagem, adequando tais níveis aos objetivos que se pretendem alcançar em cada caso. Nesse contexto, os autores afirmam que a seleção das tarefas Matemáticas assume papel primordial na relação ensino e aprendizagem, pois a mesma se constitui como uma ferramenta que fará um vínculo entre os objetivos que pretendem ser atingidos e o caminho percorrido pelos níveis de raciocínio do estudante em meio ao entendimento do conteúdo Matemático.
Assim, em estudos desenvolvidos por Litoldo (2021, p. 94), baseados em estudos de Stein; Grover; Henningsen, (1996), tarefa Matemática é definida como:
“uma atividade em sala de aula, cujo objetivo é focar a atenção dos estudantes em um determinado assunto” (STEIN; GROVER; HENNINGSEN, 1996, p. 460, tradução nossa). “Essa atividade só será classificada como uma nova tarefa, ou diferente, caso a ideia matemática dessa nova tarefa seja diferente da tarefa subjacente a ela (STEIN; GROVER; HENNINGSEN, 1996).”
De fato, a citação dos autores acima, traz a ideia de que a tarefa Matemática serve como uma ferramenta, em que o objetivo está em atrair a atenção dos estudantes para determinado, conteúdo, assunto, definições, conceitos Matemáticos, de forma a nortear todos os caminhos que deverão ser percorridos para se chegar ao objetivo final no caso, a aprendizagem do conteúdo Matemático.
Assim, considerando a importância da seleção das Tarefas Matemáticas no processo de ensino e aprendizagem, pois segundo Groenwald et al, (2019) baseados nos estudos de Pennalva e Llinares (2011), a seleção das Tarefas Matemáticas, configura-se como uma das atividades docentes que tem maior impacto em relação ao processo de ensino e de aprendizagem dos estudantes. Onde tal importância se justifica no fato de tais tarefas representarem a forma mais direta de interação entre professor, aluno e conteúdo bem como a forma em que o estudante irá se relacionar diretamente com a aprendizagem do conteúdo Matemático. Ainda segundo Groenwald et al, (2019), sendo as tarefas Matemáticas uma ferramenta que está presente diretamente no dia- dia da sala de aula, se faz necessário uma observação e um cuidado por parte do professor com relação a seleção de tais tarefas de forma a atender a diferentes níveis cognitivos (Demandas Cognitivas) dos estudantes, ofertando ao aluno diferentes experiências de aprendizagem. O termo Demanda Cognitiva, segundo Groenwald et al, (2019), em estudos de Pennalva Llinares (2011) apresenta a seguinte definição: “Demanda Cognitiva”, se refere a classe e nível de pensamento que se é exigido dos estudantes para a resolução da tarefa, apontando o que se alcança e o que se aprende em cada nível”. O mesmo autor classifica os níveis de Demandas Cognitivas exigidos em cada tarefa da seguinte forma: (NÍVEL 1) – Memorização ; (NÍVEL 2) – Procedimentos sem Conexões; (NÍVEL 3) – Procedimentos com conexões e (NÍVEL 4) – Fazer Matemática.
De acordo com Barros e Justulin (2024), baseados nas definições de Stein et al (2001), as características correspondentes a cada nível são:
Nível 1 – Memorização: tarefas que exigem apenas aplicação direta do algoritmo, fórmulas ou definições, e não exigem a interpretação ou procedimentos metodológicos para resolução do problema.
Nível 2 – Procedimentos Sem Conexões: tarefas que exigem a aplicação de algoritmos e requer o uso de procedimentos que geralmente são solicitados na própria tarefa, onde tais procedimentos não possuem conexão direta com o procedimento utilizado.
Nível 3- Procedimentos Com Conexões: tarefas que envolvem o uso de procedimentos de modo a desenvolver um nível de raciocínio mais elevado com relação aos conceitos envolvidos, onde se sugerem caminhos a serem seguidos, mas ainda sim requer um esforço cognitivo maior, pois tais caminhos não podem ser seguidos automaticamente, sem pensar.
Nível 4 – Fazer Matemática: tarefas que envolvem um pensamento mais complexo e não-algorítmico. Onde o caminho percorrido para se chegar a resolução da tarefa não se apresenta descrito na mesma, exigindo que o aluno faça conexões entre conhecimentos prévios, definições e conceitos para chegar a resolução.
Ainda segundo Barros e Justulin (2024), de acordo com Hsu (2013), as tarefas matemática que são classificadas como de alta demanda cognitiva tem como foco principal o uso de procedimentos voltados para técnicas de resolução de problemas, pois o objetivo da aprendizagem se baseia no protagonismo do aluno, que irá construir passo a passo o caminho da resolução do problema. Assim, os autores concordam que para resolver problemas que exigem um alto nível de Demanda Cognitiva, o aluno deverá recorrer a altos níveis de interpretação, criatividade, conexões com diversos conceitos, e tais habilidades, não são exigidas dos alunos quando esses se deparam com tarefas de baixo nível de Demanda Cognitiva.
Diante do exposto acima, os autores Barros e Justulin, (2024), baseados nos estudos de Pennalva e Llinares (2013), ainda ressaltam que a gestão das tarefas tem papel fundamental na aprendizagem Matemática, uma vez que são capazes de proporcionar ao estudante situações de aprendizagem que exigem um alto nível de demanda Cognitiva do tipo “ Fazer Matemática”, exigindo procedimentos que envolvam criatividade, combinação de conceitos, conexões com a realidade, onde tais procedimentos não encontram-se ofertados em um ensino que se utiliza de tarefas com baixo Nível de Demanda Cognitiva.
Atividades Realizadas
No curso de Mestrado do Profmat, como uma das aulas apresentadas na disciplina “Tópicos de Matemática”, ministrada pela professora Ana Paula Perovano, no campus da Uesb, localizada em Vitória da Conquista – Bahia, foi realizada uma aula referente a apresentação e análise dos diferentes níveis de demandas cognitivas que podem ser exigidos dos alunos através das atividades que lhes são apresentadas.
Num primeiro momento, foi feita a análise e contextualização da importância da observação das atividades propostas aos alunos nos livros didáticos segundo a visão dos diferentes níveis de demandas cognitivas e expostos os conceitos referentes ao tema. Logo após a apresentação dos conceitos, iniciou-se uma conversa com os alunos presentes sobre os níveis de demandas cognitivas nas atividades propostas em sala de aula. De modo geral, a maioria dos presentes na aula relatou que observavam tais demandas, mas que de forma inconsciente em seu planejamento, pois procuravam sempre adequar os níveis exigidos nas tarefas, aos objetivos e graus de dificuldades, relacionando-os à realidade e contexto no qual se apresentavam.
Em seguida a professora pediu que os alunos da sala fossem organizados em duplas, e de acordo com o livro didático de Matemática levado por cada aluno, foi feita a escolha, pela professora, de um Capítulo do livro para que fossem observadas e posteriormente classificadas algumas atividades, relacionando-as aos diferentes níveis de demandas cognitivas.
O Livro Didático escolhido foi referente ao conteúdo Matemático do Ensino Médio, Titulado: Matemática Multiversos (2020), do autor Joamir Souza e editora FTD, e o capítulo escolhido trata do estudo de Estatística referente ao conteúdo: “Medidas de Posição”.
Abaixo é apresentada uma análise de três atividades escolhidas, bem como a classificação de tais atividades quanto aos níveis de demandas cognitivas:
Nível 1: Memorização (Baixo Nível)

Observa-se que a atividade apresentada acima se classifica como tarefa de Memorização (Nível 1), pois requer apenas a aplicação direta de fórmulas e conceitos, não exigindo maiores esforços com relação ao conteúdo apresentado. Dessa forma, representam atividades de baixo nível de demanda cognitiva.
Nível 2: Procedimentos Sem Conexões ( Baixo Nível)
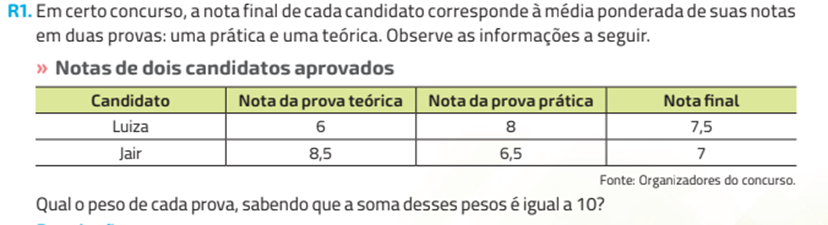
A atividade acima é classificada como de Procedimentos sem conexões (Nível 2), pois ainda apresenta sua ênfase com base na resposta final a ser apresentada. No caso da atividade acima o autor pergunta apenas qual o peso de cada prova, onde o aluno para obter a resposta correta recorrerá, de forma simples, a aplicação de formulas de maneira direta. Assim, atividades como estas, segundo Stein e Smitn ( 1998), estão focadas na produção de respostas corretas ao invés do desenvolvimento da compreensão matemática.
Nível 3:Procedimentos com Conexões ( Alto Nível)

A atividade acima pode ser classificada como Procedimento com Conexões (Nível3), pois observa-se que existe um indicativo do conhecimento matemático que deverá ser aplicado, no caso, Média aritmética, mas para isso será exigido do aluno uma interpretação prévia um pouco mais apurada, exigindo assim um esforço cognitivo maior por parte do aluno, pois o mesmo deverá recorrer a interpretação prévia de obter a média de todos os números apresentados na tabela e depois compara-lo a porcentagem de 80% de 15 Mbps.
Analisando as atividades referentes ao capítulo: “Medidas de Posição”, não foram encontradas aquelas do tipo: “Fazer Matemática”, pois grande parte das atividades realizadas sempre fazia alguma referência na própria questão, do conceito a ser utilizado, indicando ao aluno o caminho a ser seguido para resolução, bem como o algoritmo a ser utilizado.
Após a análise das atividades por escrito como as expostas acima, a professora propôs que as mesmas fossem apresentadas e discutidas com toda a turma e ao final da aula foi solicitado que os alunos escolhessem algumas questões em meio as que foram analisadas para que fossem modificadas ou adaptadas, transformando-as de certo nível de Demanda Cognitiva para outro nível diferente do inicialmente proposto. Essa parte final da aula foi bastante interessante, pois pode-se perceber a importância em se observar os níveis de Demandas Cognitivas nas tarefa analisadas, e como tais observações são importantes no sentido de se procurar adequar determinadas tarefas aos diferentes contextos de aprendizagem, proporcionando ao aluno o contato com diferentes tipos de Demandas Cognitivas. Pois como no exemplo do capítulo analisado não foram encontradas atividades do tipo “Fazer Matemática”, contudo através da experiência apresentada em “ transformar a questão” de um nível cognitivo em outro, o professor acaba por ter a oportunidade de ofertar ao aluno diferentes tarefas, abarcando diversos níveis de Demandas Cognitivas. Dessa forma, reiteramos a importância de ofertar ao aluno diferentes situações de aprendizagem, que poderá ser oportunizada através da aplicação de tarefas de diferentes níveis de Demandas Cognitivas, pois como reforça Litoldo (2019, p. 124), baseado nos estudos dos autores (CARRILLO; CONTRERAS; ZAKARYAN, 2013, p. 789) e (STEIN; SMITH, 1998, p. 269):
“Conseguintemente, “a resolução de tarefas de diferentes demandas cognitivas apresenta oportunidades para ativar diferentes processos cognitivos” (CARRILLO; CONTRERAS; ZAKARYAN, 2013, p. 789,tradução nossa). Assim, o trabalho em sala de aula com essa pluralidade de oportunidades de tarefas cognitivamente diferentes, ao longo do processo de aprendizagem, “conduz ao desenvolvimento de ideias implícitas nos estudantes sobre a natureza da Matemática”
Conclusões
Através da experiência vivenciada por esse relato, pode-se perceber a importância referente aos diferentes Níveis de demandas Cognitivas. Assim, a escolha das tarefas, que antes poderia ser feita de forma a não observar os graus e níveis de dificuldades exigidos para resolvê-las, agora passam a ser observadas sobre outra ótica, onde o professor poderá escolher com maior segurança a tarefa mais adequada ao objetivo que ele pretende alcançar, dentre as diferentes condições de ensino. Nesse sentido o professor poderia introduzir atividades que exigem um baixo nível de Demanda Cognitiva, a fim de estabelecer uma relação de incentivo e confiança com o aluno frente ao conteúdo e um pouco mais adiante ir avançando para atividades com níveis de demandas cognitivas mais elevadas como o “Fazer Matemática”.
Independente das atividades a serem escolhidas pelo professor, que irão compor parte do seu planejamento seja diário ou anual, o fato é que, através do estudo e observação referente aos diferentes níveis de Demandas Cognitivas, o professor terá a oportunidade de conseguir reunir um maior embasamento teórico com relação ao caminho a ser alcançado através da aplicação de determinada tarefa.
Dessa forma, de acordo com as reflexões expostas acima, podemos observar que os autores dialogam no sentido de expor os conceitos sobre os níveis de demandas cognitivas e como tais conceitos podem contribuir com os objetivos da atividade docente, através da seleção consciente das tarefas a partir da observação sobre os níveis de demandas cognitivas exigidos em cada uma delas. Com isso, acredita-se que o professor poderá, de maneira mais coerente, adequar os níveis de demandas exigidos em cada atividade proposta, aos reais objetivos de aprendizagem nos mais diferentes contextos nas aulas de Matemática.
Referências
PESENTE, Ilisandro; GREOENWALD, Claudia Lisete Oliveira; LLINARES,
Salvador C. Olhar profissionalmente a sala de aula: demanda cognitiva de
atividades matemáticas. Anais do VII CIEM, ULBRA, 2017. Acesso em:
http://www.conferencias.ulbra.br/index.php/ciem/vii/paper/viewFile/8899/4351
BARROS, Felipe Aparecido Baldin; JUSTULIN, Andresa Maria. A Resolução de Problemas nos anos iniciais: possibilidades a partir das demandas cognitivas. Educação Matemática em Revista, Brasília, v. 29, n. 82, p. 01-16, 2024.
CALAZANS, Marcos Vinicius Fernandes; GROENWALD, Lisete Oliveira; Llinares, Salvador Ciscar. Demanda Cognitiva e a Competência Observar com Sentido: análise de atividades com a temática Funções Exponenciais. In: Conferencia Interamericana de Educación Matemática, 15., 2019, Medellín: Ed. Universsidade de Medellín, 2019.
FREITAS, Isabel Maria Sabino de; SALES, Josenete de Oliveira Castelo Branco; BRAGA, Maria Margareth Sampaio de Carvalho; FRANÇA, Maria do Socorro Lima Marques. Didática e Docência – aprendendo a profissão. 3 ed. Brasília- DF : Autores Associados, 2011.
HAYDTH, Regina Célia Cazaux. Curso de Didática Geral. 1°ed. São Paulo: Ática, 2011.
LITOLDO, Beatriz. A Contextualização e os níveis de Demandas Cognitivas de Tarefas de Geometria presentes em Livros didáticos de Matemática sob a perspectiva do opportunity-to-learn. 202. Tese de Doutorado – Multiunidades em Ensino de Ciências e Matemática do Instituto de Física “Gleb Wataghin”, Unicamp, Campinas – SP, 2021.
Smith, Margareth Schwan; Stein, Mary Kay. Selecting ans Creating Mathematical Tasks: Foram Research to Practice. Matehmatics Teaching in the Middle Scholl, (1998) . 3, 344-50.
SOUZA, Joamir Roberto de. Matemática Multiversos: Matemática Financeira, gráficos e sistemas: Ensino Médio. 1° ed. São Paulo: Ftd, 2020.
STEIN, Mary Kay ;SMITH, Margareth Schwan. Tarefas matemáticas como quadro para reflexão. Educação e Matemática, n.105, 2009, p. 22 – 28
FILIAÇÃO
