REGISTRO DOI: 10.5281/zenodo.12788414
Paulo Henrique de Faria1;
Vanessa Benko².
RESUMO: Este trabalho explora as muitas e possíveis interseções entre o ensino de Matemática e o jogo de xadrez nas séries iniciais do Ensino Fundamental, de acordo com as diretrizes da Base Nacional Comum Curricular (BNCC) para todo o Ensino Fundamental. O objetivo principal é integrar essas duas áreas, propondo métodos alternativos para abordar os conteúdos matemáticos no contexto escolar. A proposta aqui apresentada busca ensinar os alunos de uma maneira que evite estratégias repetitivas e desinteressantes, que muitas vezes resultam em desistência ou bloqueio frente ao conhecimento. A ideia central é que o professor possa desafiar seus alunos, estimulando-os a superar os obstáculos através do desenvolvimento do raciocínio e da necessidade do saber.
PALAVRAS-CHAVE: Xadrez; Xadrez Pedagógico; Matemática; Ensino; BNCC.
ABSTRACT: This work explores the many potential intersections between the teaching of Mathematics and the game of chess in the early grades of Elementary School, in accordance with the guidelines of the Base Nacional Comum Curricular (BNCC) for the entire Elementary School. The main objective is to integrate these two areas by proposing alternative methods to approach mathematical content within the school context. The proposal presented here aims to teach students in a way that avoids repetitive and uninteresting strategies, which often lead to disengagement or a mental block towards knowledge. The central idea is for the teacher to challenge their students, stimulating them to overcome obstacles through the development of reasoning and the need for knowledge.
KEYWORDS: Chess; Educational Chess; Mathematics; Teaching; BNCC.
1 INTRODUÇÃO
O jogo de xadrez há muito tem sido objeto de diversos estudos em diferentes áreas do conhecimento. Este jogo ganha cada vez mais popularidade no mundo e é praticado por um número crescente de adeptos de todos os níveis sociais, intelectuais e culturais.
Em nossa vida, estamos constantemente adquirindo habilidades para resolver problemas, mesmo na infância. Conforme avançamos nas etapas naturais da vida, a atenção e outras habilidades se tornam cada vez mais importantes. Com o aumento da expectativa de vida e o surgimento de novas doenças cerebrais, manter uma boa memória tornou-se extremamente importante para garantir uma melhor qualidade de vida.
Dentro desse contexto, a Base Nacional Comum Curricular (BNCC) destaca a importância do desenvolvimento de competências e habilidades que vão além dos conteúdos tradicionais, promovendo uma educação integral que abrange aspectos cognitivos, emocionais e sociais em todo o Ensino Fundamental. A integração do xadrez como ferramenta pedagógica no ensino da Matemática pode ser vista como uma estratégia alinhada a esses princípios, proporcionando aos alunos uma abordagem diferenciada que favorece o desenvolvimento do raciocínio lógico e crítico.
Nesse sentido, entendemos que:
O xadrez é uma atividade que além de proporcionar o lazer também dá a possibilidade de valorizar o raciocínio através de um exercício lúdico, podendo alcançar, dentre outros, os seguintes objetivos: · Desenvolver o raciocínio lógico; · Desenvolver habilidades de observação, reflexão, análise e síntese; · Desenvolver habilidades e hábitos necessários à tomada de decisões; · Compreender e solucionar problemas pela análise do contexto geral em que estão inseridos (SILVA, 1997 apud BEZERRA; ZANELLA, 2007, p. 66)
Por ajudar a realizar esse exercício mental, o jogo de xadrez pode melhorar a qualidade de vida de pessoas de todas as idades. Neste artigo, trataremos de algumas relações entre o xadrez e a Matemática e veremos como esses conteúdos podem ser inter-relacionados dentro e fora da sala de aula, tornando ambas as atividades mais atraentes.
Hoje em dia, é comum falar sobre o uso do xadrez na educação, mas infelizmente muitos o utilizam apenas como atividade extracurricular ou nas aulas de educação física como uma modalidade esportiva, o que minimiza a prática do jogo.
No contexto escolar, Vygotsky (2001) explica que é importante que o professor desenvolva as capacidades do aluno de forma holística, em campos variados. Para isso, é necessário trabalhar com o aluno os aspectos relacionados ao desenvolvimento das diferentes faculdades de concentração sobre os diversos conteúdos escolares. Assim, quando o professor estimula os processos internos de desenvolvimento do aluno, pode alcançar os objetivos e propósitos esperados.
O jogo de xadrez é um dos mais completos a ser praticado no ambiente escolar. Pode ser considerado uma prática esportiva, regulamentada por federações mundiais, nacionais e regionais, além de ser uma ciência, devido às diversas investigações sobre suas quase infinitas posições, postulados gerais e estudos teóricos. Como arte, o xadrez oferece posições artísticas e brilhantes, encontradas em milhões de partidas registradas, exigindo que quem as examina compreenda os princípios do jogo, sendo impactado como um apreciador das mais belas pinturas.
O xadrez possui um caráter criativo muito presente, produzindo posições praticamente infinitas, sempre oferecendo algo novo para aprender ou pesquisar. O jogador deve investigar continuamente a melhor forma de resolver seus problemas durante o jogo ou em torneios.
Bezerra e Zanella (2007) defendem que, ao ensinar xadrez no ensino fundamental, é possível transmitir valores éticos e potencializar habilidades. A prática do xadrez vai além da ética, do respeito e da lógica do bom comportamento. Há um respeito inerente em permitir que o adversário realize suas ideias e jogadas, e o xeque-mate, o ponto alto da partida, é seguido por uma nova partida, sem dano físico, apenas uma luta simbólica no tabuleiro. A derrota leva o jogador a refletir sobre ação e consequência, onde o erro é visto como um amigo do crescimento.
O xadrez também possui um caráter socializador, podendo ser praticado por pessoas de todas as idades e níveis sociais, culturais e educacionais. Existem kits de peças em diversas faixas de preço, e o jogo não exige força física, pois o embate é intelectual e mental. Neto (2004, p.1) indica que:
A atividade enxadrística realizada no contexto educacional permite trabalhar a melhoria da autoestima dos estudantes, visto que a sua iniciação não requer pré-requisitos (características físicas, sociais, etc.) e é acessível aos estudantes situados em qualquer altura da grade escolar.
Neste artigo, exploraremos algumas das relações entre xadrez e matemática. A escolha dessa relação se deve à ideia de que há inúmeras competências e habilidades conectadas à prática educativa do xadrez, comprovadamente benéficas para os alunos. Se bem trabalhadas no âmbito escolar, essas competências podem ajudar a diminuir a aversão às ciências exatas, incentivando os alunos a vencer obstáculos e resolver problemas no xadrez, habilidades que podem ser transferidas para o aprendizado da matemática, evitando o “fracasso escolar” (PATTO, 1999) causado pelo sistema educativo que faz os alunos acreditarem que não conseguem aprender.
Como Fadel (2016, p. 2) explica,
Fica evidente a necessidade de se buscar estratégias pedagógicas que contribuam para o aprimoramento de competências e habilidades com vistas à melhoria do desempenho escolar dos alunos. Ou seja, o aluno tem que ter a capacidade de “aprender” a desenvolver determinadas atividades, bem como a habilidade de “saber fazer”, de dominar os conhecimentos apreendidos.
Há um vasto conjunto de conhecimentos teóricos e práticos, advindos de anos de pesquisas realizadas em diversos países, que torna evidente que é possível, com base no xadrez, estender a aplicação de diversos aspectos trabalhados dentro do cotidiano escolar. Concluímos que o processo cognitivo da Matemática e do xadrez possui ampla relação, já que ambos “têm necessidade de utilizar o cálculo, o raciocínio lógico e a habilidade em lidar com elementos abstratos e limitados, por exemplo, com as peças no xadrez e com os números, nas práticas matemáticas” (JULIÃO, 2008, p. 5).
2 O TEMA
O fato de que, no xadrez, as peças têm valores pré-fixados – cada uma com uma pontuação diferente no início da partida – pode servir como um suporte eficaz para o desenvolvimento do raciocínio matemático básico. Ao considerar conteúdos fundamentais da matemática, como adição e subtração, que são trabalhados sistematicamente com alunos mais jovens, o xadrez oferece uma oportunidade prática e envolvente para reforçar esses conceitos. Relacionar essas duas áreas faz muito sentido, porque
O ensino da matemática, no caminhar de sua história, foi sobrecarregado de estereótipos, os quais, muitos autores afirmam serem uma das causas do repúdio que esta disciplina enfrenta na escola. Na busca de sanar estas dificuldades, muitos educadores têm trazido para o ensino da matemática uma didática lúdica, quebrando com algumas barreiras e preconceitos, buscando respaldos para esta prática nos jogos. (PEREIRA; LÔBO; SANTOS, 2013, p. 2)
Ainda,
Nos jogos de estratégia, parte-se da realização de exemplos práticos que levam ao desenvolvimento de habilidades específicas para a resolução de problemas e os modos típicos do pensamento matemático. Os jogos constituem uma forma interessante de propor problemas, pois permitem que estes sejam apresentados de modo atrativo e favorecem a criatividade na elaboração de estratégias de resolução e busca de soluções. (SANTOS, 2009, p. 70)
Ao introduzir o jogo de xadrez como um recurso de aprendizagem, o professor transcende o convencional e busca alternativas inovadoras para enriquecer sua prática pedagógica. Isso permite que o aluno desenvolva habilidades e conhecimentos práticos que beneficiem não apenas seu desempenho escolar, mas também sua vida em geral. Ao aprimorar sua capacidade de raciocínio, por exemplo, o aluno pode melhorar em diversos outros campos, já que:
O raciocínio é associado a outros conceitos, como inteligência, resolução de problemas e compreensão/pensamento. (…) O raciocínio é um dos elementos mais importantes da resolução de problemas, principalmente quando as tarefas a serem resolvidas exigirem descobertas de relações, comparação de elementos e a escolha de uma entre várias alternativas propostas como resposta. O raciocínio pode ser encarado como uma capacidade cognitiva exigida na resolução de problemas simples e complexos. (ALMEIDA, 1988 apud SANTOS, 2009, p. 65)
E na tentativa de evitar que haja uma resistência aos conteúdos ensinados nas escolas por ausência de certas habilidades nos alunos, percebemos que por exemplo, numa pesquisa feita por Pereira, Lôbo e Santos (2003, p. 7) “os alunos não conseguiam perceber a matemática como algo importante no seu dia-a-dia, tabu este quebrado quando eles começaram a conciliar o xadrez com a matemática, parecia que nesse momento, eles conseguiam ver sentido no aprender”.
2.1 Conteúdos Matemáticos
O campo de inserção do jogo de xadrez na Matemática e vice-versa é vasto, e Zanella e Bezerra (2007) apontam muitas sugestões de conteúdos matemáticos que podem ser explorados no xadrez. Entre eles estão: frações, noção de equivalência, noção de simetria, razão e proporção, lateralidade, potenciação, geometria plana, plano cartesiano, entre outros que serão apresentados junto as habilidades da BNCC mais a frente.
2.1.1 Valor absoluto das peças
Como exemplo, podemos pensar no valor individual e imutável das peças que formam o jogo, no qual cada uma delas sempre vale uma mesma pontuação independentemente da posição que ocupa, ou da atividade que exerce no tabuleiro. Exemplo: (Peão=1 ponto; Cavalo= 3 pontos; Bispo= 3 pontos; Torre= 5 pontos; Dama= 9 pontos e o Rei vale a vitória na partida)
Na posição inicial seguindo a lógica da pontuação pré-estabelecida cada lado possui 39 pontos ao somar todas as peças, e na total quantidade delas, com a seguinte disposição de pontos tabelados peça a peça:
Quadro 1 – Valor das peças

Fonte: Elaborado pelos autores
Figura 1 – Posição inicial das peças

Fonte: Elaborado pelos autores
Aplicando a Matemática, cada número independentemente da posição que ele ocupa não tem seu valor modificado. Os números podem possuir um caráter imutável, por exemplo: 1.234.567.890- caráter imutável
Onde contrariando a lógica do valor posicional de nosso sistema numérico não leríamos um bilhão, duzentos e trinta e quatro milhões, quinhentos e sessenta e sete mil, oitocentos e noventa. E sim, leríamos apenas a disposição dos números onde o 1 continua sendo 1, o 2 continua sendo o 2 e o 3 continua sendo o 3 e assim por diante. Já no próximo exemplo veremos a relatividade dos valores das peças e números de acordo com a posição que ocupam.
2.1.2 Valor relativo
A habilidade de atribuir um valor relativo as peças é de ir além do obvio, pois exige conhecimento prévio. Uma criança pode aprender facilmente a nomear os números de maneira isolada, mas terá uma dificuldade natural na hora de transpor o que esse conjunto de números forma em sentido maior. No xadrez também há essa dificuldade natural que exige conhecimentos prévios.
O aspecto do raciocínio lógico, no jogo de Xadrez, a criança passa a ter contato com diversos exercícios que lhe são propostos, nos quais ela deve buscar a melhor combinação dos lances a serem realizados, tendo a sua frente inúmeras possibilidades. Isso resultará em um ganho material (peças). (CHRISTOFOLETTI, 2005, p.2)
Poderá obter também uma posição mais favorável, mesmo possuindo menos pontos em peças. 1.234.567.890 – caráter mutável:
Figura 2 – O lado branco prestes a vencer

Fonte: Elaborado pelos autores
Figura 3 – O lado branco vence com material mínimo

Fonte: Elaborado pelos autores
No exemplo acima o jogador das peças pretas possuía todas as peças como no início da partida, o que representa 39 pontos. O lado das brancas possuía apenas um peão, e ao avançá-lo e atacar o rei preto, este não terá saída (estará em xeque-mate). Então, podemos dizer que o peão na partida, tem um valor relativo maior que as demais peças pretas, devido a posição que ele ocupa no tabuleiro.
Assim se dá também com o conjunto dos números naturais onde a posição que o número ocupa dentro do conjunto lhe garante maior ou menor valor.
Exemplo: 1<2<3<4<5<6<7<8<9<10… que significa que um é menor que 2, que é menor que 3 e assim por diante. Note agora a questão do valor posicional do número:
1.234.567.890 – um bilhão, duzentos e trinta e quatro milhões, quinhentos e sessenta e sete mil oitocentos e noventa.
No número citado o algarismo 1 tem um valor relativo de 1 (um) bilhão e por conta da posição que ocupa no número tem valor maior que os demais.
Além dessa distinção entre valor relativo e absoluto das peças, qual relação pode ser aplicada entre Matemática e xadrez? São inúmeras, como veremos nos exemplos seguir.
2.1.3 Adição
O jogador faz uso da soma de quantos pontos em peças ele capturou. Figura 4 – Calculando as adições

Fonte: Elaborado pelos autores
Na situação acima, partindo da ideia que as brancas capturaram das pretas dois bispos, um cavalo, uma torre e dois peões. O jogador vai fazendo as somas na ordem de captura.
1º capturou um cavalo = 3 pontos
2º capturou um peão= 1 ponto
3º capturou uma torre= 5 pontos
4º capturou um bispo= 3 pontos
5º capturou outro bispo= 3 pontos
6º capturou um peão= 1 ponto
Somando as parcelas 3+1+5+3+3+1= ele teria: 16 pontos capturados. Pode também realizar as somas das peças que o adversário capturou, por exemplo:
1º capturou um bispo = 3 pontos
2º capturou uma torre= 5 pontos
3º capturou um cavalo= 3 pontos
4º capturou um peão= 1 ponto
5º capturou outro cavalo= 3 pontos
6º capturou um peão= 1 ponto
Somando as parcelas 3+5+3+1+3+1= o adversário teria também: 16 pontos capturados. Também é possível utilizar-se do contrário da adição.
2.1.4 Subtração
O jogador calcula quanto de material ele possuía e quanto perdeu para o adversário. Ou numa troca de peças, o quanto ele ganhou ou perdeu de material através das trocas. Usando a ideia da adição, mas de forma inversa o jogador das brancas ou pretas poderia pensar usando o exemplo anterior: Figura 5 – Calculando as subtrações

Fonte: Elaborado pelos autores
Para trabalhar a subtração: partindo da ideia que as brancas perderam dois cavalos, um bispo, uma torre e dois peões. O jogador vai fazendo as subtrações na ordem de captura. Ele possuía 39 pontos.
1º perdeu um bispo = 39 – 3 pontos= Sobrou 36 pontos
2º perdeu um torre= 36 – 5 ponto= 31 pontos
3º perdeu uma cavalo= 31 – 3 pontos= 28 pontos
4º perdeu um peão= 28 – 1 pontos= 27 pontos
5º perdeu outro cavalo= 27 – 3 pontos= 24 pontos
6º perdeu outro peão= 24 – 1 ponto= 23 pontos
Subtraindo teríamos 39 – 3 – 5 – 3 – 1 – 3 – 1 = ele teria: 23 pontos de resto ou diferença.
2.1.5 Noções de geometria plana
O tabuleiro de xadrez é composto por linhas que estimulam nas crianças o que podemos chamar de imaginação geométrica. Os alunos precisam imaginar os cruzamentos de linhas e colunas para analisar se há alguma casa sob a influência de suas peças (Revista Cálculo, 2011, p.46).
A partir dessa atividade, podemos constatar que as peças de xadrez, através de suas movimentações, servem como apoio didático em aulas de geometria. Elas permitem que os alunos construam figuras geométricas, com o número de movimentos determinando o número de lados e, consequentemente, a figura correspondente. Por exemplo, os movimentos dos bispos podem ensinar sobre retas inclinadas e paralelas ao apontarem juntos para a mesma direção. Além disso, os bispos, ao se moverem sozinhos e formarem a letra X, ilustram retas concorrentes e perpendiculares. Figura 6 – Movimento do bispo, retas concorrentes e perpendiculares
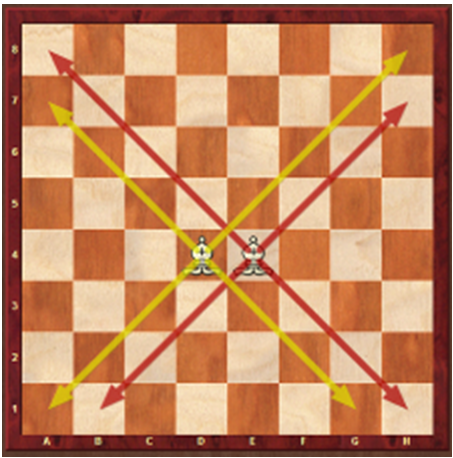
Fonte: Elaborado pelos autores
Retas perpendiculares com o movimento da torre.
Figura 7 – Movimento da torre, retas perpendiculares pois formam ângulos de 90º
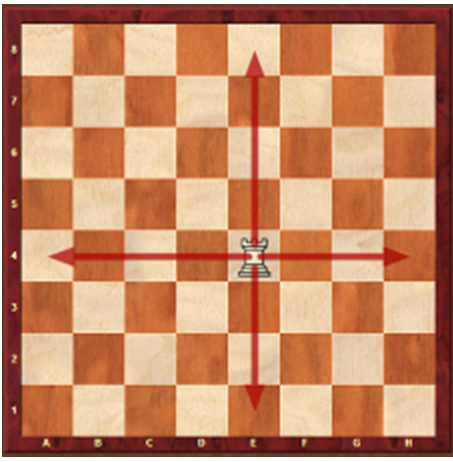
Fonte: Elaborado pelos autores
Semirretas de linhas verticais e horizontais com o movimento da torre.
Figura 8 – Movimento da Torre, semirretas, que são infinitas em uma direção

Fonte: Elaborado pelos autores
Ângulo de 90 graus com o movimento da torre.
Figura 9 – Movimento da torre

Fonte: Elaborado pelos autores
Semirretas horizontais, inclinadas e verticais com os possíveis movimentos da Dama.
Figura 10 – Movimento da dama, semirretas, infinitas em uma direção
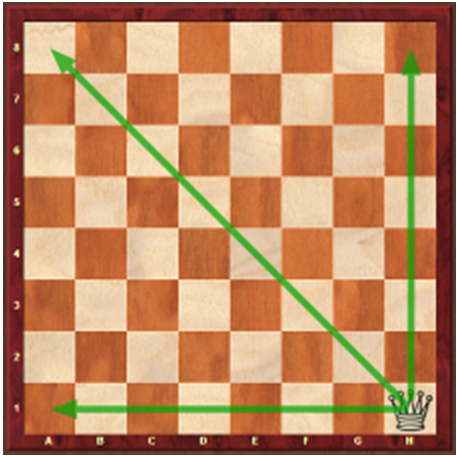
Fonte: Elaborado pelos autores
Retas perpendiculares e concorrentes com os possíveis da Dama.
Figura 11 – Movimento da dama, retas perpendiculares e concorrentes
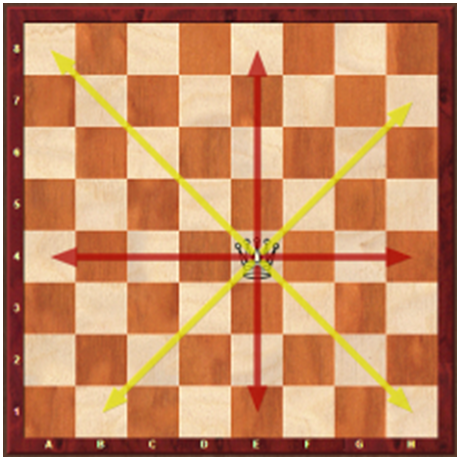
Fonte: Elaborado pelos autores
Ou ainda a pergunta: quantas retas passam pelo ponto e4 onde está a dama?
Figura 12 – Resposta: Infinitas retas passam por um ponto

Fonte: Elaborado pelos autores
2.1.6 Lógica
A lógica, conceito este discutido por inúmeros autores, pode ser apresentada também:
Por meio dos jogos as crianças não apenas vivenciam situações que se repetem, mas aprendem a lidar com símbolos e a pensar por analogia: os significados das coisas passam a ser imaginados por elas. Ao criarem essas analogias, tornam-se produtoras de linguagens, criadoras de convenções, capacitando-se para se submeterem a regras e darem explicações. (PASIN, 2011, p. 22)
2.1.7 Adições com símbolos e números
Supondo que o aluno não conhecesse ainda o valor das peças, ele poderia aprender por tornar verdadeira a adição abaixo:
Figura 13 – Exemplo de adição
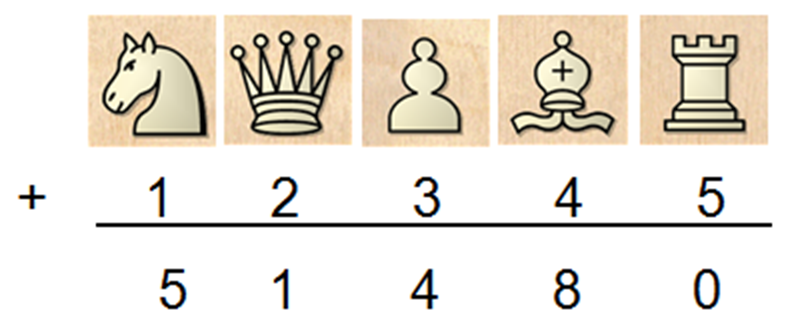
Fonte: Elaborado pelos autores
A adição acima seria equivalente a 39.135 + 12.345= 51.480. Nela, as peças do xadrez são símbolos com um valor pré-determinado e que em uma operação matemática poderia ser usado para representar números ou constantes.
2.1.8 Subtração com símbolos e números
Figura 14 – Exemplo de subtração
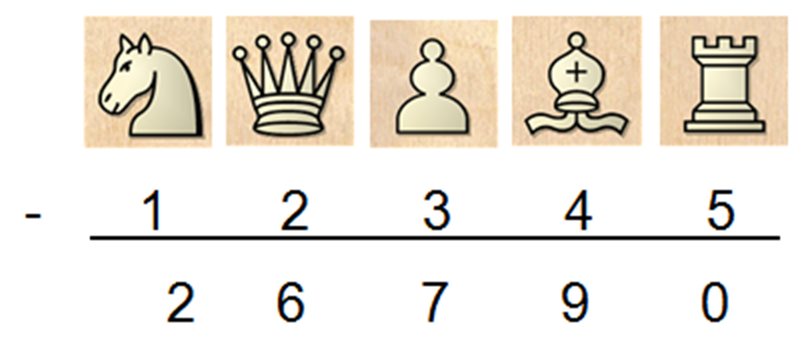
Fonte: Elaborado pelos autores
A subtração acima seria equivalente a 39.135 – 12345= 26790. Além das somas e subtrações é possível trabalhar as multiplicações e divisões. Vamos nos ater agora a parte da relação, Matemática e xadrez, com respeito ao conhecimento de frações.
2.1.9 Frações
No estudo das frações podemos destacar o uso do tabuleiro com e sem as peças nas aulas de Matemática.
Com as peças por exemplo podemos destacar as frações próprias que são aquelas com o Numerador (número que vai em cima na fração) e como Denominador que é o número que vai embaixo como sendo o todo do tabuleiro. É verdade que ensinar de uma maneira geral é um grande desafio, principalmente por meio de estratégias que não se renovam, ao falarmos sobre o ensino de frações (…) é difícil encontrar novas propostas circulando no ensino, nos deparamos apenas com métodos antigos, os quais dão prioridade a nomenclaturas e as figuras geométricas planas divididas e pintadas. Por ser um dos conteúdos mais difíceis, acredito que deveria ser dispensado um tempo maior a sua aprendizagem, e claro, uma maior dedicação por parte dos professores, mas isso não seria suficiente, os alunos precisam de novas práticas, pois como sabemos pela afirmação anterior, as que são usadas atualmente tem surtido um baixo efeito no aprendizado desses alunos. (SÁ, 2011, p. 15)
Observe agora a disposição do tabuleiro com somente as peças brancas. Figura 15 – Fração ocupada do tabuleiro apenas com as peças brancas

Fonte: Elaborado pelos autores
Representa a fração 16/64, que é lida por dezesseis sessenta e quatro avos. Essa fração é redutível e pode ser transformada ao dividirmos o Numerador e Denominador pelo maior divisor comum entre eles que é 16 como ¼, que se lê um quarto. O mesmo ocorre com a visão do tabuleiro a partir das peças pretas. Confira agora:
Figura 16 – Fração ocupada do tabuleiro apenas com as peças pretas

Fonte: Elaborado pelos autores
A fração seria também 16/64 como no exemplo anterior.
O próximo exemplo demonstra como somar frações com mesmo denominador. Ao juntarmos a montagem das peças brancas que representa 16/64 e das peças pretas que também representam 16/64 temos uma área do tabuleiro formada pela fração 32/64 que lê-se trinta e dois sessenta e quatro avos.
Figura 17 – Fração ocupada do tabuleiro com todas as peças

Fonte: Elaborado pelos autores
Essa também é uma fração redutível e 32/64 pode se transformar na fração equivalente ½ que significa que o conjunto das peças na posição inicial do jogo de xadrez ocupa exatamente metade das casas do tabuleiro.
Vejamos agora outras frações no tabuleiro sem as peças:
Figura 18 – Outros exemplos de frações
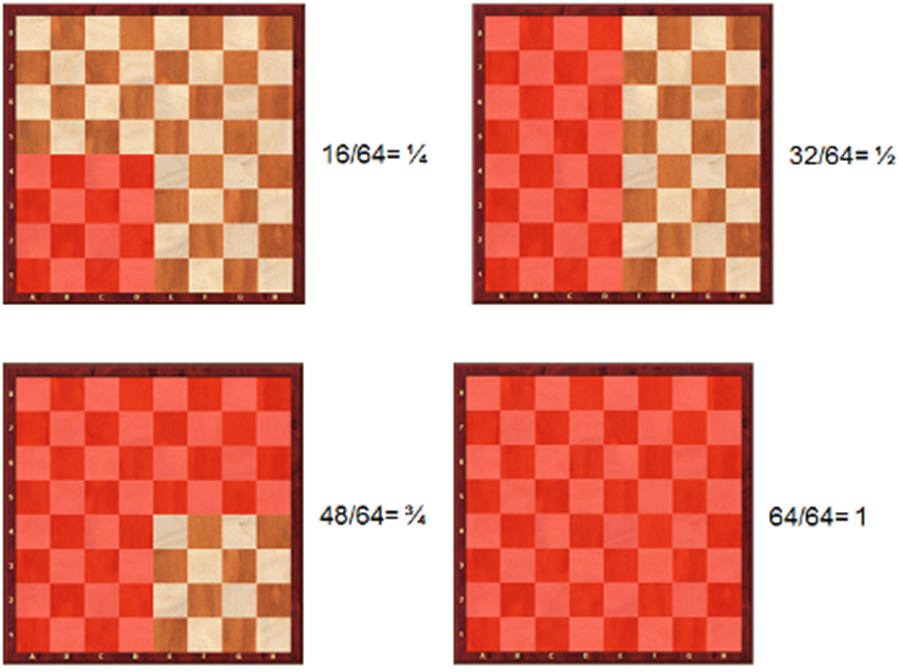
Fonte: Elaborado pelos autores
3. Relações possíveis entre as habilidades da Base Nacional Comum Curricular (BNCC) e o jogo de xadrez no ensino da Matemática
A leitura das habilidades citadas abaixo se faz assim:
Habilidade EF01MA04
BNCC – EF= Ensino Fundamental; 01= 1º ano; MA= Matemática; 04= Número da habilidade.
Texto da BNCC:
“Classificar e seriar objetos e figuras de acordo com suas semelhanças e diferenças, como forma, cor, textura, tamanho e outras propriedades observáveis.”
Explicação Simples:
Essa habilidade é sobre ensinar as crianças a identificar e agrupar objetos e figuras com base em características que eles podem observar, como a forma (redondo, quadrado), a cor (vermelho, azul), a textura (liso, rugoso) e o tamanho (grande, pequeno).
EF01MA04: Classificar e Seriar Objetos e Figuras
Habilidade BNCC: Classificar e seriar objetos e figuras de acordo com suas semelhanças e diferenças, como forma, cor, textura, tamanho e outras propriedades observáveis.
Relação com o Xadrez: As peças de xadrez podem ser classificadas e seriadas conforme suas características: peões, cavalos, bispos, torres, damas e reis. Cada peça possui formas, tamanhos e cores distintas, permitindo aos alunos praticarem a observação e a classificação. Isso desenvolve habilidades de discriminação visual e categorização, essenciais para a compreensão inicial de conceitos matemáticos.
3.1 EF02MA10: Estratégias de Cálculo Mental
Habilidade BNCC: Explorar estratégias de cálculo mental, utilizando propriedades das operações para adicionar ou subtrair números.
Relação com o Xadrez: No xadrez, os jogadores frequentemente somam e subtraem pontos para avaliar a situação no tabuleiro. Cada peça tem um valor específico (peão=1, cavalo=3, bispo=3, torre=5, dama=9). A prática de calcular rapidamente os pontos das peças capturadas ou sacrificadas durante o jogo promove o desenvolvimento de habilidades de cálculo mental.
3.2 EF03MA15: Resolver Problemas com Estimativa e Cálculo Mental
Habilidade BNCC: Resolver problemas utilizando estratégias de estimativa e cálculo mental com adição, subtração, multiplicação e divisão.
Relação com o Xadrez: Os jogadores de xadrez precisam estimar a força de suas posições e fazer cálculos rápidos para tomar decisões estratégicas. Resolver problemas no tabuleiro, como decidir qual peça mover ou capturar, envolve a aplicação de operações matemáticas e estratégias de estimativa.
3.3 EF03MA17: Multiplicação e Divisão para Resolver Problemas
Habilidade BNCC: Utilizar a multiplicação e a divisão para resolver problemas envolvendo essas operações, com significado e propriedades.
Relação com o Xadrez: A contagem dos pontos das peças pode ser usada para ensinar multiplicação e divisão. Por exemplo, calcular o valor total de um grupo de peças capturadas (3 peões, 2 cavalos, etc.) envolve multiplicar o número de peças pelo valor de cada uma e, em seguida, somar os resultados.
3.4 EF04MA12: Valor Posicional dos Números
Habilidade BNCC: Reconhecer, representar e analisar o significado do valor posicional dos números no sistema de numeração decimal.
Relação com o Xadrez: As posições das peças no tabuleiro podem ser entendidas em termos de valor relativo e absoluto. Por exemplo, a posição de uma torre em uma coluna aberta pode ser mais valiosa do que em uma coluna bloqueada. Esta analogia ajuda os alunos a compreenderem conceitos de valor posicional no sistema numérico.
3.5 EF05MA07: Grandezas Diretamente Proporcionais
Habilidade BNCC: Identificar e resolver problemas que envolvem grandezas diretamente proporcionais, como razão e proporção.
Relação com o Xadrez: A compreensão das proporções e relações entre diferentes peças do xadrez (por exemplo, a relação entre o valor de uma dama e dois cavalos) ajuda os alunos a desenvolverem o entendimento de razão e proporção.
3.6 EF05MA23: Identificar Ângulos
Habilidade BNCC: Explorar e identificar ângulos como mudança de direção ou giros, e utilizar instrumentos de medida e estimativa para encontrar ângulos.
Relação com o Xadrez: O movimento das peças, especialmente do bispo, da torre e da dama, envolve a compreensão de ângulos e direções. Por exemplo, o bispo move-se em ângulos diagonais, o que pode ser utilizado para ensinar conceitos de ângulos.
3.7 EF06MA10: Análise de Gráficos e Tabelas
Habilidade BNCC: Analisar gráficos e tabelas, para inferir e prever informações de situações cotidianas.
Relação com o Xadrez: Os gráficos e tabelas podem ser usados para registrar e analisar jogos de xadrez. Estatísticas de jogos, como número de vitórias, empates e derrotas, podem ser representadas graficamente para análise.
3.8 EF06MA11: Regularidades em Sequências Numéricas e Geométricas
Habilidade BNCC: Reconhecer e explorar regularidades em sequências numéricas e geométricas.
Relação com o Xadrez: Os padrões de movimento das peças de xadrez e a formação de figuras geométricas no tabuleiro ajudam os alunos a reconhecerem e explorarem regularidades.
3.9 EF07MA11: Medidas de Comprimento, Área, Volume, Capacidade, Massa e Tempo
Habilidade BNCC: Resolver problemas que envolvam medidas de comprimento, área, volume, capacidade, massa e tempo, utilizando as unidades de medida padronizadas.
Relação com o Xadrez: O movimento das peças no tabuleiro, que pode ser dividido em quadrantes, ajuda a compreender conceitos de espaço e medidas. Por exemplo, calcular a distância que uma peça precisa percorrer para atingir um determinado ponto no tabuleiro.
4. Benefícios do Xadrez no Desenvolvimento de Habilidades Socioemocionais Alinhados a BNCC
O xadrez, além de ser um jogo estratégico e intelectual, pode ser uma ferramenta eficaz no desenvolvimento de habilidades socioemocionais, conforme estabelecido pela Base Nacional Comum Curricular (BNCC). A BNCC destaca a importância das competências socioemocionais para o desenvolvimento integral dos alunos, e o xadrez se alinha perfeitamente com esses objetivos. Aqui estão alguns exemplos de como o xadrez pode contribuir para essas habilidades:
_A_
Educacao_dono_Campo_na_Base_Nacional_Comum_
Curricular_e_na_reforma_do_novo_Ensino_
Medio_desafios_para_o_ensino_de_Matematica
4.1 Tomada de Decisão e Responsabilidade
BNCC – Competência Geral 1: Conhecimento
Cada movimento no xadrez envolve a análise de opções e suas possíveis consequências. Essa prática constante de tomada de decisão ajuda os alunos a desenvolverem habilidades críticas de avaliação e a assumirem a responsabilidade por suas escolhas.
4.2 Perseverança e Resiliência
BNCC – Competência Geral 2: Pensamento científico, crítico e criativo
No xadrez, os alunos enfrentam derrotas e aprendem com seus erros, desenvolvendo perseverança e resiliência. Essa experiência ensina-os a lidar com fracassos de maneira positiva e a continuar tentando até alcançar o sucesso.
4.3 Planejamento e Estratégia
BNCC – Competência Geral 3: Repertório cultural
O xadrez ensina os alunos a pensar estrategicamente e a planejar suas jogadas com antecedência. Eles aprendem a considerar várias etapas à frente e a desenvolver um plano para alcançar seus objetivos, habilidades valiosas para a vida acadêmica e pessoal.
4.4 Controle Emocional
BNCC – Competência Geral 4: Comunicação
O xadrez ajuda os alunos a lidarem com a pressão e a manterem a calma em situações difíceis. O controle emocional desenvolvido no tabuleiro pode ser aplicado em várias situações da vida, ajudando os alunos a gerenciarem o estresse e a reagirem de forma equilibrada diante de adversidades.
4.5 Empatia e Cooperação
BNCC – Competência Geral 5: Cultura digital
Em ambientes onde o xadrez é jogado em pares ou em grupos, os alunos têm a oportunidade de desenvolver empatia e habilidades de cooperação. Eles aprendem a trabalhar juntos, a ajudar uns aos outros e a valorizar as perspectivas dos colegas, promovendo um senso de comunidade e apoio mútuo.
4.6 Paciência e Autocontrole
BNCC – Competência Geral 6: Trabalho e projeto de vida
O xadrez ensina os alunos a esperar pelo momento certo para fazer suas jogadas, promovendo a paciência e o controle da impulsividade. A prática constante de planejar e esperar desenvolve a capacidade de pensar a longo prazo e de manter a calma em situações de pressão.
4.7 Argumentação
BNCC – Competência Geral 7: Argumentação
No contexto do xadrez, os alunos são desafiados a argumentar suas jogadas e estratégias. Cada movimento requer justificativas baseadas em análises de possibilidades e antecipação das ações do oponente. Essa prática constante de argumentação desenvolve nas crianças e adolescentes habilidades de expressão clara, organização de ideias e defesa de pontos de vista.
4.8 Concentração e Foco
BNCC – Competência Geral 8: Autoconhecimento e autocuidado
O xadrez exige um alto nível de concentração para avaliar as jogadas do oponente e planejar as próprias estratégias. Essa habilidade de manter o foco em tarefas específicas é transferível para outras áreas acadêmicas e da vida.
4.9 Autoconfiança e Autoestima
BNCC – Competência Geral 9: Empatia e cooperação
À medida que os alunos melhoram suas habilidades no xadrez, eles ganham confiança em suas capacidades intelectuais e de resolução de problemas. Essa autoconfiança pode se refletir em outras áreas da vida, incentivando-os a enfrentar novos desafios com coragem.
4.10 Respeito e Esportividade
BNCC – Competência Geral 10: Responsabilidade e cidadania
O xadrez promove um ambiente de respeito mútuo, onde os jogadores aprendem a valorizar seus oponentes e a aceitar vitórias e derrotas com dignidade. Essa atitude esportiva é fundamental para o desenvolvimento de relações saudáveis e colaborativas.
Integrar a prática do xadrez no ambiente educacional, conforme as diretrizes da BNCC, proporciona um desenvolvimento abrangente das habilidades socioemocionais dos alunos. Essas competências são essenciais para o sucesso acadêmico e pessoal, preparando-os para enfrentar os desafios da vida com resiliência, empatia e confiança. O xadrez, portanto, vai além de um simples jogo, tornando-se uma ferramenta educativa poderosa para o desenvolvimento integral das crianças.
5. CONSIDERAÇÕES FINAIS
Ao longo deste estudo, exploramos a interseção entre o ensino da Matemática no Ensino Fundamental e o uso do xadrez como ferramenta pedagógica. Observamos como o xadrez não apenas oferece um meio lúdico e motivador para aprender, mas também desenvolve habilidades cognitivas fundamentais, alinhando-se com as competências gerais propostas pela Base Nacional Comum Curricular (BNCC). Estas incluem o raciocínio estratégico, a capacidade de planejamento, a análise crítica e a tomada de decisões sob pressão, essenciais para uma educação integral.
A integração do xadrez no currículo escolar vai além de simplesmente ensinar regras e movimentos; ela permite aos alunos aplicar conceitos matemáticos de maneira prática e contextualizada, promovendo o desenvolvimento de competências matemáticas básicas conforme preconizado pela BNCC. Por exemplo, o jogo ensina sobre valores numéricos atribuídos às peças e estratégias de contagem, fundamentais para a formação de uma base sólida em matemática desde os primeiros anos escolares.
Além disso, ao utilizar o jogo de xadrez, os educadores têm a oportunidade de cultivar um ambiente onde os alunos não apenas absorvem informações, mas também são incentivados a explorar, questionar e experimentar, desenvolvendo habilidades socioemocionais como autonomia, colaboração e respeito mútuo, conforme preconizado pela BNCC.
É crucial que os professores continuem a buscar formas criativas e inovadoras de apresentar o conteúdo escolar, alinhadas com os princípios da BNCC, proporcionando uma educação que prepare os alunos para enfrentar os desafios complexos de um mundo em constante mudança. O xadrez, com sua combinação única de desafio intelectual e diversão, desempenha um papel vital nesse processo educacional, transformando a maneira como os estudantes aprendem e se relacionam com o conhecimento.
Portanto, ao integrar o xadrez de maneira mais profunda e estruturada na educação, não estamos apenas enriquecendo o aprendizado acadêmico, mas também alinhando-nos com as competências gerais e habilidades socioemocionais propostas pela Base Nacional Comum Curricular (BNCC). Estamos preparando os alunos para se tornarem indivíduos críticos, criativos e resilientes, capazes de enfrentar os desafios do século XXI com confiança e competência.
REFERÊNCIAS BIBLIOGRÁFICAS
ALMEIDA, Jose Wantuir Queiroz. O jogo de xadrez e a educação matemática: como e onde no ambiente escolar. Campina Grande: Universidade Estadual da Paraíba – UEPB, 2010
ALMEIDA, L. S. O raciocínio diferencial dos jovens. Porto: Instituto Nacional de Investigação Científica. 1988.
BEZERRA, Renata Camacho; ZANELLA, André Ildemar. Xadrez: um recurso metodológico facilitador do processo de ensino e aprendizagem de matemática. Foz do Iguaçu: Ideação. Revista do centro de Educação e Letras da UNIOESTE – Campus de Foz do Iguaçu. v.9 n.10/11, p. 59-69, 2007
BRASIL. Ministério da Educação. Base Nacional Comum Curricular.
BRASIL. Referencial Curricular Nacional para a Educação Infantil. Brasília: Ministério da Educação e do Desporto. Secretaria da Educação Fundamental MEC/SEF. 2000.
BRASIL. Parâmetros Curriculares Nacionais. Brasília: Ministério da Educação e do Desporto. Secretaria da Educação Fundamental MEC/SEF. 2000.
BECKER, I. Manual de xadrez. São Paulo: Nobel. 1989.
CARVALHO, M. T. O jogo de xadrez e a aprendizagem Matemática: uma análise de possibilidades. Guaratinguetá: Faculdade de Engenharia do Campus de Guaratinguetá, Universidade Estadual Paulista. 2011.
CHRISTOFOLETTI, Danielle Ferreira Auriemo. O jogo de Xadrez na Educação Matemática. Revista Digital. Buenos Aires, año 10, n.80. 2005.
FADEL , Jacqueline Gisele Rosas; MATA , Vilson Aparecido da. O xadrez como atividade complementar na escola uma possibilidade de utilização do jogo como instrumento pedagógico. Paraná: Secretaria de Estado da Educação do Estado do Paraná. 2016.
JOSÉ, F.; MEDEIROS, F. Xadrez um novo aliado escolar. 2003. Disponível em: <http://www.tabuleirodexadrez.com.br/24-08-2003-reportagem-gazeta-de-alagoas.html>. Acesso em: 21 ago. 2016.
JULIÃO, T. Uma etnografia do xadrez: símbolos e representações. 2008. Disponível em <http://www.clubedexadrezonline.com.br/artigo.asp?doc=1028>. Acesso em: 21 ago. 2016.
LASKER, Edward. História do xadrez. São Paulo: IBRASA, 1999.
LOCATELI, MARIZA HELENA. Xadrez Na Escola: Ferramenta Pedagógica na melhoria do rendimento escolar através de uma abordagem interdisciplinar. Francisco Beltrão: Secretaria do Estado do Paraná. 2011.
NETO, Jaime Sunye, Xadrez Escolar: Um Instrumento Multidisciplinar numa Escola de Qualidade. 2004. Disponível em <http://www.tabuleirodexadrez.com.br/xadrez-escolar-um-instrumento-multidisciplinar-numa-escola-de-qualidade.html>. Acesso em: 21 ago. 2016.
PASIN, Silvia Dalla Corte. Uma Proposta para a aprendizagem dos números inteiros: Regras da adição e subtração. Porto Alegre: Universidade Federal do Rio Grande do Sul. 2011
PATTO, Maria Helena Souza. A produção do fracasso escolar: histórias de submissão e rebeldia. 2.ed. São Paulo: Casa do Psicólogo, p. 9-75. 1999
PEREIRA , Patricia Santos; LÔBO , Wériton de Souza; SANTOS, Silmary Silva dos. Xadrez uma prática lúdica e suas contribuições para o ensino da matemática. Anais do XI Encontro Nacional de Educação Matemática. 2013
SÁ, Fernanda Bartz de. Aprendizagem de frações no Ensino Fundamental. Porto Alegre: Universidade Federal do Rio Grande do Sul. 2011
SANTOS, Marciel Silveira. A abstratividade das ciências químicas, físicas e matemáticas – o xadrez como auxílio no desenvolvimento das habilidades cognitivas.Porto Velho: Saber Científico, 2009.
TIRADO, A.; SILVA, W. Meu Primeiro Livro de Xadrez: curso para escolares.Curitiba: Expoente. 1999.
VYGOTSKII, L.S.; LURIA, A. R.; LEONTIEV, A. N. Linguagem, desenvolvimento e aprendizagem. São Paulo: Ícone. 2001.
¹https://orcid.org/0009-0005-4294-6157
Mestrando em TICs, Universidad Europea del Atlántico- Santander-España
Pedagogo Universidade de São Paulo- USP/Ribeirão Preto- SP
Matemático, FIDE Arbiter e FIDE Instructor
Árbitro e Instrutor da Federação Internacional de Xadrez
profpaulohdefaria@gmail.com
²https://orcid.org/0009-0001-9094-0340
Graduanda em Letras, Universidade Virtual do Estado de SP- Univesp-
Administradora, Universidade de São Paulo- USP/Ribeirão Preto- SP
Contadora, Escritora e Organizadora de eventos da Confederação Brasileira de Xadrez
vanessa.benko@hotmail.com
