VERIFICATION OF THE SERVICE LIMIT STATE (ELS) OF EXCESSIVE DEFORMATIONS IN REINFORCED CONCRETE BEAMS ACCORDING TO NBR 6118 (2023) AND EUROCODE 2 (2004)
REGISTRO DOI: 10.69849/revistaft/th102412191009
André Luis Dalri Andreghetoni [1]
Marcos Wiese [2]
Resumo
A verificação do estado limite de serviço de deformação excessiva é essencial. É necessário considerar que na viga deformada podem haver seções Estádio I e outras seções que estejam no estádio II de deformação. Além da consideração dos efeitos causados pela fissuração é necessário considerar ainda a deformação lenta (fluência). O objetivo deste estudo é comparar os métodos propostos pelas normas técnicas ABNT NBR 6118 (2023) e Eurocode 2 (2004) para a verificação de deformações excessivas (flechas) para vigas de concreto armado. Foram moldadas quatro vigas de concreto armado, bi-apoiadas, com vão de 2,8m. Duas das vigas foram moldadas com seção transversal de 15×30 e duas com seção transversal de 20×40. As vigas foram submetidas a ensaio de flexão de 4 pontos. Os resultados experimentais foram comparados com os deslocamentos determinados pelos métodos da NBR 6118(2023) e Eurocode 2 (2004). Para as vigas com seção 15×30 verificou-se de maneira geral o método proposto pela norma europeia revelou-se ser o mais assertivo. Para vigas com seção 20×40 os resultados obtidos pelos dois métodos foram muito divergentes entre si e novamente que o método do Eurocode 2 (2004) foi o que mais se aproximou do comportamento obtido no ensaio com significativa assertividade.
Palavras-chave: Vigas. Concreto armado. Deformações excessivas. Estados Limites de Serviço.
1 INTRODUÇÃO
Os estados limites de serviço são os relacionados a durabilidade da estrutura, sua aparência, conforto do usuário e a boa utilização funcional das mesmas. Um destes estados limites de serviço está relacionado às deformações excessivas dos elementos estruturais. Deformações excessivas podem prejudicar o uso de uma edificação de diferentes maneiras, como por exemplo: efeito visual desagradável, vibrações indesejáveis, mau funcionamento de elementos não estruturais, deslocamentos que possam impedir a utilização adequada da construção e até deslocamentos que afetem o comportamento dos elementos estruturais. A dificuldade em prever tais deformações se dá no fato de que, em uma viga posta em serviço, diferentes seções transversais podem vir a trabalhar em estádios distintos – no caso, I e II, e, portanto, os momentos de inércia nestas seções serão diferentes.
A previsão destas deformações é essencial, pois desta maneira, torna-se possível evitar danos em elementos não-estruturais e evitar o desconforto ao usuário, quando as deformações se tornam visíveis (ABNT, 2014). Entre os métodos utilizados para determinação das deformações em vigas de concreto armado estão os propostos pelas normas NBR 6118 (2023) e Eurocode 2 (2004). O objetivo deste estudo é determinar os deslocamentos (deformações) em vigas de concreto armado através de modelos propostos pelas normas NBR 6118 (2023) e Eurocode 2 (2004) e comparar com resultados obtidos experimentalmente.
2 REFERENCIAL TEÓRICO
2.1 Estado Limite de Deformação excessiva
Como especificado anteriormente, o estado limite de deformações excessivas é atingido quando as deformações ultrapassam os limites estabelecidos para possibilitar a utilização normal da edificação como um todo. E quanto ao tipo de combinação utilizada para determinar as deformações excessivas, utiliza-se as combinações quase permanentes de serviço (ARAÚJO, 2010). A ABNT NBR 6118(2023) determina os deslocamentos limites, ou seja, valores práticos para verificação em serviço do estado limite. A norma também os classifica em quatro grupos, sendo eles:
a) Aceitabilidade sensorial: limite é caracterizado por vibrações indesejáveis ou efeito visual desagradável;
b) Efeitos específicos: os deslocamentos podem impedir a utilização adequada da construção.
c) Efeitos em elementos não estruturais: deslocamentos estruturais podem ocasionar o mau funcionamento de elementos que, apesar de não fazer parte da estrutura, estão a ela ligados;
d) Efeitos em elementos estruturais: os deslocamentos podem afetar o comportamento do elemento estrutural, provocando afastamento em relação as hipóteses de cálculo adotadas. Se os deslocamentos forem relevantes para o elemento considerado, seus efeitos sobre as tensões ou sobre a estabilidade da estrutura devem ser considerados, incorporando-os ao modelo estrutural adotado.
Segundo Chust e Rodrigues (2014), as deformações excessivas devem ser analisadas através de modelos que considerem a rigidez efetiva da seção da peça estrutural, devido ao fato de que, em uma viga sob ações de serviço, é observado na Figura 1 presença dos estádios de deformação I e II em diferentes seções, tornando-se inevitável a consideração dos efeitos da fissuração e retração, e a fluência do concreto.
Figura 1 – Estádios e diagramas de tensão na flexão de uma viga de concreto armado
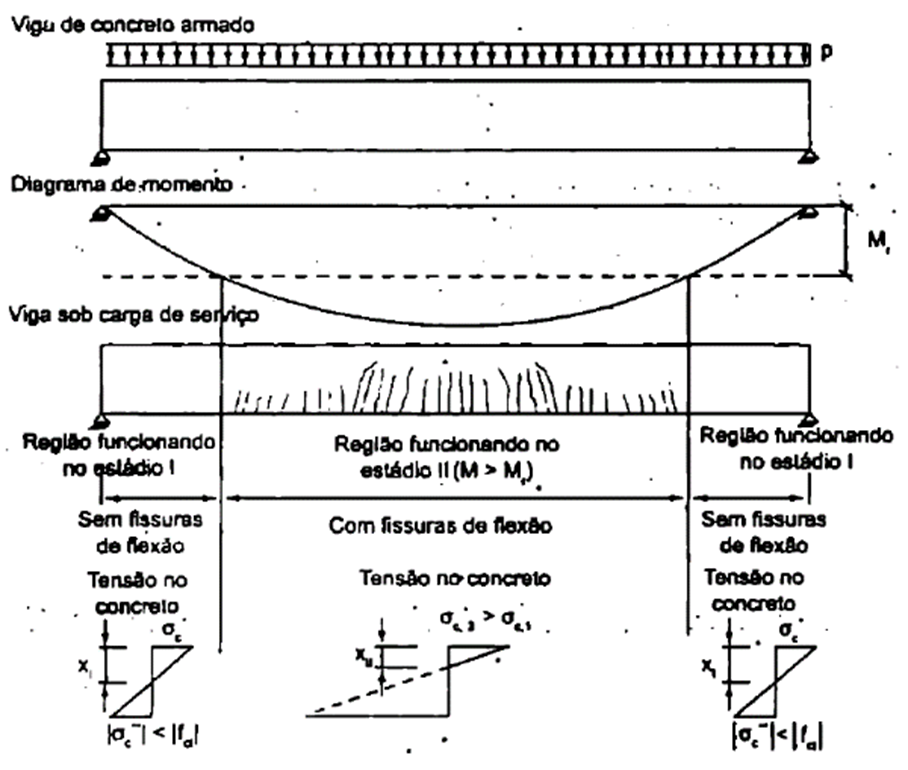
Fonte: Chust e Rodrigues (2014)
Na Figura 2, exemplifica-se o comportamento entre carga e deformação em uma viga submetida a flexão. Quando a seção do concreto fissura, verifica-se que o momento de inércia diminui, o que consequentemente diminui a rigidez, e então as deformações aumentam.
Figura 2 – Estádios e diagramas de tensão na flexão de uma viga de concreto armado
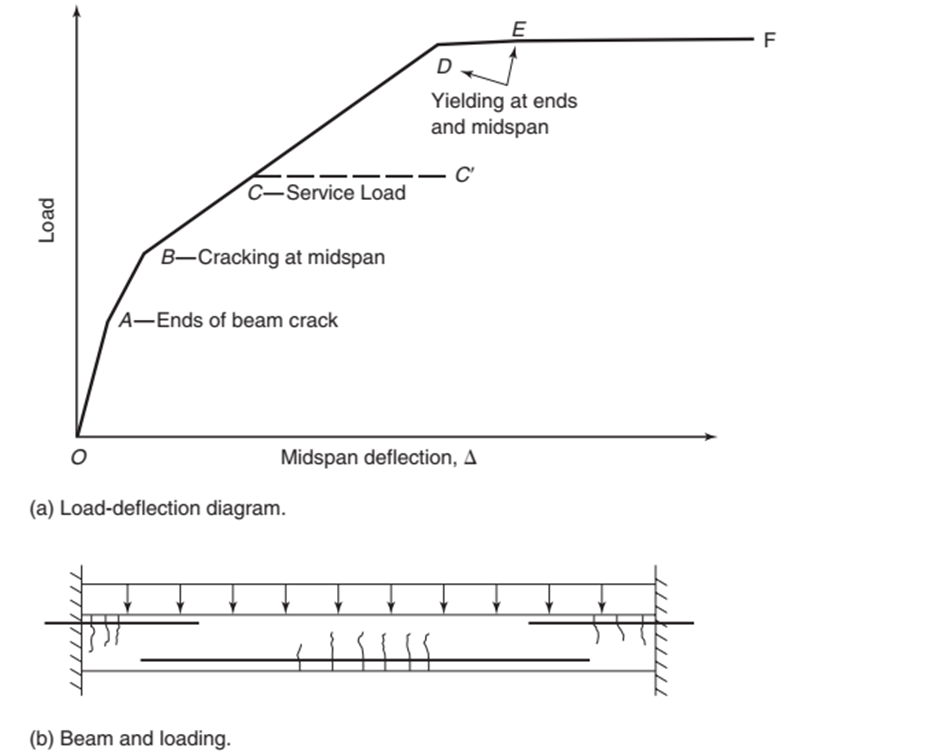
Fonte: Wight e MacGregor (2012)
2.2 Estádios do Concreto Armado
O estádio I, também chamado de estado elástico, ocorre quando um momento fletor de pequena intensidade gera tensões tão baixas que não ultrapassam a sua resistência característica a tração do concreto, ou seja, o concreto nesse estádio ainda está resistindo a esforços de tração. Nesse estádio não há fissuras, e o diagrama de tensão normal ao longo da seção é linear. O estádio II, ou estado de fissuração, acontece quando o momento fletor aumenta de tal maneira que as tensões geradas ultrapassem a resistência característica a tração do concreto. Neste estádio, o concreto sofre fissurações e já não suporta mais as tensões normais de tração, sendo totalmente resistidas pelo aço em si (ARAÚJO, 2010). Na Figura 3, observa-se os estádios I (beforecracking) e II (effectivesectionaftercracking) nas seções transversais de uma viga submetida a flexão.
Figura 3 – Estádios I e II em uma seção transversal de uma viga

Fonte: Wight e MacGregor (2012)
Assim, segundo Chust e Rodrigues (2014), diferentes seções em diferentes estádios implicam em rigidezes diferentes, o que significa que na determinação das flechas, é necessário saber as características geométricas da viga em cada estádio, para assim, definir uma inércia que represente esta situação.
2.3 Efeito da Fissuração
Visto que os estádios de deformação possuem relação direta com as deformações excessivas devido as diferenças das características geométricas promovidas pela fissuração do concreto, Branson (1968) desenvolveu um modelo que determina uma única inércia, que contempla os trechos fissurados e não fissurados de um elemento, ou seja, considera as diferenças de características geométricas em cada estádio (CHUST; RODRIGUES, 2014). O modelo está representado na Equação 1.
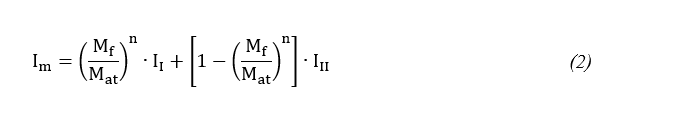
onde:
Im = momento de inércia efetivo/médio para uma seção ou para toda a peça no caso de vigas simplesmente apoiadas;
II = momento de inércia da peça no estádio I;
III = momento de inércia da peça no estádio II;
Mf = momento de fissuração do concreto;
Mat = momento atuante de serviço, na seção mais solicitada;
n = índice de valor igual a 4 para situações quando a análise é feita em apenas uma seção da peça, ou igual a 3 quando a análise é feita para todo o seu comprimento.
Segundo Pinheiro (2007), para uma viga de seção retangular, pode-se determinar o momento de inércia no estádio I e II, como exposto nas Equações 2 e 3, respectivamente.
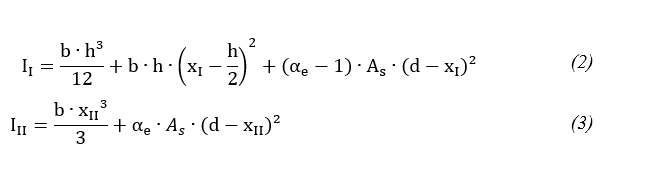
onde:
b = comprimento da base de uma seção retangular;
h = comprimento da altura de uma seção retangular;
xI = posição da linha neutra para o estádio I;
xII = posição da linha neutra para o estádio II;
αe = relação entre os módulos de deformação longitudinal do aço e doconcreto;
As = área de aço de tração;
d = comprimento da altura útil da seção.
E ainda segundo Pinheiro (2007), para uma seção retangular, têm-se as Equações 4 e 5 para obter-se a posição da linha neutra para uma viga trabalhando nos Estádios I e II, respectivamente. Como resultado da aplicação dessas equações, obtém-se a cota a partir da face superior da viga até sua linha neutra.
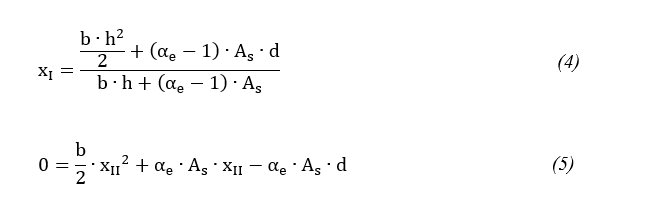
onde:
b = comprimento da base de uma seção retangular;
h = comprimento da altura de uma seção retangular;
xI = posição da linha neutra para o estádio I;
xII = posição da linha neutra para o estádio II;
αe = relação entre os módulos de deformação longitudinal do aço e doconcreto;
As = área de aço de tração;
d = comprimento da altura útil da seção.
Martin e Purkiss (2006) estabelecem as Equações 6 e 7 para a determinação da posição da linha neutra a partir da face superior da viga, para os Estádios I e II, respectivamente.
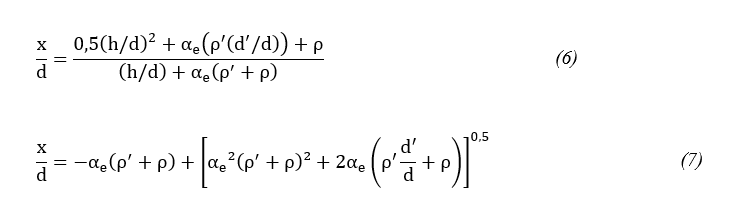
onde:
x = posição da linha neutra a partir da face superior da viga;
d = comprimento da altura útil da seção;
d’ = comprimento da altura da seção menos sua altura útil;
h = comprimento da altura de uma seção;
αe = relação entre os módulos de deformação longitudinal do aço e do concreto;
ρ = coeficiente dado por As/bd;
ρ’ = coeficiente dado por As’/bd;
E o momento de inércia da seção, para ambos os Estádios I e II são determinados através das Equações 8 e 9, respectivamente.
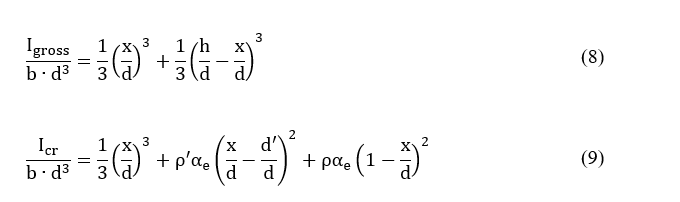
onde:
b = comprimento da base da seção;
d = comprimento da altura útil da seção;
d’ = comprimento da altura da seção menos sua altura útil;
h = comprimento da altura da seção;
x = posição da linha neutra para o Estádio I e II.
ρ = coeficiente dado por As/bd;
ρ’ = coeficiente dado por As’/bd;
2.4 Efeito da Fluência
A fluência pode ser definida como um fenômeno em que surgem deformações ao longo do tempo em um corpo solicitado por carga constante. Este fenômeno é parcialmente reversível, o que significa que, caso seja retirado o carregamento que originou a deformação, uma parte dessa deformação é recuperada imediatamente, outra parte é recuperada com o tempo, e uma outra parte é permanente na estrutura (CHUST; RODRIGUES, 2014).
O aumento da fluência é relativamente pequeno após um ano de carregamento na estrutura. Para efeitos meramente práticos, é determinado que 25% da fluência após um carregamento de 20 anos é obtida em 2 semanas, 50% da fluência é obtida em 3 meses, e 75% da fluência é obtida em 1 ano. A fluência do concreto pode ser crítica em vigas de concreto armado, pois a sua ocorrência aumenta as deflexões. Também podem ser críticas em pilares esbeltos carregados excentricamente, levando-os facilmente a flambagem (BROOKS; NEVILLE, 2013).
2.5 Método Proposto pela ABNT NBR 6118 (2023) para a Determinação de Deformações em Vigas.
A ABNT NBR 6118 (2023) propõe a seguinte expressão, representada pela Equação 10 para a determinação rigidez da peça para o cálculo de flechas imediatas.
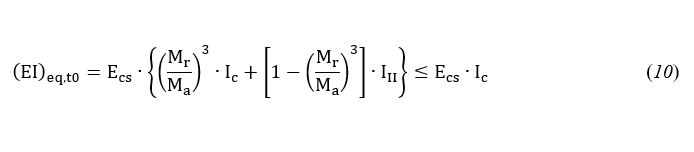
onde:
Ic = momento de inércia da seção bruta de concreto;
III = momento de inércia da peça no estádio II;
Ma = momento fletor na seção crítica do vão considerado;
Mr = momento de fissuração do elemento estrutural;
EI = rigidez;
Ecs = módulo de elasticidade secante do concreto.
Verifica-se que a expressão proposta pela ABNT NBR 6118 (2023) é uma adaptação da expressão proposta por Branson (1968) para o momento de inércia efetivo/médio.
A ABNT NBR 6118 (2023) estabelece a Equação 11 para a obtenção do módulo de elasticidade secante do concreto. Vale ressaltar que a Equação 7 considera o agregado graúdo como sendo granito.
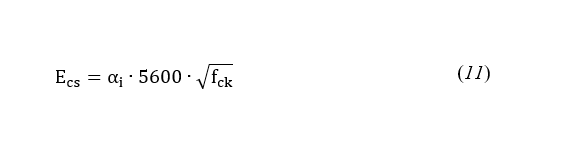
onde:
Ecs = módulo de elasticidade secante do concreto;
αi = coeficiente em função da resistência característica do concreto;
fck = resistência característica do concreto;
A ABNT NBR 6118 (2023) também informa que o momento de fissuração é dado pela Equação 12.

onde:
α = coeficiente relacionado a forma da seção;
Ic = momento de inércia da seção bruta de concreto;
yt = distância do centro de gravidade até a fibra mais tracionada;
fct,m = resistência média a tração do concreto, dada pela Equação 13, segundo a ABNT NBR 6118 (2023)

E, a partir dos resultados obtidos, é possível obter a flecha imediata através das tradicionais equações de flechas obtidas pela resistência dos materiais.
Para a determinação de flechas diferidas pelo tempo, ou seja, causadas pela fluência do concreto, a ABNT NBR 6118 (2023) recomenda que seja obtida através da multiplicação da flecha imediata pelo coeficiente αf, dado pela Equação 14.

onde:
ρ’ = coeficiente dado pela Equação 16;
ξ = coeficiente em função do tempo, dado pela tabela 17.1 da ABNT NBR 6118 (2023) ou calculado pela Equação 15.

onde:
As’ = área de aço de compressão;
b = comprimento da base de uma seção retangular;
d = comprimento da altura útil da seção.

onde:

2.6 Método Proposto pelo Eurocode 2 (2004) para a Determinação de Deformações em Vigas.
O Eurocode 2 (2004) propõe a seguinte expressão para o cálculo de flechas, conforme mostrado na Equação 17.

onde:
a = flecha total calculada;
aI e aII = parâmetros de curvatura calculados para os estádios I e II, respectivamente;
ξ = coeficiente de distribuição, calculado pela Equação 18.

onde:
b = coeficiente que leva em consideração a duração do carregamento, sendo 1,0 para carregamento único de curto prazo e 0,5 para um carregamento mantido a longo prazo;
M = momento fletor atuante no vão;
Mcr = momento de fissuração do elemento estrutural, que segundo Martin e Purkiss (2006) pode ser dado pela Equação 19;

onde:
fct,m = resistência média a tração do concreto, dado pelo Eurocode 2, da mesma maneira da ABNT NBR 6118, identificada neste trabalho como Equação 14.
h = comprimento da altura da seção;
x = posição da linha neutra para o Estádio I;
Igross = momento de inércia da seção bruta de concreto.
Para o cálculo da curvatura de deformação devido a retração do elemento estrutural, o Eurocode 2 (2004) dá como expressão a Equação 20.

onde:
S = momento estático da seção (deve-se considerar para ambos os Estádios I e II);
I = momento de inércia da seção (deve-se considerar para ambos os Estádios I e II);
αe = relação entre o módulo de elasticidade do aço e do módulo de elasticidade efetivo do concreto;
εcs = deformação específica de retração, dado no item 3.1.4 da norma e é apresentada abaixo, como Equação 21, a expressão para obtê-lo;

onde:
εca = tensão de encolhimento autógena, dada pelo Eurocode 2 (2004) pela Equação 22.

onde:
βas(t) = coeficiente dado pela Equação 23, sendo t a idade do concreto;
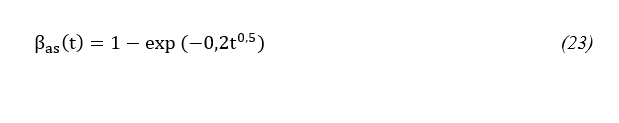
εca(ꝏ)= coeficiente dado pela Equação 24, sendo fck a resistência característica do concreto;

εcd = tensão de encolhimento por retração, dada pelo Eurocode 2 (2004) pela Equação 25.

onde:
εcd,0 = valor nominal de retração, dependente da umidade relativa do ar, dado pela Tabela 3.2 do Eurocode 2 (2004);
kh = coeficiente que depende do tamanho nocional da seção, obtido através da Tabela 3.3 do Eurocode 2 (2004);
βds(t) = coeficiente que depende de parâmetros de idade e cura do concreto, dado pela Equação 26.
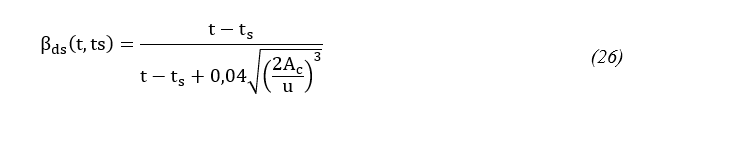
onde:
t = idade do concreto;
ts = tempo de cura do concreto;
Ac = área da seção bruta de concreto
u = perímetro da seção exposta a cura do concreto.
Para a obtenção do coeficiente αe, é necessário que seja obtido o módulo de elasticidade efetivo do concreto. A expressão para a obtenção do módulo de elasticidade efetivo do concreto está apresentada abaixo, na Equação 27.

onde:
Ecm = módulo de elasticidade secante do concreto, dado segundo Eurocode 2 (2004) por 22((fck+8)/10)0,3;
φ(t,t0) = coeficiente de fluência do concreto, dado pelo Anexo B da norma e é apresentado abaixo como Equação 28, a expressão para obtê-lo.

onde:
βc(t,t0) = coeficiente que considera o desenvolvimento da fluência com o tempo após o carregamento, dado pelo Eurocode 2 (2004) pela Equação 29.

onde:
t = idade do concreto;
t0 = tempo de cura do concreto;
βH = coeficiente que depende da umidade relativa do ar e o tamanho nocional da seção, dado pelo Eurocode 2 (2004) para concretos menores que C35 pela Equação 30.
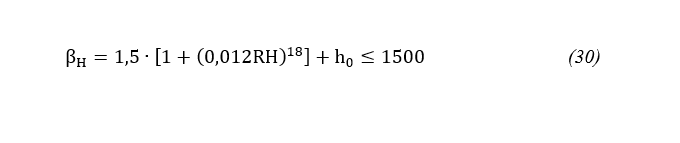
onde:
RH = umidade relativa do ar;
h0 = tamanho nocional da seção.
e:
φ0 = coeficiente de fluência nocional, dado pelo Eurocode 2 (2004) pela Equação 31.

onde:
β(t0) = coeficiente que permite considerar o efeito da idade do concreto ao carregamento no coeficiente de fluência, dado pelo Eurocode 2 (2004) pela Equação 32, sendo t0 o tempo de cura do concreto;

β(fcm) = coeficiente que permite considerar o efeito da força do concreto no coeficiente de fluência, dado pelo Eurocode 2 (2004) pela Equação 34, sendo fcm = fck + 8;

φRH = coeficiente que permite considerar o efeito da umidade relativa no coeficiente de fluência, dado pelo Eurocode 2 (2004) pela Equação 34 para concretos menores que C35, sendo RH a umidade relativa do ar e h0 o tamanho nocional da seção;

Para a obter-se as curvaturas devido ao momento fletor na seção, Martin e Purkiss (2006) estabelecem, segundo o Eurocode 2 (2004), a Equação 35 para a determinação da curvatura no Estádio I:

onde:
fct = tensão de tração na seção de concreto, dada por Msd.(h-x)/Igross;
Ec,eff = módulo de elasticidade efetivo do concreto;
h = comprimento da altura da seção;
x = posição da linha neutra para o Estádio I;
E a Equação 36 para o Estádio II:

onde:
fcs = tensão de compressão na seção de concreto, dada por Msd.x/Icr;
Ec,eff = módulo de elasticidade efetivo do concreto;
x = posição da linha neutra para o Estádio I;
3 METODOLOGIA
3.1 Materiais
Utilizou-se concreto usinado de resistência característica de 25 MPa, o cimento utilizado foi do tipo CPV ARI-RS – Cimento Portland do tipo V com alta resistência inicial e resistente ao sulfato -, este tipo de cimento não possui adições em sua composição e tem alta reatividade em suas primeiras horas de aplicação, o que concede um ganho alto de resistência em pouco tempo. O agregado graúdo utilizado para a fabricação foi a brita 1, com granulometria de 9,5 a 19 mm.
O concreto foi solicitado com abatimento (slump) de 12 ± 2 cm, e ao realizar-se o ensaio de abatimento (slumptest) in loco, seguindo os procedimentos prescritos nas recomendações da ABNT NBR NM 67 (1998), obteve-se como resultado um Slump de 13,5 cm, conforme Figura 4.
Figura 4 – Ensaio de abatimento realizado no recebimento do concreto

Moldou-se 20 corpos de prova para a realização do ensaio de determinação da resistência a compressão do concreto, sendo este número determinado através das exigências da ABNT NBR 12655 (2014). A moldagem dos corpos de prova cilíndricos foi realizada de acordo com as recomendações da ABNT NBR 5738 (2015), com suas dimensões sendo 10 cm de diâmetro de 20 cm de altura. Os procedimentos de rompimento foram realizados aos 28 dias de cura do concreto. Para a realização do rompimento dos corpos de prova, utilizou-se uma prensa servo controlada com capacidade de 2000 kN, seguindo as orientações da ABNT NBR 5739 (2015). A Figura 5 mostra os 20 corpos de prova que foram moldados para rompimento aos 28 dias de cura do concreto.
Figura 5 – Corpos de prova moldados para rompimento aos 28 dias

Os resultados obtidos no ensaio de rompimento dos corpos de prova aos 28 dias estão apresentados na Tabela 1, assim como a determinação da resistência a compressão do concreto.
Tabela 1 – Resultados do rompimento dos corpos de prova aos 28 dias
CP01: 25,0 MPa CP02: 24,0 MPa CP03: 25,7 MPa CP04: 24,3 MPa CP05: 28,1 MPa CP06: 27,4 MPa CP07: 31,3 MPa CP08: 25,7 MPa CP09: 29,8 MPa CP10: 27,0 MPa CP11: 24,2 MPa CP12: 28,5 MPa CP13: 28,1MPa CP14: 28,1 MPa CP15: 26,6 MPa CP16: 26,4 MPa CP17: 26,2 MPa CP18: 27,2 MPa CP19: 27,1 MPa CP20: 29,0 MPa
Com as resistências individuais de cada corpo de prova obtidas, é possível utilizar-se a Equação 38, de acordo com a ABNT NBR 12655 (2014), referente a amostragem parcial com 20 ou mais exemplares, para a determinação da resistência característica estimada aos 28 dias.

onde:
fck,est = valor da resistência característica estimada (MPa);
fcm = valor da resistência média dos exemplares do lote (MPa);
Sd = desvio padrão da amostra (MPa);
Aplicando-se a Equação 38 para as 20 amostras rompidas aos 28 dias, obteve-se como resistência característica (fck) o valor de 23,84MPa.
3.2 Amostras
Optou-se por confeccionar dois tipos de vigas: o Tipo 1, com seção transversal 15×30 (cm) e o Tipo 2, com seção transversal 20×40 (cm), ambas com 3 metros de comprimento. A classe de agressividade, segundo a ABNT NBR 6118 (2023) escolhida para a confecção das vigas foi a I – Fraca, com risco de deterioração da estrutura como sendo insignificante; portanto o cobrimento adotado para o dimensionamento das vigas foi de 2,5 cm. O dimensionamento das vigas foi feito através do método proposto por Araújo (2014), de acordo com a ABNT NBR 6118 (2023). O carregamento característico, determinado somente para efeito de dimensionamento da viga, foi de 23kN para as vigas do Tipo 1, com seção transversal de 15×30 cm, e 40kN para a vigas do Tipo 2. As condições de carregamento utilizadas para dimensionamento foram idênticas para ambas as vigas: vigas bi-apoiadas com aplicação de duas cargas concentradas com valor sendo metade das cargas previamente informadas – 11,5kN e 20 kN – a cada terço do comprimento da viga. A Figura 6 a seguir exemplifica esta condição de carregamento.
Figura 6 – Condição de carregamento utilizada para dimensionamento das vigas
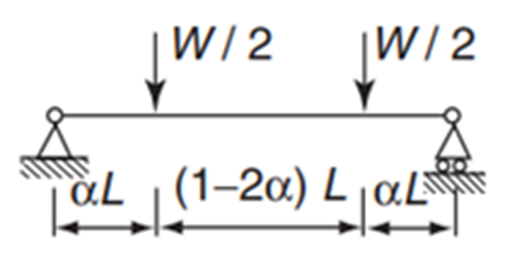
Fonte: Martin e Purkiss (2006)
O motivo da escolha por este tipo de carregamento é que, desta forma, têm-se no centro da viga, flexão pura, ou seja, há apenas o momento fletor atuando no terço central. A Figura 7 representa o detalhamento da armadura referente às vigas do Tipo 1.
Figura 7 – Detalhamento da armadura das vigas do Tipo 1 – 15×30
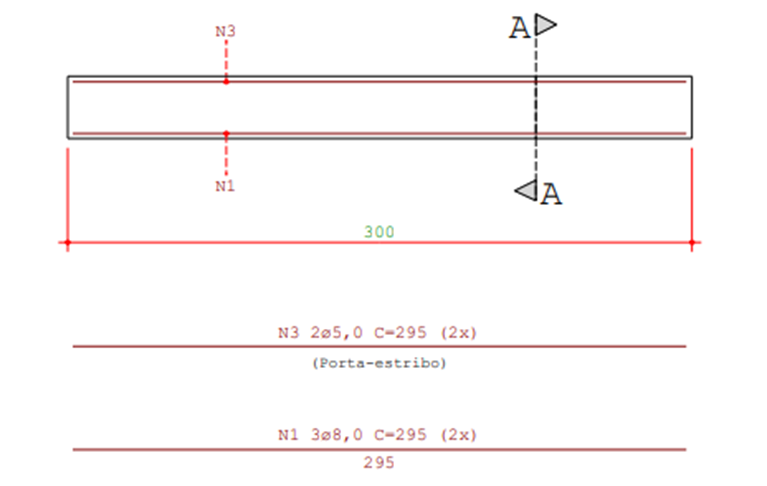
Na Figura 8, é possível observar no corte AA, a seção transversal deste mesmo tipo de viga.
Figura 8 – Corte AA da seção transversal das vigas do Tipo 1
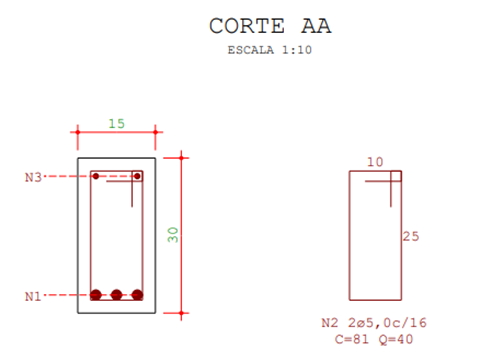
A Figura 9 representa o detalhamento da armadura referente às vigas do Tipo 2.
Figura 9 – Detalhamento da armadura das vigas do Tipo 2
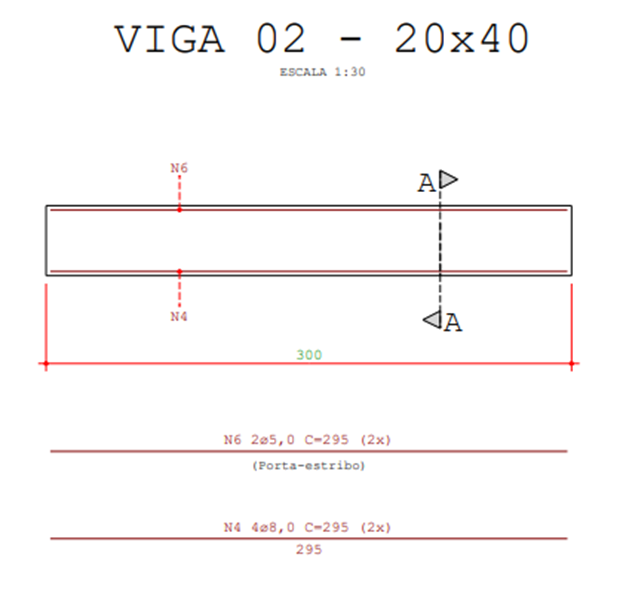
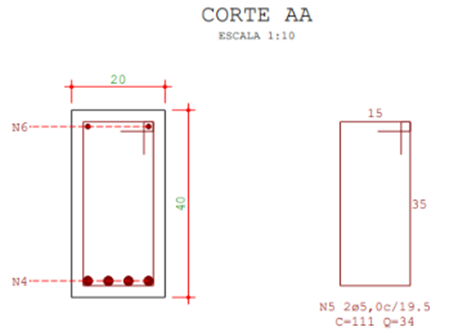
Na Figura 10, é possível observar no corte AA, a seção transversal deste mesmo tipo de viga.
Figura 10 – Corte AA da seção transversal das vigas do Tipo 2
Com o detalhamento propriamente feito, foi possível então realizar a moldagem das vigas em laboratório. A Figura 11 demonstram as armaduras das vigas antes de serem concretadas.
Figura 11 – Armadura das vigas do Tipo 1

Nas Figuras 12 e 13, é demonstrado as fôrmas das vigas antes e depois de serem concretadas.
Figura 12 – Fôrmas das vigas antes de serem concretadas

Figura 13 – Fôrmas das vigas depois de serem concretadas

Com as vigas devidamente moldadas foi possível então, após os 28dias de cura do concreto, levar as vigas novamente a laboratório para realizar-se o ensaio para determinar-se as deformações.
3.1 Ensaio de Flexão
Como sequência, determinou-se efetivamente as deformações nas vigas propostas. Foram realizadas majoritariamente de duas diferentes maneiras: por meio de ensaios realizados em laboratório, e por meio dos métodos simplificados das normas técnicas ABNT NBR 6118 (2023) e Eurocode 2 (2004). Na primeira maneira, como demonstrado, fez-se a moldagem das vigas em laboratório, respeitando-se minuciosamente as condições e dados propostos nas etapas iniciais do trabalho. Em seguida, foram determinadas e medidas as deformações, a partir dos ensaios realizados em duas máquinas universais de ensaios, uma com carga máxima de 50 toneladas e com controle de carga, e outra com tensão máxima de 400 bar e com controle de carga, e deformações medidas com um relógio comparador com precisão de 0,0001mm, como demonstrado no esquema da Figura 13.
Figura 13 – Esquema do ensaio
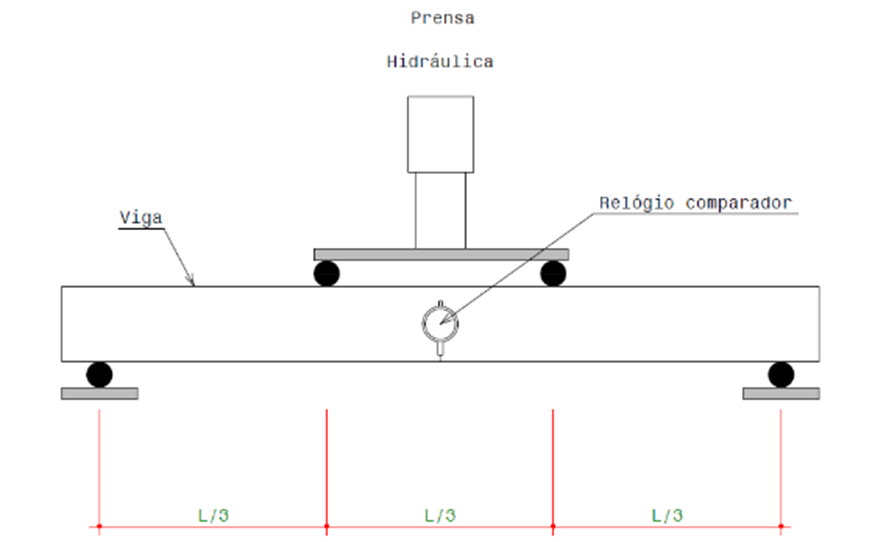
A Figura 14 demonstra o ensaio realizado em laboratório, aplicando-se as condições apresentadas na Figura 13.
Figura 14 – Esquema do ensaio em laboratório

É importante salientar que as vigas foram ensaiadas com um intervalo entre o incremento de cargas, para que a deformação tenha tempo para se consolidar e se estabilizar, e que também foram levadas até ultrapassarem o estado limite último.
No segundo procedimento, empregando-se os métodos simplificados, a obtenção das deformações é foi feita através da utilização de equações propostas pelos métodos de ambas as normas, que já foram anteriormente demonstradas. É importante ressaltar que as flechas obtidas e analisadas neste trabalho são referentes ao tempo 0, ou seja, as flechas imediatas.
4 RESULTADOS E DISCUSSÕES
Neste capítulo são apresentados os resultados obtidos nas aplicações dos métodos simplificados para obtenção de deformações imediatas, nas vigas dos Tipos 1 e 2, através da ABNT NBR 6118 (2023) e Eurocode 2 (2004), bem como os resultados obtidos experimentalmente através do ensaio de flexão da viga. Também são apresentados os resultados obtidos nos ensaios de determinação da resistência a compressão do concreto.
4.1 Método Simplificado da ABNT NBR 6118 (2023)
Foram determinadas as flechas máximas para as vigas, para incrementos de carga de 1 kN, iniciando em zero até a carga correspondente ao estado limite último considerado para dimensionamento. Os resultados foram plotados no gráfico P x f (carga x deslocamento). É importante ressaltar que os momentos de fissuração, estão destacados, o que significa que é com esse carregamento em que ocorre a troca de Estádios do concreto, do I para o II. Os resultados estão apresentados nas figuras 15 e 16 para as vigas do Tipo 1 e 2, respectivamente.
Figura 15 – Gráfico P (kN) x f(t=0) (mm) das vigas do Tipo 1 segundo NBR 6118 (2023)
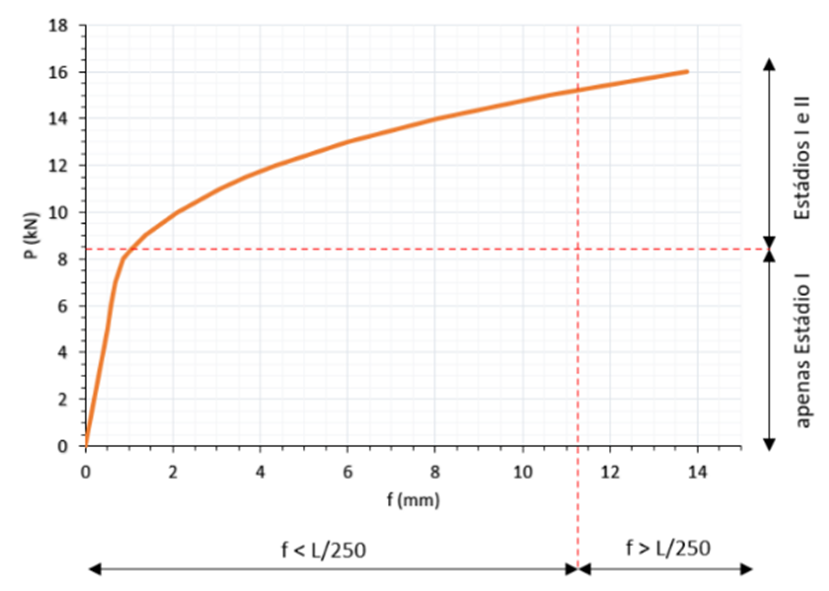
Figura 16 – Gráfico P (kN) x f(t=0) (mm) das vigas do Tipo 2 segundo NBR 6118 (2023)
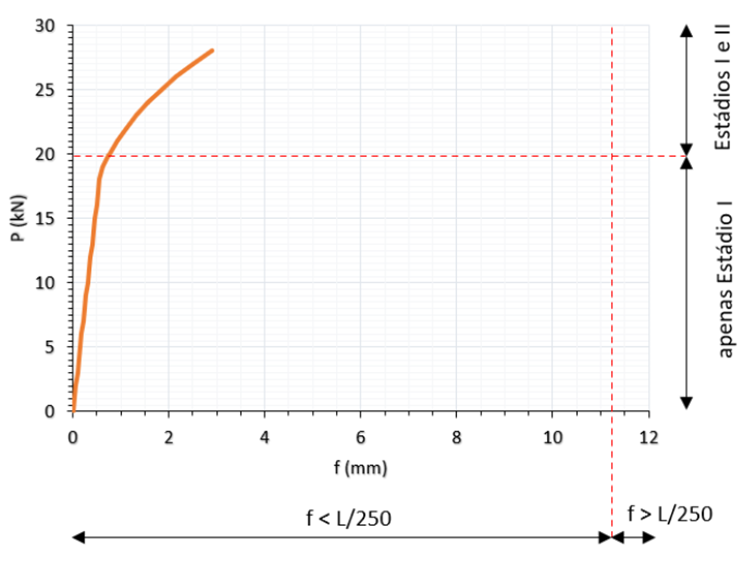
Nos gráficos apresentados, observa-se o ponto em que o concreto entra no estádio II em
ambas as vigas. Nota-se também que, para a viga do Tipo 1 alcança-se a deformação limite proposta pela norma, L/250, entre a carga de 15 e 16 kN, já para a viga do Tipo 2, este limite não é alcançado, sendo alcançado primeiro o estado limite último.
4.2 Método Simplificado do Eurocode 2 (2004)
As flechas máximas para as vigas foram determinadas pelo método simplificado do Eurocode 2 (2004) considerando incrementos de carga de 1 kN, iniciando em zero até a carga correspondente ao estado limite último considerado no dimensionamento. Os resultados foram plotados em um gráfico P x w (carga x deslocamento). Os momentos de fissuração, estão destacados, o que significa que é com esse carregamento em que ocorre a troca de Estádios do concreto, do I para o II. Os resultados foram apresentados nas figuras 17 e 18 para as vigas do Tipo 1 e 2, respectivamente.
Figura 17 – Gráfico P (kN) x w (mm) das vigas do Tipo 1 segundo Eurocode 2 (2024)
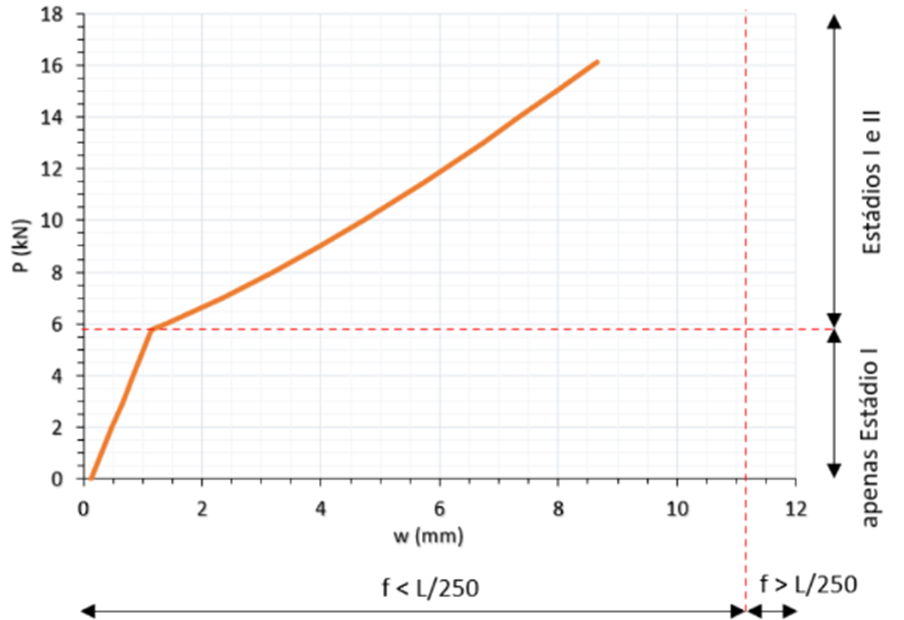
Figura 18 – Gráfico P (kN) x w (mm) das vigas do Tipo 2 segundo Eurocode 2 (2024)
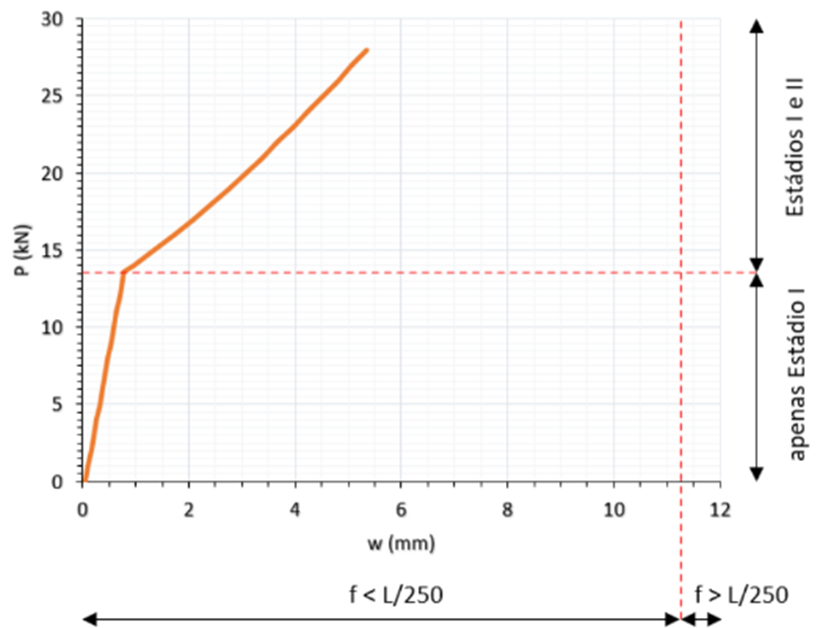
Observa-se nos gráficos o início do estádio II para os dois tipos de vigas. Nota-se também que a deformação limite proposta pela norma, L/250, não é alcançada em nenhuma das vigas, com o estado limite último sendo atingido primeiro.
4.3 Método Experimental
Após 42 dias da cura do concreto, encaminhou-se as quatro vigas ao laboratório e realizou-se o ensaio de flexão de 4 pontos. Para a execução do ensaio, utilizou-se dois tipos de prensas hidráulicas: uma menor, com capacidade de tensão de 400 bar, que utiliza um martelo com 2 cm de diâmetro para transmitir a carga, e outra maior, com capacidade de carga de 50 tf. Utilizou-se a prensa hidráulica menor para uma das vigas do Tipo 1, com seção 15×30, e para o restante das vigas utilizou-se a prensa maior. A Figuras 19 ilustra para uma das vigas do Tipo 1, o ensaio realizado em laboratório. Nota-se nestas figuras, o incremento de carga aplicado nas vigas, bem como a evolução da deformação e fissuração.
Figura 19 – Evolução do ensaio realizado em uma das vigas do Tipo 1

O incremento de carga utilizado no ensaio, ou seja, o aumento de carga a cada intervalo de ensaio, devido as estrutura e programação dos equipamentos, foi de 100 bar para a prensa hidráulica menor e 0,5 tf para a prensa hidráulica maior. É importante ressaltar que a prensa hidráulica maior tem como carga de partida uma grandeza de 2 tf, o que significa que foi a partir desta carga que as deformações nas vigas foram contabilizadas, exceto em uma das vigas do Tipo 1, onde utilizou-se primeiramente a prensa hidráulica menor e depois utilizou-se a maior.
Apresenta-se abaixo, como Tabelas 2 e 3, as cargas aplicadas na viga A do Tipo 1 e suas respectivas flechas imediatas obtidas. A Tabela 2 apresenta as deformações obtidas com a prensa menor, com capacidade de 400 bar, e a Tabela 3 apresenta as deformações obtidas com a prensa maior, com capacidade de 50 tf.
Tabela 2 – Determinação das flechas imediatas para a viga A do Tipo 1 pelo método experimental utilizando a prensa hidráulica de 400 bar
Pprensa P (kN) M (kN.m) f (mm) 0 0 0 0 100 bar 1,57 1,57 0,4245 200 bar 3,14 3,14 0,7605 300 bar 4,71 4,71 0,9660
Tabela 3 – Determinação das flechas imediatas para a viga A do Tipo 1pelo método experimental utilizando a prensa hidráulica de 50 tf
Pprensa P (kN) M (kN.m) f (mm) 2,0 tf 10 10,00 7,4015 2,5 tf 12,5 12,50 8,0300 3,0 tf 15 15,00 9,3270 3,0 tf 15 15,00 11,4900
É importante destacar que, após a retirada da primeira prensa hidráulica, de 400 bar, o relógio comparador demonstrou não haver deformação permanente na viga, com ela retornando à posição indeformada.
Com a execução dos ensaios, constatou-se que nesta viga alcançou-se o Estádio II do concreto no intervalo entre o carregamento de 4,71 e 10 kN. E com o carregamento de 15 kN constatou-se que a viga alcançou o escoamento do aço, ou seja, com este carregamento a viga já não suportava mais carga e a deformação registrada para os 15 kN somente aumentava conforme se tentava realizar um incremento de carga. É importante destacar que a deformação limite proposta pelas normas técnicas, L/250, foi atingida após alcançar-se o escoamento do aço
Abaixo, apresenta-se na Tabela 4 os resultados de flechas imediatas obtidas para a viga B do Tipo 1 e suas respectivas cargas.
Tabela 4 – Determinação das flechas imediatas para a viga B do Tipo 1 pelo método experimental utilizando a prensa hidráulica de 50 tf
Pprensa P (kN) M (kN.m) f (mm) 0 0 0 0 2,0 tf 10 10,00 7,3150 2,5 tf 12,5 12,50 8,1520 3,0 tf 15 15,00 9,6595 3,0 tf 15 15,00 16,2275
Com a execução dos ensaios, constatou-se que nesta viga alcançou-se o Estádio II do concreto antes de ser aplicada a primeira carga, de 10 kN. E, novamente, com o carregamento de 15 kN constatou-se que a viga alcançou o escoamento do aço.
A Tabela 5 apresenta os resultados de flechas imediatas obtidas através do ensaio realizado para a viga A do Tipo 2 e suas respectivas cargas. Porém, devido a falhas no ensaio relacionados ao equilíbrio do relógio comparador, os resultados aqui apresentados devem ser desconsiderados para análise e discussão.
Tabela 5 – Determinação das flechas imediatas para a viga A do Tipo 2 pelo método experimental utilizando a prensa hidráulica de 50 tf
Pprensa P (kN) M (kN.m) f (mm) 0 0 0 0 2,0 tf 10 10 1,5905 2,5 tf 12,5 12,5 3,5475 3,0 tf 15 15 3,8640 3,5 tf 17,5 17,5 4,1990 4,0 tf 20 20 4,7860 4,5 tf 22,5 22,5 5,2955 5,0 tf 25 25 5,9165 5,5 tf 27,5 27,5 6,8400 6,0 tf 30 30 7,2385 6,5 tf 32,5 32,5 7,9900 6,5 tf 32,5 32,5 8,8105
Na Tabela 6 abaixo, apresenta-se as flechas imediatas obtidas com o ensaio realizado para a viga B do Tipo 2 e suas respectivas cargas.
Tabela 6 – Determinação das flechas imediatas para a viga B do Tipo 2 pelo método experimental utilizando a prensa hidráulica de 50 tf
Pprensa P (kN) M (kN.m) f (mm) 0 0 0 0 2,0 tf 10 10,00 0,4890 2,5 tf 12,5 12,50 0,8530 3,0 tf 15 15,00 1,8020 3,5 tf 17,5 17,50 2,6365 4,0 tf 20 20,00 3,2785 4,5 tf 22,5 22,50 3,8260 5,0 tf 25 25,00 4,2715 5,5 tf 27,5 27,50 5,2015 6,0 tf 30 30,00 5,8530 6,5 tf 32,5 32,50 6,4310 6,5 tf 32,5 32,50 8,6550
Com a execução do ensaio, constatou-se que nesta viga alcançou-se o estádio II do concreto no intervalo entre o carregamento de 12,5 e 15 kN. E com o carregamento de 32,5 kN constatou-se que a viga alcançou o escoamento do aço. A deformação limite, para esta viga, não foi atingida em nenhum dos carregamentos aplicados.
4.4 Discussão dos Resultados
Com os resultados obtidos através das três maneiras: método da ABNT NBR 6118 (2023), método do Eurocode 2 (2004) e método experimental através dos ensaios realizados em laboratório, comparou-se as flechas obtidas por meio de gráficos de dispersão ligados por retas onde se relaciona a carga exercida nas vigas com as respectivas flechas, para os três métodos.
Primeiramente, comparando-se os dados obtidos para a viga do Tipo 1 e aplicando-os graficamente, obteve-se a Figura 20 como resultado.
Figura 20 – Comparação dos resultados obtidos para viga do Tipo 1 segundo os três métodos
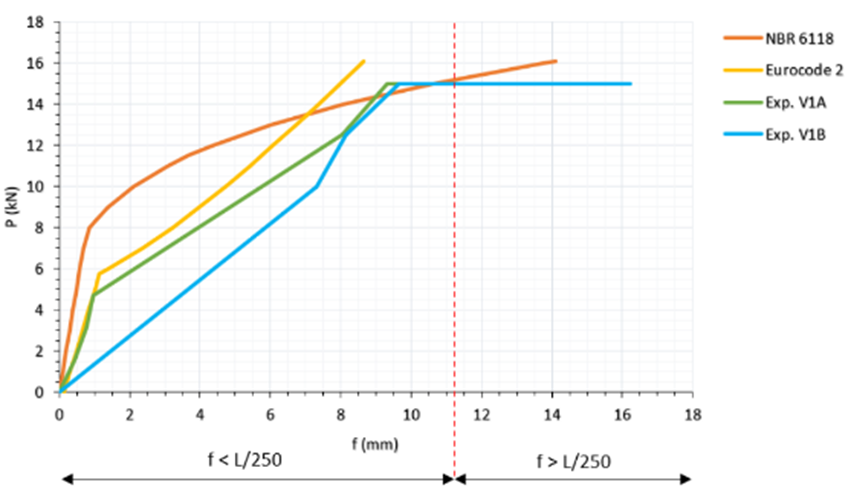
Observando primeiramente os resultados obtidos pelo método experimental aplicado nas duas vigas, é percebido que as flechas obtidas para as vigas com seção transversal 15×30 possuem um comportamento muito semelhante quando se compara o carregamento a partir dos 10 kN, a diferença percebida se dá apenas na primeira casa decimal do milímetro. É muito importante destacar também que, o trecho inicial da viga 1-B não representa bem o comportamento real, visto que o primeiro incremento de carga se deu com 10 kN, e a fissuração ocorreu antes desta carga.
Analisando-se a curva de deformação obtida com a Viga 1-A, onde utilizou-se as duas prensas hidráulicas para determinar-se as deformações, percebe-se que há uma lacuna entre os 4,71 kN e os 10 kN. Tal lacuna é observada devido a impossibilidade de realizar-se incrementos de carga como inicialmente desejou-se, pois as prensas hidráulicas possuídas pelo laboratório inviabilizam uma maior precisão para precisão, visto que esta viga ensaiada possui uma capacidade de carga baixa, e que o incremento de carga deve também ser baixo, pois assim se observaria uma curva de deformação com maior veracidade.
Outro fator importante a ser destacado que a lacuna obtida impossibilitou de ser analisado com maior precisão o início da ocorrência da fissuração, e consequentemente o início da ocorrência de seções no estádio II. Observa-se que, para a viga ensaiada, enquanto toda a viga estava no estádio I, o método do Eurocode 2 (2004) se mostra bastante assertivo no que se diz as deformações obtidas nesta etapa. O método proposto pela ABNT NBR 6118 (2023) se mostrou menos preciso para a viga quando estava totalmente no estádio I, apresentando flechas menores do que as que foram obtidas através dos métodos do Eurocode 2 (2004) e do método experimental aplicado a Viga 1-A.
Comparando as flechas obtidas em uma carga na faixa de 10 kN, observando-se as deformações, notou-se diferenças significativas entre os resultados do ensaio e dos métodos simplificados de cálculo. Enquanto observou-se deformações na grandeza de 7 mm em ambas as vigas ensaiadas em laboratório, a ABNT NBR 6118 (2023) previu 2,0985 mm, e o Eurocode 2 (2004) previu 4,7137 mm, demonstrando-se assim que o método simplificado que mais se aproximou dos ensaios, foi o Eurocode 2 (2004).
Esta diferença continuou sendo observada até próximo de atingir o estado limite último. No ponto de 15 kN, percebeu-se uma melhor aproximação do método da ABNT NBR 6118 (2023). A previsão da norma brasileira para esta carga foi de uma grandeza de 10,6223 mm, e, se comparado com o que obteve-se nos experimentos, 9,3270 mm para a viga 1-A e 9,6596 mm para a viga 1-B, conclui-se próximo ao estado limite último, observou-se uma maior assertividade da ABNT NBR 6118 (2023) sobre o Eurocode 2, que previu uma flecha de 7,9798 mm. A viga não conseguiu alcançar a carga de 17,5 kN (próximo incremento da prensa hidráulica).
É importante evidenciar também que, a deformação limite proposta pelas normas somente foi alcançada nos experimentos após o escoamento do aço ser atingido, diferentemente do que se previu segundo a ABNT NBR 6118 (2023), onde esta flecha foi alcançada entre 15 e 16 kN.
De uma forma geral, pode-se constatar que, analisando-se singularmente cargas e deformações, o método que mais se aproximou dos ensaios foi o método apresentado pelo Eurocode 2 (2004), principalmente quando nos primeiros incrementos de carga, quando a viga toda estava trabalho no estádio I. Já próximo a atingir o estado limite último, o método da NBR 6118 (2023) foi mais preciso. Verificou-se que na maior parte do ensaio, os métodos simplificados previram flechas menores do que foram verificadas em ensaio, logo, para a viga em questão, se mostraram pouco conservadores.
Ao comparar-se os dados obtidos pelos métodos para a viga do Tipo 2, e aplicando-os em um gráfico, assim como foi feito para a viga do Tipo 1, obteve-se como resultado a Figura 28. Novamente salienta-se que para a análise dos resultados, excluiu-se a amostra viga 2-B, pois verificou-se erros durante a execução do ensaio importante destacar também que, o trecho inicial da viga 1-B não representa bem o comportamento real, visto que o primeiro incremento de carga se deu com 10 kN, e a fissuração ocorreu antes desta carga.
Analisando-se a curva de deformação obtida com a Viga 1-A, onde utilizou-se as duas prensas hidráulicas para determinar-se as deformações, percebe-se que há uma lacuna entre os 4,71 kN e os 10 kN. Tal lacuna é observada devido a impossibilidade de realizar-se incrementos de carga como inicialmente desejou-se, pois as prensas hidráulicas possuídas pelo laboratório inviabilizam uma maior precisão para precisão, visto que esta viga ensaiada possui uma capacidade de carga baixa, e que o incremento de carga deve também ser baixo, pois assim se observaria uma curva de deformação com maior veracidade.
Outro fator importante a ser destacado que a lacuna obtida impossibilitou de ser analisado com maior precisão o início da ocorrência da fissuração, e consequentemente o início da ocorrência de seções no estádio II. Observa-se que, para a viga ensaiada, enquanto toda a viga estava no estádio I, o método do Eurocode 2 (2004) se mostra bastante assertivo no que se diz as deformações obtidas nesta etapa. O método proposto pela ABNT NBR 6118 (2023) se mostrou menos preciso para a viga quando estava totalmente no estádio I, apresentando flechas menores do que as que foram obtidas através dos métodos do Eurocode 2 (2004) e do método experimental aplicado a Viga 1-A.
Comparando as flechas obtidas em uma carga na faixa de 10 kN, observando-se as deformações, notou-se diferenças significativas entre os resultados do ensaio e dos métodos simplificados de cálculo. Enquanto observou-se deformações na grandeza de 7 mm em ambas as vigas ensaiadas em laboratório, a ABNT NBR 6118 (2023) previu 2,0985 mm, e o Eurocode 2 (2004) previu 4,7137 mm, demonstrando-se assim que o método simplificado que mais se aproximou dos ensaios, foi o Eurocode 2 (2004).
Esta diferença continuou sendo observada até próximo de atingir o estado limite último. No ponto de 15 kN, percebeu-se uma melhor aproximação do método da ABNT NBR 6118 (2023). A previsão da norma brasileira para esta carga foi de uma grandeza de 10,6223 mm, e, se comparado com o que obteve-se nos experimentos, 9,3270 mm para a viga 1-A e 9,6596 mm para a viga 1-B, conclui-se próximo ao estado limite último, observou-se uma maior assertividade da ABNT NBR 6118 (2023) sobre o Eurocode 2, que previu uma flecha de 7,9798 mm. A viga não conseguiu alcançar a carga de 17,5 kN (próximo incremento da prensa hidráulica).
É importante evidenciar também que, a deformação limite proposta pelas normas somente foi alcançada nos experimentos após o escoamento do aço ser atingido, diferentemente do que se previu segundo a ABNT NBR 6118 (2023), onde esta flecha foi alcançada entre 15 e 16 kN.
De uma forma geral, pode-se constatar que, analisando-se singularmente cargas e deformações, o método que mais se aproximou dos ensaios foi o método apresentado pelo Eurocode 2 (2004), principalmente quando nos primeiros incrementos de carga, quando a viga toda estava trabalho no estádio I. Já próximo a atingir o estado limite último, o método da NBR 6118 (2023) foi mais preciso. Verificou-se que na maior parte do ensaio, os métodos simplificados previram flechas menores do que foram verificadas em ensaio, logo, para a viga em questão, se mostraram pouco conservadores.
Ao comparar-se os dados obtidos pelos métodos para a viga do Tipo 2, e aplicando-os em um gráfico, assim como foi feito para a viga do Tipo 1, obteve-se como resultado a Figura 21. Novamente salienta-se que para a análise dos resultados, excluiu-se a amostra viga 2-B, pois verificou-se erros durante a execução do ensaio.
Figura 21 – Comparação dos resultados obtidos para viga do Tipo 2 segundo os três métodos
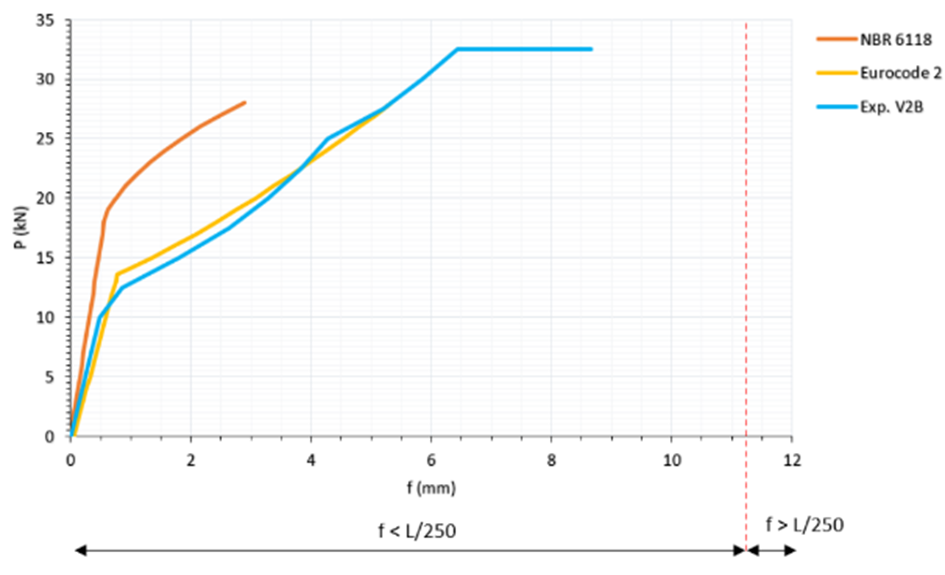
Observando as curvas de deformação obtidas para a viga do Tipo 2, percebe-se rapidamente que a configuração e aspecto obtidos com o método experimental se assemelha muito com o que foi calculado através do método proposto pelo Eurocode 2 (2004).
Enquanto trabalhando no estádio I, a viga ensaiada em laboratório, apresentou deformações intermediárias, se comparado com o que se previu utilizando os métodos simplificados.
Por este Tipo de viga possuir uma capacidade de carga maior do que o Tipo 1, no ensaio foi possível observar o início da ocorrência de seções trabalhando no estádio II, que ocorreu no intervalo entre os 12,5 e 15 kN, o que se assimila com o que foi determinado pelo método do Eurocode 2 (2004), onde a norma europeia previu que a carga de fissuração seria de 13,576 kN. Já a ABNT NBR 6118 (2023), apresentou menor precisão ao estabelecer a carga de fissuração, estabelecida como sendo 19,880 kN.
De uma forma geral, a curva de deformação apresentada pelo método simplificado da ABNT NBR 6118 (2023) pouco se assemelhou ao que foi observado tanto no Eurocode 2 (2004), quanto nos ensaios de laboratório. As flechas calculadas foram excessivamente baixas, se comparado com os outros dois métodos, e pode-se dizer que a curva obtida pouco representa a realidade encontrada.
O Eurocode 2 (2004), para esta viga, apresentou forma e grandezas muito semelhantes com o que foi obtido através dos ensaios, demonstrando que o método foi muito acurado nesta ocasião.
5 CONCLUSÃO
Na aplicação dos métodos de cálculo simplificados, propostos pelas duas normas analisadas, a ABNT NBR 6118 (2023) e o Eurocode 2 (2004), observou-se algumas diferenças entre os resultados obtidos através destes métodos. Inicialmente, analisando os resultados apresentados na previsão de flecha para as vigas do Tipo 1, verificou-se que os valores obtidos na aplicação dos dois métodos não foram tão discrepantes, porém, com uma análise gráfica, notou-se uma significativa diferença no aspecto que as curvas de deformação se apresentaram. E após, com a aplicação do método experimental, averiguou-se que de uma maneira geral, que o método proposto pela norma europeia revelou-se ser o mais assertivo.
Diferentemente das vigas do Tipo 1, as vigas do Tipo 2, apresentaram para a aplicação dos métodos propostos pelas normas, resultados muito divergentes. Novamente também se notou que diferentes perfis foram identificados na análise gráfica, com suas devidas proporções. E posteriormente, na comparação com o método experimental, verificou-se novamente que o método do Eurocode 2 (2004) foi o que mais se aproximou, desta vez com uma grande assertividade.
Alguns fatos podem explicar a discrepância entre os métodos e a maior assertividade do Eurocode 2 (2004). A norma brasileira, em comparação com a europeia, possui menos variáveis para a aplicação do seu método, citando-se por exemplo a umidade relativa do ar, idade do concreto, tamanho nocional, entre outros. Isso acabou por demonstrar que o método do Eurocode 2 (2004) é mais versátil e por consequência, mais assertivo. Vale destacar o método da norma brasileira, é uma adaptação de um modelo relativamente antigo, proposto por Branson em 1968, e o avanço dos materiais nesse período até os tempos atuais podem ter modificado parâmetros de análise. De maneira geral, pode-se concluir que para as vigas ensaiadas, o método simplificado do Eurocode 2 (2004) se mostrou mais próximo dos resultados na determinação do estado limite de serviço de deformações excessivas, se comparado com o da ABNT NBR 6118 (2023).
REFERÊNCIAS
ARAÚJO, José Milton de. Curso de Concreto Armado: Volume 1. 3. ed. Rio Grande: Dunas, 2010. 257 p. 1 v.
ARAÚJO, José Milton de. Curso de Concreto Armado: Volume 2. 3. ed. Rio Grande: Dunas, 2010. 395 p. 1 v.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 5738:2015 Concreto — Procedimento para moldagem e cura de corpos de prova. Rio de Janeiro, 2015.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 5739:2018 Concreto – Ensaio de compressão de corpos de prova cilíndricos. Rio de Janeiro, 2018.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118:2014: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 12655:2015: Concreto de Cimento Portland – Preparo, controle e aceitação – Procedimento. Rio de Janeiro, 2015
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM 67:1998 Concreto – Determinação da consistência pelo abatimento do tronco do cone. Rio de Janeiro, 1998.
BRANSON, D. E. Design Procedures for ComputingDeflections.ACI Journal, New York, n. 65, set. 1968.
BROOKS, J. J.; NEVILLE, A. M. Tecnologia do Concreto. 2. ed. Porto Alegre: Bookman, 2013. Disponível em:https://integrada.minhabiblioteca.com.br/books/9788582600726. Acesso em: 17 maio 2020.
CARVALHO, Roberto Chust; FIGUEIREDO FILHO, Jasson Rodrigues de. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado: segundo a NBR 6118:2014. 4. ed. São Carlos: Edufscar, 2014. 415 p.
COELHO, Jano D`araujo. Confiabilidade de vigas de concreto armado no estado limite de serviço. 2011. 272 f. Tese (Doutorado) – Curso de Engenharia Civil, Universidade Federal de Santa Catarina, Florianópollis, 2011. Disponível em: https://repositorio.ufsc.br/handle/123456789/95593. Acesso em: 17 maio 2020.
EUROPEAN COMMITTEE FOR STANDARDIZATION. Eurocode 2: Design of Concrete Structures – Part 1-1: General rulesandrules for buildings. Brussels: Cen, 2004.
FELIPE, Túlio Raunyr Cândido et al. Verificação do Estado limite de Deformação Excessiva para Vigas de Concreto Armado Submetidas à Ação Térmica. In: CONGRESSO BRASILEIRO DE PONTES E ESTRUTURAS, 9., 2016, Rio de Janeiro. Disponível em: http://www.abpe.org.br/trabalhos2016/90.pdf. Acesso em: 17 maio 2020.
JUNGES, Elisabeth. Estudo comparativo entre métodos simplificados e modelos de elementos finitos não lineares para o cálculo de flecha imediata em vigas de concreto armado. 2011. 360 f. Dissertação (Mestrado) – Curso de Engenharia Civil, Universidade Federal de Santa Catarina, Florianópolis, 2011.Disponível em: http://repositorio.ufsc.br/xmlui/handle/123456789/95129. Acesso em: 17 maio 2020.
MARTIN, Lawrence; PURKISS, John. Concrete Design: ToEN 1992. 2. ed. Londres: Butterworth-Heinemann, 2006.
PARIZOTTO, Liana. Concreto Armado. Porto Alegre: Sagah, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788595020917/cfi/1!/4/4@0:0.00. Acesso em: 26 abr. 2020.
PINHEIRO, Libânio M.. FUNDAMENTOS DO CONCRETO E PROJETO DE EDIFÍCIOS. São Carlos: Usp – Eesc – Dep. Eng. de Estruturas, 2007.
WIGHT, James K.; MACGREGOR, James G. Reinforced Concrete: Mechanics&Design. 6. ed. Nova Jersey: Pearson Prentice Hall, 2012.
[1] Engenheiro Civil – Universidade Regional de Blumenau e-mail: andrel.dalri@gmail.com
[2] Docente do Curso Superior de Engenharia Civil da Universidade do Estado de Santa Catarina – Centro de Educação Superior do Alto Vale do Itajaí e-mail: marcos.wiese@udesc.com.br
