REGISTRO DOI: 10.69849/revistaft/ch10202507091316
Andrilene Maciel1
Anderson Apolônio2
Resumo
Os mapas auto-organizáveis de Kohonen (SOM) têm sido amplamente utilizados na classificação de padrões e análise multivariada de dados em diversas áreas. Este artigo propõe uma abordagem baseada em SOM para classificação de sinais biomédicos de eletrocardiograma (ECG), focando na identificação de gargalos computacionais durante o processamento em CPUs convencionais. O sistema desenvolvido em MATLAB recebe os sinais de ECG e os parâmetros da rede neural para gerar mapas topográficos (matriz-U), possibilitando a identificação de padrões relacionados às arritmias cardíacas. Os resultados sugerem que o modelo pode ser ajustado para execução em arquiteturas paralelas (GPU), viabilizando sua aplicação em tempo real no apoio ao diagnóstico clínico.
Palavras-chave: Mapas Auto-organizáveis, ECG, Redes Neurais Artificiais, Mineração de Dados,
1 . Introdução
Estimativas da Organização Mundial de Saúde (OMS) apontam que as doenças crônicas não transmissíveis (DCNT) já são responsáveis por 17,8 milhões de mortes em todo o mundo anualmente (MENDIS,2014). Medidas governamentais são necessárias para alcançar as metas mundiais que visam a redução da carga das doenças crônicas não transmissíveis e prevenir mortes prematuras antes dos 70 anos, causadas pelas cardiopatias1,, acidentes cerebrovasculares, câncer e pela diabetes (PORTO,2005;MENDIS,2014). De acordo com o novo relatório da OMS (MENDIS,2014), a maioria das mortes prematuras causadas por doenças crônicas não transmissíveis são evitáveis.
No Brasil, as DCNT seguem o padrão de crescimento, tendo incidências em número semelhante ao que ocorre a nível mundial, sendo responsáveis por 19,4% de mortes prematuras entre pessoas com 30 e 70 anos (MENDIS,2014). Dentre elas destacam-se as doenças cardiovasculares, câncer, diabetes e doenças respiratórias (MENDIS,2014).
Essas doenças têm um forte impacto na qualidade de vida dos indivíduos afetados, ocasionando a morte prematura, gerando grandes e subestimados efeitos econômicos adversos para as famílias, comunidades e a sociedade em geral (PORTO,2005), (MACIEL,2015).
Recentemente, estudos que empregam mapas auto-organizáveis (SOM) e redes neurais como classificadores estão se tornando cada vez mais presentes, e essas abordagens têm sido aplicadas como ferramentas alternativas no contexto de análise de dados multivariados – incluindo mineração de dados com níveis satisfatórios de desempenho MUSTAQ(2007), JAIN (1988), (MACIEL A, 2023). Estudos recentes abordam a rede neural SOM para identificar os componentes de agrupamento intervalares (ALMEIDA,2013). Classificação usando arritmia cardíaca com redes neurais (LEITE,2010). Detecção de anomalia cardíaca usando mapas de Kohonen semisupervisionado (TRIQUI,2019). Aplicações de Redes Neurais de Kohonen para resolver problemas cardiovasculares (LYOZINA,2024). Preprocessamento e análise de sinais de ECG usando os Mapas de Kohonen (CACEK,2011). Análise de patologias cardíacas usando redes neurais (RADHWANE,2013). Os mapas de Kohonen representam a relação entre um objeto (por exemplo, fumante ou não) relacionado a um paciente específico. O grande problema de utilizar a rede de Kohonen para realizar a classificação de dados, está relacionada ao tempo de processamento da matriz U, o que poderá impossibilitar seu uso em sistemas de tempo real, quando utilizada em CPU’s convencionais.
Este artigo propõe uma mineração de dados usando as redes neurais de Kohonen (Self-Organizing Maps – SOM ), para classificar os sinais de arritmia cardíaca e gerar as vizinhanças entre as classes em função do tempo de processamento do algoritmo em CPU’s distintas e identificar os gargalos computacionais, os quais impossibilitam o melhor desempenho de processamento do algoritmo.
O sistema desenvolvido recebe parâmetros da rede neural, os sinais biomédicos e a saída da rede SOM, gera automaticamente um mapa unificado dessa estrutura em formato de clusters com objetivo de possibilitar um diagnóstico das arritmias a partir da classificação desses dados, que possa ser executadas em tempo considerado viável pelo médico e atribuir um possível diagnostico.
2. Métodos
2.1. Self-Organizing Maps – SOM
O principal objetivo da rede SOM é transformar um padrão de entrada de dimensão arbitrária em um mapa discreto unidimensional ou bidimensional. Há três processos envolvidos na SOM: a competição, a cooperação e a adaptação. A modelagem por rede SOM pode ser resumida da seguinte forma: quando um padrão de entrada x é apresentado à rede, o algoritmo SOM procura a unidade mais semelhante a x. Durante a fase de treinamento, a rede aumenta a similaridade do nó escolhido e de seus vizinhos com o padrão x. A rede SOM utiliza um algoritmo de aprendizado competitivo, onde os nós da camada de saída competem entre si para se tornarem ativos entre aqueles que geram a maior saída. Para cada padrão de entrada, apenas uma saída ou nó (dentro de um grupo de neurônios) se torna ativo (LUDEMIR,2000). O vetor de pesos sinápticos para cada neurônio na rede tem a mesma dimensão que o espaço de entrada. Tomando x = [x1, x2,…, xn]T, seja o vetor de pesos do neurônio j denotado por:
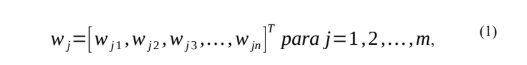
Fonte: LUDEMIR at. all,2000.
Onde m representa o número total de neurônios na rede. Agora, usamos o índice i(x) para identificar o neurônio que melhor corresponde ao vetor de entrada x, onde, aplicando a condição à distância euclidiana, determinamos i(x):
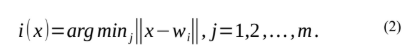
Fonte: LUDEMIR at. all,2000.
O neurônio vencedor, identificado por i(x), mapeia uma área de entrada para um conjunto discreto de neurônios. A resposta vem da atualização dos pesos vetoriais associados ao neurônio vencedor de acordo com a vizinhança topológica. Ao minimizar a distância entre os vetores x e w com base na maximização do produto interno de Ludemir (LUDEMIR,2000), o neurônio vencedor é aquele que tem a menor distância dos dados x (que melhor representa os dados). No processo de cooperação, o produto interno de requer que os neurônios próximos a ele também tenham seus vetores de peso sináptico ajustados na direção do vetor de dados. Assim, o neurônio vencedor deve excitar os neurônios que pertencem à sua vizinhança. Essa observação nos leva a fazer a vizinhança topológica ao redor do neurônio vencedor i decair suavemente com a distância lateral. Seja Nj,i a vizinhança centrada no neurônio vencedor i e abrangendo um conjunto de neurônios excitados, um típico dos quais é denotado por j. Seja di,j a distância lateral entre o neurônio vencedor e o neurônio excitado, então podemos assumir que a vizinhança topológica é uma função unimodal da distância lateral, aqui representada por:
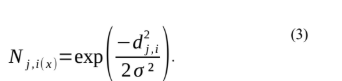
Fonte: LUDEMIR at. all,2000.
Para manter essa cooperação, é necessário que a vizinhança topológica dependa da distância lateral no espaço de saída, e não de alguma medida de distância no espaço de entrada original. Essa distância lateral pode ser definida como:

Fonte: LUDEMIR at. all,2000.
Onde o vetor discreto rj define a posição do neurônio excitante e ri define a posição discreta do vencedor, ambos medidos no espaço discreto de saída. No processo adaptativo, o vetor de peso do neurônio mais ativado, com distância rj, é atualizado em direção ao vetor de entrada x. O processo de adaptação dos vetores de peso sináptico do neurônio j no instante k é:
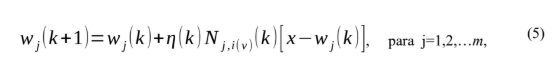
Fonte: LUDEMIR at. all,2000.
Onde η(k) define a taxa de aprendizagem, N j,i(x) define o grau de adaptação do neurônio em relação à vitória. A taxa de aprendizagem η(k) deve mudar gradualmente com o tempo, a fim de permitir uma convergência adequada da rede SOM [9]. Normalmente, η(k)→ 0 quando k→ ∞, sendo este requisito atendido pela escolha de um decaimento exponencial para η(k)[9][19]:
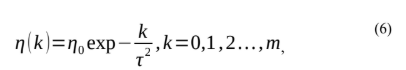
Fonte: LUDEMIR at. all,2000.
Onde τ2 é outra constante de tempo do algoritmo da rede SOM.
3. Sinais de Arritmia de Eletrocardiograma
3.1. Anatomia do Coração
A atividade mecânica cardíaca é precedida por um estímulo elétrico responsável pela ativação miocárdica (MOFFA,2001a). O estímulo elétrico tem origem no nó sinusal, representado por uma estrutura oval e alongada, semelhante a uma vírgula, com 5 mm de espessura, 10mm a 20mm de comprimento e a 1mm da superfície epicárdica atrial, localizada posteriormente ao ângulo de união na veia cava superior com o átrio direito e pode ser visto na figura 4.2 (MOFFA,2001a), (MOFFA,2010b).
O suprimento arterial do nó sinusal é realizado por ramos na artéria coronária direita, em 55% a 60% dos casos, e por ramos na circunflexa em 40% a 45% dos casos restantes(MOFFA,2001a).
O nó sinusal inicia a atividade elétrica normal do coração porque representa o marca-passo mais rápido e dominante, despolarizando-se espontaneamente. Em adultos, a frequência cardíaca é representada a partir de 60 a 100 bpm (batimentos por minutos) e define os limites normais do ritmo sinusal, formado pelas células nodais, transicionais e musculares atriais (MOFFA,2001a), (MOFFA,2010b).
As células nodais (figura 4.2), ou células P, recebem essa denominação por terem aparência pálida ao microscópio comum e representadas em pequenas dimensões (3mm a 10mm)(MOFFA,2001a).
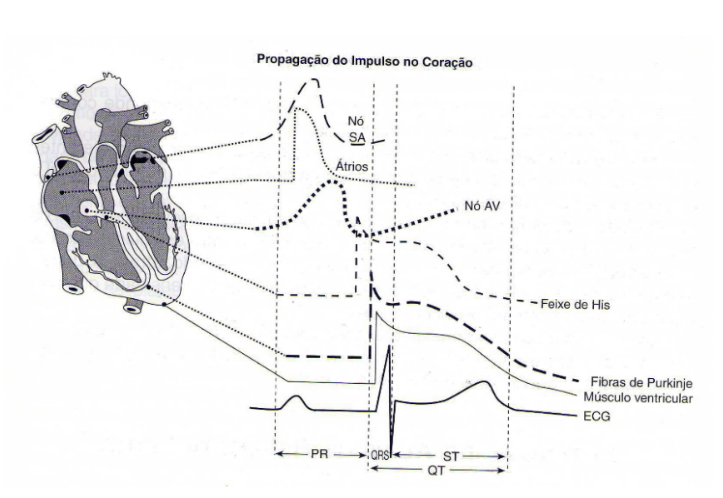
Figura 1. Curvas de potencial de ação das diferentes estruturas cardíacas e a correspondentes gêneses do ECG. Fonte: MOFFA,2001a.
As células P são células com função de marca-passos; e são menos estriadas (primitivas), quando comparadas às células miocárdicas ordinárias. Elas possuem menor número de mitocôndrias e miofibrila que as células contráteis e estão agrupadas em pequenos feixes fascículos interconectantes que se conectam entre si, em meio à matriz de tecido fibroso (MOFFA,2001a). As células transicionais ou células T, são assim denominadas devido à estrutura intermediária entre as células P, apresentam forma alongada e estreita, estão localizadas às margens do nó (figura 2), cujas células nodais tornam-se contíguas com o miocárdio atrial. As células T próximas às células nodais apresentam conexões intercelulares simples, enquanto discos intercalares mais desenvolvidos são encontrados na célula T; as nodais, por sua vez, comunicam-se entre si com as células miocárdicas atriais (MOFFA,2001a). Do ponto de vista funcional, as células T são vias de ligação entre as células P e o restante da musculatura cardíaca. O terceiro tipo de célula é a célula miocárdica atrial ordinária.
Segundo Moffa (2001a), a célula P representada pelo nó sinusal seja responsável pelo automatismo fundamental do coração e pelo tipo peculiar de potencial transmembrana de ação; ao passo que às células T têm a função de transmitir o estímulo elétrico às células miocárdicas atriais contráteis.
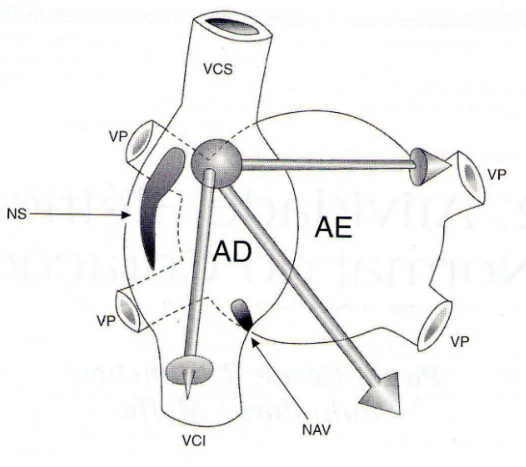
Figura 2. Relação espacial do átrio direito (AD) e do átrio esquerdo (AE). NS = Nó sinusal; NAV = nó atrioventricular; VCS=veia carva superior; VCI = veia carva inferior; VP=veia pulmonar. orientação dos vetores de ativação atrial, direito, esquerdo e resultante. Fonte: MOFFA,2001a.
3.2. Características básicas do eletrocardiograma
O equipamento necessário para o registro do eletrocardiograma (ECG) é o eletrocardiógrafo, esse aparelho é basicamente um galvanômetro, cuja função é detectar as diferenças de potenciais geradas no campo elétrico do coração. O eletrocardiógrafo promove a amplificação do sinal, filtragem das interferências da rede elétrica e das contrações musculares esqueléticas e o registro dos fenômenos elétricos (MOFFA,2001a).
Segundo Moffa (2001a),para o registro do ECG é necessário que se feche o circuito elétrico entre o coração e o eletrocardiógrafo. Para esse fim colocam-se eletrodos metálicos na sua superfície corporal, especificamente nos braços (punhos) e nas pernas (tornozelos), constituindo as derivações nos membros, na parede torácica (anterior [V1-V6] e, eventualmente, posterior [V7-V9]), derivações precordiais. Esses eletrodos exploradores são conectados ao aparelho de registro por fios condutores.
As derivações bipolares registram as diferenças de potenciais elétricos entre dois eletrodos posicionados em diferentes locais, uma vez que, não se conhece o potencial real de cada eletrodo (MOFFA,2001a).
As derivações bipolares, D1, D2 e D3, registram as diferenças de potenciais elétricos no plano frontal (PF). Assim, D1 registra as diferenças de potenciais elétricos entre o braço esquerdo (polo positivo) e o braço direito (polo negativo); D2, entre a perna esquerda (polo positivo) e o braço direito (polo negativo), e D3, entre a perna esquerda (polo positivo) e o braço esquerdo (polo negativo). O eletrodo da perna direita é considerado conexão terra (MOFFA,2001a).
4. Metodologia
4.1. Modelagem dos Dados na Rede Neural – SOM
A metodologia para seleção de dados de eletrocardiograma (ECG), tem como principais características a modelagem dos dados a ser integrada na rede neural de Kohonen. Primeiramente, busca-se identificar o tipo de doença cardiológica a ser estudada, para poder realizar a coleta do sinal de ECG no portal do Physiobank (PHYSIONET,2025). O algoritmo foi desenvolvido usando MATLAB R2025a, para seleção dos dados, conversão dos dados originais, definição dos parâmetros da rede neural e classificação dos sinais de ECG, usando o módulo da Toolbox da rede SOM (JODAH,2025). A transposição da amostra de dados se torna importante para o processo de modelagem de dados, a qual é definida por x = [x1, x2,…, xn]T , para manter a uniformidade dos dados na matriz- U, na formação das classes (figura 3). No algoritmo da rede neural SOM é necessário definir os parâmetros da rede neural, por exemplo: a dimensão do mapa topográfico na matriz-U, os quais representam o número de neurônios na grade, com pode ser visto nafigura 3. O tamanho da dimensão da grade de neurônios, interfere diretamente no custo computacional e no tempo de execução do algoritmo, necessitando de configurações específicas de hardware para seu processamento.
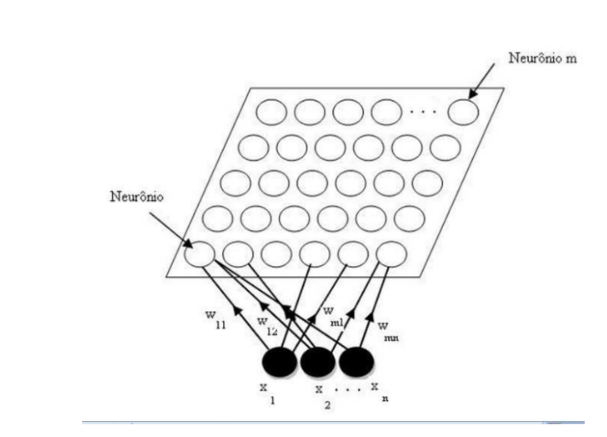
Figura 3. Arquitetura do mapa auto-organizaveis Fonte: HAYKIN,2001.
A figura 3, apresenta as principais características da arquitetura convencional da rede SOM a partir de uma grade bidimensional de neurônios integrada com um conjunto de vetores de entrada. Assim, quando um padrão de entrada e apresentado a rede, a mesma procura a unidade mais parecida com e durante o seu processo de treinamento, a rede aumenta a semelhança do nodo escolhido e de seus vizinhos ao padrão, construindo um mapa topológico onde os nodos que estão topologicamente próximo respondem de forma semelhante aos padrões de entrada (HAYKIN,2001).
A rede SOM utiliza um algoritmo de aprendizado competitivo, em que os nodos da camada de saída competem entre si para se tornarem ativos, ou seja, para ver quem gera a maior saída. Para cada padrão de entrada, apenas um nodo de saída ou nodo por grupo se torna ativo, esta competição e chamada “o vencedor leva tudo” (LUDEMIR at. at.,2000) e (KOVACZ,2002). Uma maneira de implementar esta competição e a utilização de conexões laterais inibitórias entre nodos de saída. A função de chapéu de mexicano representa bem este processo de acordo com o que segue:
As conexões laterais da rede podem ser representadas a partir da função de chapéu de mexicano, onde os neurônios que estão espacialmente ordenados dentro das áreas de raio (R1,R2 e R3) tendem a responder a padrões de estímulos semelhantes a partir do resultado obtido através da competição. Assim, quando um nodo vence uma competição e produz a maior saída para uma dada entrada, não apenas ele mas também os nodos localizados na sua vizinhança topológica tem seus pesos ajustados. Essa ordenação topológica e resultado do uso do feedback lateral entre as células do córtex cerebral. Na função de chapéu de mexicano cada neurônio influencia no estado de ativação de seus neurônios vizinhos de tres formas possíveis: excitatória (se os vizinhos de neurônios estão próximos ao neurônio vencedor e dentro de uma área de raio R1);inibitória (se os vizinhos estão fora da área anterior R1, mas dentro de uma segunda área R2, onde (R2 > R1); levemente excitatória ( se os vizinhos estão fora das áreas anteriores mas dentro de uma terceira área R3, mas fora das áreas de raios R1 e R2 , onde (R3 > R2 > R1) (LUDEMIR at. All,2000). Desta forma, quando um nodo vence uma competição produzindo a maior saída para uma dada entrada, nao apenas ele mas também os nodos localizados na sua vizinhança tem seus pesos ajustados. Com isso, os mapas de Kohonen consegue um resultado semelhante aquele obtido com a utilização da função chapéu de mexicano, proporcionando menor custo computacional (LUDEMIR at. All,2000). Em seguida, define-se os parâmetros da rede neural, conforme a função chapéu de mexicano e seus raios (figura 4).
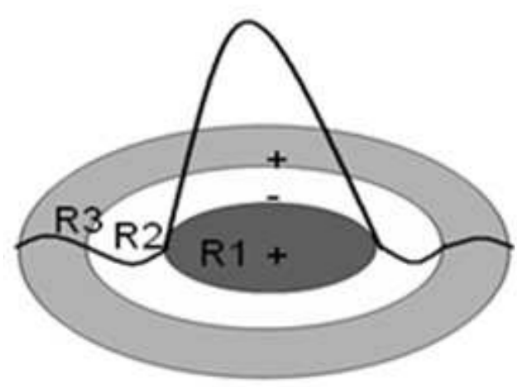
Figura 4.Tipos de estímulos produzidos de acordo com a função chapéu de mexicano. Fonte: LUDEMIR at. All,2000.
Os vetores de pesos dos neurônios, podem ser representados pelo plano bidimensional (2-D), conforme as equações (1-6). Assim, i (x) pode ser representado pelo indice para o neurônio de saída (neurônio vencedor) conhecido como neurônio BMU (Best Matching Unit) e ||•|| e a norma Euclidiana. Portanto, pode-se usar a equação 2, para mapear um espaço continuo de entrada sobre um arranjo discreto de neurônios. A resposta provem da atualização do vetor de pesos associado ao neurônio vencedor segundo a sua vizinhança topológica. O neurônio BMU e adaptado, seu vetor de pesos sinápticos e alterado no sentido de se aproximar ainda mais do dado apresentado, aumentando a probabilidade de que este mesmo neurônio volte a vencer numa subsequente apresentação do mesmo dado (Fonte: LUDEMIR at. All,2000).
4.2. Análise de Dados – Regressão Logística
Segundo Jeffrey (2014), a regressão logística é uma forma especializada de regressão formulada para prever e explicar uma variável categórica binária. A forma da variável estatística de regressão logística é semelhante à da variável estatística de regressão múltipla, representa uma relação multivariada com os coeficientes da regressão, e indica o impacto relativo de cada variável para fim de predição (JEFFREY,2014).
O processo de análise de dados baseado na regressão logística segue as seguintes etapas:
1. Identificar o conjunto de variáveis dependentes: o conjunto de n variáveis dependentes será representado pelo vetor x = [x1, x2,…, xn]T , onde n ∈ ℕ compondo o conjunto das ondas do ECG, conforme a figura 5.
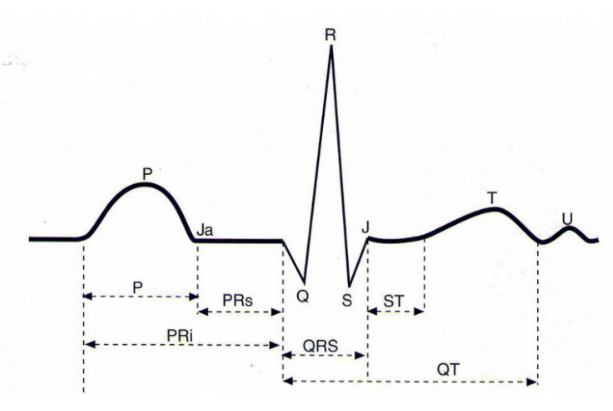
Figura 5. As deflexões, segmentos e intervalos do eletrocardiograma normal. Fonte: MOFFA,2001a.
As características dessas ondas e os intervalos do ECG normal são variáveis e sofrem a influência de inúmeros fatores tais como: idade, etnia, sexo e frequência cardíaca, os quais serão discutidos:
- Onda P: constitui a primeira onda registrada pelo ECG, representando a ativação dos átrios, após o estímulo sinusal. A morfologia da onda P normal é arredondada, monofásica, e apresenta, ocasionalmente, detalhes de modo que a distância entre um pico e outro não seja superior a 0,03 segundos (MOFFA,2001a) .
- Intervalo PR e Segmento PR: medem a duração do intervalo (PR), desde o princípio da onda P até o início do complexo QRS, começando pela onda Q ou R (MOFFA,2001a) .
- O segmento PR (segmento inscrito do final da onda P até o início do QRS): deve ser nivelado com a linha de base no traçado do ECG. Os infradesníveis têm importância menor e são de avaliação mais difícil do que os supradesníveis, já que o sentido normal da onda de repolarização atrial se opõe à onda P (BSOUL,2009;CARNEIRO,1986).
- Complexo QRS: representa a ativação ventricular; o contorno desse conjunto de ondas é pontiagudo, em vez de arredondado como as ondas P e T, pelo fato de ser composto por sinais de alta frequência. Duração: é medido no início da primeira onda, seja ela Q ou R, até o fim da última, que pode ser as ondas R, S, R’ (MOFFA,2001a).
- Onda Q: registrada uma derivação toda vez que as forças iniciais do QRS se afastarem do eletrodo positivo. A orientação das forças iniciais que se originam principalmente no septo interventricular e a da região apical dos ventrículos é variável no plano frontal. Essa onda Q constitui a primeira onda do complexo QRS, segunda onda do ECG padrão, com amplitude de 25% da onda R (FERREIRA,2011).
- Onda R: a onda R apresenta maior amplitude encontrada nos leads V4 e V5; a onda R de V6 é menor que a de V5. O limite superior da amplitude nessas derivações é de 25 mm. Estas correspondem à segunda onda do complexo QRS e à terceira onda do ECG padrão. Elas surgem quando o impulso elétrico de despolarização alcança as paredes dos ventrículos com amplitude de 1,60mV (FERREIRA,2011).
- Onda S: representa a onda mais profunda nas derivações precordiais direitas, com maior profundidade na derivação V2. O limite superior que representa a amplitude é negativo e chega a 30 mm em adultos jovens. Quando inferior a 3 mm, é considerada anormal, costumeiramente secundária ao infarto do miocárdio (FERREIRA,2011).
- Caracterizada pela última onda do complexo QRS, quarta onda do ECG padrão, ela ocorre quando a onda de despolarização atinge a região de alta posterior do septo interventricular (FERREIRA,2011).
- Onda T: representa a repolarização ventricular, processo que se realiza na mesma direção da ativação ventricular (MOFFA,2001a). Corresponde à repolarização do miocárdio ventricular, que progride no epicárdio para o endocárdio. Ela normalmente é perpendicular e arredondada, sua inversão indica processo isquêmico e a configuração (FERREIRA,2011).
- Onda U: representa a última onda e a menor deflexão do ECG; localiza-se logo após a onda T e antes da P, do ciclo seguinte, com polaridade igual a T e precedente; possui amplitude entre 5% e 25% da onda T. Essa onda geralmente é resultante da repolarização das células médio miocárdicas(FERREIRA,2011).
O vetor x = [x1, x2,…, xn]T , compõem a formação das ondas do ECG na classe por paciente, para cada paciente existe a composição do eletrocardiograma completo, formado pelo conjuntos das onda P, Q, R, S, T, U e seus leads V1,V2,V3,V4,V5,V6, sucessivamente.
– O módulo após a visualização da matriz-U, define o modelo de regressão linear:
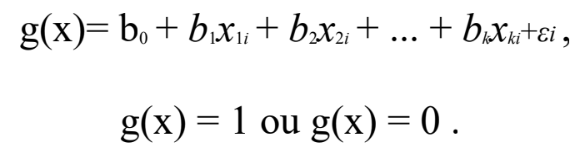
Equação A.1 Fonte: JOHN,2010.
A variável dependente só pode assumir dois valores (zero e um), torna-se necessário obter valores que possam ser interpretados em termos de probabilidades associadas a cada observação, em razão de chance (Odds Ratio), que representa a probabilidade de sucesso comparada à probabilidade de fracasso (CARVALHO,2012).
- Calcular a resposta esperada representada pela fórmula:
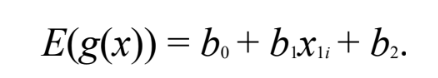
Equação A.2. Resposta esperada. Fonte: JOHN,2010.
- Calcular g(x) representa uma distribuição de probabilidade:
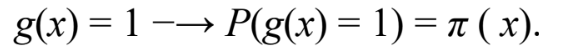
Equação A.3. Fonte: JOHN,2010. (A.3)
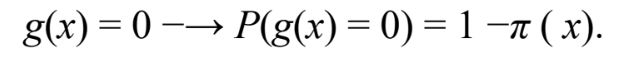
Equação A.4. Distribuição de Probabilidade. Fonte: JOHN,2010. (A.4)
- Calcular o Logit equivale ao logaritmo natural (base e) da chance:
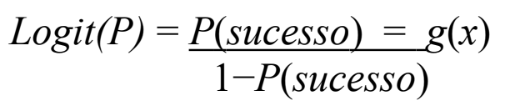
Equação A. 5. Logit . Fonte.CARVALHO,2012 (A.5)
- Calcular a razão de chances (ODDS RATIO), considerando CPU1 (Tempo de Processamento/ Dimensão do Mapa) = P1 e CPU 2 (Tempo de Processamento/ Dimensão do Mapa) = P2.
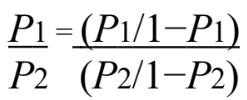
Equação A. 6. Fonte: Fonte.CARVALHO,2012.
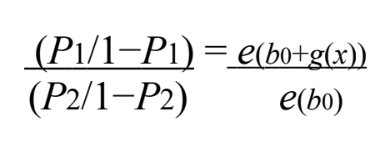
Equação A. 7. Fonte: Fonte.CARVALHO,2012.
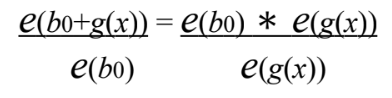
Equação A. 8. Fonte.CARVALHO,2012 (A.8)
- Calcular a razão de chance de e(g(x));
- Analisar a chance de sucesso de P1 obter processamento rápido em relação a P2:
- Caso eg(x) for maior que uma unidade, a chance de sucesso em P1 é maior em P2;
- Caso eg(x) for menor que uma unidade, a chance de sucesso em P1 é menor em P2;
A base de cálculo para a tabela 3, será definida conforme as respectivas equações:
- Calcular P1: tempo de execução do algoritmo por ciclo, considerando uma derivação.
- Calcular P2: tempo de execução do algoritmo por ciclo, considerando uma derivação.
- Calcular o modelo de regressão baseado nas equações A.1 e A.2, para calcular g(x).
- Calcular a distribuição de probabilidades equações A.3 e A.3, para calcular DP1(CPU1);
- Calcular a distribuição de probabilidades equações A.3 e A.3, para calcular DP2(CPU2);
- Calcular ODDS RATIO equações A.6 a A.8, para calcular OD1(CPU1);
- Calcular ODDS RATIO equações A.6 a A.8, para calcular OD2(CPU2); • Calcular o ganho (G) do algoritmo CGAADT na CPU:
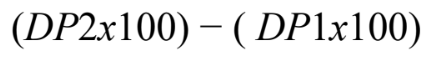
Equação A.9. Ganho do algoritmo . Fonte: Autor.
5. Arquitetura e principais processos do algoritmo da rede de Kohonen
No mapa auto-organizáveis de Kohonen, os neurônios são dispostos em um arranjo discreto finito, geralmente unidimensional ou bidimensional e totalmente conectados com a entrada, possibilitando mapear um conjunto de dados. O algoritmo responsável pela formação do mapa auto-organizável começa primeiramente inicializando os pesos sinápticos na rede. Isto pode ser feito atribuindo-lhes valores pequenos tomados a partir de um gerador de números aleatórios; fazendo desta forma, nenhuma organização previa a qual e imposta ao mapa características Ham (HAM, 2001), Kovacz (KOVACZ,2002). De acordo com Haykin (2001), Kohonen (1997) e Zuchini (2003),a formação de um mapa auto-organizáveis pode ser dividida em três principais processos:
- Competição. Para cada padrão de entrada, os neurônios da grade calculam seus valores em relação a ele e competem entre si pelo direito de representá-lo. O neurônio que melhor representa os dados é aquele que utiliza alguma métrica preestabelecida, o qual é considerado o vencedor (KOHONEN,1997).
- Cooperação. O neurônio vencedor determina a localização espacial de uma vizinhança topologica de neurônios excitados, fornecendo acima base para a cooperação entre os neurônios vizinhos(KOHONEN,1997).
- Adaptação Sináptica. Este último processo permite que os neurônios excitados (incluindo os vencedores) aumentem seus valores individuais em relação ao padrão de entrada através de ajustes adequados aplicados a seus pesos sinápticos. Os ajustes são feitos de tal forma que a resposta do neurônio vencedor a aplicação subsequente de um padrão de entrada similar e melhorada (KOHONEN,1997).
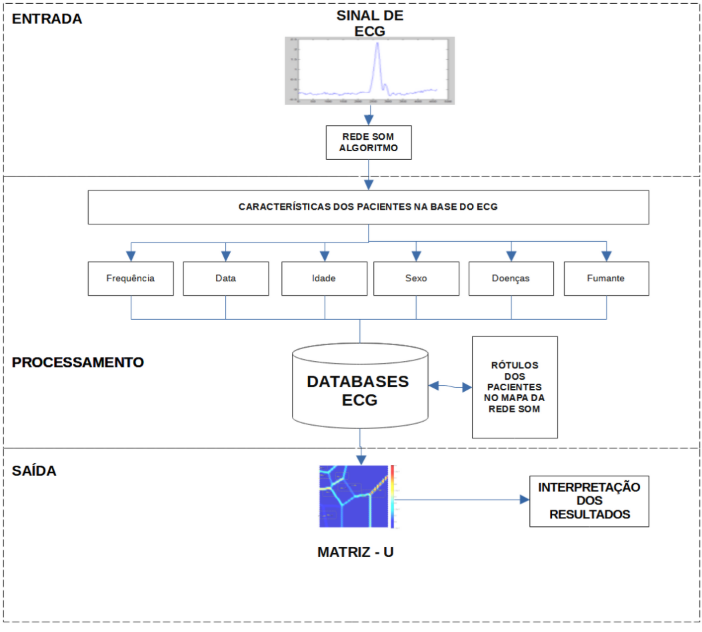
Figura 6. Diagrama de Blocos da Arquitetura da Rede SOM no Processamento de Sinais de ECG. Fonte: Autor.
A figura 6, representa o processo do algoritmo da rede SOM. Os sinais de ECG representam a entrada de dados pelo algoritmo da rede SOM. Em seguida, as características relevantes dos dados dos pacientes são distribuídas no cabeçalho da base de dados de ECG e na lateral direita são distribuídos os rótulos dos dados dos pacientes na exibição do mapa topográfico na rede SOM de acordo com a distância euclidiana, em um aprendizado não supervisionado, para que a matriz-U seja extraída como a saída do sistema. Diante da visualização do mapa topográfico, as similaridades comuns entre os pacientes serão vistas, para que o médico possa interpretar os resultados e propor o diagnóstico ou correlacionar os clusters de dados.
5. Estudo de Caso
5.1. Sinais Biomédicos – Pacientes com Doenças Cardiovasculares
A base de dados é composta pelo conjunto de dados de 10(dez) pacientes portadores de obesidade, gastrite, hipertensão e infarto do miocárdio. A idade média destes pacientes evolui no intervalo de 46 a 81 anos (tabela 1). Os sinais de eletrocardiograma utilizados nos experimentos são compostos de 12(doze) derivações do ECG, divididos nas derivações unipolares e bipolares, identificada pelos leads: DI, DII, DIII, Avr, Avf, Avl, V1,V2, V3, V4, V5, V6, são formadas pelos dados de arritmia do MIT-BIH/Phisionet (PHYSIONET,2025), apresentada na tabelas 1, descritas abaixo:
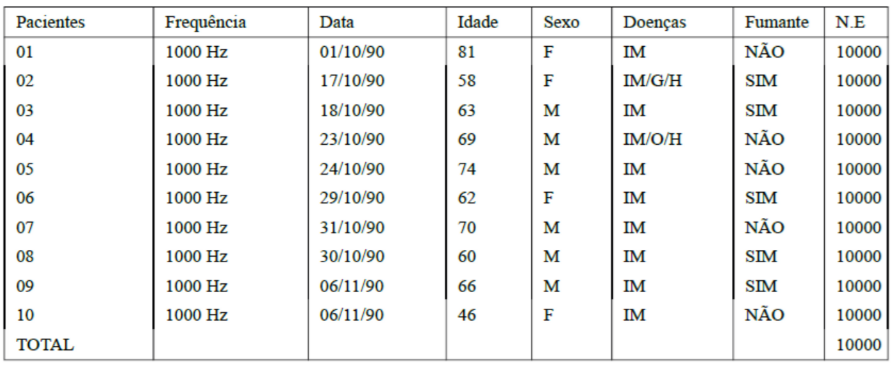
Tabela 1. Características base de dados ECG. Legenda : (F) Feminino, (M) Masculino, (IM) Infarto do Miocárdio, (G) Gastrite, (H) Hipertensão, (O) Obesidade e (N.E) Número de Exemplos de dados. Fonte: Physionet, MIT-BIH Arrhythmia Databases. Fonte: PHYSIONET,2025.

Figura 7. Mapa Contextual do Sinais de Eletrocardiograma (Matriz-U) . Fonte : Autor.
O mapa contextual apresenta oito classes ou clusters. A classe I é formada por P04 (paciente 4), possui características isoladas por obter infarto do miocárdio, obesidade, hipertensão e não ser fumante. As classes II e III, formadas por P08 (paciente 08) e P03 (paciente 03), os sinais possuem idades próximas, mesmo sexo, infarto do miocárdio para não fumantes, porém a distinção e proximidade das idades, permite que a classificação pela SOM, possa modelar uma linha distribuídas em as classes. As classes IV e V são formadas pelos sinais dos pacientes P01(paciente 01) e P09 (paciente 09), ambos sinais possuem sexos distintos, e características comuns (infarto do miocárdio, não fumante e idosos), observa-se que existe uma proximidade da classe e uma leve divisão entre eles devido a diferença de sexo. A classe VI formada por P10 (paciente 10) , existe uma característica comum com o infarto de miocárdio (classe formada), vista em p09, por isso existe uma divisão mediana trazendo uma parte da classe em proximidade com P09. Considerando que, P02 (paciente 02) e P05 (paciente 05) são subclasses de P10, apesar de possuírem idades distintas, sendo p02 (58) anos e p05(74) anos, ambos possuem características similares de infarto do miocárdio, obesidade e hipertensão, existe uma aproximação aparente entre as classes, por meio de uma divisão leve classificando-as, a pesar da condição de fumante e sexo serem distintas. As classes VII e VIII , P06 (paciente 6) e P07 (paciente 7), ambos sinais possuem sexo distintos, porém, características de similaridade de idosos pelo fator idade, ambos obtiveram infarto do miocárdio. Como possuem sexo e a situação de fumante distintos, as classes são subdivididas de forma o que permite distinguir entre as classes por meio de classificação. As classes que representam as divisões de sinais claros, possuem características semelhantes formando um pequena subclasse individualizada, as classes com divisões mais escuras representam a dissimilaridade dos sinais.
Usando um mapa contextual de 55×55 de dimensão, vizinhança hexagonal, dados padronizados, 30 vezes a primeira fase de 3 → 1 para um mapeamento mais espesso e para o seu refinamento usado em 20 ciclos com vizinhança fixa de 1 → 1, para um melhor refinamento do mapa, o erro de quantização e QE = 0,000 ET = 0,90.
6. Implementação e Resultados
A implementação da rede neural de Kohonen, para a realização da simulação, foram utilizados dois tipos de hardware, com a mesma configuração de dimensionalidade e números de neurônios constantes na matriz-U. A primeira configuração de hardware foi utilizado uma CPU com processador Intel Core i7, 10thGen – 1.80 GHz – 16GB RAM. A segunda configuração de hardware, foi utilizado uma CPU Core i7, 13thGen – 2.60 GHz – 32 GB RAM com o software MATLAB R2025a, Kohonen Toolbox MATLAB, versão 1.0.0.0., e algoritmo ajustado da última versão de Kohonen, para a modelagem da arquitetura vista na figura 6.
Na definição da dimensão dos dados, se torna importante, definir o número de neurônios na grade do mapa de Kohonen, o qual aumenta o erro topográfico e o erro de quantização vetorial da rede. Poderá ser ajustado o mapeamento inicial da rede neural SOM, definindo o número de épocas ou ciclo para 30, reduzindo a vizinhança decrescente em média de 5→ 1, considera-se a vizinhança de 1 → 1 , no mapeamento final , reduzindo os ciclos para um melhor refinamento do mapa topográfico.
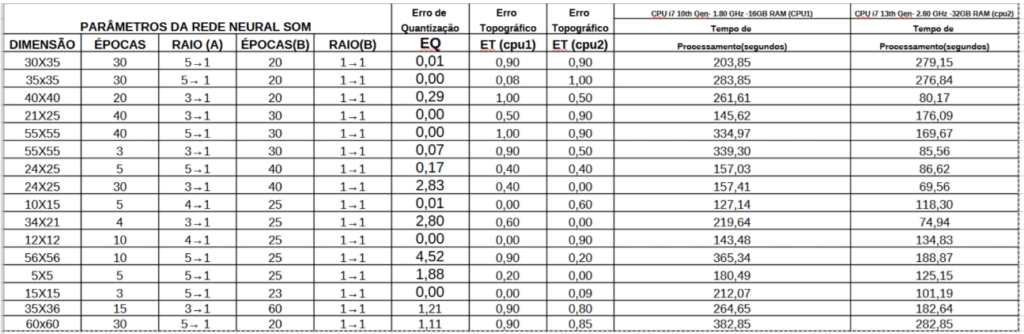
Tabela 2. Parametros da rede neural SOM nos sinais de eletrocardiograma. Fonte: Autor.
De acordo com a tabela 2, múltiplos experimentos foram executados, considerando mapeamentos com dimensões iguais e outros distintos. Os mapas topográficos com as dimensões maiores de 55×55, aumenta significadamente o tempo de processamento do algoritmo, conforme a excução das equações 1 a 6 e demais parâmetros da rede SOM. Os mapas com as dimensões distintas e menores que 55×55, não conseguem representar todas as características dos sinais de ECG de forma satisfatória, muitas variáveis não foram exibidas no mapa topográfico. O mapeamento topográfico da rede neural SOM, visto na figura 7, classifica de forma satisfatória as variáveis constantes na tabela 1, sendo utilizado um mapa topográfico de 55×55 (dimensão da grade de neurônios), 40 ciclos no refinamento do mapa inicial, refinando o mapa topográfico com a redução no número de ciclos para 30 de forma decrescrente de 1→1 , com erro topográfico (ET) de 0,90, para que seja visualizada todas as variáveis da base de dados do ECG.
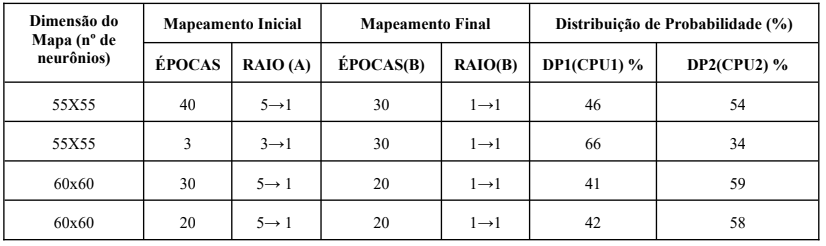
Tabela 3. Distribuição de Probabilidades. Fonte: Autor
De acordo com os resultados apresentados nas tabelas 2 e 3, os mapas com dimensões entre 55×55, apesar de obterem o erro topográfico de 0,90 (CPU1) e (0,80), conseguiram obtiveram um ganho de 7,6%, no mapa topográfico de 55×55, utilizando um mapeamento inicial de 40 épocas por ciclo, reduzindo a vizinhança decrescente de 5→1, no mapeamento final de 30 épocas por ciclo reduzindo a vizinhança decrescente de 1→1 . Observa-se que a probabilidade do processamento do algoritmo na CPU1, obtem ganho em relação a CPU2 é de 7,6 %, baseado na equação A.9. Considerando que, o ODDs Radio na CPU1 foi de 0,86 e na CPU2 foi de 1,17.
Nos casos, dos mapas 55×55, reduzindo os ciclos para 3, no mapeamento inicial de 3 →1 e 20 épocas de 1→1 no mapeamento final, houve um deficit de ganho de 32,8, devido a falta de classificação de todas as variáveis no mapa topográfico, essa mesma situação ocorreu com os mapas de 60×60 com épocas 30 e 20, no mapeamento decrescente e inicial do mapa, com deficit de ganho de 18,3 e 15,0, quando executado em CPU1’s tradicionais. Portanto, se torna necessário projetar a rede neural som, em um novo algoritmo distribuindo essa rede para seu processamento ser distribuído parte em CPU e outra em GPU com objetivo de minimizar os impactos no tempo de execução do algoritmo, para sistemas em tempo real e melhorar o ganho computacional.
7.Conclusões
Considerando que, os sinais de ECG, possuem características específicas de acordo com a morfologia do sinal e que dependendo do tipo de doença, medicação, e outros fatores poderão alterar a morfologia do sinal de ECG, inclusive ruídos, poderão afetar diretamente na classificação dos sinais, na coleta de resultados e no processamento da rede neural. Como a rede neural de Kohonen executa o processo de competição, neste processo ao mesmo tempo realiza a filtragem do sinal, melhorando a integridade dos dados e a classificação, se tornou satisfatória, apesar do aumento no processamento do algoritmo. Os sinais de eletrocardiograma se comportam diferente no processamento da Rede SOM, devido a complexidade da amostra de dados. As redes SOM não avaliam objetos dessa classe que estão no limiar definido pela classe, ou quando um objeto, que está dentro da faixa normal de migração para uma nova fase, identifica que essa medida pode fazer parte de uma nova classe com características de anormalidade.
A classificação realizada pela rede SOM, com uso de sinais biomédicos ECG, poderá ser usado para outros tipos de sinais, por exemplo, COVID19, categorizado ou não, ou a integração do modelo da rede SOM com a lógica nebulosa, para determinar limiares no sinal de ECG. Em casos de arritmia, o que influencia a complexibilidade do ruído do sinal, uma vez que, os ruídos constantes nas arritmias (representam qualquer alteração na regularidade, frequência, local de origem do impulso, ou anormalidade na condução desse impulso), poderão se caracterizar doenças cardiológicas, alterações por medicamentos, ou esconder a onda U, rara em sinais de ECG. A integração de modelos de rede SOM baseados em regras fuzzy a ser abordada em trabalhos futuros, mostra que a projeção não linear de dados fornecida por mapas auto-organizados não permite a identificação de intervalos de classe ou quaisquer medidas que possam representar um limite mínimo, dependendo do tipo de dados a ser usado na rede neural. A implementação de controladores fuzzy baseados em regras apresenta algumas vantagens práticas facilmente compreendidas e seu propósito e resultado podem ser facilmente interpretados. Além disso, todas as funções de controle associadas às regras podem ser testadas individualmente e também podem aumentar a facilidade de manutenção, pois a simplicidade das regras permite o uso por pessoal menos treinado. Vários tópicos relacionados a este trabalho podem ser citados como sugestão para pesquisas futuras: o uso de algoritmos genéticos para elaborar e implementar as regras básicas de controle baseadas em programação evolutiva, adotando uma abordagem paramétrica usando o método Takagi-Sugeno e também adotando um modelo de mapeamento topograficamente generativo.
A utilização de redes SOM na classificação de sinais biomédicos de ECG mostrou-se eficaz na identificação de padrões associados a diferentes condições cardíacas. Apesar das limitações computacionais observadas em CPUs tradicionais, os resultados indicam que a arquitetura pode ser otimizável por meio de paralelização em GPU ou FPGA, tornando-a adequada para aplicações em tempo real. Como perspectivas futuras, propõe-se a integração com lógica fuzzy para tratar incertezas em sinais limiares, bem como a aplicação do modelo a outras condições médicas. A implementação de métodos híbridos, como a combinação com algoritmos genéticos, também é sugerida para otimizar o desempenho da rede.
REFERÊNCIAS
ALMEIDA C.W.D at all. Fuzzy Kohonen Clustering Networks for Interval Data. Volume 99-1, Neurocomputing, pages 65-75,2013. URL: https://doi.org/10.1016/j.neucom.2012.06.019.
BSOUL, K.; JI, S. W. and Detection of p, qrs, and t components of ecg using wavelet transformation, IEEE, 2009.
CACEK A. Preprocessing and analysis of ECG signals – A self-organizing maps approach. Volume 38, Issue 7, Expert Systems With Applications, Pages 9008-9013. DOI: https://doi.org/10.1016/j.eswa.2011.01.119, 2011.
CARNEIRO, E. F. O Eletrocardiograma, 3ª. Edição, Atheneu, Rio de Janeiro, 1986.
CARVALHO, E. P. A. at al. Análise Multivariada de Dados: para cursos de Administração, Ciências contábeis e economia. 2012.
FERREIRA, A. M. V. Uma Especificação do Algoritmo Genético Baseado em Tipos Abstratos de Dados para Diagnóstico de Arritmias Ventriculares a ser Aplicada a partir do Eletrocardiograma, Dissertação de Mestrado, Universidade Federal de Alagoas, 2011.
KOVACZ Z. L. Redes Neurais Artificiais: fundamentos e aplicações. Livraria da Física, São Paulo, 2002.
KOHONEN T. Self-Organizing Maps. Springer, Berlin, 1997.
HAM F. M. Principles of neurocomputing for science and engineering. New York : McGraw-Hill, 2001.
HAYKIN, S. Neural Networks: a comprehensive foundation, Pearson, 2001.
JEFFREY, D.; RAJARAMAN A. Mining of Massive Datasets. Stanford University Press, 2014
JODAH A. MATLAB. R2025a. Self Organizing Map Kohonen Neural Network – Tollbox. Version 1.0.0.0. URL: https://ch.mathworks.com/matlabcentral/fileexchange/46481-self-organizing-mapkohonen-neural-network,2025.
JAIN, A. at. All. Algorithms for Clustering Data. New Jersey : Prentice-Hall, 1988.
JOHN, G.; PROAKIS, V. Digital Signal Processing using Matlab. Third Edition, Cengage Learning, 2010.
MENDIS, S. Global Status Report: on non communicable diseases. WHO Library Cataloguing, 2014. URL: https://iris.who.int/bitstream/handle/10665/148114/9789241564854_eng.pdf? ua=1. Último Acesso: 02/05/2025.
MACIEL A. Um Filtro Adaptativo de Alto Desempenho Instanciado do Algoritmo GAADT para o Processamento de Sinais de Eletrocardiograma. Centro de Informática, Universidade Federal de Pernambuco.Tese de Doutorado, 2015. URL:https://repositorio.ufpe.br/bitstream/123456789/18044/1/TESE_IMPRESS%C3%83O_ANDRILENE_VF INAL_bib.pdf. Último Acesso: 04/05/2025.
MACIEL A. Mineracao de Dados com Redes Neurais: uma abordagem com mapas auto-organizáveis para processamento de sinais de glicemia. 1ª Edição, Recife, 2003. URL: https://clubedeautores.com.br/.
MOFFA, P.; SANCHES, P; Eletrocardiograma: normal e patológico, 7ª edição, Roca, São Paulo, 2001a.
MOFFA, P.; SANCHES, P.; Eletrocardiograma: Uma abordagem didática. 1ª edição, Roca, São Paulo, p. 356 ,2010b.
MUSTAQ H., EAKINS J.P. Component-based visual clustering using the self-organizing map, Neural Networks, pp. 260-273, 2007.
LEITE C.R M. at all. Classification of Cardiac Arrhythmias using Competitive Networks, 2010. Annual International Conference of the IEEE Engineering in Medicine and Biology. IEEE Xplore, Bueno Aires, Argentina. DOI: 10.1109/IEMBS.2010.5626728,2010.
LYOZINA I.V, IASHIN D.I. Applying the Kohonen Neural Network to Solve the Problem of Determining Diseases of the Cardiovascular System Based on the Results of Electrocardiography. Conference: 2024 X International Conference on Information Technology and Nanotechnology (ITNT), 2024. DOI:10.1109/ITNT60778.2024.10582291
LUDEMIR. T. B., BRAGA. A. P, CARVALHO. A. C. P. L. Redes Neurais Artificiais : teoria e aplicacoes. Rio de Janeiro – RJ, 2000.
RADHWANE B. Analyse du signal ECG par un réseau adaptatif d’ondelettes en vue de la reconnaissance de pathologies cardiaques. Laboratoire de Genie Biomedical. République Algérienne Démocratique et Populaire Ministère de l’enseignement supérieur et de la recherche scientifique Université Abou BEKR BELKAID, 2013. URL:bhttps://www.researchgate.net/publication/281237494_Analyse_du_signal_ECG_par_reseau_adaptatif_d%27ondelettes_en_vue_de_la_reconnaissance_de_pathologies_cardiaques
PORTO, C. C. Doenças do Coração : prevenção e tratamento. Guanabara, 2005.
PHYSIONET, MIT-BIH Arrhythmia Databases. Disponível em:<http://www.physionet.org/physiobank/database/mitdb>. Último Acesso em: 02 de maio de 2025.
TRIQUI B., BENYETTOU A. Semi-Supervised Kohonen Map for Cardiac Anomalies Detection. International Review on Modelling and Simulations, Vol 12, Nº 3. https://doi.org/10.15866/iremos.v12i3.16953 , 2019.
ZUCHINI M.H, Zuchini. Aplicações de mapa auto-organizáveis em mineração de dados e recuperação de informações, dissertação de mestrado do departamento de engenharia de computação e automação industrial. Universidade Estadual de Campinas da Faculdade de Engenharia Elétrica. Campinas – SP, 2003.
1Universidade Federal Rural de Pernambuco
Postal Code 52.171-900 – R. Dom Manuel de Medeiros, s/n – Dois Irmãos, Recife – Brazil
2 Instituto Federal de Pernambuco, IFPE – Paulista
Postal Code 53.441-601 – Maranguape I, Paulista – PE – Brazil, {andrilene.maciel@ufrpe.br , aalq@cin.ufpe.br}
