REGISTRO DOI: 10.69849/revistaft/ni10202511302106
Gustavo Eduardo Araújo Da Silva Sandes1
Antonio Nilson Laurindo Sousa2
Juliermes Carvalho Pereira3
Sergio Nolêto Turibus4
RESUMO
Este trabalho tem como objetivo apresentar uma abordagem das Equações Diferenciais Ordinárias (EDO) aplicadas em circuitos elétricos. Inicialmente, é feito um resgate histórico do desenvolvimento das equações diferenciais e do eletromagnetismo, destacando contribuições de cientistas como Newton, Leibniz, Euler e Maxwell. O estudo se aprofunda na classificação das equações diferenciais quanto ao tipo, ordem e linearidade, além de apresentar métodos de resolução como separação de variáveis, fator integrante e uso da equação característica. Na parte aplicada, são analisados elementos de circuitos elétricos (resistores, capacitores, indutores) e suas relações com as EDOs, evidenciando como a modelagem matemática contribui para compreender e resolver problemas físicos e tecnológicos. A pesquisa adota uma abordagem bibliográfica e exploratória, baseada em autores clássicos e contemporâneos.
Palavras-chave: Equações diferenciais ordinárias. Circuitos elétricos. Modelagem matemática. Física aplicada.
1 INTRODUÇÃO
As equações diferenciais (EDs) desempenham uma função fundamental na modelagem Matemática, sendo constantemente utilizadas em cursos de exatas como Matemática, Física, Química e Engenharia. Sua importância tem como objetivo aprimorar cálculos e realizar análises mais detalhadas de seus processos e comportamento. No entanto, as EDs não se restringem apenas ao campo das exatas, tendo uma vasta utilidade em outras áreas do conhecimento, como Biologia, Medicina e outras ciências. O que as transforma em uma ferramenta indispensável para a humanidade, proporcionando uma base Matemática que constitui em conhecimento mútuo sobre o processo dinâmico que ocorre na natureza e na sociedade, o que traz mudanças significativas e interações complexas, resultando em progressos científicos e tecnológicos.
Diante disso, com a crescente presença de dispositivos eletrônicos em nosso cotidiano, seja em nossas casas ou trabalho, mostra que estamos rodeados de tecnologia. Desse modo, compreender os princípios que regem o funcionamento dos circuitos elétricos tornou-se uma habilidade cada vez mais valorizada, tanto na formação acadêmica quanto na prática profissional. Os circuitos elétricos representam sistemas físicos que envolvem componentes como resistores, capacitores e indutores, os quais, quando organizados em um circuito, obedecem a leis fundamentais da Física, como as Leis de Ohm e de Kirchhoff. No entanto, o comportamento dinâmico dessas estruturas, especialmente em situações com fontes variáveis de corrente ou tensão, exige um tratamento matemático mais profundo, no qual as equações diferenciais ordinárias desempenham papel essencial.
As equações diferenciais possibilitam a modelagem de sistemas que evoluem com o decorrer do tempo, fornecendo uma descrição precisa das variações de grandezas elétricas, como corrente e tensão. Em especial, os circuitos do tipo RC, RL e RLC, que envolvem elementos com capacidade de armazenar energia, são classicamente estudados com base em equações diferenciais de primeira ou segunda ordem. O estudo desses circuitos permite ao futuro professor ou profissional da Matemática reconhecer na prática a potência das ferramentas matemáticas na resolução de problemas concretos.
Além da aplicação prática, este trabalho reforça a relação entre a Matemática e áreas como a Física. A interdisciplinaridade favorece uma aprendizagem mais integrada e significativa. Ao abordar equações diferenciais aplicadas aos circuitos elétricos, busca-se superar abordagens didáticas que tratam a Matemática de forma isolada.
Desse modo, a presente pesquisa tem como objetivo compreender o estudo das equações diferenciais ordinárias (EDOs). Para alcançar este propósito, o trabalho se propõe a cumprir os seguintes objetivos específicos: mostrar o contexto histórico das equações diferenciais e do eletromagnetismo; classificar os diferentes tipos de equações diferenciais; e demonstrar estratégias metodológicas eficazes para facilitar a compreensão e o domínio das Equações Diferenciais Ordinárias (EDOs) aplicada em circuitos elétricos.
Portanto, a proposta central deste estudo vai além da resolução de equações ou da apresentação de circuitos. Ela se ancora na valorização do conhecimento matemático como linguagem universal da ciência, capaz de interpretar fenômenos naturais e tecnológicos com clareza e precisão. Acredita-se que essa abordagem contextualizada, que alia teoria, história e aplicação, possa inspirar o leitor a enxergar a Matemática não apenas como um conjunto de fórmulas, mas como ferramenta para compreender e transformar a realidade.
2 EQUAÇÕES DIFERENCIAIS ATRAVÉS DA HISTÓRIA
A história das equações diferenciais, segundo diversos estudos, teve início no século XVII, com as contribuições de Isaac Newton (1642–1727) e Gottfried Wilhelm Leibniz (1646–1716), considerados os pioneiros e formuladores dessa importante ferramenta matemática, cuja aplicação se mostrou fundamental para o avanço da ciência e da humanidade. No entanto, conforme destaca Bassanezi e Ferreira Jr. (1988), as equações diferenciais já vinham sendo desenvolvidas, ainda que de forma inicial, por estudiosos anteriores a Newton e Leibniz, por meio de investigações voltadas à mecânica. Fenômenos como a rotação dos planetas, a oscilação de pêndulos e o movimento de queda livre já eram objeto de análise por cientistas como Leonardo da Vinci (1452–1519), Johannes Kepler (1571–1630), Galileu Galilei (1564–1642) e Christiaan Huygens (1629–1695). Apesar dessas contribuições significativas, ainda faltavam, à época, conceitos matemáticos mais sofisticados que permitissem a modelagem precisa desses fenômenos. Lacuna essa que foi suprida com os avanços promovidos por Newton e Leibniz.
Newton e Leibniz tiveram grandes contribuições no estudo das equações diferenciais. Por meio deles foram desenvolvidas novas maneiras de derivação e integração. Newton, em particular, destacou-se ao classificá-las como equações de primeira ordem, considerando três formas distintas:
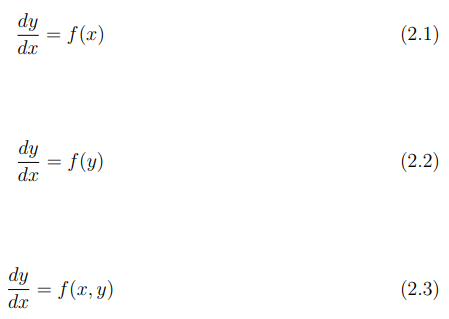
A qual a formula (2.3) ele desenvolveu um método de resolução, em que f(x,y) é um polinômio em x e y em uma série infinita. Já Leibniz desenvolveu notação que conhecemos hoje dx/dy , além de contribuir para o sinal de integral. Descobriu o método de separação de variáveis, redução de equações homogêneas separáveis e procedimentos para a resolução de equações lineares de primeira ordem, assim inúmeros problemas Mecânicos, conseguiram ser resolvidos pelas contribuições de Newton e Leibniz o que incentivou a outros cientistas a pesquisar mais sobre as equações diferenciais como destaca (Bassanezi; Ferreira Jr., 1988, p.07):
A partir desta época surgiu a questão da resolução dos problemas matemáticos apresentados por estes modelos. Vários deles foram resolvidos explicitamente e de maneira elegante por matemáticos de extraordinária habilidade operacional, como os da família Bernoulli: Jacques (1655 – 1705), Jean (1667 – 1748), Nicholas (1695 – 1726), Daniel (1700 – 1782) e principalmente por seus alunos, insuperável L. Euler (1707 1783) cuja obra (incompleta) preenche 74 grandes volumes.
Em particular, a família Bernoulli, representada pelos irmãos Jakob (1654-1705) e Johann (1667-1748), teve um papel importante no progresso das equações diferenciais, conforme Boyce e Diprima (2015), os irmãos fizeram grande contribuições ao qual eles resolveram muitos problemas relacionados a Mecânica formuladas através das equações diferenciais a qual vale destacar equações diferencial

do tipo resolvida por Jakob, a qual ficaria conhecida como a famosa equação “Bernoulli”, já Johann foi capaz de solucionar a equação do tipo:

Jakob também apresentou pela primeira vez a expressão “integral” como um termo moderno em seu artigo. Por outro lado, o filho de Johann, Daniel Bernoulli (1700-1782), foi um notável matemático extraordinário ao qual tinha um interesse mútuo em equações diferenciais parciais, ele ficou conhecido por desenvolver a famosa equação de Bernoulli da mecânica dos fluidos e o primeiro a encontrar que, tempos depois, seriam funções de Bessel.
Entre os cientistas que mais contribuíram para o desenvolvimento das equações diferenciais, destaca-se Leonhard Euler (1707–1783), eminente matemático suíço e discípulo de Johann Bernoulli. Euler teve um papel fundamental nesse campo, oferecendo avanços teóricos e metodológicos que revolucionaram a matemática e suas aplicações. Segundo Boyce e DiPrima (2015), Euler é considerado por muitos o matemático mais memorável de todos os tempos, tendo deixado uma vasta produção intelectual composta por mais de 70 volumes, abrangendo praticamente todas as áreas da matemática, além de diversos campos do conhecimento.
Dentre suas contribuições mais notáveis, destaca-se a formulação do método do fator integrante, essencial na resolução de equações diferenciais lineares homogêneas com coeficientes constantes. Euler também se dedicou ao estudo de equações diferenciais não lineares, propondo soluções inovadoras que influenciaram diretamente o desenvolvimento da matemática aplicada. Sua genialidade transcendeu os limites da matemática pura, estendendo-se à física, à engenharia, à astronomia e à mecânica dos fluidos, consolidando-o como uma figura central na história da ciência. Suas contribuições não apenas fortaleceram os fundamentos teóricos da matemática, mas também abriram caminhos para aplicações práticas que permanecem relevantes até os dias atuais.
2.1 Equações Diferenciais
Conforme Boyce e DiPrima (2015, p.54), “o estudo de Equações Diferenciais é uma busca para entender algum processo Físico representado pela modelagem Matemática, seja ela simples ou complexo.” Já para Bassanezi e Ferreira Jr (1988), as equações diferenciais, talvez sejam as únicas no ramo da Matemática que têm mais interações com outras ciências desde de sua origem.
Ainda nesse contexto o mesmo autor nos afirmam, que as equações diferenciais que descrevem algum processo Físico são conhecidas como modelos matemáticos. Modelos esses, que se tornaram indispensável para Mecânica clássica desde sua descoberta no século XVII o que nos mostra que a Mecânica é um estudo importante nas equações diferencias como ressalta Bassanezi e Ferreira Jr (1988).
Segundo Bassanezi (2002), a modelagem Matemática é uma arte de reformular e resolver problemas do cotidiano por meio da Matemática, interpretando sua linguagem e adaptando-a às situações do mundo real. Ainda nesse contexto, o autor ainda afirma que:
Muitos problemas que serviram para testar métodos matemáticos ou estimular desafios e competições entre matemáticos nos séculos XVII e XVIII, tiveram sua origem na observação de processos mecânicos geralmente simples.(Bassanezi, 2002, p.21)
A construção de um modelo matemático exige, primeiramente, o reconhecimento de que cada problema apresenta um comportamento único, com características e peculiaridades próprias. Nesse sentido, os autores enfatizam que a modelagem não é uma habilidade que pode ser completamente sistematizada por meio de regras fixas ou procedimentos padronizados. Apesar disso, o conhecimento dessas regras pode ser útil como ponto de partida, auxiliando na compreensão e na estruturação do modelo, especialmente em contextos mais complexos Boyce e DiPrima (2015).
Já Bassanezi (2002), destaca que os modelos matemáticos são uma síntese da reflexão sobre a realidade, cujo objetivo principal é explicar e compreender situações estudadas para intervir sobre elas.
Em contra partida Bassanezi e Ferreira Jr. (1988), destacam que problemas reais não podem ser representados de maneira precisa, mas ao trabalhar com variáveis, os modelos matemáticos podem reproduzir de maneira aproximada o problema real vividos em nosso cotidiano. Assim, os modelos e a modelagem Matemática representam a formulação e dedução de vários problemas que podem ser resolvidos por meio de equações diferenciais ordinárias e parciais, tornando-se uma ferramenta essencial para a solução de problemas e o avanço do conhecimento intelectual na resolução de problemas reais do nosso cotidiano.
Assim, esta pesquisa introduz os princípios fundamentais das Equações Diferenciais (ED), apresentando algumas definições e técnicas de resolução por meio de exemplos selecionados. Para uma análise das equações diferenciais ordinárias, são Utilizados exemplos extraídos de obras reconhecidas, como as de Boyce e DiPrima (2015), Zill e Cullen (2001), Bassanezi e Ferreira Jr. (1988), Bronson e Costa (2008), entre outros autores, ao longo do estudo, para obter uma análise mais aprofundada das Equações Diferenciais Ordinárias.
2.2 Equações diferenciais e suas classificações
Uma equação diferencial pode ser compreendida como uma expressão matemática que estabelece uma relação entre uma função desconhecida e suas derivadas, envolvendo, portanto, variáveis dependentes e independentes. Essas equações surgem quando se busca descrever fenômenos dinâmicos, nos quais há variação de uma grandeza em função de outra. Podem ser classificadas de acordo com diferentes critérios, como o tipo (ordinária ou parcial), a ordem (relativa ao maior grau da derivada presente) e a linearidade. Tais características serão abordadas nas próximas seções, visando a compreensão mais aprofundada dessa importante ferramenta matemática.

2.2.1 Classificação em relação ao tipo
As equações diferenciais podem ser classificadas, de forma geral, em dois tipos distintos: equações diferenciais ordinárias (EDOs) e equações diferenciais parciais (EDPs). No caso das EDOs, trata-se de equações nas quais as derivadas envolvidas referem-se a uma única variável independente. Em outras palavras, a função desconhecida depende de apenas uma variável, e todas as suas derivadas são tomadas em relação a essa mesma variável. Esse tipo de equação é amplamente utilizado na modelagem de sistemas que evoluem ao longo do tempo ou em função de uma única dimensão (Zill; Cullen, 2001).
Exemplo: 2.1

A equação (2.6), que representa o modelo de crescimento populacional, é classificada como uma equação diferencial ordinária porque envolve derivadas em relação a uma única variável independente, neste caso, o tempo (t). Isso significa que a função desconhecida P(t), que descreve a população em função do tempo, depende exclusivamente dessa variável, e todas as derivadas presentes na equação são tomadas com relação a (t). Esse é o critério essencial que diferencia as equações diferenciais ordinárias das equações diferenciais parciais, as quais, por sua vez, envolvem derivadas em relação a duas ou mais variáveis independentes.
Outro exemplo de equação diferencial ordinária pode ser observado na análise do movimento de corpos em queda livre, conforme ilustrado no Exemplo (2.2).
Exemplo: 2.2


Exemplo: 2.3
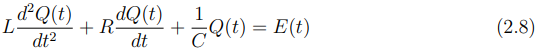
O exemplo 2.3, é uma equação diferencial ordinária, pois envolve derivadas de uma função desconhecida Q(t) em relação a uma única variável independente, o tempo t.
Exemplo: 2.4

O exemplo 2.4 é uma equação diferencial ordinária, porque relaciona a derivada de uma função y(x) em relação a uma única variável independente x.
Exemplo: 2.5

O exemplo (2.5) é uma equação diferencial ordinária, porque envolve derivadas da função y(x) em relação a uma única variável independente x.
As equações diferenciais parciais são aquelas em que as derivadas estão relacionadas a duas ou mais variáveis independentes. Diferente das equações diferenciais ordinárias, que lidam com variações em apenas uma direção, as equações parciais são utilizadas para descrever fenômenos em que a variação ocorre em múltiplas direções ao mesmo tempo Zill e Cullen (2001).
Essas equações aparecem com frequência em situações do mundo real, especialmente na física e na engenharia. Um exemplo clássico é a equação da onda unidimensional, que descreve como uma vibração se propaga ao longo de uma corda ou superfície como vista no exemplo (2.6).
Exemplo 2.6:


Exemplo 2.7:

O exemplo (2.7) é uma equação diferencial parcial, pois u e v são variáveis dependentes de duas variáveis independente x e y o que resulta que u = u(x,y) e v = v(x,y) ou seja a equação irá se relacionar as taxas de variação de u em relação a y com as de v em relação a x
Outro exemplo em que as equações diferenciais parciais (EDPs) aparecem é na equação de Laplace.
Exemplo 2.8

Essa é a forma bidimensional da equação de Laplace. A função f (x,y) é a incógnita da equação e depende de duas variáveis independentes, x e y.
Essa equação é classificada como uma equação diferencial parcial (EDP) de segunda ordem, homogênea e linear, e é amplamente utilizada na modelagem de fenômenos físicos e de engenharia.
2.2.2 Classificação em relação a ordem
A ordem de uma equação diferencial está relacionada a derivada de maior ordem que nela aparece. De modo geral, as equações podem ser de 1ª ordem , 2ª ordem, 3ª ordem…, ou de ordem n, podendo ser escrita na forma:
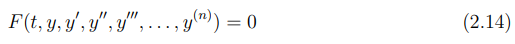
Em que y é uma variável dependente apenas de uma variável independente t.
Exemplo 2.9:


2.2.3 Classificação em relação a linearidade
A linearidade de uma equação diferencial pode ser classificada como linear ou não-linear. Uma equação é considerada linear quando apresenta uma função F que envolve incógnita e suas derivadas, é uma função linear em relação às variáveis y,y′,y′′…yn. Dessa forma, dizemos que a equação diferencial de ordem n é linear quando pode ser expressada pela forma:
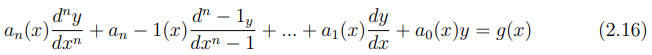
Veja que as equações diferenciais lineares são caracterizadas de acordo com duas propriedades:
- A variável dependente y e todas as suas derivadas aparecem em primeiro grau, ou seja, a potência de cada termo envolvendo y é igual a 1.
- Cada coeficiente depende apenas da variável independente x.
As equações diferenciais ditas não-lineares são equações que não podem ser escrita na forma (2.16), de acordo com Boyce e Diprima um caso simples que envolve uma equação diferencial não-linear são os problemas que inclui pêndulos a qual tem como equação:

Onde, (θ) a variável dependente e o (t) e a variável independente, o (θ) irá representar a oscilação do pêndulo em um determinado instante de tempo(t). A constante (g) representa a aceleração da gravidade em metros por segundo (m/s2), e (L) corresponde ao comprimento da corda ou fio, em metros (m). Trata-se de uma equação não linear, pois envolve o termo (senθ), o que descaracteriza a linearidade da equação. Outro exemplo pode ser encontrado no livro de Zill e Cullen (2001, p.04).

A equação diferencial ordinária (2.18) não é linear, devido à presença do termo y2, pois não obedece a primeira propriedade de linearidade.
2.3 Métodos de solução
As soluções de uma equação diferencial podem ser classificadas em gerais e particulares. A solução geral corresponde ao conjunto de todas as soluções possíveis da equação, geralmente expressas por meio de constantes arbitrárias. Já as soluções particulares são aquelas que satisfazem condições iniciais ou outras condições complementares específicas, conforme destacado por Bassanezi e Ferreira Jr. (1988).
Sobre esse tema, Zill e Cullen em seu livro traz algumas definições do que seria realmente uma solução particular e geral de uma equação diferencial, conforme será apresentado a seguir.

Vale ressaltar que o intervalo I, a depender do contexto em que é utilizado, pode assumir diferentes formas. Ele pode representar um intervalo aberto (a,b), um intervalo fechado [a,b], ou ate mesmo um intervalo infinito, como (0,∞).
2.3.1 Problema de Valor inicial (PVI)
O problema:

Sujeito a condições iniciais:


2.4 Teorema de existência de uma única solução
De acordo com Boyce e Diprima(2015), Antes mesmo de iniciarmos a solução de um problema de valor inicial, é fundamental investigar previamente a existência e a unicidade da solução. Essa análise pode ser guiada por três questões principais:
- A equação diferencial em questão admite solução?
- Caso exista uma solução, ela é única?
- Há alguma solução que satisfaça uma condição inicial específica?
Responder a essas perguntas é essencial para garantir que estamos lidando com um problema bem definido e que nossos esforços não serão em vão. Para isso, contamos com o Teorema de Existência e Unicidade, que estabelece as condições sob as quais uma equação diferencial de primeira ordem possui uma solução única associada a um dado valor inicial. Teorema a seguir pode ser encontrado em Zill e Cullen (2001, p.40):

Zill e Cullen (2001) afirmam que o teorema (2.1) é um dos mais populares entre os teoremas de equações diferenciais, uma vez que os critérios de continuidade tornam a sua verificação relativamente simples. No entanto, não é possível estabelecer um intervalo específico para I onde uma solução possa está definida sem resolver a solução diferencial.
3 EQUAÇÕES DIFERENCIAS DE PRIMEIRA ORDEM
Segundos os autores Boyce e Diprima (2015), Zill e Cullen (2001), Bassanezi e Ferreira Jr (1988), uma equação diferencial ordinária de primeira ordem pode ser escrita da seguinte forma:

Seguindo analogia dos autores que traz também a forma escrita de uma equação diferencial ordinária linear de primeira ordem, a qual tem a forma:

Sendo p e q funções que dependem apenas de uma variável independente t, a solução da equação (3.2) pode ser obtida utilizando o método do fator integrante. Esse método permite encontrar uma solução geral em um intervalo I, no qual as funções p(t) e q(t) são contínuas.
Ao multiplicar a equação diferencial (3.2) por uma função µ(t), a equação é transformada em uma forma integrável, o que facilita sua resolução, pois permite aplicar a regra da derivada do produto. A função µ(t) é chamada de fator integrante.
O objetivo e provar que µ(t) é um fator integrante da equação diferencial (3.2). A resolução a seguir será baseada na análise dos autores Zill e Cullen (2001), a fim de proporcionar maior embasamento teórico.
Multiplicando ambos lados da equação diferencial (3.2) pelo termo µ(t) temos que:
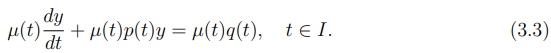
Observe que o objetivo é fazer com que o lado esquerdo seja dado por µ(t)y(t). Utilizando a regra da cadeia na equação (3.3), tem-se que:
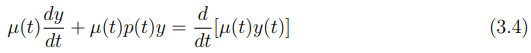
Resolvendo a equação (3.4) pela regra do produto temos que:
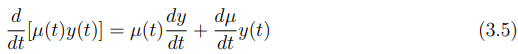
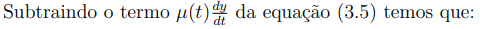

Eliminando y(t) da equação (3.6), sob a suposição de que y(t) = 0 , temos:

A equação (3.7) é uma equação separável, sendo possível resolvê-la por meio de integração:

Onde:

3.1 Equações Diferenciais Separáveis
De acordo com Boyce e DiPrima (2015), uma equação diferencial de primeira ordem escrita na forma da equação (3.1) pode, em muitos casos, não ser linear. Isso dificulta sua resolução, pois, para equações não lineares, muitas vezes não existe um método de solução universalmente aplicável. No entanto, quando a equação pode ser reescrita na forma:

torna-se possível aplicar o método de separação de variáveis, já que as variáveis x e y podem ser isoladas em lados opostos da equação. Reorganizando a equação, temos:

Essa forma evidencia uma equação diferencial separável. A solução, então, pode ser obtida por integração direta de ambos os lados, resultando em:
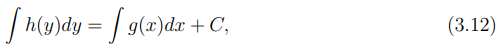
em que C representa uma constante arbitrária de integração.
3.2 Equações diferenciais Exatas
Dentro do estudo das equações diferenciais ordinárias de primeira ordem, destaca-se uma classe conhecida como equações exatas. Essas equações possuem uma estrutura particular que permite sua resolução por meio da identificação de uma função potencial, ou seja, uma função cujo gradiente reproduz a equação original. Esse tipo de equação se mostra relevante não apenas pela elegância matemática de sua resolução, mas também pelas diversas aplicações em áreas como a física, a engenharia e a modelagem de sistemas dinâmicos.
Neste tópico, será apresentado o conceito de equações exatas, a condição necessária para sua caracterização, bem como o método sistemático de resolução. Essa abordagem é essencial para a compreensão de certos problemas práticos.
Uma equação diferencial de primeira ordem é dita exata quando admite uma função potencial g(x,y), tal que:

A equação (3.13) é a diferencial total de g(x,y), ou seja:
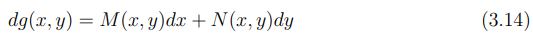
Em outras palavras, existe uma função g(x,y) cuja diferencial total coincide com a equação dada. Dessa forma, resolver a equação (3.13) equivale a determinar a função g(x,y). Para que a equação (3.13) seja considerada exata, é necessário que sejam satisfeitas as condições estabelecidas no teorema (3.1), o qual será apresentado a seguir, pois é esse teorema que assegura a exatidão da equação:

Fonte: Zill e Cullen (2001, p. 61)
Em outras palavras, o teorema estabelece que, caso as funções M(x,y) e N(x,y) admitam derivadas parciais contínuas em uma certa região, a equação pode ser considerada exata.
Supondo que a equação (3.13) seja exata, o próximo passo consiste em determinar a função g(x,y) tal que:

Desse modo a solução de uma equação exata seguir o seguinte método que é Integra a função M(x,y) em relação a x, tratando y como constante:
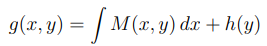
onde h(y) é uma função de y que surge como constante de integração. Deriva-se a expressão obtida para g(x,y) em relação a y e iguala-se a N(x,y):
Dessa equação, determina-se h′(y) e, posteriormente, integra-se para obter h(y).
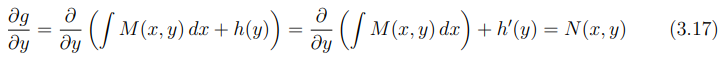
Por fim, a solução geral da equação diferencial é dada implicitamente por:

onde c ∈ R é uma constante arbitrária.
4 EQUAÇÕES DIFERENCIAIS DE SEGUNDA ORDEM
De acordo com Boyce e DiPrima (2015), uma equação diferencial de segunda ordem tem a forma:

A equação (4.1) será considerada uma equação diferencial linear se estiver na forma:
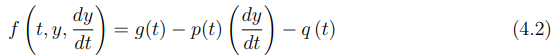


ou
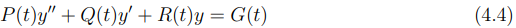
As equações que se apresentam nas formas (4.3) ou (4.4) serão classificadas como lineares, onde p, q e g são continuas em I. As equações que não se enquadrarem nas formas anteriormente apresentadas serão classificadas como não lineares.
Se caso a função g(t) = 0 a equação será classificada como homogênea, caso contrario, será classificada como não-homogênea. Assim considerando a equação (4.3) em que p(t), q(t) e g(t) são funções contantes em a, b e c em que a equação (4.3) torna-se na forma:
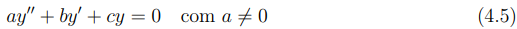
A equação (4.5) será denominada equação linear homogênea de segunda ordem com coeficientes constantes, cuja solução será discutida nas próximas seções, abordando tanto os casos lineares quanto os não lineares, com o auxílio da obra literária de Zill e Cullen (2001).
4.1 Solução de uma equação linear homogênea
Antes de começamos a soluciona a equação (4.5) iremos aplicar o teorema do principio da suposição, também conhecido como método da solução por tentativa a qual está representado no teorema 4.1 :

O teorema 4.1, retirado da obra de Zill e Cullen (2001), estabelece que a soma ou superposição de duas ou mais soluções de uma equação diferencial linear homogênea também constitui uma solução dessa equação.
Utilizando o método da tentativa, supõe-se que a solução da equação (4.5) pode ser encontrada na forma exponencial y(t) = ert. Onde suas derivadas são:

Fazendo a substituição das derivadas na equação (4.5) tem-se que:

Ou inclusive:

Visto que a função exponencial ert é diferente de zero para todo t ∈ R, pode-se desconsiderá-la uma equação algébrica em que obtém-se uma equação polinomial em r, conhecida como equação característica:

A solução da equação característica depende dos valores de suas raízes, que podem ser obtidas pela fórmula de Bhaskara. O tipo dessas raízes influencia diretamente a forma da solução da equação diferencial original. Três casos principais podem ocorrer:
- Duas raízes reais e distintas: a solução geral é dada por uma combinação linear das funções exponenciais associadas a cada raiz:

onde r1 e r2 são as raízes reais distintas da equação característica.
- Duas raízes reais e iguais: neste caso, há uma raiz dupla r, e a solução geral assume a forma:

- Duas raízes complexas conjugadas: quando as raízes são da forma r = α ± βi, a solução geral pode ser escrita como:
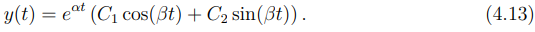
Esses três formatos abrangem todas as possíveis soluções para equações diferenciais lineares homogêneas de segunda ordem com coeficientes constantes, e a escolha da forma apropriada depende do discriminante da equação característica.
4.2 Equações Diferenciais Lineares Não-Homogêneas
As equações diferenciais lineares não homogêneas de segunda ordem aparecem com frequência na modelagem de sistemas físicos, como oscilações mecânicas forçadas, circuitos elétricos com fonte externa e fenômenos de propagação de ondas. A forma geral dessas equações é dada por:
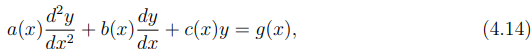
Onde a(x),b(x),c(x) e g(x) são funções contínuas em um intervalo I ⊆ R, com a(x) = 0. O termo g(x) representa a fonte ou entrada externa e é o responsável por tornar a equação não homogênea. Quando g(x) = 0, a equação torna-se homogênea.
Um caso comum e importante ocorre quando os coeficientes a(x),b(x) e c(x) são constantes. A equação assume então a forma mais simples:

A solução geral de uma equação diferencial linear não homogênea é sempre a soma de duas partes distintas:
- Solução geral da equação homogênea associada, isto é:

cuja solução, denotada por yh(x), depende das raízes da equação característica associada:

- Uma solução particular yp(x) da equação não homogênea completa:

Assim, a solução geral da equação não homogênea é dada por:

Para encontrar a solução particular yp(x), os métodos mais utilizados são:
- Coeficientes a determinar: Utilizado quando g(x) é uma função polinomial, exponencial, seno ou cosseno, ou uma combinação dessas. Consiste em propor uma forma funcional para yp(x) com coeficientes desconhecidos e substituí-la na equação para determinar tais coeficientes.
- Variação de parâmetros: Método mais geral, que pode ser aplicado mesmo quando (g(x)) não é de forma simples. Esse método baseia-se nas soluções da equação homogênea para construir uma solução particular da equação completa.
O estudo dessas equações é de extrema importância, uma vez que muitos fenômenos naturais e artificiais são modelados por equações diferenciais de segunda ordem com termos não homogêneos, como por exemplo sistemas massa-mola com forças externas ou circuitos RLC sujeitos a uma fonte de tensão variável. A compreensão teórica dessas soluções permite prever e controlar o comportamento desses sistemas.
5 ELETROMAGNETISMO ATRAVÉS DA HISTÓRIA
De acordo com Wentworth (2009), o eletromagnetismo teve seus primeiros indícios com o grego Thales de Mileto por volta de 600 a.C. Ele evidenciou os primeiros vestígios da atração magnética com a pedra âmbar que significa (elektron), em grego.
A partir dessa descoberta, desencadeou-se uma série de estudos, porém independentes em relação à eletricidade e ao magnetismo, que duraram por vários séculos e que, de acordo com Halliday e Resnick (2016, p.13) afirmam que:
Figura 1 – Pedra âmbar

Fonte: Disponivel em:https://pt.vecteezy.com/foto/25279437-macro-ambar-mineral-pedra-com-aranha-em-branco-fundo acesso em: 30 de abr de 2025
A partir dessa origem modesta na Grécia antiga, as ciências da eletricidade e do magnetismo se desenvolveram independentemente por muitos séculos até o ano de 1820, quando Hans Christian Oersted descobriu uma ligação entre elas: uma corrente elétrica em um fio é capaz de mudar a direção da agulha de uma bússola. Curiosamente, Oersted fez essa descoberta, que foi para ele uma grande surpresa, quando preparava uma demonstração para seus alunos de física.
O primeiro estudo mais esboçado foi com o cientista Pierre de Maricourt (1220 – 1270), que escreveu o primeiro trabalho chamado “O Magneto”, a qual, de acordo com Barbosa (2021, p.09) foi o primeiro estudo organizado sobre o magnetismo do ímã natural. Nele, Maricourt descreve como a repulsão e a atração de uma agulha magnética poderiam ser utilizadas para orientar viajantes. Foi também nesse estudo que ele formulou a ideia de que as linhas de força convergiam para dois pontos opostos do ímã, os quais denominou de polos.
Em 1600, O médico da rainha Elizabeth I William Gilbert (1544–1603) expandiu os estudos sobre o magnetismo com sua obra “De Magnete”. Segundo Barbosa (2021, p. 09), Gilbert sugeriu que a Terra funcionava como um grande ímã e concluiu que, além do âmbar, outras substâncias também poderiam apresentar propriedades similares após serem atritadas. Para demonstrar isso, ele desenvolveu um experimento chamado Versorium que possibilitou identificar a atração dessas substâncias friccionadas por um corpo de massa reduzida, que se tornaria o primeiro instrumento para estudar a energia elétrica. O Versorium é um instrumento básico, composto por uma agulha rotativa reforçada por um plano.
Figura 2 – Versorium.
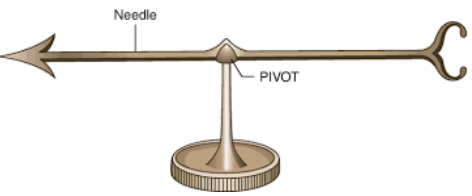
Fonte: Disponivel em: https://link.springer.com/chapter/10.1007/978-3-031-62994-5_1
Acesso em: 02 de abr de 2025
O cientista norte-americano Benjamin Franklin (1706 – 1790) desenvolveu uma teoria que transformou profundamente a compreensão da eletricidade ao postular que, por meio da fricção, um “fluido elétrico” poderia ser transferido de um corpo para outro. Nesse processo, o objeto que recebia esse fluido passaria apresentar uma carga positiva, enquanto o que o perdia ficaria com carga negativa. Tal formulação está alinhada com a concepção apresentada por Sousa (2021, p.36), ao citar Rocha (2002):
No século XVIII, o físico americano Benjamin Franklin (1706–1790) formulou que o elétron e os raios das tempestades possuíam as mesmas propriedades, e que a carga elétrica era conservada. (Rocha, J. F., 2002, apud Sousa, 2021, p.36)
Segundo Ribeiro (2015, p.01), Charles Augustin de Coulomb (1736-1806) foi um cientista francês que elaborou a lei de Coulomb, que declarava que a força entre duas cargas elétricas era proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas. Nesse cenário, Coulomb realizou diversas pesquisas na área da física mecânica e realizou um experimento em sua balança de torção, chegando à lei do inverso do quadrado da distância. Essa lei teve um grande impacto nas novas tecnologias e nos estudos futuros, o que ajudou também a compreensão da interação de moléculas dentro de fluidos e sólidos, o que iria contribuir para o estudo da eletricidade e magnetismo.
De acordo com Wentworth (2009, p. 17), Alessandro Volta (1745–1827) criou a pilha voltaica, permitindo o controle em estudos com correntes elétricas. Hans Christian Orsted (1777–1851) descobriu que essas correntes geram campo magnético, e Michael Faraday (1791–1867) mostrou que a variação do campo magnético induz um campo elétrico. Essas descobertas foram unificadas por James Clerk Maxwell (1831–1879) em quatro equações fundamentais do eletromagnetismo.
De acordo com Lima (2019, p.02), Maxwell apresentou suas equações do eletromagnetismo pela primeira vez em seu artigo “Sobre Linhas de Força Física”, relacionando características elétricas e magnéticas à luz. Sua contribuição foi essencial para formular a teoria eletromagnética da luz, solidificando a noção de que a luz e as manifestações eletromagnéticas são expressões de um único éter.
6 INTRODUÇÃO AO CIRCUITOS ELÉTRICOS
Os circuitos elétricos constituem um dos conteúdos mais relevantes no estudo do eletromagnetismo, sendo amplamente abordados em diversos cursos, especialmente nas áreas de ciências exatas, como Engenharia Elétrica, Matemática e Física. Sua aplicação abrange inúmeros aspectos da vida cotidiana, incluindo a geração de energia, o funcionamento de máquinas elétricas e o uso de aparelhos eletrônicos. Trata-se, portanto, de um tema com ampla aplicabilidade nas áreas da Matemática e da Física, sendo frequentemente explorado em trabalhos acadêmicos e projetos científicos (Alexander; Sadiku, 2013).
Ainda segundo os autores, um circuito elétrico pode ser definido como a interconexão de elementos elétricos. Dessa forma, entende-se o circuito como o caminho pelo qual as cargas elétricas se deslocam por meio dos fios condutores, permitindo o transporte de elétrons de um ponto a outro do sistema.
6.1 Lei de Ohm
Quando os elétrons se movem por um condutor, eles colidem com os átomos do material, perdendo energia na forma de calor. A aplicação de uma tensão faz com que voltem a ganhar energia, mas novas colisões continuam ocorrendo, criando um ciclo constante de perdas e ganhos. Essa dificuldade no movimento dos elétrons é chamada de resistência elétrica. Ela exige uma tensão para manter a corrente fluindo e é representada pela letra (R), sendo medida em ohms (Ω). Em muitos condutores, a corrente elétrica I cresce proporcionalmente à tensão V OMalley (2014). A relação entre elas é dada equação

Em que:
- (V ) é a tensão (ou queda de potencial) no resistor.
- (R ) é a resistência elétrica do componente (medida em ohms(Ω)).
- (I ) é a corrente elétrica que passa pelo resistor (medida em amperes).
Para Halliday e Resnick (2016), um componente só obedece à Lei de Ohm se a corrente elétrica que o atravessa variar linearmente com a diferença de potencial aplicada, independentemente do valor dessa diferença.
6.2 Elementos de um circuito
6.2.1 Resistor
O resistor é um dos componentes mais básicos de um circuito elétrico. Ele tema função de oferecer resistência à passagem da corrente elétrica, transformando parte da energia elétrica em calor. Quando dizemos que um resistor é ôhmico, estamos afirmando que ele obedecer a Lei de Ohm representada na equação (6.1), ou seja quando atravessado por uma corrente elétrica ocorre uma queda de potencial (Nussenzveig, 2015).
Ainda de acordo com Nussenzveig (2015), a conversão de energia elétrica em energia térmica ocorre por meio do efeito Joule, quando essa energia é dissipada. Essa dissipação pode ser representada pela fórmula (6.2):

“Deve-se destacar que nem todos os resistores obedecem à Lei de Ohm. Aqueles que a obedecem são denominados resistores lineares”(Alexander; Sadiku, 2013, p. 30). Já para OMalley (2014), do ponto de vista matemático, o resistor é um componente no qual existe uma relação algébrica entre a tensão e a corrente instantânea, definida pela equação (6.1). Os componentes que não seguem essa relação são conhecidos como resistores não lineares, sendo tratados separadamente. Exemplos de resistores lineares e não lineares podem ser observados na figura 03.
Figura 3 – Resistores lineares e Não-lineares

O resistor “a” será linear, enquanto o resistor “b” será não linear. Desse modo, existem diferentes tipos de resistores em um circuito, desde aparelhos eletrônicos como televisores, micro-ondas e secadores de cabelo, nos quais os resistores dividem ou limitam correntes e voltagens. Tais circuitos podem possuir muitos resistores (Youg; Freedman, 2016).
Figura 4 – Diversos tipos de resistores encontrados em circuitos elétrico

Fonte: Disponivel em :<https://viverdeeletrica.com/tipos-de-resistores-variaveis/>
acesso em 30 de Maio de 2025
Um exemplo prático de resistor não linear é o termistor, cujo valor de resistência varia de forma significativa com a temperatura. Existem dois tipos principais: NTC (coeficiente de temperatura negativo) e PTC (coeficiente de temperatura positivo). A Figura 05 apresenta a representação de um termistor.
Figura 5 – Termistor

Fonte: Disponivel em : https://pt.vecteezy.com/arte-vetorial/27775539-termistor-icone-conjunto-em-branco-fundo-ntc-termistor-resistor-placa-plano-estilo
acesso em 24 de julho de 2025
6.2.2 Capacitor e Capacitância
Os capacitores são dispositivos utilizados para armazenagem de carga elétrica na forma de campo eletrostático. Eles são “formados por duas placas condutoras separadas por um material isolante ou dielétrico” (Alexander; Sadiku, 2013, p. 190). Essa configuração impede o fluxo direto de corrente entre as placas, permitindo no entanto, o acúmulo de cargas elétricas opostas em cada uma delas, como observado na figura 06.
Figura 6 – Capacitor Comum
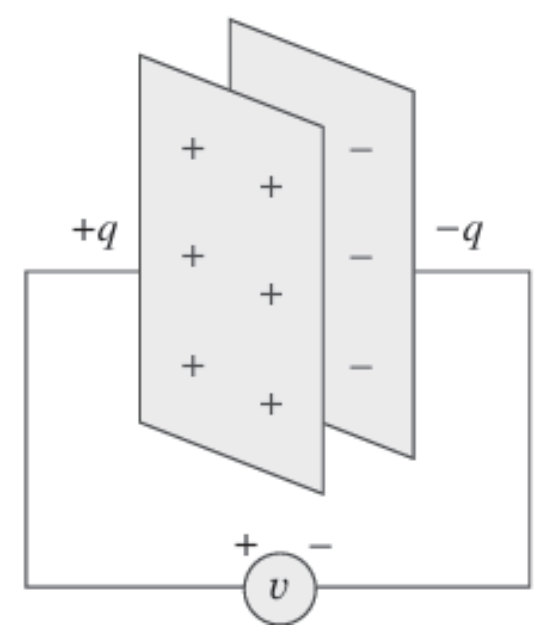
Geralmente o capacitor irá possuir carga liquida igual a zero, mas quando esse condutor é ligado a uma fonte de tensão (v), ocorre a movimentação de elétrons de uma placa para outra em que uma placa acumula carga positiva (+Q) e a outra, carga negativa (−Q). Apesar de cada placa estar carregada, o sistema como um todo possui carga líquida nula, pois as cargas são de mesmo módulo, mas de sinais opostos. Desse modo dizemos que o capacitor está em equilíbrio eletrostático quando essa distribuição se estabiliza e não há mais movimento de cargas. A diferença de potencial entre as placas do capacitor é diretamente proporcional à carga armazenada e inversamente proporcional à capacitância do dispositivo. A placa com carga (+Q) encontra-se em um potencial elétrico mais elevado, enquanto a de carga (−Q) apresenta potencial mais baixo (Young; Freedman, 2016). Nos esquemas de circuitos elétricos, o símbolo do capacitor é representado na figura 07.
Figura 7 – Diagrama de um capacitor em um circuito elétrico
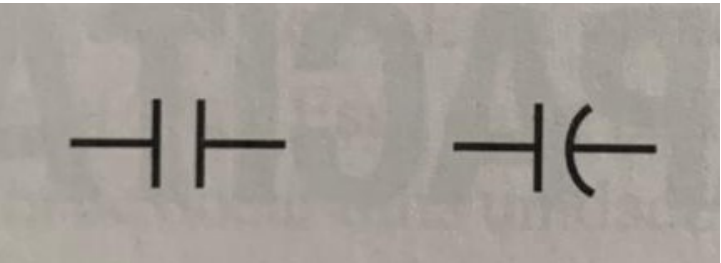
Sobre a capacitância de capacitor Young e Freedman (2016, p.112) afirma quer será “a medida da capacidade de armazenar energia de um dado capacitor”, desse modo vários capacitores conseguem alcançar uma capacitância bastante alta, entre (1−1000µF), porém em frequências mais baixas. Por outro lado, existem capacitores que funcionam melhor em frequências mais altas, mas com uma capacitância limitada, geralmente entre (5pF − 1µF) esse capacitores são chamados de capacitores de cerâmica Wentworth (2009) a equação para calcular a capacitância fica:

A unidade de medida da capacitância é o Farad, nome dado em homenagem ao grande físico Michael Faraday. Um Farad equivale a (1C/V), ou seja, um coulomb por volt. Nessa relação, C representa a constante de proporcionalidade, enquanto (Q) corresponde ao módulo da carga armazenada. Já Vab indica a diferença de potencial entre os condutores, sendo que o condutor (a) possui a carga (+Q) e o condutor (b), a carga (−Q) (Young; Freedman, 2016).
Alexander e Sadiku (2013) afirma que, embora a capacitância C seja definida como a razão entre a carga Q e a tensão V , ela não depende exclusivamente desses dois fatores. Na verdade, a capacitância também está relacionada às características físicas do capacitor, como a área das placas e a distância entre elas. A fórmula (6.3) é utilizada especificamente para o cálculo da capacitância de capacitores de placas paralelas, sendo expressada por:

Nessa equação, (ϵ) representa a permissividade do material dielétrico entre as placas, (A) corresponde à área de cada placa e (d) é a distância entre elas. Dessa forma, é possível encontrar diversos tipos de capacitores, como ilustrado na figura 08.
Figura 8 – Diversos tipos de capacitores
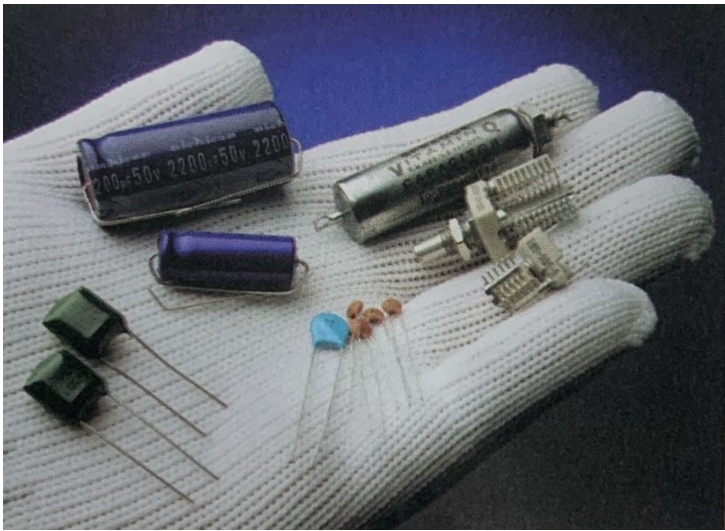
6.2.3 Indutor e Indutância
Indutor é um componente eletrônico cuja principal função é armazenar energia na forma de campo magnético, quando percorrido por uma corrente elétrica. Ele é geralmente constituído por um fio condutor enrolado em forma de espiral, chamado de bobina. Sua principal característica é a indutância, que mede a capacidade do indutor de se opor a variações na corrente elétrica (Halliday; Resnick, 2016) em que pode ser representada pela seguinte relação:

Na equação (6.5), o termo (N) representa o número de espiras de um solenoide que está envolvido por um fluxo magnético. Já o produto (NΦ) corresponde ao enlaçamento do fluxo magnético. A indutância magnética, representada por (L), indica o quanto de enlaçamento de fluxo magnético o indutor é capaz de produzir para uma determinada corrente elétrica. No Sistema Internacional (SI), sua unidade de medida é o Tesla-metro quadrado por ampère (T · m2/A), que recebe o nome de Henry (H), em homenagem ao físico Joseph Henry (Halliday; Resnick, 2016)
Segundo OMalley (2014), a indutância de um indutor está diretamente ligada às suas características físicas e ao modo como ele é construído. Fatores como o formato da bobina, o número total de espiras, o tipo de material ao redor (ou dentro), do núcleo e o espaço entre as voltas do fio são determinantes para o valor final da indutância. Quanto mais voltas e maior a área da seção transversal, maior tende a ser a indutância. Para bobinas simples, feitas em uma única camada, existe uma fórmula aproximada para calcular a indutância, levando em conta a permeabilidade do material, a área da seção transversal, o número de espiras e o comprimento total da bobina. Essa relação é dada na seguinte equação:

Onde (N) é o número de espiras, (µ) a permeabilidade do material, (A) a área da seção transversal e (ℓ) o comprimento da bobina.
Em circuitos elétricos e eletrônicos, os indutores têm diversas aplicações, como filtrar sinais, suavizar variações de corrente, armazenar energia temporariamente ou compor circuitos ressonantes, quando associados a capacitores. Sua representação simbólica nos circuitos é mostrada na figura 09:
Figura 9 – Diagrama de um indutor em circuitos elétricos

Como a indutância irá depender diretamente da forma e dimensões do indutor, existirá vários tipos de indutor a qual pode ser observados na figura 10:
Figura 10 – Diversos tipos de indutores
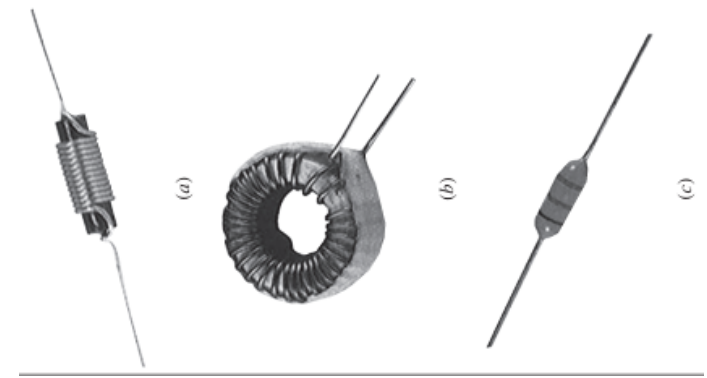
6.2.4 Tensão
A fonte de tensão é um dos elementos fundamentais em circuitos elétricos e eletrônicos, desempenhando o papel de fornecer a energia necessária para o funcionamento dos dispositivos conectados ao circuito. Em termos conceituais, uma fonte de tensão é um componente ou sistema capaz de manter uma diferença de potencial elétrico constante entre seus terminais, independentemente da corrente que a ela esteja sendo solicitada dentro de certos limites operacionais (OMalley, 2014). Sua equação pode ser representada na equação (6.7):

Além disso, a tensão elétrica também pode ser representada por meio de diagramas de circuitos, como ilustrado na figura 11. Nesses diagramas, os componentes são representados por símbolos padronizados, sendo que a fonte de tensão é indicada por um círculo com um sinal positivo e negativo. O indutor, por sua vez, é simbolizado por duas retas paralelas de comprimentos diferentes: a linha maior representa o terminal de maior potencial, enquanto a menor indica o terminal de menor potencial (Barbosa, 2021).
Figura 11 – Representação da tensão em circuitos elétricos
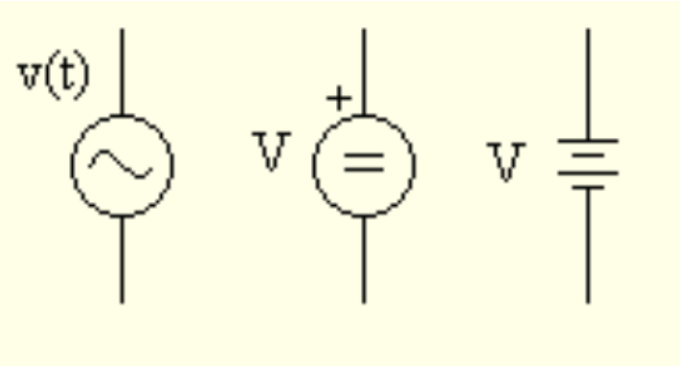
Fonte: Disponivel em :https://www.maxwell.vrac.puc-rio.br/10/10_002.HTM
acesso em 16/06/2025
Uma aplicação prática dessa representação esquemática pode ser observada nas pilhas, como exemplificado na figura 12, onde a disposição dos polos positivo e negativo remete diretamente ao conceito de diferença de potencial elétrico.
Figura 12 – Representação da tensão em pilhas
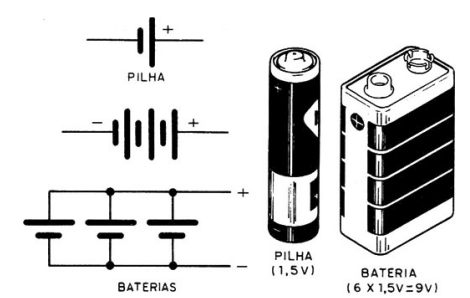
Fonte: Disponível em: https://www.newtoncbraga.com.br/como-funciona/10805-como-funcionam-as-pilhas-e-baterias-art2506.html
acesso em 19/07/2025
6.3 Leis de Kirchhoff
6.3.1 Primeira lei de Kirchhoff
A primeira lei está relacionada ao princípio da conservação da carga elétrica, que afirma que “a soma algébrica das correntes que entram em um nó (ou em um limite fechado) é zero” (Alexander; Sadiku, 2013, p.34). Em outras palavras, a quantidade total de corrente que chega a um ponto de conexão em um circuito (o nó) é exatamente igual à quantidade que sai desse mesmo ponto. Isso garante que não há acúmulo de carga elétrica no nó, refletindo diretamente a conservação da carga. Essa lei é uma importante ferramenta de análise de circuitos, conhecida como Lei das Correntes de Kirchhoff (LKC) ou Lei do Nó, está representada matematicamente pela equação (6.8):

6.3.2 Segunda lei de Kirchhoff
A segunda lei é conhecida lei de Kirchhoff para tensão (LKT) ou lei das malhas, e afirma que “a soma algébrica das variações de potencial encontradas ao longo de uma malha completa de um circuito é zero” (Halliday; Resnick, 2016, seção 27.01). Ou seja, ao percorrer um caminho fechado dentro de um circuito, a soma das quedas e elevações de tensão deve resultar em zero. Representada pela equação (6.9):

6.4 Circuito de Primeira e Segunda ordem
Os circuitos elétricos do tipo RC e RL são classificados como circuitos de primeira ordem, pois possuem apenas um elemento armazenador de energia (capacitor ou indutor). Isso resulta em uma equação diferencial de primeira ordem. Por outro lado, o circuito RLC é considerado um circuito de segunda ordem, já que contém dois elementos de armazenamento de energia (capacitor e indutor), o que leva à formulação de uma equação diferencial de segunda ordem (Alexander; Sadiku, 2013).
Para resolver problemas envolvendo circuitos elétricos simples, é fundamental ter conhecimento prévio das Leis de Kirchhoff e da Lei de Ohm.
Segundo Zill e Cullen (2001), como discutido anteriormente, a Segunda Lei de Kirchhoff para Tensões (LKT) aplicada a circuitos elétricos estabelece que a soma algébrica das quedas de tensão ao longo de um circuito fechado é igual à força eletromotriz aplicada. Essa análise envolve componentes como indutores, capacitores e resistores, cujas tensões podem ser expressas, respectivamente, em função da derivada da corrente, da carga acumulada e da própria corrente elétrica. As expressões matemáticas que descrevem essas tensões dependem diretamente das constantes características de cada componente: indutância; capacitância e resistência, conforme apresentado a seguir:
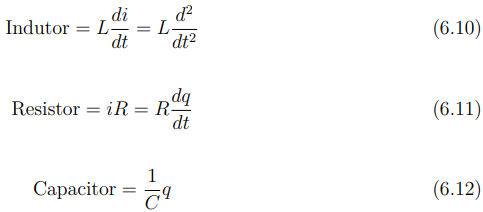
Dessa forma igualando as equações obtemos a segunda lei Kirchhoff com suas derivadas.


6.4.1 Circuito RC
Esse tipo de circuito é composto por um resistor e um capacitor, sendo alimentado por uma fonte de tensão variável no tempo. Aplicando a Segunda Lei de Kirchhoff, podemos obter a seguinte equação que descreve o comportamento dos circuitos elétricos do tipo RC:

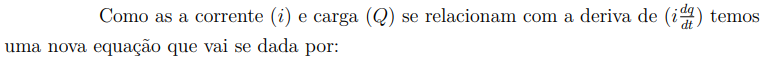

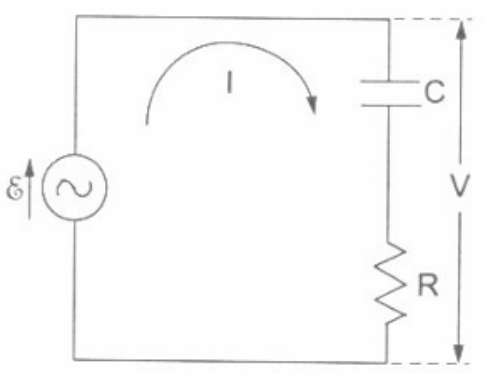
Representação do Diagrama de um circuito RC pode ser observado na figura 11
Figura 13 – Circuito RC
6.4.2 Circuito RL
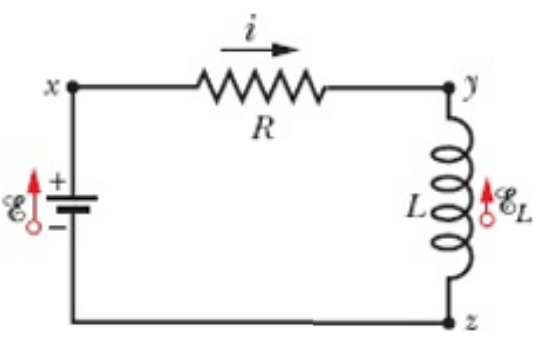
O circuito RL é composto por um resistor e um indutor. Seu funcionamento baseia-se no controle da corrente elétrica, sendo que o indutor atua como um elemento de armazenamento de energia. Ao se opor à variação da corrente, ele gera uma força eletromotriz contrária.
Quando a chave do circuito é fechada, estabelece-se uma tensão constante. Ao ser aberta, o indutor passa a se comportar como um curto-circuito, pois (Ldi/dt = 0). Antes de receber energia, o circuito não armazena nenhuma energia Nilsson e Riedel (2015). Aplicando a segunda Lei de Kirchhoff, a equação diferencial que descreve o circuito fica:

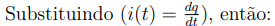

Essa equação é classificada como uma equação diferencial ordinária de primeira ordem, pois envolve apenas a derivada de primeira ordem da corrente i ( t ). Além disso, como os coeficientes (R) e (L) são constantes, trata-se de uma equação com coeficientes constantes.
A representação do diagrama do circuito RL pode ser observado na figura 14:
Figura 14 – Circuito RL
6.4.3 Circuito RLC
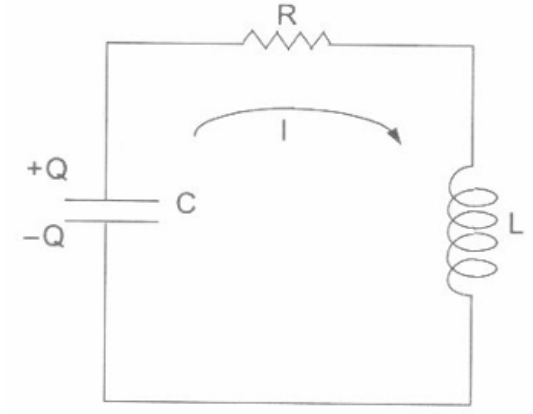
O circuito RLC se destaca por reunir resistor, indutor e capacitor em um único sistema. Apesar de sua aparência simples, sua análise exige a aplicação da Segunda Lei de Kirchhoff, que resulta em uma equação diferencial de segunda ordem, como a apresentada na equação (6.13). Esse modelo matemático é essencial para compreender como as grandezas elétricas se relacionam no tempo e como o circuito responde a diferentes estímulos. A representação do diagrama do circuito RLC pode ser observado a abaixo:
Figura 15 – Circuito RLC
7 METODOLOGIA
Para Marconi e Lakatos (2003), o método cientifico é uma série de atividades organizadas sistematicamente de forma racional, em que traz uma melhor estruturação e ajuda o pesquisador a chegar aos seus objetivos de forma segura e com firmeza evitado erros e promovendo economia, ainda nesse contexto as autoras trazem a definição a que se refere uma pesquisa cientifica.
A pesquisa, portanto, é um procedimento formal, com método de pensamento reflexivo, que requer um tratamento científico e se constitui no caminho para conhecer a realidade ou para descobrir verdades parciais. (Marconi; Lakatos, 2003, p.155) Desse modo, o presente trabalho caracteriza-se como uma pesquisa bibliográfica de natureza exploratória, com ênfase na aplicação das Equações Diferenciais Ordinárias (EDOs) em circuitos elétricos. Explorando conceitos fundamentais por meio da modelagem matemática. A pesquisa foi fundamentada em obras clássicas e contemporâneas como Boyce e DiPrima (2015), Zill e Cullen (2001), Bassanezi e Ferreira Jr. (1988), Bronson e Costa (2008), entre outros autores, além do uso de dissertações, teses e artigos científicos obtidos por meio de plataformas como Google Acadêmico, Scielo e Periódicos Capes.
No que diz a respeito sobre pesquisa bibliográfica Gil (2002), destacar que esse tipo de estudo será constituído através materiais já elaborados através de fontes bibliográficas o que a também a carateriza também uma pesquisa exploratória já que seu principal instrumento se configura através de analise de dados sobre diversas visões em relação a um problema. Gil (2002), ainda destaca a vantagem de utiliza-la:
A principal vantagem da pesquisa bibliográfica reside no fato de permitir ao investigador a cobertura de uma gama de fenômenos muito mais ampla do que aquela que poderia pesquisar diretamente. Essa vantagem torna-se particularmente importante quando o problema de pesquisa requer dados muito dispersos pelo espaço. Por exemplo, seria impossível a um pesquisador percorrer todo o território brasileiro em busca de dados sobre população ou renda per capita; todavia, se tem a sua disposição uma bibliografia adequada, não terá maiores obstáculos para contar com as informações requeridas. A pesquisa bibliográfica também é indispensável nos estudos históricos. Em muitas situações, não há outra maneira de conhecer os fatos passados se não com base em dados bibliográficos.(Gil, 2002, p.45)
Com relação a pesquisa exploratória, esta tem como objetivo ampliar a compreensão sobre a aplicação das equações diferenciais ordinárias no contexto dos circuitos elétricos. Segundo Gil (2002), esse tipo de pesquisa busca proporcionar maior familiaridade com o tema, visando torná-lo mais claro e acessível. Assim, pode-se afirmar que o trabalho tem como propósito o aprimoramento do conhecimento e o desenvolvimento de novas ideias a partir da análise teórica existente.
De acordo com Zanella (2011), o levantamento de dados envolve um processo de leitura e interpretação dos resultados, o qual se divide em diferentes fases. O objetivo principal desse processo é ampliar o conhecimento acerca do objeto de estudo de forma mais clara e fundamentada. A autora destaca que as etapas para a elaboração de uma pesquisa são leitura exploratória, leitura seletiva, leitura reflexiva e leitura interpretativa.
A leitura exploratória, segundo Marconi e Lakatos (2003), consiste em uma sondagem inicial de materiais de pesquisa e obras já publicadas. Essa etapa tem como objetivo obter uma visão geral do que já foi produzido sobre o tema. Nesse sentido, a presente pesquisa realizou uma prospecção de trabalhos acadêmicos por meio de plataformas especializadas, anteriormente mencionadas, além da consulta a livros disponíveis tanto na biblioteca física quanto na biblioteca digital da Universidade Estadual do Maranhão – Campus Balsas, com a finalidade de aprofundar o conhecimento sobre o tema investigado.
Segundo Gil (2002), a leitura seletiva corresponde ao processo de triagem do material coletado, focando naquilo que, de fato, é relevante para os objetivos da pesquisa. Nessa fase, a partir dos dados obtidos na leitura exploratória, realizou-se a seleção criteriosa dos conteúdos pertinentes, descartando-se os que não apresentavam relação direta com o foco do estudo. Para isso, foram analisados os títulos e resumos das produções encontradas, a fim de verificar sua adequação ao escopo da presente investigação.
Sobre a leitura reflexiva, conforme, Marconi e Lakatos (2003), é a etapa que proporciona maior profundidade ao estudo, sendo responsável por reunir e analisar as informações mais relevantes para a pesquisa. Trata-se do momento de fechamento conceitual, no qual se comparam ideias, estabelecem-se relações e são feitos julgamentos críticos a respeito do tema investigado, nesta etapa, a presente pesquisa procedeu a uma análise criteriosa de todos os trabalhos selecionados nas fases anteriores, organizando os dados e estruturando as ideias que fundamentaram o delineamento final da investigação.
No que diz respeito à última fase, foi realizada uma leitura interpretativa dos trabalhos, o que proporcionou um melhor entendimento e um aprofundamento sobre o tema em questão.
O primeiro capitulo é destinado a introdução desse trabalho. Já o segundo capítulo, é apresentado o contexto histórico das equações diferenciais, destacando seu desenvolvimento ao longo dos séculos. A análise baseia-se nas obras de Boyce e DiPrima (2015) e de Bassanezi e Ferreira Jr. (1988), que traçam a evolução desse campo por meio da contribuição dos principais matemáticos responsáveis pela formulação e consolidação das equações diferenciais ao longo do tempo.
Os capítulos três e quatro abordam as equações diferenciais de Primeira e Segunda Ordem, apresentando a fundamentação teórica dessas equações lineares, tanto homogêneas quanto não homogêneas. Além disso, explicam os principais métodos de resolução, como o fator integrante, a separação de variáveis e a equação característica. Essa análise está bastante baseada nos métodos sugeridos por Boyce e DiPrima (2015), Zill e Cullen (2001) e Bronson e Costa (2008).
O capítulo cinco foi destinado a apresentar o conceito histórico do eletromagnetismo e seu desenvolvimento ao longo do tempo. Já o capítulo seis teve como foco o debate sobre os circuitos elétricos, seus principais componentes, tipos e as leis fundamentais que os regem, como as leis de Kirchhoff e Ohm.
O capítulo sete foi destinado à discussão da metodologia adotada para alcançar a aplicação apresentada no capítulo oito deste trabalho, que consistiu na aplicação das equações diferenciais em circuitos RC, RL e RLC, com base em obras literárias como Boyce e DiPrima (2015), Bronson e Costa (2008) e Zill e Cullen (2001).
8 APLICAÇÃO DE EDOS EM CIRCUITOS ELÉTRICOS
Este capítulo será dedicado à aplicação das equações diferenciais em circuitos elétricos, abordando os circuitos do tipo RC, RL e RLC. Utilizaremos os conceitos desenvolvidos ao longo deste trabalho para a resolução de alguns problemas, os quais foram selecionados a partir das obras de Bronson e Costa (2008) e Zill e Cullen (2001).

Resolução: Neste problema, temos os seguintes dados, a força eletromotriz E = 5V, resistência R = 10Ω e capacitância C = 102 F. Com base nessas informações, podemos estabelecer a seguinte equação:

Substituindo os valores fornecidos na equação (8.1) fica da seguinte forma:

Multiplicando ambos os temos por 100 para que possamos simplificar posteriormente, dessa forma a equação (8.2) fica da seguinte forma:

Reorganizando fica:

A equação (8.4) é uma equação diferencial linear de primeira ordem, cuja forma geral pode ser expressada por:

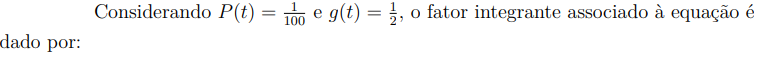

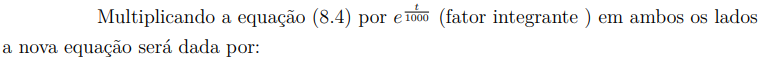
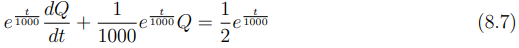

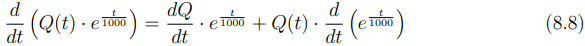
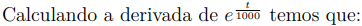
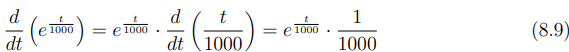
Substituindo este resultado de volta na regra do produto, obtemos que:
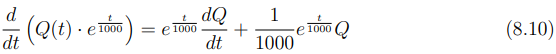
Comparando este resultado com o lado esquerdo da Equação (8.7), verifica-se que são idênticos. Portanto, a equação (8.7) pode ser reescrita como a derivada de um produto:

Integrando ambos os lados da equação (8.11) fica:
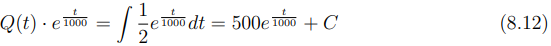
Logo:

Utilizando a condição inicial dado no problema Q(0) = 5, temos:

Portanto, a carga no capacitor em função do tempo é dada por:

A corrente do circuito e dada:

Derivando Q(t) na equação (8.15) temos que:
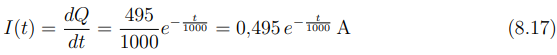
Portanto, a corrente transitória do circuito é representada pela equação (8.17), que mostra que a corrente no circuito RC não se mantém constante com o tempo. Logo após a ligação da fonte, a corrente tem seu valor máximo, que é 0,495A. A partir desse ponto, ela começa a diminuir gradualmente, seguindo um decaimento exponencial, até se aproximar de zero. Isso acontece porque a energia armazenada no capacitor vai sendo dissipada pelo resistor. Com o tempo, o circuito atinge o regime permanente, momento em que não há mais corrente circulando. Esse comportamento confirma a natureza transitória do circuito, ou seja, um processo que muda com o tempo até estabilizar.

Utilizando a Segunda Lei de Kirchhoff, a soma das quedas de tensão nos componentes é igual à tensão fornecida pela fonte. A equação diferencial que modela um circuito RL em série é:

Substituindo os dados fornecidos:

Para resolver a equação (8.19), podemos primeiro dividi-la por 0,5 para simplificar:

Trata-se de uma equação diferencial linear de primeira ordem. O fator integrante é dado por:

Multiplicando ambos os lados da equação (8.20) por e100t:
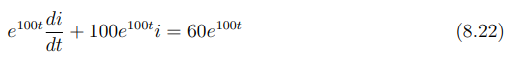
O lado esquerdo da equação (8.22) é a derivada do produto:

Integrando ambos os lados da equação (8.23):
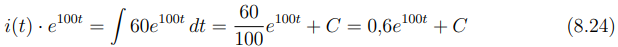
Isolando i(t) da equação (8.24):

Aplicando a condição inicial fornecida pelo problema temos que i(0) = 0:

Portanto, a expressão da corrente elétrica no circuito em função do tempo é:

A equação (8.27), descreve o comportamento da corrente elétrica em um circuito RL sob a ação de uma fonte de tensão constante. Observa-se que, no instante inicial (t = 0), a corrente é nula, como indicado pela condição inicial, e que ela cresce gradualmente com o tempo, aproximando-se de um valor máximo de 0,6A à medida que t → ∞. Esse valor corresponde ao regime permanente do circuito. O termo exponencial negativo representa a parte transitória do sistema, que decai rapidamente devido à constante de tempo associada à razão RL. Assim, o resultado mostra como a corrente evolui de forma suave, partindo do repouso até atingir seu valor final estável.

Sabemos que a equação para um circuito série RLC com força eletromotriz E(t) é:

Os valores fornecido pelo problema é:
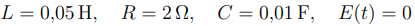
Substituindo:
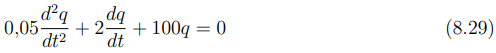
Dividindo a equação (8.29) por 0,05:

A equação (8.30) é classificada como uma equação diferencial linear homogênea de segunda ordem com coeficientes constantes. Devido a essas características, é adequado aplicar o método da equação característica, por meio do qual a equação diferencial é transformada em uma equação algébrica:

Para resolver a equação característica (8.31) aplicamos Bhaskara:

Desse modo a solução geral fica:
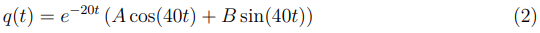
Aplicando condições iniciais:

Usando q(0) = 5:
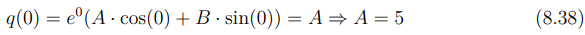
Derivando q(t):
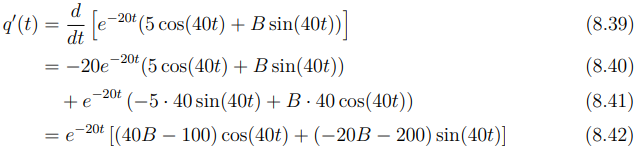
Aplicando q′ (0) = 0:
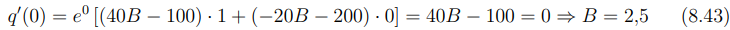
Solução final para q(t):
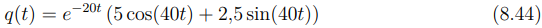
Como o valor de q = (0,01) Substituímos na equação (8.44) a qual fica:
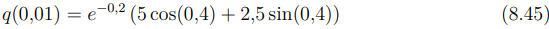
Resolvendo a equação (8.45) temos que:
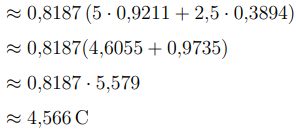
Desse modo, a carga no instante t = 0,01s é aproximadamente 4,566C.
Agora, vamos determinar o primeiro instante em que a carga se anula, isto é, quando q(t) = 0:
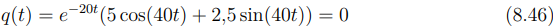
Como e-20t ≠ 0, basta:
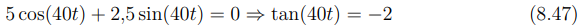
Desse modo a solução fica:
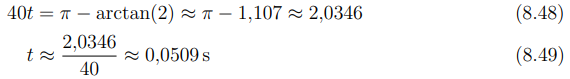
Desse modo o instante em que q(t) = 0 é aproximadamente 0,0509s
Assim o resultado obtido indica que a carga elétrica no capacitor, que inicialmente era de 5C (coulombs), diminui ao longo do tempo devido à ação combinada da resistência, da indutância e da capacitância do circuito. No instante aproximado de 0,0509 segundos, essa carga torna-se igual a zero pela primeira vez.
Esse fenômeno ocorre porque o circuito RLC está oscilando de forma amortecida: a energia elétrica inicialmente armazenada no capacitor é transferida entre o indutor e o capacitor, ao mesmo tempo em que parte dessa energia é dissipada na resistência do circuito.
Portanto, o instante t ≈ 0,0509s representa o primeiro momento em que toda a carga armazenada no capacitor foi descarregada, ainda que temporariamente, antes de possíveis oscilações residuais, típicas desse tipo de circuito, ocorram.
9 CONSIDERAÇÕES FINAIS
A presente pesquisa foi motivada pelo interesse em compreender, de maneira mais aprofundada, a aplicação da modelagem Matemática na Física, especificamente no âmbito dos circuitos elétricos. Paralelamente, almejou-se fomentar a curiosidade e o engajamento de outros pesquisadores acerca da temática, evidenciando sua relevância para a formação acadêmica e para o avanço científico.
Ao longo do desenvolvimento deste trabalho, adotou-se uma metodologia pautada na clareza e objetividade, sustentada por um referencial teórico sólido que abordou, de forma sistemática, conceitos fundamentais e técnicas de resolução de equações diferenciais ordinárias, tais como o método do fator integrante, o tratamento de problemas de valor inicial e a classificação das equações quanto à ordem, tipo e linearidade.
Além disso, foram discutidos aspectos históricos do eletromagnetismo e dos circuitos elétricos, com ênfase na apresentação dos elementos constituintes desses sistemas resistores, capacitores e indutores e nas leis fundamentais que os regem, como a Lei de Ohm e as Leis de Kirchhoff. A investigação incluiu ainda a análise de circuitos de primeira e segunda ordem, permitindo verificar, de forma concreta, a aplicabilidade das equações diferenciais na modelagem de sistemas físicos reais.
Dessa forma, a pesquisa demonstrou a importância das equações diferenciais ordinárias como instrumento essencial na compreensão e solução de fenômenos eletromagnéticos, reforçando a necessidade de sua inclusão e valorização no estudo da Matemática aplicada, especialmente nas ciências exatas e tecnológicas.
Vale destacar que, ao aliar fundamentos teóricos, históricos e aplicações práticas, este trabalho buscou não apenas contribuir para a formação técnica e científica do pesquisador, mas também evidenciar a potência das equações diferenciais como linguagem universal para interpretar os fenômenos naturais e tecnológicos. Ao tratar de circuitos elétricos por meio da modelagem matemática, reforça-se o caráter interdisciplinar da Matemática, incentivando abordagens educacionais que integrem teoria e prática de forma mais significativa.
Por fim, espera-se que este estudo possa servir de base para futuras investigações, promovendo a reflexão sobre novas metodologias de ensino e pesquisa que envolvam a modelagem matemática e sua aplicação em sistemas físicos. Acredita-se que, ao tornar os conceitos mais acessíveis e contextualizados, contribui-se não apenas para o avanço acadêmico, mas também para a popularização da ciência e o fortalecimento do pensamento crítico e analítico nas novas gerações de estudantes e pesquisadores.
REFERÊNCIAS
ALEXANDER, Charles K; SADIKU, Matthew NO. Fundamentos de circuitos elétricos. [S.l.]: AMGH Editora, 2013. Citado 4 vezes nas páginas 22, 25, 29 e 30.
BARBOSA, Mauro José. Monografia, Equações diferenciais ordinárias: aplicações nos circuitos elétricos. 2021. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Instituto Federal de Educação, Ciência e Tecnologia de Rondônia, Campus Cacoal. Citado 2 vezes nas páginas 20 e 28.
BASSANEZI, Rodney Carlos. Ensino e Aprendizagem com Modelagem Matemática. Campinas: Autores Associados, 2002. Citado na página 5.
BASSANEZI, Rodolfo Ilari; Ferreira Jr., Wilfredo. Equações diferenciais: teoria e problemas. São Paulo: Atual, 1988. Citado 5 vezes nas páginas 3, 4, 6, 33 e 34.
BOYCE, William E.; DIPRIMA, Richard C. Equações Diferenciais e Problemas de Valores de Contorno. 9. ed. Rio de Janeiro: LTC, 2015. Tradução da 9ª edição norte-americana. Citado 8 vezes nas páginas 4, 5, 6, 7, 14, 16, 33 e 34.
BRONSON, Richard; COSTA, Gabriel. Equações diferenciais. 3. ed. Porto Alegre: Bookman, 2008. Tradução de Fernando Henrique Silveira. Coleção Schaum. 400 p. Citado 5 vezes nas páginas 6, 7, 33, 34 e 35.
GIL, Antonio Carlos. Como elaborar projetos de pesquisa. 4. ed. São Paulo: Atlas, 2002. Citado 2 vezes nas páginas 33 e 34.
HALLIDAY, David; RESNICK, Robert. Fundamentos de Física, Volume 3: Eletromagnetismo. 10. ed. Rio de Janeiro: LTC – Livros Técnicos e Científicos Editora, 2016. Tradução de: Fundamentals of Physics, 10th edition. ISBN 978-85-216-3208-5. Citado 5 vezes nas páginas 19, 22, 26, 29 e 32.
LIMA, Marcelo Costa de. Sobre o surgimento das equações de maxwell. Revista Brasileira de Ensino de Física, v. 41, n. 4, p. e20190079, 2019. Disponível em: https://www.scielo.br/j/rbef/a/YOUR-LINK-HERE. Citado na página 21.
MARCONI, Marina de Andrade; LAKATOS, Eva Maria. Fundamentos de Metodologia Científica. 5. ed. São Paulo: Atlas, 2003. ISBN 85-224-3397-6. Citado 3 vezes nas páginas 32, 33 e 34.
NILSSON, James W.; RIEDEL, Susan A. Circuitos Elétricos. 10. ed. São Paulo: Pearson Education do Brasil, 2015. Revisão técnica: Antônio Emílio Angueth de Araújo, Ivan José da Silva Lopes. ISBN 978-85-4301-812-6. Citado na página 31.
NUSSENZVEIG, Herch Moysés. Curso de física básica: Eletromagnetismo (vol. 3). [S.l.]: Editora Blucher, 2015. v. 3. Citado 4 vezes nas páginas 22, 23, 31 e 32. OMALLEY, John. Análise de circuitos. [S.l.]: Bookman Editora, 2014. Citado 4 vezes nas páginas 22, 23, 27 e 28.
RIBEIRO, Daniel. Charles-augustin de coulomb. Revista de Ciência Elementar, v. 3, n. 3, p. 039, 2015. Faculdade de Ciências da Universidade do Porto. Disponível em: http://doi.org/10.24927/rce2015.039. Citado na página 21.
SOUSA, Damião Franceilton Marques de. TCC, Equações diferenciais ordinárias aplicadas na física clássica. 2021. Trabalho de Conclusão de Curso (Licenciatura em Física) – Universidade Federal de Campina Grande, Centro de Educação e Saúde, Cuité, PB. Citado na página 21.
WENTWORTH, Stuart M. Eletromagnetismo aplicado: abordagem antecipada das linhas de transmissão. [S.l.]: Bookman Editora, 2009. Citado 3 vezes nas páginas 19, 21 e 25.
YOUNG, Hugh D.; FREEDMAN, Roger A. Física III, Sears e Zemansky: Eletromagnetismo. 14. ed. São Paulo: Pearson Education do Brasil, 2016. Título original: University Physics with Modern Physics. Citado na página 25.
ZANELLA, Liane Carly Hermes. Metodologia de Pesquisa. 2. ed. Florianópolis: Universidade Federal de Santa Catarina, 2011. Material do Curso de Administração a Distância, Departamento de Ciências da Administração, UFSC. ISBN 978-85-7988-111-3. Citado na página 33.
ZILL, Dennis G.; CULLEN, Michael R. Equações diferenciais: volume 1. 3. ed. São Paulo: Pearson Makron Books, 2001. Revisão técnica de Antonio Pertence Jr. Tradução da obra: Differential Equations with Boundary-Value Problems. ISBN 85-346-1291-9. Citado 11 vezes nas páginas 6, 7, 8, 10, 15, 30, 33, 34, 35, 37 e 39.
1Discente do Curso Superior de Licenciatura em Matemática da Universidade Estadual Do Maranhão Campus Balsas-MA. e-mail: gustavouema22@gmail.com
2Docente do Curso Superior de Licenciatura em Matemática da Universidade Estadual Do Maranhão Campus Balsas-MA. Doutor em Física e Astronomia (UNIVAP). e-mail: nilsonlaurindo@cesba.uema.br
3Docente do Curso Superior de Licenciatura em Física da Universidade Estadual Do Maranhão Campus Caxias-MA. Doutor em Engenharia e Ciências dos Materiais (UFC). e-mail: juliermesufc@gmail.com
4Docente do Curso Superior de Licenciatura em Matemática da Universidade Estadual Do Maranhão Campus Balsas-MA.
Doutor em Engenharia Nuclear(UFRJ). e-mail: sergioturibus@professor.uema.br
