REGISTRO DOI: 10.5281/zenodo.7581462
Danilo do Nascimento Souza
Resumo
O mercado global de energia elétrica está crescendo a uma taxa de cerca de 100 GW por ano e até recentemente, essa demanda era atendida por meio de plantas de geração centralizadas. No entanto, essa estrutura centralizada é ineficiente e poluente. Por isso, muitas nações estão se voltando para a geração distribuída de energia utilizando recursos naturais renováveis para atender a demanda crescente de energia, aumentar a eficiência e reduzir as emissões de gases poluentes. A geração distribuída permite aos usuários controlar a produção e demanda, impõe uma melhoria na eficiência pela redução das perdas por transmissão e distribuição, e aprimora a segurança energética. As pilhas a combustível do tipo PEM (Proton Exchange Membrane) são amplamente pesquisadas devido à sua eficiência elevada, capacidade de funcionar de forma discreta e produzir água e calor como subprodutos. Com a crescente presença de geração distribuída (GD) na rede elétrica, é necessário que as unidades de GD compartilhem a responsabilidade de manter a estabilidade da rede. Além disso, as unidades conectadas podem ser usadas para suporte de tensão através da injeção de potência reativa. Esses requisitos são atualizados e revisados com base no desenvolvimento e nível de inserção das unidades e são emitidos como procedimentos de rede. Este estudo propõe um sistema de microgeração formado por uma pilha a combustível e um inversor monofásico conectado à rede, que atenda especificações de procedimentos de rede. Além disso, é apresentado e analisado o controle do inversor multinível para rastreamento de referências de potência em condições normais de operação e em operação Fault Ride Through.
Palavras – chave: Pilha a combustível, Geração Distribuída, inversor monofásico, PEM, FRT.
Abstract
The global electricity market is growing at a rate of about 100 GW per year and until recently, this demand was met through centralized generation plants. However, this centralized structure is inefficient and polluting. Therefore, many nations are turning to distributed generation of energy using renewable natural resources to meet the growing demand for energy, increase efficiency, and reduce emissions of pollutants. Distributed generation allows users to control production and demand, imposes an improvement in efficiency by reducing transmission and distribution losses, and improves energy security. Proton Exchange Membrane (PEM) fuel cells are widely researched due to their high efficiency, ability to function discreetly and produce water and heat as by-products. With the increasing presence of distributed generation (DG) in the electricity grid, it is necessary for DG units to share the responsibility of maintaining grid stability. Additionally, connected units can be used for voltage support through reactive power injection. These requirements are updated and reviewed based on the development and level of insertion of the units and are issued as grid codes. This study proposes a microgeneration system consisting of a fuel cell and a single-phase inverter connected to the grid, meeting grid code specifications. Additionally, the control of the multi-level inverter for power reference tracking in normal operation and Fault Ride Through operation is presented and analyzed.
Keywords: Fuel Cell, Distributed Generation, single phase inverter, PEM, FRT
1. Introdução
A crescente preocupação com o desenvolvimento sustentável e formas de geração mais eficientes de energia têm proporcionado um aumento no interesse por combustíveis alternativos e novos processos de geração de energia. A dependência dos combustíveis fósseis tem resultado em uma inexorável poluição do ar e em dificuldades crescentes para exploração das reservas de petróleo do mundo. Ademais, o mundo precisa de formas de gerar energia com baixa emissão de gases poluentes, com eficiência elevada e cujos principais insumos energéticos tenham suprimento ilimitado para atender a demanda de uma população em expansão.
O mercado global de energia elétrica está crescendo a uma taxa de cerca de 100 GW [1] por ano e até recentemente, essa demanda era atendida por meio de plantas de geração centralizadas com linhas de transmissão para distribuição. No entanto, essa estrutura centralizada é ineficiente e poluente. Por isso, muitas nações estão se voltando para a geração distribuída de energia utilizando recursos naturais renováveis para atender a demanda crescente de energia, aumentar a eficiência e reduzir as emissões de gases poluentes. A geração distribuída permite aos usuários controlar a produção e demanda, impõe uma melhoria na eficiência pela redução das perdas por transmissão e distribuição, e aprimora a segurança energética.
As pilhas a combustível do tipo PEM (Proton Exchange Membrane) são amplamente pesquisadas devido à sua eficiência elevada, capacidade de funcionar de forma discreta e produzir água e calor como subprodutos. Elas podem ser aplicadas em diversas situações, incluindo estacionárias, transporte e portáteis. O objetivo desse estudo é analisar a utilização estacionária dessas pilhas. Pequenas centrais estacionárias operam na faixa de potência de 1 kW a 10 kW [2]. De acordo com a Norma da Light para microgeração, o sistema com potência de geração instalada inferior a 10 kW tem a opção de operar de forma monofásica.
2. Pilhas a Combustível
Uma pilha a combustível é um dispositivo que converte energia química em energia elétrica, utilizando dois reagentes, o combustível (geralmente hidrogênio) e um oxidante (normalmente oxigênio presente no ar ambiente). A energia é gerada a medida que os reagentes são consumidos. As reações eletroquímicas ocorrem nos eletrodos, produzindo ou consumindo elétrons e íons. Elétrons são gerados no anodo e consumidos no catodo, movendo-se através de um circuito externo, resultando em corrente elétrica. Íons fluem entre o anodo e o catodo e é necessário um catalisador para que a reação ocorra. Como resultado, é produzido água e calor como subprodutos. A Figura 1 ilustra o esquema básico dessa pilha.
Figura 1 – Diagrama básica da Pilha a Combustível [3]
2.1 Pilhas PEM
O estudo utilizará pilhas do tipo PEM, também conhecidas como pilhas a combustível de polímero de eletrólito médio. Essas pilhas foram inventadas na General Electric no início da década de 1960 por Thomas Grubb e Leonard Niedrach. A GE desenvolveu uma pilha pequena para uso militar, alimentada por hidrogênio gerado a partir de água e hidreto de lítio. No início da década de 1960, a NASA utilizou pilhas do tipo PEM no Projeto Gemini, mas devido a problemas com contaminação e vazamento de oxigênio, as pilhas foram descontinuadas [4].
A GE continuou seu trabalho nas pilhas PEM na década de 1970 e desenvolveu uma tecnologia de eletrólise da água para pilhas do tipo PEM, que foi utilizada na Planta de Geração de Oxigênio da Marinha Americana [5]. A Marinha Real Britânica também utilizou pilhas do tipo PEM no início da década de 1980 para a sua frota de submarinos. A partir do ano 2000, pilhas do tipo PEM foram extensivamente estudadas por companhias comerciais para aplicações veiculares, estacionárias e portáteis [5].
Atualmente, a abordagem de pesquisas em pilhas do tipo PEM é feita a partir de três pontos de vista: custo, desempenho e durabilidade. O material é o principal custo em uma pilha do tipo PEM, mas com o aumento do preço dos combustíveis fósseis, o preço dessas pilhas tem se tornado cada vez mais competitivo. A durabilidade média de uma pilha do tipo PEM é da ordem de 1000 horas de operação, mas para ser viável economicamente, a vida útil precisaria aumentar significativamente [6]. Além disso, pesquisadores também estão trabalhando em soluções para os desafios relacionados a condições de operação a frio, condições de eficiências mais favoráveis e a produção e mudança de fase da água.
3. Modelo da Pilha a Combustível
Existem vários tipos de modelos de pilhas a combustível propostos na literatura, que podem ser classificados em três categorias: químico, experimental e elétrico. Os modelos químicos incluem processos químicos complexos e fenômenos eletrodinâmicos, mas necessitam de muitos parâmetros que podem ser difíceis de obter com precisão. Os modelos experimentais derivam de experimentos e representam a pilha por tabelas de consulta ou expressões empíricas, mas não incluem a termodinâmica da pilha e podem não considerar os efeitos de parâmetros de operação como pressão, vazão, composição do gás e temperatura. Por outro lado, os modelos elétricos representam a pilha a partir de um circuito elétrico e são adequados para simulação de sistemas de pilhas a combustível, mas também não incluem a termodinâmica da pilha. Em todas as abordagens de modelagem, os parâmetros do modelo são obtidos empiricamente através de testes na pilha real.
O modelo elétrico simplificado representa a pilha por meio de uma fonte de tensão controlada conectada em série com uma resistência constante, como mostrado na Figura 2. Neste modelo, parâmetros como pressão, temperatura, composição dos gases e vazões de ar e hidrogênio podem variar. Esses parâmetros afetam o coeficiente angular de Tafel (A), a corrente de troca (i0) e a tensão de circuito aberto (Eoc). Para determinar esses parâmetros, é preciso considerar as pressões de entrada, vazões, temperatura da pilha e composição dos gases. A fonte de tensão controlada (E) é descrita pela equação 3.1.
Figura 2 – Modelo Elétrico Simplificado da Pilha a Combustível [3]
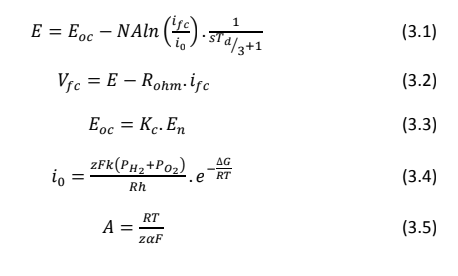
em que
Eoc = tensão de circuito aberto (V),
N = número de células,
A = coeficiente angular de Tafel (V),
i0= corrente de troca (A),
Td = tempo de resposta (s),
Rohm = resistência interna (Ω),
R = 8, 3145 J/(mol · K),
F = 96485 A s/mol,
z = número de elétrons em movimento (z = 2), En =Tensão de Nernst (V),
α =coeficiente de transferência de carga,
PH2= pressão parcial do hidrogênio no interior da pilha (atm), PO2= pressão parcial do oxigênio no interior da pilha (atm), k = constante de Boltzmann (1, 38 × 10^−23 J/K), h = constante de Planck (6, 626 × 10^−34 J s),
∆G = energia livre de Gibbs (J),
T = temperatura de operação da pilha (K),
Kc =constante de tensão em condições normais de operação, ifc= corrente da pilha (A),
Vfc = tensão da pilha (V).
4. Operação em modo FRT
Com a crescente presença de geração distribuída (GD) na rede elétrica, é necessário que as unidades de GD compartilhem a responsabilidade de manter a estabilidade da rede. A desconexão dessas unidades durante eventos de afundamento de tensão não é mais aceitável, pois pode resultar em perda repentina de potência ativa e colapso do sistema de energia. Além disso, as unidades conectadas podem ser usadas para suporte de tensão através da injeção de potência reativa. Essas exigências já são comuns em alguns países e são fornecidas como requisitos de rede. Esses requisitos são atualizados e revisados com base no desenvolvimento e nível de inserção das unidades e são emitidos como procedimentos de rede.
Por exemplo, nos requisitos de rede da Alemanha, as unidades de geração devem operar em modo FRT (Fault Ride Through) e suportar a tensão da rede em situações de falta. Requisitos similares podem ser observados em outros países como a Dinamarca, Itália, Espanha e Estados Unidos, onde a geração distribuída representa uma parcela significativa na malha energética do país [3]. A capacidade de operar em modo FRT é definida de modo que a unidade GD permaneça conectada à rede durante um curto período e injetando uma quantidade de potência reativa para sustentar a rede na presença de uma falta. Diferentes curvas FRT são mostradas de acordo com os requisitos de cada país (Figura 3). Neste trabalho, a norma E.ON é seguida para determinar a injeção de reativo durante a falta, conforme ilustrado na Figura 4.
No Brasil, de acordo com as normas da ABNT NBR-16149 para sistemas fotovoltaicos, sistemas com capacidade nominal superior a 6 kW devem manter a conexão com a rede em casos de afundamentos de tensão de acordo com a Fig.5. Apesar de não existir uma norma especificamente para pilhas a combustível devido à baixa inserção na malha energética, a tendência é que no futuro as normas aplicadas à pilha sejam as mesmas que são aplicadas aos painéis fotovoltaicos atualmente. Por isso, neste trabalho será utilizada a norma ABNT NBR-16149 e a norma da Light para microgeração como uma primeira referência para as pilhas a combustível.
Figura 3 – Critério de tensão para o modo FRT para Sistemas de Distribuição em diferentes países [3]
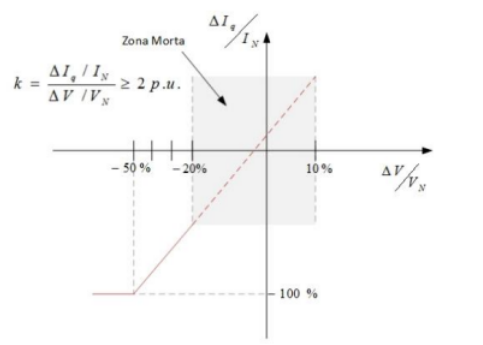
Figura 4 – Critério para Suporte de Tensão em Situações de Falta [3]
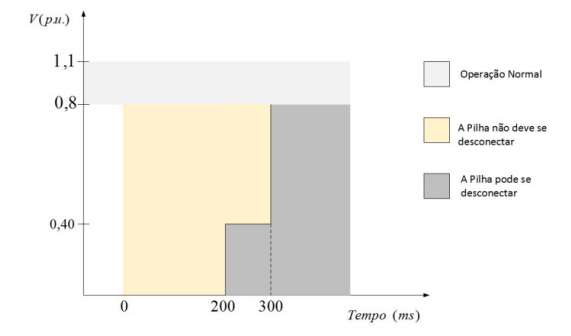
Figura 5 – Critérios de suportabilidade a subtensões decorrentes de falta na rede [3]
A Fig.6 ilustra a estrutura geral do sistema de geração de energia a pilha a combustível conectado à rede de distribuição.
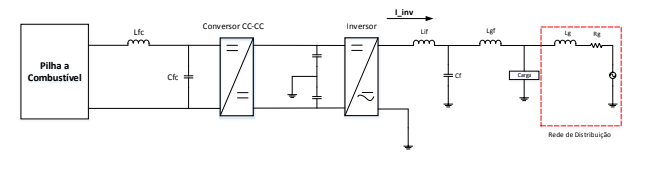
Figura 6 – Diagrama Geral de um Sistema a Pilha a Combustível conectado à Rede
Conversor CC-CC
As fontes de energia utilizadas na geração distribuída frequentemente apresentam características de saída que não são compatíveis com a rede elétrica. Por essa razão, são geralmente utilizados conversores eletrônicos para conectar essas fontes de energia à rede. Por exemplo, a pilha de combustível tem uma tensão de saída de baixa amplitude e uma corrente contínua que varia com a carga. Dessa forma, é necessário elevar a tensão de saída da pilha e convertê-la em tensão alternada para que possa ser conectada à rede elétrica.
Devido às suas vantagens, como a elevada relação de transformação e o baixo ripple de corrente, o conversor push-pull fonte de corrente é considerado o mais adequado para esse estudo. Além disso, é conhecido que o desequilíbrio de fluxo no transformador não é uma preocupação significativa devido à alta impedância de entrada do conversor push-pull com tap central [7].
Inversor
O uso de conversores multiníveis tem sido cada vez mais comum em aplicações como FACTS (Flexible AC Transmission Systems) e personalizadas. Isso se deve ao fato de que essas topologias de conversores são convenientes para usar com fontes de tensão CC múltiplas, como capacitores, baterias e fontes renováveis [8]. A função principal de um conversor multinível é produzir uma forma de onda CA a partir de níveis de tensão CC. Por isso, esses conversores são ideais para serem conectados em série ou paralelo a uma rede CA com fontes renováveis como fotovoltaica, pilhas a combustível e dispositivos de armazenamento de energia como capacitores e baterias. Além disso, eles são usados para ajuste de velocidade de motores, compensação reativa, restauração dinâmica de tensão e filtro harmônico.
Com a crescente inserção de fontes de geração distribuída na malha elétrica, o uso de conversores multiníveis para controlar a frequência e tensão de saída a partir de fontes renováveis traz benefícios significativos devido à sua rápida resposta e controle autônomo. Eles também podem controlar os fluxos de potência ativa e reativa de uma fonte de energia renovável conectada à rede. Isso os torna atraentes para o controle contínuo do comportamento dinâmico do sistema e para reduzir problemas de qualidade de potência, como harmônicos de tensão, desequilíbrio e afundamentos [9].
A utilização de conversores multiníveis foi proposta devido à sua facilidade de integração com fontes renováveis de energia, como fotovoltaica, eólica e pilhas a combustível, além de produzir sinais com baixa distorção harmônica. No entanto, é importante avaliar se eles atendem aos requisitos dos procedimentos de rede para geração distribuída e como se comportam em condições anormais de operação, como será discutido mais adiante.
Determinação da Potência para o modo de operação FRT
A pilha opera de maneira eficiente e com fator de potência próximo à unidade em condições normais de operação. No entanto, de acordo com alguns requisitos de rede, em caso de falhas, o inversor deve injetar potência reativa na rede para ajudar a manter a estabilidade de tensão durante o período de falha. A potência reativa injetada é determinada pelo afundamento de tensão ocorrido durante a falha. As potências fornecidas à rede em coordenadas d-q podem ser expressas como [3]:

Os subscritos “gd” e “gq” representam as componentes d e q da tensão e corrente na rede. Conforme a Fig. 4, a corrente reativa é expressa como
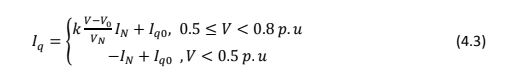
V, V0 e VN são as amplitudes da tensão instantânea da rede, o valor inicial da tensão da rede antes da falta e a tesão norminal da rede respectivamente. IN e Iq0 representam a corrente nominal e corrente reativa inicial antes da ocorrência da falta e k ≥ 2. pu.
A corrente Id é dada por
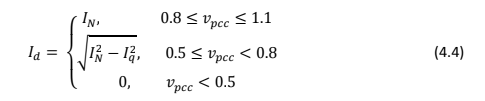
De posse da eq. (4.3) e substituindo nas eqs. (4.1) e (4.2), a potência ativa P∗ e reativa Q∗ de referência no modo falta podem ser expressas como

Estratégia para Injeção de Potência Reativa
Durante a operação normal do sistema da pilha, a potência ativa de referência é determinada a partir do ponto de operação da pilha e o sistema normalmente opera com fator de potência unitário ou de acordo com requisitos do operador de rede. Quando uma falha é detectada, o sistema da pilha passa a operar no modo FRT. Durante esse período, o sistema mantém a tensão regulada e, ao mesmo tempo, fornece suporte reativo durante a recuperação de tensão. Considerando a proteção de sobrecorrente do inversor e os requisitos de injeção de potência reativa em caso de falhas na rede, a estratégia de controle consiste em manter a amplitude de corrente limitada, evitando assim o risco de desligamento do inversor devido a sobrecorrente. A corrente reativa é calculada de acordo com a equação (4.3) e a corrente de pico é ajustada como o valor nominal da corrente do inversor em condições normais de operação.
Desse modo,

Em que vpcc representa a tensão no PCC (ponto de acoplamento comum), 0.5 ≤ < 0.8 e k ≥ 2. Se vpcc < 0.5 p.u o inversor fornece somente potência reativa ( Iq = IN). . O diagram da Fig. 7 ilustra a estratégia de controle adotada.
Figura 7 – Diagrama de correntes para a estratégia de corrente de pico constante [3]. a) 0.5 ≤ vpcc < 0.8 b) vpcc < 0.5
Malha de Controle de Corrente
Os métodos de controle Proporcional Ressonante (PR), Controle Ressonante (RSC), Controlador Repetitivo (RC) e Controlador Deadbeat podem ser aplicados diretamente na malha de corrente devido à sua capacidade de seguir sinais senoidais sem erro de regime permanente. Adicionando um Compensador Harmônico (HC) ao controlador, é possível obter um melhor desempenho do controle. Os métodos de controle Proporcional Ressonante (PR), Controle Ressonante (RSC), Controlador Repetitivo (RC) e Controlador Deadbeat podem ser aplicados diretamente na malha de corrente devido à sua capacidade de seguir sinais senoidais sem erro de regime permanente [3]. Adicionando um Compensador Harmônico (HC) ao controlador, é possível obter um melhor desempenho do controle.
A função de transferência do controlador de corrente é dada por:
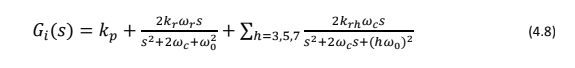
em que kp é o ganho proporcional, kr é o ganho fundamental do controle ressonante, krℎ é o ganho de controle de order h-ressonante e w0 é a frequência fundamental da rede. A Fig. 8 ilustra o diagrama da malha de corrente e a Fig. 9 mostra o controlador proporcional ressonante com compensador de harmônicos descrito pela eq. (4.8).
Figura 8 – Diagrama da Malha de Controle de Corrente
Figura 9 – Diagrama de Resposta em Frequência para o PRHC para kp-22, kr-500, wc=1rad/s e krh = 5000.
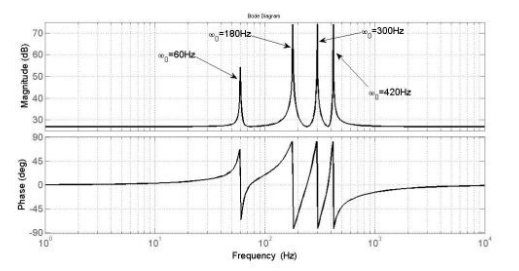
Figura 9 – Diagrama de Resposta em Frequência para o PRHC para kp-22, kr-500, wc=1rad/s e krh = 5000.
Malha de Controle de Potência
A malha externa de potência estabelece as condições de funcionamento do sistema (amplitude de tensão e frequência da rede) e gera a corrente de referência utilizada na malha interna de corrente. Portanto, essa malha permite a implementação de métodos de controle para determinar a corrente da rede operando no modo FRT. Com base na Teoria de Potência Instantânea para sistemas monofásicos, a referência da corrente do inversor pode ser obtida regulando as potências ativa e reativa.
A referência da corrente do inversor pode ser dada por [3]:
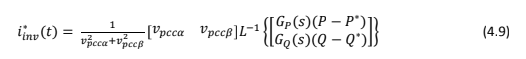
em que vpccα e vpccβ são as componentes ortogonais da tensão do PCC, P e Q são respectivamete as potências ativa e reativa, P∗ e Q∗ são as referências de potência ativa e reativa e e GP(s) e GQ(s) são os controladores PI para as potência ativa e reativa respectivamente.
Figura 10 – Malha de Controle de Potência
A Fig.10 ilustra o sistema de controle para a malha de potência. Nessa figura, Vcc representa a tensão do elo CC e Pfcff representa a potência feedforward fornecida pela pilha.
Resultados para o Modo de operação FRT
Em seguida, serão mostradas as formas de onda de potência em cenários de falha para avaliar o controle do inversor durante o modo FRT.
Afundamento de 0.65 pu de tensão no PCC
As figuras 11 e 12 mostram as variações da potência ativa e reativa, respectivamente, diante de uma queda de tensão de 0.65 p.u. A oscilação observada na referência da potência ativa é causada pela
regulação da tensão no elo CC do inversor, que apresenta uma componente de segundo harmônico. Os valores das potências são calculados de acordo com as equações (4.5) e (4.6).
As referências de corrente durante a falta podem ser determinadas segundo as eqs. (4.4) e (4.7) e, portanto as referências de potência podem ser determinadas utilizando-se das equações (4.5) e (4.6). Logo,

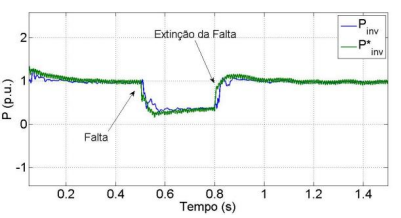
Figura 11 – Curva de Potência Ativa diante do afundamento de tensão de 0.65 pu.
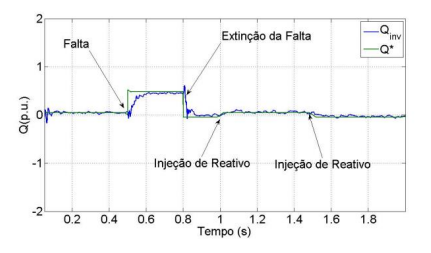
Figura 12 – Curva de Potência Reativa diante de afundamento de tensão de 0,65 p.u.
Fig.13 ilustra o rastreamento da corrente do inversor. Pode-se notar nessa figura que durante o período de falta o valor de pico da corrente permanece limitado conforme a técnica de controle utilizada. A Fig.14 mostra em detalhe o rastreamento da corrente.
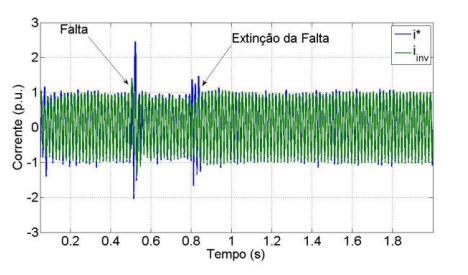
Figura 13 – Rastreamento da Corrente no Inversor com falta de 0.65 p.u
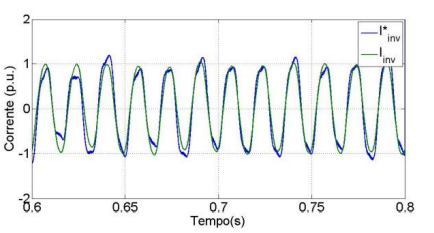
Figura 14 – Detalhe para o Rastreamento da Corrente no Inversor para afundamento de 0.65 p.u
O THD para o intervalo anterior a falta foi de 3,11 %, para o intervalo durante a falta de 4,89 % e pós falta de 3,73 %. A norma da Light estabelece que a corrente no inversor deve possuir distorção harmônica total inferior a 5 %.
5. Conclusão
Este estudo abordou um sistema de microgração a pilha a combustível conectado à rede de distribuição por meio de circuitos de eletrônica de potência que utilizam um conversor CC e um inversor de potência.
A operação em modo FRT mostrou-se como uma alternativa eficaz para suporte de tensão da rede mediante situações de falta com injeção adequada de reativo a partir do cálculo da corrente de referência do inversor. Esse cálculo foi obtido a partir de malhas de controle tanto de corrente quanto de potência. Foi demonstrado ainda que o PRHC tornou-se fator fundamental para que a corrente obtida estivesse dentro dos níveis de distorção harmônica adotados por procedimentos de rede.
Dessa forma, mediante a proposta de controle adotada, as unidades de geração podem se manter conectadas à rede em situações de falta, evitando assim a perda repentina de potência ativa e colapso do sistema de energia.
6. Referências Bibliográficas
[1] COLLEEN, S., Designing and building fuel cells. Mcgraw-hill New York, NY, USA, 2007.
[2] NAIL, J. M., ANDERSON, G., CEASAR, G., et al., “The evolution of the pem stationary fuel cell in the us innovation system”. In: International Conference on Innovation in Energy Technologies, Washington, DC, pp. 29–30, 2003.
[3] DO NASCIMENTO SOUZA., D., “Análise e simulação de um sistema de microgeração distribuída com pilha a combustível de catodo aberto e conversor multinível monofásico”, Dissertação de Mestrado, COPPE-UFRJ, BRAZIL, 2015.
[4] BASU, S., Channel Two-phase Flow and Phase Change in Polymer Electrolyte Fuel Cells. ProQuest, 2008
[5] BARBIR, F., PEM fuel cells: theory and practice. Academic Press, 2012
[6] WIND, J., SPÄH, R., KAISER, W., et al., “Metallic bipolar plates for PEM fuel cells”, Journal of Power Sources, v. 105, n. 2, pp. 256–260, 2002
[7] KWON, J.-M., EUNG-HO, K., KWON, B.-H., et al., “High-efficiency fuel cell power conditioning system with input current ripple reduction”, Industrial Electronics, IEEE Transactions on, v. 56, n. 3, pp. 826–834, 2009
[8] RODRIGUEZ, J., LAI, J.-S., PENG, F. Z., “Multilevel inverters: a survey of topologies, controls, and applications”, Industrial Electronics, IEEE Transactions on, v. 49, n. 4, pp. 724–738, 2002
[9] TOLBERT, L. M., PENG, F. Z., “Multilevel converters as a utility interface for renewable energy systems”. In: Power Engineering Society Summer Meeting, 2000. IEEE, v. 2, pp. 1271–1274, 2000
