REGISTRO DOI: 10.5281/zenodo.10365751
Ian Ronsoni Peixoto1
Jefferson Jacques Andrade2
Giovani Marcelo Schmidt3
Vanderlei Freitas Junior4
INTRODUÇÃO
Esse artigo apresenta uma parte da realização do II Prêmio ACIVA (Associação Comercial e Industrial do Vale do Araranguá) de Matemática. Realizada em duas etapas por turmas do nono ano do Ensino Fundamental e terceiro anos do Ensino Médio de escolas do município de Araranguá/SC. O projeto foi desenvolvido pelos professores do Projeto de Extensão do Instituto Federal Catarinense – Campus Avançado Sombrio (IFC-CAS), em parceria com o Instituto Federal de Santa Catarina (IFSC) – Campus Araranguá, Campus da UFSC (Universidade Federal de Santa Catarina).
Antes de existir a proposta de provas e questões matemáticas organizadas como “Olimpíadas”, na Itália no século XVI, onde desafios matemáticos eram realizados, e renomados matemáticos participavam para conseguir recompensas. A recompensa de maior prestígio era uma cátedra para professor universitário na Itália, onde muitos matemáticos se empenhavam a encontrar soluções para problemas que poderiam ser envolvidos. A cadeira de professor universitário garantia reconhecimento público, uma condição financeira mais privilegiada, e prestígio sobre seu cargo e sua relevância na área. Muitos matemáticos jovens buscavam vencer esses desafios contra os matemáticos mais experientes, como “duelos” entre os matemáticos, buscando poder e ambição a partir da vitória desses desafios. Durante esse momento, diversas equações e resolução de problemas matemáticos foram desenvolvidos.
Em 1894, com intenção mais nobres, os matemáticos húngaros passaram a organizar uma competição chamada “Eotvos”, com um modelo de estrutura pioneira do que temos hoje como “Olimpíadas de Matemática”. A primeira Olimpíada de Matemática “moderna” ocorreu em 1934 na União Soviética, na cidade de Leningrado. Em 1959, ocorreu a primeira Olimpíada Internacional de Matemática[4] (IMO), na cidade de Bucareste, na Romênia, junto com a participação da Bulgária, Hungria, Polônia, Tchecoslováquia e União Soviética. A primeira edição da IMO em que o Brasil participou foi em 1979, disputando com outros 23 países, ocorrendo na cidade de Londres, Inglaterra.

Dentre as Olimpíadas Brasileiras de Matemáticas organizadas pelo Instituto de Matemática Pura e Aplicada (IMPA) em escala nacional, tem a Olimpíada Brasileira de Matemática (OBM) e a Olimpíada Brasileira de Matemática em Escolas Públicas (OBMEP), além de torneios e competições (como Torneio de Meninas na Matemática, e a Competição Elon Lages Lima para universitários) (OBM, 2022a).
A OBM foi organizada, pela primeira vez, em 1979 pela Sociedade Brasileira de Matemática (SBM), buscando estimular o Ensino da Matemática, a melhoria do ensino, aperfeiçoar a capacitação de professores, e descobrir jovens talentos dentro da área (OBM, 2022b).
Houve, com o tempo adaptações que são importantes para o contexto da OBM atual, como a divisão em três níveis (I: 5ª e 6ª série; II: 7ª e 8ª série; e III: Ensino Médio) e três fases (1ª etapa: múltipla escolha com 20 ou 25 questões; 2ª etapa: prova aberta com seis questões; e 3ª etapa: cinco questões para o nível I e II, e seis questões para o nível III) em 1998 (OBM, 2022b).
Em 2017 a OBM se integra à OBMEP, realizando fase única para os três níveis, mas em 2020, o nível universitário, que era realizado em duas fases, passa a ser só um e passa a ser conhecido como Competição Elon Lages Lima (OBM, 2022b). A OBMEP é a maior Olimpíada estudantil no mundo, com 18 milhões de estudantes participando e cerca de 47 mil instituições de ensino participando do projeto. Teve sua primeira edição organizada em 2005, que busca promover uma Olimpíada de Matemática entre os estudantes de escola pública, desde a sexta série (todas as séries do Ensino Fundamental), até o Ensino Médio. É realizado pelo IMPA, com o apoio da SBM, junto com a promoção do Ministério da Educação (MEC). A OBMEP tem bastante semelhanças com a OBM em relação aos seus objetivos, como estimular o ensino da matemática, identificar jovens talentos, e o aperfeiçoamento da capacitação dos professores.
Junto a isso, os objetivos da OBMEP busca contribuir com melhorias no ensino básico e no material didático das escolas; ingressos de estudantes em universidades, nas áreas de ciências e tecnologias; integração das escolas com sociedades científicas; e a inclusão social (OBMEPa; OBMEPb, 2022c). A prova possui duas fases, sendo a primeira uma fase de classificação da escola, desde que o aluno não tenha zerado na prova, com 20 questões com cinco alternativas para o estudante responder.
Após a classificação, o estudante passa para a segunda fase, uma prova com seis questões em aberto, com cada uma valendo 20 pontos (totalizando 120). Ocorre a premiação, com distribuição de medalhas e menções honrosas. Do nível 1 (sexto ao sétimo ano) ao 2 (oitavo ao nono ano) são até 200 medalhas de ouro, 500 medalhas de prata e 1990 medalhas de bronze para o primeiro nível e 1440 para o segundo. Para o nível 3, que engloba o Ensino Médio, são até 100 medalhas de ouro, 500 de prata, e 1070 de bronze (OBMEPc, 2022c). O número de menções honrosas, da 16ª edição é de 46.200 (15.400 para cada nível).
Destaca-se também outras Olimpíadas de Matemática que são realizadas em outros países, tendo em consideração a proximidade do idioma (Portugal e Espanha), como também sua influência e destaque no meio matemático, referente às questões que são colocadas na prova (Índia e Rússia), que serão importantes para o embasamento das questões que foram aplicadas na prova ACIVA de Matemática.
A Olimpíada Portuguesa de Matemática (OPM) teve sua origem em 1980, três integrantes da Sociedade Portuguesa de Matemática organizaram “mini-olimpíadas de matemática”, que se popularizou e se expandiu para todo Portugal em 1983, com o nome de Olimpíada Nacional de Matemática. Em 1999, mudaram o nome para Olimpíada Portuguesa de Matemática, levando em conta a internacionalização do evento. Os “níveis” da prova da OPM são semelhantes ao que tem na OBMEP: duas turmas para o Ensino Fundamental (sexto – sétimo, oitavo – nono) e um nível para todas as turmas de Ensino Médio. As provas são organizadas em três etapas: a primeira se dá pela classificação dos 50 melhores classificados de cada região[5]; a segunda, classifica os 10 melhores de cada região, e a final, distribui três medalhas de ouro e prata, e seis medalhas de bronze. A pontuação da prova possui no total 40 pontos e exige conhecimentos que são superiores ao nível exigido na escola, trabalhando com problemas que envolvam a criatividade e o engenho dos estudantes (PORTUGAL, 2022c).
A Olimpíada Matemática Espanhola[6] (OME), em 2022, estava em sua 58ª edição do projeto, mas, diferente dos já listados anteriormente, ocorre entre estudantes dos cursos de bacharelado. O processo de etapas é semelhante ao de Portugal, mas difere por ter somente duas etapas, sendo a primeira em nível regional, e a segunda em nível nacional, onde os 36 melhores colocados serão premiados com medalhas de ouro, prata e bronze, seguindo a proporção 1:2:3 (OME, 2007).
A Olimpíada Nacional de Matemática da Índia[7] (ONMI) é uma competição realizada para classificar os seis estudantes que irão representar o país na IMO, sendo uma prova com seis questões para responderem em quatro horas. Antes dessa prova, é realizado duas provas: a Olimpíada Regional Indiana de Matemática[2] (ORIM) e a Olimpíada Pré-regional Indiana de Matemática[3] (OPre-RIM), mas que se fundiu em uma prova só de 2020 para cá, nomeada de Olimpíada Indiana de Qualificação em Matemática[4] (OIQM). Entretanto, para fins de estudo, foi selecionado o modelo das duas provas para a classificação da ONMI. A OPre-RIM é a primeira etapa das Olimpíadas de Matemática na Índia, até chegar na classificação indiana para formação da equipa na IMO. Essa fase consiste em 30 questões abertas para serem respondidas em três horas. A resposta é um número de até dois dígitos. As dificuldades variam de uma escala 2 à 5, envolvendo problemas de álgebra, teoria dos números, combinação e geometria. (AoPS Onlinea, s.D.). Na fase seguinte, os classificados participarão da ORIM, formada por seis questões com três horas para responder, com resposta em aberta e considerada sua forma de resolução, mesmo que não tenha um resultado (AoPS Onlineb, s.D.). Após o participante ser classificado, ele participa da ONMI, em que busca classificar para representar a Índia nas Olimpíadas Internacionais de Matemática. A OIQM teria o mesmo objetivo da ORIM, só que, agora, é realizada em somente uma única fase.
A Olimpíada Russa de Matemática[11] (ORM) é uma das olimpíadas que faz parte da All-Russian Olympiad for Schoolchildren (Todas as Olimpíadas Russas para Estudantes, tradução livre), em que engloba outras olimpíadas voltadas a outra disciplinas (economia, química, idioma russo, inglês, ciências sociais, ecologia, etc.). Em matemática, ela se divide em cinco etapas: a fase de convite, a fase escolar, a fase municipal, a fase regional, e a fase final. A primeira fase, a fase de convite, inclui as turmas do 3º ano até o 11º ano (o que englobaria o “Ensino Médio”, comparando com o sistema brasileiro) com oito questões abertas, ela não é necessária para participar da fase escolar. Na fase escolar, somente as turmas do 4º ano até o 11º ano participam dessa etapa, compondo oito questões em aberto para cada série, com um nível de complexidade maior de acordo com o que se avança nas fases das olimpíadas. Após o estudante passar nessa fase, ele participará das olimpíadas municipais, contemplando somente as turmas do 7º ano até o 11º ano, mas com um modelo de prova semelhante: oito questões
Os estudantes do 9º ano até o 11º ano participam, sequentemente, da olimpíada regional, onde cada turma possui dois dias para responder dez questões abertas (cinco questões por dia). Por fim, os estudantes que passaram para a fase final terão dois dias para responder oito questões, ficando quatro por dia. Os melhores classificados nessa última fase são convocados para representarem a Rússia na IMO (ALL-RUSSIAN…, 2021-2022; STAGES OF…, 2021).
Conhecendo sobre como são as olimpíadas em outros cantos do mundo, é possível observar que esses eventos possuem muita influência na educação daquele país, agregando positivamente no ensino da matemática, o que se reflete no empenho, no destaque e no investimento nessa área. Essas oportunidades são fundamentais para que a matemática se torne algo de valor para o estudante e, não somente para ele, mas para a escola, para o professor, para as metodologias de ensino da matemática, que se aperfeiçoam e acompanham as mudanças no ambiente escolar. Esses valores se unem com uma percepção de que a matemática é uma questão de treino, disciplina e empenho, em contrapartida a percepção da matemática inacessível e distante, uma luta diária para quem trabalha com o ensino da matemática. A partir disso, traça-se a justificativa do projeto do artigo, onde busca-se agregar valor na educação matemática na região, como influenciar positivamente na percepção individual (do estudante) sobre a matemática e o rompimento de estigmas limitantes da matéria.
JUSTIFICATIVA
Baseado no histórico das olimpíadas de matemática ao longo dos tempos e tendo por base escolhida o modelo atual da OBMEP foi submetido ao edital de extensão o projeto intitulado Prêmio ACIVA de matemática que justifica-se pelo impacto positivo que atividades como as Olimpíadas de Matemática agregam ao estudante que participa dessas atividades, bem como ser uma oportunidade de divulgar o IFC CAS e os cursos que o campus oferece e em especial o Curso Superior de Licenciatura em Matemática.
Dentre outras ainda podemos mencionar que poderá trazer uma relação do estudante (bolsista) com a matemática torna-se diferente daquela que é proposta dentro da sala de aula do curso, fazendo com que o estudante bolsista tenha outras experiências e assim possa receber uma formação que possa ser um diferencial no futuro mercado de trabalho e até quem sabe divulgador das propostas de Prêmios de Matemática, Olimpíadas ou Feiras de Matemática.
Por conta, por vezes, de descrenças e práticas pedagógicas construtivistas/formalistas, que distorcem uma perspectiva de uma matemática mais aberta a reflexões, criatividade e desafios que instigam o uso do raciocínio-lógico e outras habilidades para resolução de problemas. É inevitável o impacto do ambiente externo sobre a percepção individual dos estudantes da matemática, destacado por Ponte (1992, p. 15 – 16) alguns preceitos sobre a área do saber como “[a Matemática ser] o domínio absoluto, a perfeição total.
Nela, não há lugar para erros, dúvidas, hesitações ou incertezas”. Outra concepção que o autor destaca é a que: “nada de novo nem de minimamente interessante ou criativo pode ser feito em Matemática, a não ser pelos “génios”” (PONTE, 1992 p. 16).
Essas concepções são resultados de um processo histórico, onde o elitismo predominava no ensino e a matemática era vista como uma “ciência para poucos”, além de reforçar padrões sobre a função do estudante no processo de aprendizado: “ter total domínio do conteúdo matemático da forma mais pura o possível”. Ter essas noções enraizadas possui efeitos prejudiciais no empenho e vontade de se aprofundar nessa área de estudo, reforçada por mitos e falsas crenças.
É a partir do ambiente escolar onde se torna fundamental para a ruptura dessas descrenças, possibilitando os estudantes a expandirem e explorar criativamente os seus conhecimentos matemáticos e suas aplicações, respeitando as suas potencialidades e motivando sua evolução. Nisso, as Olimpíadas de Matemática possuem um papel importante para estimular e promover o Ensino da Matemática entre os estudantes, reconhecendo novos talentos, integrando o ambiente escolar ao projeto e o aperfeiçoamento de professores (PEREIRA et. al., 2020 p. 799). Moreira, et. al. (2003, p. 17. apud. PEREIRA et. al., 2020 p. 799 – 800) escreve sobre a importância das Olimpíadas de Matemática no Ensino:
As Olimpíadas de Matemática são hoje reconhecidamente um poderoso instrumento não só para a descoberta de talentos, mas também para a difusão desta área fundamental do conhecimento, a que são expostas nossas crianças desde bem cedo. De fato, quando organizadas em várias etapas ou fases para o mesmo grupo de crianças ou jovens, pode-se ir desde testes amigáveis e atraentes até a etapa mais seletiva da descoberta de talentos, muitos deles tornando-se mais tarde excelentes cientistas ou profissionais em geral. (MOREIRA et. al. 2003, p. 17. apud. PEREIRA et. al., 2020 p. 799 – 800)
Junto a isso, é relevante fazer um recorte sobre a importância de organizar projetos regionais e com interação à comunidade escolar do local, reconhecendo talentos e habilidades dos alunos na área, engajamento à Olimpíada, aqui queremos ao Prêmio ACIVA e ao ensino da matemática, como também, o empenho e o Ensino da Matemática da região em questão.
A matemática é, ainda, uma matéria que é popularmente como algo de pouco domínio, então, elaborar provas que consigam visualizar esse cenário, que consiga desafiar sem que sobressaia a capacidade do aluno, é fundamental para a elaboração do projeto e resultados que vão além do resultado da Olimpíada.
Considerando a região de Araranguá e suas particularidades, pode-se trabalhar e elaborar provas que promovam o ensino da matemática aplicado às práticas cotidianas dos estudantes, viabilizando uma perspectiva da matemática muito mais presente no dia-a-dia do estudante, capaz de compreender seu uso e a resolução de problemas por meio dela.
A seguir apresentaremos a metodologia utilizada na realização do II Prêmio ACIVA de matemática que contou com a participação daquela que faz a frente que é a ACIVA dando todo o suporte do prêmio em relação a espaço de encontro, impressão das provas, logísticas, contato com as escolas e o espaço em que se realizou a 2ª Etapa do Prêmio. As instituições IFC, UFSC, IFSC e UNESC que juntas por meio de docentes da área de matemática construíram a metodologia em conjunto com o estagiário do projeto de extensão.
METODOLOGIA
O projeto foi desenvolvido com mais instituições parceiras sendo que inicialmente se reuniram no auditório da ACIVA para planejamento do andamento do projeto no que tange a realização das etapas de execução. Optou-se em fazer reuniões virtuais via Google Meet em virtude que os professores das entidades parceiras eram de diferentes cidades.
Figura 01 – Link de uma das reuniões de planejamento

Fonte: Os autores, 2022
Durante as duas primeiras reuniões foram revistos pontos do Regulamento da 1ª Edição do Prêmio, buscando deixar ainda mais organizado e também aproveitando que houve uma reunião com os professores dos alunos que participaram no dia da segunda etapa da 1ª Edição de avaliação e nesta houve então uma avaliação onde poderiam ser apontados pontos positivos, negativos e sugestões para uma possível segunda edição. Esta não acontece por dois anos pelo motivo da COVID 19 e é retomada então em 2022 com a 2ª Edição. No terceiro encontro foi desenvolvido o cronograma a ser apresentado a comunidade escolar do município de Araranguá, novamente apenas com a participação das escolas públicas municipais e estaduais. Foi encaminhado para todos os diretores de escolas via secretaria de educação municipal para as escolas municipais e via GERED (Gerência de Educação) para as escolas estaduais. Estes convites foram encaminhados pelo setor de comunicação da ACIVA que ficou responsável por esta parte do processo.
Figura 02 – Crocnograma da 2ª Edicação do Prêmio ACIVA de Matemática

Fonte: Os autores, 2022.
Conforme calendário realizou-se no dia 23 de maio uma reunião com a participação da equipe organizadora do Prêmio com os diretores das escolas interessadas em participar onde foi apresentado o regulamento, objetivos, importância do prêmio para os estudantes e futuros impactos que possam gerar, bem como a proposta geral do Prêmio.
Figura 03 – Reunião com os diretores das escolas públicas interessadas

Fonte: Os autores, 2022.
Enquanto as escolas se inscreviam para participar do prêmio os professores das instituições parceiras foram se reunindo e organizando a primeira etapa da prova dividindo os conteúdos de forma abrangente aos professores, que por meio de uma documento do drive iam alimentando o arquivos com as questões que vinham sendo produzidas pelos professores.
Figura 04 – Drive usado como repositório para as questões em Elaboração
Fonte: Os autores 2022
Durante semanas em trabalho de leituras e releituras e conversas nas reuniões e pelo grupo de Whatsapp as questões foram sendo lapidadas e escolhidas de acordo com o que os professores entendiam ser importante ser abstraído dos estudantes visto que estávamos em um ano pós pandemia. Importante destacar que durante este processo houve sempre por parte dos professores o senso de pensar no melhor para o Prêmio deixando de lado suas ideias particulares ou institucionais, prevalecendo a democracia na escolha das questões e sempre buscando diversificar ao máximo os campos da matemática e a forma de elaboração das questões.
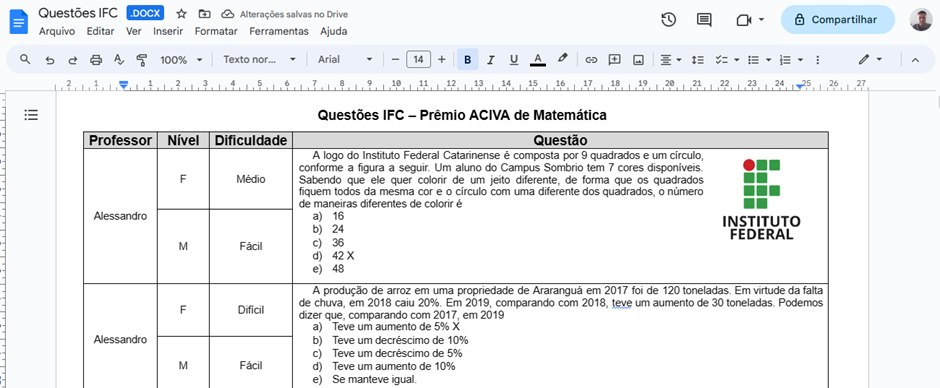
Segue uma parte da prova para visualização de algumas das questões aplicadas na prova de 20 questões de múltipla escolha. As questões apresentadas a seguir foram elaboradas pelos professores de matemática do projeto e o bolsista nos encontros presenciais no IFC CAS e apresentadas nas reuniões onde se discutiu quais questões iriam compor a prova de 20 questões.
Em duas elas aparece a instituição IFC e na terceira não, contudo vale ressaltar que estes momentos de criação e organização foram momentos em que se percebeu a necessidade de um bolsista no projeto auxiliando e trazendo ideias de alguém que a pouco tempo antes ainda estava em sala de aula na educação básica.
Figura 05 – Recorte de questões da 1ª Etapa da prova do nono ano, 2022
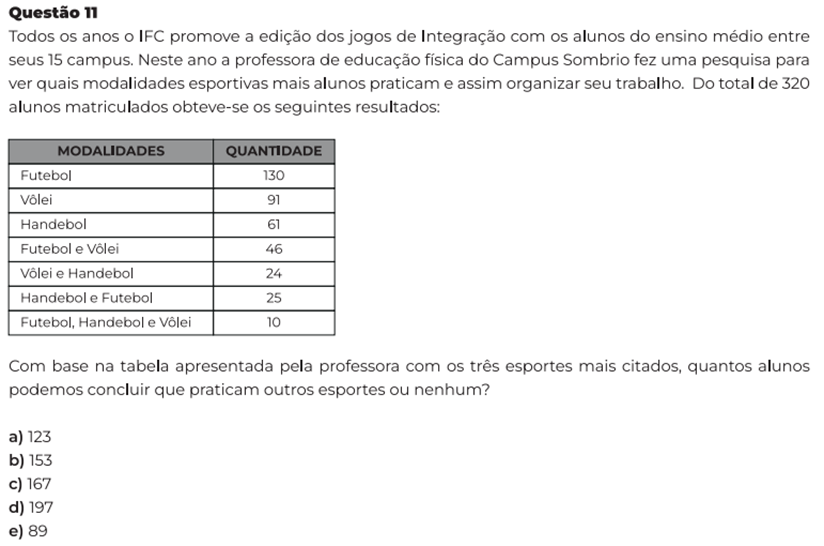


Fonte: Os autores, 2022.
A aplicação da 1ª Etapa foi realizada em cada escola participante sendo aplicada no mesmo dia e horário pelos professores de matemática que encaminharam os cartões resposta para a ACIVA que posteriormente direcionou ao bolsista do projeto.
Figura 06 – Aplicação da 1ª Etapa do Prêmio em uma turma de 9º Ano

Fonte: Os autores, 2022.
O bolsista corrigiu todos os cartões respostas e ranqueou os alunos por turmas e por escolas participantes sendo feita a divulgação via e-mail para doas as escolas e junto com a classificação foi também enviado o convite para os alunos classificados na primeira etapa a participar da segunda Etapa, sendo que esta aconteceu nas dependências da ACIVA.
Figura 07 – Registro da aplicação da 2ª Etapa

Fonte: Os autores
RESULTADO
Como resultado observou-se inicialmente que houveram menos participantes na segunda Edição do Prêmio do que na primeira. Vários comentários foram na linha de que estavam com medo e temor de que os alunos não conseguissem resolver as questões das provas ou na 1ª Etapa ou na 2ª Etapa. Principalmente na segunda por ser descritiva. Observou-se que houveram mais acertos em média pelos estudantes participantes na 1ª Etapa, sendo que este resultado continua em análise para verificar qual a causa.
Outro resultado é uma melhora no nível das questões pontuada pelos professores e o trabalho coletivo entre a ACIVA e as instituições parceiras, fazendo com que houvesse uma integração e oportunidade de os professores junto com acadêmicos mostrarem habilidades de criação de questões e produção acadêmica e científica.
Também cabe ressaltar que o Curso de Licenciatura em Matemática do Campus Sombrio e o campus como um todo também se beneficia já que na composição de algumas das questões escolhidas são mencionados o campus e cursos que o mesmo oferece.
Como resultado da importância deste projeto continuar em outros anos, trazemos a importância que o Prêmio ACIVA já proporcionou a uma participante, a salientar a entrevista em portal de notícias da cidade de Araranguá trazendo o relato de oportunidade criada pela 1ª Edição do Prêmio lá em 2019. Conforme trecho retirado da reportagem
Figura 08 – Trecho de uma reportagem com ex participante

Fonte: Assessoria de imprensa do Portal Agora, 2022.
Cabe ressaltar que o número de estudantes atingidos nesta segunda edição foi de 864, sendo que a previsão inicial era de atingir 1500.
CONSIDERAÇÕES FINAIS
O Prêmio ACIVA, baseado em Olimpíadas Matemáticas, tem por objetivo potencializar o estudo da matemática e sua aplicação no dia a dia, bem como trazer ao público talentos na matemática de jovens do município de Araranguá e assim fazer junto aos associados da ACIVA olhar com mais atenção para a juventude local buscando oportunizar o protagonismo juvenil dentro das empresas.
O Projeto quanto a divulgação do IFC em âmbito regional recebeu mais destaque podendo por meio do projeto projetar também o Curso Superior de Licenciatura em Matemática do Campus Sombrio.
REFERÊNCIAS
ALL-RUSSIAN SCHOOLCHILDREN OLYMPIAD in Mathematics for Moscow Schoolchildren. Tradução russo-inglês. 2022. Disponível em: https://olympiads.mccme.ru/vmo/. Acesso em: 6 nov. 2022
AOPS ONLINE. Pre-Regional Mathematical Olympiad. 2022c. Disponível em: https://artofproblemsolving.com/wiki/index.php/Pre-Regional_Mathematical_Olympiad. Acesso em: 6 nov. 2022
_______________. India Regional Mathematical Olympiad. 2022c. Disponível em: https://artofproblemsolving.com/wiki/index.php/India_Regional_Mathematical_Olympiad. Acesso em: 6 nov. 2022
IMO. 63ª Olimpíada Internacional de Matemática (tradução). 2022. Fonte em inglês. Disponível em:https://www.imo-official.org/year_info.aspx?year=2022. Acesso em: 6 nov. 2022
MACIEL, Marcos Vinícius Milan Maciel; BASSO, Marcus Vinícius de Azevedo. Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP): Qualificação do Ensino de Matemática na Educação Básica. X Encontro Gaúcho de Educação Matemática, Comunicação Científica – Ijuí/RS. 2009. Disponível em: http://www.projetos.unijui.edu.br/matematica/cd_egem/fscommand/CC/CC_19.pdf. Acesso em: 6 nov. 2022
OBM. Competições Nacionais. 2022. Disponível em: https://www.obm.org.br/competicoes/nacionais/. Acesso em: 6 nov. 2022
OBMEP. Apresentação. 2022c. Disponível em: http://www.obmep.org.br/apresentacao.htm. Acesso em: 6 nov. 2022
_______________. Integração das Olimpíadas nacionais de Matemática. 2022c. Disponível em: http://www.obmep.org.br/noticias.DO?id=467#:~:text=Em%20pouco%20mais%20de%20uma,ensino%20da%20Matem%C3%A1tica%20no%20Brasil. Acesso em: 6 nov. 2022.
_______________. Premiados da OBMEP. 2021. Disponível em: http://www.obmep.org.br/premiados.htm. Acesso em: 6 nov. 2022
OME. Olimpiada Matemática Española: ¿Qué son las Olimpiadas Matemáticas?. 2007. Disponível em: http://www.olimpiadamatematica.es/platea.pntic.mec.es/_csanchez/olimpque.htm. Acesso em: 6 nov. 2022
PEREIRA, et. al. Pensando sobre Matemática: uma análise das concepções de estudantes que participam de programas de incentivo à Matemática. Universidade Estadual de Ponta Grossa (UEPG), Ponta Grossa/PG. Revista Thema, v. 17, n. 3, 2020. p. 791 – 800. Disponível em: https://periodicos.ifsul.edu.br/index.php/thema/article/view/1712/1628. Acesso em: 6 nov. 2022.
PONTE, João Pedro da. Concepções dos Professores de Matemática e Processos de Formação. Repositório da Universidade de Lisboa. 1992. Instituto de Inovação Educacional. p. 1 – 23. Disponível em: http://hdl.handle.net/10451/2985. Acesso em: 6 nov. 2022
PORTUGAL, Ministério da Educação. Olimpíadas Portuguesas de Matemática. 2022c. Disponível em: https://olimpiadas.spm.pt/. Acesso em: 6 nov. 2022
STAGES OF THE ALL-RUSSIAN OLYMPIAD FOR SCHOOLCHILDREN IN MOSCOW: Maths. 2022. Disponível em: https://vos.olimpiada.ru/archive/table/tasks/years/2021_2022/#math. Acesso em: 6 nov. 2022
agorasul.com.br/jovem-estudante-de-medicina-relata-experiencia-apos-vencer-premio-aciva-de-matematica/
[4] International Mathematics Olympiad.
[5] Essas são regiões que coincidem com o posicionamento geográfico dos distritos em Portugal. Os que compõem a região Norte são: Braga, Bragança, Porto, Viana do Castelo e Vila Real. No Centro: Aveiro, Castelo Branco, Coimbra, Guarda, Leiria, Portalegre, Santarém e Viseu. No Sul: As ilhas dos Açores e da Madeira, Beja, Évora, Faro, Lisboa e Setúbal.
[6] Olimpiada Matemática Española.
[7] Indian National Mathematical Olympiad.
[8] Regional Mathematical Olympiad.
[9] Pre-Regional Mathematical Olympiad.
[10] Indian Olympiad Qualifier in Mathematics.
[11] All-Russian Olympiad in Mathematics (Всероссийская олимпиада по математике, em russo)
Ian Ronsoni Peixoto – Estudante do Curso Superior em Licenciatura em Matemática no Instituto Federal Catarinense – Campus Avançado Sombrio (IFC-CAS) e bolsista do projeto de extensão “Prêmio ACIVA de Matemática”. E-mail para contato: peixotoian@hotmail.com1
Jefferson Jacques Andrade – Mestre em matemática, professor no curso de licenciatura em matemática no IFC-CAS, e co-orientador do projeto de extensão “Prêmio ACIVA de Matemática”. E-mail para contato: jefferson.andrade@ifc.edu.br2
Giovani Marcelo Schmidt – Mestre em matemática, professor no curso de licenciatura em matemática, orientador do projeto de extensão “Prêmio ACIVA de Matemática”. E-mail para contato: giovani.schmidt@ifc.edu.br3
Vanderlei Freitas Junior
