REGISTRO DOI: 10.5281/zenodo.8072255
Matheus Berbel Barusso1
RESUMO
Este artigo tem como principal objetivo a análise da sequência recursiva de Fibonacci, seu funcionamento, peculiaridades, comportamento e como sua sequência descreve a proporção áurea. O estudo também analisa as aplicações do número áureo em projetos feitos pela humanidade e apropriações naturais dessa proporção e sequência que fornecem uma estética harmoniosa. A análise será realizada através de revisões da sequência, da forma a qual ela é representada e como quanto mais longe do início na sequência mais perto chegamos da constante Φ, sua dedução e relações.
Palavras-chave: Número de Ouro. Sucessão de Fibonacci. Razão áurea.
ABSTRACT
This article has the main goal of analyzing the Fibonacci Recursive Sequence and how it works, peculiarities, how it behaves and how this sequence describes the Golden Ratio. This study will analyze the enforcement of the Golden ratio in humanmade projects and where the ratio and sequence are present in the nature, creating a harmonious aesthetic. The analysis will be realized through the revision of the sequence, how it can be represented e how close we can get to the Φ constant as we go further from the start, during the project will be analyzed its deduction and relation with numbers.
Keywords: Golden Number. Fibonacci Sequence. Golden Ratio.
INTRODUÇÃO
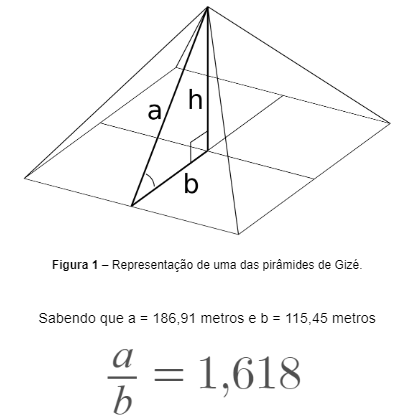
A descoberta da razão áurea aconteceu muito antes mesmo de Leonardo Pisano, criador da sequência de Fibonacci, praticar matemática, datando aproximadamente 2.500 a.C. com o matemático Euclides. A proporção de ouro tem sido estudada desde então por inúmeros estudiosos e escolas que sempre apreciaram a estética e harmonia que essa constante irracional traria para suas criações em diversas áreas, desde a engenharia até a música. Essa proporção foi utilizada em diversas aplicações que existem até os dias atuais como a pirâmides de Gizé, no Egito, que foram arquitetadas e construídas utilizando a Razão Áurea como grande fundamento, e isso fica explícito ao dividirmos a altura de uma face da pirâmide pela metade da base, obtendo então a constante Φ, ou, o aproximadamente o número 1,618.
Distante do Egito, o número áureo seria também utilizado na construção do Partenon, na Grécia, um templo construído aproximadamente em 430 a.C. possui a proporção áurea descrita em diversas partes da sua fachada, que foi pensada em criar um sentimento de estética harmoniosa que agradasse os visitantes, perpetuando os conceitos gregos da época.

Figura 2 – Partenon, na Grécia, juntamente do retângulo de ouro que representa a proporção áurea.
Porém, mesmo com todo o conhecimento já existente em relação ao número áureo, foi somente com os avanços do matemático Leonardo Pisano em 1202 d.C., estudante da matemática islâmica, que a sequência recursiva que conteria a proporção de ouro teria a sua descoberta realizada, mostrando consequentemente novas maneiras de se obter a constante Φ que ainda não eram conhecidas pela humanidade.
Além das aplicações humanas, a razão áurea aparece na natureza em diversas instâncias que vão desde as cascas de caracóis e a formação do corpo de moluscos como o Nautilus até a formação de furacões. É incerto o motivo de esse padrão se repetir por toda a natureza, porém isso complementa a afirmação sobre essa proporção ser especial e ser considerada desde a antiguidade como uma proporção divina.
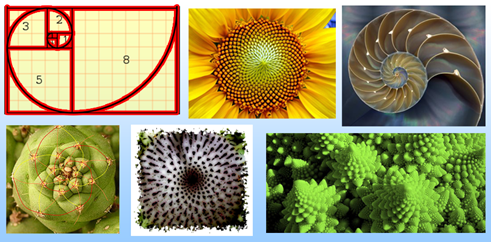
Figura 3 – Presença da proporção áurea em retângulos áureos em diversas ocasiões na natureza
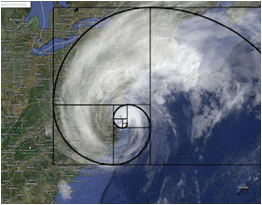
Figura 4 – Presença da proporção áurea na formação de ciclones
ORIGEM E ESTUDOS DE LEONARDO FIBONACCI
Leonardo Pisano, ou, Leonardo Fibonacci, também conhecido assim devido ao nome de seu pai Bonaccio, foi um estudioso da matemática nascido em 1170 em Pisa, na Itália. Fez diversas viagens pelo mediterrâneo e conheceu a matemática islâmica que serviu de grande inspiração e fonte para os seus trabalhos, que tem como mais conhecidos as obras Lider Abbaci (1202), Pratica Geometrae (1220) e Liber Quadratorum (1225). A primeira dessas obras é um estudo sobre cálculo aritmético e é considerado a referência para estudos de Álgebra na época em que foi escrito. Nele estão descritas novas regras para cálculo, utilizando os numerais indo-arábicos e problemas de diversas áreas, como cálculo de lucros, problemas de movimento, conversão monetária entre outros. Porém um dos problemas deste livro se destaca, sendo esse o problema dos coelhos, que se refere ao número de casais de coelhos que irão existir em uma população após 12 meses levando em conta algumas considerações:
1 – No primeiro mês existirá apenas um casal;
2 – Os casais poderão se reproduzir somente após o segundo mês de vida;
3 –Desconsidera-se problemas genéticos por conta de cruzamento consanguíneo;
4 – Todos os meses cada casal fértil irá dar a luz para um novo casal;
5 – Os coelhos nunca morrem.
E esse problema tem como principal questionamento a seguinte questão: Quantos casais de coelhos serão gerados por um casal de coelhos em um ano?
No primeiro mês existirá apenas o casal inicial, recém-nascido que não pode ainda procriar. No segundo mês o casal inicial será agora um casal adulto e poderá ter um casal de filhos. No terceiro mês existirão dois casais de coelhos, o casal inicial e o casal de filhos que ainda será recém-nascida. No quarto mês existirão 3 casais de coelhos, o casal inicial, a primeira prole do casal inicial que agora será adulto e poderá procriar e o novo casal filhos do casal inicial.
No início do quinto mês dois casais serão adultos que já produziram um filho cada e mais um par que acaba de completar um mês de vida, totalizando 5 casais. No sexto mês existirão 3 casais adultos que já produziram um casal cada e dois casais que ainda serão jovens e não poderão ainda procriar.
Essa lógica se mantém pelos 12 meses propostos por Pisano e assim é obtido a sucessão de Fibonacci, que tem como seus primeiros 12 termos os seguintes:
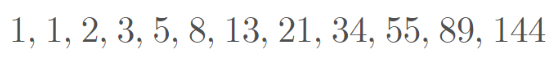
E que após os 12 meses continuará a crescer conforme a sequência recursiva descrita por

A relação de tal sucessão com a proporção áurea vem do fato que ao dividirmos algum dos elementos da sequência pelo seu anterior iremos obter uma aproximação da constante Φ. Nota-se que isso só acontecerá caso n ≥ 4. Percebe-se também que conforme nos distanciamos dos termos iniciais o resultado cada vez mais irá se aproximar da constante:
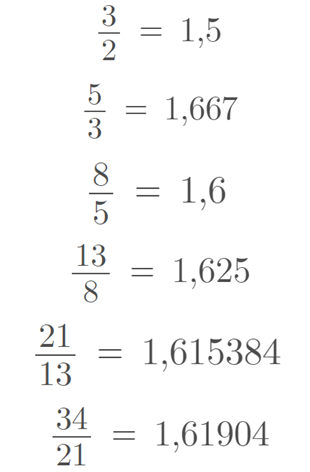
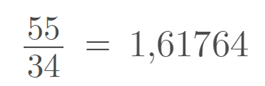
E finalmente, ao dividirmos o décimo elemento pelo nono chegaremos a aproximação utilizada na matemática
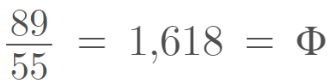
O gráfico a seguir mostra a tendência da razão se aproximar cada vez mais da constante, conforme demonstrado acima:
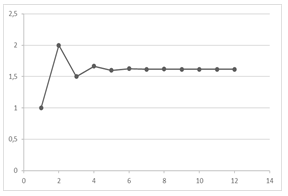
Figura 5 – Gráfico da sequência da razão entre f(n) e f(n-1), uma sequência divergente a 1,618
E as peculiaridades dessa sequência não se limitam a obtenção do número áureo, ela também permite a criação de teoremas, como por exemplo o demonstrado a seguir, que servem para todas as funções recursivas de formato f(n+2) = f(n+1) + f(n), ou, f(n+1) = f(n-1) + f(n), ou representada de outra maneira. Teorema: A soma S dos quadrados dos n primeiros números de Fibonacci é dada por:
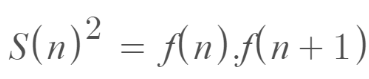
E isso pode ser exemplificado como, por exemplo, fazendo a soma dos quadrados dos 8 primeiros números da sucessão de Fibonacci: 714
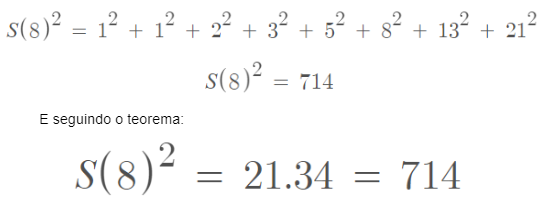
A CONSTANTE Φ
Sabemos que a proporção áurea é de 1,618 mas ainda não foi explicado o motivo de a constante assumir tal valor. Sabemos que dois valores positivos estão em razão áurea se sua razão é igual a razão da sua soma pelo maior dos números. Utilizaremos a e b para essa demonstração e levaremos em conta que a > b > 0.
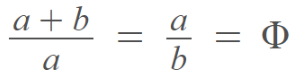

Obtemos uma equação quadrática de forma ax²+bx+c=0, onde a = 1, b = -1 e c = -1. Utilizando a fórmula de resolução de equações quadráticas temos que:

CONSIDERAÇÕES FINAIS
O presente artigo mostrou relações entre uma sequência recursiva, primeiramente estudada para definir populações, que demonstraria sua importância ao estar diretamente ligada a uma proporção presente em muitas ocasiões na natureza e também em construções humanas, muitas vezes sendo significado de harmonia. Os estudos acerca da sucessão de Fibonacci não se limitam aos apresentados nesse trabalho, porém como descrito anteriormente seriam analisadas a sequência e a proporção e seria criada a correlação entre elas. Com esse projeto foi possível também ratificar a infinidade dos mistérios matemáticos e suas relações com o universo que vivemos, procurando encontrar as relações para que o entendamos.
REFERÊNCIAS
BACELAR, Flávio. A Sucessão de Fibonacci na Natureza. Nove de Novembro de 2018. Disponível em: https://profmbacelar.blogspot.com/2018/11/a-sucessao-de-fibonacci-na-natureza.html. Acesso em 29 out. 2022.
BELUSSI, Giuliano; GERALDINI, Daniel; PRADO, Enéias. NÚMERO DE OURO. Departamento de Matemática, Universidade Estadual de Londrina – PR – Brasil.
PEREIRA, Lívia; FERREIRA, Marcio. SEQUÊNCIA DE FIBONACCI: HISTÓRIA PROPRIEDADES E RELAÇÕES COM A RAZÃO ÁUREA. Disc. Scientia. Série: Ciências Naturais e Tecnológicas, S. Maria, v. 9, n. 1, p; 67-81, 2008.
Sequência de Fibonacci: veja as suas aplicações na natureza e na arte – HIPERCULTURA – Ciência. Disponível em: https://www.hipercultura.com/sequencia-fibonacci/. Acesso em 28 out. 2022.
SAHD, Luíza; O que é a sequência de Fibonacci?. 28 set. 2011. Superinteressante – Editora Abril. Disponível em: https://super.abril.com.br/mundo-estranho/o-que-e-a-sequencia-de-fibonacci/. Acesso em 29 out. 2022
The Golden Ratio (why it is so irrational) – Numberphile. 08 mai. 2018. Canal Numberphile. Disponível em: https://www.youtube.com/watch?v=sj8Sg8qnjOg&t=376s&ab_channel=Numberphile. Acesso em 27 out. 2022.
1Graduando em Engenharia de Computação pela UTFPR-TD. E-mail: barusso@utfpr.edu.br
