REGISTRO DOI: 10.5281/zenodo.790525610.5281/zenodo.7905433
Sérgio Henrique Lopes Cabral1
Andreza Sartori2
Romeu Hausmann3
Luiz Henrique Meyer4
Rafael Eduardo Werlich5
Pedro Henrique Bertoldi Meyer6
Resumo: Este trabalho traz um estudo teórico e experimental do desempenho de um filtro passivo conhecido como LCL, aplicado em conversor de frequência. O estudo advém de um projeto desenvolvido na Universidade de Blumenau, cuja motivação foi uma demanda da indústria, em que esses filtros raramente conseguem alcançar um desempenho satisfatório, embora tenham custos consideráveis. O estudo começa pela análise teórica de filtros passivos, de ordens 1 a 3, com simulações computacionais, seguida pela análise experimental do comportamento de conversores sob a presença de harmônicos de tensão e de corrente e suas influências na distorção da forma de onda da tensão da rede, estando o conversor acionando um motor de indução sem e com carga. Finalmente, um filtro LCL é projetado e implementado, se avaliando o grau de filtragem através da análise da distorção da tensão da rede. O resultado é um necessário ajuste-fino do projeto, implementado de forma empírica e totalmente centrado no re-projeto dos indutores uma vez que o capacitor é comercialmente disponível. Ainda, os condutores utilizados nos indutores tiveram seção retangular super dimensionada, de forma a se evitar aquecimento excessivo. Tais medidas permitiram a obtenção de êxito na filtragem dos harmônicos advindos do conversor, mas evidenciaram a complexidade de casos de natureza industrial, em que potências maiores são envolvidas. Os resultados são de utilidade para o setor produtivo, por trazer importantes dados experimentais que permitem orientar adequadamente projetos de indutores, que em muito diferem dos de transformadores, apesar da relativa semelhança construtiva, que faz com que sejam assim dimensionados.
Palavras-chave conversor de frequência, filtros, harmônicos, indutores.
Abstract: This paper brings a theoretical and experimental study of the performance of a passive filter known as LCL, applied in a frequency inverter. The study comes from a project developed at the University of Blumenau, whose motivation was a demand from industry, in which these filters rarely achieve satisfactory performance, although they have considerable costs. The study starts with the theoretical analysis of passive filters, from order 1 to 3, with computer simulations, followed by the experimental analysis of converter behavior under the presence of voltage and current harmonics and their influence on the distortion of the grid voltage waveform, with the converter driving an induction motor with and without load. Finally, an LCL filter is designed and implemented, and the degree of filtering is evaluated by analyzing the distortion of the grid voltage. The result is a necessary fine-tuning of the design, implemented in an empirical way and totally centered on the re-design of the inductors since the capacitor is commercially available. Also, the conductors used in the inductors had an oversized rectangular section, in order to avoid excessive heating. These measures allowed the success in filtering the harmonics coming from the inverter, but showed the complexity of industrial cases, in which larger powers are involved. The results are useful for the productive sector, as they bring important experimental data that allows for the proper orientation of inductor designs, which differ greatly from transformer designs, despite the relative constructive similarity, which causes them to be non-adequately designed.
Keywords: VFD, filtering, power harmonics, inductors.
1 INTRODUÇÃO
Na indústria brasileira os motores elétricos de indução são aplicados em diversos setores e várias finalidades, sendo responsáveis por cerca de 40 % do consumo de energia no Brasil (Stahelin et al., 2016). Na maioria dos casos mais novos de implantação e grandes sistemas de acionamentos de motores, o acionamento se dá por conversores de frequência, que são retificadores-inversores de estado sólido, com potência cada vez maior, já atingido a faixa de alguns MW (IEEE, 1991) e (IEEE, 2014). Esse tipo de acionamento permite maior eficiência e melhor desempenho do motor, com controle preciso de velocidade, em diversos processos industriais. Por outro lado, inerentemente à operação dos conversores, tanto o processo de retificação a tensão de entrada quando o de inversão da tensão retificada, fazem com que o conversor gera harmônicos de tensão e de corrente, que invariavelmente distorcerão a forma de onda senoidal da tensão de toda uma instalação, causando uma série de problemas, que vão desde o mal-funcionamento de diversos equipamentos até problemas tarifários consideráveis. A fim de se evitar isso, a medida mais viável é a adoção de filtros, dentre os quais os passivos são os mais amplamente utilizados, comercialmente disponíveis e economicamente viáveis. Dentre as configurações mais comumente utilizadas, casos de sucesso têm sido reportados com a adoção do LCL, indutor-capacitor-indutor, como em Mattar et al. (2013), Fitzgerald et al. (1992) e Cigré (1999), o que motivou a adoção desse tipo de configuração para este trabalho. Não obstante, também se consideraram os dados de frequente insucesso da adoção desse filtro, principalmente pelo ajuste dos valores de indutores, que se tornaram obrigatoriamente como tendo núcleo ferromagnético, por conta dos elevados valores de indutância requeridos (Kassick, 2005) e (Cabral et al., 2008). Ainda assim, os resultados positivos superam, em larga escala, a adoção de outras configurações, como a CLC, a LC e a CL, por exemplo em (Pena-Alzola et al., 2014). Neste contexto, este trabalho parte de uma análise teórica geral de filtros passivos, convergindo rapidamente para o filtro LCL e sua aplicação para o caso do acionamento de um motor de apenas 1 cv, mostrando o quanto o ajuste-fino se torna necessário, sendo que esse ainda tem que ser realizado de forma empírica, dificultando significativamente o processo de se projetar os indutores, por requer mudanças de valores de indutância de 1:3, que é relativamente alto. Não obstante, os resultados obtidos apontam para uma condição favorável de se encontrar um procedimento menos empírico, para aplicações industriais de grande porte.
2 DESENVOLVIMENTO
Com o intuito de estabelecer uma base teórica para melhor análise de resultados experimentais, contendo dados de tensão e de corrente de um conversor que acionará um motor, se apresenta uma breve análise sobre filtros voltados para a aplicação em questão. No início, se analisam dois dos mais básicos filtros passivos, que são os filtros de primeira ordem passa-baixa e o passa-alta, convergindo para filtros de segunda-ordem, conhecidos como passa/rejeita-faixa e culminando com o de terceira ordem, LCL.
2. FILTROS PASSIVOS APLICADOS A CONVERSORES
Essencialmente, há dois grandes tipos de filtros, que são os ativos e os passivos. Os do primeiro tipo, tal como o nome sugere, atuam através da geração de harmônicos em oposição de fase com aqueles presentes, causando o seu cancelamento. É um tipo muito pouco utilizado, por ser muito caro e, portanto, não será abordado neste trabalho. Já os filtros passivos, amplamente disponíveis e fáceis de se projetar e instalar, realizam a filtragem por faixas de frequências, definidas com base nos valores de seus componentes e a topologia do circuito. Dentre os mais utilizados filtros passivos estão o passa-baixa e o passa-alta, que são de primeira ordem, bem como o rejeita-faixa e o passa-faixa, que são de segunda ordem.
Inicialmente, quanto aos filtros passa-baixa e passa-alta, convém reiterar que sua importância se deve à sua ampla aplicação industrial, sendo seus projetos baseados no ajuste de valores de indutância, ou de capacitância, para se definir a faixa de frequência desejada.
Para se analisar essa a influência dos valores de componente se procedeu a um estudo teórico através da modificação do valor do capacitor à cada simulação, verificando a faixa de frequência filtrada, condicionando o filtro à situação de se filtrar cada vez mais o sinal de entrada. Os resultados são mostrados a seguir.
2.1.1 Filtro Passa-baixa
O nome deste filtro se dá por conta de filtrar frequências mais altas do espectro. No caso deste trabalho, se refere àqueles presentes na tensão, na forma de harmônicos. A utilização desse filtro é clássica na eletrônica, em que se dá para circuitos de controle de subwoofers, transmissão de ondas de rádio em que se filtram os harmônicos presentes no sinal, entre outras aplicações.
Nas Figuras 1.a a 1.c se mostram o circuito de simulação, no programa online Multisim®, considerando o gerador como aplicando uma onda triangular, com frequência fundamental de 60 Hz e 10 V de pico, no filtro, sendo a tensão no capacitor como sendo a tensão de saída. O filtro passa-baixa é composto pela associação série de um resistor de 10 kΩ e um capacitor, que atua como elemento de saída e cujo valor é ajustado em 1 mF,1 μF e 1 nF, respectivamente.
Figura 1.a – O circuito de um filtro passa-baixa submetido a um gerador de onda triangular de 60 Hz – Formas de onda de entrada (verde) e saída (azul). R = 10 kΩ e C = 1 mF.
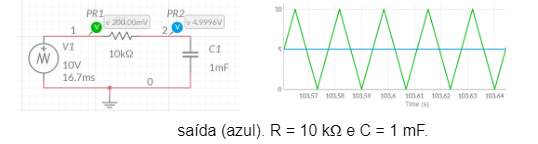
Figura 1.b – Circuito de um filtro passa-baixa submetido a um gerador de onda triangular de 60 Hz – Formas de onda de entrada (verde) e saída (azul). R = 10 kΩ e C = 1 nF.
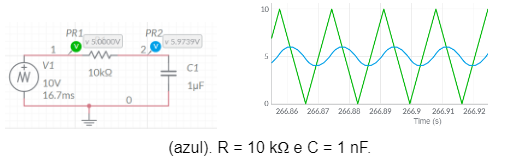
Figura 1.c – Circuito de um filtro passa-baixa submetido a um gerador de onda triangular de 60 Hz – Formas de onda de entrada (verde) e saída (azul). R = 10 kΩ e C = 1 μF.
Com base nesses resultados, se verifica que um filtro passa-baixa elementar começa por filtrar todas as frequências presentes na onda retangular, quando o capacitor é de 1 mF. Dessa forma, as frequências baixas permitidas estão abaixo de 60 Hz. Por sua vez, à medida em que a capacidade de saída é reduzida há uma tendência do valor de corte do filtro aumentar e assim permitir a manifestação na saída de todo o sinal de entrada. Neste caso, conforme (Cigré ,1999), é importante considerar que a mudança do valor do capacitor per se não é responsável pelo ajuste da faixa de passagem, mas sim o produto RC. Assim, considerando o espectro de frequências presentes no sinal de entrada, se verifica que para C = 1 mF, nenhuma frequência é permitida a se manifestar na saída. Já para C = 1 nF, todas as frequências têm essa permissão, enquanto a condição de C = 1 μF corresponde a um valor intermediário. Em outras palavras, houve uma variação do valor da frequência de corte, tendo essa sido aumentada.
Similarmente, um outro importante tipo de filtro passivo é analisado.
2.1.2 Filtro Passa-alta
Um segundo filtro passivo simulado foi o filtro passa-alta, que atua, tal como o seu nome diz, filtrando as baixas frequências que compõem o sinal de entrada. Uma das aplicações em que esse tipo de filtro é comumente encontrado é em alto-falantes do tipo tweeters, que são para frequências superiores a 5 kHz.
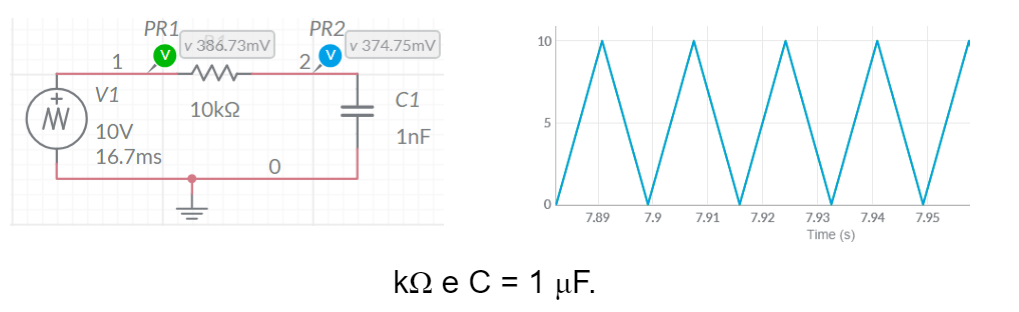
Nas Figuras 2.a, 2.b e 2.c se mostram então o circuito de simulação, no programa online Multisim®, considerando o gerador como aplicando uma onda triangular, com frequência fundamental de 60 Hz e 10 V de pico, no filtro, sendo a tensão no resistor como sendo a tensão de saída. O filtro passa-baixa é composto pela associação série de um capacitor com um resistor de 10 kΩ, que atua como elemento de saída. O capacitor tem, similarmente, seu valor ajustado em 1 mF, 1 μF e 1 nF, respectivamente.
Figura 2.a – Circuito de um filtro passa-baixa submetido a um gerador de onda triangular de 60 Hz – Formas de onda de entrada (verde) e saída (azul). R = 10 kΩ e C = 1 mF.
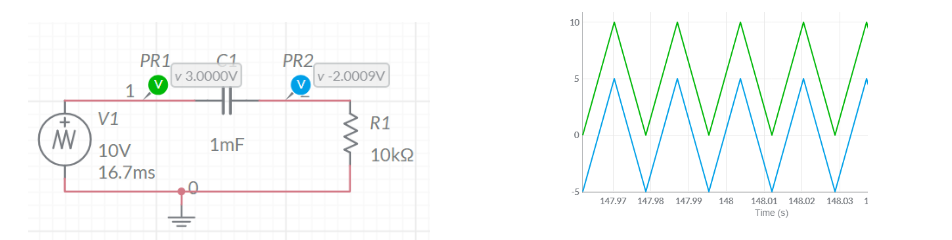
Figura 2.b – Circuito de um filtro passa-baixa submetido a um gerador de onda triangular de 60 Hz – Formas de onda de entrada (verde) e saída (azul). R = 10 kΩ e C = 1 μF.
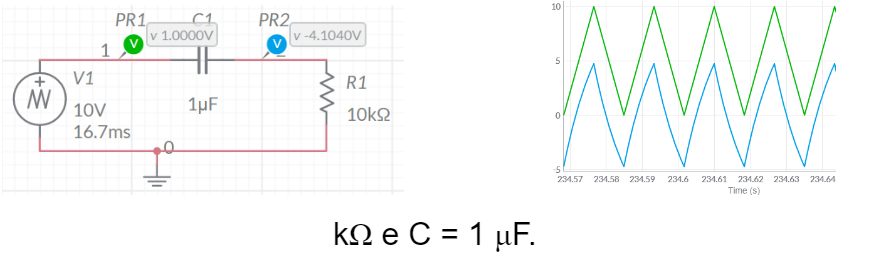
Figura 2.c – Circuito de um filtro passa-baixa submetido a um gerador de onda triangular de 60 Hz – Formas de onda de entrada (verde) e saída (azul). R = 10 kΩ e C = 1 nF.
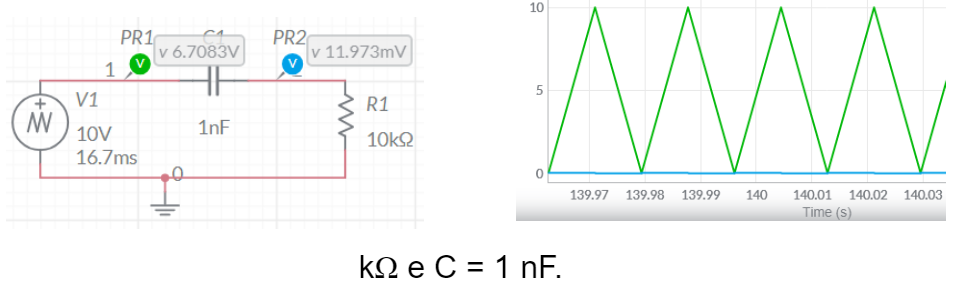
A análise dos gráficos mostrados, considerando a mudança topológica realizada no circuito, em comparação com o circuito das Figuras 1.a a 1.c, permite deduzir um comportamento antagônico ao do circuito anterior. Ou seja, à medida em que o valor da capacitância série diminui, as frequências presentes no sinal de entrada vão sendo cortadas e não se manifestam na saída. Da mesma forma que anteriormente mencionado, a influência não é somente do capacitor, mas do valor da constante RC, de forma que quanto menor for o valor dela maior será a faixa de frequências cortadas.
Assim, uma vez analisados dois dos mais elementares filtros passivos, se analisam mais brevemente dois filtros passivos com configuração um pouco mais complexa que as dos demais. São filtros de segunda ordem por comportar um indutor e um capacitor, além do resistor, o que causa a definição de faixas de frequências para serem cortadas ou permitidas, caracterizando os filtros rejeita-faixa e passa-faixa, brevemente comentados a seguir e que se mostram como aplicáveis a conversores.
2.1.3 – Filtro Rejeita-faixa
Esses filtros rejeita-faixa têm essa denominação por filtrar frequências de um intervalo definido, permitindo que frequências com valores maiores e/ou menores do que os dos limites do intervalo desejado, presentes no sinal de entrada, se propaguem para a saída. Dentre diversas aplicações pode ser encontrado em consoles de mixagem usados em estúdios e em processadores de efeito em áudio.
A grandeza-base que define a frequência do centro da faixa de rejeição é a raiz quadrada do produto LC. A Figura 3 ilustra um circuito típico desse tipo de filtro de faixa.
Figura 3 – Filtro rejeita-faixa – LC série
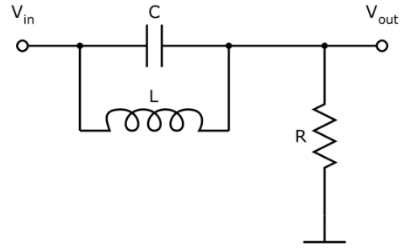
A essência da filtragem está na ressonância propiciada pela combinação e indutor e capacitor.
De forma semelhante à dualidade entre os filtros passa-baixa e passa-alta, o filtro do rejeita-faixa é brevemente descrito a seguir.
2.1.4 – Filtros Passa-faixa
Em contraposição aos filtros rejeita-faixa, existem os filtros conhecidos por passa-banda, ou passa-faixa, que podem ser compreendidos como sendo constituídos por um filtro passa-alta e um passa-baixa, ajustados de forma a filtrar frequências acima e abaixo dos valores de limites pré-estabelecidos. A sua aplicação é bastante ampla, inclusive em nível industrial, 60 Hz. Um circuito dos mais elementares do filtro em destaque pode ser representado por um resistor, R, associado com um circuito LC-série, tal como mostrado na Figura 4, em que se utiliza apenas um capacitor, um indutor e um resistor.
Figura 4 – Filtro passa-faixa – LC paralelo.
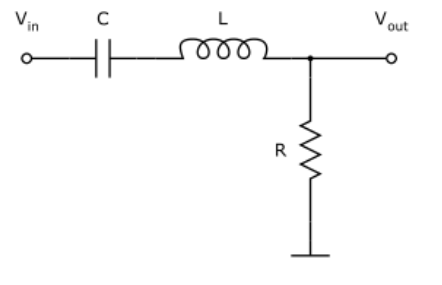
Para calcular os valores dos componentes do circuito a partir dos valores de frequência de corte, que correspondem aos valores de frequência inicial e de frequência final, se deve considerar que

, sendo XL e XC os respectivos valores de rematrículas.
Uma vez definido o valor de R, utilizam-se os valores das frequências inicial e final desejados para se determinar a diferença entre esses valores, ∆f, e definir o valor da indutância, L, incluindo o valor da resistência, através de

e após o conhecimento do valor do valor do indutor, L, se calcula XL por e, através de (1) , se obtém o valor da capacitância, C.
Finalmente, uma configuração mais utilizada, no âmbito industrial, que não faz uso específico de resistores, sendo que esse surge naturalmente na forma da impedância de carga, no circuito de saída, é o filtro LCL. Trata-se de um filtro cuja topologia dos elementos estão mostrados na Figura 5, junto com sua resposta em frequência de amplitude e de fase, caracterizando seu diagrama de Bode. Nesse diagrama fica evidenciada a seletividade do filtro passa-faixa que, no caso de aplicação em conversores, deve ser ajustada na frequência fundamental, 60 Hz, com considerável atenuação para todas as frequências harmônicas superiores, incluindo o sinal de sincronismo do conversor.
Figura 5 – Filtro passa-faixa – L C L : Arranjo topológico do circuito e diagrama de amplitudes e fase – Bode.
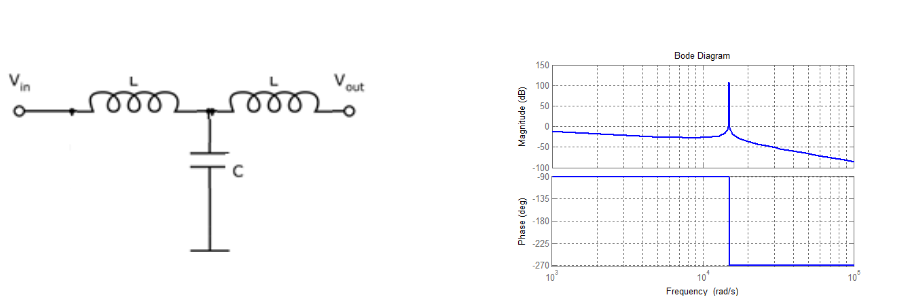
Feita essa breve análise, se apresentam a seguir os resultados experimentais da aplicação e filtros, obtidos pelos autores
3. CONVERSORES EM OPERAÇÃO – CARACTERÍSTICAS E FILTRAGEM
Com o intuito de reforçar o conhecimento teórico sobre a composição harmônica da tensão de saída de um conversor, que se aplica no estator de um motor, um primeiro experimento foi realizado visando analisar o comportamento da forma de onda de tensão ao se variar a frequência de acionamento do conversor desde 10 até 60 Hz, passando por 20 e 40 Hz . Para isso foi utilizado o conversor de frequência CFW11-WEG®, alimentado pela tensão da rede, acionando um motor trifásico e com registro da forma de onda em um osciloscópio, conforme mostrado esquematicamente na Figura 6. O motor acionado esteve sem carga mecânica e, portanto, solicitando uma corrente relativamente baixa, propositalmente assim escolhido para não provocar distorção na tensão de alimentação do conversor, provida pela rede.
Figura 6 – Diagrama esquemático de ligação dos equipamentos e instrumentos.

Nas Figuras 7 e 8, de a a d, são apresentadas as formas de onda de tensão aplicada ao estator do motor e de sua corrente, respectivamente, obtidas pelo osciloscópio.
Figura 7 – Forma de onda de tensão – a. 60 Hz; b. 40 Hz; c. 20 Hz e d. 10 Hz
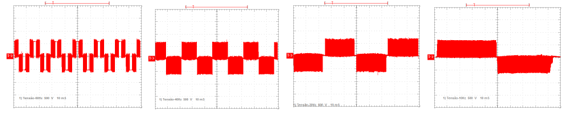
Figura 8 – Forma de onda de corrente – a. 60 Hz; b. 40 Hz; c. 20 Hz; d. 10 Hz.
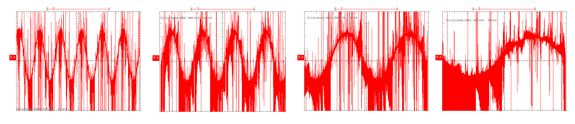
Pelos gráficos mostrados, tendo todos a mesma base de tempo, se observa que para a tensão, numa mesma base de valor de amplitudes, a diminuição da frequência implica no aumento do período, por terem uma relação inversa. Já quanto à corrente, a diminuição da frequência se reflete na diminuição da amplitude e no aumento do período, o que se deve ao fato de que o motor opera em vazio e, portanto, não solicita, em menor frequência, a mesma corrente que solicita a 60 Hz. Em todos os casos, fica evidenciada a intensa presença de harmônicos a serem filtrados, em ambos os tipos de sinal.
Após o ensaio inicial, anteriormente apresentado, se realizou o principal e mais importante ensaio , no qual se verificou a deformação da forma de onda de alimentação do conversor, a partir da alimentação desse ao motor com carga em teste , deformação essa representada pelas distorções em formas de ruídos e de harmônicos.
Na Figura 8 se apresenta o arranjo de acionamento do motor pelo conversor, estando o motor agora com carga, realizado no laboratório de engenharia elétrica da FURB.
Figura 8 – Aparato de acionamento de motor por conversor e medição de corrente e tensão.

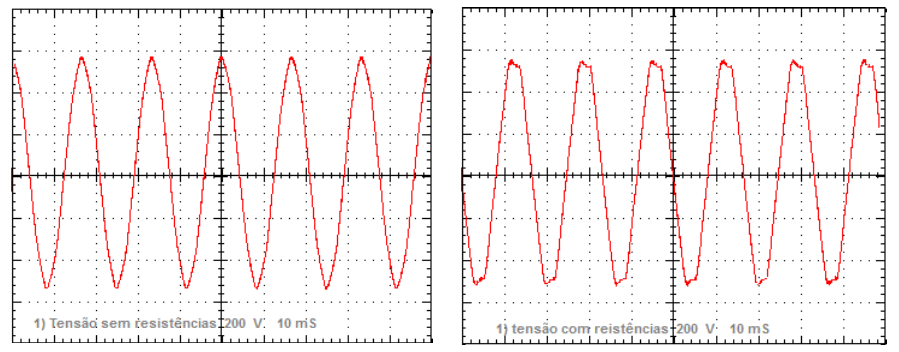
Nas Figuras 9.a e 9.b se apresentam as formas de onda nas condições de motor sem carga e com carga nominal, respectivamente, que permite confirmar o quanto o conversor distorce a tensão da rede, podendo trazer vários prejuízos e mau-funcionamento a outros equipamentos que estejam operando na instalação.
Figura 9 – Tensão da rede. a. Sem a carga no motor – conversor ligado; b conversor acionando motor com carga nominal;
Na Figura 10 se mostra o espectro de amplitudes de harmônicos da tensão distorcida, tal como na Figura 9.b, permitindo o início do projeto do filtro LCL a ser adotado.
Figura 10 – Espectro de harmônicos da tensão distorcida da rede.
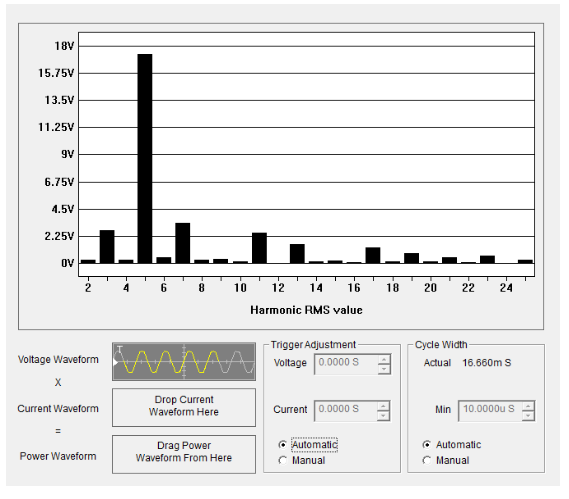
Esses importantes resultados obtidos permitiram o início do projeto do filtro LCL. Mais especificamente, o projeto dos indutores, uma vez que o capacitor a ser utilizado é um elemento comercial amplamente disponível.
Um primeiro passo foi, de posse do espectro de harmônicos, considerar o destaque com que aparece a quinta harmônica, cuja amplitude representou cerca de 5% da tensão de entrada. Tal resultado permitiu delimitar a faixa de rejeição do filtro LCL neste harmônico, diminuindo as restrições para se projetar os indutores adequados.
4. PROJETO DE FILTRO E APLICAÇÃO
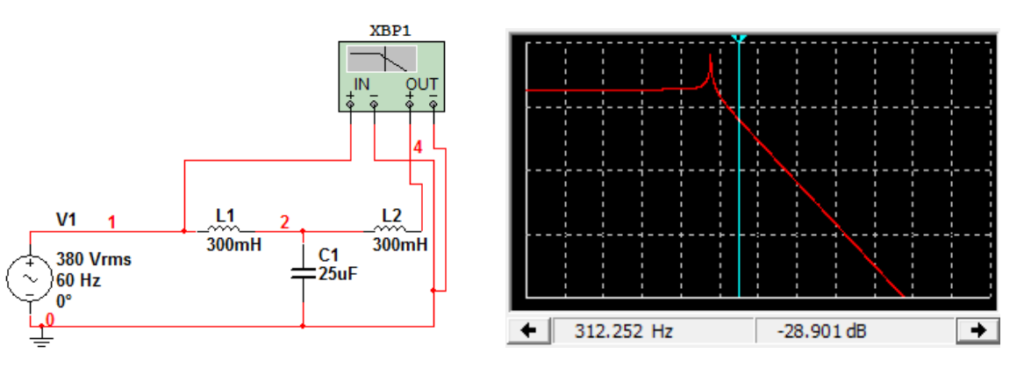
Tendo por base a utilização de um filtro LCL no circuito entre a rede e o conversor, se iniciaram os trabalhos de projetar os indutores a serem dimensionados, através do programa Multisim, pelo qual se pôde definir, após várias tentativas e de posse dos valores de capacitores disponíveis, o circuito com ambos os indutores valendo 300 mH, tal como mostrado no circuito da Figura 11. Neste caso, o capacitor disponível e utilizado foi de 25 μF, de escala comercial e, portanto, amplamente disponível. Já quanto aos indutores, por terem um valor relativamente alto, tiveram que ser montados, na própria instituição, em núcleo ferromagnético, tendo ainda elevada capacidade de condução de corrente e de dissipação de calor, dada a perniciosa presença do quinto harmônico. Complementarmente, se apresenta o diagrama de bode para o arranjo projetado.
Figura 11 – a. Circuito LCL projetado, com ênfase na escolha de valor e projeto dos indutores;
b. Diagrama de bode do filtro sintonizado em 60 Hz e com atenuação de cerca de 30 dB para o quinto harmônico.
Uma vez definidos os valores dos componentes do filtro, a partir das simulações, se iniciou a parte de montagem e implementação do filtro com os indutores projetados. Entretanto e tal como previsível, por conta da não-linearidade dos núcleos de material ferromagnético e da indisponibilidade de material suficiente para se produzir indutores com núcleo de ar, menos sujeito a esse tipo de problema, se verificou que havia ainda uma distorção significativa na tensão, quando do acionamento do motor pelo conversor.
Desta forma, se prosseguiu ao ajuste empírico dos valores de indutores, ajustando a associação série e paralelo, contando com alguns deles disponíveis e outros que tiveram que ser montados, tal como mostrado na Figura 12.
Figura 12 – a. Arranjo experimental de ajuste do filtro LCL; b. Projeto de associação série e paralelo para ajuste-fino empírico dos indutores de filtragem LCL.

Após um longo período de ensaios, finalmente se chegou a uma combinação adequada entre os parâmetros, combinando uma capacitância de 70 μF, facilmente disponível, e um projeto de associação de indutores que equivaleu a 100 mH, cada, permitindo que tensão da rede pudesse ficar sem distorção, tal como na Figura 9.a.
Na Figura 13 se mostram o circuito final projetado e implementado, bem como seu diagrama de Bode.
Figura 13 – a. Circuito LCL ajustado e implementado com indutores projetados; b. Resposta em frequência do circuito de filtro projetado – ênfase na atenuação de cerca de 28 dB para o quinto harmônico.
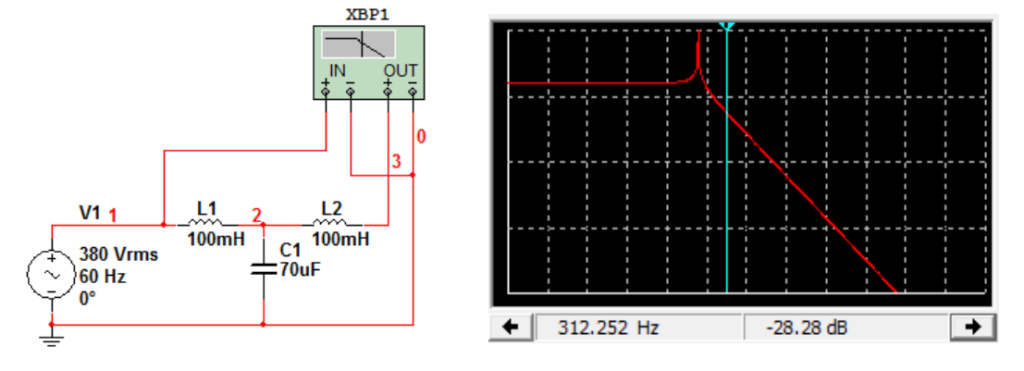
Para enfatizar a complexidade do projeto dos indutores, convém mencionar que o arranjo montado com os valores dos componentes suficientes para a filtragem adequada se deu em três estágios para cada indutor de 100 mH, sendo requerido um carrinho para comportá-los, tal como mostrado na Figura 13.b. Por outro lado, cabe salientar a natureza específica do ajuste-fino do filtro, que depende substancialmente da rede em que o conjunto filtro + motor + conversor operam. Isso porque por detrás de toda a rede há uma impedância equivalente, inerente, que interfere na resposta em frequência do filtro e, portanto, na sua capacidade de atuação. Ainda, cabe considerar que o valor dessa impedância possui uma parcela considerável que é variável ao longo do dia, por conta da variação e carregamento do sistema elétrico, de forma que o grau de satisfação para a filtragem para cada aplicação de filtro LCL , na indústria, deve ser criteriosamente analisada, servindo os resultados teóricos como uma aproximação muitas vezes razoável.
5 CONSIDERAÇÕES FINAIS
De posse de informações obtidas a partir de estudos teóricos, incluindo simulações computacionais, a respeito de filtros passivos, se pôde concluir que servem muito adequadamente para se chegar a resultados aproximados em seus projetos voltados para conversores de frequência. Principalmente, no que diz respeito ao projeto dos indutores, nos casos de filtros mais utilizados, tal como o LCL. Um dos pontos mais críticos vem a ser, em seguida aos estudos teóricos, o ajuste fino nos valores dos parâmetros capacitor e principalmente, indutor, cuja variação pode se tornar significativa e proibitiva. No caso deste trabalho, o motor utilizado a ser acionado foi de pequena potência, o que provavelmente permitiu uma forte e indesejável influência da impedância intrínseca da rede de energia. Por outro lado, no caso de motores de plantas industriais, com potências de pelo menos cem vezes a que foi utilizada neste trabalho, se tal influência se mostrar persistente, além da dificuldade que causará em se variar os parâmetros e realizar testes, a possível necessidade de troca de componentes indutores e capacitores pode tornar inviável a medida de filtragem, o que de certa forma explica a ocorrência de tantos casos de insucesso dessa implementação, na indústria.
Tal conjunto de resultados apontam para uma necessidade cada vez maior de estudos dessa natureza, dado que o acionamento de motores por conversores encontra-se em franco crescimento.
REFERÊNCIAS
CABRAL, S.H. L.; PEREIRA, E. T. ; MEYER, L. H. ; WERLICH, R. E. & RIBEIRO, J. M. Localização de Faltas em Redes de Distribuição com o Uso de Bobinas de Rogowski. Revista Eletricidade Moderna , v. XXXIV, p. 178-187, 2005.
CIGRÉ. Guide to The Specification and Design Evaluation of AC Filters for HVDC Systems, Apr. 1999.
FITZGERALD, A. E. ; KINGSLEY JR. C. & UMANS, S. D., Electric Machinery. 5a edição. Londres: McGraw-Hill. 1992.
IEEE. Recommended Practices and Requirements for Harmonic Control in Electric Power Systems. Project IEEE-519. October 1991.
IEEE. Recommended Practice and Requirements for Harmonic Control, Electric Power System IEEE Standard 519;2014, March 2014.
KASSICK, E. V. Harmônicas em Sistemas Industriais de Baixa Tensão. UFSC, 2008.
MATTAR, J. R.; STRUTZ J. C.; HAUSMANN, R.; OLIVEIRA, S. V. G. & PÉRES, A. A Single Phase Active Filter as a Harmonic Compensator. Brazilian Power Electronics Conference, Gramado, Brazil, 2013, pp. 1234-1238;
PENA-ALZOLA, R.; LISERRE, M.; BLAABJERG, F.; ORDONEZ, M. & KEREKES, T. Self-commissioning Notch Filter for Active Damping in Three Phase LCL-filter Based Grid-tie converter, Power Electronics, IEEE Transactions on, vol. PP, pp. 1-1, 2014.
STAHELIN, A. L. Estudo do Filtro LCL em Aplicações com Conversor de Frequência Regenerativo. Dissertação de Mestrado Eng. Elétrica – PPGEE/FURB, 2016;
1scabral@furb.br / Universidade Regional de Blumenau
2asartori@furb.br / Universidade Regional de Blumenau
3romeuh@furb.br / Universidade Regional de Blumenau
4meyer@furb.br / Universidade Regional de Blumenau
5rwerlich@furb.br / Universidade Regional de Blumenau
6pmeyer@furb.br / Universidade Regional de Blumenau
