REGISTRO DOI: 10.5281/zenodo.10802645
Johnny Luís Mércuri1
RESUMO
O presente trabalho tem por finalidade apresentar uma proposta bastante simples e pedagogia sobre o porquê todo número elevado a zero sempre é igual a 1. Inicialmente apresentamos algumas propriedades de potência, necessárias para que a ideia seja compreendida e por fim faremos uma análise por inspeção sobre um número da forma ab com a ≠ 0 real e como esse valor se comporta ao decorrer que b vai variando próximo a zero.
Palavra-Chave: Potenciação, Um número elevado a zero, Tende a um.
1. INTRODUÇÃO
O presente artigo tem por objetivo apresentar de forma intuitiva e um pouco formal a ideia de porque todo número elevado a uma potência zero sempre é igual a 1. Assim adotaremos um valor fixo para a base, nesse caso usaremos a base dois para facilitar os cálculos, e analisaremos o que acontece quando a potência b se aproxima de zero, nos casos para b > 0 e b < 0.
1.1 UMA BREVE IDÉIA SOBRE POTENCIAÇÃO
Potenciação é a multiplicação de fatores iguais, onde a potência representa quantas vezes multiplicamos o valor da nossa base.
Por exemplo:
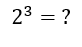
No caso acima o valor 2 é nossa base e o valor 3 é nossa potência ou expoente, assim, queremos saber qual o valor dessa igualdade quando multiplicamos o termos 2 com ele mesmo 3 vezes. Logo queremos o valor de 2x2x2 que é 8, por tanto 23 = 8.
No exemplo acima estamos trabalhando com a base sendo maior do que 1, mas podemos aplicar essa ideia também para valores entre zero e um.
Por exemplo:
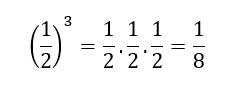
Aplicando a mesma ideia aplicada anteriormente conseguimos determinar o valor de:
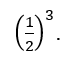
Podemos ter o caso onde nossa potência é negativa onde devemos ajustá-la para que possamos determinar o seu valor.
Por exemplo:
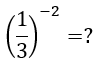
Aplicando a propriedade de potência temos:
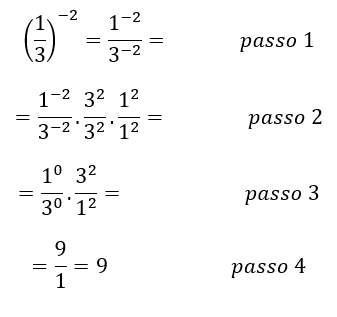
Logo nossa resposta é 9.
Muitos alunos ficam com dúvida na passagem 3 para a 4, não sabendo ao certo por que todo número elevado a zero sempre é igual a 1. Assim, apresentaremos uma forma clara e intuitiva de porque todo número elevado a zero sempre resulta em 1.
2. POR QUE UMA POTÊNCIA ELEVADA A ZERO SEMPRE É IGUAL A UM ?
Sabemos que toda potência é da seguinte forma:
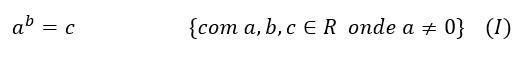
Onde a é nossa base, b é nosso expoente e c é a solução. Assim temos que b representa quantas vezes devemos multiplicar nossa base a para determinar o valor de c. Então podemos reescrever (I) como sendo.
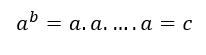
Tendo b termos a se multiplicando obtendo assim o valor c, e ainda, a potência de cada a vale 1.
Mas nossa dúvida é a seguinte, por que se tivermos b = 0 nosso c sempre será igual a 1?
i) Vamos analisar um caso para tentar verificar um padrão, usaremos nossa base valendo 2 e iniciaremos com a potência 5.

Tabela 1
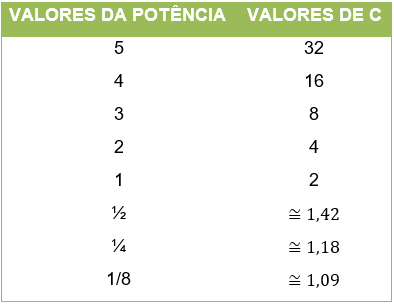
Fonte: Tabela criada pelo autor
Analisando a variação de b, vemos que o valor de 2b se torna cada vez menor se b se torna um número muito pequeno, se tomarmos b =1 /10000 temos que c≅ 1,0000693 um valor bem próximo de 1. Então para valores bem pequenos de b (chegando próximos a zero), ou melhor, se b = 1/d onde d ∈N – {0} e d tende ao infinito temos que 2b = c se aproxima cada vez mais de 1.
ii) Analisemos agora se b for um valor negativo, onde nossa potência será -5 com a base valendo 2.

Tabela 2
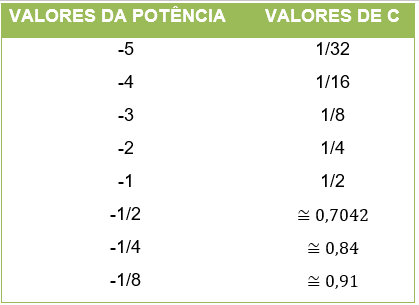
Fonte: Tabela criada pelo autor
Assim, tomando b < 0 temos que 2b se torna bem próximo de 1 a cada vez que b se aproxima de zero. Contudo, se b de aproxima de zero pelo lado direito da reta numérica e b se aproxima de zero pelo lado esquerdo (figura 1) temos que 2b tende a se aproximar cada vez mais de 1.
Figura 1
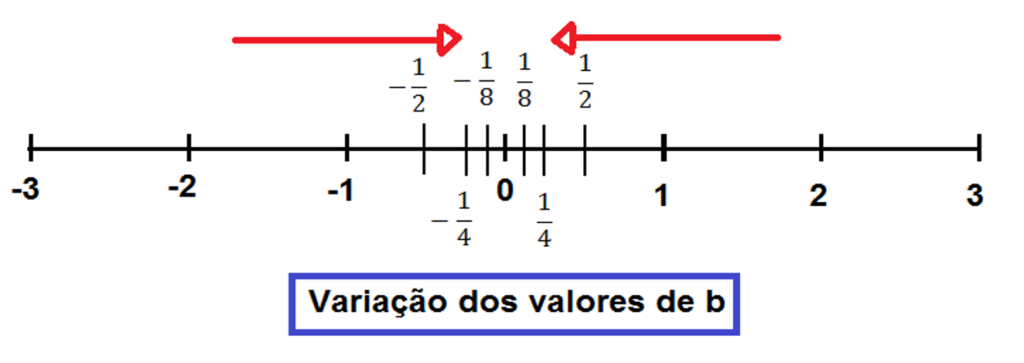
Fonte: Figura criada pelo autor
3. CONCLUSÃO
Logo, podemos concluir que para valores de b se aproximando cada vez mais de zero, tanto para b > 0 quanto para b < 0, temos que 2b se aproxima cada vez mais de 1. Portanto se tivermos b = 0 temos que 20 = 1. Assim todo número real a ≠ 0 na forma ab com b ∈ R é igual a 1.
BIBLIOGRAFIA
[1] SILVA, Sebastião Medeiros da; SILVA, Elio Medeiros da; SILVA, Ermes Medeiros da. Matemática: para os cursos de economia, administração e ciências contábeis. 3. Ed, São Paulo: Atlas, 1988. Página(17).
[2] CAVALLANTE; Sidney L; NETO, Aref A; NILTON, Lapa; SAMPAIO, José Luiz P; NILTON, Lapa. Introdução à análise matemática. Vol 8. São Paulo: Ed. Moderna, 1985.
1johnnymatematica@hotmail.com
