CONSTRAINED OPTIMIZATION VIA H ∞ CONTROL WITH UNSTRUCTURED UNCERTAINTIES USING LINEAR MATRIX INEQUALITIES
REGISTRO DOI: 10.69849/revistaft/ch10202506241850
Ivanildo Silva Abreu1; Marlos Luís Rocha Martins2; Alan Jefferson Lima Aragão3; Karllos Alexandre Sousa Pereira4; Anne Karine Cherrin de Sousa5; Cristovam Filho Dervalmar Rodrigues Teixeira6; José Ribamar Ferreira Silva7; Maciel dos Santos Silva8
Resumo
Neste trabalho de pesquisa, usa-se as desigualdades matriciais lineares (LMIs), uma poderosa ferramenta matemática usada na área de controle robusto, que tem como base o teorema de Lyapunov. Esta pesquisa apresenta tanto a análise quanto a síntese de controle robusto H ∞ pela técnica clássica de realimentação dos estados para sistemas lineares invariantes no tempo sujeito a incertezas não estruturadas. O objetivo deste trabalho é projetar um controlador que seja robusto mesmo diante a incertezas usando a norma H ∞. Usando o Complemento de Schur e o Bounded Real Lemma, formula-se um problema de otimização restrito a essas LMIs. Com o valor de ganho por realimentação dos estados, a saída apresentou um overshoot e em seguida o sistema se estabilizou. Nesta avaliação usando a norma H ∞ não estamos preocupados com o desempenho e sim com a estabilidade sendo que o comportamento é típico de um controlador ótimo ou robusto, onde o esforço de controle é maior no início para minimizar o tempo de assentamento. O controlador H ∞ projetado via LMIs estabiliza o sistema com convergência suave e sem sobressinal. O ganho K calculado equilibra desempenho e robustez, como evidenciado pela resposta dos estados e do sinal de controle e a ausência de oscilações em u(t).
Palavras-chave: Função de Lyapunov, LMIs, Bounded Real Lemma, Controle H∞, Controle por Realimentação dos Estados.
Abstract
In this research work, we employ Linear Matrix Inequalities (LMIs), a powerful mathematical tool used in robust control theory, which is based on Lyapunov’s theorem. This study presents both analysis and synthesis of robust H ∞ control through the classical state feedback technique for linear time-invariant systems subject to unstructured uncertainties. The objective of this work is to design a controller that remains robust even in the presence of uncertainties using the H ∞ norm. By applying the Schur Complement and the Bounded Real Lemma, we formulate a constrained optimization problem based on these LMIs. With the obtained state feedback gain, the system output exhibited an overshoot before stabilizing. In this H ∞ norm evaluation, we are not primarily concerned with performance but rather with stability, as the behavior is typical of an optimal or robust controller where control effort is initially higher to minimize settling time. The H ∞ controller designed via LMIs stabilizes the system with smooth convergence and no overshoot. The calculated gain K balances performance and robustness, as evidenced by the state responses and control signal, along with the absence of oscillations in u(t). The results demonstrate the effectiveness of the proposed method in achieving robust stability while maintaining satisfactory dynamic performance.
Keywords: Lyapunov function, LMIs ,H∞ robust control, linear matrix inequality, state-feedback control.
1. INTRODUÇÃO
Sistemas de controle modernos frequentemente operam sob incertezas – seja devido a erros de modelagem, perturbações externas ou variações de parâmetros. A teoria de controle robusto, particularmente o controle H ∞, fornece um arcabouço para garantir estabilidade e desempenho do sistema apesar dessas incertezas. Entretanto, métodos tradicionais podem levar a projetos conservadores ou falhar no tratamento eficaz de incertezas não estruturadas (como dinâmicas não modeladas ou perturbações não lineares).
Para enfrentar esse desafio, as Desigualdades Matriciais Lineares (LMIs) surgem como uma ferramenta poderosa, permitindo a formulação de problemas de controle em um framework de otimização convexa restrito a essas desigualdades matriciais lineares. Um elemento-chave nesta abordagem é a função de Lyapunov, que naturalmente introduz LMIs para certificar estabilidade e desempenho. Ao aproveitar o Complemento de Schur, desigualdades matriciais não lineares podem ser transformadas em LMIs, possibilitando soluções computacionalmente tratáveis.
Os objetivos deste trabalho consistem em desenvolver um framework de otimização baseado em LMIs para controle H ∞, sob incertezas não estruturadas, explorar formulações baseadas em Lyapunov para garantir robustez e minimizar conservadorismo, aplicar o Complemento de Schur para converter restrições matriciais não lineares em LMIs, facilitando soluções numéricas, validar a abordagem em um problema de otimização restrita por meio do Bounded Real Lemma demonstrando desempenho superior a métodos clássicos.
Este trabalho de pesquisa tem como justificativa e contribuições a indagações tais como, Incertezas não estruturadas (como perturbações no domínio da frequência) são comuns em sistemas reais, mas desafiadoras de modelar precisamente, o controle H ∞, garante robustez contra perturbações no pior caso, mas sua aplicação direta pode levar a problemas de otimização intratáveis e LMIs fornecem uma maneira sistemática de codificar restrições de estabilidade e desempenho, enquanto o Complemento de Schur possibilita soluções numéricas eficientes numa estrutura de otimização que tem como modelo a aplicação do Bounded Real Lemma.
As contribuições esperadas deste trabalho podem ser uma nova formulação LMI integrando funções de Lyapunov e restrições H ∞, para incertezas não estruturadas, redução do conservadorismo comparado a métodos tradicionais de controle robusto, algoritmos computacionalmente eficientes para aplicações de controle em tempo real e validação prática em estudos de caso (ex.: aeroespacial, robótica), demonstrando aplicabilidade.
Neste trabalho de pesquisa, usa-se as desigualdades matriciais lineares (LMIs), uma poderosa ferramenta matemática usada na área de controle robusto, que tem como base o teorema de Lyapunov. Esta pesquisa apresenta tanto a análise quanto a síntese de controle robusto H ∞ pela técnica clássica de realimentação dos estados para sistemas lineares invariantes no tempo sujeito à incertezas não estruturadas.
O sistema a ser usado será a tempo contínuo. Para isso, utiliza-se uma forma sistemática para modelar essas incertezas não estruturadas. A ideia desse tipo de procedimento será inicialmente separar o sistema nominal Gnom (s) da parte com incertezas que será denominada de G(∆), tendo uma entrada de controle u, y como saída, w e z são interfaces (ramos de entrada e de saída) que são artificiais.
Elas indicam como essas incertezas interagem com o sistema nominal. Usando o Complemento de Schur e o Bounded Real Lemma, formula-se um problema de otimização restrito a essas LMIs.
Com o valor de ganho de realimentação dos estados, a saída apresentou um overshoot e em seguida o sistema se estabilizou. Nesta avaliação usando a norma H ∞ não estamos preocupado s com o desempenho e sim com a estabilidade sendo que o comportamento é típico de um controlador ótimo ou robusto, onde o esforço de controle é maior no início para minimizar o tempo de assentamento. O controlador H ∞ projetado via LMIs estabiliza o sistema com convergência suave e sem sobressinal.
O ganho K calculado equilibra desempenho e robustez, como evidenciado pela resposta dos estados e do sinal de controle e a ausência de oscilações em u(t) corrobora a estabilidade do sistema em malha fechada.
O sistema a ser usado será a tempo contínuo. Para isso, utiliza-se uma forma sistemática para modelar essas incertezas não estruturadas. A ideia desse tipo de procedimento, será inicialmente separar o sistema nominal G_nom (s) da parte com incertezas que será denominada de G(∆), tendo uma entrada de controle u(t), y(t) como saída, w e z são interfaces (ramos de entrada e de saída) que são artificiais. Elas indicam como essas incertezas interagem com o sistema nominal.
Usando o Complemento de Schur e o Bounded Real Lemma, formula-se um problema de otimização restrito a essas LMIs. Com o valor de ganho de realimentação dos estados, a saída apresentou um overshoot e em seguida o sistema se estabilizou. Nesta avaliação usando a norma H ∞ não estamos preocupado com o desempenho e sim com a estabilidade sendo que o comportamento é típico de um controlador ótimo ou robusto, onde o esforço de controle é maior no início para minimizar o tempo de assentamento. O controlador H ∞ projetado via LMIs estabiliza o sistema com convergência suave e sem sobressinal. O ganho K calculado equilibra desempenho e robustez, como evidenciado pela resposta dos estados e do sinal de controle e a ausência de oscilações em u(t) corrobora a estabilidade do sistema em malha fechada.
2. FUNDAMENTAÇÃO TEÓRICA
O controle robusto H ∞, surgiu na década de 1980 (Zames, 1981; Doyle et. al., 1989) para sistemas sujeitos a perturbações e incertezas. A norma H ∞, quantifica o ganho máximo (pior caso) entre perturbações w e saídas z, garantindo estabilidade e desempenho mesmo sob incertezas não estruturadas (ex.: dinâmicas não modeladas). A formulação clássica minimiza γ tal que


Esta técnica é essencial para reformular problemas de controle robusto (Scherer & Weiland, 2000).

Os Solvers como LMIlab (Gahinet et al., 1995) ou YALMIP (Loftberg, 2004) resolvem o problema de otimização convexa acima, Eq. (7). A evolução histórica do Controle H ∞ via LMIs tem como marco o ano de 1982 com os trabalhos de Zames intitulado Fundamentos do Controle H ∞. Os pesquisadores Doyle, Glover, Khargonekar e Francis, em 1989 deram sua contribuição na solução do problema de controle H ∞usando as equações de Riccati. A formulação por LMIs se deu por volta de 1994 com a contribuição de Boyd et al. O uso de LMIs para incertezas não estruturadas se deu em 1994 pelo pesquisador Gahinet & Apkarian. A unificação teórica via BRL ocorreu em 1996 por zhou, Doyle, Glover e em 2000 as LMIs foram usadas em sistemas incertos por Scherer & Weiland.
A integração de funções de Lyapunov, Complemento de Schur, e Bounded Real Lemma permite reformular problemas complexos de controle robusto em otimizações convexas via LMIs, visto que essa abordagem fornece garantias teóricas de estabilidade robusta, eficiência computacional para sistemas servadorismo e estender LMIs para sistemas não lineares.
3. METODOLOGIA
Esta é a parte na qual se diz como foi feita a pesquisa. Existem várias formas de se explicitar uma metodologia. Deve-se optar por uma maneira que dê suporte adequado para realização da pesquisa ou sua replicação.
Nesta parte do trabalho são realizadas descrições dos passos dados e dos Procedimentos / recursos que foram utilizados no desenvolvimento da pesquisa. Assim, devem ser mostrados, de forma detalhada, os instrumentos, procedimentos e ferramentas dos caminhos para se atingir o objetivo da pesquisa, definindo ainda o tipo de pesquisa, a população (universo da pesquisa), a amostragem (parte da população ou do universo, selecionada de acordo com uma regra), os instrumentos de coleta de dados e a forma como os dados foram tabulados e analisados.
Todos os tipos de pesquisa devem apresentar material e métodos.
Nesta parte da pesquisa descreve-se a sua realização de maneira sistemática, onde o resultado final é um problema de otimização restrita a LMIs vis controle robusto H ∞. O objetivo será projetar um controlador robusto que minimize para um sistema com incertezas não estruturadas, por exemplo, incertezas não estruturadas nos parâmetros da dinâmica do sistema ou ruído no atuador, de maneira que possa garantir estabilidade e desempenho robusto.
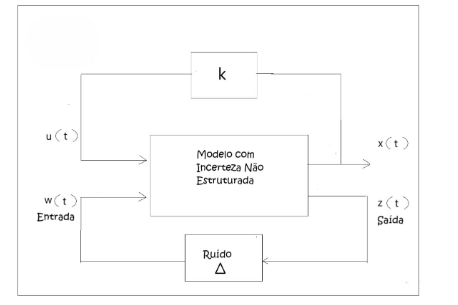
A ideia desse tipo de sistemática, é inicialmente separar o sistema nominal Gnom(s) da parte com incertezas que será denominada de G(∆), tendo uma entrada de controle u, y como saída, w e z são interfaces (ramos de entrada e de saída) que são artificiais. Elas indicam como essas incertezas interagem com o sistema nominal, conforme a Figura (1).
Onde o modelo com incertezas não estruturadas é dado pelo conjunto de equações:
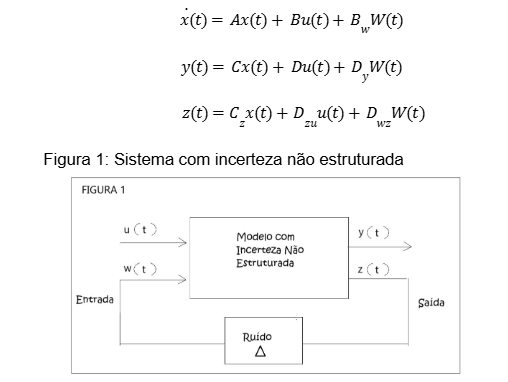
Fonte: (Autor, 2025).
Então, cria-se um sistema similar a uma malha de realimentação, que na verdade é fictícia, mas que é modelada para se aplicar as ferramentas conhecidas para esse tipo de modelo. Na equação de estados tem-se uma entrada W(t) que vai estar associada à matriz Bw. na equação de saída, y(t) é a saída do sistema, que também pode ser afetado pela incerteza w, assim como a incerteza poderia afetar diretamente o sensor e z(t) modela-se como uma saída linear nos estados na entrada w e também na saída z. Os elementos incertos, ou seja, as dinâmicas que iremos modelar estão contidas no ∆.
Para aplicar a metodologia, utiliza-se o sistema cuja representação em espaço de estados é dado por:
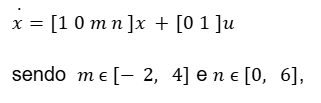
Os elementos incertos. Os valores de m e n são desconhecidos, porém sabemos o intervalos onde eles estão variando. Assim, este é um sistema que está sendo afetado por incertezas que são os parãmetros m e n, porém não se sabe os valores das incertezas, mas se conhece os intervalos delas, isto é, os limitantes das mesmas. Pode-se dizer que mesmo não conhecendo esses parâmetros m e n, tem-se uma noção do tamanho delas. Então, essa é a idéia da modelagem robusta.
Agora inicia-se a modelagem, separando a parte nominal da parte com incerteza. Para isso, considere:
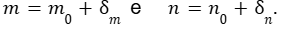
. Os valores nominais serão as médias aritmética dos intervalos, com suas respectivas variações:


Assim, a dinâmica do sistema é modelada da maneira abaixo:

O próximo passo será, escrever a parte da realimentação que envolvem o Bloco das Incertezas ∆ com o sinal de saída fictício (interface)

Em outras palavras, deseja-se determinar os parâmetros matriciais constantes Cz, Dzu e Dzu do sinal ficitício de saída da Eq. (17). A abordagem de busca desses parâmetros não é única. Uma interpretação para o bloco das Incertezas ∆, nos diz como as incertezas estão afetando a dinâmica do sistema, Eq.(17). Percebe-se claramente que a matriz Bw afeta a dinâmica da variável de estado x2, uma vez que ele está afetando a segunda linha da Eq. (15) a seguir. Ele não afeta diretamente a dinâmica da variável de estado x1.
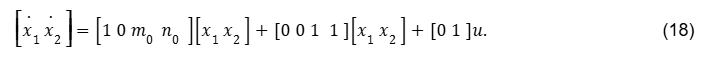
Nesta abordagem, observa-se que no Loop que envolve o sinal de entrada fictício (interface),w(t), como sendo o sinal de saída da aplicação de z pelo bloco de Incerteza ∆, ou seja, w=∆.z. Para realizar a modelagem, supõe-se que o bloco de incertezas, não possui dinâmica, ou seja, é estático. Então ele será apenas um bloco de ganho. A modelagem não possui solução única.
O próximo passos será selecionar os parâmetros matriciais da Eq.(17). Uma vez que
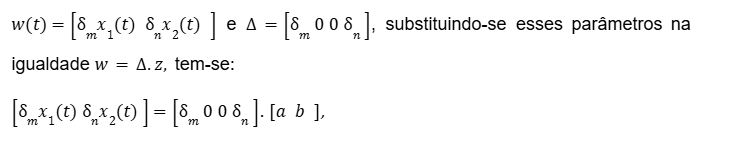
para as variáveis a e b.
Resolvendo o sistema de equações, tem-se que a variável de saída são os próprios estados. Assim z=[x1(t) x2(t)] indica quais são as variáveis que estão sendo afetadas pelas incertezas do sistema e quem indica é a variável de entrada w. esta variável indica como a incerteza afeta o sistema dinâmico. Esta seria uma interpretação para z e w, respectivamente.
Substituindo todas essas informações na Eq.(17):
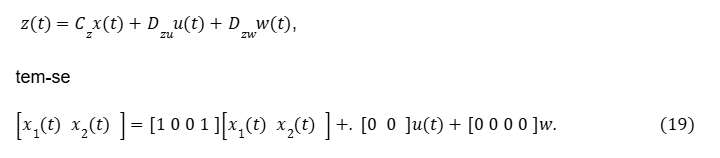
Portanto, definiu-se os parâmetros matriciais constantes a seguir
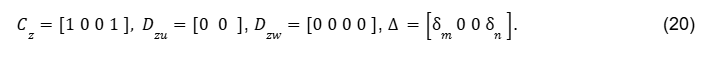
Até este momento, focamos em modelar sistema com incertezas não estruturada seguindo esta forma sistemática, apresentada acima. Assim, a idéia da incerteza não estruturada, consiste em separar a parte conhecida, ‘Parte Nominal’ da ‘Parte Incerta’ e descreveu-se o laço externo como uma relação entre o sinal de entrada w (ruído) e o sinal de saída z para descrever como é no geral o modelo da incerteza.
A análise de estabilidade será estabelecida pelo Teorema do Pequeno Ganho. será verificada se a estabilidade do sistema nominal está sendo afetada ou não, pela atuação do bloco da Incerteza ∆, que neste trabalho, está sendo um ruído externo. A análise de estabilidade será dada pelo cálculo da norma H ∞ da função de transferência do sinal de entrada w(t) para o sinal de saída z(t):
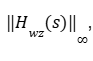
que em termos de resposta em frequência, corresponde ao maior ganho possível que o sistema pode resultar. A partir da definição do Diagrama de Bode, esta norma corresponde ao máximo valor de magnitude.
No caso MIMO, multiple input multiple outputs, calcula-se os valores singulares e eles são os máximos dos máximos de todos os valores de magnitude especificados no diagrama de Bode da magnitude.
Supondo que H(s) seja um sistema internamente estável, e que H_wz (s) é a função de transferência entre a entrada w(t) e a saída z(t). Então o sistema da Figura (1) é Internamente Estável para todas as incertezas, ∆, desde que satisfaça uma das condições a seguir:
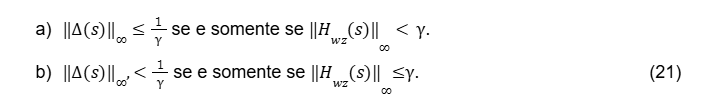
No caso SISO, single input single output, que é o nosso estudo de interesse, essa modelagem usa o teorema do pequeno ganho para projetar controladores, de maneira que o sistema controlado seja robusto a essa incerteza (ruído).
Assim, iremos projetar um sinal de controle u(t) de modo a interferir na função de transferência da entrada w(t) para a saída z(t), Hwz (s). Para sua construção, iremos usar o sistema de realimentação normal, seguindo alguns critérios. Inicialmente iremos usar uma condição para estabilidade, usando o teorema de Lyapunov: AT P+PA<0. Em seguida, usa-se a representação do sistema em malha fechada para realizar a síntese de controladores que irá substituir a matriz A por (A+BK), sendo K o controlador desejado, conforme a Figura (2).
Figura 2: Sistema com realimentação de estados
Fonte: (Autor).
Neste trabalho, iremos realizar apenas a análise e em seguida realizar a síntese com alteração de parâmetros no código estabelecido pelo projetista, simulando no MATLAB. Para realizar o cálculo da norma
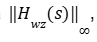
usaremos então uma outra definição da norma infinita, que nos diz:

Para um sistema estável, a norma H∞ será caracterizada por meio da função quadrática de Lyapunov:
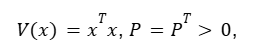
Simétrica Definida Positiva sob a condição

Logo se existe um escalar γ que é um limitante superior da norma
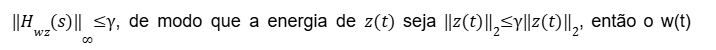
está intrinsecamente relacionado à ideia do diagrama de Bode. Isto é se a energia de w(t) para z(t) for menor que para todas as possíveis situações de w que é um sinal de energia finita, então a desigualdade

Agora é necessário garantir a estabilidade do sistema, admitindo que a Eq. (19) seja satisfeita. Para isso, incorpora-se a Eq.17 na condição de estabilidade de Lyapunov, que gera o conjunto das Desigualdades Matriciais Lineares (LMIs) a seguir:
Quando se realiza esta metodologia, está se usando a descrição do sistema sem controle, apenas com a condição de análise; veja Eq. (27):

Quando se realiza esta metodologia, está se usando a descrição do sistema sem controle, apenas com a condição de análise; veja Eq. (27):
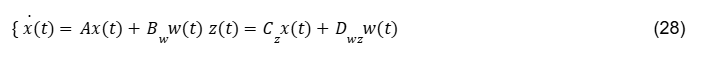
Desenvolvendo o lado esquerda da Eq.(27)
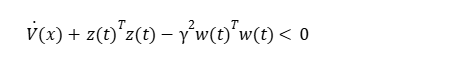
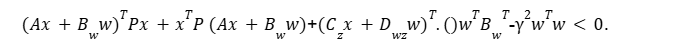
Aplicando a propriedade distributiva, tem-se
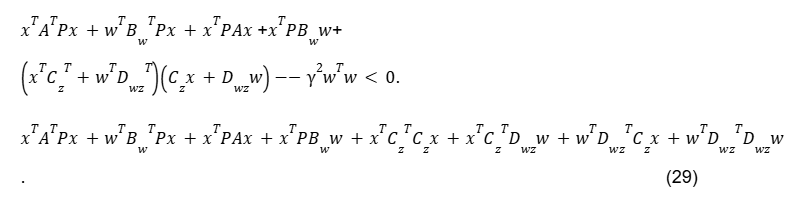
Este desenvolvimento é equivalente a
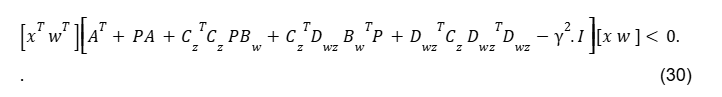
A Desigualdade (29) deve ser válida para todo x e todo w, ou seja, a matriz
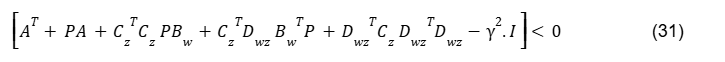
Isso é equivalente a um dado inicialmente que satisfaz a Desigualdade (22), irá satisfazer também a Desigualdade (25). Então vamos chamar P tal que esse satisfaz a desigualdade (31). Como deseja-se calcular a norma H∞ do sistema, então precisa-se achar o menor que satisfaz a Desigualdade (30), e em seguida, iremos minimizar a sensibilidade ou ruído. Assim, iremos transformar a busca do gama num problema de otimização, isto é, minimizar o γ.Um passo a mais será incluído na Eq.(25), que é o Complemento de Schur,para realizar as condições de análise. Portanto, para calcular a
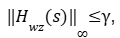
deve-se mostrar que existe uma matriz P=PT>0 (Simétrica definida positiva) que satisfaça a Eq. (30), (LMIs).
O Complemento de Schur é um artifício frequentemente utilizado para converter uma desigualdade (convexa) não-linear em uma LMI (Equação matricial linear) ou vice versa.
Em particular, para matrizes simétricas do tipo M=MT=[M1 M2 M2T M3 ]. Define-se o Complemento de Schur em relação ao bloco M3 como:
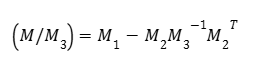
Para isso, iremos reescrever a LMIs (30) da seguinte maneira:
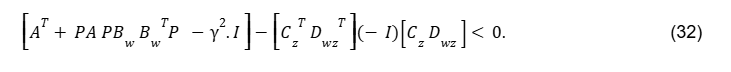
Percebe-se claramente que Eq. (31) está na forma do Complemento de Schur, e que também pode se ter esta condição
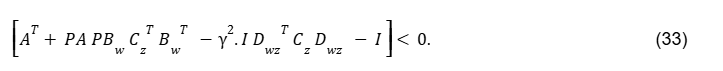
Então, pode-se observar que a Eq.(22) é equivalente à Eq.(33). Portanto, uma forma particular de realizar a computação da norma H∞ é obter a solução P>0 da equação algébrica de Riccati associada à desigualdade de Riccati anterior.
O Bounded Real Lemma (BRL) é um resultado fundamental na teoria de controle robusto. Ele estabelece uma condição equivalente para que o ganho H de um sistema linear seja menor que um valor especificado . Ele transforma uma condição de desempenho em uma desigualdade matricial linear (LMI), permitindo análise e síntese de controladores robustos e a existência de uma solução.
Considere um sistema linear invariante no tempo (LTI):
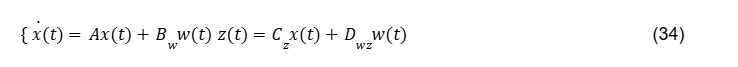
sendo
{xϵRn estado do sistema wϵRm entrada de distúrbio zϵRp sinal de desempenho.
O objetivo desta metodologia é garantir que o ganho
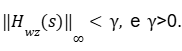
Numa forma erudita, o Bounded Real Lemma é enunciado da seguinte maneira:

sendo que cada bloco tem seu papel:
- Bloco (1,1): AT+PA (estabilidade do sistema).
- Bloco (1,2): PBw (acoplamento entre distúrbio e dinâmica).
- Bloco (1,3): CzT (saída de desempenho).
- Bloco (2,2): y2.I (limitação de energia de w para z).
O (Bounded Real Lemma) BRL é usado para:

maximizando a relação sinal-ruído.
Diante da exposição do Bounded Real Lemma, pode-se adaptar para projeto a computação do valor exato da norma H∞ para sistemas precisamente conhecidos (Primal), ou seja, encontrar a solução do problema de otimização semidefinida associado ao Bounded Real Lemma e descrito abaixo, utilizando a mudança de variável linearizante μ≜2:
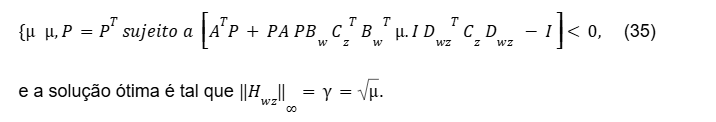
A versão para a computação da norma H∞ de representação do sistema Dual linear invariante no tempo, possui a mesma função de transferência do sistema original (Primal), com algumas alterações. Veja a seguir:

e aplica-se o Bounded Real Lemma
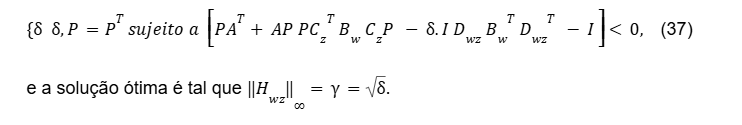
A solução deste tipo de problema de otimização, com restrições descritas por LMIs e função objetivo linear, pode, em princípio, ser obtida empregando-se algum método de programação do tipo exclusão de espaços com aproximação externa como, por exemplo, o método de planos de corte. No entanto,atualmente existe uma grande família de algoritmos dedicados a resolver este tipo de problema convexo de programação semi-definida com características próprias e de fácil utilização.
A seguir, são listados alguns dos mais conhecidos pacotes de otimização utilizados para resolver de forma bastante eficiente problemas sobre LMIs: LMILAB, LMITOOL, SeDuMi, LMISol.
Já a bastante tempo, as LMIs aparecem como uma das mais importantes ferramentas dentro da teoria de controle, particularmente, o controle robusto. Por volta dos meados dos anos de 1990, as descrições por LMIs despontaram como uma nova vestimenta e de fácil manipulação, alternativa a uma vasta gama de abordagens de controle e estimação fortemente baseadas, até aquele momento, nas desigualdades algébricas de Riccati como, por exemplo, LQR, LQE, LQG e o controle ótimo H∞ e H2, atualmente denominados de abordagens padrões (Doyle et al., 1989).
Para desenvolver este estudo do controle, toma-se como base a Figura (2) Iremos admitir que o sistema incerto seja modelado desta forma. Pode-se dizer que temos uma entrada w(t) (ruído externo) que indica como essa incerteza afeta a dinâmica do sistema e a saída z(t) que indica quais variáveis são afetadas pela incerteza.
E fizemos a condição de análise fundamentada no Teorema do Pequeno Ganho, com base na norma H do sistema. Basicamente, se
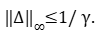
então o sistema permanece estável e admitindo que a parte nominal é estável, então o bloco das incertezas ∆(s)≤1/2 não iria interferir na estabilidade do sistema se ‖∆‖∞≤1/ γ. Isto foi o que vimos na condição de análise com fundamentação em LMIs, onde adequo o Bounded Real Lemma, Condição de Lyapunov, a computação de gama e por fim, o problema de otimização restrito à LMIs. Cálculo de gama.
Agora iremos trabalhar com as condições de Síntese de Controle em sistemas Incertos. Inicialmente serão considerados apenas ganhos de realimentação de estados u(t)=Kx(t). Portanto, devemos encontrar um valor de ganho K que garanta a estabilidade e robustez do sistema diante das incertezas. Daí, surge o seguinte questionamento: como se pode projetar uma lei de controle u(t) para controlar o sistema independentemente da incerteza?
Agora acrescentou-se um bloco com o controlador K juntamente com a partes nominal e incerta (ruído), e iremos admitir que a saída erá os estados x(t). Então temos que construir um ganho de realimentação de modo que, quando se constrói o controle dessa maneira, o sistema de controle em malha fechada inicialmente seja estável, pois pode ser que o sistema agora em malha aberta não necessariamente seja estável, visto que normalmente é o caso.
Logo esse K vai garantir a estabilidade do sistema nominal e também a robustez do sistema com essa incerteza ∆(s), isto é, ele deverá satisfazer o Teorema do Pequeno Ganho. Então inicialmente em termos algébricos tem-se o modelo matemático do sistema a seguir:
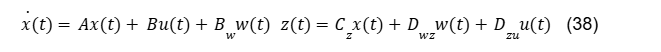
Na Eq.(29) não foi levada em consideração a equação de saída, porque estamos admitindo que as saídas são os estados, conforme foi nossa hipótese. Em malha fechada, quando se usa u(t)=Kx(t), na Eq.(29), tem-se:
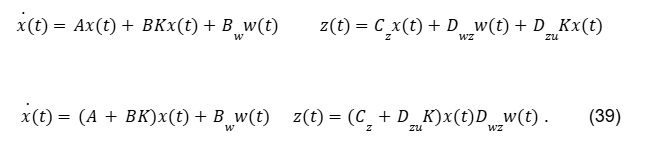
As condições de síntese serão utilizadas para realizar o controle. Daí, utiliza-se a mesma sistemática para a síntese de ganhos de controle de realimentação de estados para sistemas conhecidos, usando o Teorema de lyapunov. Faz-se a substituição de A⟶(A+BK) e Cz⟶(Cz+DK) em seguida, realizam-se todos os procedimentos já vistos. A sequência de desenvolvimento, pouco se altera e iremos gerar a condição de análise e em seguida, aplicar o controle na condição de análise e para finalmente gerar a condição de síntese.
O Bounded Real Lemma será obtido a partir do Sistema Dual, que possui a mesma função de transferência do sistema original (sistema Primal):
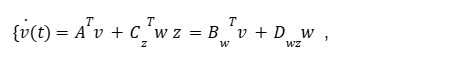
aplicando o Bounded Real Lemma, tem-se a condição de análise, Eq.(40).
O próximo passo será realizar o cálculo da norma H∞ usando o Sistema Dual, que é formulado pela estrutura de otimização restrita a seguir:
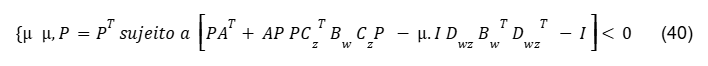
A norma H∞ do sistema em malha fechada tal que ‖Hclosed‖∞≤γ, se somente se, ∃P=PT>0 tal que
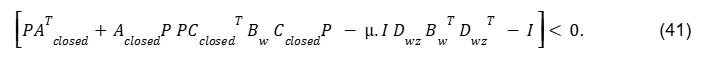
Fazendo KP=Z, a norma H∞ do sistema em malha fechada com o ganho de realimentação de estados ut=Kx(t) é tal que ‖Hclosed‖∞≤γ, ∃P=PT>0 e Z=KP tais que
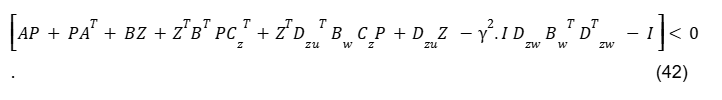
e K=ZP-1 é o ganho de realimentação dos estados.
Na Eq.(42) tem-se uma condição de LMIs, isto é, todos os termos são lineares, desde que u=γ2, por questões de programação. Daí pode-se resolver efetuando o cálculo de P, Z e . Assim, K=ZP-1 é o ganho de realimentação dos estados, que garante a Estabilidade do Sistema e também a norma infinita de w para z do sistema de malha fechada ‖Hclosed‖∞≤γ. Então realiza-se o controle que garante a estabilidade e robustez.
A submatriz AP+PAT+BZ+ZTBT da Eq.(42) corresponde à Condição de Síntese para que essa LMI seja negativa. É uma condição necessária mas não suficiente, que os elementos da diagonal principal sejam negativos. Portanto, o sistema nominal estável, é uma condição necessária, porque é uma condição necessária para estabilidade e do sistema e também garante-se que se tenha‖Hclosed‖∞≤γ. Logo essas condições irão garantir a robustez de sistemas aos ruídos, às incertezas predominantes.

É possível minimizar a norma H∞ do sistema em malha fechada a partir da estrutura de Otimização Restrita
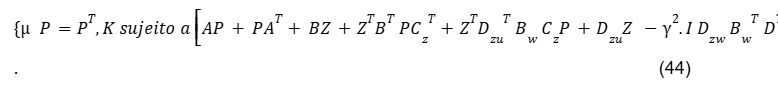
Para exemplificar a teoria de sistemas incertos que pode afetar o sistema, por exemplo, usou-se neste trabalho parâmetros incertos e ruídos no atuador. Eles são responsáveis por produzir movimento atendendo a comandos manuais ou mecânicos, que convertem energia pneumática, hidráulica ou elétrica em energia mecânica.
Isto é, se o atuador tem um ganho aplicado ao valor nominal u(t), o que normalmente é usado para representar falha no atuador, então
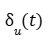
será um valor negativo, visto que ele vai representar uma perda de potência no atuador.
Admita fisicamente que o atuador insira um ruído na entrada de controle u(t), e além disso, o ruído seja também proporcional ao estado x1(t) Assim a entrada real do

O ruído do sensor será representado por ∆=δu(t), mas no caso do sensor, ele somente irá afetar quando se tiver uma realimentação. Uma vez que se está fazendo o caso da análise, o ruído no sensor não irá afetar na análise do sistema. A representação dada pela Eq.(36) separa o sistema nominal da parte com ruído.
O primeiro desafio na teoria de controle robusto, é representar matematicamente as incertezas do sistema. Iremos separar em dois blocos com uma realimentação interna, chamada Linear Fractional transformation (LFT).
Considere o sistema incerto

que pode ser reescrito na forma matricial:

Todas as matrizes dependem do parâmetro δ. A forma da Eq.(46) é uma sistematização, pois a idéia é apresentar a interpretação desse tipo de modelagem, ou seja, separar o sistema na parte nominal (matrizes constantes) Snom e na parte ruidosa S∆ que é a parte incerta. Neste caso, tem-se como meta obter as matrizes Bw, Cz e Dzw de modo que a Eq.(46) seja equivalente à Eq.(47) a seguir:
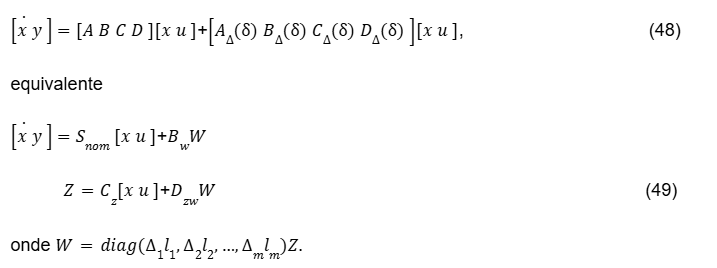
A LFT É essa transformação e existem metodologias para calcular de forma numérica esses parâmetros matriciais. Realizando o procedimento de otimização, elimina-se W, de modo que equivalente a
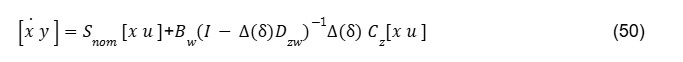
isto é, o elemento incerto se consegue representa na Eq.(41). Para determinar essas matrizes, exige-se que
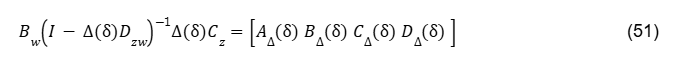
Usando a Eq.(1), o sistema pode ser reescrito como
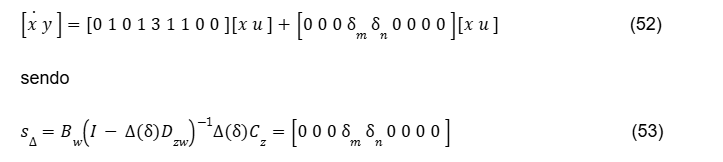
Então temos que encontrar as matrizes Bw, Dzw, Cz e ∆(δ) com coeficientes constantes de modo a satisfazer a Eq.(44). Efetuando manipulações algébricas, tem-se
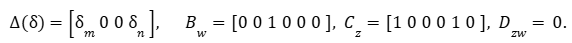
Logo com essas matrizes, a Eq. (53) é verificada.
4 RESULTADOS E DISCUSSÕES
Para exemplificar este trabalho de pesquisa, considera-se o sistema representado na forma de espaço de estado cujas matrizes são; o sistema nominal é estável.
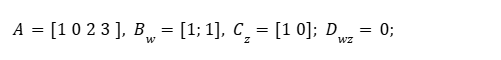
Cálculo da computação (Simulação Computacional)
Tabela 1
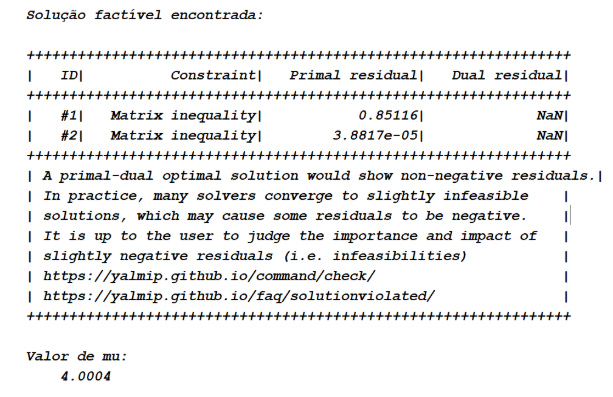
Como a ‖Hwz‖∞≤2, então o sistema vai aceitar valores de ∆(s) de magnitude até ½. Logo se ∆(s) tiver energia até 1/2, ‖∆‖∞≤1/2, ela não vai desestabilizar o sistema. Caso este valor seja ultrapassado, ‖∆‖∞>1/2, não se pode garantir mais nada e provavelmente o sistema vai se tornar instável. Desta forma, fez-se a computação da ‖Hwz‖∞ para sistemas com incertezas não estruturadas usando as condições LMIs.
Para esta etapa do controle usando ruídos no atuador, usa-se a mesma dinâmica
A seguir:
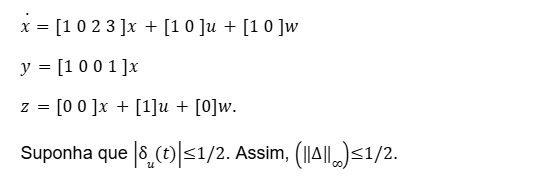
Pelo Teorema do Pequeno ganho, a estabilidade do sistema não está comprometida para a magnitude desse ruído. Então ‖Hclosedwz‖∞≤2. Daí, pode-se gerar um ganho de realimentação K de modo a estabilizar o sistema nominal, só que para garantir que ele seja robusto, com esta falha no atuador, (modelagem para falha até 50% da potência máxima), é uma falha superior a este percentual, o controle não vai conseguir estabilizar o sistema; portanto, para que o sistema seja robusto com falha de magnitude de até 50%, a ‖Hclosedwz‖∞≤2. Em outras palavras, o γ<2.
Vamos inicialmente minimizar a norma H∞ do sistema em malha fechada, Eq.(35), ou seja, qual é o máximo valor de robustez que se consegue garantir. Precisa-se de 2. O algoritmo gerou um ganho de realimentação dos estados de:
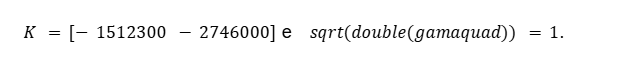
Então o máximo que se consegue garantir de estabilidade seria uma a ‖Hclosedwz‖∞=1. Aplicando o Teorema do Pequeno Ganho, ‖∆‖∞<1, isto é -1< δu<1. O problema exige ½, só que estou conseguindo até erro estritamente de até 1. Menor ou igual, nunca se irá obter. Se δu(t)=-1 Por exemplo, isso equivale a um atuador totalmente falho, ele está desligado, não está funcionando e não importa qual o controle que vou submeter ele não irá atuar no sistema. Logo, não se consegue o controle robusto.
O custo que se tem são os valores de ganho extremamente altos. Portanto, esse é o grande problema do controle usando a Norma H∞. Quando se otimiza (minimiza), o projetista se prepara para a maior robustez possível e isso vai implicar em ganhos extremamente elevados. Na prática, não se consegue implementar com estes valores.
Figura (3): estabilidade assintótica dos estados.
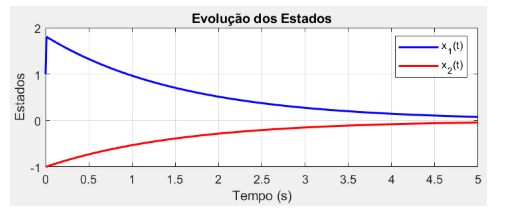
Fonte: (Autor)
Já o sinal de controle, Figura (4), apresenta uma magnitude elevada mostrando-se que o controle é bastante ruidoso, pois qualquer mudança nos estados, ele vai ter uma sensibilidade extremamente alta devido a magnitude do ganho K.
Figura (4): Sinal de controle elevado
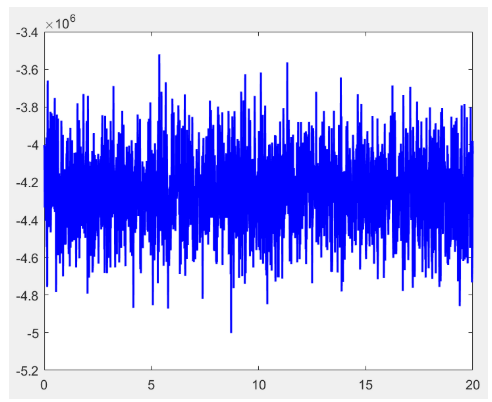
Fonte: (Autor)
Para contornar esse problema, vejamos o procedimento a ser feito, uma vez que deve-se utilizar a hipótese do controle H∞.Não iremos usar o ganho ótimo. Aqui, precisa-se garantir até ½ de Problema (Ruído). Para o problema ilustrado, usa-se um ganho suficiente. Neste caso, como estou querendo preparar até 50 % (1/2), admito que se for inferior a 50%, deve-se substituir o atuador. Então o controle precisa garantir que o gama seja 2.
Fazendo essas modificações e realizando as simulações computacionais, tem-se um valor para o ganho de realimentação dos estados, bem mais realista e suficiente para garantir a robustez do sistema.

Caso desejássemos um ganho de magnitude menor em comparação ao apresentado.
Uma vez que estamos lidando apenas com a questão da robustez, percebe-se claramente que não estamos conseguindo controlar a magnitude, do ganho do desempenho do sistema. A preocupação maior é com a robustez. Embora o valor do ganho na Eq.(45) possa até ser elevado para este exemplo, mas está sendo robusto pois resolve o problema. A questão do desempenho está associado a norma H2.
Com esse novo valor de ganho de realimentação dos estados, a saída apresentou um overshoot e em seguida o sistema se estabilizou. Nesta avaliação usando a norma H não estamos preocupados com o desempenho e sim com a estabilidade.
Figura 5: Estados e sinal de controle
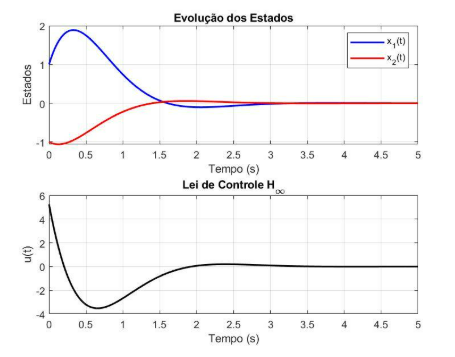
Fonte: (Autor, 2025).
Análise do Gráfico dos Estados e do Sinal de Controle
1. Gráfico dos Estados x1t e x2t
Comportamento Observado:
- Ambos os estados decaem para zero ao longo do tempo.
- x1t converge mais rapidamente que x2t indicando que a dinâmica associada a x1t é mais rápida.
- Não há oscilações significativas, sugerindo que o controlador H∞projetado fornece amortecimento crítico ou superamortecido.
- Interpretação:
- A estabilização é eficaz, pois os estados convergem para zero em aproximadamente 5 segundos.
- A diferença na taxa de decaimento pode estar relacionada aos autovalores da matriz em malha fechada A+BK.
2. Gráfico do Sinal de Controle u(t)
- Comportamento Observado:
- O sinal de controle u(t) é mais intenso no início (t≈0) e decai rapidamente à medida que os estados se aproximam de zero.
- O pico inicial sugere que o controlador age de forma enérgica para corrigir os estados iniciais x0=[1; -1].
- Após t≈1.5 segundos, u(t) se aproxima de zero, indicando que o sistema está próximo do equilíbrio.
- Interpretação:
- O comportamento é típico de um controlador ótimo ou robusto, onde o esforço de controle é maior no início para minimizar o tempo de assentamento.
- A ausência de oscilações em u(t) corrobora a estabilidade do sistema em malha fechada.
Conclusões
- Desempenho do Controlador:
- O controlador H∞ projetado via LMIs estabiliza o sistema com convergência suave e sem sobressinal.
- O ganho K calculado equilibra desempenho e robustez, como evidenciado pela resposta dos estados e do sinal de controle.
- Sugestões para Melhoria (se necessário):
- Se ut for demasiadamente agressivo, pode-se ajustar (ganho H ) para suavizar o controle.
- Se a convergência de x2t for lenta, ponderar mais esse estado na matriz Cz da saída de desempenho.
- Validação Adicional:
- Simular o sistema com perturbações para testar a robustez.
- Verificar os autovalores de A+BK para garantir que estão no semiplano esquerdo.
Referências
1. Boyd, S., El Ghaoui, L., Feron, E., & balakrishnan, V. (1994). Linear Matrix Inequalities in System and Control Theory. SIAM.
2. Benton, S. E., & Smith, D. (1998). IEEE Transactions on Automatic Control, 43(7), 961-966.
3. Doyle, J. C, et al. (1989). State-Space Solutions to Standard H2 and H Control problems. IEEE Transactions on Automatic Control, 34 (8), 831-847.
4. Gahinet, P., & Apkarian, P. (1994). A Linear Matrix Inequality Approach to HControl. International Journal of Robust and Nonlinear Control, 4(4), 421-448.
5. Iwasaki, T., & Skelton, R. E. (1994). All Controllers for the General H∞ Control Problem: LMI Existence Conditions and State Space Formulas. Automativa, 30(8), 1307-1317.
6. LMI Control Toolbox – MATLAB Documentation.
7. Loftberg, J. YALMIP: A Toolbox for Modeling and Optimization in Matlab. Proceedings of the CACSD Conference (2004).
8. MIT Open Course Ware (Course 6.241 – Dynamic Systems and Control).
9. Scherer, C., & Weiland, s. (2005). Linear Matrix Inequalities in Control. Lecture Notes, Dutch Institute for Systems and Control.
10. Scherer, C.;Weiland, S. (2000). Linear matrix inequalities in Control. Lecture Notes, Delft University of Technology.
11. Skogestad, S., & Postlethwaite, I. (2005). Multivariable Feedback Control: Analysis and design. Wiley.
1Pós-Doutor em Automação e Controle pela Universidade de São Paulo (USP) Instituição: Universidade Estadual do Maranhão (UEMA) – Campus São Luís, E-mail: ivanildoabreu@yahoo.com.br
2Mestrando em Matemática pela Universidade Estadual do Maranhão Instituição: Centro de Ensino Professor Robson Campos Martins, E-mail: solramluis@hotmail.com
3Mestrando em Matemática pela Universidade Estadual do Maranhão Instituição: Secretaria de Educação do Governo do Estado do Maranhão (SEDUC – MA), E-mail: alanjeffersonlima@gmail.com
4Mestrando em Matemática pela Universidade Estadual do Maranhão Instituição: Secretaria Municipal de Educação, Ciência e Tecnologia de Magalhães de Almeida (SEMECT), E-mail: karllos-alexandre@hotmail.com
5Mestranda em Matemática pela Universidade Estadual do Maranhão Instituição: Centro Educa Mais Professora Maria do socorro Almeita
6Mestre em Engenharia da Computação e Sistemas (UEMA). Cidade Universitária Paulo VI, São Luís, Brasil. Email: cristovamfilho17013@gmail.com
7Mestre em Matemática pela Universidade Estadual do Maranhão Instituição: Complexo Habitacional no Maranhão, E-mail: joseribsila@hotmail.com
8Mestre em Matemática pela Universidade Federal do Piauí / PROFMAT Instituição: Centro Universitário de Nassau, E-mail: macieleu@hotmail.com
