REGISTRO DOI: 10.69849/revistaft/cl10202504301802
Rafael Santos Silva
José Phelipe de Oliveira Albuquerque
Gabriel Rodrigues da Silva
Gilson Santos Coutinho
Resumo
Este artigo apresenta uma abordagem que une a teoria da probabilidade com a lógica proposicional. Primeiro, foi feito um breve resumo sobre a origem e o desenvolvimento da probabilidade e da lógica. Em seguida, mostramos como é possível utilizar sentenças lógicas para representar e resolver problemas de probabilidade. A proposta é resolver as questões usando a lógica, de forma intuitiva, sem recorrer diretamente às fórmulas tradicionais. Assim, a lógica proposicional se mostra uma ferramenta eficaz para interpretar e solucionar problemas envolvendo incerteza.
Palavras-chave: probabilidade, lógica proposicional, resolução de problemas, raciocínio lógico, matemática.
Abstract
This article presents an approach that combines probability theory with propositional logic. First, a brief overview of the origin and development of probability and logic is provided. Then, we show how logical sentences can be used to represent and solve probability problems. The proposal is to solve the problems intuitively using logic, without directly relying on traditional formulas. Thus, propositional logic proves to be an effective tool for interpreting and solving problems involving uncertainty.
Keywords: probability, propositional logic, problem solving, logical reasoning, mathematics.
Introdução
A teoria da probabilidade surgiu para resolver problemas envolvendo situações de incerteza, como os jogos de azar. Com o passar do tempo, a probabilidade foi sendo estudada e aprimorada, tornando-se uma ferramenta importante em diversas áreas, como a matemática, a estatística e a ciência de dados. Seu desenvolvimento começou de forma mais organizada no século XVII, com os trabalhos de Blaise Pascal e Pierre de Fermat. Também, é um dos eixos de matemática mais abordados em livros didáticos (Haubrichs, Amadeo, 2021).
A lógica, por outro lado, é estudada desde a antiguidade. Com Aristóteles, ela se desenvolveu como uma forma de organizar o pensamento e o raciocínio. Mais tarde, com o avanço da matemática, surgiu a lógica proposicional, que trabalha com proposições simples e compostas, utilizando conectivos como “e”, “ou” e “não”. A lógica proposicional trouxe um jeito mais preciso e rigoroso de representar o raciocínio.
Neste artigo, foi feito um resumo da história da probabilidade e da lógica proposicional, e mostramos como essas duas áreas podem se unir. Usando apenas a lógica, sem depender diretamente de fórmulas tradicionais, conseguimos resolver problemas de probabilidade de forma mais intuitiva e organizada. Assim, a lógica proposicional é apresentada como uma ferramenta útil para interpretar e resolver situações de incerteza.
Breve História da Teoria da Probabilidade
Podemos compreender a probabilidade como “[…] o ramo da matemática que pretende modelar fenômenos não determinísticos, isto é, aqueles fenômenos em que o ‘acaso’ representa um papel preponderante.” (VIALI, 2008, p.143).
Dessa forma, destaca-se, conforme a autora, a relevância do termo ‘acaso’ na definição de eventos indeterminados, sendo esse conceito uma peça fundamental na construção da Teoria das Probabilidades. Conforme Viali (2008, p. 144), podemos entender “acaso” como “[…] um conjunto de forças, em geral, não determinadas ou controladas, que exercem individualmente ou coletivamente papel preponderante na ocorrência de diferentes resultados de um experimento ou fenômeno.”.
Tomando como exemplo o sorteio de uma bola numerada de 1 a 6 em uma caixa, onde se pode obter qualquer um dos seis números e o “acaso” encontra-se impossibilitado de antecipar quais bolas numeradas serão observadas em lançamentos futuros, não sendo viável a determinação prévia de seus respectivos resultados. Este “acaso” relaciona-se também com diversos outros exemplos, como o lançamento de uma moeda, lançamento de um dado, previsões do tempo, etc.. Deste modo, podemos observar que o “acaso” pode estar relacionado aos jogos de azar, eventos ocorridos no dia-a-dia ou aos fenômenos naturais.
Os eventos ligados ao acaso desempenharam um papel crucial no surgimento dos seguros, criados com o intuito de minimizar prejuízos e perdas decorrentes de fenômenos naturais ou outras eventualidades. Registros históricos indicam que práticas de seguro já eram adotadas por comerciantes marítimos da Mesopotâmia e da Fenícia, que enfrentavam riscos constantes de roubos e acidentes durante suas rotas. Embora os critérios exatos para o cálculo desses seguros não sejam conhecidos, é provável que tenham se baseado nas probabilidades de incidentes ocorrerem. Por exemplo, em trechos marítimos com altos índices de acidentes, é natural que as taxas cobradas fossem superiores à média estipulada (SILVA, s/d). Nesta mesma perspectiva, segundo Viali (2008), é provável que as tentativas de quantificação dos riscos associados a naufrágios, acidentes, mortes, etc. foram os fatores pioneiros para o início da Teoria das Probabilidades.
A Teoria da Probabilidade começou a se consolidar como um ramo da Matemática por volta do século XV, tendo suas raízes fortemente ligadas aos jogos e apostas. Há indícios históricos do uso de objetos semelhantes a dados já em 1200 a.C., como fragmentos de ossos talhados com faces numeradas. No Egito, por volta de 3500 a.C., já se praticavam jogos com ossinhos.
Durante os séculos XV e XVI, matemáticos italianos foram os primeiros a explorar cálculos ligados à probabilidade. Eles foram além da simples contagem de possibilidades, aplicando esses conceitos à análise de frequências e resultados em jogos de azar. No entanto, nessa fase inicial, os estudos não avançaram para formulações teóricas ou teoremas; os italianos se concentraram principalmente na resolução de problemas práticos.
O frei Luca Pacioli (1445 – 1517), posteriormente mudou seu nome para Luca di Borgo após entrar na ordem dos franciscanos, por mais que não tenha publicado nada de inédito é reconhecido por uma obra de tamanha grandiosidade na época. O trabalho que o colocou na história da probabilidade foi denominado de Summa de arithmetica, geometria, proportioni e proportionalità ou simplesmente Summa e foi publicada em Veneza no ano de 1494. Pacioli dedicou-se ao estudo do problema dos pontos (divisão da aposta), ainda que sua solução estivesse incorreta. Embora sua abordagem não tenha sido original, sua obra teve grande relevância devido à influência exercida por seu livro ao longo do tempo. O problema dos pontos por ele analisado é semelhante àquele que, mais tarde, seria resolvido por Pascal e Fermat, sendo este considerado o marco inicial da Teoria da Probabilidade.
Girolamo Cardano (1501 – 1576) é um dos nomes mais importantes no desenvolvimento de estudos sobre probabilidade. Ele iniciou a pesquisa das probabilidades associando-as ao arremesso de dados (ROQUE, 2012). Em suas pesquisas, concluíram que na ordenação de 2 dados deve ser obtido 36 pares ordenados de possíveis resultados e não somente 21 (não ordenados).
Com um histórico de forte envolvimento com jogos de azar, Cardano investiu grande parte de sua vida no estudo dessas práticas. Em sua autobiografia, relata ter jogado xadrez por mais de quatro décadas e se dedicado ao jogo de dados por cerca de vinte e cinco anos. Ao participar frequentemente de apostas com dinheiro, percebeu que, para aumentar suas chances de vitória e obter ganhos, seria essencial desenvolver estratégias eficazes. Com isso, ele dedicou boa parte de seu tempo desenvolvendo técnicas para obter esses resultados. Entre suas contribuições à área da probabilidade, destaca-se a obra Liber de Ludo Aleae, voltada ao universo dos jogos de azar. Apesar de seu conteúdo enxuto, o livro funciona como um guia prático para jogadores (GIANELLA, 2006).
A obra Liber de Ludo Aleae apresenta uma análise ampla sobre os jogos, propondo uma classificação baseada em suas principais características. Cardano distingue dois grupos: o primeiro reúne jogos de azar que envolvem força, habilidade e sorte; o segundo inclui jogos puramente aleatórios, como os de cartas, dados e gamão. Embora seja essencialmente um manual sobre jogos de azar, o autor ressalta que, em certas modalidades, a destreza do jogador pode influenciar os resultados, especialmente quando há elementos ocultos, como no caso das cartas. Cardano também faz uma abordagem estatística da probabilidade, podendo inclusive ter sido o primeiro a fazer isso.
Na parte técnica do livro, Cardano discutiu equiprobabilidade, esperança (o montante correto da aposta a ser feita por um jogador que tem p de ganhar a importância s), estabeleceu a lei Pn=Pn, que dá a probabilidade de que um evento de probabilidade P ocorra, independentemente, n vezes sucessivas, achou tábuas de probabilidades para dados e usou a chamada lei dos grandes números (de modo rudimentar) – questão em que foi o pioneiro (PAIVA, 1995, p. 75).
Outro matemático importante que se dedicou bastante ao estudo das probabilidades foi Niccolo Fontana de Brescia, conhecido como Tartaglia (1500 – 1557). Seu nome está ligado ao triângulo numérico que, mais tarde, ficou famoso como Triângulo de Pascal (GIANELLA, 2006). Além disso, Tartaglia escreveu um tratado completo sobre números e medidas, que foi publicado pela primeira vez em 1543.
Já partindo para os estudiosos franceses, Blaise Pascal (1623 – 1662) trocou cartas com Pierre de Fermat (1601 – 1665) sobre jogo de dados e o problema dos pontos. Juntos conseguiram solucionar o problema e averiguaram diversas outras situações de jogos de azar, de Cardano e Pacioli, contribuindo para o avanço dos estudos probabilísticos. Coutinho (2007, p. 60) faz uma observação de suma importância sobre as cartas trocadas entre Pascal e Fermat:
Observamos aqui os primeiros indícios de uma dualidade da noção de probabilidade, dualidade essa que é devida ao conflito entre a apreensão perceptiva das chances de realização de um evento (grau de credibilidade) e a relação entre resultados favoráveis e possíveis.
Segundo Coutinho (2007, p. 60), Christiaan Huygens (1629–1695) identificou nas trocas de cartas entre Fermat e Pascal um ponto de partida para suas próprias contribuições à teoria das probabilidades, especialmente ao desenvolver o conceito de ‘direito de esperar’, também conhecido como ‘valor da chance’. Em 1657, Huygens publicou a obra De Ratiociniis in Ludo Aleae (O Raciocínio nos Jogos de Azar). Anos depois, Jacob Bernoulli (1654–1705) aprofundou esse campo ao lançar, em 1713, a obra Ars Conjectandi (A Arte de Conjecturar), onde introduziu de forma mais sistemática a definição clássica da probabilidade, além de explorar detalhadamente os conceitos de permutação e combinação.
Após um século, Pierre Simon Laplace (1749 – 1827) consolidou a definição clássica de probabilidade apresentada por Bernoulli, onde afirma que “A probabilidade de um evento é igual à razão entre o número de casos favoráveis e o número de casos possíveis” (Coutinho 2007, p. 61).
Segundo Viali (2008, p. 151), “Até Laplace a probabilidade estava essencialmente restrita ao cálculo em jogos de azar. Foi com Laplace que o campo de aplicação da teoria se expandiu significativamente, abrangendo áreas como a teoria dos erros, a matemática atuarial e a mecânica estatística”. Vialli (2008) ressalta que após a contribuição de Laplace e os valorosos avanços no estudo da probabilidade outros matemáticos também se destacaram: Johann Friedrich Gauss (1777- 1855), Andrei Andreyevich Markov (1856-1922), Siméon Denis Poisson (1781-1840), Henri Léon Lebesgue (1875-1941), Jean Le Rond d’Alembert (1717-1783), dentre outros.
Lógica proposicional
A lógica proposicional, também conhecida como lógica sentencial, é uma parte da lógica formal responsável por estudar como as proposições se relacionam e como podemos estruturar argumentos dedutivos. Assim, usando conectivos como negação (não), conjunção (e), disjunção (ou), condicional (se… então) e bicondicional (se e somente se), ela nos ajuda a entender o que torna um raciocínio válido.
Segundo Hegenberg (1994, p. 18), “Aristóteles foi o primeiro a sistematizar a lógica como disciplina, elaborando um corpo teórico voltado à análise dos argumentos válidos, o que lhe confere um papel fundador no desenvolvimento da lógica ocidental”. Essa referência histórica é importante porque mostra o impacto duradouro das ideias de Aristóteles, mesmo na lógica proposicional moderna. A lógica proposicional tem aplicações diretas na matemática e na ciência da computação, essas são áreas nas quais a formalização de linguagens, algoritmos e sistemas de inferência são indispensáveis. Como destacam Copi e Cohen (2007, p. 23), “a lógica é uma ferramenta essencial para qualquer investigação racional, pois fornece os critérios para distinguir raciocínios válidos dos inválidos”.
Proposições e Conectivos Lógicos
Na lógica proposicional, as proposições são sentenças declarativas que podem ser classificadas como verdadeiras ou falsas e nunca poderá ter uma terceira opção. Essa propriedade é conhecida como o princípio do terceiro excluído. Uma proposição simples, como “O céu é azul”, expressa uma única ideia. Já uma proposição composta une duas ou mais proposições simples por meio de conectivos lógicos. Cada proposição é representada por uma letra minúscula, a qual normalmente é p, q, r, s e assim por diante.
Entre os conectivos mais comuns, estão:

De acordo com Machado e Garcia (2012), ao estudar sistematicamente os conectivos, é possível desenvolver sistemas formais que representem, de forma computacional, o raciocínio humano. Esses estudos servem como base essencial para áreas como a lógica de programação.
Tabelas-Verdade e Equivalências Lógicas
A tabela-verdade é um recurso fundamental para avaliar a validade de proposições compostas, também conhecidas como sentenças moleculares na lógica proposicional. Ela funciona como uma matriz que organiza todas as combinações de valores de verdade das proposições envolvidas, e em seguida mostrando claramente o resultado final da fórmula composta. Então a tabela verdade é usada para analisar a validade dos argumentos ou seja se é verdadeiro (V) ou falso (F) certa molécula.

p é o termo antecedente e p será o consequente.
Logo a mesma só será falsa na situação em que p seja verdadeira e q seja falsa. A tabela verdade torna esse processo mais claro e estruturado, ajudando a classificar as proposições em três grupos distintos: as tautológicas, que sempre serão verdadeiras; as contraditórias, que são sempre falsas; e as contingentes, cujo o valor de verdade depende diretamente das proposições que as compõem.
Como afirmam Lima (2013) e Copi e Cohen (2007), compreender a estrutura formal dos argumentos permite não apenas analisar deduções, mas também busca simplificar e representar simbolicamente o que é essencial para o desenvolvimento de algoritmos e linguagens de programação.
A lógica proposicional é uma das formas mais simples, porém extremamente eficazes, de raciocínio formal, originada no pensamento aristotélico, ela evoluiu ao longo do tempo e tornou-se uma ferramenta essencial em diversas áreas do conhecimento. Sua força está na clareza, precisão e na habilidade de estruturar o raciocínio de maneira lógica. O estudo dessa lógica não só aprimora a capacidade de argumentação e o pensamento crítico, mas também sustenta avanços tecnológicos em campos como a computação, a matemática e a engenharia.
Aplicando a Lógica em Problemas de Probabilidade
Depois de termos visto uma breve história da probabilidade e alguns conceitos de lógica proposicional, vejamos agora como podemos aplicar a lógica na resolução de problemas de probabilidade. Para isso, selecionamos alguns problemas de forma a colocar em prática essa técnica, evidenciando o passo a passo para que seja possível repeti-los.
Problema 1.
Em uma urna há 5 bolas vermelhas, 3 bolas azuis e 2 bolas verdes. Uma bola é retirada ao acaso. Qual é a probabilidade de ela não ser azul?
1. Definição das proposições
A partir das informações que o enunciado nos forneceu, definamos as proposições:
p: 5 bolas vermelhas de 10.
q: 3 bolas azuis de 10.
r: 2 bolas verdes de 10.
Nesse caso, as proposições foram feitas como probabilidades de sair bolas de cada cor. Assim sendo, cada proposição nada mais é do que uma probabilidade.
Por fim, é-nos perguntado qual é a probabilidade de sair uma bola que não é da cor azul. Dessa forma, teremos que criar as expressões lógicas.
Construção da sentença molecular
Utilizando as proposições definidas, representamos o problema com sentenças moleculares:
Sentença molecular do problema 1.
(p v s)
A sentença molecular p v s pode ser lida como p ou s. Logo, a conjunção nada mais é do que a soma das probabilidades de p e de s, sendo, então, excluídas as probabilidades das bolas azuis.
Em notação matemática teríamos:
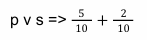
Tendo como resultado:

Problema 2.
Agora vejamos a probabilidade de ser tirada uma bola azul, sabendo-se que uma bola verde já foi retirada.
1. Definição das proposições
Seja o conjunto original de bolas na urna composto por:
- 5 bolas vermelhas
- 3 bolas azuis
- 2 bolas verdes
Total: 10 bolas
Suponhamos agora que uma bola verde foi retirada. Restam:
- 5 bolas vermelhas
- 3 bolas azuis
- 1 bola verde
Total: 9 bolas
Com base nisso, definimos as seguintes proposições simples, agora sob o novo espaço amostral (após a retirada da bola verde):
p: “A próxima bola é vermelha”
q: “A próxima bola é azul”
r: “A próxima bola é verde”
Cada proposição representa logicamente a escolha de uma bola de determinada cor.
Assim, temos as seguintes distribuições probabilísticas associadas a cada proposição, que também podem ser interpretadas como sua frequência relativa no novo universo:
p: 5 ocorrências de 9 possíveis
q: 3 ocorrências de 9 possíveis
r: 1 ocorrência de 9 possíveis
2. Construção da sentença molecular
Sabendo que uma bola verde foi retirada inicialmente, tomamos como verdadeiro o evento “uma bola verde foi retirada anteriormente”. Essa condição pode ser representada por uma proposição v.
A pergunta é: qual é a chance de se tirar uma bola azul, dado que v é verdadeiro?
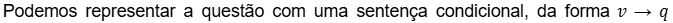
Essa sentença pode ser lida como:
“Se uma bola verde foi retirada, então a próxima bola será azul.”
No entanto, para fins de interpretação probabilística sob a lógica proposicional, nos interessa considerar a ocorrência de q sob a hipótese de v. Como v é verdadeira, a atenção volta-se para as ocorrências em que q também é verdadeira, dentro do novo espaço amostral.
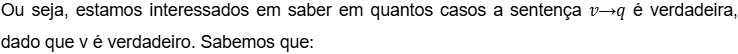
O número total de possibilidades (após a retirada de uma verde) é 9; Em 3 dessas possibilidades, a próxima bola é azul (q verdadeira).
Logo, dentro do contexto onde v é verdadeiro, há 3 situações em que q também é verdadeiro.

3. Conclusão lógica

Problema 3.
Qual é a probabilidade de não sair uma bola vermelha, sabendo-se que uma bola azul foi retirada?
1. Situação inicial
Temos uma urna com:
- 5 bolas vermelhas
- 3 bolas azuis
- 2 bolas verdes
Total: 10 bolas
Agora, uma bola azul é retirada. Com isso, o novo conjunto de bolas é:
- 5 bolas vermelhas
- 2 bolas azuis
- 2 bolas verdes
Total: 9 bolas
2. Definição das proposições
Com base nesse novo cenário (após retirada da azul), definimos as seguintes proposições:
p: “A próxima bola é vermelha”
q: “A próxima bola é azul”
r: “A próxima bola é verde”
a: “Uma bola azul foi retirada”
Deseja-se saber a probabilidade de não sair uma bola vermelha, sob a condição de que a é verdadeira.

3. Construção da sentença molecular
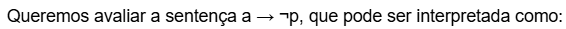
“Se uma bola azul foi retirada, então a próxima bola não é vermelha.”

Vamos verificar isso no novo espaço amostral:
Total de bolas: 9

4. Conclusão lógica

Conclusão
A análise da história da probabilidade, aliada à aplicação da lógica proposicional na resolução de problemas probabilísticos, evidencia uma interface conceitual significativa entre esses dois domínios. A Teoria da Probabilidade, desenvolvida a partir do estudo de jogos de azar e da necessidade de quantificação de riscos, fornece ferramentas essenciais para a modelagem de situações incertas.
Por sua vez, a Lógica Proposicional, fundamentada na estrutura formal de proposições e conectivos, constitui um mecanismo eficaz para a formalização do raciocínio sobre eventos, possibilitando a representação e análise das relações lógicas entre eles. A utilização da lógica na definição de eventos e na formulação de sentenças compostas permite uma abordagem sistemática para o cálculo de probabilidades condicionais e a análise de eventos compostos. Essa integração não substitui os métodos tradicionais da probabilidade, mas os complementa, ao oferecer uma estrutura formal que traduz conceitos probabilísticos em termos lógicos, favorecendo maior rigor e clareza na resolução de problemas.
Conclui-se, portanto, que a incorporação da lógica proposicional ao estudo da probabilidade não apenas enriquece a análise conceitual, como também amplia as possibilidades metodológicas no tratamento de fenômenos aleatórios, ao oferecer um arcabouço lógico para a interpretação e resolução de questões probabilísticas.
Referências
COPI, Irving M.; COHEN, Carl. Introdução à lógica. 12. ed. São Paulo: Pearson Prentice Hall, 2007.
COUTINHO, C. Q. S. Conceitos probabilísticos: quais contextos a história nos aponta? Revemat, Florianópolis, SC, v. 2, n. 1, p. 50-67, 2007. Disponível em: https://periodicos.ufsc.br/index.php/revemat/article/view/12991/12092. Acesso em: 26 abr. 2025.
DAVID, F. N. Games, Gods and Gambling: the origins and history of probability and statistical ideas from the earliest times to the Newtonian era. New York: Hafner Publishing Company, 1962.
GIANELLA, Renato. Teoria das Probabilidades: Aleae Geometria Principia Mathematica (o futuro administrando o presente). São Paulo: Edição Mandacaru Letra e Arte, 2006.
HAUBRICHS, Cleber; AMADEO, Marcello. História da Matemática nas Coleções do PNLD 2018: um estudo preliminar. Hipátia: Revista de Educação Matemática, v. 6, n. 2, 2021. Disponível em: https://ojs.ifsp.edu.br/hipatia/article/view/1851. Acesso em: 26 abr. 2025.
HEGENBERG, Leônidas. Lógica. 3. ed. São Paulo: EPU, 1994.
LIMA, Roberto R. Lógica matemática. São Paulo: Saraiva, 2013.
MACHADO, João R.; GARCIA, Maria A. Fundamentos de lógica computacional. Rio de Janeiro: LTC, 2012.
PAIVA, Manoel. Matemática. Vol. 2. São Paulo: Editora Moderna, 1995. Probabilidades no Ensino Médio.
ROQUE, Tatiana. História da Matemática: uma visão crítica, desfazendo mitos e lendas. Rio de Janeiro: Zahar, 2012.
RUSSELL, Stuart; NORVIG, Peter. Inteligência artificial. 3. ed. Rio de Janeiro: Elsevier, 2013.
SILVA, M. N. P. da. Matemática e o surgimento dos seguros. s/d. Disponível em: https://mundoeducacao.uol.com.br/matematica/matematica-surgimento-dos-seguros .htm. Acesso em: 26 abr. 2025.
VIALI, L. Algumas considerações sobre a origem da Teoria das Probabilidades. Revista Brasileira de História da Matemática, n. 16, v. 8, p. 143-153, out. 2008.
