REGISTRO DOI: 10.69849/revistaft/ma10202212291733
Thiago Braga Nobre
RESUMO
Este artigo propõe uma nova abordagem para entender a organização dos números. O estudo começa com uma análise visual utilizando o conceito de blocos para decompor um produto até identificar seus fatores próximos, ou confirmar que é um número primo. Além disso, a metodologia visual será aplicada também em cálculos, proporcionando uma compreensão mais intuitiva e prática da estrutura dos números primos.
Palavras-chave: Números primos; Decomposição de produto.
1 INTRODUÇÃO
Os números primos são frequentemente comparados aos átomos na matemática, pois são os blocos fundamentais de construção dos números inteiros. Seguindo essa analogia, propomos que, para identificar os fatores próximos de um produto ou determinar se um número é primo, é útil visualizar a decomposição dos produtos como blocos unitários. Através da manipulação desses blocos, podemos chegar a conclusões gráficas e intuitivas sobre a formação dos números. Neste trabalho, demonstramos que é possível um padrão simples de organização, facilitando a compreensão e a análise dos números primos e compostos.
2 REGRA DE ORGANIZAÇÃO DOS BLOCOS
A regra é simples: Para validar qualquer número que seja maior que 2, e seja ímpar, vamos organizar inicialmente o valor em duas linhas, cada uma com o valor (n−1)/2, e uma terceira linha com o valor 1.
Ajustamos as colunas deslocando os valores até que todas as linhas tenham o mesmo número de colunas. Se a primeira coluna estiver preenchida, então o número é primo. Se as colunas excederem o número disponível, ajustamos com o valor anterior e movemos o restante para a próxima linha até que todas as linhas estejam equilibradas.
Um grande detalhe nesse padrão, é que ao chegar na segunda coluna (exceto os números 3, 5) sem conseguir se formar em colunas iguais, já sabemos que é primo, ou seja, antes de chegar na primeira coluna, pois o que acontece é que ele retorna ao seu estado inicial, ele começa com uma organização inicial em 2 linhas e chega até uma mesma organização, porém em 2 colunas, ao invés de linhas.
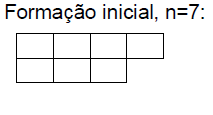
Vamos verificar que ele chega na mesma organização, porém em colunas, aqui já identificamos que ele é um número primo, antes mesmo de retornar a primeira coluna.
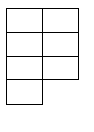
Exceto nos casos de 3 e 5, que não necessita de movimentação para identificar a primalidade.
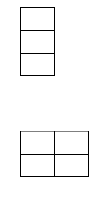
3 DECOMPOSIÇÃO DE UM PRODUTO SOBRE A ABORDAGEM DE BLOCOS
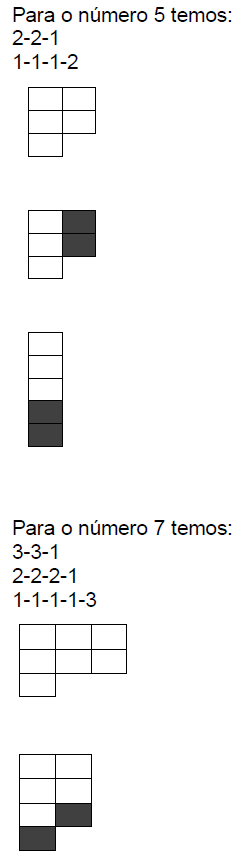
Imagine que temos um produto, um número ímpar inteiro positivo maior que 1. Para este estudo, começamos com dois blocos, um em cima do outro. Todos os números pares, por serem formados com dois blocos, serão compostos e não primos. Já os números ímpares, em sua formação inicial, terão dois blocos empilhados e um bloco adicional ao lado direito, formando duas linhas. Vamos ilustrar isso com um exemplo:
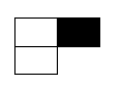
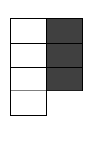
Para validar, deslocamos o bloco destacado abaixo dos outros 2 blocos. Isso cria 3 linhas e 1 coluna, o que indica que o número é primo, pois não conseguimos formar blocos adicionais e não encontramos fatores. Porém se observarmos com atenção na formação que ele se encontrava já poderíamos identificar o padrão de um primo.

4 NÚMERO COMPOSTO
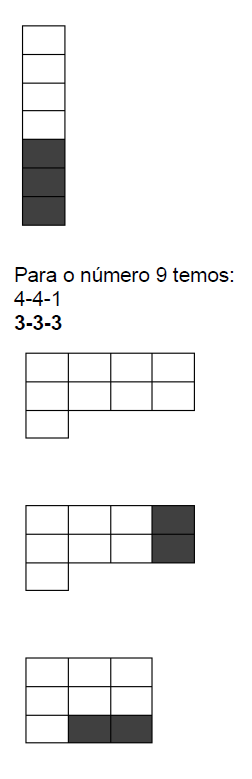
Já o comportamento de um número composto como o 9 é diferente.
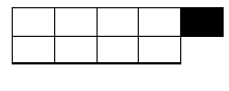
Seguindo o mesmo princípio, iremos mover a última coluna para uma nova linha.
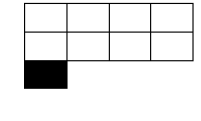
Após uma primeira formação, podemos perceber que na terceira linha existe uma lacuna, ou seja, as colunas de todas as linhas não estão iguais, precisam ser ajustadas. Então vamos mover as últimas colunas para a última linha.
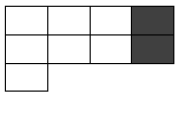
E então perceberemos que neste caso todas as colunas entre as linhas são da mesma quantidade.
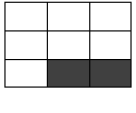
5 NÚMERO PRIMO
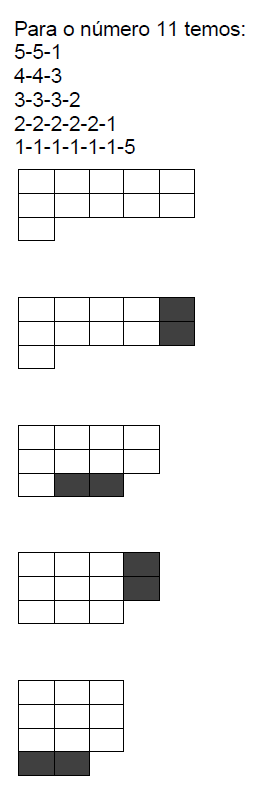
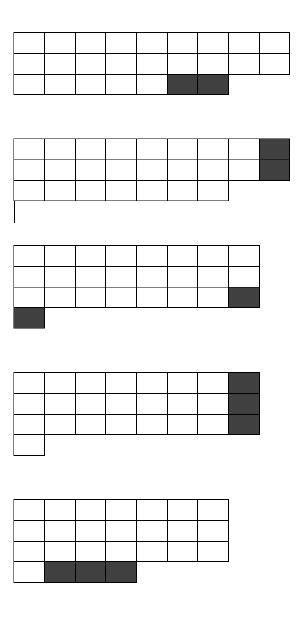
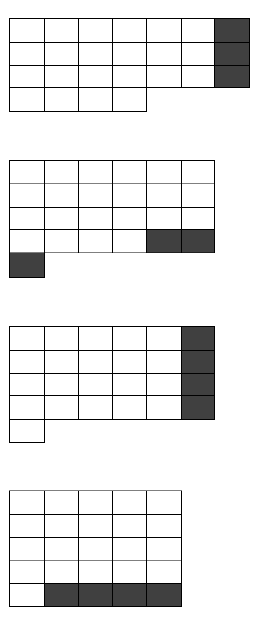
Caso ao mover os blocos a quantidade transportada seja maior que a quantidade da coluna anterior, o restante será transferido para a próxima linha.
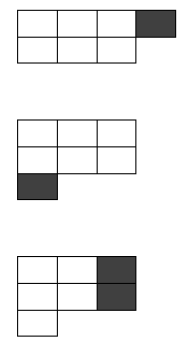
Pode parar aqui
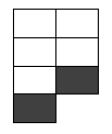
Ou prosseguir até a primeira coluna
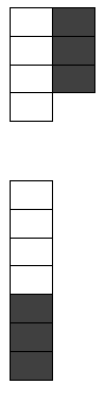
E finalizamos com a comprovação de que o número 11 é primo sendo formado em uma única coluna. Porém, se percebermos que antes de retornar à primeira coluna, ele retornou a sua formação inicial passando de colunas para linhas.
6 CÁLCULO DE DECOMPOSIÇÃO DO PRODUTO
Para representarmos em cálculos as representações gráficas, sempre iniciaremos em 3 colunas sendo a primeira e a segunda (n -1 ) / 2 e a terceira o valor 1, então subtrai-se 1 da primeira e segunda coluna e a terceira coluna recebe os valores subtraídos. Exemplificando o número 3
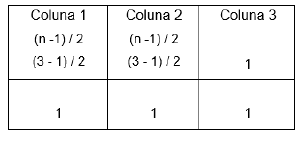
No caso dos números primos 2 e 3, nem é necessário transpor os valores, pois já iniciam com o valor 1 nas colunas 1 e 2, ou seja, já estão na primeira coluna, logo, são primos.
Para o número 2 temos:
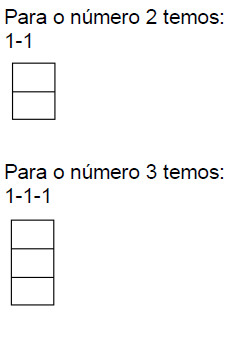


7 CONSIDERAÇÕES FINAIS
A representação gráfica e numérica apresenta uma nova abordagem de como os números se organizam, como podemos identificar se um número é primo ou composto, sem precisar dividir pelos antecessores numéricos por tentativas, com isso conseguimos achar o menor caminho dos fatores de um produto, ou afirmar que um número é primo.
Esse trabalho pode ser aperfeiçoado com novos pontos não vislumbrados nesta pesquisa, e que seja de grande valia para estudiosos e quiçá abra novos horizontes e perspectivas em relação a esse fascinante mundo. Espero que contribua para a didática dentro das salas de aula e que tragam novas descobertas no campo da ciência.
