MODELING SHOPPING APP IN SMALL ENTERPRISES DEVELOPED IN MIT APP INVENTOR 2, FOCUSING ON MATHEMATICS TEACHING IN BASIC EDUCATION
REGISTRO DOI: 10.5281/zenodo.10666572
Alex Dias de Freitas1
Anderson Amaro Vieira2
Fábio José da Costa Alves3
RESUMO
Este artigo é resultado da elaboração de um programa criado na plataforma Mit App Inventor 2, para realizar a transposição didática no ensino de Matemática em situações reais do cotidiano. Está atividade foi parte constituinte da avaliação da disciplina de Tecnologias de Informática no Ensino de Matemática, do curso de Mestrado Profissional em Ensino de Matemática, ofertado pelo Programa de Pós-Graduação (Stricto Sensu) em Ensino de Matemática, da Universidade do Estado do Pará (UEPA). Convém destacar que o objeto matemático principal abordado é destinado no material é a Matemática Financeira e o secundário e com a mesma relevância do primeiro, será tratado a Adição e Multiplicação de Números Racionais, que faz parte do cotidiano da população, e no caso de Parauapebas – PA, local onde foi realizado a tratativa das informações que geraram o material original é uma realidade bastante recorrente. Aqui neste artigo, reportamos o aplicativo desenvolvido e seus meios de instalação, assim como algumas sugestões de uso em sala de aula. Concluímos que a utilização do aplicativo, associado a uma metodologia de ensino eficaz, pode ser promissora e trazer resultados significativos, se aplicada adequadamente no processo de ensino.
Palavras–Chave: Ensino de Matemática. App Inventor 2. App de Compras. Matemática Financeira.
ARTICLE
This article is the result of the development of a program created on the Mit App Inventor 2 platform, to carry out the didactic transposition in the teaching of Mathematics in real everyday situations. This activity was part of the evaluation of the discipline of Information Technology in Mathematics Teaching, of the Professional Master’s Degree in Mathematics Teaching, offered by the Graduate Program (Stricto Sensu) in Mathematics Teaching, at the State University of Pará (UEPA). It should be noted that the main mathematical object approached and destined in the material is Financial Mathematics and the secondary and with the same relevance of the first, the Addition and Multiplication of Rational Numbers, which is part of the daily life of the population, and in the case of Parauapebas – PA, where the treatment of the information that generated the original material was carried out is a very recurrent reality. Here in this article, we will report the developed application and its installation means, as well as some suggestions for use in the classroom. We conclude that the use of the application, associated with an effective teaching methodology, can be promising and bring significant results, if properly applied in the teaching process.
Keywords: Mathematics Teaching. App Inventor 2. Shopping App. Financial math.
1. ENSINO DE MATEMÁTICA: DO TRADICIONAL A NOVA ERA TECNOLÓGICA
O estudo da disciplina de matemática no âmbito escolar é encarado como uma forma de se traduzir a realidade e estabelecer as diferenças e conjecturar novas possibilidades que possam variar de uma situação inicial. Assim, esta área do conhecimento deve ser vista como uma estratégia para realizar mediações entre o meio e suas transformações. Mesmo sabendo da importância da matemática tanto na aplicação do dia a dia quanto para o desenvolvimento do raciocínio e criatividade do homem, em situações pontuais, principalmente na escola, a disciplina é tratada com insatisfação por exigir do aluno uma linha de raciocínio mais complexa.
As dificuldades inicialmente impostas pela complexidade ou profundidade da discussão no processo de aprendizagem podem fazer com que o aluno desassocie a disciplina de seu cotidiano. Não é à toa que a matemática é a disciplina que mais gera medo entre os alunos, pois eles não sentem uma aproximação com a realidade que vivem. No tocante do ensino de Matemática, o professor ao problematizar as dificuldades que os alunos apresentam ao estudar os conceitos matemáticos, Stoica (2015) traz outra questão: a organização das aulas; diz ele que:
em classes tradicionais de Matemática os estudantes são ensinados pela primeira vez a teoria e, em seguida, eles são convidados a resolver alguns exercícios e problemas que têm mais ou menos soluções algorítmicas usando mais ou menos o mesmo raciocínio e que raramente são conectados com as atividades do mundo real (Stoica, 2015, p. 702).
Existe uma questão que está muito difundida na memória de longo prazo dos estudantes da equação básica que é a ideia de que a disciplina Matemática é muito difícil, o que faz com que os estudantes já apresentem aversão à disciplina mesmo que ainda não tenham passado por situações de dificuldade.
Segundo Damasceno, Oliveira e Cardoso (2018, p. 114), a disciplina de Matemática, “continua sendo considerada uma das maiores vilãs dentre as disciplinas, sendo responsável por altos índices de reprovação de alunos”. Isto porque, a grande maioria dos alunos já possui um pré-conceito sobre o estudo da disciplina.
Os documentos oficiais que norteiam o ensino de Matemática no Brasil já vêm apresentando a necessidade de uma transição do ensino tradicional para um novo modelo de ensino que faça uso das tecnologias digitais em sala de aula. Segundo os Parâmetros Curriculares Nacionais (PCN), “as técnicas, em suas diferentes formas e usos, constituem um dos principais agentes de transformação da sociedade, pelas implicações que exercem no cotidiano das pessoas” (Brasil,1997, p. 34).
Os Parâmetros Curriculares Nacionais para o Ensino Médio (PCNEM) preveem a influência do uso das Tecnologias Digitais da Informação e Comunicação (TDIC’s) no ensino da Matemática e a mudança no seu paradigma de ensino e aprendizado quando afirmam que:
o impacto da tecnologia, cujo instrumento mais relevante é hoje o computador, exigirá do ensino de Matemática um redirecionamento, sob uma perspectiva curricular, que favoreça o desenvolvimento de habilidades e procedimentos com os quais o indivíduo possa se reconhecer e se orientar nesse mundo do conhecimento em constante movimento (Brasil, 2002, p. 41).
Seguindo a mesma ideia, a Base Nacional Comum Curricular (BNCC), ao propor as dez competências gerais que materializam, no âmbito pedagógico, os direitos de aprendizagem e desenvolvimento, trata da importância do uso das TDIC’s de forma crítica e reflexiva no contexto escolar, “nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva” (Brasil, 2017, p. 9).
É importante ponderar que não é somente um recurso tecnológico que vai fazer com que um aluno aprenda determinados conceitos matemáticos, afinal a atividade deve ser organizada pelo professor no sentido de desenvolver um raciocínio em que possa criar conjecturas, abstrair suas ideias tornando-as conhecimentos formais com ajuda do computador.
De acordo com Moran (2015a, p. 16), os “métodos tradicionais, que privilegiam a transmissão de informações pelos professores, faziam sentido quando o acesso à informação era difícil”; com o advento da Internet podemos aprender “em qualquer lugar, a qualquer hora e com muitas pessoas diferentes”. Diz ele que o “ensinar e aprender acontece numa interligação simbiótica, profunda, constante entre o que chamamos mundo físico e mundo digital”.
Desse modo, “a educação formal é cada vez mais blended, misturada, híbrida, porque não acontece só no espaço físico da sala de aula, mas nos múltiplos espaços do cotidiano, que incluem os digitais”. Daí o professor precisa comunicar-se não só “face a face com os alunos, mas também digitalmente, com as tecnologias móveis, equilibrando a interação com todos e com cada um”.
Portanto, o ensino da matemática deve propiciar de modo panorâmico aos alunos não somente o conhecimento teórico específico da disciplina de Matemática, mas também despertar a curiosidade e a postura crítica, objetivando um desenvolvimento de competências e habilidades matemáticas para aplicar em sua vida cotidiana.
2. USO DA TECNOLOGIA NO ENSINO DE MATEMÁTICA
As escolas atuais, de modo análogo às do século passado, não mudaram muito. Elas continuam com o professor à frente na sala de aula e os alunos sentados organizados em fila ouvindo a explicação do conteúdo, de modo totalmente passivo. Mesmo diante dos avanços tecnológicos, as aulas continuam ocorrendo, majoritariamente, no método tradicional, ou seja, com conteúdo transmitido aos alunos de forma passiva (Bacich, L.; Tanzi Neto, A.; Trevisani, 2015).
Ainda de acordo com estes autores, verifica-se que crianças e jovens, estão cada vez mais conectadas às tecnologias digitais, como por exemplo, smartphones, tablets e notebooks, com acesso à internet. Essa geração estabelece novas relações com o conhecimento, em simbiose com essas tecnologias e que, por conseguinte, tais relações exigem transformações no modo de ensinar e aprender, de modo que se alcance uma aprendizagem significativa.
De acordo com Vidal e Miguel (2020), o século XXI é sinônimo de mudanças significativas para a sociedade, com inúmeras transformações em todas as dimensões da vida humana, podendo ser citado dentro deste contexto evolutivo a expansão das mídias digitais onde esse progresso tecnológico é notável, reconfigurando a forma de organização social e profissional, maneiras de comunicação e a relação entre os indivíduos.
No campo educacional a presença das tecnologias na sociedade por si só, já justificam sua integração no campo da educação, sendo plausível levar em consideração que a maioria dos alunos já nascem imersos ao mundo digital, e que também aprendem em ambientes externos a escola, a exemplo do meio social e cultural em que vive fora da escola (Palfrey, 2011).
Inicialmente considera-se que o desenvolvimento acelerado das TDIC’s, tem propiciado inúmeras mudanças na sociedade atual, sobretudo na forma de se comunicar e de interagir. A necessidade de automatizar processos atualmente é indispensável, principalmente quando há uma quantidade considerável de informações que precisam ser analisadas, verificadas e monitoradas.
Discute-se por docentes e pesquisadores sobre a inserção e utilização de tecnologias nos processos de ensino e de aprendizagem. Para Valente (1999), a utilização de tecnologias pode ser voltada a “[…] uma pedagogia que proporcione a formação dos alunos, possibilitando o desenvolvimento de habilidades que serão fundamentais na sociedade do conhecimento”.
É dentro do espaço escolar, de acordo com Vidal e Miguel (2020), que o ser humano se constitui nos principais aspectos de desenvolvimento e inserção social, compreendendo o mundo no qual está inserido em seus aspectos e dimensões ideológicas, políticas, sociais, epistemológicas e filosóficas, é perante a esse pressuposto que enfatiza-se ainda mais a importância de uma evolução necessária das instituições de ensino na representação social necessária para a construção e/ou continuidade de diversas culturas, contribuindo para uma educação global, que de acordo com Cabezudo, et al., (2010) tem por objetivo:
Desenvolver uma cultura de avaliação entre as pessoas envolvidas no processo de escolarização, é um desafio para a educação global. O processo de avaliação tem, obviamente, de estar em sintonia com as questões da educação global. A educação global prepara as pessoas para lidarem com contradições e estereótipos, e para desenvolverem capacidades de pensamento crítico e análise, pesquisa e abordagem de problemas comuns considerando múltiplas perspectivas (Cabezudo, et al., 2010, p. 54).
Se for concebido a tecnologia como o conjunto de conhecimentos que permite a intervenção do sujeito no mundo, utilizando de um leque de ferramentas matemáticas ou de instrumentos, tecnológicos e sociais é possível concretizar o real sentido de “saber fazer educação” utilizado de diversas fontes da experiência, obtendo contribuições das diferentes áreas do conhecimento.
Um saber fazer que, se não quiser ser mecanicista e rotineiro, deve levar em consideração as contribuições dos diferentes âmbitos científicos, constituindo-se, por sua vez, em fonte de novo conhecimento. Diante disso, torna-se necessário conceituar o termo tecnologia, (re)pensar como estão sendo inseridas no ambiente escolar e quais suas implicações no ensino de matemática. Deve-se considerar sob qual método seria mais funcional a sua utilização.
Nesse viés, as tecnologias mudaram de forma substancial e funcional como as pessoas realizam muitas atividades no seu cotidiano, como produz, como consome, interage até mesmo como exercem a sua cidadania. Agora é a vez da tecnologia mudar a forma como aprendemos e ensinamos. Se antes educamos os alunos para usar a tecnologia, hoje usamos a tecnologia para educar os alunos. Desta forma, conseguiremos avançar na superação de grandes desafios da educação brasileira. Logo, faz-se necessário a inclusão dessas tecnologias como estratégias metodológicas no viés de consolidar as aprendizagens dos alunos e ainda aumentar o interesse nas aulas, possibilitando aos mesmos serem protagonistas do seu próprio saber.
Todavia, é importante ponderar que essas tecnologias devem ser um meio e não um fim do processo de construção de conhecimento, os atores envolvidos no processo não devem utilizá-las como única ferramenta disponível.
Desse modo, é necessário que o professor esteja preparado para o uso de tecnologias (Pocinho; Gaspar, 2012), pesquisando constantemente sobre metodologias de ensino condizentes com essa nova realidade, além de aprimorar seus conhecimentos com o uso efetivo das TDIC’s em sua formação inicial e continuada.
Assim, foi pensando em uma proposta a fim de tornar as aulas de Matemática mais interessantes e dinâmicas e, principalmente, mais próximas da realidade dos alunos, acostumados com as tecnologias no seu dia a dia. Também levamos em consideração, o fato de ser necessário a introdução às operações de mercado (Matemática Financeira) desde as séries iniciais, pois desde crianças somos instigados a usar o dinheiro, desde as considerações as idas à padaria, mercadinho, supermercado e entre outros estabelecimentos.
Portanto, julgamos adequado a realização do presente trabalho, a fim de contribuir com os colegas de área, a apreciação, construção e utilização de uma ferramenta didática com potencial a contribuir com o processo de ensino de Números Racionais e Introdução à Matemática Financeira.
3. MIT APP INVENTOR, O QUE É?
O MIT App Inventor, também conhecido como App Inventor for Android originalmente criada pela Google Education, e atualmente mantida pelo Massachusetts Institute of Technology (MIT) é um ambiente de programação visual intuitivo que permite que todos – até mesmo crianças – criem aplicativos totalmente funcionais para telefones Android, iPhones e tablets Android/iOS.
O Aplicativo foi disponibilizado através de solicitação em 12 de julho de 2010, e lançado publicamente em 15 de dezembro de 2010.
O App Inventor Team foi liderado por Hal Abelson e Mark Friedman. No segundo semestre de 2011, a Google lançou o código fonte, rescindiu o seu servidor e forneceu o financiamento para a criação do MIT Center for Mobile Learning liderados pelo criador do App Inventor Hal Abelson e colegas professores do MIT, Eric Klopfer e Mitchel Resnick. A versão do MIT foi lançada em março de 2012.
Em 6 de Dezembro de 2013, MIT App Inventor 2 foi lançado, renomeando a versão original como “App Inventor Classic“. As principais diferenças são:
- O Editor de Blocos na versão original funcionou em um processo Java em separado, usando a biblioteca aberta “Blocks JAVA” para a criação de blocos visuais de linguagens de programação;
- Open Blocks é distribuído pelo Scheller Teacher Education Program (STEP) e é derivado da pesquisa de mestrado tese por Ricarose Roque. Os professores Eric Klopfer e Daniel Wendel do programa Scheller apoiaram a distribuição de BLOCKS abertas no âmbito da licença MIT.
Assim, aqueles que são novos no MIT App Inventor podem ter um primeiro aplicativo simples instalado e funcionando em menos de 30 minutos. Além disso, a ferramenta baseada em blocos, facilita a criação de aplicativos complexos e de alto impacto em um tempo significativamente menor do que os ambientes de programação tradicionais. O projeto MIT App Inventor busca democratizar o desenvolvimento de software, capacitando todas as pessoas, especialmente os jovens, a passar do consumo de tecnologia para a criação de tecnologia.
Uma pequena equipe de funcionários e alunos do MIT CSAIL, liderada pelo professor Hal Abelson, forma o núcleo de um movimento internacional de inventores. Além de liderar a divulgação educacional em torno do MIT App Inventor e realizar pesquisas sobre seus impactos, essa equipe principal mantém o ambiente de desenvolvimento de aplicativos online gratuito que atende a mais de 6 milhões de usuários registrados.
Os programas de codificação baseados em blocos inspiram o empoderamento intelectual e criativo. O MIT App Inventor vai além disso para fornecer capacitação real para que as crianças façam a diferença – uma maneira de alcançar um impacto social de valor imensurável para suas comunidades. Na verdade, os inventores de aplicativos na escola e fora dos ambientes educacionais tradicionais se uniram e fizeram exatamente isso.
Com mais de um milhão de visitantes únicos mensais de 195 países criando coletivamente quase 30 milhões de aplicativos, o MIT App Inventor está mudando a maneira como o mundo cria aplicativos e a maneira como as crianças aprendem sobre computação.
Outro fator de grande relevância, é que, por ser uma ferramenta de código aberto (open source), isto é, pode ser visualizada e acessada por qualquer pessoa, o App Inventor torna a programação e criação de aplicativos acessíveis para uma grande variedade de públicos, como: educadores, governo, empresas, organizações, pesquisadores e a sociedade como um tudo.
O MIT App Inventor é uma ferramenta de utilização online que possui tradução para português e ainda é preciso ter uma conta de e-mail do gmail (ex.: seunome@gmail.com) para acessar e por fim um celular Android para que os aplicativos desenvolvidos no site do App Inventor possam ser testados.
Desta forma, democratizar a criação e desenvolvimento de softwares e aplicativos, especialmente os jovens, para o consumo de tecnologia para a criação de novas tecnologias, especialmente ao processo de ensino, podem contribuir de modo significativo no processo de aprendizagem, assim como também contribui na motivação para o ensino de Matemática.
4. OBJETO MATEMÁTICO DO APLICATIVO
Nesta seção, iremos descrever de modo pontual, o conteúdo matemático que pode ser explorado com o referido material.
Assim, o conteúdo matemático a ser explorado com a ferramenta é:
i. Matemática Financeira: aqui iremos reportar apenas a uma breve introdução, sem aprofundamentos, pois faremos uso de valores monetários (Real=R$), apenas como grandeza ou unidade de medida.
ii. Operações com Números Racionais: aqui como trataremos de dinheiro (valores monetários) e de variação da quantidade de mercadorias ou produtos é esperado que surjam valores decimais exatos ou não-exatos a depender da quantidade definida pelo usuário.
Dessa forma, das operações pertinentes de Números Racionais, de modo mais recorrente iremos utilizar apenas a adição e a multiplicação para demonstração da variação de quantidade e preço a ser pago pelos produtos.
A Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de investimentos ou financiamentos de bens de consumo. Consiste em empregar procedimentos matemáticos para simplificar uma operação financeira. Ela tem por objetivo estudar as diversas formas de evolução do valor do dinheiro no tempo, bem como as formas de análise e comparação de alternativas para aplicação / obtenção de recursos financeiros, compras ou vendas a depender do produto ou serviço.
O Capital é o valor aplicado por um determinado produto ou serviço prestado que através de alguma operação financeira de compra, aluguel ou venda. Ele é qualquer valor expresso em moeda (dinheiro ou bens comercializáveis) disponível em determinada época.
No trabalho iremos propor apenas a utilização do Real (moeda brasileira utilizada nas operações de compra e venda). A família do real é constituída por:
Tabela 1 – Quadro com a família do Real (R$).

Logo, em todas as operações que será feito pelo aplicativo, obrigatoriamente fará uso da família do Real (R$), seja em valores inteiros ou em valores fracionários, já que tomando por base operações reais do cotidiano, as mesmas sempre ocorrem com valores não inteiros..
Segundo Manoel Paiva (2005, p. 16-17), indica-se por Q o conjunto dos números racionais e por Q* o conjunto dos números racionais não-nulos:
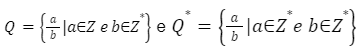
Portanto, número racional é todo aquele valor que pode ser representado como a razão de dois números inteiros, com o segundo não-nulo. Assim, concluímos que todo número inteiro também é racional, pois pode ser considerado como uma razão de denominador 1.
Vale destacar que a seguinte relação de inclusão é verdadeira:
N⊂Z⊂Q .
A seguir, teremos uma representação gráfica (mostrada via Diagrama de Venn) da relação de inclusão que indicamos acima, a fim de mostrar a ordem de indicação dessa inclusão, a fim de proporcionar uma melhor visualização:
Figura 1 – Esquema de inclusão do Conjunto dos Naturais (N), Inteiros (Z) e Racionais (Q).
Fonte: Manoel Paiva (2005).
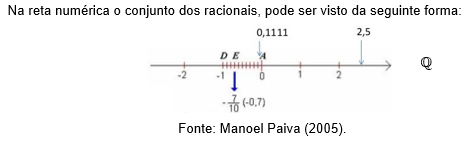
Logo, o conjunto dos números racionais é formado por todos os números naturais, inteiros, as frações e seus resultados com representação decimal exata e finita ou não-exata (dízimas periódicas simples ou compostas).
Quando utilizamos o conjunto dos números racionais, as seguintes propriedades são válidas:
P.1 → A soma de dois números racionais quaisquer é um número racional.
P.2 → A diferença de dois números racionais quaisquer é um número racional.
P.3 → O produto de dois números racionais quaisquer é um número racional.
P.4 → O quociente de dois números racionais quaisquer, sendo o divisor diferente de zero, é um número racional.
No aplicativo que é proposto neste trabalho, faremos uso das propriedades acima descritas, pois os valores das mercadorias, são dados em reais e são todos valores racionais exatos, cujas operações podem gerar novos números racionais, a partir da escolha do consumidor final.
5. DOWNLOAD DO APLICATIVO E TREINO DAS FUNÇÕES NO SMARTPHONE
Após a conclusão do aplicativo, foi gerado a versão para funcionar no celular Android, que poderá ser instalada através do apk do programa ou de um QR Code. Assim, para instalar no smartphone o aplicativo, basta escanear o “QR Code” gerado que indicamos abaixo, com o leitor do seu celular. Caso você não possua leitor de QR Code no seu aparelho é possível baixar um leitor na sua loja de aplicativos “Play Store”. Após baixar o leitor, caso você não possua no seu smartphone, escaneie o “QR Code” abaixo, para instalação do aplicativo no seu celular:
Figura 2 – Print do QR Code para download do aplicativo.
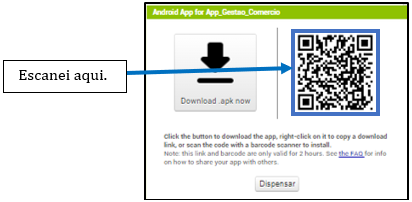
Fonte: Autores, 2023
Essa deverá ser a apresentação da tela do seu smartphone após ler o código acima:
Figura 3 – Imagem após leitura do QR Code.
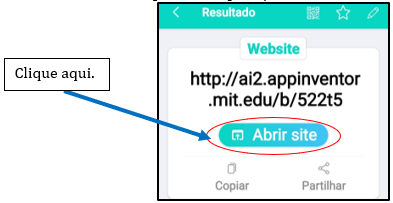
Fonte: Autores, 2023.
Clique em abrir site. Após essa ação, será exibido na sua tela, a pergunta se deseja “fazer o download do arquivo?” A ação a ser seguida é “fazer o download”. Se por equívoco você baixar ou escanear mais de uma vez, será feita a pergunta abaixo.
Figura 4 – Tela de download do aplicativo da web para o smartphone.
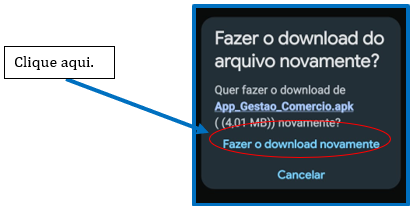
Fonte: Autor, 2023.
Depois vá na sua pasta de download na memória do seu smartphone e clique no arquivo baixado. Em seguida, aparece a tela abaixo, a qual deve ser clicado em instalar aplicativo:
Figura 5 – Tela de instalação do aplicativo.
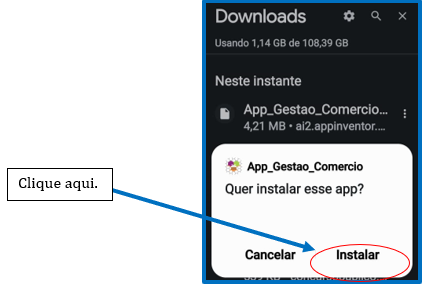
Fonte: Autor, 2023.
Após o sistema, concluir a instalação do aplicativo, que deverá ocorrer de modo rápido, devido o aplicativo possuir pouco mais de 4 megabytes (MB) de memória é esperado que a pergunta apresentada na Figura 4, mude para “App Instalado”. Abaixo terá duas opções, uma com o nome “Concluído” e a outra “Abrir”.
Aqui faremos uma observação muito importante, que depois de instalado o aplicativo no seu smartphone não existe atualização automática. Logo, se for necessário realizar alguma mudança no projeto original ou algum ajuste é necessário a realização de todos os passos elencados até este momento, pois no momento que for gerado um novo “QR Code”, o sistema entenderá se tratar de um novo programa.
Portanto, se faz necessário a exclusão da versão anteriormente instalada, ou mude o nome de exibição da versão para facilitar a sua performance de qual é a versão mais recente. Após essas considerações, iremos clicar em “Abrir” para acessar o aplicativo.
Figura 6 – Aplicativo instalado no smartphone.
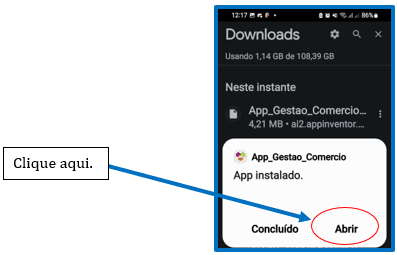
Fonte: Autor, 2023.
Se porventura você clicar em “Concluído”, basta procurar o ícone do aplicativo na sua tela de aplicativos instalados.
Figura 7 – Print da Tela do Smartphone com destaque do app criado.
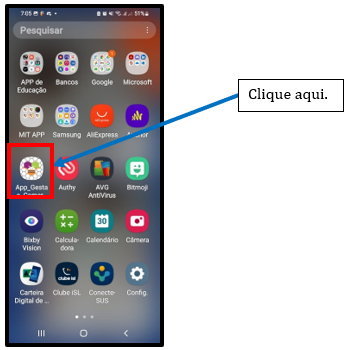
Fonte: Autor, 2023.
Utilizando uma ação ou a outra, iremos acessar o aplicativo. Abaixo (Tabela 2), temos alguns prints da tela do smartphone mostrando as principais telas, o que elas fazem, e aqui iremos organizá-las em uma tabela, com uma pequena descrição.
Tabela 2 – Funcionalidades do Aplicativo.


Fonte: Autor, 2023.
As informações contidas na Tabela 2, são as funcionalidades que o aplicativo criado possui e estão à disposição para serem utilizadas pelo usuário. Após o aplicativo instalado e revisado todas as suas funcionalidades, precisamos efetuar testes de situações que poderiam acontecer no cotidiano de uma família, de uma comunidade ou de uma pessoa a fim de realizar uma compra rápida e em um determinado local ou estabelecimento. Tomando por base o avanço da tecnologia e das redes sociais presentes no cotidiano das pessoas, esse indivíduo poderia simplesmente solicitar um orçamento prévio de uma compra para saber se o mesmo teria dinheiro suficiente para comprar aqueles produtos ou não.
Assim, na sessão do treino, iremos considerar uma situação aplicada que faz uso do aplicativo desenvolvido com a finalidade de ensino de Números Racionais e Introdução à Matemática Financeira de uma forma bem espontânea e sem o rigor dos cálculos e operações matemáticas necessárias, mas, que apresentaram os resultados esperados. Passemos agora à análise da situação que pode ser resolvida com o uso do aplicativo desenvolvido, sem a necessidade de papel, lápis, borracha ou de contas.
- Situação 1
José precisa de tomate, cebola e batata para pôr no seu ensopado especial de domingo. Porém ao procurar por esses três ingredientes em sua geladeira, notou que todos haviam acabado. Desta forma, ele foi a Frutaria da Irmã Nega, que vende esses e outros produtos, com o objetivo de comprar 3,5 kg de tomate, 2,75 kg de cebola e 5,3 kg de batata. Com base nessa compra, quanto custará essa compra para José?
Sol.: Para resolver esse problema iremos fazer uso do aplicativo desenvolvido e que já está instalado no smartphone dos alunos e do professor.
Inicialmente, com o aplicativo aberto e atualizado, vamos selecionar os produtos necessários e quantidade desejada um por vez. Assim, seguiremos os passos descritos na Tabela 3.
Tabela 3 – Sequência de ações utilizando o aplicativo.


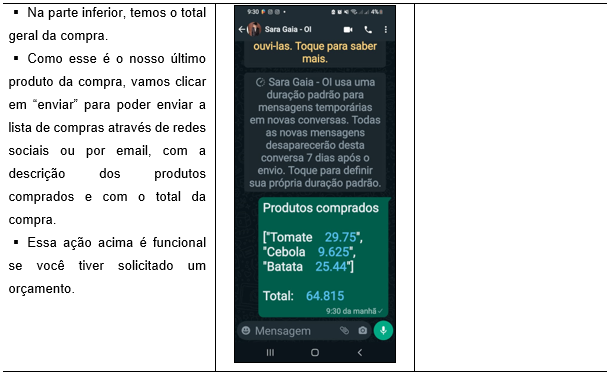
Fonte: Autores, 2023.
Resposta Final: Com base nas observações realizadas na tela do aplicativo ao final das compras, concluímos que as mesmas custaram a José um total de R$64,80.
Sol. 2: Vamos resolver a Situação 1, pelo método usual de sala de aula.
Inicialmente temos os produtos a serem comprados, a quantidade e o valor corresponde a cada quilograma de produto. Dessa forma, vamos organizar essas informações na Tabela 4.
Tabela 4 – Dados da Situação 1.
PRODUTO QUANTIDADE PREÇO POR KG OPERAÇÃO RESULTADO Tomate 3,5 kg R$ 8,50 3,50 kg . R$ 8,50 R$ 29,75 Cebola 2,75 kg R$ 3,50 2,75 kg . R$ 3,50 R$ 9,625 Batata 5,30 kg R$ 4,80 5,30 kg . R$ 4,80 R$ 25,44 Total da Compra: R$ 64,815
Fonte: Autores, 2023.
Resposta Final: Com base nas informações observadas na Tabela 13, as compras custaram a José um total de R$64,80.
Após a conclusão das duas soluções, observamos que o aplicativo fez as contas certinhas como deveriam ser e do ponto de vista de ensino é bastante funcional porque permite a utilização de um aplicativo no processo de ensino que favorece o envolvimento dos alunos e ao mesmo tempo, pode ser uma ferramenta motivante para que o aluno realize novos problemas e testes já que a mesma pode-se configurar como uma novidade.
CONCLUSÕES E APONTAMENTOS
Com base nos objetivos da proposta e ainda considerando os resultados obtidos na construção e testes do aplicativo, consideramos que o uso do MIT App Inventor 2 é versátil e de utilização fácil, pois utiliza uma base de programação por blocos deixando mais intuitivo para construção de aplicativos e também evita aquela linguagem de programação complexa e que por conta das suas especificidades acaba sendo abandonada pelo usuário que é iniciante e que não pretende seguir carreira nessa área.
O objetivo deste trabalho é auxiliar os alunos a entrarem neste novo mundo tecnológico e despertar a curiosidade dos mesmos sobre esta tecnologia que cria aplicativos onde eles deixam de ser meros repetidores de informações e passam a criar novas formas de aprender matemática utilizando apenas o aplicativo , bem como o passo a passo que é guiado neste livro.
Já sobre a construção do aplicativo “Modelando App de Compras em Pequenos Empreendimentos”, voltado para o ensino de Números Racionais e Introdução à Matemática Financeira, voltado para o público do Ensino Fundamental, concluímos que o mesmo é bastante promissor e funcional, uma vez que permite a construção de uma ferramenta que permite a conjectura de várias situações hipotéticas de produtos e quantidades, pois podemos notar que qualquer valor inteiro ou racional a ferramenta é capaz de calcular com exatidão.
Nesse viés o (a) professor (a), poderia com o auxílio do aplicativo, demonstrar aos alunos as diferenças e propriedades inerentes a cada resultado de uma situação prática, o que a nosso ver criaria uma aprendizagem significativa e iria inserir essas aprendizagens na memória de longo prazo, o que no futuro é fundamental para novos desdobramentos.
REFERÊNCIAS BIBLIOGRÁFICAS
BACICH, L., NETO, A.T, & TREVISANI, F.M. Ensino híbrido: personalização e tecnologia na educação. Hibrideducação: Personalização e Tecnologia na Educação. Porto Alegre: Penso. 2015.
BRASIL. Ministério da Educação. Secretaria da Educação Fundamental. Parâmetros Curriculares Nacionais: matemática. 3. ed. Brasília: MEC/SEF, 1997. Disponível em: < http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf >. Acesso em: 10 set. 2022.
_______. Parâmetros Curriculares Nacionais do Ensino Médio (PCNEM) -Ciências da Natureza, Matemática e suas Tecnologias. Brasília, Ministério da Educação/Secretaria de Educação Média e Tecnologia, 2002.
_______. Ministério da Educação. Base Nacional Comum Curricular (BNCC). Brasília: MEC/SEB, 2017. Disponível em: <http://basenacionalcomum.mec.gov.br>. Acesso em: 18 ago. 2022.
CABEZUDO, Alicia. et al. Guia prático para a educação global conceitos e metodologias no âmbito da educação global para educadores e decisores políticos. Lisboa: Global Education Guidelines Working Group, 2010.
DAMASCENO, A. A.; OLIVEIRA, G. S.; CARDOSO, M. R. G. O ensino de matemática na educação de jovens e adultos: a importância da contextualização. Monte Carmelo/MG: Cadernos da Fucamp, v.17 n. 29, p. 112-124, 2018. Disponível em: https://www.fucamp.edu.br/editora/index.php/cadernos/article/download/1347/93. Acesso: 18 mar 2022.
GASPAR, J. P. M.; POCINHO, R. F. da S. “O uso das TIC e as alterações no espaço educativo”. Exedra, Coimbra, Portugal, n. 6, pp. 143-154, 2012.
MITE INVENTOR: O que é? Disponível em: https://aedmoodle.ufpa.br/pluginfile.php/170097/mod_book/chapter/2317/MITAPP_I nventor_apostila.pdf. Acesso em 11 mar 2022.
MORAN, J. Mudando a educação com metodologias ativas. Coleção mídias contemporâneas. Convergências midiáticas, educação e cidadania: aproximações jovens, v. 2, nº 1, p. 15-33, 2015a.
PAIVA, M. Matemática, Volume Único/Manoel Paiva. – 1. Ed. – São Paulo: Moderna, 2005.
PALFREY, J. Nascidos na era digital: entendendo a primeira geração de nativos digitais. Porto Alegre: Artmed, 2011.
STOICA, A. Using Math Projects in Teachingand Learning. Procedia – Social and Behavioral Sciences. 2015. v.180.p.702-708. Disponível em: <http://www.sciencedirect.com/science/article/pii/S187704281501527X > Acesso em: 26 set 2022.
VALENTE, J. A. (Org.) Análise dos diferentes tipos de softwares usados na educação. In:
VALENTE, J.A. O computador na sociedade do conhecimento. Campinas: UNICAMP/NIED, 1999. p.89-110.
VIDAL, A. S.; MIGUEL, J. R. As Tecnologias Digitais na Educação Contemporânea. Id on Line Rev. Mult. Psic., Maio/2020, vol.14, n.50, p. 366-379. ISSN: 1981-1179. Disponível em: <https://idonline.emnuvens.com.br/id/article/viewFile/2443/3877>. Acesso em: 20 de set. de 2022.
1Mestrando em Ensino de Matemática e Graduado em Matemática pela Universidade do Estado do Pará.
2Mestrando em Ensino de Matemática pela Universidade do Estado do Pará e Graduado em Matemática pela Universidade Federal do Sul e Sudeste do Pará.
3Pós-Doutor em Ensino de Ciências e Matemática da Universidade Federal do Rio Grande do Norte. Doutor e Mestre em Geofísica pela Universidade Federal do Pará. Engenheiro Civil pela Universidade Federal do Pará.
