REGISTRO DOI: 10.69849/revistaft/cl10202411131812
Edvan Barbosa de Sousa1
RESUMO
Um dos problemas do ensino fundamental no ensino da matemática surge através da necessidade de compreender determinados questões e assuntos que venham surgir no decorrer do ensino de aprendizagem relacionado à dificuldade de compreensão das quatros operações no quinto ano do ensino fundamental, sendo assim, surge à necessidade de procurarmos novas metodologias que estimule a prática pelo gosto do ensino da matemática nesse sentido.
O trabalho compartilhado de métodos de resolução de problemas e a utilização de meios práticos, com recursos concretos envolvendo as quatros operações no ensino fundamental contribuem para exploração de novas táticas ou meios de investigação e, consequentemente para o estímulo de práticas dos alunos, pois a linha de raciocínio de um pode ser o ponto de partida para outros e, ainda mais, a concretização do estudo sobre a utilização de materiais concretos ou jogos para a aprendizagem das quatros operações no Ensino fundamental, sendo essa a principal finalidade deste trabalho.
Para Soares (2008, p.15) “a educação tem se tornado fundamental na formação das pessoas, pois é a partir dela que, em geral, o cidadão consegue atender para patamares sociais mais elevados”.
Na concepção de Dante. L.R, 1979, resolver problemas e desafios, trocar ideias, observar ao redor, ler, trabalhar em equipe para uma compreensão coletiva de procedimentos eficientes e argumentar, são meios inteiramente contribuintes e estimulantes para despertar o prazer pela resolução de problemas.
Os problemas matemáticos são fundamentais, pois permitem ao aluno colocar-se diante de questionamentos e pensar por si próprios, possibilitando o exercício do raciocínio lógico e não apenas o uso padronizado de regras. Sendo assim, para que se resolva um problema envolvendo as quatros operações é necessário traduzir um enunciado para uma linguagem apropriada, até porque cada problema pode ter um procedimento semelhante ou diferente para a resolução.
Palavra-chave: Prática simples das quatro operações:
1. INTRODUÇÃO
Uma das principais dificuldades dos alunos na compreensão de resolver atividades matemáticas é compreender qual o tipo de operação que deve ser utilizada e principalmente conhecer o procedimento da operação em questão? Como proceder inicialmente para a resolução da operação? Quais os passos necessários? Como identificar, entre as quatros operações, qual a que o problema necessita para resolver?
De acordo com a concepção de Granado (2000, p, 28) comprova que:
O Professor de Matemática se apresenta como um dos grandes responsáveis pelas atividades a serem desenvolvidas em sala de aula. Portanto, qualquer mudança necessária a ser realizada no processo ensino-aprendizagem da matemática estará sempre vinculada à ação transformadora do Professor.
Deste modo, certifica-se que o trabalho do Professor deve ser novo e agradável constantemente para que o ensino aconteça de forma satisfatória e assim possibilite o processo ensino-aprendizagem acontecer.
A Matemática sempre foi vista como “um bicho papão”, levando os alunos a não apreciarem a disciplina e, assim, consequentemente venha surgir o fracasso. Como se não bastasse, hoje observamos que essa matemática continua sendo aplicada em nossas escolas como antigamente, não se atentando para as imposições da vida atual. Desta forma, D’Ambrósio salienta que:
A grande expansão da educação a partir do final do século passado e que se manifesta com maior intensidade nos países menos desenvolvidos a partir de meados deste século, a universalização da Educação Matemática. Universalização no sentido pleno: Ensinar Matemática para todos e, praticamente, a mesma Matemática em todo o mundo.
A perspectiva deste trabalho é a busca de estratégias de ensino que coloque o aluno não só para executar cálculos por meios de materiais concretos repassados pelo Professor, mas compreender o processo de desenvolvimento da operação que lhes permitam resolver, adicionando, subtraindo, multiplicando e dividindo, além de estar apto cognitivamente a resolver problemas que tem relação com essas operações.
Uma das principais rejeições de matemáticas e motivo de muito desempenho baixo nesta disciplina está na dificuldade de resolver problemas matemáticos envolvendo as quatros operações, na difícil interpretação de uma questão, no fato de encontrar um caminho que possa facilitar a resolução de um problema. Qual seria um meio simples de compreender o desenvolvimento das quatro operações de modo simples, utilizando material concreto (palitos, tampinhas e softwares), já que todos os conteúdos matemáticos têm como a base envolvendo essas quatros operações?
Identificar o tipo da operação e resolvê-la, não se resume em compreender o que foi proposto e, em dar respostas aplicando procedimentos adquiridos. Aprender a dar uma resposta correta, que tenha sentido, pode ser suficiente para que ela seja aceita e até seja convincente, mas não é garantia de apropriação de conhecimentos envolvidos.
Uma parte dos problemas no ensino da matemática está relacionada também ao processo de formação tanto inicial quanto de formação continuada, pois é necessário que o professor tenha conhecimento para compreender as dificuldades e origens para então proceder com precisão no desenvolvimento de soluções que possam contribuir no desempenho da resolução de problema envolvendo as quatros operações.
Um fato importante na visão de um procedimento é destacar como problema, a situação em questão, no entanto, não basta apenas propor e resolvê-los usando fórmulas prontas, enfim, é preciso uma interpretação eficaz no que foi proposto, pois além de ser importante encontrar uma resposta, e mais ainda, é aprender o procedimento de como se chegou a essa resposta.
No intuito de aproveitar os conhecimentos que os alunos já trazem para resolver problemas envolvendo as quatros operações na sala de aula, pode-se complementar esse conhecimento ensinando-os a seguir meios capazes de facilitar a resolução de problemas envolvendo as quatros operações.
Nessa visão, pretende-se buscar meios de ensinos que permita ao aluno não só realizar cálculos por meios desses recursos, mas compreender o processo operatório e encontrar outras formas de raciocínio que lhe permita operar, adicionando, subtraindo, multiplicando e dividindo, além de ser capaz de resolver problemas que envolvam essas operações.
Verifica-se hoje que diversos alunos possuem dificuldades no desenvolvimento de assuntos básicos, como o envolvimento das quatros operações, e que pode ser notado nos alunos do ensino fundamental, até mesmo maior, e médio. Além disso, pode ser notado nos resultados do Sistema Nacional de Avaliação da Educação Básica (Saeb), prova Brasil, Enem e concursos, fazendo com que a matemática seja vista como vilã e como principal fator dos baixos rendimentos em relação às demais disciplinas. No entanto, esse fator é caracterizado pela falta de uma base sólida cognitiva que deveria ser constituída gradativamente ao longo dos anos (D’Ambrósio, 2001, p.6).
A situação se agrava porque no sistema educacional atual, requer muito a questão numérica de aprovação e, por essa razão, alguns alunos são aprovados para o ano seguinte sem as condições mínimas de resolver questões matemáticas, aplicando as noções básicas dessa disciplina no cotidiano.
Segundo a concepção de Freire (1979):
O Educador, que aliena a ignorância, se mantém sempre em posições fixas, enquanto os educandos serão sempre o que não sabem. A rigidez destas posições nega a educação e o conhecimento como processo de busca.
Com isso, necessitamos estar aptos às novas formas de ensinar. O ensino com materiais concretos (tampinhas, baralho, software) quando bem planejados, pode ser uma estratégia um ensino onde os alunos tenham possibilidade de pensar, criar soluções, fazendo surgir definições matemáticas.
2. BUSCANDO ALTERNATIVAS PARA O ENSINO MATEMÁTICO COM MATERIAL CONCRETO.
O ensino com material concreto não requer que os alunos inventem meios para a formulação de definições de algo abstrato e concretizado negativamente pela falta de orientação do Professor.
Espera-se que o ensino como material concreto possibilite que Professores e alunos se envolvam no processo de ensino, possibilitando o surgimento de novas formas de pensar, observar e descobrir meios para a construção do conhecimento.
De acordo com a concepção de PONTE,2005, o ensino exploratório pode ser executado com atividades que surjam na forma de problemas, jogos ou com uso de mídia, por exemplo.
Quadro 1- Organização do material concreto
Tarefas Conteúdo Objetivos Tampinhas As quatros operações – Raciocínio lógico; -Socializar o desenvolvimento das quatros operações por meio de tampinhas. Baralho Adição, multiplicação e divisão – Desenvolver o raciocínio lógico Software Multiplicação e divisão -Raciocínio lógico; -Estimular raciocínio rápido.
Nota-se que esses materiais como palitos, tampinhas e softwares da divisão ou labirinto da tabuada, que podem ser úteis na compreensão de problemas envolvendo as quatros operações no ensino fundamental e, assim, sanar possíveis dificuldades de compreensão.
Quando se trabalha com materiais com materiais concretos, consequentemente se trabalha de forma lúdica, então o Professor deve tomar diversos cuidados ao planejar atividades com esses materiais para que não provoque bagunça e nem ultrapasse o tempo da aula. Além disso, um dos principais também é o foco no objetivo que pretende atingir e consequentemente se os alunos estão assimilando corretamente.
A habilidade do Professor é fundamental para adotar papéis, normas e valores na profissão e na construção do aspecto cognitivo matemático como também no aspecto didático pedagógico, da circunstância educativa, dos alunos e suas propriedades, dos materiais e programas de comando e organização da sala de aula, de sua autoconfiança, recursos e etc.
Sabe-se que é conveniente que busquemos metodologia que oportune aos nossos alunos a busca de novos entendimentos e que esses entendimentos os qualifiquem para indivíduos mais autônomos. Cabem a nós, Professores de matemática, estarmos envolvidos com o ensino de uma matemática criativa, que vai além do que os livros didáticos nos oferecem, dando importância ao espaço social e físico de nossos alunos.
Podem-se citar as Diretrizes Curriculares da Educação Básica na área da Matemática:
Pela Educação Matemática, almeja-se um ensino que possibilite aos estudantes, análises, discussões, conjectura, apropriação de conceitos e formulação de ideias. Aprendesse Matemática por sua beleza ou pela consistência de sua teoria, mas, para que, a partir dela, o homem amplie seus conhecimentos e, por conseguinte, contribua para o desenvolvimento da sociedade. (PARANÁ, 2008, p.48)
No que diz respeito ao trabalho com materiais concretos nas aulas de matemática, o objetivo do ensino é sempre importante, não permitindo que materiais concretos não sejam o principal foco, mas sim um aliado do ensino.
Além desses materiais concretos (tampinhas, baralho e labirinto da tabuada), a calculadora pode ser utilizada nas tarefas do dia a dia no ensino da matemática, tornando agradável o modo de pensar e agir dos alunos. Dessa forma, eles podem criar soluções das atividades propostas.
Esse objeto, a calculadora, é um instrumento que amplia a capacidade no processo de ensino aprendizagem, descartando a hipótese de que ela diminui o aprendizado.
Baseado nisso, FOLLADOR (2011, p.20) sustenta que:
Do ponto de vista da aprendizagem, a utilização da calculadora, bem como de outras mídias, não destaca a necessidade de o aluno raciocinar para resolver ou reformular problemas, mas muda o modo como esse aluno irá raciocinar, levando-o a usar outro elemento além de lápis r de papel.
É um material que também precisa ser planejado de forma que o Professor dê oportunidades aos alunos e criarem definições no que diz respeito a assuntos matemáticos.
3. METODOLOGIA
Na pesquisa bibliográfica, serão verificados e apontados meios necessários para o desenvolvimento dos aspectos cognitivos relacionados às quatro operações no ensino fundamental, como:
- Lendo cuidadosamente o problema;
- Identificando o tipo da operação existente;
- Aplicando atividades com materiais concretos (palitos, tampinhas, material dourado e softs) para melhor compreensão do conteúdo.
- Propondo situações problemas envolvendo as quatro operações;
- Identificando palavras-chaves que possam de imediato, dar um ponto de partida para resolução;
- Propondo a repetição da questão envolvendo as quatro operações para facilitar à interpretação e consequentemente a resolução do referido problema;
- Aplicação de exercícios para medir o conhecimento do aluno em relação ao tema colocado, e testes para acompanhamento do desenvolvimento do trabalho, no entanto, podem-se formar grupos em sala de aula para a resolução de diferentes problemas com observações individuais de como o aluno chegou às soluções;
- Refazendo problemas para a verificação e concretização do processo realizado para se obter respostas, pois a repetição da construção do problema constitui uma das formas de compreensão de um problema matemático.
- Fazendo a verificação da operação através da prova real para verificação da autenticidade da mesma.
Com o propósito de facilitar o estudo da matemática com material concreto, no ensino fundamental, pode-se verificar o ensino aplicado nas quatro operações especificamente.
A seguir um detalhamento de como esses materiais concretos (tampinhas, baralho, e software da divisão ou labirinto da tabuada) deve ser manuseado de forma simples, após um cuidadoso planejamento.
3.1 Tampinhas
- A adição é uma operação com menos dificuldades por parte dos alunos.
A utilização das tampinhas na adição acontece quando se separa as parcelas para, em seguida, juntá-las formando o total. Ex: 2 + 2 = 4

- Na subtração, as tampinhas são retiradas de quantidade menor são retiradas de uma quantidade maior. Nessa operação os alunos podem ter uma dificuldade quando forem resolver a operação tentando inverter o termo minuendo com o subtraendo. Ex: 3 – 1 = 2

- Na multiplicação, as tampinhas são posicionadas com a quantidade de acordo com o multiplicando e o multiplicador, ou seja, a soma deles tantas vezes quantas forem as unidades do outro. Assim, o procedimento a se observar, será que vai existir com 3 fileiras de duas tampinhas em cada fileira. Ex: 2 x 3 = 6

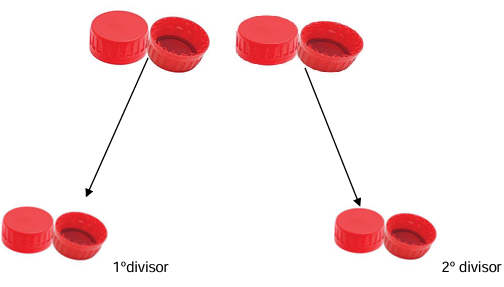
- Na divisão, as tampinhas serão separadas de acordo com o dividendo e distribuídas de acordo com o divisor. O divisor pode ser um pequeno espaço onde receberão os itens a serem distribuídos. Sendo assim, a distribuição deverá acontecer cuidadosamente, colocando para cada divisor sempre a mesma quantidade de tampinhas. Caso não seja possível colocar de forma igual, a sobra será o resto. Ex: 4 / 2 = 2
3.2 Baralho
Na atividade com o baralho, pode-se desenvolver a adição e multiplicação com mais facilidade e desenvolvimento do raciocínio lógico.
- Na adição, a atividade acontece com dois participantes, onde cada participante de cada vez pega uma carta, no monte, virada para baixo e coloca na própria testa. O Professor, como um juiz, fala em voz alta o resultado da adição. Logo em seguida cada participante, como não está vendo a própria carta, irá dizer qual a carta que está na sua testa. O participante mais rápido que falar a própria carta, será o vencedor.
- Com o baralho também pode ser trabalhado a multiplicação utilizando o mesmo processo da adição.
Imagem 1 – Jogo de adição e multiplicação com o baralho
3.3 Softwares da divisão ou labirinto da tabuada
Este recurso é um jogo que consiste em descobrir o caminho do gol, passando pelas casas que contém os resultados de uma ou duas tabuadas que o aluno escolher. Veja a ilustração.
Imagem 2- labirinto da tabuada
Neste jogo o aluno é deixado livre para que ele crie sua própria estratégia. Alguns podem até utilizar a multiplicação como estratégias para constatar a veracidade da operação.
A habilidade do professor, aderi funções, normas e valores que são necessários na profissão e na construção de aspectos cognitivos na matemática, do aspecto didático pedagógico, da circunstância educativa, dos alunos e sua propriedade, dos materiais e programas, de comando e organização da sala de aula, de sua autoconfiança, recurso e etc.
4. REFERENCIAL TEÓRICO
Segundo “Pólya”, 1979 a resolução de problemas tem como objetivo a análise baseada em exemplos, a melhoria dos passos para a resolução e a adoção de técnicas fundamentais propostas.
Ainda de acordo com “Pólya”, (1979) o uso de uma tática para investigar e compreender os conteúdos, o uso de questões do cotidiano, a busca de uma metodologia para resolver diversos problemas, a verificação e compreensão dos resultados, a firmeza para usar os procedimentos matemáticos e a unificação dos resultados e metodologias, podem levar aos alunos conhecimentos suficientes para resolução de problemas.
O ensino das quatros operações pode ser utilizado com atividades que se apresentem em forma de problemas, investigações, jogos e com uso da mídia, como exemplo, no entanto, não importam como as tarefas são nomeadas, elas devem dar oportunidades para que o aluno raciocine matematicamente sobre ideias fundamentais e atribua sentido ao conhecimento matemático que surge a partir da discussão coletiva dessas tarefas, PONTE, (2005).Neste sentido de ensino, a função do professor é importante e começa na escolha e preparação das atividades, tendo claros os objetivos e aprendizados que almejam atingir.
5. RESULTADOS E DISCUSSÃO
O presente trabalho coloca a disposição de alternativas para ensino das quatros operações no ensino fundamental menor com materiais concretos, assim como obter noção de resolução.
Acredita-se que inicialmente pode ser detectada dificuldade de adaptação, referente à compreensão das atividades envolvendo as quatros operações. Poderá ser observado também se os alunos utilizarão formas diferentes de raciocínio e resolução como o cálculo mental ou relação entre as operações.
Pode haver também momentos de dificuldades, principalmente quando se tratar da falta de compreensão nas questões propostas, até porque o ensino com material concreto é preciso paciência e compreensão diante de cada participação interativa.
Este trabalho pode disponibilizar momentos grandiosos de aprendizagem e processos cognitivos envolvendo as quatros operações. Além disso, esses materiais (tampinhas, baralho, software ou labirinto da tabuada) podem facilitar a execução das atividades e possibilitar uma resolução concreta.
Deste modo, pode-se concluir que o ensino com materiais concretos são enriquecedores e formulam grandes ideias conceituais, o que constitui uma estratégia reflexiva, onde todos os momentos de descontração sejam transformados em aspectos cognitivos matemáticos.
6. CONSIDERAÇÕES FINAIS
Ao final pode-se destacar a importância de pensar, refletir, analisar e concluir para que o aluno seja capaz de dominar os conhecimentos através de sua confiança, entretanto, para que seja possível é necessária mudança de uma metodologia com foco de atenção para uma que conduza o aluno se envolver de forma dinâmica, integrativa e contínua.
AGRADECIMENTOS
A Deus pelo dom da vida, pela fé, confiança, força e perseverança para vencer mais esta jornada, me incentivar mesmo diante a tantos obstáculos.
À minha família pelo apoio e carinho que recebo, em especial a minha filha Gabrielly e minha esposa Francineusa e a meus pais, que são meus maiores incentivadores e também meus amigos mais próximos que sempre torcem por mim.
Resumidamente, sou grato a todos que de alguma forma colabora para a execução de meus objetivos.
REFERÊNCIAS
DANTE, L. R. Didática da resolução de problemas de matemática. 2. Ed. São Paulo: Ática, 1991;
FREIRE, P. Pedagogia do oprimido. Rio de Janeiro: Editora Paz e Terra, 1979.
FOLLADOR, D. Metodologia do Ensino da Matemática e Física: Tópicos Especiais no Ensino da Matemática: Tecnologias e Tratamento da Informação. 2.Ed. v. 7. Curitiba: Ibpex, 2011.
PONTE, J.P. Gestão curricular Matemática. In GTI (Ed.), O Professor e o desenvolvimento curricular. P. 11-34. Lisboa: APM, 2005.
D’AMBRÓSIO. Ubiratan. Educação Matemática: Uma visão do estado da arte. Proposições. Campinas, v. 4, n. 1[10], março 1993. Disponível em: ,: http://mail.fae.unicamp.br/~proposicoes/textos/10-artigos-d%5C’ambrosiou.pdf.
Parâmetros Curriculares Nacionais volume três, Brasília, 1997;
PÓLYA, George. 1887. A arte de resolver problemas: Um novo aspecto do método matemático.
CANAVARRO, A.; OLIVEIRA, H.; MENEZES, L. Práticas de ensino exploratório da matemática: o caso de célia. In: Encontro de Investigação em Educação Matemática 2012: Práticas de Ensino da Matemática, 2012, Castelo de Vide. Actas…Porto Alegre: SPIEM, p. 255- 256, 2012.
DANTE, L.R. Didática da resolução de problemas. São Paulo: Ática, 1989;
CANAVARRO, A.P. Ensino exploratório da Matemática: Práticas e desafios. Educação e Matemática, Lisboa, n.115, p. 11-17, 2011.
1Graduado do Curso de Licenciatura em Matemática da Universidade Federal do Piauí-PI; Pós-graduado 1 pelo Curso de Metodologia do Ensino da Matemática no Ensino Infantil, Fundamental e Médio da Faculdade de Teologia e Ciências do alto Parnaíba – MG, Pós-graduação 2 do Curso de Docência no Ensino Superior da Faculdade de administração, Ciências, Educação e Letras – PR, edvanbarbosa07@hotmail.com
