REGISTRO DOI: 10.5281/zenodo.10854961
Ruan de Aguiar Silva1
Francisco Diego de Aguiar Silva2
Andreane Matias da Silva3
Elane Pereira de Moraes4
Cosmo Lustosa da Silva5
RESUMO
No presente trabalho busca abordar um problema do cotidiano, usando as equações diferenciais, que pode ser utilizado através da lei do resfriamento de Newton, e tentando associar teoria e prática. Sendo que o presente trabalho tem por objetivo comprovar a eficiência de dois tipos de garrafas térmicas (rosca e pressão) tem melhor eficácia para manter líquidos quentes e frios. Sendo que se faz necessário modelagens matemáticas para formular a lei do resfriamento de Newton.
Palavra chave: lei do resfriamento de Newton, teoria, prática, modelagens matemáticas.
ABSTRACT
The present work seeks to address a daily problem, using differential equations, which can be used through Newton’s law of cooling, and trying to associate theory and practice. The present work aims to prove the efficiency of two types of thermoses (screw and pressure) has better effectiveness to keep liquids hot and cold. Therefore, mathematical modeling is necessary to formulate Newton’s law of cooling.
Keywords: Newton’s law of cooling, theory, practice, mathematical modeling.
1. INTRODUÇÃO
A Modelagem Matemática pode ser descrita como uma arte que, além de ilustrativa e deslumbrante, tem seus pontos particulares de importância, por tratar de aspectos de extrema relevância para o desenvolvimento de análises e soluções de inúmeras situações problema no decorrer da história da humanidade. Segundo Biembengut e Hein (2003, p. 11),
[…] o ser humano sempre recorreu aos modelos, tanto para comunicar-se com seus semelhantes como para preparar uma ação. Nesse sentido, a modelagem, arte de modelar, é um processo que emerge da própria razão e participa da nossa vida como forma de constituição e expressão do conhecimento.
Com a modelagem podemos tornar as aulas mais dinâmicas, discutir diferentes temas, selecionar informações relevantes para a compreensão de um problema, realizar e analisar simulações, identificar padrões, fazer previsões e conjecturas, e obter uma equação matemática que descreva um problema. Ao partir de um problema não matemático e realizar a modelagem, o aluno deve abstrair e esse processo o motiva a pesquisar, a querer aprender sempre mais. Segundo D’Ambrosio (1996, p. 31), isso é importante, pois
[…] a matemática que se ensina hoje nas escolas é morta. Poderia ser tratada como um fato histórico. […] Interessa à criança, ao jovem e ao aprendiz em geral aquilo que tem apelo às suas percepções materiais e intelectuais mais imediatas. Por isso proponho um enfoque ligado a situações mais imediatas.
Usar a modelagem como metodologia de ensino e aprendizagem pode trazer inúmeros benefícios para a aprendizagem dos alunos, ainda que demande um tempo maior do professor, no que diz respeito ao planejamento e desenvolvimento das aulas.
As equações diferenciais são muito utilizadas no dia-a-dia para descrever problemas da física, que podem ser o fluxo de corrente elétrica, resfriamento ou aquecimento, entre outros processos físicos.
Neste caso, o presente trabalho tem por objetivo estudar, compreender e aplicar a lei do resfriamento de Newton , como também alguns problemas que envolvem equações diferenciais ordinárias (EDO ‘s) em problemas reais, permitindo a comparação entre a solução analítica e a dados experimentais.
As equações diferenciais ordinárias têm ampla aplicabilidade em vários contextos. Em particular, a lei de resfriamento de Newton permite, de maneira simples, modelar problemas reais e fornecer previsão de resultados. Tal lei, descreve problemas reais de pequena e grande complexidade, como observar a temperatura do líquido em uma garrafa térmica, ao resfriamento de um cadáver, para que, através de algumas adaptações, o modelo matemático fornece resultados consistentes com a situação analisada.
A área criminalística, por exemplo, “é responsável pela identificação, coleta, processamento e correta interpretação dos vestígios de um crime”, com isso, utiliza-se da principal lei de Newton “ A lei de resfriamento de Newton” para identificar o tempo em que o crime ocorreu através da temperatura do corpo.
2. FUNDAMENTAÇÃO TEÓRICA
2.1. Lei do resfriamento de Newton
A Lei do Resfriamento de Newton descreve uma situação de equilíbrio térmico entre um corpo e o ambiente em que ele se encontra. “A taxa de variação da temperatura de um corpo (sem fonte interna) é proporcional à diferença entre sua temperatura e a do meio ambiente” (BASSANEZI; FERREIRA JR., 1988, p. 43). Embora pareça simples, envolve outras variáveis como a superfície de contato do corpo com o meio, o calor específico que quanto maior exigirá mais energia e o tempo de contato.

Lembrando que a derivada de uma função representa uma variação, a lei pode ser expressa pela equação diferencial ordinária de primeira ordem,

A partir do que é apresentado na literatura, desenvolvemos um experimento a fim de relacionar a teoria com a prática, ou seja, estudar, analisar e comparar o comportamento do fenômeno real com o que está presente na teoria.
Segundo Newton a taxa de resfriamento de um corpo é proporcional à diferença entre a temperatura do corpo e a temperatura do meio.
Silva (2014), um corpo com temperatura T que não possui nenhuma fonte de calor em seu interior, quando deixado em um meio ambiente, tende a uma temperatura (Ta) do meio que o cerca. Desse modo, se a temperatura T do corpo é menor que a temperatura ambiente Ta, este corpo se aquecerá e, caso contrário, se esfriará. A temperatura do corpo é uma função contínua do tempo, T(t).

3. METODOLOGIA: Estudo de caso
3.1. Características do Problema
Problema 1: Foi encontrado pelas 04h00min na esquina da rua A com a rua B o corpo de um homem aparentando 30 anos. Moradores do local disseram ter ouvido tiros por volta da 00h00min também em torno das 03h00min da madrugada. A polícia já encontrou ambos os autores dos disparos. Somente após o legista identificar a hora da morte é que a polícia poderá prender um dos suspeitos.
Surge então um questionamento: como podemos saber quando a vítima morreu?
De acordo com a Lei de Newton de resfriamento/aquecimento, a taxa de variação de um corpo em um determinado ambiente é diretamente proporcional à diferença entre a temperatura do corpo e a temperatura local (meio) onde o corpo se encontra.
Para a solução do problema vamos utilizar a seguinte fórmula:
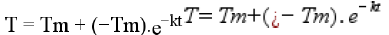
(1) Onde, Tm é a temperatura ambiente, To é a temperatura
inicial do corpo quando encontrado , k é a constante de proporcionalidade e t é o tempo.
Primeiramente, calcula-se a constante k, tal que: T= 23° C , t=2 horas , Tm=20°C , to=30°C.
Desenvolvendo:
T(t)=Tm+( T0 – Tm). e^-kt
T(2)=20+(30-20). e^-2k
3=10.e^-2k
0,3= e^-2k ln 0,3=lne^-2k k=ln (0,3/-2)
K= 0,6
Assim, após encontrar a constante k iremos a procura do tempo no qual ocorreu a morte da vítima.
Temos:
Substituindo:
T = Tm + (T0 – Tm). e^-kt
30=20+(37-20). e^-0,6t
10=17. e^-0,6t
0,5882= e^-0,6t
(0,5882)= ln^(e^-0,6t)
-0,531= -0,6t
0,885=t
0,885*60=t t=53 min
Conclui- se que encontraram o corpo às 4 horas e o instante de sua morte foi 53min antes, então é possível concluir que a vítima morreu aproximadamente às 3h 07 min.
Para melhor visualização utilizaremos o software GeoGebra para analisar de forma geométrica o resultado da equação ( figura 1) Considerando o instante t e a temperatura T do corpo como o par ordenado (t ,T). Então se obtém T1(3.07 , 37), T2(4.00 , 30) e T3(6.00 , 23), como mostra a figura a seguir.
Figura 1: Gráfico da solução .
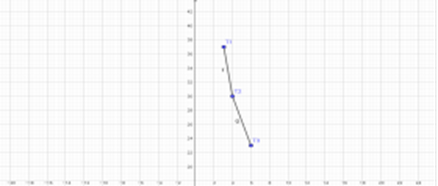
Fonte: Liliane, Any e Josimeire (2017).
Observando o gráfico, nota-se que à medida que o tempo t aumenta, a temperatura T do corpo diminui, até atingir um ponto em que, entrará em equilíbrio com a temperatura do meio em um determinado tempo t.
Concluímos que é possível adaptar um conteúdo teórico a um contexto e com isso analisar soluções de diferentes formas, em situações-problema que possibilitem maior envolvimento por parte dos alunos, despertando a participação na aula por meio de aulas envolvendo práticas, uso de softwares no laboratório. Dessa forma, podemos proporcionar motivação por parte de quem está ensinando (professores) e de quem está aprendendo (alunos).
Problema 2- Observação experimental frasco de Dewar, será utilizando os seguintes objetos: dois termômetros de mercúrio com medição de -10° C a 110° C, um termômetro digital, um termômetro de temperatura ambiente e duas garrafas térmicas, sendo uma de rosca e uma de pressão. O mesmo tem por objetivo manter a temporada na garrafa por uma maior quantidade de tempo, sendo que a função da garrafa térmica é dificultar as trocas de calor com o ambiente.
Com isso, apesar de não haver um isolamento térmico perfeito, foram tomados os devidos cuidados para manter a temperatura alta depois de certo tempo após colocar a água quente até atingir o equilíbrio térmico ( figura 2)
Figura 2: Garrafa Térmica
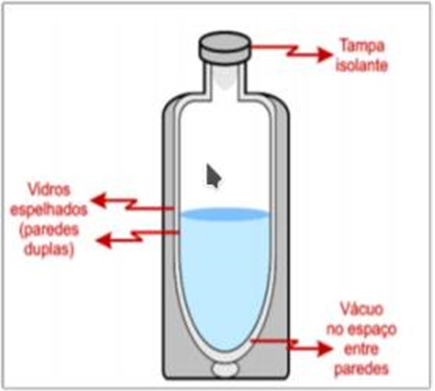
Fonte: Marques, 2009, p. 50.
4. Análise dos resultados
Após montado o experimento foi calculado através da lei de resfriamento de Newton com o líquido quente. Sabendo que, dada a média das temperaturas nos dias que foram realizados os experimentos Tm= 27°C, e usando esse valor como constante temos:

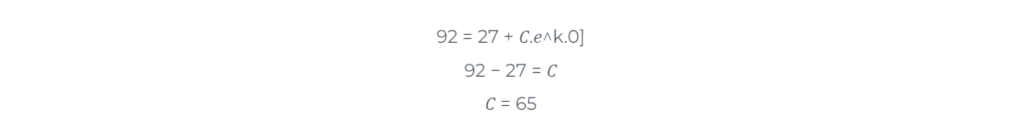
Portanto passa a ser


4.1. Resultado obtidos:
Após a realização do experimento obtivemos os seguintes resultados
Tabela 1: temperatura da prática na garrafa de rosca
Líquido Quente t(h) 0 12 24 36 48 60 72 T (ºC) 92 70 57 50 44,5 42 38
Tabela 2: Temperatura da prática na garrafa de pressão
Líquido Quente t(h) 0 12 24 36 48 60 72 T (ºC) 92 64 50 50 43 36 33
Tabela 3: Temperatura da prática na garrafa de rosca
Líquido frio t(h) 0 12 24 36 48 T (ºC) 2 16 22,1 26,2 27,7
Tabela 4: Temperatura da prática na garrafa de pressão
Líquido frio t(h) 0 12 24 36 48 T (ºC) 2 13,2 19,3 24,3 26,4
Pode-se perceber que a garrafa de pressão é eficiente para manter os líquidos frios e a garrafa de pressão é mais eficaz para manter os líquidos quentes.
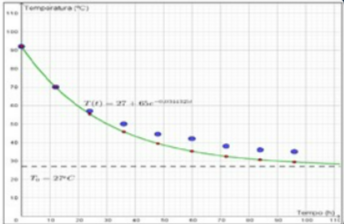
Figura 3: Curva exponencial da garrafa de rosca com líquido quente.
Fonte: Aline, Claudemir e Priscila ( 2019).
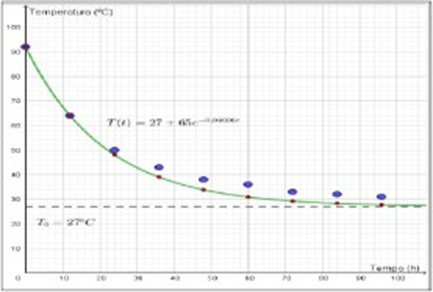
Figura 4: Curva exponencial da garrafa de pressão com líquido quente.
Fonte: Aline, Claudemir e Priscila ( 2019).
Ao analisar o gráfico acima percebe-se que os pontos em vermelho referem-se aos pontos do experimento na teoria pelo cálculo da lei do resfriamento de Newton, os pontos em azul são os retirados na temperatura na prática e na cor verde a curva da função exponencial .
A partir do experimento nota-se que a garrafa de rosca chega a uma temperatura ambiente em 100 horas e a garrafa de pressão em aproximadamente 80 horas, o gráfico também mostra que os pontos em azul são os que foram retirados na prática, nas duas figuras acima, ficaram distantes da curva, isso se dá pela troca de calor com o meio, e pela variação de temperatura.
Figura 5: Curva exponencial da garrafa de rosca com líquido frio.

Fonte: Aline, Claudemir e Priscila ( 2019).
Figura 6: Curva exponencial da garrafa de pressão com líquido frio

Fonte: Aline, Claudemir e Priscila ( 2019).
Logo qunado o líquido atingir a temperatura ambiente em aproximadamente 80 horas, porém isso não aconteceu pelo menos motivo do primeiro gráfico.
4.2. Erro
Os erros podem acontecer no processo de modelagem na qual estariam relacionados à aproximando da situação física e também no processo de resolução onde ocorrem erros de truncamento e arredondamento.
4.2.1 Temperatura no líquido quente
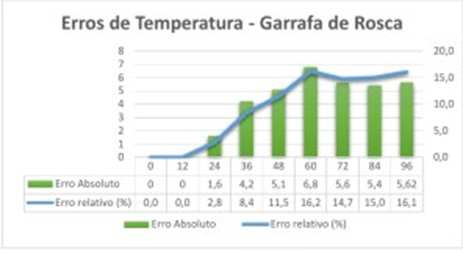
Gráfico 1: Erro (líquido quente)
Fonte: Aline, Claudemir e Priscila ( 2019).
Gráfico 2: Erro (líquido quente).
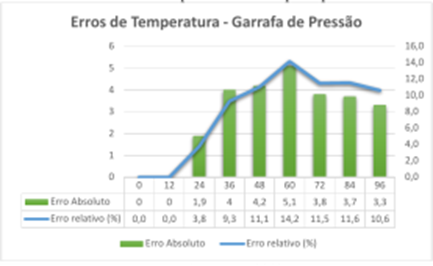
Analisando o primeiro gráfico perceber-se que o erro absoluto ficou abaixo 7,0°0 e o erro relativo ficou abaixo de 17%, isso mostra que os valores das temperaturas registradas na prática ficaram distante na teoria.
No gráfico 2 aconteceu o mesmo, já que o erro absoluto ficou abaixo de 6,0°C e o erro relativo ficou abaixo de 15%, mostrando que os valores ficaram aproximados aos cálculos da lei do resfriado de Newton
4.2.1 Temperatura no líquido frio
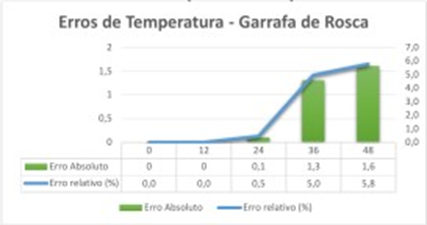
Gráfico 3: Erro (líquido frio)
Fonte: Aline, Claudemir e Priscila ( 2019).
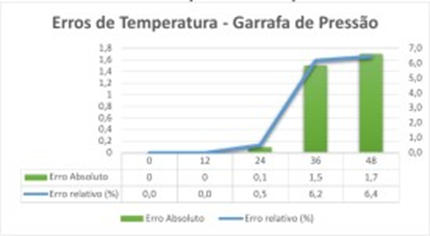
Gráfico 4: Erro (líquido frio)
Fonte: Aline, Claudemir e Priscila ( 2019).
Em relação aos líquidos frios, o gráfico mostra que os erros foram menores nos dois casos, porém a perda de calor foi mais alta, chegando a temperatura ambiente em 80 horas, percebe-se tambem que no terceiro gráfico ouvi uma variação de temperatura bem maior e o erro absoluto chegou há 1,6°C, já o erro relativo em 5,8% isso quer dizer que os erros nos líquidos frios foram menores.
No gráfico 4 os erros foram um pouco maiores chegando a 1,7°C para o erro absoluto 6,4% para o erro relativo, com isso os líquidos frios ganharam mais calorias por estarem mais próximos da temperatura ambiente
5. CONCLUSÃO
O presente trabalho teve por finalidade mostrar que através da lei do resfriamento de Newton e utilizando os estudos desenvolvidos sobre as equações diferenciais ordinárias, questionando o modelo de garrafas térmicas é mais eficaz e o tempo que um líquido qualquer frio ou quente demora para atingir a temporada ambiente.
Após fazer a verificação de cada valor na teoria e na prática e fazendo os estudos de erros absolutos e relativos, a partir daí percebemos que a conservadores de líquidos ocorre de maneiras diferentes nos tipos de garrafas estudados, sendo que podemos perceber que a garrafa de rosca conserva melhor os líquidos quentes e a garrafa de pressão conserva melhor os líquido frias.
6. REFERÊNCIAS
ALMEIDA, L. M.W.; SILVA, K. A. P. Modelagem Matemática em Foco. ed. Rio de janeiro: Editora Ciência Moderna Ltda, 2014.
BASSANEZI, R. C. Ensino-aprendizagem com modelagem matemática: uma nova estratégia. São Paulo: Contexto, 2002.
BIEMBENGUT, M. S,; HEIN, N. Modelagem matemática no ensino. São Paulo: Contexto, 2003. p. 13- 17, 2010.
BOYCE, W. E.; DIPRIMA, R. C. Equações Diferenciais elementares e problemas de valores de contorno. Richard C. DiPrima; tradução e revisão técnica Valéria de Magalhães Iorio. Rio Janeiro: LTC, p.23, 2010.
BRONSON, R.; COSTA, G. Equações diferenças. 3º ed. Porto Alegre: Bookman, p. 64, 2008.
BASSANEZI, R. C.; FERREIRA, W. C. F. Jr. Equações diferenciais com aplicações. São Paulo: Harbra, 1988.
D’AMBROSIO, U. Educação Matemática: da teoria à prática. 10. ed. Campinas: Papirus, 1996.
SILVA, J. S. F. da. Sobre o problema da variação de temperatura de um corpo. CONNECTIONLINE, n. 5, 2014.
1 ruan.rdas69@gmail.com
2fdas.diego@gmail.com
3andreane.matias@hotmail.com
4elane423@gmail.com
5cosmolustosa2@gmail.com
