Implementation of Solver and Operational Research Fundamentals in the programming of an electronic board factory.
REGISTRO DOI: 10.5281/zenodo.7951479
Eduardo Alves Diana;
Gabriel Oliveira Souto;
Gabriela Costa de Carvalho;
Nicolli Arão;
Thalita Maria Olyntho.
Orientador: Prof. Dr. Rogerio Lobo
Resumo: Este artigo tem como base teórica a pesquisa bibliográfica em livros e artigos, com isso serão apresentadas as ferramentas que serão utilizadas. Depois seguirá com a apresentação do estudo de caso, realizado em uma indústria de placas eletrônicas, localizada na cidade de São Paulo, que possui problemas na sua produção, por não conseguir atender a demanda de sua principal cliente, que compra em média 300 mil de placas por mês, devido a suas limitações operacionais e o mal planejamento da sua linha de produção.
Com isso, foi realizado o mapeamento da capacidade produtiva da linha e análise da demanda mensal solicitada pela sua cliente, com o auxílio da ferramenta Solver, do MS-Excel, agregando os fundamentos de Pesquisa Operacional, para tentar solucionar os problemas de restrições operacionais que a empresa possui em sua linha produtiva.
Após analisar a produtividade da fábrica, e estudar a sua capacidade produtiva, foi percebido que a fabricante possuía disponibilidade em sua linha para atender a demanda da fabricante, porém, estava sendo mal planejada a produção, com isso, o Solver auxiliou na organização da linha, com a informação de qual o mix de produção diário e quais as quantidades a serem produzidas. Ao final do estudo, notamos que a realocação da produção, permitiu que fosse atendida demanda do fornecedor, sem que as restrições de capacidades produtivas fossem ultrapassadas.
Palavras-chave: Solver, MS-Excel, Pesquisa Operacional, Análise de Sensibilidade.
Abstract: This article is theoretically based on bibliographical research in books and articles, with which the tools that will be used will be presented. Then it will continue with the presentation of the case study, carried out in an electronic board industry, located in the city of São Paulo, which has problems in its production, for not being able to meet the demand of its main customer, who buys an average of three hundred thousand of boards per month, due to its operational limitations and poor planning of its production line.
As a result, the production capacity of the line was mapped and the monthly demand requested by its client was analyzed, with the help of the Solver tool, from MS-Excel, adding the fundamentals of Operational Research, to try to solve the problems of restrictions operations that the company has in its production line.
After analyzing the productivity of the factory, and studying its production capacity, it was noticed that the manufacturer had availability in its line to meet the demand of the manufacturer, however, the production was being poorly planned, with that, Solver helped in the organization of the line, with information on the daily production mix and the quantities to be produced. At the end of the study, we noticed that the reallocation of production allowed the supplier’s demand to be met, without exceeding the restrictions of productive capacities.
Keywords: Solver, MS-Excel, Operational Research, Sensitivity Analysis.
1. INTRODUÇÃO
Uma indústria, seja ela de grande ou pequeno porte, necessita de um planejamento e controle da produção. Pois essa atividade é de importante na organização para que tenha total controle da sua fábrica, de qual é a sua capacidade produtiva, do que produzir e quando produzir. Um bom setor de planejamento tem principal função realizar todo o gerenciamento da sua linha produtiva, elaborar e monitorar os indicadores de performance, encontrar possíveis problemas de gargalos ou falhas que podem ocorrer e encontrar ferramentas para solucionar qualquer ineficiência que possa ocorrer.
Com este cenário, as empresas estão buscando também profissionais qualificados e que tenham conhecimento em ferramentas de otimização ou simulação, para que os auxiliem nas tomadas de decisões. Neste estudo apresentaremos o Solver, ferramenta que possui capacidade analítica de hipóteses, que agregado aos fundamentos de Pesquisa Operacional, pode solucionar diversos problemas de restrições operacionais que as empresas encontram no dia a dia. E como parte prática do estudo, foi realizado o mapeamento na linha de produção de uma empresa fabricante de placas eletrônicas, localizada em São Paulo. Esta empresa possuía grandes problemas no planejamento das suas linhas de produção, pois ela tinha como principal cliente uma empresa que comprava o todo o seu volume de produção, mas por conta desse mal planejamento não conseguia atender os pedidos de alta sazonalidade. E o Solver auxiliará no planejamento do que será produzido por dia e quanto será produzido para atender a demanda mensal comprada pela sua principal cliente.
1.1 JUSTIFICATIVA E PROBLEMÁTICA
Este trabalho tem como justificativa o mal planejamento de produção da empresa de placas eletrônicas, localizada em São Paulo, o não atendimento da demanda total de seu principal cliente, com isso, surgiu-se a necessidade de realizar um mapeamento da produtividade da sua empresa e com encontrar ferramentas de simulações ou otimizações, para auxiliar na tomada de decisões, fazendo com que a empresa possua uma melhor produtividade e eficiência na sua linha de produção, para que assim consiga atender a demanda mensal solicitada pela sua cliente.
1.2 OBJETIVOS (GERAL E ESPECÍFICOS)
Neste capítulo serão apresentados os objetivos gerais e específicos do trabalho.
1.2.1. Objetivo Geral
O presente trabalho tem como objetivo geral apresentar a ferramenta Solver do Excel, que junto com os fundamentos de Pesquisa Operacional, é uma ferramenta de análise que pode auxiliar na tomada de decisão.
1.2.2. Objetivos Específicos
Utilizar o Solver como principal ferramenta para auxiliar uma empresa fabricante de placas eletrônicas em sua tomada de decisão, desenhando o faseamento da produção para atender a demanda de seu principal cliente, respeitando as restrições de capacidade produtiva que a empresa possui.
2. REVISÃO BIBLIOGRÁFICA
Neste capítulo mostra o referencial teórico do estudo que tem como base teórica a pesquisa bibliográfica em livros e artigos.
2.1 PESQUISA OPERACIONAL
Segundo Moreira (2015), pesquisa operacional lida com o problema de como realizar e coordenar certos procedimentos em uma organização, baseado em métodos científicos para resolver problemas.
Segundo Andrade (2012) O termo Pesquisa Operacional surgiu pela primeira vez durante a Segunda Guerra Mundial, quando pesquisadores tentavam desenvolver métodos para alguns problemas operacionais militares, e os utilizavam como ferramentas de otimização para melhor aproveitamento de recursos como armas, munições, alimentos, água, etc.
Os principais aspectos da pesquisa operacional podem ser resumidos da seguinte forma: É utilizado em ampla gama de governos e instituições, manufaturas, empresas comerciais e de serviços; aplica-se questões relacionadas com a execução e coordenação de operações ou atividades dentro de uma organização; adota uma abordagem sistemática para a resolução de problemas; procura a solução ótima e utiliza métodos de trabalho em equipe (engenharia, computação, economia, estatística, administração, matemática, ciências comportamentais). (MARINS, Fernando Augusto Silva 2011)
De acordo com Rabenschlag (2005) e Marins (2011), é possível dividir a solução do problema de pesquisa operacional em cinco fases:
- Identificação do problema – Etapa é necessária identificar o objetivo principal do estudo; além de mapear as restrições, limites e tudo que pode ser limitante do controle do projeto; identificar alternativas das decisões existentes.
- Construção do Modelo matemático – Na construção do modelo matemático, é a etapa onde acontece a modelagem do problema, é onde são construídas as equações ou formando um sistema matemático, indicando quais são as ligações importantes entre as variáveis, quais são as informações relevantes e quais são as variáveis.
- Solução do Modelo – Nesta etapa pode ser utilizado diversos modelos matemáticos de pesquisa operacional, e existem softwares apropriados para auxiliar na resolução desses problemas, por exemplo, o Solver do Excel que irá atuar com planilhas. Ferramenta capaz de otimizar um sistema, esse método irá buscar a solução ótima obtida mais próxima da solução ótima do sistema.
- Teste de validação do modelo – Na validação do modelo, serão realizados os testes para verificar se o modelo matemático é viável de ser solucionado ou não.
- Implementação da solução – Após a validação do modelo, a implementação da solução após ser testada a aprovada, será realizado um acompanhamento da utilização do produto para serem retirados resultados e correções de possíveis erros atípicos.
Conforme citado anteriormente, o Solver é uma das ferramentas de Pesquisa Operacional, que podem auxiliar na tomada de decisão, no próximo capítulo, teremos mais detalhes dessa ferramenta.
2.2 SOLVER
O Solver é um software disponível no Excel ou em softwares personalizados desenvolvidos com programação. Essa ferramenta tem a capacidade de auxiliar na resolução de problemas de otimização, seja maximizando ou minimizando um sistema matemático ou alcançando um valor específico, desde que o sistema seja viável. A ferramenta pode ser aplicada em uma variedade de cenários, em cada caso, envolvendo várias decisões que precisam ser tomadas da melhor maneira possível, enquanto simultaneamente satisfazem um conjunto de condições lógicas ou restrições. A “melhor” solução pode significar maximizar os lucros, minimizar os custos ou alcançar a melhor qualidade possível.
Como parametrizar o Solver do Excel para atender ao modelo matemático?
Para parametrizar o Solver é necessário ter um modelo matemático definido, pois é de extrema importância para seguir as etapas, sendo elas:
- Definir a célula objetivo, ou seja, qual o resultado se quer chegar, sendo eles máximo, mínimo ou algum resultado específico.
- Definir as células variáveis, ou seja, as decisões que serão tomadas, ou quais serão as células que a ferramenta irá simular valores, para se atender a função objetivo.
- Definir as restrições do problema matemático, e em quais as células elas estarão, essas restrições geralmente são os limitantes do problema.
- Após todas as etapas concluídas, a ferramenta simulará valores nas células varáveis até encontrar os valores ideais que satisfazem as restrições e soluciona a célula objetivo, seja maximizando, minimizando ou chegando em um resultado desejado. Esses valores encontrados nas células variáveis é a tomada de decisão sugerida pela ferramenta, de acordo com o modelo tomado.
Em outros Softwares Personalizados, geralmente são utilizados código em uma linguagem de programação como Visual Basic, C#, Java ou C/C++. Variáveis ou matrizes no programa contêm as variáveis de decisão e outros dados necessários enquanto o código é escrito para calcular valores para as restrições e objetivos.
O Solver consegue resolver esses tipos de sistemas matemáticos devido aos fundamentos de Programação Linear que ele possui, vamos aprofundar um pouco mais sobre esse método.
2.3 PROGRAMAÇÃO LINEAR
Moreira (2015), diz que essa programação é um dos modelos matemáticos mais populares, desenvolvido para resolver problemas que apresentem variáveis mensuráveis e cujos relacionamentos possam ser exibidos através de equações e/ou inequações lineares.
Os modelos devem ser formulados de acordo com os parâmetros das variáveis de decisão, que são valores fixos e que não devem ser alterados. Essas variáveis podem assumir diversos valores. A função objetivo pode ser maximizada ou minimizada a partir da combinação. O resultado dessa combinação é a solução do problema de programação linear. (MOREIRA 2015).
Segundo Prado (2016), a Programação Linear é uma técnica de planejamento que surgiu no final da década de 1941, encontrou seu aliado natural com o advento dos computadores na década de 1950, depois se acelerou. A Programação Linear é o tópico científico da Pesquisa Operacional, que inclui outros tópicos como Teoria das filas, Simulação, Teoria dos jogos, programação dinâmica PERT/CPM etc.
De acordo com Prado (2016), estudos estatísticos mostram que a Programação Linear é uma das técnicas de pesquisa mais populares atualmente. É comum que os aplicativos, como o Solver e outros que possuem essa técnica, façam parte do processo de planejamento diário nas mais diferentes empresas, desde empresas com equipes de planejamento estabelecidas até empresas que simplesmente adquirem software para determinadas funções de planejamento. É possível conceituar a Programação Linear da seguinte maneira:
- É uma técnica de otimização
- É uma ferramenta utilizada para maximizar ou minimizar resultados, onde temos múltiplas opções sujeitas a algum tipo de restrição ou regulamentação
Sendo assim, Prado (2016) comenta que a Programação Linear é uma técnica de planejamento baseada em matemática e economia e tem sido aplicada em vários campos, como neste presente trabalho, onde auxiliará no faseamento da produção para a melhor utilização da capacidade produtiva, atendendo as restrições impostas pelo cliente. E em outros campos como mostram os seguintes cenários abaixo:
- Alimentos: Quais alimentos as pessoas devem comer para minimizar custos, ter a quantidade certa de nutrientes e atender à variedade, aparência, sabor e outros requisitos da refeição.
- Rotas de Transporte: Qual deve ser a roteirização dos veículos de carga para movimentar todas as mercadorias no menor tempo e com o menor custo total.
- Siderurgia: Qual minério deve ser carregado em um alto-forno para produzir um determinado aço dentro das especificações de um determinado elemento químico ao menor custo.
- Fabricação: Qual deve ser a composição do produto fabricado pela empresa para obter o máximo lucro, respeitando as restrições ou exigências do mercado comprador e a capacidade produtiva da fábrica.
Vimos que a Programação Linear é um modelo que pode ser aplicado em diversas áreas e de diversos modos, mas esta técnica agregada com a Análise de Sensibilidade, outro método dentro da Pesquisa Operacional e que o Solver também possui como ferramentas, pode se tornar mais assertiva ainda, pois falaremos sobre seus benefícios e sua definição no próximo capítulo.
2.4 ANÁLISE DE SENSIBILIDADE
Para Colin (2011), a análise de sensibilidade é o estudo do impacto que o valor objetivo terá, ao sofrer alterações nos parâmetros de acordo com a modelagem do problema. Tais parâmetros pode ser: o coeficiente das variáveis nas restrições ou o coeficiente b de alguma restrição (lado direito da restrição), ou na função objetivo, entre outros. É possível visualizar a aplicação desse estudo em organizações que trabalham com modelos quantitativos de gestão, como por exemplo, valor gasto com matéria prima ou quantidade de produtos que serão vendidos.
Dessa forma, “a análise de sensibilidade é fundamental no estudo de problemas de programação linear, já que tem como objetivo investigar os efeitos que determinadas alterações nos parâmetros do modelo causariam na solução ótima” (FÁVERO, BELFIORE, 2013, p. 174).
Consequentemente, as finalidades da análise de sensibilidade são: encontrar os parâmetros sensíveis (parâmetros que podem alterar a solução ótima); e para os parâmetros não sensíveis, definir os possíveis intervalos de valores (que não possuem relação com a alteração da solução ótima) (HILLIER, LIEBERMAN, 2013). Assim, a análise de sensibilidade auxilia na avaliação de como mudanças no modelo e na aplicação real podem influenciar na solução, de forma positiva ou negativa (COLIN, 2013), além de detectar o nível de dependência de uma determinada constante ou coeficiente em relação à solução (LACHTERMACHER, 2006).
Segundo Lachtermacher (2006), Fávero e Belfiore (2013), podemos enquadrar a análise de sensibilidade em dois grupos específicos. O primeiro é caracterizado pelo estudo da probabilidade de variações e influências na solução ótima de um problema, nos casos de apenas uma alteração por vez; já o segundo considera mais de uma alteração de forma simultânea.
Para o primeiro grupo, chamado de análise de sensibilidade, “estuda-se a variação que os coeficientes da função objetivo e as constantes do lado direito de cada restrição podem assumir (limites inferiores e superiores), sem alterar a solução ótima do modelo inicial ou sem alterar a região de factibilidade”. Nesse caso a avaliação dos dados pode ocorrer através de cálculos algébricos, gráficos, diretamente pelo Solver do Excel ou outros softwares como o LINDO. Fávero (2013, p.174 apud LOPES, 2019, p. 23).
O segundo grupo, chamado de análise de sensibilidade pós-otimização, “é empregado quando, após mudanças nos parâmetros do modelo, a solução ótima do modelo é afetada (a solução passa a ser sub-ótima ou infactível), sendo necessário recalcular a nova solução ótima do modelo” (FÁVERO, BELFIORE, 2013, p. 174). Para esse tipo de análise são usados gráficos (para até duas variáveis) e o método Simplex.
2.5 MÉTODO SIMPLEX
Segundo Andrade (2012), o Método Simplex é a ferramenta que em geral pode ser utilizada para a resolução de problemas de alocação de recursos que pertence a um capítulo da pesquisa operacional chamado de programação linear.
Após a definição de todos os componentes que serão utilizados nesse presente artigo, no próximo capítulo será realizado o detalhamento do estudo de caso realizado.
3. DETALHAMENTO DA PROBLEMÁTICA (ESTUDO DE CASO)
A empresa estudada é uma fabricante de placas eletrônicas, localizada em São Paulo, que comercializa o os seus produtos para clientes de diversos seguimentos. Um de seus principais clientes é uma empresa de aparelhos celulares e notebooks, onde sua linha de produção é dedicada para a produção de placas deste grande cliente.
Apesar de dedicar quase toda sua linha de produção para a sua cliente montadora de aparelhos eletrônicos, a empresa fabricante de placas possui grandes problemas no atendimento da demanda acordada em contrato, pois trata-se de 10 placas diferentes para serem produzidas, que somando os volumes podem chegar até 300 mil placas por mês.
Por se tratar de um serviço muito customizado para esse cliente, o maquinário utilizado é muito restrito e teria que ser desenvolvido novamente do zero, acarretando grandes custos para a aquisição desse novo equipamento. Como a empresa não possuía um setor de Planejamento e Controle de Produção, um analista da empresa de eletrônicos resolveu se juntar com os seus colegas de faculdade e mapear a produção da fornecedora, para entender se é possível realizar o atendimento da demanda, ou se terão que buscar novas alternativas para atender ao volume mínimo necessário.
Após a equipe mapear durante 2 meses o planejamento e a produção da fabricante de placas, foram detectadas algumas restrições na produção. Onde cada uma das placas possuía um desempenho produtivo diferente, devido a sua complexidade na montagem dos componentes, foi identificado também que a empresa só consegue produzir 15 mil placas por dia, considerando os 3 turnos, pois o seu maquinário precisa de uma limpeza após a produção das 15 mil placas, caso não fosse realizada a limpeza poderia comprometer a qualidade e o funcionamento das placas. Abaixo a quadro com a capacidade produtiva de placas por dia:
Quadro 1: Capacidade produtiva de placas por dia
Código Texto breve material Capacidade Diária 628220-P PLACA ARGENTINA 4.500 625220-P PLACA FRANÇA 3.400 623220-P PLACA BRASIL 3.000 627220-P PLACA INGLATERRA 2.000 619127-P PLACA SUÍÇA 1.000 628220-P PLACA PORTUGAL 1.200 612127-P PLACA ITALIA 1.000 615127-P PLACA CANADÁ 1.000 611127-P PLACA BELGICA 800 610127-P PLACA ESPANHA 800
Em seguida ao mapeamento da produtividade total da fábrica de placas diárias, foi realizada a análise do histórico de compras de placas pela cliente e qual o comportamento mensal dos meses nos períodos de sazonalidades, onde a demanda atinge a capacidade total produtiva de 300 mil placas por mês, com isso separamos os 6 meses com os maiores valores compras no ano, e no quadro abaixo mostra a quantidade comprada por tipo de placa em cada mês:
Quadro 2: Meses com maiores demandas de compras de placas
Código Texto breve material Janeiro Março Abril Maio Junho Julho 628220-P PLACA ARGENTINA 72.084 79.131 80.345 78.025 77.408 77.785 625220-P PLACA FRANÇA 24.172 20.448 21.812 18.304 18.772 18.261 623220-P PLACA BRASIL 43.579 57.022 59.823 62.839 61.371 62.796 627220-P PLACA INGLATERRA 43.017 41.087 40.173 41.363 40.128 41.320 619127-P PLACA SUÍÇA 15.672 8.041 8.339 8.261 9.165 8.218 628220-P PLACA PORTUGAL 31.017 32.741 33.376 34.359 34.317 34.513 612127-P PLACA ITALIA 22.607 23.001 20.010 20.460 20.449 20.015 615127-P PLACA CROACIA 18.996 15.464 17.820 18.172 18.643 18.129 611127-P PLACA BELGICA 15.134 8.991 10.674 10.700 11.498 10.657 610127-P PLACA ESPANHA 13.722 14.074 7.628 7.517 8.249 8.306
Em seguida foi realizada a análise do que era produzido diariamente pela empresa fabricante e percebeu-se que mesmo que a empresa tivesse a capacidade de produção que atenda e demanda de 300 mil placas por mês, foi percebido que o mal faseamento de produção das placas estava atrapalhando a produtividade e o atendimento da fábrica, pois em alguns dias a empresa estava com a capacidade no seu limite e outros dias a fábrica estava com ociosidade, isso por conta da priorização das produções, abaixo um quadro que mostra a os resultados coletados da produção diária para atendimento do mês de Abril.
Quadro 3: Produção diária de Placas para atendimento da demanda de abril.
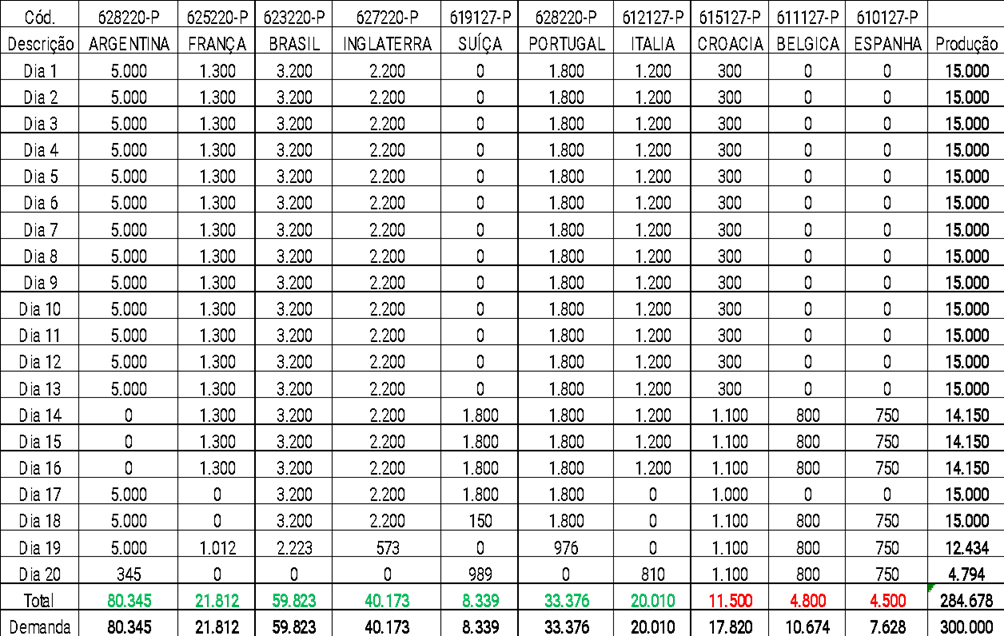
Conforme citado, foi percebido que devido à falta de planejamento da produção, a empresa fabricante de placas possuía problemas com o faseamento da produção, de quais SKU’s produzir e quanto produzir nos dias. No quadro (3) acima, podemos notar que a empresa adotava como estratégia atender as placas com maiores demandas do mês nos primeiros dias do mês. E no final do mês a capacidade ficava ociosa, devido a capacidade diária de produção de cada placa, conforme mostra o Gráfico 1 abaixo:
Gráfico 1: Total da produção diária de placas x capacidade total produtiva
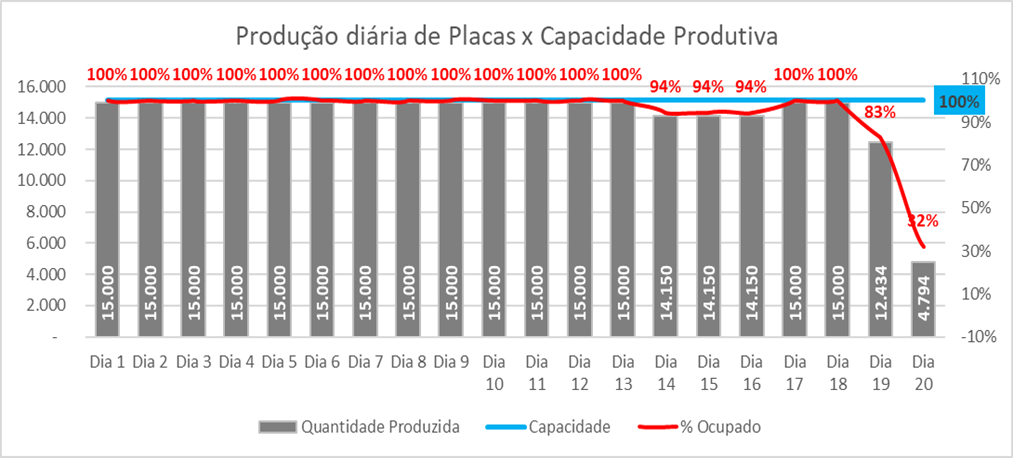
No Gráfico 1, é possível identificar que os primeiros dias do mês estão com a sua capacidade lotada, porém há ociosidade de produção nos últimos dias úteis do mês, conforme já citado, isso ocorre devido ao mal faseamento da produção de placas.
Após a análise realizada sobre como a empresa produzia diariamente as suas placas (Gráfico 1) e a análise das demandas dos meses com maior volume de compras de placas pela grande cliente, foi traçado como estratégia a utilização do Solver, como já citado anteriormente, é um importante componente que faz parte de um pacote de programas MS- Excel chamados de ferramentas de teste de hipóteses e pode auxiliar nas tomadas de decisões. Com os recursos disponíveis na ferramenta, foi possível criar um simulador onde ele auxiliará na tomada de decisão de como realizar um planejamento de produção adequado para a obtenção da melhor produtividade da fábrica e de acordo com as restrições de produção citadas anteriormente.
Para criar um simulador igual ao que foi criado para a fabricante de placas, são necessárias ter algumas premissas bem definidas, sendo elas, qual o objetivo principal do problema, neste caso é o atendimento da demanda mensal da empresa, atendendo as 300 mil placas no mês, conforme acordado em contrato. A segunda premissa, são as quantidades mínimas de produção para atender o Plano Mestre de Produção mensal por placas, de acordo com o Quadro 2. Em terceiro, são quais as restrições/capacidade de produção diária por placas que a empresa possui, conforme ilustrado no Quadro 1.
3.1. PREPARAÇÃO DO SIMULADOR NO EXCEL E SOLVER
A preparação do Excel é o primeiro passo para a solução do problema, onde é preciso deixar organizadas as informações, para que não tenha problemas na parametrização do Solver. Abaixo a figura 1, mostra como foi organizado os componentes necessários para a elaboração do simulador:
Figura 1: Simulador do Solver no Excel
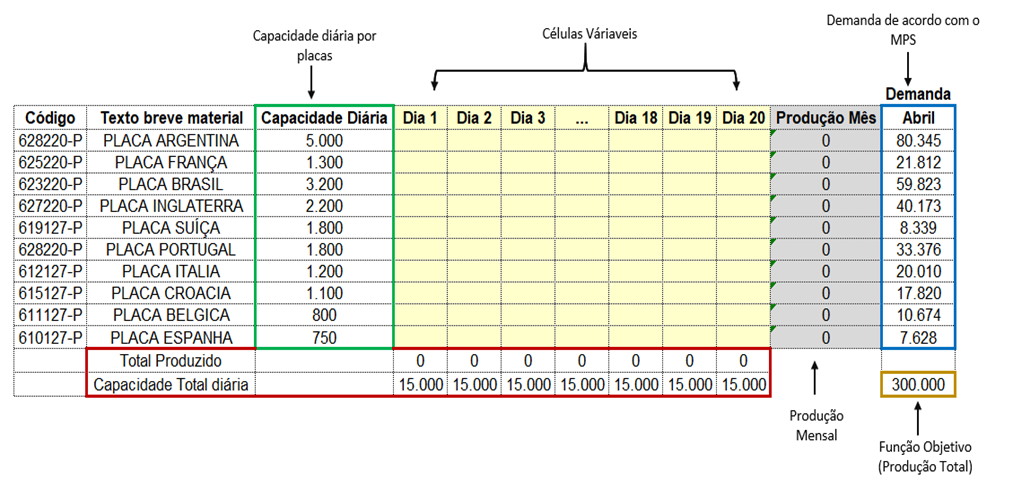
Na figura 1, mostra como foi esquematizado no Excel para a melhor apresentação dos dados de produção diária. Nela mostra a função objetivo, neste caso, a produção total que a empresa deverá realizar para atender a demanda de placas, as capacidades de produção diárias por placas e em sua totalidade, a demanda mensal referente ao mês de março, temos as células variáveis, onde o Solver realizará as hipóteses para viabilizar a produção de acordo com as restrições.
Figura 2: Tela de Parametrização do Solver
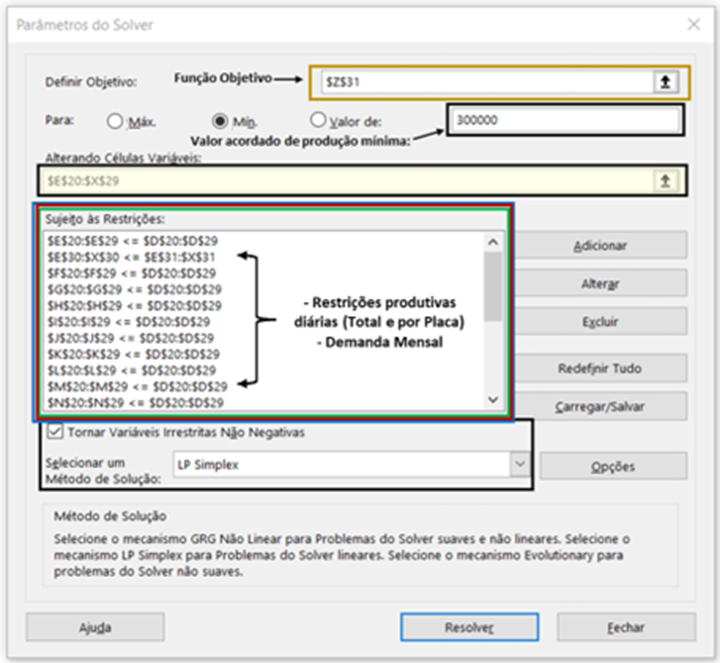
Afigura 2, representa a parametrização do Solver para que seja calculada a produtividade diária de placas, temos a função objetivo, o Solver disponibiliza a opção de escolher qual será o valor atingido na célula objetivo, sendo eles valor máximo, mínimo ou igual à determinado valor. Neste exemplo, pode ser definido tanto como volume mínimo a produzir ou igual a 300 mil placas, conforme informado no contrato com a sua cliente.
A imagem mostra também os locais onde são adicionadas as restrições, sendo elas das capacidades máximas de produção da linha, identificadas como capacidade total diária, e as restrições mínimas de produção mensal, ou seja, qual o mínimo a ser produzido no mês para atender a demanda do MPS da empresa compradora das placas, identificado como demanda, ambas no apresentadas na figura 1. E por último, o local onde é preenchido com as células variáveis que serão alteradas, ponto importante para essa análise é a seleção do campo “Tornar Variáveis Irrestritas Não Negativas”, para que que os resultados não fiquem com números negativos, pois o estudo fala sobre de produção de peças e não é possível produzir peças em quantidades negativas.
Além de o método de solução para LP Simplex, ferramenta que em geral se utiliza para a resolução de problemas de alocação de recursos. Após a parametrização do Excel e do Solver, foramsimulados os resultados e serão discutidos no próximo capítulo.
4. RESULTADOS E DISCUSSÃO
Para demonstrar como poderia ser o faseamento de produção da fabricante de placas eletrônicas, foram escolhidos dois nesses meses, para demostrar que o simulador criado através do Solver é uma ferramenta que auxiliará a empresa nas tomadas de decisões.
Figura 3: resultado da simulação do faseamento de produção referente ao mês de abril
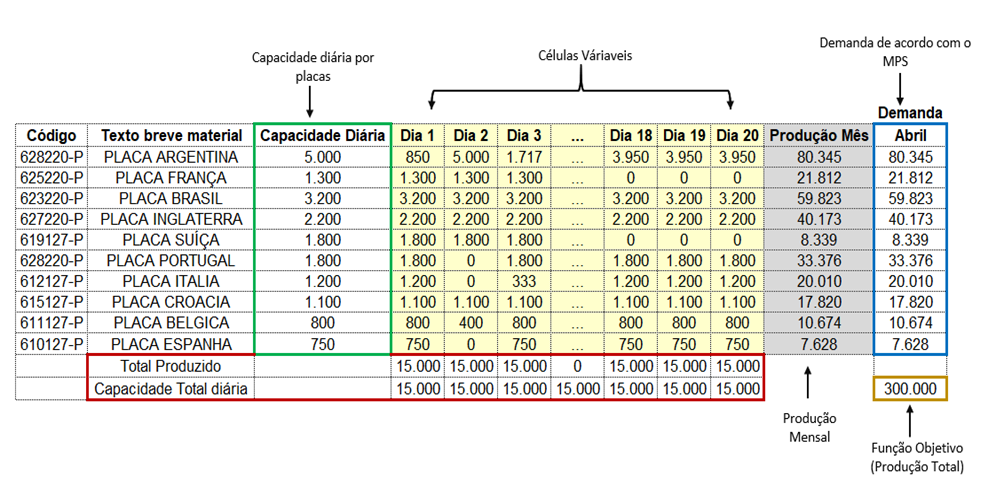
Nafigura 3, mostra que o simulador do Solver conseguiu realizar a simulação dos valores para atingindo todas as restrições impostas no modelo matemático criado. Com esse resultado, é possível perceber que para solucionar o problema de atendimento da demanda, o Solver teve como papel auxiliar na alocação da produção dos itens e na quantidade a ser produzida por dia, ou seja, o que produzir, qual a quantidade e em quais os dias a serem produzidos. Abaixo veremos o quadro (4) com a produção diária detalhada.
Quadro 4: Faseamento da produção referente ao mês de abril simulado no Solver
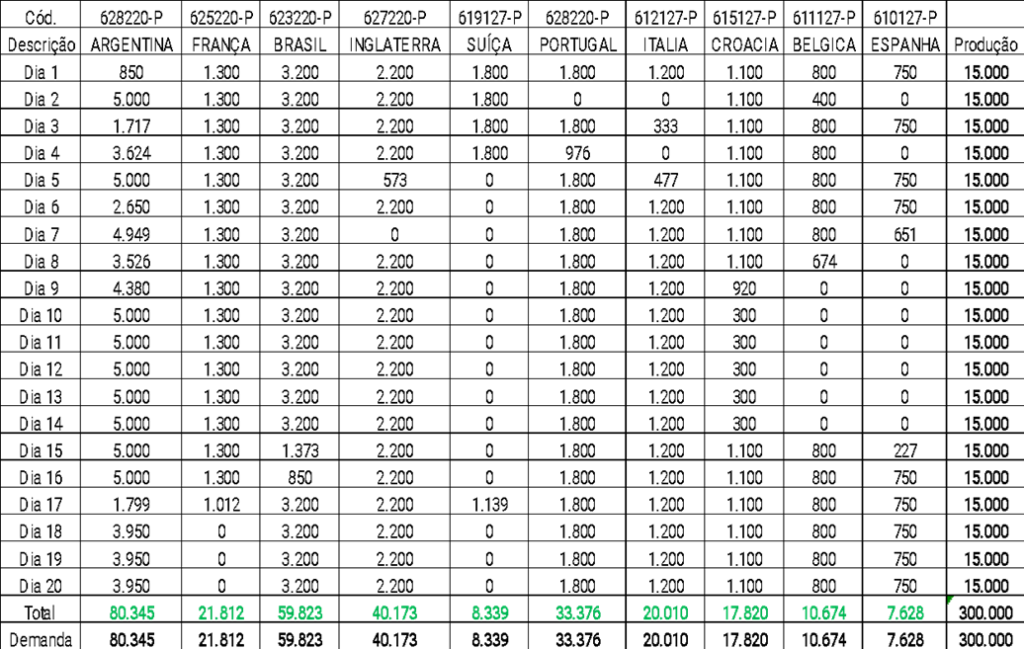
No quadro 4, mostra uma das possíveis soluções de faseamento na produção de placas, o Solver simulou o quanto produzir por placa e por dia, para atender a demanda a demanda de 300 mil placas no mês e atender a demanda do MPS do seu cliente. Podemos notar que além do atendimento das demandas a produção, os resultados simulados por dia não ultrapassaram os limites de capacidades produtivas, sejam elas a capacidade total por dia e a capacidade diária por placa.
Quadro 5: Faseamento da produção referente ao mês de maio simulado no Solver
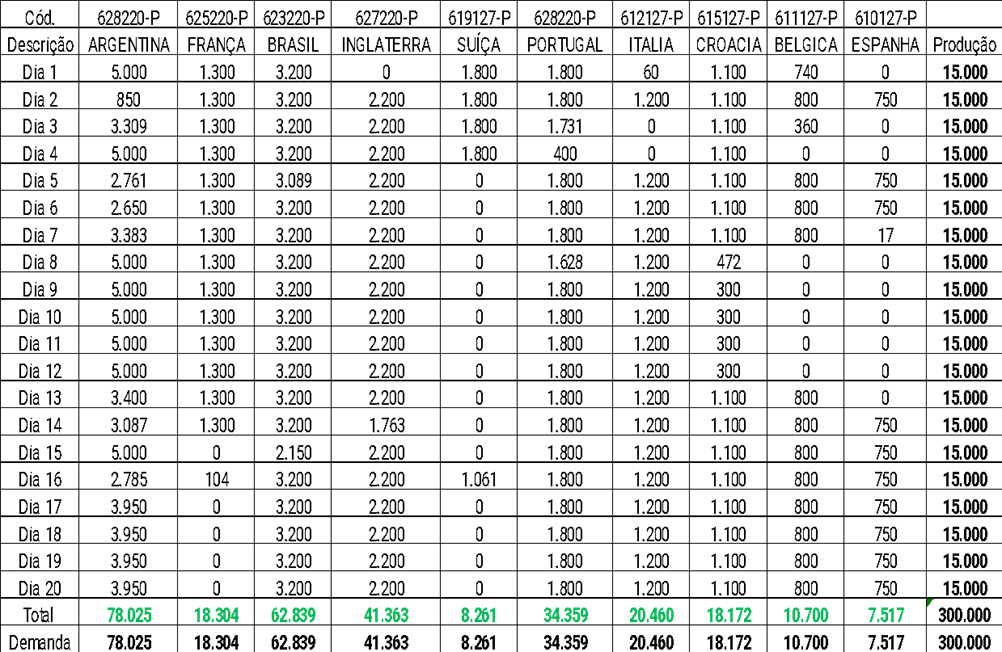
Podemos notar nos dois quadros (4 e 5), que o Solver encontrou os resultados de faseamento de produção das placas para que as demandas fossem atendidas e a fábrica não tivesse dias de ociosidade na sua produção, esses valores sugeridos, são considerados como as variáveis de decisões, é o que auxilia ao gestor a tomar decisões no dia a dia, nestes dois simulados podemos ver que a capacidade produtiva da fornecedora de placas é atingida 100%, conforme mostra o gráfico abaixo:
Gráfico 2: Total da produção diária de placas x capacidade total produtiva
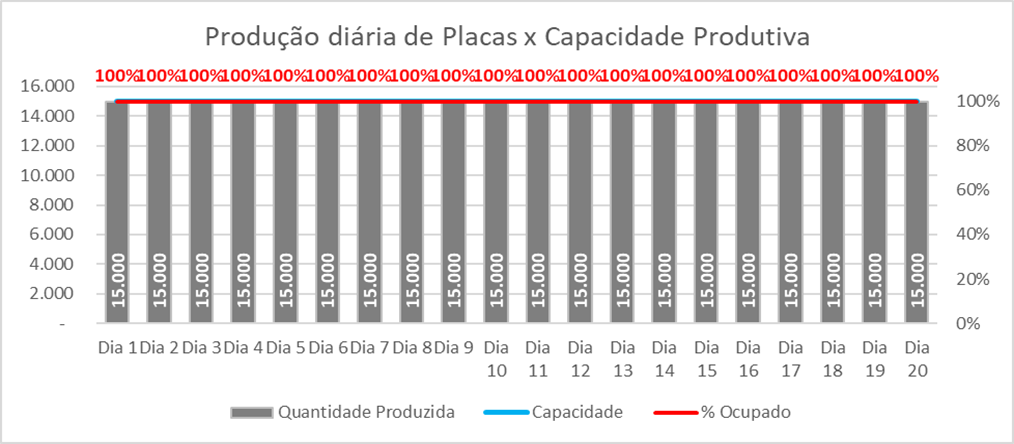
Ao analisarmos o gráfico (2) com a solução proposta pelo Solver, notamos que a capacidade da fabricante está sendo utilizada 100%, ou seja, caso tenha algum acréscimo na demanda, não será possível produzir em sua totalidade. O Solver permite realizar a análise de sensibilidade da forma em que o valor objetivo reage as alterações das variáveis, de acordo com a modelagem do problema. Para obter o relatório que permite analisar estes dados basta habilitar a função conforme ilustrado na figuram (4) abaixo:
Figura 4: Tela do Solver para habilitar o relatório de Sensibilidade
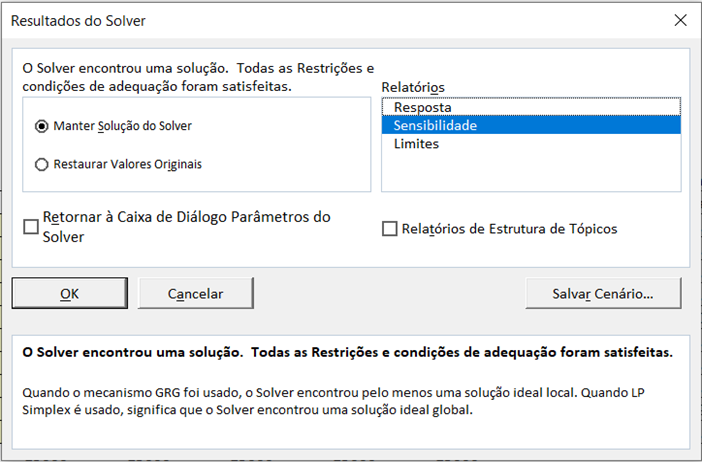
Após habilitar o relatório de sensibilidade o Solver irá gerar um relatório igual a quadro 6 abaixo, nele podemos ver a resposta final de acordo com a simulação e a coluna com os limites no que é permitido aumentar ou diminuir, sem que haja alteração do valor na função objetivo.
Quadro 6: Relatório de Análise de Sensibilidade
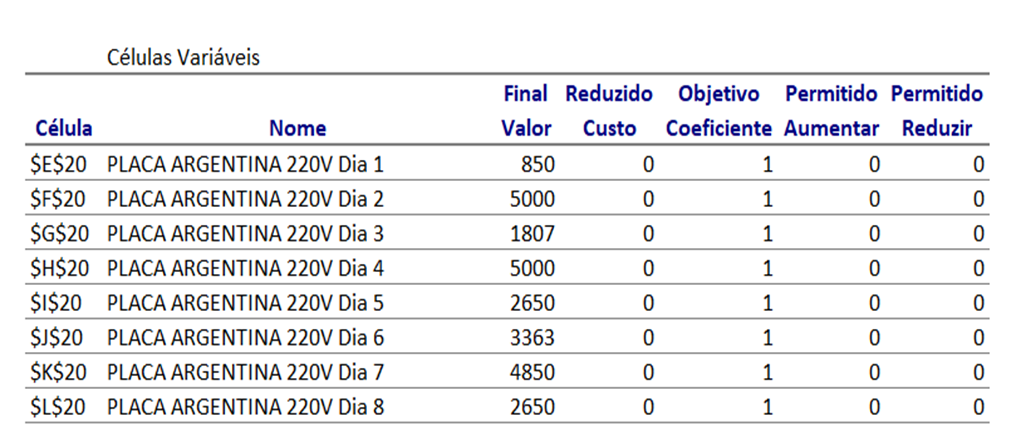
Neste estudo, como notamos que a capacidade está 100% ocupada, então a folga para ajuste é igual a zero, conforme mostra o quadro (6), onde não é possível aumentar a produção por dia, pois excederia a capacidade produtiva diária, o máximo que poderia ser ajustado seria a ordens dos dias de produção, conforme ilustrado no quadro (6).
5. CONSIDERAÇÕES FINAIS
Vimos que as empresas estão buscando cada vez mais a melhoria de seus processos, e para as indústrias, ter um bom setor de Planejamento e Controle de Produção que saiba mapear a capacidade produtiva, organizar a linha de produção e que consiga trabalhar com ferramentas de otimização e/ou simulação é algo muito importante para o seu sucesso, pois assim, pode evitar vários transtornos, como de não atendimento das demandas de seus fornecedores, não conhecimento da capacidade produtiva, ou até mesmo deixando a sua mão de obra ociosa.
Nos resultados obtidos, notamos que nem sempre realizar a produção da placa com maior volume, pois esta estratégia adotada pela empresa estava fazendo com que a empresa tivesse a sua capacidade total ocupada no início do mês, e no final por conta da capacidade diária de produção das demais placas, além de não atender a demanda solicitada pelo cliente. E com a solução possível que o Solver retornou, o resultado mostrou que a se bem realizado o faseamento é possível atender a demanda e não gerar ociosidade na linha de produção.
Com isso, o Solver, que éuma ferramenta de otimização e simulação, dentre outras na Pesquisa operacional, que pode auxiliar aos analistas e gestores a tomarem as decisões assertivas, com base nos modelos matemáticos construídos, para lidar com problemas de alocação e coordenar os procedimentos em uma organização, baseando-se em dados coletados e nos métodos científicos para resolver problemas.
6. REFERÊNCIAS
COLIN, Emerson Carlos. Pesquisa operacional: 170 aplicações em estratégia, finanças, logística, produção, marketing e vendas. Rio de janeiro: LTC, 2011.
COLIN, E. C. Pesquisa Operacional: 170 aplicações em estratégia, finanças, logística, produção, marketing e vendas. Rio de Janeiro: Ltda, 2013.
FÁVERO, L. P.; BELFIORE, P. Pesquisa operacional para concursos de engenharia. Rio de Janeiro: CIP-Brasil, 2013.
LACHTERMACHER, G. Pesquisa Operacional na Tomada de Decisões. 5ª. ed. Rio de Janeiro: CIP-BRASIL, v. II, 2018.
LOPES, Thaís Ferreira. Análise de sensibilidade em modelos de programação linear com solução degenerada: revisão sistemática e estudo aplicado na Agência de Aviação Civil. 2019.
MORETTI, V. et al. Aplicação da Programação Linear para maximização de lucros numa organização do setor varejista. In: X Congresso Brasileiro de Engenharia de Produção, 2020, p. 1-12.
PRADO, D. S. Programação Linear: Série Pesquisa Operacional, vol 1 – 7. 7. ed. São Paulo: Editora Blucher, 2016.
PRADO, D. Programação linear. Belo Horizonte: Editora UFMG, 1999.
MARINS, F. A. S. Introdução à pesquisa operacional. São Paulo: Cultura Acadêmica, 2011.
SUNO. Análise de sensibilidade: o que é e como aplicá-la em investimentos. Disponível em: https://www.suno.com.br/artigos/analise-de-sensibilidade/. Acesso em: 11 fev. 2023.
RABENSCHLAG, D. R. Pesquisa operacional. Santa Maria: Universidade Federal de Santa Maria, 2005.
ANDRADE, E. L. Introdução à pesquisa operacional: métodos e modelos para análise de decisões. 4. ed. Rio de Janeiro: LTC, 2012.
COLIN, E. C. Pesquisa Operacional: 170 aplicações em estratégia, finanças, logísticas, produção, marketing e vendas. São Paulo: LTC, 2011.
MOREIRA, D. A. Pesquisa Operacional: curso introdutório. 2. ed. São Paulo: Cengage Learning, 2015.
FRONTLINE SYSTEMS. Definir e resolver um problema usando o Solver. Disponível em: https://support.office.com/pt-br/article/Definir-e-resolver-um-problema-usando-o-Solver9ed03c9f-7caf-4d99-bb6d-078f96d1652c. Acesso em: 21 jan. 2023.
SOLVER. Optimization Tutorial. Disponível em: https://www.solver.com/optimization-tutorial. Acesso em: 15 fev. 2023.
