STUDY OF THE BEHAVIOR OF A SELF-EXCITED INDUCTION GENERATOR IN STEADY STATE
REGISTRO DOI: 10.5281/zenodo.10048551
Daniel Maynart Coriolano de Melo¹
Sebastião Ércules Melo²
Elkin Ferney Rodriguez Velandia²
Capítulo 1
Introdução
1.1. Apresentação
Desde a descoberta de Michael Faraday e a criação do primeiro gerador de indução em 1831, também conhecido como dínamo, a aplicação de máquinas assíncronas na indústria é crescente e cada vez mais indispensável no mundo moderno.
Atualmente geradores de indução, em sua maioria, operam em paralelo com a rede elétrica, não criando dificuldade para o funcionamento destes equipamentos, visto que a própria a rede consegue fornecer a potência reativa necessária à máquina. Uma outra maneira de funcionamento do gerador é quando o mesmo trabalha de forma isolada, ou seja, desconectado da rede elétrica. Desta forma o gerador funciona em conjunto com um banco de capacitores conectado em paralelo que, através do processo de auto excitação, consegue fornecer energia reativa suficiente para a máquina, possibilitando que o gerador passe a entregar energia elétrica a partir dos seus terminais. A operação isolada do gerador tem como uma de suas aplicações o uso associado ao fornecimento de energia em áreas remotas ou de menor infraestrutura, visto que é relativamente de baixo custo, exige pouca manutenção e pode utilizar, por exemplo, a queda da água, vento ou combustível como força motriz.
1.2. Objetivo
Este trabalho busca estudar a teoria e analisar o comportamento do gerador de indução auto excitado a partir dos ensaios feitos em laboratório e do resultado do código elaborado para simulações.
1.3. Metodologia
Inicialmente é realizada uma abordagem teórica do tema, detalhando a máquina no geral e as informações necessárias para dar prosseguimento ao trabalho. Com o entendi- mento teórico do funcionamento do gerador é possível elaborar a simulação digital, usada como referência para comparação com os ensaios práticos. Em seguida, no laboratório, são realizados ensaios básicos de curto-circuito, rotor livre e rotor bloqueado a fim de encontrar os parâmetros da máquina. Com os parâmetros do gerador foi possível construir a curva de magnetização e inserir dados de entrada no algoritmo e, assim, simular o ensaio de carga variável de velocidade fixa. Posteriormente são realizados os ensaios do gera- dor auto excitado observando os acontecimentos presencialmente e o seu desempenho. Após estes procedimentos foram comparados os resultados de ensaio de carga variável de velocidade fixa com os resultados da simulação. Por fim tem-se a conclusão do trabalho.
1.4. Organização do trabalho
No capítulo 1, introdutório, temos a ordem do trabalho escrito vista na seguinte sequência: O capítulo 2 apresenta os aspectos gerais da máquina de indução, sua curva de conjugado e seu esquemático. O capítulo 3 aborda mais especificamente o seu comporta- mento como gerador auto excitado e mostra como será o modelo teórico para simulação. Os ensaios básicos de curto-circuito, rotor bloqueado e a vazio, que possibilitam encontrar os parâmetros da máquina e a construção da curva de magnetização são encontrados no capítulo 4. O capítulo 5 apresenta os ensaios do gerador auto excitado, que permitem analisar sua performance quando se varia sua carga, velocidade e capacitância. A construção do algoritmo e o método de solução iterativa utilizado são demonstrados no capítulo 6. O capítulo 7 compara os valores práticos com os obtidos da código desenvolvido. Por fim, no capítulo 8, temos a conclusão do trabalho com comentários gerais sobre o tema.
Capítulo 2
Fundamentos Básicos
2.1. Aspectos Construtivos e Funcionamento
Uma das vantagens da máquina de indução, quando comparada a outras máquinas rotativas, é a sua construção mais simples que permite, de maneira geral, um menor custo de fabricação e manutenção. Sua característica física possibilita seu funcionamento sem ter a necessidade de uma corrente de campo contínua, como nas máquinas síncronas por exemplo.
Este equipamento, resumidamente, é composto por um estator e um rotor. O primeiro tem sua parte fixada à carcaça por onde passa a corrente elétrica alternada que produz um campo magnético variante no tempo que, pela lei de Faraday-Neumann-Lenz, induz tensão no rotor[1]. Consequentemente, tem-se uma corrente que gera um fluxo magnético que se contrapõe a variação do fluxo magnético produzido no estator. O torque desenvolvido pela máquina é produzido pela iteração entre o fluxo magnético gerado pelo estator e o rotor presente no interior da maquina. Vale ressaltar que as máquinas de indução apresentam uma falta de sincronismo entre o movimento do rotor e o campo magnético girante a fim de manter a indução de corrente necessária para o funcionamento da máquina. Este movimento do rotor é responsável pela energia mecânica da máquina. Será visto mais adiante como é o fluxo de energia de acordo com seu modo de operação.
Existem dois tipos de máquina de indução trifásica: rotor bobinado e gaiola de esquilo, sendo este último o utilizado nos ensaios deste trabalho.
O rotor bobinado, visto da figura 2.1, é construído de forma a ter os terminais do rotor disponíveis na carcaça graças ao uso de anéis no rotor e de escova no estator composição entre os seus anéis e sua escova, podendo ser adicionar resistências que permitem controlar o conjugado de partida.

Figura 2.1: Rotor Bobinado
O rotor gaiola de esquilo, visto na figura 2.2, é o mais comum comercialmente, possuindo como principal característica construtiva a conexão entre suas barras e seus anéis.

Figura 2.2: Rotor Gaiola de Esquilo
2.2. Modelo Teórico
A modelagem teórica da máquina de indução é praticamente igual a utilizada com o transformador e pode ser usada tanto para rotor bobinado ou rotor gaiola de esquilo (usado no experimento). A principal mudança se encontra no escorregamento, que é a diferença entre a velocidade do rotor e a velocidade do campo magnético girante do estator, passando a ser considerado no circuito equivalente. Vale ressaltar que a velocidade do rotor, para operação como gerador, é sempre maior que a velocidade do campo magnético gerado pela corrente no estator. O fato da máquina operar como gerador com velocidade acima da síncrona faz com que o escorregamento da máquina seja negativo, evidenciando que a máquina está injetando potência na rede em que está conectada.
2.2.1. Desenvolvimento Matemático
A primeira expressão a ser mostrada para desenvolvimento do circuito equivalente do gerador de indução trifásico é a equação da velocidade síncrona em rotações por minuto [rpm].

Em que:
- ηs-velocidade síncrona em rotações por minuto [RPM]
- fs– frequência da rede [Hz]
- P– número de polos
Para efeito de análise, é possível fazer a mudança de unidade de rotações por minuto para radianos por segundo [rad/s].

- ωs– velocidade angular síncrona em [rad/s]
O escorregamento pode ser definido nas seguintes equações:

- s– escorregamento
- r ω′– velocidade angular do campo magnético girante do rotor [rad/s]
- ωr– velocidade angular do rotor [rad/s]
Em consequência da relação das equações vistas acima, temos:

- fs– frequência da tensão do estator
- r f′– frequência induzida no rotor ou frequencia de escorregamento
2.3. Circuito Equivalente
Dadas as equações do tópico anterior, pode-se modelar o circuito equivalente do gerador de indução para sua análise[2], visto na figura 2.3
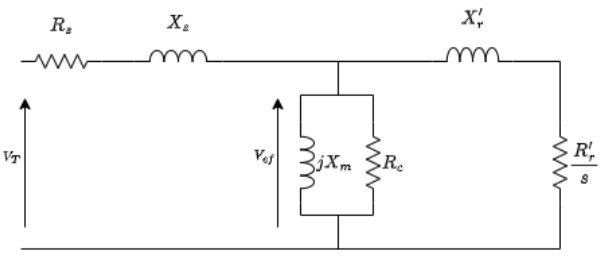
Figura 2.3: Circuito equivalente do de gerador de indução
- Rs– Resistência do estator
- Xs– Reatância do estator
- Rc– Resistência do núcleo
- Xm– Reatância de magnetização
- r R′– Resistência do rotor
- r X′– Reatância do rotor
- s– Escorregamento
- Vt– Tensão terminal
- Vef– Tensão de entreferro
r A composição entre as perdas por histerese e por corrente parasita da máquina podem ser resumidas como perdas no núcleo, que são representadas pela resistência Rc. As per- das de potência também acontecem nos enrolamentos do estator e rotor, representadas por Rse R′, respectivamente. As perdas por dispersão do fluxo magnético são representadas
r por Xs, X′e Xm, que são as reatância do estator, rotor e de magnetização, respectivamente.
2.4. Modos de Operação
Um dos estudos mais importantes da máquina de indução é a sua curva de conjugado- velocidade. Ela permite a análise do torque aplicado e seus modos de operação, além dos seus pontos de máximo e mínimo, fundamentais para avaliação de seu comportamento. Entretanto, para a construção do seu gráfico, é necessário o desenvolvimento do seu circuito equivalente, como é visto na figura 2.4. Com o objetivo de avaliar a máquina de indução de uma forma mais adequada, é possível utilizar o teorema de Thévenin a fim de remodelar seu circuito equivalente.
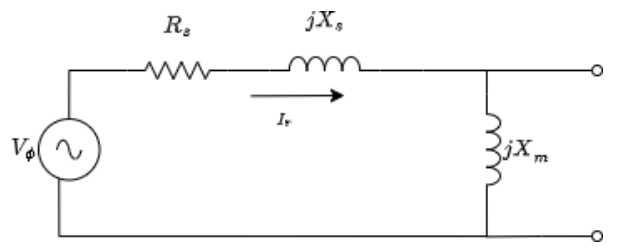
Figura 2.4: Tensão equivalente de entrada de um motor de indução
Uma que vez que a Xmé consideravelmente maior que o restante dos parâmetros da máquina, visto na figura 2.4, a equação da tensão de Thévenin pode ser simplificada ou aproximada por [1]:

Para o cálculo de impedância de Thévenin Zthtemos:
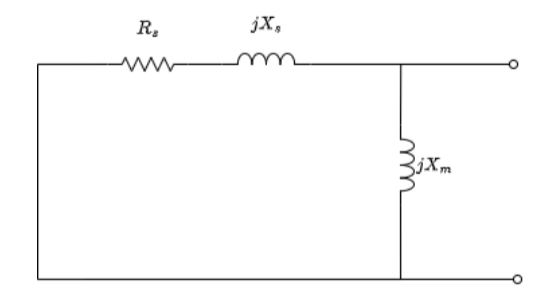
Figura 2.5: Impedância de Thévenin do circuito de entrada
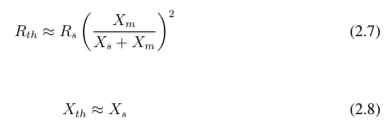
É possível ver a informação do circuito equivalente de Thevenín e o circuito do rotor na figura 2.6.
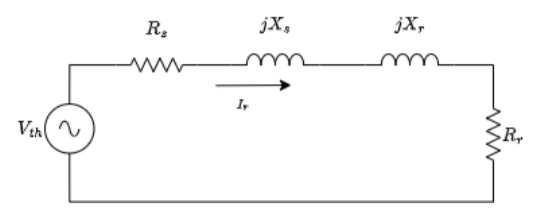
Figura 2.6: Circuito equivalente de Thévenin
Uma vez que o circuito visto na figura 2.6 tem seus elementos em série, podemos associar pela lei de Kirkchoff a corrente do rotor com a tensão de Thévenin e as impedâncias da seguinte forma:

Sendo:
- Zth= Rth+ jXth– Impedância equivalente de Thévenin
- s Zr= Rr+ jXr– Impedância do rotor
Para se chegar à equação de torque induzido, deve-se apresentar a equação que representa a potência de entreferro visto na equação 2.10. Podemos, resumidamente, defini-la como a potência que é transferida do estator ao rotor devido ao campo magnético presente no entreferro. Parte desta potência que flui no entreferro de um motor de indução é consumida como perdas no cobre do rotor e outra parte é convertida em potência mecânica para acionar o eixo do motor [1].

- Pef– Potência de entreferro
Finalmente podemos mostrar a equação de torque induzido 2.11.

- τind– Torque induzido
Fruto da combinação das equações 2.9, 2.10 e 2.11, temos a equação 2.12 para construção da curva de conjugado.
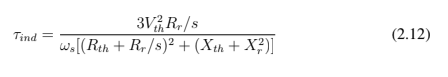
O resultado do desenvolvimento matemático visto é a relação da curva de conjugado- velocidade, observado na figura 2.7, que é fundamental para entender seu comportamento da curva para determinada velocidade e o modo de operação do motor. Como dito anteriormente, tanto para motor quanto para gerador temos uma faixa de escorregamento que mostra como é o fluxo de energia da máquina.
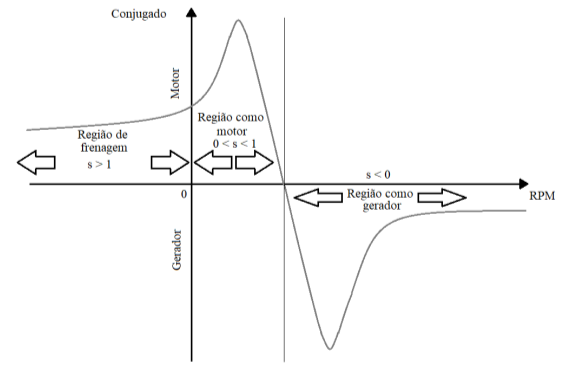
Figura 2.7: Conjugado × velocidade de rotação por minuto
Na atuação como motor, tem-se que o escorregamento varia entre 0 e 1, e seu objetivo é entregar energia mecânica recebendo energia elétrica através de seu estator. Já para atuação como gerador, o escorregamento é menor que 0, o rotor recebe energia mecânica para entregar energia elétrica pelo seu estator. Na operação por frenagem a contramarcha, o escorregamento é maior que 1, temos a mudança o sentido de rotação por inversão das fases do motor.
2.5. Fluxo de Potência
O fluxo de potência do gerador de indução é praticamente idêntico quando a máquina opera como motor. A diferença, já mencionada anteriormente, ocorre devido ao sentido do fluxo. Neste caso, o gerador recebe na sua entrada potência mecânica no seu eixo oriundo de turbinas eólicas, máquinas térmicas, quedas-d’água, entre outros e entrega potência elétrica na sua saída. Entretanto, no decorrer do fluxo ocorrem perdas por diversas causas, referenciadas abaixo, que podem ter maior interferência dependendo das condições da máquina, temperatura do ambiente e da carga.
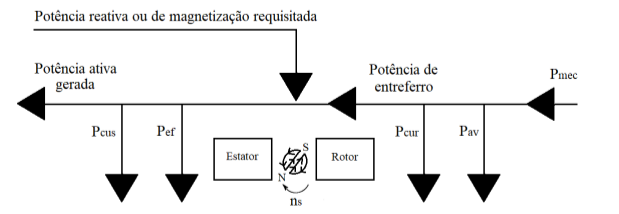
Figura 2.8: Fluxo de potência do gerador de indução
Em que:
- Pmec– Potência mecânica de entrada
- Pav– Perdas por atrito e ventilação
- Pcur– Perdas no cobre do rotor por efeito Joule
- Pef– Potência de entreferro
- PFe– Perdas no núcleo por histerese e correntes parasitas
- Pcus– Perdas no cobre do estator por efeito Joule
- P– Potência elétrica de saída
Capítulo 3
Gerador Auto excitado
3.1. Fenômeno da Auto excitação
Para o funcionamento do gerador de indução é necessária potência reativa devido à característica indutiva da máquina. Essa potência pode ser fornecida quando o gerador é ligado à rede ou por banco de capacitores quando trabalha de maneira isolada, ou seja, operando de forma auto excitada. Ao escolher a inserção de um banco de capacitores, vemos o fenômeno ressonância no gerador devido a sua característica indutiva possibilitando o aumento de tensão nos seu terminais e, consequentemente, promovendo a sua excitação já que na frequência de ressonância é possível alcançar a maior corrente que de magnetização [3].
É desta forma que a reatância capacitiva é capaz de prover a corrente de magnetização com o avanço de fase, produzindo um fluxo magnético de orientação idêntico ao encontrado pelo magnetismo residual, incrementando a magnetização da máquina que é limitada até a sua saturação.
Vale ressaltar que o processo de auto excitação necessita do movimento do rotor e do magnetismo residual, obtido de utilizações anteriores da máquina, que é essencial para permitir que haja indução de tensão no estator. No entanto, a baixa intensidade desse magnetismo remanescente não é suficiente para fornecer energia elétrica na sua saída.
A curva de magnetização é vista na figura 3.1, sendo obtida através do ensaio a vazio, cuja tensão deve ser levada até região de saturação, cerca de 120% da tensão nominal [1].
A auto excitação ocorre com a troca de energia entre o capacitor e o gerador, começando na tensão de “V1″oriundo do magnetismo residual, seguindo uma sequência na qual o capacitor é carregado e descarregado até o ponto de saturação “T“.
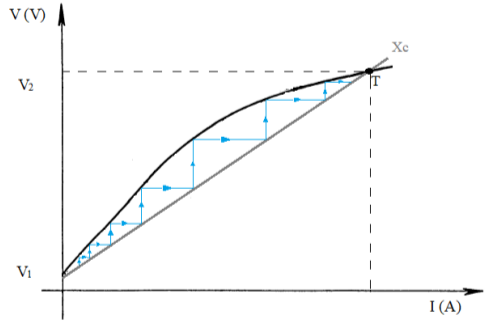
Figura 3.1: Processo de auto excitação
Com os dados da curva de magnetização da máquina, é possível avaliar os efeitos da reatância capacitiva e determinar os limites teóricos e práticos, mostrando uma faixa de valores, como é observado na figura 3.2.
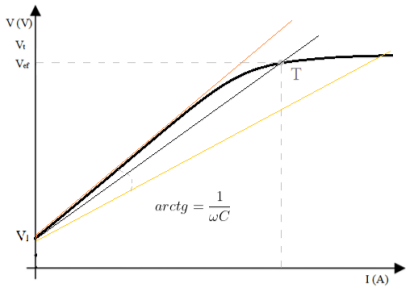
Figura 3.2: Limites de capacitância
O limite superior do capacitor deve tangenciar o ponto de maior inclinação da curva de magnetização. Isto se deve ao fato de que a reatância capacitiva não poder ser maior do que a reatância do núcleo pois, caso seja, o sentido do fluxo de potência seria invertido e o gerador não seria magnetizado adequadamente. O limite inferior deve respeitar o ponto de saturação da máquina, evitando danos a ela já que neste ponto a corrente passaria do valor nominal.
Para calcular a capacitância máxima e mínima devemos seguir as equações: 3.1 e 3.2:

Apesar de ser bastante difícil de acontecer, a máquina de indução pode perder seu magnetismo residual. Para recuperá-lo podemos escolher um dos seguintes procedimentos, sendo o primeiro o mais comum e também o utilizado experimentalmente [2]:
- Acionar a máquina de indução como motor a uma alta velocidade de rotação
- Utilizar uma bateria para causar uma corrente de pico nos enrolamentos da máquina
- Manter um capacitor de alta capacitância carregado para causar uma corrente de pico nos enrolamentos da máquina
- Usar um retificador alimentado pela rede para substituir a bateria no segundo mé- todo
3.2. Circuito equivalente do gerador auto excitado
A representação do circuito equivalente por fase do gerador auto excitado pode ser vista na figura 3.3. Basicamente é a figura 2.3 , adicionando nos terminais do estator o capacitor e a carga, que neste trabalho será apenas de caráter resistivo.
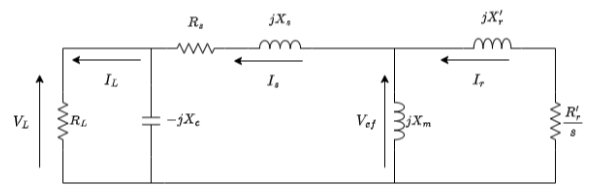
Figura 3.3: Circuito equivalente do gerador de indução com carga
- Xc– Reatância do banco de capacitores
- RL– Resistência de carga
- Is– Corrente no estator
- r I′– Corrente no rotor referido ao estator
- IL– Corrente de carga
O circuito da figura 3.3 deve ser ajustado para uma frequência e rotação por unidade pois experimentalmente o ensaio terá alterações, mesmo que sutis, que podem interferir na análise do gerador[2]. Tais considerações também são previstas na simulação. Portanto, a frequência por unidade:

Assim, o escorregamento é manipulado da seguinte forma:
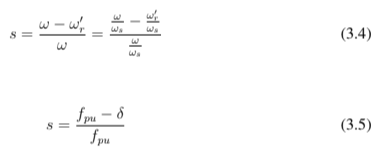
Onde:
- ω – Velocidade de rotação do campo do estator em rad/s
Cujo δ corresponde a:

Como os ensaios práticos dificilmente conseguem manter a mesma velocidade e por conseguinte o mesmo valor de escorregamento, é necessário compensar esta variação. Por este motivo, é utilizada a frequência por unidade “fpu“para corrigir esta variação nos parâmetros que estão relacionados com a velocidade e com o escorregamento, como visto na figura 3.4.
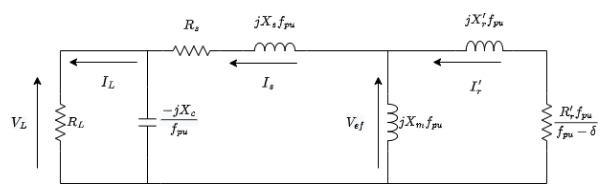
Figura 3.4: Circuito equivalente com frequência por unidade do gerador com carga
O circuito final para análise é visto na figura 3.5, ao dividir os parâmetros por fpu.
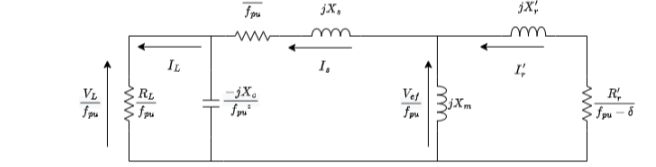
Figura 3.5: Circuito equivalente com frequência por unidade do gerador com carga
3.3. Modelo Teórico para simulação
Para comparar e pré configurar, testando valores de carga, capacitores e velocidade com o ensaio de carga variável a uma rotação fixa, foi elaborado um simulador digital. A premissa deste código se baseia na ausência de uma fonte externa de energia elétrica, permitindo assim que a única tensão no circuito seja oriunda do magnetismo residual da máquina. Entretanto essa tensão é ínfima e igualada a zero. Portanto, temos a equação 3.7 como base para o desenvolvimento teórico do código:

Já que para a magnetização da máquina temos uma corrente circulando então resta igualar a impedância equivalente a zero, como é observado na equação 3.8 , dividindo em parte real e imaginária [4] [5].
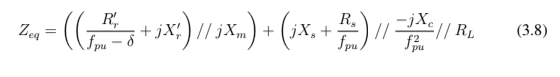
Assim:
- Re{Zeq}= 0
- Im{Zeq}= 0
Por simplificação para elaboração da simulação teremos:
- r Rs= R′= R
- r Xs= X′= X
Das equações 3.7 e 3.8, temos as seguintes deduções:
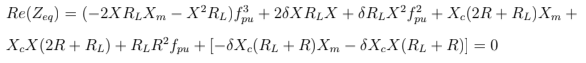
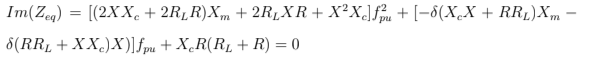
As variáveis Xme fpudevem ser satisfeitas ao mesmo tempo e são valores constantes ponto a ponto que podem ser encontrados através de métodos computacionais, apesar de inicialmente serem encontradas em outros ensaios experimentais. Com estes parâmetros será possível calcular, para cada ponto da simulação, os valores de Is, IL, Vte Ic[4] [5][6][7] .
Em que:
- Is– Corrente do estator
- IL– Corrente de carga
- Vt– Tensão terminal
- Ic– Corrente do capacitor
O primeiro resultado a ser encontrado é a corrente do estator, representada pela equação 3.9. Ela é formulada a partir da malha correspondente aos parâmetros do estator, reatância de magnetização e do capacitor, vistos na figura 3.5.
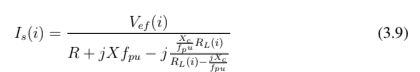
Uma vez definido o valor da corrente do estator podemos formular à equação 3.10, referente a corrente de carga, por um divisor de corrente:
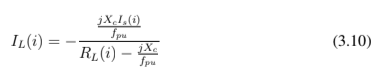
Pela lei de Kirchoff, temos a equação 3.11, para calcular o valor da corrente do capacitor:

Por fim, o cálculo da tensão terminal se dá pela equação 3.12.

Mais adiante no capítulo 6, o código e suas variáveis de entrada e saída serão discutidos com mais profundidade.
Capítulo 4
Ensaios para determinação de parâmetros
4.1. Máquina, equipamentos e ensaios
A máquina disponível é usada como motor e tem suas informações disponíveis na tabela 4.1.
Tabela 4.1: Dados de placa do motor
Fabricante WEG Modelo A56 0297 Potência 1/3 CV Tensão 220/380 V Corrente 1,60/0,92 A RPM 1745 Frequência 60 Hz Isolamento B Categoria N FS 1,35 Grau de Proteção 21 Ligação Triângulo / Estrela Modo de Operação Motor
Os principais equipamentos utilizados, vistos na figura 4.1, são:
- Gossen-Metrawatt MAVOWATT 30
- Disjuntor padrão DIN
- Máquina CC EGC1.3A
- Máquina de indução WEG A56 0297
- Fios
- Autotrafo variável 440V (Variac)

Figura 4.1: Bancada de ensaio
Softwares para tratamento de dados:
- Excel 2021
- Matlab 2018a
Os ensaios para determinação dos parâmetros são:
- Ensaio de curto-circuito
- Ensaio de rotor livre
- Ensaio de rotor bloqueado
4.2. Forma de ligações
A máquina de indução utilizada nos ensaios é de 6 terminais, podendo então ser ligada em delta ou estrela, como na figura 4.2. Para simplificar as medições, utiliza-se a ligação em estrela.
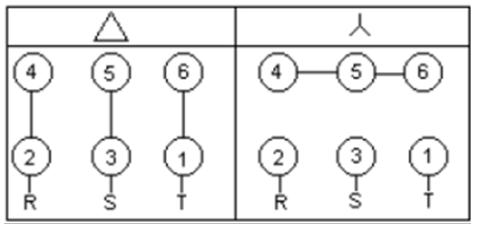
Figura 4.2: Tipos de conexão
4.3. Ensaio de corrente contínua
4.3.1. Objetivo
- Encontrar o valor de resistência do estator.
4.3.2. Material
- Amperímetro Alicate Minipa ET-3350
- Multímetro Fluke 77
4.3.3. Experimento
Aplica-se uma corrente contínua no enrolamento do estator. Como a corrente é contínua, não haverá tensão induzida no circuito do rotor. Além disso, a reatância do motor é zero com corrente contínua pois a mesma está condicionada à frequência[1]. A configuração pode ser observada na figura4.3. A equação 4.1 é responsável por achar o valor da resistência do estator.
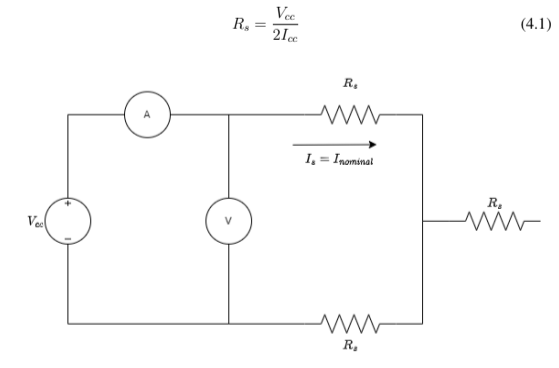
Figura 4.3: Esquemático do ensaio de curto-circuito
O experimento foi realizado para cada fase da máquina e posteriormente calculado os valores médios para encontrar Rs. Na tabela 4.2 vemos os valores por fase e na tabela 4.3 os valores médios.
Tabela 4.2: Valores por fase do ensaio de curto-circuito

Tabela 4.3: Valor médio do ensaio de curto-circuito
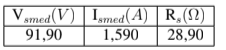
Portanto:
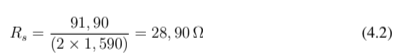
4.4. Ensaio de rotor livre
4.4.1. Objetivo
Medir os dados de tensão e corrente terminais para montar a curva de magnetização com o intuito de encontrar os limites de capacitância com as quais a máquina pode operar. Além disso, calcular o parâmetro de magnetização Xm.
4.4.2. Material
- Gossen-Metrawatt MAVOWATT 30
- Autotrafo variável 440V (Variac)
- Disjuntor padrão DIN
- Fios
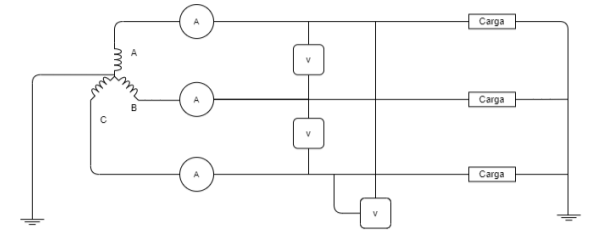
Figura 4.4: Esquemático da aplicação para medição
4.4.3. Experimento
O ensaio de rotor livre (ou a vazio) foi realizado ligando a máquina em indução como um motor em estrela sem carga à frequência nominal. A alimentação é feita por um autotransformador variável elevando o nível de tensão terminal até cerca de 120 % do valor nominal de placa, recomendado pela referência [1]. Desta forma a máquina é capaz de alcançar a região de saturação e pode-se encontrar o limite inferior da reatância capacitiva, uma vez que a corrente deve estar próxima de seu valor nominal para não ter danos ao motor. Pelo fato de a máquina operar a vazio, seu escorregamento é muito pequeno, próximo a zero, o que possibilita a redução do circuito equivalente já que as perdas no rotor são desprezíveis. Assim, temos o circuito aproximado do motor na figura 4.5, não levando em consideração a resistência do núcleo, visto que ela é consideravelmente maior que a reatância de magnetização.
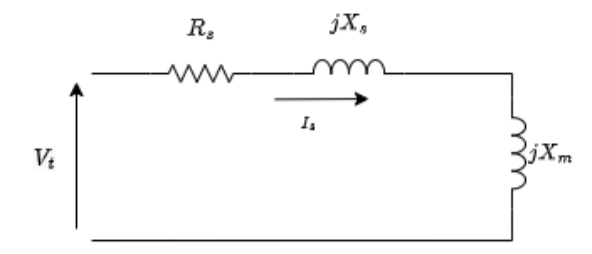
Figura 4.5: Circuito de rotor livre
O cálculo da reatância capacitiva e do capacitor, que serão colocados nos terminais da máquina, vem da equação 4.3. Durante o ensaio foi possível perceber a excitação da máquina a partir do sétimo ponto das tabelas 4.4 e 4.5. A partir deste ponto encontramos o limite de capacitância máximo, cujo valor não ultrapasse mais de 120% o valor de tensão e que fique próximo do valor de corrente nominal, evitando danos à máquina.

Tabela 4.4: Valores por fase do ensaio a vazio
Nº Vsa(V) Vsb(V) Vsc(V) Isa(A) Isb(A) Isc(A) 1 9,80 10,01 10,15 0,126 0,126 0,133 2 21,70 22,42 22,47 0,325 0,339 0,350 3 29,87 30,50 30,56 0,466 0,482 0,492 4 40,79 41,19 41,63 0,654 0,670 0,682 5 50,24 51,35 51,60 0,802 0,830 0,842 6 60,45 60,92 60,99 0,852 0,849 0,857 7 72,15 71,78 71,68 0,313 0,312 0,311 8 80,16 80,74 80,70 0,316 0,315 0,316 9 88,81 88,88 88,76 0,316 0,317 0,323 10 94,67 94,99 94,91 0,318 0,324 0,330 11 100,10 100,60 100,40 0,323 0,331 0,334 12 109,60 109,50 109,20 0,343 0,340 0,345 13 119,50 120,30 120,40 0,349 0,364 0,373 14 129,10 129,50 129,40 0,375 0,379 0,388 15 141,30 142,30 142,30 0,397 0,415 0,418 16 148,60 149,40 149,20 0,418 0,429 0,434 17 162,60 163,40 163,30 0,457 0,470 0,476 18 170,10 170,60 170,50 0,482 0,488 0,495 19 178,20 179,70 178,80 0,504 0,523 0,515 20 191,00 191,90 191,70 0,544 0,557 0,561 21 200,00 200,20 200,00 0,586 0,583 0,594 22 211,00 211,90 211,50 0,627 0,635 0,638 23 219,60 219,50 219,50 0,673 0,664 0,680 24 227,60 228,70 228,20 0,714 0,720 0,720 25 242,50 242,80 242,80 0,813 0,804 0,820 26 249,10 249,30 249,20 0,869 0,851 0,872 27 263,70 264,50 263,90 1,006 0,987 1,006
Tabela 4.5: Valor médio do ensaio a vazio
Nº Vsmed(V) Ismed(A) C (µF) Xc(Ω) 1 9,99 0,128 34,09 77,81 2 22,20 0,338 40,39 65,67 3 30,31 0,480 42,01 63,15 4 41,20 0,669 43,05 61,62 5 51,06 0,825 42,84 61,92 6 60,79 0,853 37,21 71,29 7 71,87 0,312 11,52 230,36 8 80,53 0,316 10,40 255,12 9 88,82 0,319 9,52 278,71 10 94,86 0,324 9,06 292,77 11 100,37 0,329 8,70 304,76 12 109,43 0,343 8,30 319,36 13 120,07 0,362 8,00 331,68 14 129,33 0,381 7,80 339,75 15 141,97 0,410 7,66 346,26 16 149,07 0,427 7,60 349,10 17 163,10 0,468 7,61 348,75 18 170,40 0,488 7,60 348,94 19 178,90 0,514 7,62 348,05 20 191,53 0,554 7,68 345,73 21 200,07 0,588 7,79 340,44 22 211,47 0,633 7,94 333,89 23 219,53 0,672 8,12 326,52 24 228,17 0,718 8,34 317,78 25 242,70 0,812 8,88 298,77 26 249,20 0,864 9,20 288,43 27 264,03 1,000 10,04 264,12
4.4.4. Curva de magnetização
Com os valores da tabela 4.5 levantou-se a curva de magnetização com o software MATLAB2018a, apresentada na figura 4.6. Utilizou-se o comando de interpolação para auxiliar e mostrar a reta que tangencia o ponto de maior inclinação obtido no ensaio a vazio. Para a elaboração descartou-se os pontos iniciais obtidos do ensaio pois a máquina não conseguia superar a inércia, ou seja, não girava.
A capacitância mínima é calculada pelas equações 4.4, 4.5 e 4.6 com os valores de tensão representados pelo 16º ponto da tabela 4.5, onde a corrente média é de 0,427A e tensão de fase média de 149,07V.
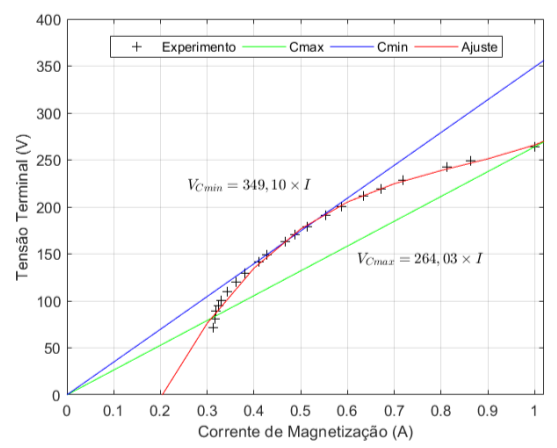
Figura 4.6: Curva de magnetização
Isto ocorre porque o ajuste da curva ultrapassa a reta de capacitância mínima, já que foram descartados apenas os pontos em que a máquina não girava, assim o sentido do fluxo de potência seria invertido e o gerador não seria magnetizado adequadamente. Desta forma:
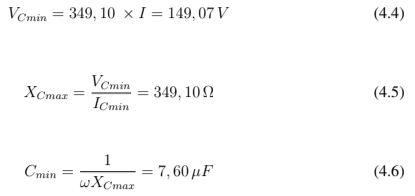
O cálculo de capacitor máximo é realizado a partir do 27o ponto da tabela 4.5 pelas equações 4.7, 4.8 e 4.9. Este ponto é o último ponto antes da reta passar a ter valores acima da reatância de magnetização, o que não manteria o giro da máquina. Além disso, como dito anteriormente, a tensão e corrente já estão acima dos valores nominais.
Assim, temos:

Outro ponto a se destacar no ensaio a vazio é a possibilidade de calcular, aproximadamente, a reatância de magnetização Xm, da mesma forma observada na equação 4.10. Pelo gráfico da figura 4.6, vemos uma pequena faixa de pontos que tangência a reta de capacitância mínima, isto porque inicialmente a máquina aumenta a velocidade gradualmente até estabilizar no valor de 1800 rotações por minutos. Posteriormente vemos a curva em vermelho sair da região linear e começar a fazer uma curva, o que indica que máquina está entrando na região de saturação. Logo, pelo 16º ponto da tabela 4.5, temos:
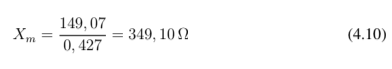
4.5. Ensaio de rotor bloqueado
4.5.1. Objetivo
Determinar resistência e reatância do rotor e do estator referidos ao lado do estator.
4.5.2. Material
- Gossen-Metrawatt MAVOWATT 30
- Autotrafo variável 440V (Variac)
- Disjuntor trifásico 5A
- Fios
- Chave de grifo
4.5.3. Experimento
Este ensaio tem seu rotor travado com uma chave grifo, impossibilitando o giro do eixo que resulta em um escorregamento igual a um. Como os valor da reatância do núcleo é bem superior aos outros componentes, despreza-se o mesmo para determinação dos parâmetros do estator e do rotor [1]. Assim, o circuito máquina pode ser visto na figura 4.7.
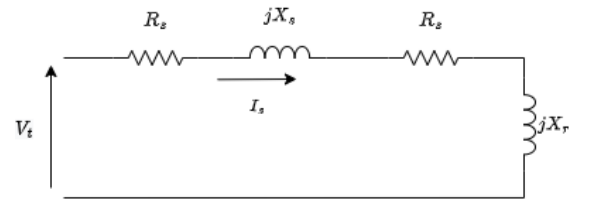
Figura 4.7: Circuito de rotor bloqueado
A obtenção dos dados é feita com aumento gradativo da tensão de entrada que alimenta o motor até alcançar a corrente nominal da máquina, observado nas tabelas 4.6 e 4.7.
Tabela 4.6: Valor por fase do ensaio de rotor bloqueado
Vsa(V) Vsb(V) Vsc(V) Isa(A) Isb(A) Isc(A) 1,23 1,16 1,07 0,048 0,031 0,037 24,92 25,23 25,26 0,391 0,400 0,407 49,39 50,37 50,51 0,826 0,852 0,865 72,96 74,05 74,02 1,236 1,268 1,280 99,12 100,10 99,84 1,602 1,634 1,642
A tabela 4.7, feita a partir da dos valores médios da tabela 4.6, possibilita a construção da figura 4.8, com a interpolação do dados.
Tabela 4.7: Valor médio de tensão e corrente do ensaio de rotor bloqueado
Vsmed(V) Ismed(A) 1,16 0,039 25,14 0,399 50,09 0,848 73,68 1,261 99,69 1,626 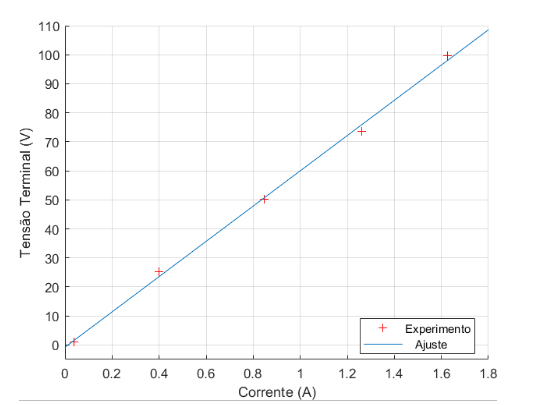
Figura 4.8: Tensão Terminal x Corrente com dados experimentais e sua interpolação
Como é possível perceber, os dados possuem uma tendência linear, confirmando queo ensaio foi feito corretamente, sendo possível seguir para análise das potências a partir da tabela 4.8.
Tabela 4.8: Valor de potência ativa do ensaio de rotor bloqueado
Psa(W) Psb(W) Psc(W) Pmed(W) 0,010 0,010 0,010 0,010 8,015 8,289 8,481 8,262 34,900 36,710 37,410 36,340 78,110 81,370 82,150 81,113 142,100 146,200 146,700 145,000 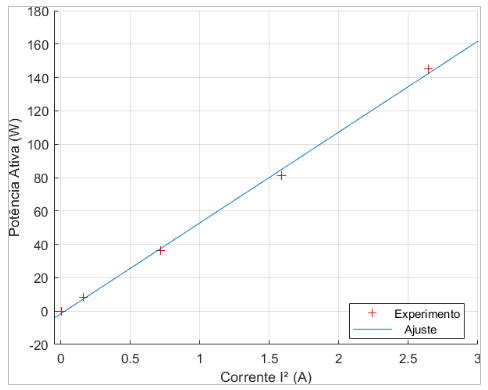
Figura 4.9: P× I2 com dados experimentais e interpolados
Com o uso do Mavowatt foi possível medir todos os tipos de potência concomitante- mente, permitindo a construção do gráfico da figura 4.9. No eixo da abscissa foi corres- ponde à corrente elevada ao quadrado, pois o cálculo da resistência equivalente do sistema é feito utilizando a corrente deste modo. Nota-se uma tendência linear com a interpolação dos dados, acompanhando a o mesmo comportamento visto anteriormente no gráfico 4.8.
Tabela 4.9: Valor de potência reativa do ensaio de rotor bloqueado
Qsa(VAR) Qsb(VAR) Qsc(VAR) Qmed(VAR) 0,010 0,010 0,010 0,010 5,329 5,682 5,624 5,545 20,770 22,040 21,870 21,560 43,860 46,650 45,240 45,250 71,100 73,700 72,100 72,300 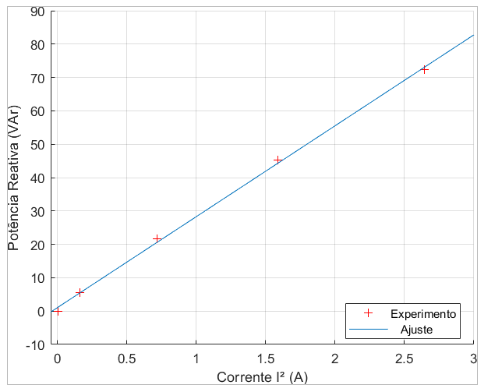
Figura 4.10: Q× I2 com dados experimentais e interpolados
A potência reativa seguiu o mesmo comportamento da potência ativa. Assim, como é mostrado o gráfico da figura 4.10 será possível calcular a reatância equivalente de uma maneira aproximada, que será visto no próximo subtópico.
Tabela 4.10: Valor de potência aparente do ensaio de rotor bloqueado
Ssa(VA) Ssb(V A) Ssc(VA) Ssc(VA) 0,059 0,036 0,040 0,045 9,758 10,100 10,310 10,056 40,830 42,970 43,710 42,503 89,830 93,620 94,410 93,550 159,300 163,800 164,400 162,500 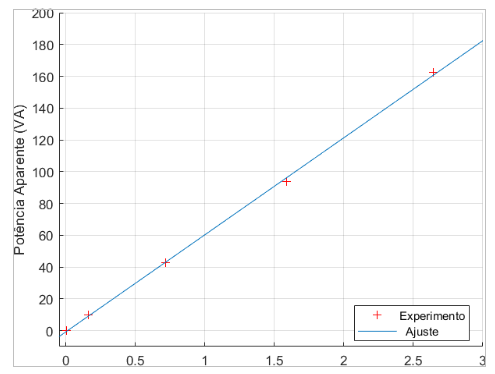
Figura 4.11: S× I2 com dados experimentais e interpolados
Os dados da potência aparente, apresentados na tabela 4.10, permitem a construção do gráfico da figura 4.11, que segue a mesma tendência vista nos dados coletados da potência reativa e ativa, confirmando que o ensaio foi realizado corretamente.
4.5.4. Cálculo dos parâmetros
É possível calcular os parâmetros através do coeficiente linear da reta ajustada, entre- tanto as reatâncias de dispersão são afetadas significativamente pela saturação e frequência do rotor. Assim é importante realizar o ensaio de rotor bloqueado com valor de cor- rente próximo ao nominal [8]. Desta forma, como os valores possuem baixa discrepância será utilizado o último ponto da tabela 4.9 para o cálculo da reatância equivalente, que no caso é soma da reatância do estator e do rotor. Importante ressaltar que os cálculos a seguir são aproximados. Portanto:
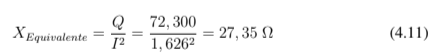
Antes de prosseguir com o cálculo da resistência, é necessário calcular a impedância total do circuito com rotor bloqueado. Assim, temos:
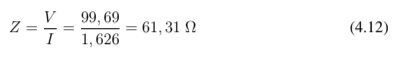
Como já foi calculado o valor da reatância equivalente, é possível encontrar o valor da resistência da seguinte maneira:

Pelo ensaio de curto-circuito temos o valor de resistência do estator já calculado. Portanto
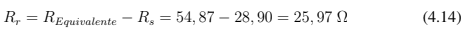
A indicação pelo perfil da máquina, por simplificação, para a reatância do estator e do rotor é assumir que ambos são iguais, portanto:
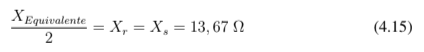
Capítulo 5
Ensaios Gerador auto excitado
5.1. Equipamentos e Material
Para a máquina operando como gerador foi necessário o uso de um motor de CC (corrente contínua) fornecendo energia mecânica ao eixo do gerador. Os dados das máquinas podem ser vistos nas tabelas 5.1 e 5.2.
Tabela 5.1: Dados de placa do Gerador de indução
Fabricante WEG Modelo A56 0297 Potência 1/3 CV Tensão 220/380 V Corrente 1,60/0,92 A RPM 1745 Frequência 60 Hz Isolamento B Categoria N FS 1,35 Grau de Proteção 21 Ligação (Triângulo/Estrela) Modo de Operação Gerador
Tabela 5.2: Dados de placa do Motor CC
Fabricante Equacional Modelo EGC1.3A Número 4087 Potência 0.75 kW Tensão 190 V Corrente 5 A RPM 1800 Frequência CC.
Outros materiais que compõem os ensaios, em geral, são:
- Gossen-Metrawatt MAVOWATT 30
- Amperímetro Alicate Minipa ET-3350
- Disjuntor padrão DIN
- Tacômetro Minipa MDT-2238
- Lâmpadas Incandescentes [25W− 75W]
- Fios
- Autotrafo variável 440V (Variac)
- Banco de capacitores [5 µF– 105 µF]
Os ensaios realizados em laboratório são:
- Ensaio de faixa de capacitores
- Ensaio de carga variável
- Ensaio de velocidade variável
5. Considerações
A fonte de força motriz do gerador de indução é o motor de corrente contínua, referenciado na tabela 5.2, possibilitando o controle do giro do eixo através da corrente de enrolamento de campo. A potência deste motor é aproximadamente três vezes maior do que a potência do gerador. Tal diferença permite a sustentação do giro do rotor em diversas circunstâncias de carga aplicada.
O conjunto motor-gerador é ligado pelo acoplamento mecânico, visto na figura 5.1, sendo possível a conexão entre os eixos do motor e do gerador

Figura 5.1: Acoplamento mecânico
Para os ensaios uma série de combinação de capacitores foram feitas, de maneira que fosse possível alcançar valores próximos aos limites encontrados de capacitância.

Figura 5.2: Banco de capacitores
5.3. Configuração
Para o funcionamento do gerador auto excitado é necessária a inserção de um banco de capacitores em paralelo quando atribuída uma carga. Toda conexão é feita em estrela e possui o modelo teórico mostrado na figura 5.3.
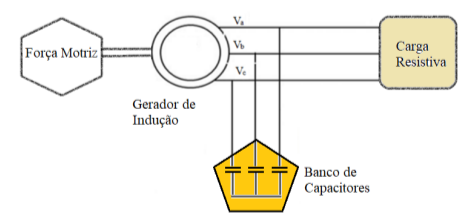
Figura 5.3: Esquemático com banco de capacitores em Y
5.4. Ensaio de faixa de capacitância
5.4.1. Objetivo
Verificar os valores de capacitância por fase que mantém a magnetização do gerador.
5.4.2. Material
- Gossen-Metrawatt MAVOWATT 30
- Disjuntor padrão DIN
- Banco de capacitores
- Fios
- Tacômetro Minipa MDT-2238
5.4.3. Experimento
O ensaio de faixa de capacitores foi realizado de dois modos, com referência aos valores limites de capacitância observados no ensaio a vazio. Em ambos os métodos o gerador foi ligado inicialmente sem capacitância.
O primeiro teste contou com a inserção de capacitores de forma crescente e gradativa, apresentados nas tabelas5.3 e 5.4, com um valor de capacitância inicial pequeno de 5 µF por fase a fim de descobrir se seria possível a magnetização com valor inicial baixo, o que não ocorreu. Isto acontece porque o capacitor se encontra fora da faixa de magnetização calculada no subtópico 4.4.4, não sendo capaz de excitar a máquina de indução. Além disso, o gerador interpreta o aumento da capacitância como uma adição de capacitor em paralelo ao capacitor inicial, o que interfere na excitação por conta da divisão de corrente no momento em que se descarrega o capacitor no inicio do processo de auto excitação.
Tabela 5.3: Valores por fase do primeiro ensaio de faixa
RPM C (µF) Vsa(V) Vsb(V) Vsc(V) Isa(A) Isb(A) Isc(A) 1856 5,00 5,50 4,28 5,45 0,035 0,020 0,022 1861 6,67 5,85 4,38 5,98 0,035 0,020 0,024 1858 7,14 6,22 4,65 6,38 0,035 0,021 0,025 1860 7,50 6,27 4,61 6,40 0,035 0,021 0,025 1859 7,78 7,47 4,67 7,29 0,036 0,024 0,026 1863 8,08 7,59 5,08 7,37 0,037 0,024 0,026 1853 8,33 6,97 4,89 7,39 0,037 0,024 0,027 1862 8,57 6,97 4,90 7,15 0,037 0,023 0,028 1864 8,94 7,48 5,13 7,54 0,037 0,025 0,029 1862 9,38 8,41 5,41 8,72 0,040 0,028 0,031 1860 9,81 10,22 6,22 10,24 0,043 0,033 0,036 1857 10,00 12,05 6,69 11,91 0,047 0,038 0,040 1858 11,05 13,82 7,70 13,71 0,054 0,047 0,048
Tabela 5.4: Valor médio do primeiro ensaio de faixa
RPM C (µF) Vsmed(V) Ismed(A) 1856 5,00 5,08 0,026 1861 6,67 5,40 0,026 1858 7,14 5,75 0,027 1860 7,50 5,76 0,027 1859 7,78 6,48 0,029 1863 8,08 6,68 0,029 1853 8,33 6,42 0,029 1862 8,57 6,34 0,029 1864 8,94 6,72 0,030 1862 9,38 7,51 0,033 1860 9,81 8,89 0,037 1857 10,00 10,22 0,042 1858 11,05 11,74 0,050
No segundo ensaio de faixa, observados nas tabelas 5.5 e 5.6, temos um procedimento feito de maneira oposta, começando com um determinado valor de capacitância e diminuindo seu valor gradativamente. Inicialmente foi escolhido um capacitor de 35µFde modo que se chegue próximo ao maior valor de corrente visto no ensaio a vazio, já que valores acima poderiam danificar a máquina. Logo ao inserir o capacitor escutou-se um ruído e uma queda na rotação da máquina, que já estava ligada porém sem o capacitor.
Tabela 5.5: Valores por fase do segundo ensaio de faixa
RPM C (µF) Vsa(V) Vsb(V) Vsc(V) Isa(A) Isb(A) Isc(A) 1034 35,00 173,30 79,53 177,30 0,988 1,002 0,998 1105 30,00 186,40 84,89 192,20 0,978 0,994 0,997 1194 25,00 202,10 92,37 208,20 0,963 0,978 0,974 1305 20,00 219,60 100,40 227,80 0,926 0,938 0,935 1377 17,50 228,60 105,00 240,50 0,886 0,908 0,907 1450 15,00 233,80 107,30 247,30 0,823 0,842 0,844 1540 12,00 237,60 109,50 250,40 0,723 0,738 0,738 1595 11,05 236,70 108,90 248,70 0,682 0,700 0,695 1647 10,00 227,80 105,00 239,60 0,610 0,625 0,623 1686 9,38 218,00 101,00 228,70 0,554 0,568 0,566 1733 8,57 207,60 96,09 216,60 0,497 0,512 0,510 1862 7,78 7,58 5,10 8,00 0,039 0,025 0,027
Tabela 5.6: Valor médio do segundo ensaio de faixa
RPM C (µF) Vsmed(V) Ismed(A) 1034 35,00 143,38 0,996 1105 30,00 154,50 0,990 1194 25,00 167,56 0,972 1305 20,00 182,60 0,933 1377 17,50 191,37 0,900 1450 15,00 196,13 0,836 1540 12,00 199,17 0,733 1595 11,05 198,10 0,692 1647 10,00 190,80 0,619 1686 9,38 182,57 0,563 1733 8,57 173,43 0,506 1862 7,78 6,89 0,030
Gradativamente diminuiu-se a capacitância até o ponto em que se perdeu a magnetização em 7,78 µF, visto na tabela 5.6, quando percebe-se que a corrente de saída tem uma queda abrupta e a rotação volta a subir. É possível notar também que a velocidade sobe a medida que o valor de capacitância desce. Isto ocorre porque a reatância é referenciada com diferentes valores de rotação, como visto na figura 3.5. Assim, tomando o último ponto antes da desmagnetização do gerador (correspondente ao capacitor de 8,57µF), temos:
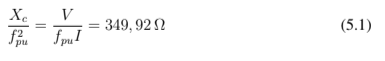
Tais resultados são bem próximos da faixa de capacitores calculada no subtópico 4.4.4 o que valida os valores encontrados.
5.5. Ensaio de carga variável e velocidade fixa
5.5.1. Objetivo
Analisar o comportamento do gerador em diferentes valores de carga resistiva com capacitor e rotação fixos.
5.5.2. Material
- Gossen-Metrawatt MAVOWATT 30
- Disjuntor padrão DIN
- Banco de capacitores
- Fios
- Tacômetro Minipa MDT-2238
- Amperímetro Alicate Minipa ET-3350
- Lâmpadas Incandescentes
5.5.3. Experimento
Este ensaio foi executado 3 vezes, cada um com diferentes valores de capacitância a fim de se observar o comportamento da tensão, corrente (estator, capacitor e carga) e, visualmente, o brilho das lâmpadas até seu desligamento.
A resistência da carga foi calculada a partir de valores nominais de potência. Isto significa que temos uma aproximação de seus valores, visto que as resistências das lâmpadas incandescentes não são lineares, oscilando principalmente com a temperatura. Portanto, como referência, temos a equação 5.2 para cálculo aproximado da resistência.

Abaixo temos os gráficos referentes aos ensaios de 9,4 µF, vistos também nas tabelas 5.7, 5.8 e 5.9, e 10,0 µF, pois o ensaio de 13,6 µF apresenta apenas dois pontos.
Tabela 5.7: Valores de ensaio de carga variável – 9,4 µF
RPM P (W) R (Ω) Vsa(V) Vsb(V) Vsc(V) 1826 25 1970,77 293,00 145,40 305,40 1825 40 1106,00 225,10 218,20 222,60 1826 50 771,20 199,00 216,50 215,50
Tabela 5.8: Valores de corrente do ensaio de carga variável – 9,4 µF
Isa(A) Isb(A) Isc(A) Ica(A) Icb(A) Icc(A) Ila(A) Ilb(A) Ilc(A) 0,815 0,837 0,844 0,759 0,781 0,773 0,123 0,126 0,128 0,766 0,788 0,780 0,709 0,717 0,728 0,178 0,179 0,182 0,739 0,747 0,758 0,654 0,669 0,663 0,211 0,212 0,218
Tabela 5.9: Valor médio de ensaio de carga variável – 9,4 µF
RPM P (W) R (Ω) Vsmed(V) Ismed(A) Icmed(A) Ilsmed(A) Psada(W) s (%) 1825 25 1970,77 221,97 0,778 0,771 0,126 102,7 -2,7 1826 40 1106,00 210,33 0,748 0,718 0,180 101,5 -4,5 1826 50 771,20 196,37 0,712 0,662 0,214 88,0 -5,9
Nota-se que apenas três pontos foram medidos na tabela 5.9. Isto porque para cargas acima de 50W, com capacitor de 9,4 µFo gerador perde a excitação, ou seja, as lâmpadas apagam, já que o aumento de potência requisitada reduz a corrente de magnetização ao ponto de desmagnetizar a máquina.
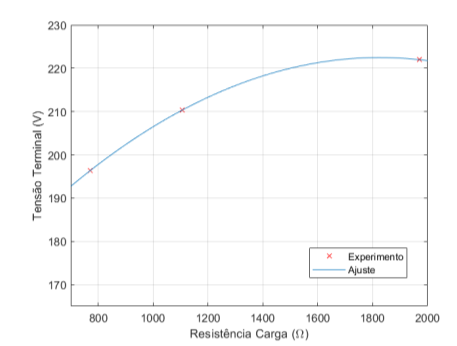
Figura 5.4: Tensão Terminal × Resistência de Carga – 9,4 µF
É importante ressaltar a queda de tensão à medida em que se aumenta a potência demandada, visto na figura 5.4. Deste forma para atender maiores potências é necessário aumentar o capacitor fazendo a máquina operar na região de saturação. Deve-se tomar cuidado na alteração de capacitância do GIAE, pois o valor não deve ultrapassar a corrente nominal a fim de evitar danos ao gerador.
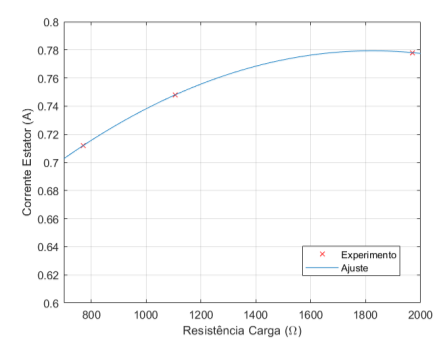
Figura 5.5: Corrente do Estator × Resistência de Carga – 9,4 µF
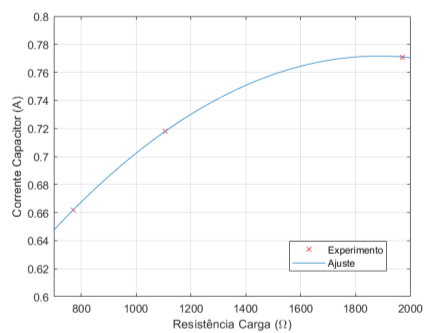
Figura 5.6: Corrente do Capacitor × Resistência de Carga – 9,4 µF
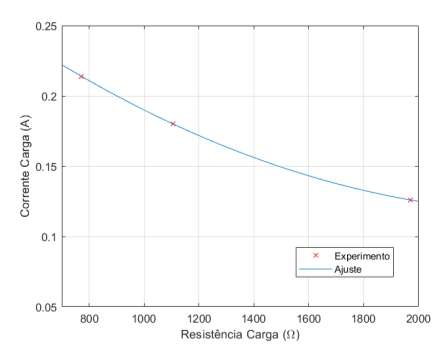
Figura 5.7: Corrente de Carga × Resistência de Carga – 9,4 µF
Percebe-se pelas figuras 5.5, 5.6 e 5.7 que a medida em que se diminui a resistência, temos um aumento da corrente de carga e queda na corrente capacitiva. Isto é esperado já que a tensão no capacitor e na resistência de carga são iguais ponto a ponto. Desta forma é possível ver que a medida em que a tensão terminal desce a corrente de carga aumenta e, devido a divisão de corrente, a corrente capacitiva diminui.
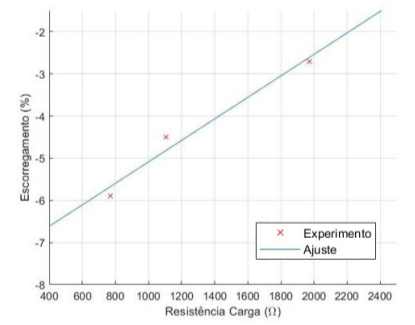
Figura 5.8: Escorregamento × Resistência de Carga – 9,4 µF
No gráfico 5.8 pode-se ver uma tendência em que o escorregamento, em módulo, aumenta e a potência de saída diminui. Também foi possível notar a queda da intensidade de brilho das lâmpadas no decorrer do ensaio.
Na sequência, aumentou-se a capacitância do ensaio para avaliar a quantidade de carga possível a ser adicionada. O ensaio manteve um comportamento parecido de quando a máquina opera com 9,4µF. Abaixo temos as tabelas 5.10, 5.11 e 5.12, além dos gráficos do ensaio com capacitor de 10µF.
Tabela 5.10: Valores de ensaio de carga variável – 10 µF
RPM P (W) R (Ω) Vsa(V) Vsb(V) Vsc(V) 1845 25 2323,88 238,60 241,50 243,00 1846 40 1347,92 220,30 239,40 236,90 1838 50 971,23 219,40 220,30 221,40 1844 60 758,99 212,30 214,00 213,90 1847 65 681,26 203,80 214,20 213,30 1845 75 508,56 194,60 196,40 194,90
Tabela 5.11: Valores de corrente do ensaio de carga variável – 10 µF
Isa(A) Isb(A) Isc(A) Ica(A) Icb(A) Icc(A) Ila(A) Ilb(A) Ilc(A) 0,902 0,928 0,920 0,888 0,914 0,906 0,125 0,124 0,123 0,880 0,893 0,903 0,863 0,876 0,886 0,176 0,179 0,178 0,841 0,865 0,857 0,800 0,822 0,815 0,209 0,219 0,213 0,829 0,850 0,842 0,780 0,799 0,792 0,233 0,238 0,234 0,825 0,837 0,843 0,751 0,762 0,767 0,239 0,244 0,242 0,784 0,802 0,794 0,697 0,713 0,706 0,282 0,290 0,285
Tabela 5.12: Valor médio de ensaio de carga variável – 10 µF
RPM P (W) R (Ω) Vsmed(V) Ismed(A) Icmed(A) Ilsmed(A) Psada(W) s (%) 1845 25 2323,88 241,03 0,917 0,903 0,124 136,2 -3,1 1846 40 1347,92 232,20 0,892 0,875 0,178 136,1 -2,6 1838 50 971,23 220,37 0,854 0,812 0,214 120,3 -4,5 1844 60 758,99 213,40 0,840 0,790 0,235 115,9 -4,4 1847 65 681,26 210,43 0,835 0,760 0,242 117,5 -7,1 1845 75 508,56 195,30 0,793 0,705 0,286 103,4 -7,0
Desta vez, pode-se ver uma amostragem maior, já que o capacitor de 10µF consegue manter a excitação para valores de potência maiores. Vale destacar que logo no primeiro ponto da tabela 5.12, vemos que a corrente do estator é bem próxima a nominal.
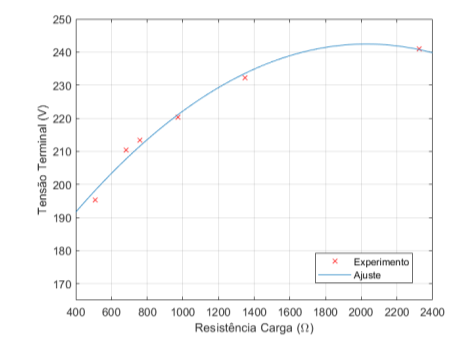
Figura 5.9: Tensão Terminal × Resistência de Carga – 10 µF
A queda de tensão do gráfico 5.9 acontece ao mesmo tempo em que cresce a potência demandada, justo como aconteceu com o ensaio de 9,4 µF, porém com uma tensão já acima da nominal, indicando operar na região de saturação da máquina.
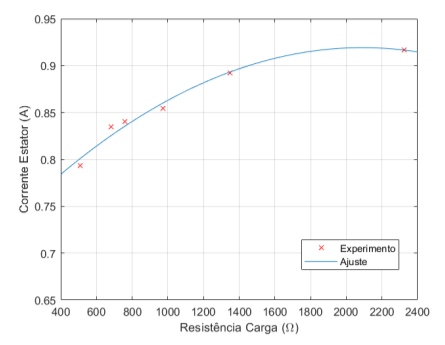
Figura 5.10: Corrente do Estator × Resistência de Carga – 10 µF
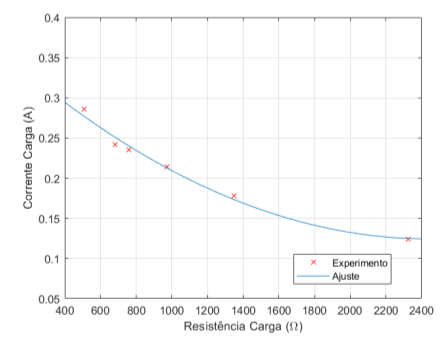
Figura 5.11: Corrente de Carga × Resistência de Carga – 10 µF
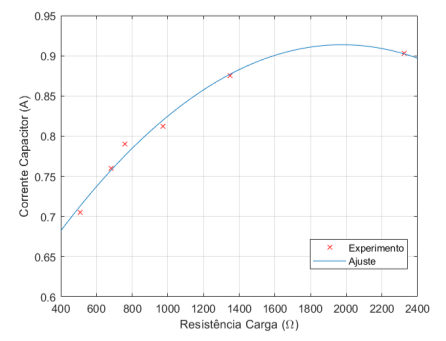
Figura 5.12: Corrente do Capacitor × Resistência de Carga – 10 µF
O comportamento das correntes, visto nos gráficos das figuras 5.10, 5.11 e 5.12, se manteve como o visto para o ensaio de 9,4 µF. Ao conectar mais lâmpadas, temos um queda resistência, resultando em aumento de corrente de carga e uma diminuição na cor- rente capacitiva.
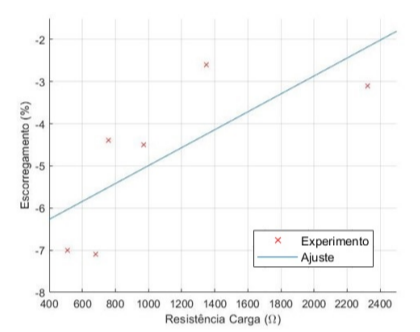
Figura 5.13: Escorregamento × Resistência de Carga – 10 µF
Também sem alterações quanto ao padrão observado no ensaio com capacitor de 9,4 µF, o escorregamento apresentado na figura 5.13 teve uma ampliação em sua faixa de valores.
Os dados obtidos para o capacitor de 13,6 µFpor fase podem ser vistos nas tabelas 5.13 5.14 e 5.15 abaixo. Com apenas dois dados experimentais, não foram construídos os gráficos como nos ensaios com 9,4 µFe 10,0 µF.
Tabela 5.13: Valores de ensaio de carga variável – 13,6 µF
RPM P (W) R (Ω) Vsa(V) Vsb(V) Vsc(V) 1849 2942,70 25 270,90 270,90 271,90 1850 1762,70 40 250,50 274,60 271,50
Tabela 5.14: Valores de corrente do ensaio de carga variável – 13,6 µF
Isa(A) Isb(A) Isc(A) Ica(A) Icb(A) Icc(A) Ila(A) Ilb(A) Ilc(A) 1,360 1,396 1,387 1,354 1,390 1,381 0,118 0,121 0,120 1,341 1,368 1,377 1,288 1,314 1,322 0,132 0,137 0,139
Tabela 5.15: Valor médio de ensaio de carga variável – 13,6 µF
RPM P (W) R (Ω) Vsmed(V) Ismed(A) Icmed(A) Ilsmed(A) Psada(W) s (%) 1849 2942,70 25 271,23 1,381 1,375 0,120 220,5 -3,8 1850 1762,70 40 265,53 1,362 1,308 0,136 230,5 -7,0
Pode-se observar que os valores de tensão e corrente acima dos valores nominais, como previsto anteriormente, mostrando que com esse valor de capacitância pode danificar a máquina.
Desta forma pode-se notar que com o aumento de potência nominal (diminuição da resistência da carga) temos uma queda gradual de tensão terminal, na corrente do estator e na corrente do capacitor até o instante em que a lâmpada apaga, pois o fluxo magnético, sustentado pela interação (auto excitação) entre o gerador e o capacitor, diminui até a desmagnetização do gerador. Percebe-se também que no decorrer do experimento que existe um declive do brilho das lâmpadas e uma oscilação de sua intensidade de iluminação.
5.6. Ensaio de velocidade variável e carga fixa
5.6.1. Objetivo
Estudar o comportamento do gerador auto excitado com uma carga fixa para diversos pontos de velocidade com o objetivo de identificar o ponto onde ocorre a desmagnetização.
5.6.2. Material
- Gossen-Metrawatt MAVOWATT 30
- Disjuntor padrão DIN
- Banco de capacitores
- Fios
- Tacômetro Minipa MDT-2238
- Amperímetro Alicate Minipa ET-3350
- Lâmpadas Incandescente
- Experimento
5.6. Experimento
Neste ensaio a carga é fixada com uma lâmpada de 25W por fase e e o capacitor de 10,0 µF, capacitância limítrofe calculado previamente em 4.4.4. Gradativamente se reduz a velocidade de rotação imposta pelo motor de corrente contínua ao eixo do gerador até que o mesmo perca a excitação e pare de fornecer energia elétrica à carga.
Tabela 5.16: Valores de ensaio de velocidade variável
RPM Vsa(V) Vsb(V) Vsc(V) 1866 248,90 242,60 247,00 1844 243,40 237,10 241,50 1824 236,40 230,30 234,40 1806 229,90 223,90 227,90 1792 226,50 220,60 224,50 1785 223,60 217,70 221,60 1771 219,20 213,30 217,10 1764 216,90 211,00 214,80 1753 210,90 205,20 208,70 1735 204,00 198,00 201,50 1723 196,90 191,50 194,70 1711 192,30 186,70 189,80 1706 189,00 183,50 186,10 1696 183,10 177,80 180,20 1689 177,20 172,30 175,50 1677 168,00 163,30 165,80 1668 152,90 148,90 151,10 1656 116,60 114,00 115,00
Tabela 5.17: Valores de corrente do ensaio de velocidade variável
Isa(A) Isb(A) Isc(A) Ica(A) Icb(A) Icc(A) Ila(A) Ilb(A) Ilc(A) 0,921 0,948 0,940 0,908 0,937 0,926 0,125 0,129 0,128 0,892 0,918 0,910 0,878 0,904 0,896 0,123 0,126 0,123 0,856 0,881 0,873 0,840 0,871 0,860 0,116 0,119 0,118 0,823 0,847 0,840 0,810 0,834 0,827 0,112 0,115 0,114 0,806 0,803 0,823 0,790 0,790 0,813 0,110 0,109 0,111 0,792 0,815 0,808 0,780 0,803 0,796 0,107 0,110 0,109 0,771 0,793 0,786 0,760 0,782 0,775 0,105 0,108 0,107 0,760 0,781 0,775 0,748 0,769 0,763 0,102 0,107 0,105 0,733 0,754 0,747 0,721 0,742 0,735 0,099 0,102 0,101 0,701 0,721 0,715 0,691 0,711 0,705 0,096 0,098 0,097 0,673 0,691 0,685 0,663 0,681 0,675 0,091 0,095 0,093 0,652 0,671 0,665 0,645 0,661 0,652 0,089 0,091 0,090 0,638 0,656 0,650 0,628 0,646 0,640 0,087 0,089 0,088 0,615 0,633 0,627 0,610 0,620 0,618 0,084 0,086 0,085 0,594 0,610 0,605 0,589 0,601 0,592 0,081 0,083 0,082 0,559 0,575 0,570 0,550 0,566 0,561 0,076 0,078 0,077 0,507 0,521 0,516 0,499 0,513 0,508 0,069 0,071 0,070 0,386 0,398 0,393 0,380 0,392 0,387 0,052 0,054 0,053
A partir das tabelas 5.16 e 5.17, são calculados os valores médios mostrados na tabela 5.18:
Tabela 5.18: Valor médio de ensaio de velocidade variável
RPM f (Hz) Vsmed(V) Ismed(A) Icmed(A) Ilsmed(A) Psada(W) s (%) 1866 59,61 246,17 0,936 0,922 0,127 135,31 -4,4 1844 59,05 240,67 0,907 0,893 0,123 129,00 -4,1 1824 58,36 233,70 0,870 0,857 0,118 119,41 -4,2 1806 57,71 227,23 0,837 0,824 0,114 113,83 -4,3 1792 56,73 223,87 0,811 0,798 0,110 108,95 -5,3 1785 57,12 220,97 0,805 0,793 0,109 106,31 -4,1 1771 56,74 216,53 0,783 0,772 0,107 98,57 -4,1 1764 56,46 214,23 0,772 0,760 0,105 98,68 -4,1 1753 56,01 208,27 0,745 0,733 0,101 92,37 -4,3 1735 55,54 201,17 0,712 0,702 0,097 85,21 -4,1 1723 55,11 194,37 0,683 0,673 0,093 78,69 -4,2 1711 54,81 189,60 0,663 0,653 0,090 75,76 -4,1 1706 54,53 186,20 0,648 0,638 0,088 72,70 -4,3 1696 54,36 180,37 0,625 0,616 0,085 67,64 -4,0 1689 54,02 175,00 0,603 0,594 0,082 62,63 -4,2 1677 53,69 165,70 0,568 0,559 0,077 55,53 -4,1 1668 53,45 150,97 0,515 0,507 0,070 46,94 -4,1 1656 53,33 115,20 0,392 0,386 0,053 25,26 -3,5
A partir das tabela 5.18 foram elaborados diversos gráficos, com os dados interpola- dos, que podem ser vistos nas figuras 5.14, 5.15,5.16 e 5.17:
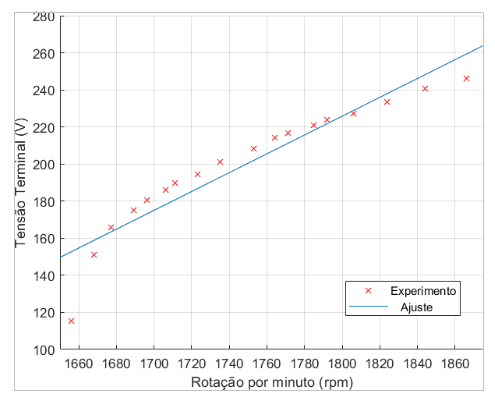
Figura 5.14: Tensão Terminal × Rotação por minuto
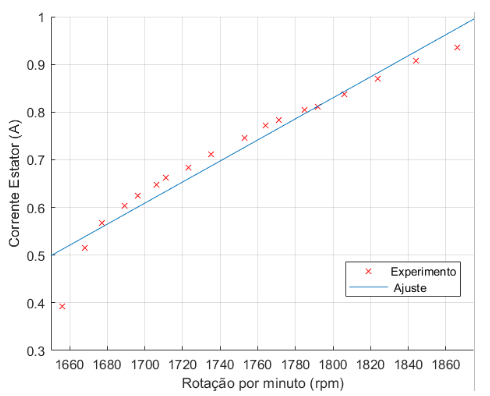
Figura 5.15: Corrente do Estator × Rotação por minuto
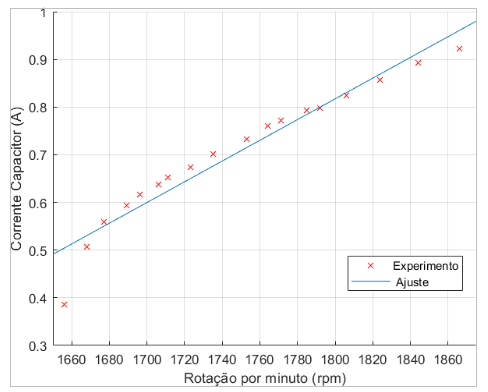
Figura 5.16: Corrente do Capacitor × Resistência de Carga
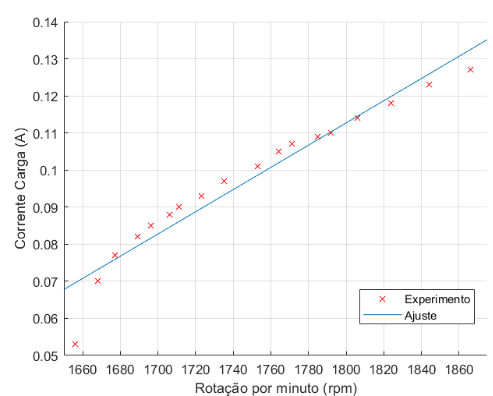
Figura 5.17: Corrente de Carga × Rotação por minuto
Pode-se observar nas figuras 5.14,5.15,5.16 e 5.17 uma relação linear com a velocidade de rotação do eixo, que muda o perfil da curva de magnetização, já que temos uma mudança na frequência de saída. Na figura 5.18 podemos observar de uma maneira mais clara a alteração de perfil.
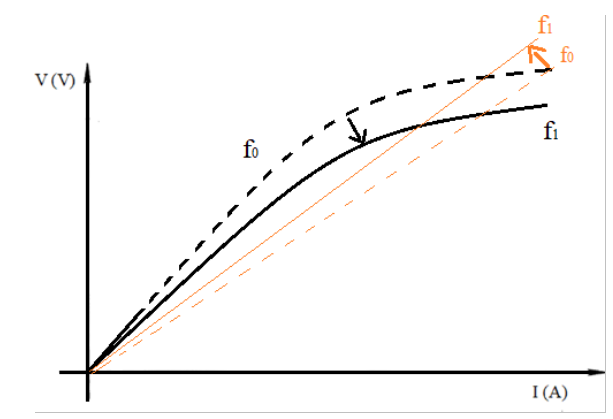
Figura 5.18: Variação da reta de reatância de acordo com a frequência
Isto leva a uma queda na reatância de magnetização ao mesmo tempo que eleva a reatância capacitiva. Estas mudanças interferem no funcionamento do gerador pois a reta capacitiva, em um determinado instante, não interceptará a curva de magnetização para determinada rotação e frequência desmagnetizando a mesma.
A partir dos gráficos 5.19 e 5.20 podemos ver que com rotações por minuto menores, temos um escorregamento, em módulo, e uma potência de saída menores também. À medida em que se diminuiu a velocidade foi possível perceber a queda do brilho das lâmpadas até o último ponto representado na tabela 4.7 (1856 rpm), em que a lâmpada começa a oscilar entre ligada e desligada. É neste ponto em que a reta de capacitância tangencia a curva de magnetização do gerador, causando instabilidade até o colapso da excitação, desmagnetizando o GIAE.
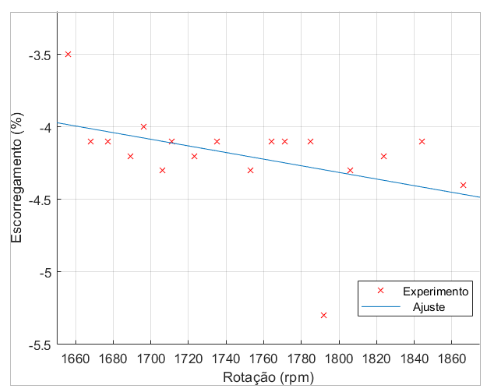
Figura 5.19: Escorregamento × Rotação por minuto
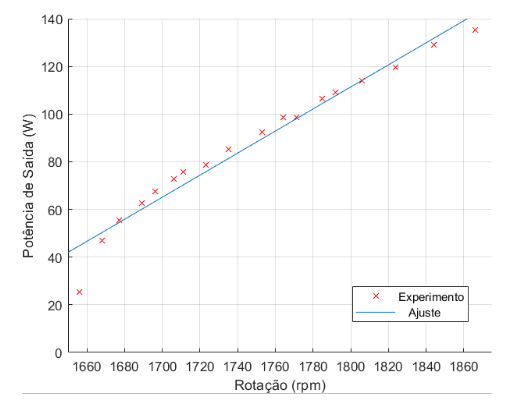
Figura 5.20: Potência de saída × Rotação por minuto
Capítulo 6
Simulação Digital
6.1. Objetivo
Encontrar as soluções das equações vistas na seção 3.3, referentes à tensão terminal, corrente de carga, corrente do capacitor e corrente do estator, comparar e servir como estimativa do ensaio de carga variável. Desta forma será possível analisar discrepâncias que podem ter ocorrido durante o experimento no laboratório.
6.2. Método Newton-Raphson
Na matemática existem diversas formas de resolver determinados problemas de cálculos mais complexos. Uma destas é o método Newton-Raphson, elaborado por Isaac Newton e Joseph Raphson, que é muito usado como algoritmos por ser de rápida convergência para estimar as raízes de um polinômio. Ele é amplamente utilizado para solucionar problemas de diversos tipos, inclusive os relacionados a engenharia elétrica.
Para um melhor entendimento, o gráfico da figura 6.1, mostra a interpretação geométrica do processo de linearização através da inclinação da reta tangente à curva que representa o polinômio [9].
A base do método de Newton-Raphson é a linearização do polinômio por série de Taylor [5] [6] [7] [9] [10] . Vale ressaltar que estipular um valor inicial próximo a raiz promove um esforço computacional menor.
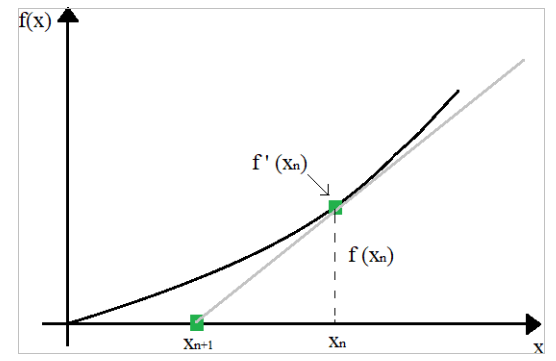
Figura 6.1: Interpretação geométrica As etapas do processo podem ser vistas a seguir:
- Atribuir condição inicial xi,i= 0
- Cálculo do valor da função no ponto (xi,(f(xi))
- Linearização da função em torno do ponto (xi,(f(xi)) pela série de Taylor
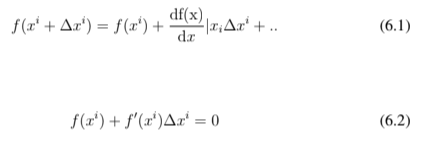
Manipulando as equações 6.1 e 6.2, temos:

4. Iteração: xi+1 = xi + ∆xi e em seguida voltar a etapa 2.
O algoritmo exige um critério de tolerância no valor da função em análise, que, na solução, deveria ser zero. Quando o valor da função atinge essa tolerância previamente estabelecida, o processo iterativo do algoritmo para e a solução é então determinada. Para isso estima-se um erro limite, normalmente o mais próximo de zero, que deve cumprir a condição da inequação 6.4:
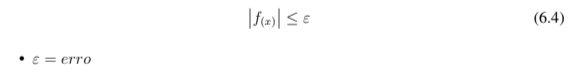
Entretanto, no ensaio de carga variável usa-se diversos vetores para análise da má- quina, o que exige o método de Newton-Raphson para um modelo multidimensional a fim de tornar viável o uso na elaboração do código. Desta forma, temos:
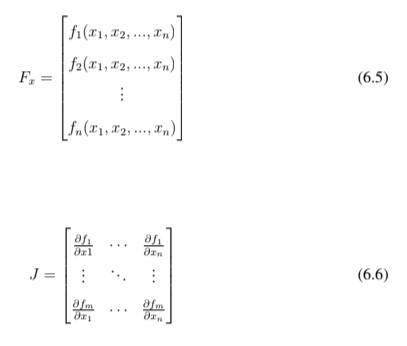
Assim, das equações 6.3, 6.5 e 6.6:
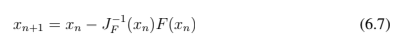
- Parâmetros
Para realizar a simulação digital é necessário a resolução das equações vistas na seção 3.4, através do método Newton-Raphson [5] [6] [7][10].
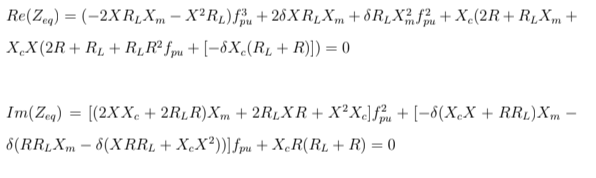
Pode-se ver que nas equações acima são necessários os dados da máquina de indução. Os valores encontrados são apresentados na tabela 6.1, decorrente dos ensaios realizados em laboratório.
Tabela 6.1: Dados dos parâmetros
Parâmetro Experimento Valor (Ω) Resistência do estator Ensaio de Corrente contínua 28,90 Resistência do rotor Ensaio de Rotor bloqueado 25,97 Reatância do estator Ensaio de Rotor bloqueado 13,67 Reatância do rotor Ensaio de Rotor bloqueado 13,67 Reatância de magnetização Ensaio a vazio 349,10
Os valores da rotação e resistência de carga são os conjuntos de dados da tabela 5.10. A tensão de entreferro é calculada utilizando a tensão e corrente terminais do ensaio de carga variável, ponto a ponto, pela equação 6.8 [5] [6] [10] .
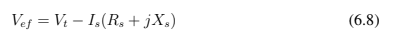
A reatância de magnetização de 349,10 Ω e a frequência de 60 Hz são as estimativas iniciais para a execução da simulação.O jacobiano fica definido por [5] [6] [10] :
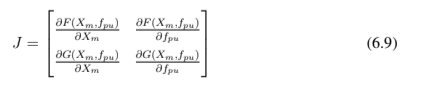
O desenvolvimento das derivadas parciais das funções F(Xm,fpu) e G(Xm,fpu), atreladas ao jacobiano, podem ser analisadas abaixo.
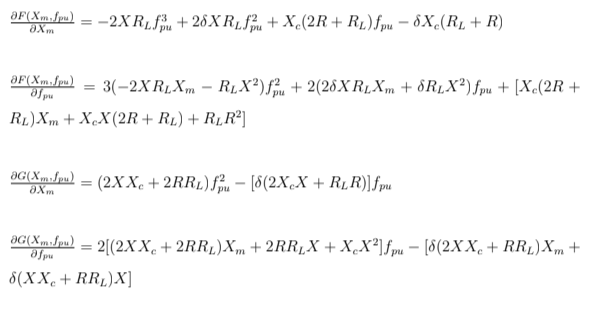
- Parte real da impedância equivalente: F(Xpu, fpu)
- Parte imaginária da impedância equivalente: G(Xpu,fpu)
Assim, para cada iteração, soluciona-se:
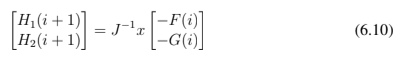
Então atualiza-se:
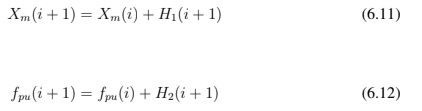
O processo iterativo continua calculando a reatância de magnetização e frequência até que seus valores absolutos sejam menores que 0,001 (erro utilizado) para todos os pontos das tabelas 5.10 a 5.12. Portanto, ao convergir, chega-se às equações 6.13, 6.14, 6.15 e
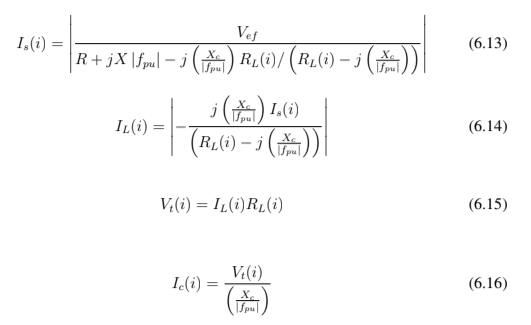
Capítulo 7
Resultados e comparações
7.1. Objetivo
Apresentar os gráficos comparativos do experimento, simulação e sua curva ajustada para as capacitâncias de 9,4 µFe 10,0 µF, respectivamente.
7.2. Gráficos para capacitância de 9,4 µF e 10,0 µF
Para facilitar a análise calcula-se as discrepâncias médias de tensão terminal, corrente do estator, corrente capacitiva e corrente de carga. Os dados podem ser visto nas tabelas 7.1 e 7.2.
Tabela 7.1: Discrepância média – 9,4 µF
Vt(%) Is(%) Ic(%) Il(%) 9% 9% 1% 10%
Tabela 7.2: Discrepância média – 10 µF
Vt(%) Is(%) Ic(%) Il(%) 10% 8% 7% 13%
Abaixo temos os gráficos com a interpolação feita a partir dos dados experimentais.
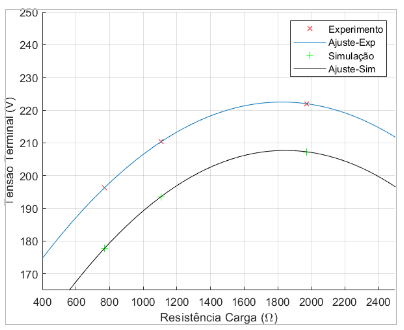
Figura 7.1: Tensão Terminal × Resistência de Carga – 9,4 µF
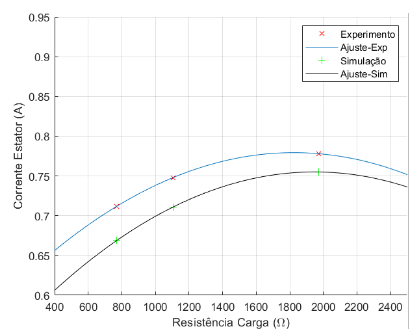
Figura 7.2: Corrente do Estator × Resistência de Carga – 9,4 µF
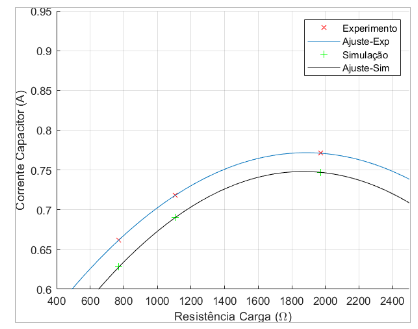
Figura 7.3: Corrente do Capacitor × Resistência de Carga – 9,4 µF
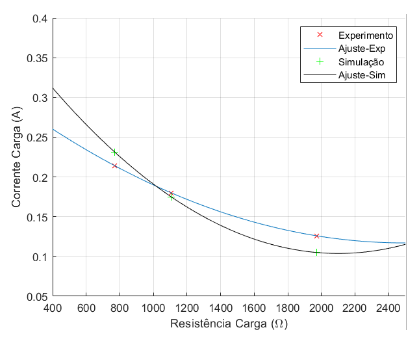
Figura 7.4: Corrente de Carga × Resistência de Carga – 9,4 µF
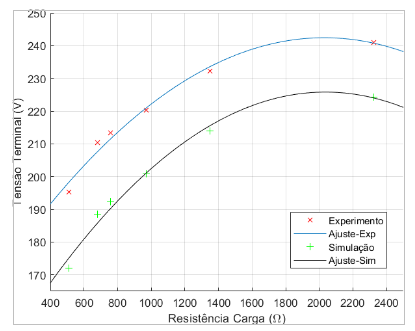
Figura 7.5: Tensão Terminal × Resistência de Carga – 10 µF
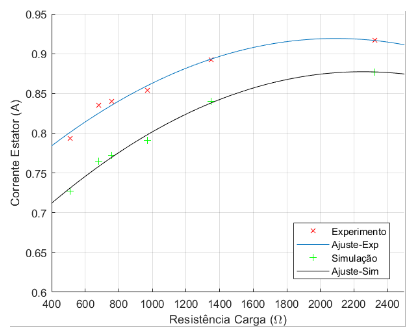
Figura 7.6: Corrente do Estator × Resistência de Carga – 10 µF
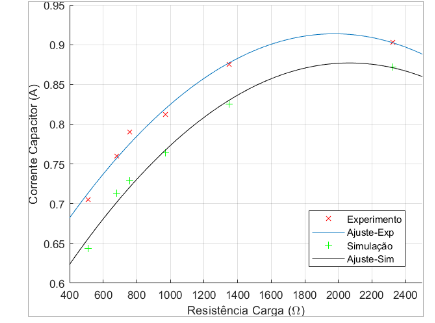
Figura 7.7: Corrente do Capacitor × Resistência de Carga – 10 µF
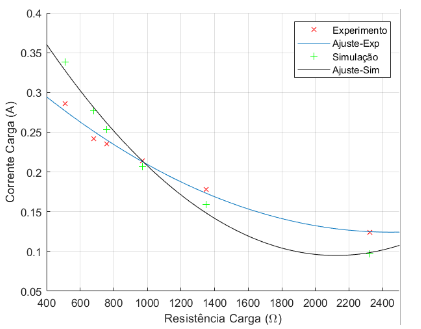
Figura 7.8: Corrente de Carga × Resistência de Carga – 10 µF
Tanto os gráficos referentes ao capacitor de 9,4 µF, vistos nas figuras 7.1,7.2,7.3 e 7.4 , quanto os gráficos referentes ao capacitor de 10,0 µF, vistos nas figuras 7.5,7.6,7.7 e 7.8, possuem valores condizentes já que várias aproximações foram realizadas, além da interferência de ventilação, temperatura, falhas de contato, harmônicos, vibração e manutenção do conjunto motor-gerador. O uso da tensão de entreferro, dado experimental, no código e o valores iniciais utilizados também interferem nos dados simulados, visto que não é possível reproduzir exatamente os componentes do gerador de indução. Além disto, vale relembrar que a resistência de carga não é linear por característica das lâmpadas incandescentes.
Notou-se que o capacitor de 10,0 µF foi uma boa escolha de capacitância, já que suportou uma quantidade de variação de carga maior do que nos ensaios de 9,4 µF e 13,6 µF. Este o último, apesar de apenas 2 pontos medidos, mostrou-se prejudicial à máquina e explicitou como seria um capacitor acima do limite teórico calculado.
Portanto o ensaio prático mostrou-se compatível com a simulação digital, principalmente pela tendência mostrada nos gráficos. O esforço computacional da simulação não foi significativo.
Capítulo 8
Conclusão
Os ensaios de curto-circuito, a vazio e de rotor bloqueado atenderam às expectativas, não possuindo nenhum impeditivo considerável que interferisse na elaboração da curva de magnetização, considerando que a resistência do núcleo seja bem maior que sua reatância. Com estes ensaios foi possível calcular os parâmetros da máquina de indução e utilizálos para elaborar o programa da simulação digital e executar, na prática, os experimentos como gerador auto excitado no laboratório.
Os ensaios do gerador de indução auto excitado por capacitores se mostrou mais desafiador devido a complexidade e as suas peculiaridades da configuração da bancada.
No primeiro experimento (ensaio de faixa) do GIAE, obteve-se êxito ao testar os limites de capacitância por fase máximo e mínimo. O maior valor é alcançado no ponto em que se chega à corrente nominal, evitando permanecer neste ponto para evitar danos à máquina. Já o limite inferior de capacitância é visto no instante em que o gerador perde a excitação, tendo uma queda brusca em sua corrente e um aumento em sua rotação. Vale ressaltar que durante o experimento escutou-se um ruído quando a máquina perdeu a magnetização.
Para o ensaio de velocidade variável e carga fixa, pode-se observar no procedimento que o brilho da lâmpada foi diminuindo a medida em que o giro do rotor foi descendo, oscilando nos últimos pontos até o gerador perder excitação quando o escorregamento aumenta e as luzes se apagam.
No ensaio de velocidade fixa e carga variável foram escolhidos três capacitores para se testar, sendo o capacitor de 10,0 µF referência, já que foi calculado como capacitor máximo no subtópico 4.4.4. Foi possível perceber que o valor de 10,0 µF foi o valor mais adequado, já que suportou uma maior quantidade de carga, quando comparado ao ensaio com capacitor de 9,4µF, a um valor de corrente abaixo da nominal, quando comparado ao ensaio capacitor de 13,6µF .
De uma maneira geral, o experimento foi bem sucedido, sendo validado pela simulação digital com resultados compatíveis, possibilitando o uso do código para trabalhos futuros.
Referências Bibliográficas
- CHAPMAN, S. J. Fundamentos de Máquinas Elétricas. 5 ed. , Mc Graw Hill, Bookman, 2013.
- SIMÕES, M. G., FARRET, F. A. Alternative Energy Systems. 2 ed. , CRC Press., 2004.
- HAQUE, M. H., MASWOOD, A. I. “Determination of excitation capacitance of a three-phase self-excited induction generator”. In: IEEE Power and Energy SocietyGeneralMeeting, pp. 1–6, San Diego, California, USA., 22-26, Julho 2012. IEEE.
- RAJ, R. E., KAMALAKANNAN, C., KARTHIGAIVEL, R. “Genetic algorithmbased analysis of wind-driven parallel operated self-excited inductiongenera- tors supplying isolated loads”, IETRenewablePowerGeneration, v. 12, Issue 4, pp. 472–483, 26, Janeiro 2018.
- VALADÃO, R. A. D. Análise do Comportamento de um gerador de indução Auto- excitadoporcapacitores. Trabalho de conclusão de curso bs.c., Universidade Federal do Rio de Janeiro, Rio de Janeiro, Rio de Janeiro, Brasil, 2012.
- NIGAM, R. R. V. P. “Steady State Analysis of Self-Excited Induction Generator”,InternationalJournalofElectricalandElectronicsEngineering, v. 2, Issue 2,pp. 77–86, Maio 2013.
- SELMI, M., REHAOULIA, H. “A simple method for the steady state performances of self-excited induction generators”. In: InternationalConferenceonElectrical EngineeringandSoftwareApplications, pp. 1–4, Hammamet, Tunisia, 21-23, Março 2013. IEEE.
- FITZGERALD, A. E., KINGSLEY, C., UMANS, S. D. MáquinasElétricas. 7 ed. , AMGH ., 2014.
- KELLEY, C. T. SolvingNonlinearEquationswithNewton’sMethod. Fundamentals of Algorithms. 1 ed. , Siam, 2003.
- CHAN, T. “Analysis of Self-Excited Induction Generators using an iterative method”, IEEE Transactions on Energy Conversion, v. 9, Issue 2, pp. 288– 296, Junho 1994.
- SANDHU, K. S. “Iterative Model for the Analysis of Self-Excited Induction Gene- rators”, ElectricPowerComponentsandSystems, v. 31, Issue 10, pp. 925–939,21 Junho 2010.
- CHAPALLAZ, J. M., GHALI, J. D., EICHENBERGER, P., et al. ManualonInductionMotorsUsedAsGenerators. 10 ed. , MHPG Series., 1992.
- TABATABAEI, N. M., AGHBOLAGHI, A. J., BIZON, N., et al. ReactivePowerControlinACPowerSystems. 1 ed. , Springer, 2017.
- LEVY, D. “Stand alone induction generators”, ElectricPowerSystemsResearch,v. 41, Issue 3, pp. 191–201, Junho 1997.
- KHAN, F., KHAN, R., ABDELLAH, K. “Three Phase Self-Excited Induction Ge- nerator for Renewable Energy Generation”, ICPEA 2013, 1st. International Conference on Power Electronics and their Applications, Novembro 2013.
- SALEHAL-SENAIDI, ALOLAH, A., ALKANHAL, M. “Parallel operation ofthree-phase self-excited induction generators with different numbers of po- les”, EngineeringScienceandTechnology,anInternationalJournal, v. 25, 8 Maio 2021.
- TRAPP, J. G. Gerador de indução isolado com tensão e frequência reguladas por conversor matricial esparso. Dissertação de Ms.c., Universidade Federal de Santa Maria, Santa Maria, Rio Grande do Sul, Brasil, 30 Junho 2008.
- JOHNSON, G. L. WindEnergySystems. 1 ed. , Prentice Hall, 1985.
Apêndice A – Rotor Bloqueado
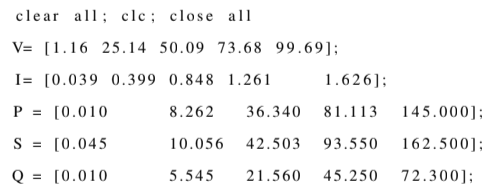
V= [ 1 . 1 6 2 5 . 1 4 5 0 . 0 9 7 3 . 6 8 9 9 . 6 9 ] ;
f i g u r e ( 1 ) ho l d on
g r i d on
p l o t ( I , V, ’ +
r ’ )
I 2 = I . * I ;
f i g u r e ( 2 )
ho l d on
g r i d on
p l o t ( I 2 , P , ’ + r ’ ) f i g u r e ( 3 )
ho l d on
p l o t ( I 2 , Q, ’ + r ’ )
%A j u s t e b a s i c f i t t i n g pos p l o t
Apêndice B – Curva de Magnetização
c l e a r a l l ; c l o s e a l l ;
T1 = r e a d t a b l e ( ’ C : \ Users \ d a n i e \ One Drive \ Area de
T r a b a l h o \ UFRJ− E n g e n h a r i a E l e t r i c a \ TCC \ Matlab . x l sx ’ ) ;
V = T1 . V; I = T1 . I ;
dVi = g r a d i e n t (V ) ; d I i = g r a d i e n t ( I ) ; v _ i = V . / I ;
t a n g = max ( v _ i ) ;
i n d i c e _ l i n e a r = f i n d ( v _ i == t a n g ) ; I i = I ( i n d i c e _ l i n e a r ) ;
Vi = i n t e r p 1 ( I , V, I i ) ;
d I i = i n t e r p 1 ( I , d I i , I i ) ; dVi = i n t e r p 1 ( I , dVi , I i ) ; I n c l i = dVi / d I i ;
Y I n t e r c e p t = Vi − I n c l i *I i
X I n t e r c e p t = − Y I n t e r c e p t / I n c l i f i g u r e
p = p o l y f i t ( I , V , 4 ) ;
f = p o l y v a l ( p , I ) ;
p l o t ( I , V, ’ + ’ , I , f , ’ − ’ )
ho l d on
p l o t ( I , I * I n c l i + Y I n t e r c e p t , ’ −b ’ ) ho l d on
g r i d
x l a b e l ( ’ I ’ )
y l a b e l ( ’ V’ )
t e x t ( I i , Vi , s p r i n t f ( ’ $V =
%.3 f \ \ t i m e s I %+.3 f \ \ r i g h t a r r o w
\ \ $ ’ , I n c l i , Y I n t e r c e p t ) ,
’ Horiz ’ , ’ r i g h t ’ , ’ Vert ’ , ’ middle ’
, ’ I n t e r p r e t e r ’ , ’ l a t e x ’ )
y_cap_max = [ 8 8 . 8 2 , 2 6 4 . 0 3 ] ; x_cap_max = [ 0 . 3 2 , 1 ] ;
c o e f = p o l y f i t ( x_cap_max , y_cap_max , 1 ) ;
r e t a_cap_max = p o l y v a l ( coef , x_cap_max ) ;
I n c l i 2 = g r a d i e n t ( y_cap_max ) / g r a d i e n t ( x_cap_max ) ;
Y I n t e r c e p t 2 = V( 3 ) − I n c l i 2 * I ( 3 ) ; p l o t ( x_cap_max , y_cap_max , ’ g ’ )
%A j u s t e s com b a s i c f i t t i n g pos c r i a c a o dos g r a f i c o s .
Apêndice C – Simulação
c l e a r a l l ; c l c ;
Vg= [ 2 1 6 . 1 6 9 7 208 . 1521 197 . 4053
190 . 7132
187 . 7487
1 7 3 . 9 7 3 7 ] ;
Rl = [ 2 3 2 3 . 8 8 1347 . 92 971 . 23 758
. 99 681 . 26
5 0 8 . 5 6 ] ;
C= 1 0 * 1 0 ^ ( − 6 ) ;
R= 2 7 . 4 2 ; X= 1 3 . 6 7 ;Xm= 3 4 9 . 1 ; f = 60 ;
k= l e n g t h ( Rl ) ;
v = [ 1 . 0 5 7 1 . 0 5 8 1 . 0 5 3 1 . 0 5 7 1 . 0 5 8
1 . 0 5 7 ]
Zbase = ( 2 2 0 ^ 2 ) / 8 1 . 7 7 ;
f b a s e = 60 ;
vbase = 220 ;
I b a s e = 8 1 . 7 7 / 2 2 0 ;
Xc = 1 / ( 2 * p i *60*C ) ;
f = f / f b a s e ;
Rl=Rl / Zbase ;
X=X/ Zbase ;
R=R / Zbase ;
Xc=Xc / Zbase ;
Xm=Xm/ Zbase ;
Vg=Vg / 2 2 0 ; f o r i = 1 : k f = 1 ;
Xm= 3 4 9 . 1 / Zbase ;
fx =( −2*X* Rl ( i )*Xm− Rl ( i )*X^ 2 )* f ^ 3 +( v ( i )* 2 *X* Rl ( i )* Xm+v ( i )* Rl ( i )*X^ 2 )* f ^ 2 +( Xc*( 2 *R+Rl ( i ) ) *Xm+Xc*
X*( 2 *R+Rl ( i ) ) +R^2* Rl ( i ) ) * f +( −v ( i )* Xc *( R+Rl ( i ) )
*Xm−v ( i )* Xc*X*( R+Rl ( i ) ) ) ;
gx = ( ( 2 *X*Xc+Rl ( i )* 2 *R)*Xm+ Rl ( i )*X*2*R+Xc*X^ 2 )
* f ^2+( − v ( i ) * ( 2 * Xc*X+Rl ( i )* R)*Xm−v ( i ) * ( Rl ( i )* R+Xc*X)*X)* f −Xc*R*( R+Rl ( i ) ) ;
dfXm=−2*X* Rl ( i )* f ^3+v ( i )* 2 *X* Rl ( i )* f ^2+Xc* ( 2 *R+Rl ( i ) ) * f −v ( i )* Xc *( R+Rl ( i ) ) ;
dgXm=( 2 *X*Xc+R*2* Rl ( i ) ) * f ^2+ ( − v ( i ) * ( 2 * Xc*X+Rl ( i )* R ) ) * f ;
d f f =3*( −2*X* Rl ( i )*Xm− Rl ( i )*X^ 2 )*f ^2+2* ( v ( i )* 2 *X* Rl ( i )*Xm+v ( i )* Rl ( i )*X^ 2 )* f +
( Xc*( 2 *R+Rl ( i ) ) *Xm+Xc*X* ( 2 *R+Rl ( i ) ) +R^2* Rl ( i ) ) ; dgf = 2 *(( 2 *X*Xc+Rl ( i )* 2 *R)*Xm+ Rl ( i )*X*2*R+Xc*X^ 2 )
* f +( −v ( i ) * ( 2 * Xc*X+Rl ( i )* R)*Xm−v ( i ) * ( Rl ( i )* R+Xc*X)*X ) ; w h i l e abs ( fx ) > = ( 0 . 0 0 1 ) | | abs ( gx ) > = ( 0 . 0 0 1 )
J =[ dfXm d f f ; dgXm dgf ] ; H=( J ^ − 1 )*[ − fx ; − gx ] ; Xm=Xm+H ( 1 ) ;
f = f +H ( 2 ) ;
fx =( −2*X* Rl ( i )*Xm− Rl ( i )*X^ 2 )* f ^3+ ( v ( i )* 2 *X* Rl ( i )*Xm+v ( i )* Rl ( i )*X^ 2 )
* f ^ 2 +( Xc*( 2 *R+Rl ( i ) ) *Xm+Xc*X* ( 2 *R+Rl ( i ) ) +R^2* Rl ( i ) ) * f +
( − v ( i )* Xc *( R+Rl ( i ) ) *Xm−
v ( i )* Xc*X*( R+Rl ( i ) ) ) ;
gx = ( ( 2 *X*Xc+Rl ( i )* 2 *R)*Xm+ Rl ( i )
*X*2*R+Xc*X^ 2 )* f ^2+( − v ( i )*
( 2 * Xc*X+Rl ( i )* R)*Xm−v ( i ) * ( Rl ( i )* R+ Xc*X)*X)* f −Xc*R*( R+Rl ( i ) ) ;
dfXm=−2*X* Rl ( i )* f ^3+v ( i )* 2 *X* Rl ( i )* f ^2+Xc*( 2 *R+Rl ( i ) ) * f −v ( i )
*Xc *( R+Rl ( i ) ) ;
dgXm=( 2 *X*Xc+R*2* Rl ( i ) ) * f ^2+( − v ( i )* ( 2 * Xc*X+Rl ( i )* R ) ) * f ;
d f f =3*( −2*X* Rl ( i )*Xm− Rl ( i )*X^ 2 )*f ^2+2* ( v ( i )* 2 *X* Rl ( i )*Xm+v ( i )* Rl ( i )*X^ 2 )*
f +( Xc*( 2 *R+Rl ( i ) ) *Xm+Xc*X* ( 2 *R+Rl ( i ) )
+R^2* Rl ( i ) ) ;
dgf = 2 *(( 2 *X*Xc+Rl ( i )* 2 *R)*Xm+ Rl ( i )*X*2
*R+Xc*X^ 2 )* f +( −v ( i )*
( 2 * Xc*X+Rl ( i )* R)*Xm−v ( i ) * ( Rl ( i )* R+
*X)*X ) ;
end
Gx ( i ) =Xm;
Gf ( i ) = f ;
I s ( i ) = abs ( Vg ( i ) / ( R+ j *X* abs ( f ) −( j *( Xc / abs ( f ) ) * Rl ( i ) ) /
( Rl ( i ) − j *( Xc / abs ( f ) ) ) ) ) ;
I l ( i ) = abs ( ( − j *( Xc / abs ( f ) ) * I s ( i ) ) /
( Rl ( i ) − j *( Xc / abs ( f ) ) ) ) ; Vt ( i ) = I l ( i )* Rl ( i ) ;
I c ( i ) = Vt ( i ) / ( Xc / abs ( f ) ) ;
end
Vt=Vt * 220 ; Gx=Gx* Zbase ; I s = I s * I b a s e ; I l = I l * I b a s e ; I c = I c * I b a s e ;
%A j u s t e s pos c r i a c a o dos g r a f i c o s
%[4] [ 5 ]
Apêndice D – Velocidade Variável
c l e a r a l l ; c l c ; c l o s e a l l
T1 = r e a d t a b l e ( ’ C : \ Users \ d a n i e \ One Drive \
Area de T r a b a l h o \ UFRJ− E n g e n h a r i a E l e t r i c a \ TCC \ D a n i e l _ v e l o c i d a d e _ v a r i a v e l . x l sx ’ ) ;
n = 1 ;
Vt_exp_ 10 =T1 . Vt_exp_ 10 ; Vt_exp_ 10 = Vt_exp_ 10 ( ~ i s n a n ( T1 . Vt_exp_ 10 ) ) ’ ;
I s_exp_ 10 =T1 . I s_exp_ 10 ; I s_exp_ 10 = I s_exp_ 10 ( ~ i s n a n ( T1 . I s_exp_ 10 ) ) ’ ;
Ic_exp_ 10 =T1 . Ic_exp_ 10 ; Ic_exp_ 10 = Ic_exp_ 10 ( ~ i s n a n ( T1 . Ic_exp_ 10 ) ) ’ ;
I l _ e x p _ 1 0 =T1 . I l _ e x p _ 1 0 ; I l _ e x p _ 1 0 = I l _ e x p _ 1 0 ( ~ i s n a n ( T1 . I l _ e x p _ 1 0 ) ) ’ ;
ns_exp_ 10 =T1 . ns_exp_ 10 ; ns_exp_ 10 = ns_exp_ 10 ( ~ i s n a n ( T1 . ns_exp_ 10 ) ) ’ ;
nr_exp_ 10 =T1 . nr_exp_ 10 ; nr_exp_ 10 = nr_exp_ 10 ( ~ i s n a n ( T1 . nr_exp_ 10 ) ) ’ ;
s_exp_ 10 =T1 . s_exp_ 10 ; s_exp_ 10 =
s_exp_ 10 ( ~ i s n a n ( T1 . s_exp_ 10 ) ) ’ ; nr_exp_ 10 = f l i p ( nr_exp_ 10 ) ;
Pmed=T1 . Pmed ; Pmed= Pmed ( ~ i s n a n ( T1 . Pmed ) ) ’ ; f i g u r e ( 1 )
p_exp_ 10 = p o l y f i t ( nr_exp_ 10 , Vt_exp_10 , 1 ) ; f_exp_ 10 = p o l y v a l ( p_exp_10 , nr_exp_ 10 ) ;
ho l d on
p l o t ( nr_exp_ 10 , f_exp_ 10 , ’ − ’ , ’ DisplayName ’ , ’ Ajuste ’ )
p l o t ( nr_exp_ 10 , Vt_exp_10 , ’ r x ’ , ’ DisplayName ’ , ’ Experimento ’ ) x l a b e l ( ’ R o t a o por minuto ( rpm ) ’ )
y l a b e l ( ’ T e n s o T e r m i n a l (V) ’ ) g r i d on
a x i s ( [ 1 6 5 0 1880 100 2 5 5 ] )
f i g u r e ( 2 )
p_exp_ 10 = p o l y f i t ( nr_exp_ 10 , Ic_exp_ 10 , 1 ) ; f_exp_ 10 = p o l y v a l ( p_exp_10 , nr_exp_ 10 ) ;
ho l d on
p l o t ( nr_exp_ 10 , f_exp_ 10 , ’ − ’ , ’ DisplayName ’ , ’ Ajuste ’ )
p l o t ( nr_exp_ 10 , Ic_exp_ 10 , ’ r x ’ , ’ DisplayName ’ , ’ Experimento ’ ) x l a b e l ( ’ R o t a o por minuto ( rpm ) ’ )
y l a b e l ( ’ C o r r e n t e C a p a c i t o r (A) ’ ) g r i d on
a x i s ( [ 1 6 5 0 1880 0 . 3 1 ] )
f i g u r e ( 3 )
p_exp_ 10 = p o l y f i t ( nr_exp_ 10 , I s_exp_ 10 , 1 ) ; f_exp_ 10 = p o l y v a l ( p_exp_10 , nr_exp_ 10 ) ;
ho l d on
p l o t ( nr_exp_ 10 , f_exp_ 10 , ’ − ’ , ’ DisplayName ’ , ’ Ajuste ’ )
p l o t ( nr_exp_ 10 , I s_exp_ 10 , ’ r x ’ , ’ DisplayName ’ , ’ Experimento ’ )
x l a b e l ( ’ R o t a o por minuto ( rpm ) ’ ) y l a b e l ( ’ C o r r e n t e E s t a t o r (A) ’ )
g r i d on
a x i s ( [ 1 6 5 0 1880 0 . 3 1 ] )
f i g u r e ( 4 )
p_exp_ 10 = p o l y f i t ( nr_exp_ 10 , I l _exp_ 10 , 1 ) ; f_exp_ 10 = p o l y v a l ( p_exp_10 , nr_exp_ 10 ) ;
ho l d on
p l o t ( nr_exp_ 10 , f_exp_ 10 , ’ − ’ , ’ DisplayName ’ , ’ Ajuste ’ )
p l o t ( nr_exp_ 10 , I l _exp_ 10 , ’ r x ’ , ’ DisplayName ’ , ’ Experimento ’ ) x l a b e l ( ’ R o t a o por minuto ( rpm ) ’ )
y l a b e l ( ’ C o r r e n t e Carga (A) ’ ) g r i d on
a x i s ( [ 1 6 5 0 1880 0 . 0 1 5 ] )
f i g u r e ( 5 )
p_exp_ 10 = p o l y f i t ( nr_exp_ 10 , s_exp_ 10 , 1 ) ; f_exp_ 10 = p o l y v a l ( p_exp_10 , nr_exp_ 10 ) ;
ho l d on
p l o t ( nr_exp_ 10 , f_exp_ 10 , ’ − ’ , ’ DisplayName ’ , ’ Ajuste ’ )
p l o t ( nr_exp_ 10 , s_exp_ 10 , ’ r x ’ , ’ DisplayName ’ , ’ Experimento ’ ) x l a b e l ( ’ R o t a o ( rpm ) ’ )
y l a b e l ( ’ E s c o r r e g a m e n t o (%) ’ ) g r i d on
f i g u r e ( 6 )
p_exp_ 10 = p o l y f i t ( nr_exp_ 10 , Pmed , 1 ) ;
f_Pmed_10 = p o l y v a l ( p_exp_10 , nr_exp_ 10 ) ; ho l d on
p l o t ( nr_exp_ 10 , f_Pmed_10 , ’ − ’ , ’ DisplayName ’ , ’ Ajuste ’ )
p l o t ( nr_exp_ 10 , Pmed , ’ r x ’ , ’ DisplayName ’ , ’ Experimento ’ )
x l a b e l ( ’ R o t a o ( rpm ) ’ )
y l a b e l ( ’ P o t e n c i a de S a i d a (W) ’ ) g r i d on
¹Graduando em engenharia elétrica pela Escola Politécnica,
Universidade Federal do Rio de Janeiro,
²Orientadores: Sebastião Ércules Mel e Elkin Ferney Rodriguez Velandia
