REGISTRO DOI: 10.5281/zenodo.11529633
Sara Nunes Moreti1;
Orientador: Giancarlo Pessoa de Jesus2
Resumo
Organizar a sequência de setups a partir dos seus tempos na produção industrial é uma maneira de aprimorar e atender às necessidades dos clientes por processos mais flexíveis. Este trabalho sugere, a partir de pesquisas bibliográficas em artigos e livros, a aplicação prática em uma injetora plástica, uma sequência de fabricação programada por meio de modelagem matemática com solução via método Evolutionary da ferramenta Solver, do Excel. A partir da análise da solução do modelo foi possível perceber a sequência mais adequada a ser seguida e que resultou em uma redução no tempo total gasto com setups de, aproximadamente, 28%. Esta solução vai ao encontro das necessidades de diversas empresas que enfrentam o problema de reduzir o tempo de setup e sequenciar a programação de produção, contribuindo na tomada de decisão, tornando os processos menos custosos e a empresa mais competitiva.
Palavras-chave: Injetora plástica; Método Evolutionary; Solver; Setup.
Abstract
Considering the area of process management, organizing the sequence of setups based on their times in industrial production is a way of improving and serving consumers, thus making it more competent. Based on bibliographical research in articles and books, this paper suggests a manufacturing sequence, programmed using a mathematical model made using the Evolutionary method of Excel’s Solver tool, which presents the best setup sequence to follow in the production of a plastic injection molding machine based on the setup time of each change, where the decision variables correspond to the sequencing of the colors of the parts. By analyzing the solution, it was possible to see the most appropriate sequence to follow, which resulted in a setup time that was almost 28% shorter. Nowadays, companies need optimal solutions in their production process, and with the help of advanced mathematical techniques, this optimization is possible, providing better strategies and contributing to decision-making, making processes less costly and the company more competitive.
Keywords: Plastic injection molding machine; Method Evolutionary; Solver; Setup.
1. INTRODUÇÃO
Atualmente as organizações têm buscado um grau elevado de desempenho e eficiência operacional, devido ao alto nível de serviço que o mercado exige. Nessa linha, o objetivo deste trabalho é desenvolver uma proposta de simulação para reformulação do sequenciamento dos setups de uma injetora plástica que fabrica peças automotivas. Com base no estudo do tempo de setup de um modelo de peça, foi proposta uma reorganização da sequência de produção.
O Setup de um processo é o tempo decorrido desde a saída da última peça boa de um determinado lote até a primeira peça boa do lote seguinte segundo Shingo (2000). A redução dos tempos de setups traz muitas melhorias como: ganhos de capacidade produtiva, mais flexibilidade para produzir a variedade que o cliente deseja e na quantidade que deseja, consequentemente, redução nos tempos de entrega, redução do problema de falta e sobra nos estoques, bem como o aumento do nível de serviço e do faturamento da empresa.
Vale ressaltar que a literatura recomenda que se trabalhe para reduzir o tempo de setup dos processos e não, necessariamente, a sequência de setup. Esse tempo deveria ser tão baixo a ponto de tornar-se irrelevante a sequência de setup. No entanto, existem muitas situações em que o tempo ainda é deveras elevado e que a aplicação de um sequenciamento é justificável, desde que não se abandone a busca incessante pela redução do tempo de setup.
A aplicação do método Single Minute Exchange of Die (SMED), conhecido no Brasil como Troca Rápida de Ferramentas (TRF) é o mais recomendado para os casos de redução do tempo. Este sistema divide as etapas realizadas durante o setup em setup interno e externo, sendo o setup interno as atividades realizadas com a máquina parada e o setup externo as atividades realizadas com a máquina em funcionamento, a partir disso o objetivo é transformar os setups internos em externos, reduzindo assim os tempos de setups resultando no aumento de produtividade. A aplicabilidade adotada neste artigo é válida, pois pode ser trabalhada e aplicada em conjunto com o sistema SMED, antes, durante ou após seu desenvolvimento.
Um fator decisivo na potencialização das operações industriais é o uso de métodos de Pesquisa Operacional na modelagem de processos. As modelagens utilizam técnicas em que procedimentos operacionais podem ser analisados criteriosamente, revelando como os recursos chaves podem ser aproveitados de maneiras mais eficientes.
Sendo assim, para atingir o objetivo do trabalho, foi desenvolvido a aplicação de um método que utiliza as características clássicas do Problema do Caixeiro Viajante (PCV) para modelar e definir a minimização da soma do tempo de setup total na injetora. Para tal, primeiramente foi feita uma revisão bibliográfica dos modelos e métodos de solução sugeridos na literatura. Em seguida, os parâmetros do processo foram levantados, incluindo restrições e objetivo do problema. Por fim, foi modelado e resolvido no Microsoft-Excel Solver usando o suplemento Evolutionary. Nas próximas linhas será apresentado uma breve revisão teórica que dá sustentação ao tema abordado.
2. REVISÃO BIBLIOGRÁFICA
Neste capítulo será apresentado o referencial teórico que foi utilizado no suporte ao conhecimento dos conceitos para a realização do trabalho.
2.1 Pesquisa Operacional
A modelagem ajuda os gestores a terem conhecimentos de cenários, restrições e deixa os objetivos mais claros e específicos nas organizações. Segundo Lachtermacher (2009), por meio dela, aumentam-se as chances de fazer simulações a fim de encontrar melhores cenários para determinadas situações. Por intermédio da aplicação da Pesquisa Operacional (PO), as organizações são auxiliadas, coordenadas e conduzidas para as melhores decisões. Ela começa por um método científico que investiga o problema ou prováveis melhorias, para depois ser montado um modelo (normalmente matemático) (HILLIER; LIEBERMAN, 2013).
Dessa forma, para Florentino (1983), a PO usa qualquer método lógico, científico ou matemático para enfrentar as dificuldades que aparecem quando a administração busca um raciocínio eficiente para encarar os problemas de decisão. Sendo assim, a PO é desenvolvida do seguinte modo: 1) elaborar o modelo; 2) produzir um modelo matemático para compor a sistemática; 3) deduzir uma solução do problema; 4) analisar o problema e a solução; 5) organizar uma supervisão em cima da solução; 6) colocar a solução em prática.
A Pesquisa Operacional pode ser aplicada em várias áreas, como por exemplo: decisões empresariais; pesquisas de mercado; eficiência e produtividade; métodos de controle de qualidade; organização e fluxos em fábricas, entre outras. Ainda, com base em Florentino (1983), observa-se que o método adequado para o desenvolvimento da proposta deste trabalho é a aplicação do Problema do Caixeiro Viajante (PCV).
2.1.1 Problema do Caixeiro Viajante (PCV)
Segundo Silva e Oliveira (2006) o Travelling Salesman Problem (TSP) ou Problema do Caixeiro Viajante tem o objetivo de oferecer, a partir da otimização combinatória, a menor rota entre um conjunto de cidades, no qual o caixeiro passa por elas apenas uma vez e finaliza na cidade em que iniciou sua jornada. Este problema tem muitas aplicações no campo da logística, transporte, produção industrial e ciência, aplicações voltadas para o planejamento de companhias aéreas, a roteirização de veículos, o mapeamento de DNA humano, o processamento de pedidos, sequenciamento das atividades produtivas, dentre outras, são muito comuns na literatura (LENSTRA; RINNOOY KAN, 1975).
No contexto deste trabalho será abordado o sequenciamento de atividades produtivas, especificamente, a “rota” de setups de uma empresa do setor automotivo. Neste caso, cada atividade requer um tempo diferente de setup, sendo este tempo maior ou menor, a depender do sequenciamento da produção, impactando diretamente na capacidade produtiva da empresa.
A Figura 1, apresenta um diagrama esquemático do TSP.
Figura 1 – Estrutura representativa do Problema do Caixeiro Viajante
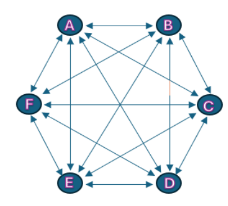
Fonte: Baseado em Rasmussen (2011)
Na figura 1 é demonstrado uma estrutura de nós interligados do Problema do Caixeiro Viajante. Há dois tipos desses problemas, os simétricos e assimétricos. Para Reinelt (1991) os simétricos são os que tem o mesmo valor de ida e volta de um determinado nó para outro, e os assimétricos são os que o valor de ida são distintos dos valores de volta. No presente trabalho, os nós se referem às cores das peças produzidas e a ligação entre os nós são os tempos de setups entre as cores, ele é assimétrico pois os valores (tempos) entre a cor A para a cor B é diferente da cor B para a cor A, e isso se repete em todas as trocas de cores possíveis.
De acordo com Miller, Tucker e Zemlin (1960) o problema do Caixeiro Viajante segue a seguinte formulação matemática:
Figura 2 – Formulação matemática do Caixeiro Viajante

Fonte: Miller, Tucker e Zemlin (1960)
A restrição (1) na Figura 2, determina que cada nó deve ser visitado apenas uma vez. A restrição (2) determina que cada nó deve ser deixado apenas uma vez. A restrição (3) impõe a eliminação de subciclos, ou seja, garante que não haja ciclos separados, e que todo nó seja visitado e não haja repetições ou exclusões. A restrição (4) estabelece que as variáveis possam assumir apenas os valores 0 ou 1 (binárias), ou seja, garantindo que o fluxo seja consistente e praticável. A solução do problema do caixeiro viajante pode ser obtida utilizando a Ferramenta Solver do Excel.
2.1.2 Ferramenta Solver do Microsoft Excel
O Microsoft Excel é um instrumento que torna possível a produção de planilhas, interações matemáticas para vários modelos de cálculos, simulações, análises, partilha e proteção de dados, dentre seu grupo de ferramentas destacamos o Solver, que é uma ferramenta utilizada para resolver problemas de otimização de uma função de variáveis (sujeita ou não a restrições) denominada função objetivo que pode ser maximizar lucros ou minimizar custos, submetendo-se a uma sequência de equações ou inequações lineares (LISBOA, 2002).
O Solver é uma importante ferramenta de otimização para várias problematizações. Com isso, a função objetivo neste artigo é a minimização do tempo total gasto nos setups, as variáveis são os tempos dos setups entre as peças e a restrição é a peça determinada como ponto de partida e chegada. No entanto, a solução pelo método simplex, no solver, pode resultar no aparecimento de subciclos gerando uma grande dificuldade, na utilização deste modelo para vários pontos. Esta comparação foi feita por Silva et al (2018). Sendo assim, para a solução do PCV foi escolhido o método Evolutionary.
2.1.3 Método Evolutionary
O método Evolutionary foi apresentado por Xie e Steven (1993), fundamentado em uma prática do Método dos Elementos Finitos (MEF), foi planejado a partir de um algoritmo evolucionário, baseado no conceito da adição de vazios, isto é, é baseado em uma definição sustentada na posição de componentes pouco usados ao longo do procedimento. Processo chamado hard-kill.
A filosofia deste método é baseada na evolução, sobrevivência e genética, sendo assim, é denominado algoritmo genético. Ele inicia formando de forma aleatória um extenso grupo de soluções candidatas, conhecidas como população. Essa população é controlada pelo Evolutionary durante todo processo de resolução. Com o cuidado das várias soluções candidatas é possível desviar-se de ciladas em um ponto ideal (HILLIER, 2014).
O método Evolutionary é uma excelente opção para solucionar problemas estruturais, como o caso do PCV.
2.2 Redução de Setup
Segundo McCarthy (2006), na maioria das organizações 50% do período de suas atividades é consumido durante o setup, assim sendo, diminuir o tempo de preparação torna se essencial no ambiente empresarial mundial competitivo. Deste modo, conseguir alternativas que torne possível a redução do tempo de setup é de extrema importância, dado que impacta claramente na capacidade produtiva.
Com objetivo de amparar nessas situações, o principal e mais propagado método para a diminuição do tempo utilizado durante os setups é o SMED, com o intuito de reduzir desperdícios (MARDEGAN et al., 2006).
2.2.1 SMED (Single Minute Exchange of Die)
O SMED foi criado por Shigeo Shingo na década de 50 com objetivo de diminuir o tempo de setup, ele diz que operações como o setup não agrega valor ao produto. No conceito de Shingo (2000), o SMED abrange técnicas que permitem realizar o setup em menos de 10 minutos. Para Flogliatto e Fagundes (2003), a TRF é uma metodologia que diminui os tempos de preparo do maquinário, proporcionando a fabricação econômica em lotes pequenos.
A Figura 3 abaixo descreve detalhadamente o processo de setup, mostrando as atividades que podem ser desempenhadas no tempo em que a máquina está parada.
Figura 3 – Demonstração do processo de setup
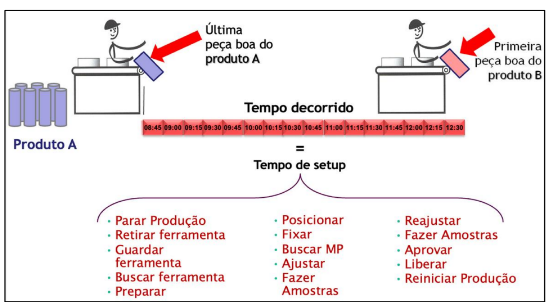
Fonte: Elaborada pelos autores (2024)
De acordo com a representação do processo da figura 3, o tempo decorrido da última peça boa de um lote até a primeira peça boa do próximo lote é chamado de setup. Segundo Shingo (1985), a divisão de setup interno e externo deve ser monitorado, visto que ambos são a chave para se alcançar o SMED. É necessário efetuar tais atividades como buscar matéria prima, ferramentas, ajustar e posicionar, durante o setup externo, ou seja, quando a máquina estiver em funcionamento. Este processo representa um ganho significativo de tempo propiciando agilidade para iniciar o setup interno.
3. ESTUDO DE CASO
3.1 A empresa estudada
A pesquisa foi realizada em uma empresa do setor de indústria de produção de peças automotivas por injeção plástica. Trata-se de uma organização de pequeno porte, com 85 fun cionários, atuando há 20 anos, neste trabalho tratada como “Empresa Estudada”. Nesta fábri ca, são realizados processos produtivos de nível médio de complexidade, com processos de fabricação e montagem, ela produz peças que abastecem as linhas de produção dos seus clien tes, todos montadoras de veículos. Este processo foi escolhido por ser importante no meio de produção e apresentar a necessidade de melhorias no tempo e na sequência de setups.
3.2 O processo de injeção plástica na empresa estudada
Segundo Martins (2014), o procedimento de injeção plástica constitui grande parte do método produtivo na fabricação de peças plásticas, por causa da sua flexibilidade e aplicação em diversos setores da indústria. O setor automotivo é o que mais utiliza esse método no Brasil, e a cada ano este consumo aumenta. O processo de injeção plástica consiste fundamentalmente em moldar a matéria-prima, o polímero (Figura 4), para transformar em peças de acordo com o molde utilizado para sua formação. O processo começa com a retirada da umidade do polímero por meio de estufas, depois disso, a matéria-prima é transportada para o maquinário (figura 5) responsável pela injeção plástica, onde é aquecida e transformada em um material pastoso, sendo injetada em um molde (Figura 6) para adquirir o formato de determinada peça. (HARADA, 2004).
Figura 4 – Polímero

Fonte: www.pinnaclepolymers.com
Figura 5 – Esquema de uma injetora plástica
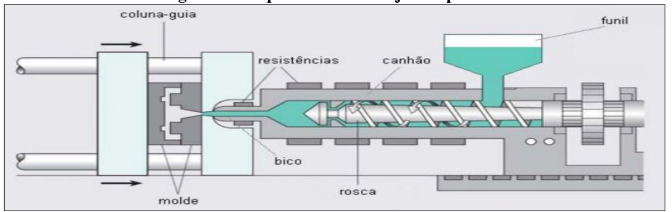
Fonte: www.researchgate.net
Figura 6 – Exemplo de molde de peça

Fonte: www.go4mould.com/automotive-injection-molding
Neste tipo de processo, o setup se torna muito crítico, uma vez que a troca dos moldes costuma ser demorada, resultando, em muitos casos, na adoção de grandes lotes de produção para compensar essas perdas. A redução do tempo de setup e a otimização do sequenciamento da produção, se torna extremamente importante para evitar o desperdício da superprodução. Nas próximas linhas, será descrito o método de pesquisa utilizado no desenvolvimento deste trabalho.
3.3 Método de pesquisa
Para Rampazzo (2005), a metodologia científica oferece o entendimento e a análise do mundo através da criação do conhecimento. O saber acontece quando as pessoas percorrem os caminhos do conhecimento, e o ensino é o protagonista desse desenvolvimento. Para atingir o objetivo deste trabalho, inicialmente foi realizada uma revisão teórica sobre o assunto, em diversas plataformas de pesquisa. Nesta fase de pesquisa exploratória, tomou-se o cuidado de selecionar materiais de artigos científicos, publicados em jornais, revistas, anais de congressos e livros.
Para este estudo, inicialmente, foi solicitada uma autorização formal da empresa estudada, que permitiu a divulgação dos dados, em caráter de sigilo de seu nome. Após esta etapa, os pesquisadores analisaram fontes documentais disponíveis na organização incluindo se documentos dos setores de gestão da qualidade e engenharia de processo tais como: relatórios de produtos não conformes, indicadores de performance etc. O objetivo desta etapa foi coletar os tempos de setup do processo de injeção.
Os dados foram organizados em uma planilha e um tratamento estatístico foi feito utilizando média, desvio padrão e coeficiente de segurança de 95%, para corrigir os desvios. A partir dos dados tratados, foi feita a modelagem pelo Método Evolutionary.
3.4 Coleta de dados
Este trabalho teve a finalidade de otimizar a sequência de fabricação a partir do tempo gasto durante os setups, ou seja, minimizá-los o máximo possível por meio da organização da sequência das cores dos produtos a serem produzidos, contribuindo assim para a redução de desperdícios e a otimização para a melhoria contínua da companhia. A Tabela 1 fornece as diferentes cores que são produzidas de determinada peça, e os tempos (em minutos) gastos durante os setups entre elas.
Tabela 1 – Cores e tempos de setups
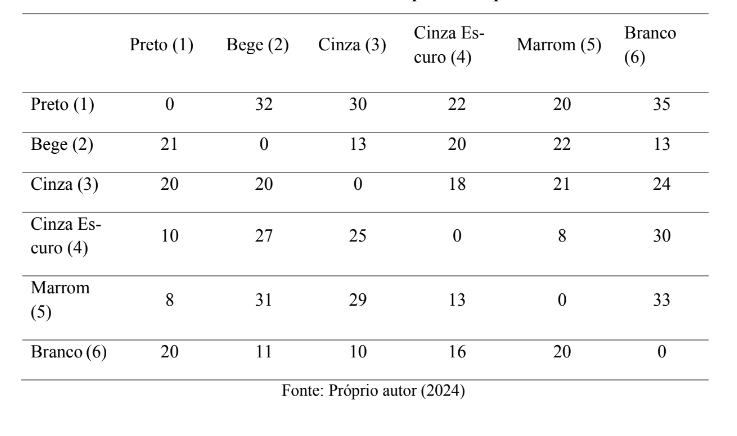
3.5 Preparação para o método Evolutionary
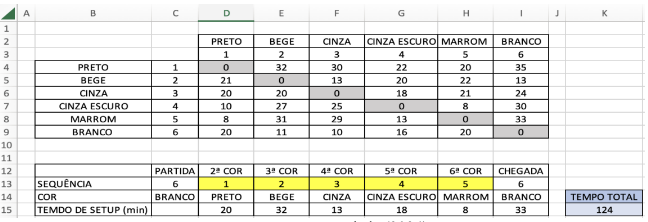
A Tabela 2 expõe os dados e as células prontas para a execução do método Evolutionary na planilha do Excel. A matriz de cores (linha 14) é formada da cor de partida e chegada (Branco) e mais 5 cores, a saber: Preto, Bege, Cinza, Cinza Escuro e Marrom, que são as cores do produto a ser fabricado.
Tabela 2 – Planilha de cores e tempos de setups
Fonte: Empresa Estudada (2024)
Antes da execução do método Evolutionary, nas células C13 e I13 foram colocados os números referentes ao ponto de partida e chegada, e entre as células D13 até H13 a sequência de cores respectivamente iguais da tabela. Depois, nas seguintes células foram colocadas as seguintes fórmulas, apresentadas no Quadro 1 a seguir.
Quadro 1 – Parâmetros do Solver

Fonte: Próprio autor (2024)
3.6 Aplicação do método Evolutionary
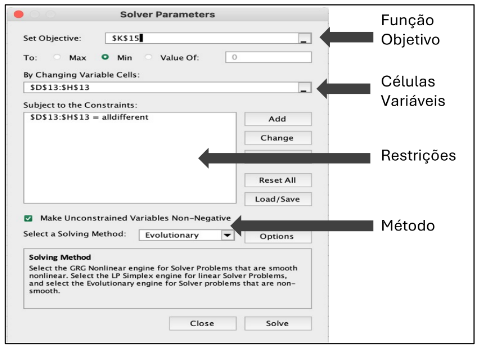
A Figura 7 oferece os parâmetros do Excel Solver, como por exemplo função-objetivo, células variáveis, restrições e o método de solução selecionado (Evolutionary).
Figura 7 – Parâmetros do solver
Fonte: Adaptado de Office 365 – Microsoft Excel
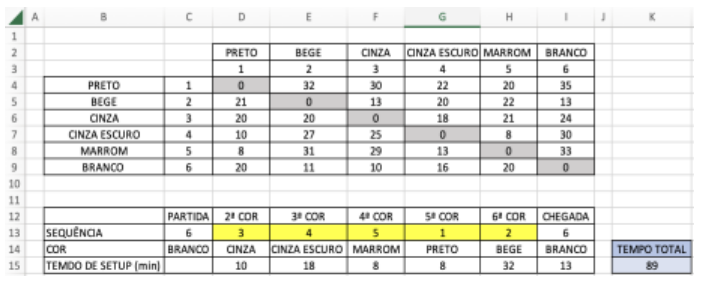
Na Tabela 3 é apresentado os resultados alcançados. A sequência de cores para se conseguir o mínimo de tempo de setup entre todas as cores e voltando para a cor inicial é: Branco – Cinza – Cinza Escuro – Marrom – Preto – Bege – Branco, e a soma de tempo total de setup é de 89 minutos.
Tabela 3 – Sequência de tempo de setup mínimo
Fonte: Próprio autor (2024)
4. DISCUSSÃO E ANÁLISE DE RESULTADOS
Fazendo uma comparação de tempos entre a Tabela 2 e a Tabela 3 é notada uma diminuição de quase 28% do tempo, ou seja, 35 minutos a menos gastos durantes os setups diariamente. A otimização deste tempo ajuda aumentar a capacidade de produção da empresa, e isso foi possível por causa da aplicação da Pesquisa Operacional que ajudou no encontro do melhor cenário possível, assim como afirmado por Lachtermacher (2009) no capítulo 2.1.
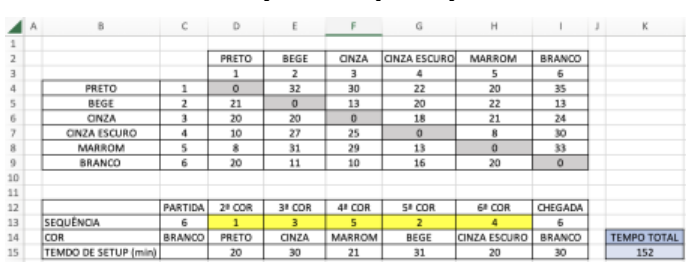
Para questões de conhecimento, na Tabela 4 mostra o tempo máximo de setup possível. O tempo máximo é de 152 min e o mínimo da Figura 3 é de 89 min, uma diferença de 63 minutos. Este conhecimento se torna importante pois a empresa estudada não trabalha com uma sequência de cores pré-definida, as peças são fabricadas conforme a entrada dos pedidos. Ou seja, o tempo de setup diário sem uma programação pode variar entre 89 até 152 min.
Tabela 4 – Sequência de tempo de setup máximo
Fonte: Próprio autor (2024)
No geral, estes cálculos apontam que a simulação feita seguindo o Problema do Caixeiro Viajante foi interessante para perceber a importância de se estudar as sequências dos processos produtivos nas empresas, sendo fundamental a utilização de ferramentas como o Evolutionary para chegar a resultados que vão fornecer melhorias nos serviços e em particular otimizar processos.
5. CONSIDERAÇÕES FINAIS
Na conjuntura apresentada, este artigo mostra um método e um software para solucionar o problema do caixeiro viajante (PCV) com a meta de definir a sequência de cores do produto a ser produzido minimizando o máximo possível o tempo gasto nos setups. O método apresentado soluciona a modelagem matemática do PCV com o recurso do método Evolutionary, que está à disposição no Microsoft-Excel-Solver. O algoritmo desse método é genético pré-programado, preparado para indicar excelentes resoluções. O software Excel está em quase todos os computadores, sendo um dos mais conhecidos e seu manuseio é simples.
Deste modo, o artigo explana um cenário que as soluções foram apontadas suficientes para o objetivo, alcançando um menor tempo durante os setups em comparação a outros sequenciamentos possíveis, otimizando todo o processo. Cabe ressaltar, que estes ganhos não se referem à redução do tempo de setup, mas a uma redução no tempo perdido por não se ter uma boa programação e sequenciamento da produção nas injetoras. O seguimento ótimo, apresentado na Tabela 3 é: 6 (branco) – 3 (cinza) – 4 (cinza escuro) – 5 (marrom) – 1 (preto) – 2 (bege) – 6 (branco). Esta sequência, tem um tempo total de setup diário de 89 minutos.
Por meio da aplicação da ferramenta Microsoft-Excel-Solver, foi possível chegar ao objetivo. Com o menor tempo nos setups é possível o aumento da produtividade conseguindo atender demandas maiores, e consequentemente diminuir custos na produção. Conclui-se, assim, que é essencial a utilização de softwares na melhoria dos processos produtivos.
A partir do trabalho realizado faz-se necessário um estudo mais aprofundado em cima do Setups das máquinas, com o objetivo de diminuir o tempo do processo de Setup na troca das cores. Para tal objetivo, indica-se a aplicação do método Single Minute Exchange of Die (SMED) conhecido como Troca Rápida de Ferramentas.
REFERÊNCIAS
FLORENTINO, A. M. Custos: princípios, cálculos e contabilização. 8ª ed. Rio de Janeiro: Fundação Getúlio Vargas, Serviço de Publicações, 1983.
FOGLIATTO, F. S.; e FAGUNDES, P. R. M. Troca rápida de ferramentas: proposta metodológica e estudo de caso. São Carlos, SP: Universidade Federal de São Carlos, 2003. Disponível em: < http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0104- 530X2003000200004>. Acesso em: 14 abr. 2024.
GO4MOULD. What makes go4 mould automotive injection molding tour top priority? Disponível em: < https://go4mould.com/automotive-injection-molding>. Acesso: 1 abr. 2024.
HARADA, J. Moldes para injeção de termoplásticos. São Paulo, Editora Artliber, 2004.
HILLIER, F. S.; e LIEBERMAN, G. J. Introdução à Pesquisa Operacional. 9aed. Porto Alegre: AMGH, 2013.
HILLIER, F. S. Introdução a ciência da gestão. modelagem e estudos de casos com planilhas eletrônicas. 4aed. São Paulo: AtlasMac Graw Hill, Bookman 2014.
LACHTERMACHER, G. Pesquisa Operacional na tomada de decisões. 4aed. São Paulo: Pearson, 2009.
LENSTRA, J. K.; e RINNOOY KAN, A. H. G. Some simple applications of the Travelling Salesman Problem. Operational Research Quarterly, Vol. 26, No4, p. 717-733, 1975.
LISBOA, E. F.A. Apostila de Pesquisa Operacional, Rio de Janeiro, RJ – Brasil, 2002.
MARDEGAN, R.; LOPES, P.; TRESIANE, R.B.; GUERRA, M.; e ROCHA, F. Estudo de caso de implementação de troca rápida de ferramenta em uma empresa metal mecânica. Anais do Encontro Nacional de Engenharia de Produção. Fortaleza, CE, Brasil, 35, 2006.
MARTINS, M. Indústria de transformação de plásticos. Ano VIII, No02. ago. 2014.
MILLER, C. E.; TUCKER, A. W.; e ZEMLIN, R. A. Integer programming formulation of traveling salesman problems. Journal of the ACM (JACM), ACM New York, NY, USA, v. 7, n. 4, p. 326–329, 1960.
MCCARTHY, R. Toolroom management: presetting increases profits and productivity. MoldMaking Technology,2006.
PINNACLE POLYMERS. Developing solutions for your polypropylene needs. Disponível em: < https://www.pinnaclepolymers.com/>. Acesso em: 18 abr. 2024.
RAMPAZZO, Lino. Metodologia científica. 3a ed. São Paulo: Loyola, 2005.
RASMUSSEN, Rasmus. TSP in spreadsheets – a fast and flexible tool. Omega, v. 39, n.1, p. 51-63, 2011.
REINELT, G. TSPLIB – A traveling salesman problem library. Informs Journal on Computing, v. 3, 4, p. 376–384, 1991.
RESEARCH GATE. Processo de MF via injeção de termoplástico. Disponível em: <https://www.researchgate.net/figure/Figura-2-Processo-de-MF-via-injecao-de termoplastico_fig2_364348497>. Acesso em: 18 abr. 2024.
SHINGO, S. A revolution in manufacturing: the SMED system. Productivity Press. Cambridge, MA, 1985.
SHINGO, S. O Sistema de Troca Rápida de Ferramentas. Porto Alegre: Bookman Editora, 2000.
SILVA, A. F.; e OLIVEIRA, A. C. Algoritmos genéticos: alguns experimentos com os operadores de cruzamento (“Crossover”) para o problema do caixeiro viajante assimétrico. XXVI ENEGEP – Fortaleza – CE, 2006.
SILVA, C. M. P; NEVES, C. E. V; OLIVEIRA, D. J.; FRAIHA NETO, E.; e MENDES, O. L. Estudo comparativo entre o método simplex e o método Evolutionary para a otimização de rotas de distribuidores na cidade de São José do Rio Preto – SP. Interface Tecnológica, DOI: 10.31510/infa.v15i2.489, 2018. XIE, M. Y.; e STEVEN, G. P. A Simple evolutionary procedure for structural optimization. Computer & Structures, v 49, p 885-896, 1993.
1Discente do Curso Superior de Tecnologia em Logística da Faculdade de Tecnologia do Estado (Fatec) Jorge Caram Sabbag, Bebedouro – SP. E-mail: sara.moreti@fatec.sp.gov.br;
2Docente do Curso Superior de Tecnologia em Logística da Faculdade de Tecnologia do Estado (Fatec) Jorge Caram Sabbag, Bebedouro – SP. Graduado em Engenharia Mecânica (UFPA). Mestre em Engenharia de Produção (UFSCar). E-mail: giancarlo.jesus@fatec.sp.gov.br
