REGISTRO DOI: 10.5281/zenodo.8318645
Ana Carolina Nobile Leiva;
Evandro da Silva Romano;
Guidyelle Silva;
Luis Eduardo de Santana da Silva;
Welton Souza Bento;
Orientadores: Prof. Me. Bernardo Goisman; Prof. Dr. Fernando Mori
Resumo: A previsão de demanda é uma ferramenta fundamental, para se obter um planejamento da organização, pois auxilia nas tomadas de decisões, permitindo o planejamento de longo, médio e curto prazo, além de ser uma variável na gestão da capacidade produtiva. Além disso, vem sendo utilizada cada vez mais, no âmbito empresarial, visando o planejamento estratégico da produção, com a finalidade de se manter ativo e competitivo no mercado. Diante disso, este trabalho tem como objetivo realizar a previsão de demanda de 14 produtos dentro de um determinado período, de uma empresa do ramo farmacêutico e no fim, comparar estas com a previsão obtida pela organização. Inicialmente, foram coletados dados do estudo de caso, onde foi possível verificar que a empresa faz o uso de dois modelos de vendas, sendo que o utilizado no estudo é o modelo Sell Out, que visa a venda ao cliente final. Com isso foi aplicado o método da Curva ABC, a fim de identificar e classificar o grau de importância de cada produto, além de determinar quais itens seriam aplicados no Software Crystal Ball, para previsão de demanda. Foram, então, criados e analisados modelos para os produtos filtrados via curva ABC.
Palavras-chave: Previsão da demanda, erros, empresa, vantagens, estudo de caso.
Abstract: The demand forecast is a fundamental tool to obtain a planning of the organization, because it helps in an important way in decision-making, allowing the planning of long, medium and short term, besides being a variable in the management of productive capacity. In addition, it has been increasingly used in the business environment, aiming at strategic production planning, in order to remain active and competitive in the market. In view of this, this work aims to carry out the demand forecast of 20 products within a certain period, of a pharmaceutical company and in the end, compare with the forecast obtained by the organization. Initially, it was analyzed the data of the case study, where it was possible to verify that the company makes use of two sales models, being Sell In and Sell Out, aiming first the sale to suppliers and finally, to the final customer. With this, the ABC Curve method was applied, in order to identify and classify the degree of importance of each product, in addition to determining which items would be applied in the Crystal Ball Software, for demand forecasting.
Keywords: Demand forecast, mistakes, company, benefits, case study.
1. Introdução
A previsão de demanda é uma atividade fundamental para o planejamento e tomada de decisões estratégicas em empresas de diversos setores, incluindo o farmacêutico. A capacidade de antecipar as necessidades do mercado e estimar a quantidade de produtos que serão demandados é essencial para garantir o abastecimento adequado, evitar estoques desnecessários e otimizar a produção (BONFA, F., SOUZA, M., & ALBINO, V., 2017).
Neste contexto, o presente artigo tem como objetivo realizar um estudo de caso em um laboratório farmacêutico sediado na cidade de Curitiba, que atua em todo o Brasil. O estudo se concentrará na previsão de demanda de 20 produtos da empresa ao longo do período de janeiro de 2022 a março de 2023.
Para atingir esse objetivo, será utilizada uma abordagem quantitativa, combinando métodos estatísticos e o uso do software Crystal Ball. Esse software é uma ferramenta poderosa que auxilia na previsão de resultados incertos e é amplamente utilizado para modelagem preditiva, previsão, simulação e otimização em diversas indústrias (ORACLE, 2008).
A metodologia adotada envolve a utilização dos dados reais fornecidos pelo laboratório farmacêutico, que incluem as vendas dos produtos ao longo de 15 meses sendo de janeiro de 2022 a março de 2023, bem como as previsões desenvolvidas pela própria empresa para o mesmo período. Em seguida, esses dados serão inseridos no Crystal Ball para realizar as previsões de dois meses (fevereiro e março de 2023).
Além disso, será aplicada a curva ABC, método criado por volta de 1897, por Wilfredo Frederico Samaso, para identificar quais produtos possuem maior relevância e merecem maior atenção no estudo de caso (DIAS, 2010).
Os resultados obtidos pelo software serão comparados com as previsões da empresa e os dados reais de vendas, para assim avaliar a acurácia dos modelos de previsão. Serão aplicadas métricas de erro, como o Erro Quadrático Médio (RMSE) e o Erro Médio Absoluto Percentual (MAPE), para avaliar o desempenho dos modelos.
A análise dos resultados obtidos permitirá identificar possíveis fatores que influenciam a precisão das previsões, bem como as possíveis causas para as divergências entre as previsões do software e da empresa.
Espera-se que este estudo de caso contribua para a compreensão da importância da previsão de demanda na indústria farmacêutica e a escolha adequada de métodos e ferramentas para aprimorar essa atividade crucial para a gestão eficiente das empresas deste e outros setores. A aplicabilidade do software Crystal Ball pode trazer insights valiosos para melhorar a tomada de decisão e garantir o sucesso no cenário competitivo do mercado.
1.1 Justificativa e Problemática
A previsão de demanda é um aspecto crítico para o sucesso de empresas, independente do ramo de atuação. Com o aumento da competitividade e a necessidade de redução de custos, torna-se essencial para as empresas incluindo as farmacêuticas adotarem métodos eficientes de previsão de demanda, a fim de otimizar o planejamento da produção, a gestão de estoques e a entrega de produtos aos seus clientes.
Todavia, o ramo farmacêutico traz desafios específicos, como a sazonalidade de determinados medicamentos, a variação de demanda causada por eventos imprevistos (por exemplo, surtos de doenças, epidemias ou pandemias como vivenciamos a de Covid-19) e a necessidade de cumprir rigorosas deliberações para garantir a disponibilidade de medicamentos para o mercado.
Assim, este artigo se justifica pela importância de verificar como as ferramentas de previsão de demanda são aplicadas no ramo farmacêutico, com base em um estudo de caso real.
Além do mais, com essa análise, espera-se contribuir para a compreensão da aplicabilidade das ferramentas, uma vez que podemos comparar resultados obtidos pelo grupo e comparar com previsões reais realizadas pela empresa e fornece recomendações práticas para aprimorar a eficiência da previsão de demanda e, consequentemente, a gestão no setor farmacêutico, estudada pelo grupo.
1.2 Objetivos
Os objetivos esquematizaram as metas a serem alcançadas para a elaboração do trabalho.
1.2.1 Objetivo geral
Utilizar ferramentas de previsão de demanda em um estudo de caso em uma empresa do ramo farmacêutico, comparando com a análise realizada pela própria empresa, visando identificar a sua eficácia na tomada de decisões estratégicas e operacionais.
1.2.2 Objetivos específicos
a) Analisar a importância da previsão de demanda e seus impactos na cadeia de suprimentos;
b) Identificar as principais ferramentas de previsão de demanda;
c) Realizar um estudo de caso em uma empresa do ramo farmacêutico, utilizando as ferramentas de previsão de demanda selecionadas;
d) Avaliar a precisão das previsões obtidas pelas ferramentas utilizadas no estudo de caso;
e) Analisar os resultados obtidos e discutir os benefícios e limitações das ferramentas de previsão de demanda no contexto do estudo de caso;
f) Propor recomendações para o aprimoramento da utilização das ferramentas de previsão de demanda na empresa estudada e em outras organizações do ramo farmacêutico.
2. Referencial teórico
Neste tópico será exibido as teorias a respeito dos temas que são a base do trabalho: Curva ABC, previsão da demanda e os modelos de erros.
2.1 Curva ABC
Este método foi criado por volta de 1897, por Wilfredo Frederico Samaso, que também era conhecido como Vilfredo Pareto. Na época ele fez uma análise referentes as rendas das pessoas e percebeu que 80% das riquezas estavam nas mãos de apenas 20% da população. Segundo Pozo (2010), Pareto utilizando este método, conseguiu identificar que a menor parte da população possuía a maior porcentagem das riquezas e a menor parte era destinada para o maior número de pessoas.
A curva ABC é muito utilizada na gestão de estoques para categorização dos produtos quanto a sua importância para empresa. Considerando esta aplicação e de acordo com os conceitos básicos, o primeiro passo é identificar todos os produtos em estoque e determinar a quantidade consumida, o preço unitário de cada item e o valor total (quantidade consumida X preço unitário). Em seguida, classifica os itens em ordem decrescente de valor total durante um período. Por fim, calcula-se as porcentagens de cada elemento em relação ao valor total de acordo com as proporções indicadas pelo método e depois classifica-se entre A, B ou C.
Segundo Martins e Alt (2005), este método consiste em analisar os itens considerando seu valor e visando classificá-los em três grupos: A, B e C.
a) classe A: os itens da classe A são imprescindíveis, e sua falta pode ocasionar a ruptura da cadeia produtiva da empresa.
b) classe B: os itens da classe B são importantes, mas sua falta em um período de curto prazo não afeta diretamente a cadeia produtiva.
c) classe C: os itens da classe C não impactam diretamente as cadeias produtivas, porém são necessários e contribuem indiretamente para o funcionamento das cadeias.
Ainda, Martins e Alt (2005) completam que os itens da classe A são mais importantes em termos de valor e de consumo, podendo representar entre 35% e 70% do valor da movimentação do estoque, com a proporção variando de 10% a 45% estão os itens da Classe B, já os itens da categoria C representam o restante.
De acordo com Ching (2007) informa que todo o valor investido nos estoques, juntos aos custos operacionais, podem ser reduzidos pela organização e direcionar o capital apenas para os itens que realmente irão atender a produção. Assim, cada item produzido visa a satisfação dos clientes, sendo uns mais rentáveis que outros ou exijam uma produção mais específica.
Segundo Dias (2010), este método é um instrumento muito importante para administrar e identificar quais itens necessitam de uma atenção especial, pois é possível evidenciá-los e classificá-los por grau de maior importância.
Por fim, é necessário classificar quais itens se enquadram dentre essas três classes e assim formar um eixo cartesiano. Martins e Alt (2005) complementam que os itens de Classe A, obtém mais valores de consumo e representam ente 35% e 70% do estoque, já os da Classe B representam cerca de 10% a 45% do estoque e por fim, os itens de Classe C, representam o restante.
Portanto, a utilização dessa ferramenta permite analisar e identificar o que demandam controles específicos, além disso, é possível gerenciar os itens que darão mais benefícios para a empresa.
2.2 Modelos de previsão da demanda
A previsão da demanda é fundamental para o planejamento das empresas, como explicitado por Gerber et. al (2013) permitindo que elas se organizem adequadamente para atender às necessidades dos consumidores, evitar desperdícios de recursos e consequentemente maximizar seu lucro.
Segundo Tubino (2000) os métodos de previsão de demanda podem ser classificados em dois modelos, em abordagem qualitativa e quantitativa, sendo, que o primeiro modelo tem referência em dados subjetivos, enquanto os métodos quantitativos em dados históricos.
2.3 Modelos Qualitativos
De acordo com Moreira (2000) modelos qualitativos são baseados em informações subjetivas, ou seja, em dados baseados nas experiências de clientes que possam contribuir com previsões futuras. Empresas utilizam destes modelos como ferramentas de análise quando desejam criar estratégias eficientes de marketing e produção para entender a demanda do consumidor.
Conforme Dias (1999) afirma, esses modelos podem ser considerados apenas para uma aproximação da realidade e que a utilização de forma única desse modelo pode gerar problemas na previsão, já que, conforme Tubino (2000) modelos qualitativos não precisam da disponibilidade de dados temporais.
2.4 Modelos Quantitativos
Os modelos quantitativos de previsão da demanda são uma das principais ferramentas utilizadas pelas empresas para estimar a demanda futura de seus produtos ou serviços. Para Pinto (2014) esses modelos se baseiam em técnicas matemáticas que analisam dados históricos, sendo utilizados como ferramentas de gestão, analisando históricos de vendas, tendências e fatores externos, como sazonalidade, mudanças econômicas e no comportamento do consumidor.
De acordo com Slack et al. (2009) esses métodos quantitativos são classificados em dois modelos, sendo eles, causais e métodos de séries temporais.
2.4.1 Modelos Causais
De acordo com Slack et al. (2013), esses modelos permitem identificar as relações de causa e efeito entre as variáveis que que influenciam no comportamento da demanda, permitindo assim a criação dos cenários possíveis no futuro para explicar as flutuações na demanda.
Segundo Arvan et al. (2019), a previsão da demanda em métodos causais é altamente associada com fatores no ambiente, como fatores econômicos e da taxa de juros de um país. Nesse modelo, os dados seguem um padrão previsível ao longo do tempo e existem relações análogas entre as informações que se deseja prever e outros fatores. Porém, é importante ressaltar que a escolha do modelo causal mais adequado deve considerar as particularidades de cada negócio e as condições do mercado em que atua. Assim, ao identificar as variáveis que influenciam a demanda, é possível criar cenários futuros possíveis e tomar decisões assertivas. Dessa forma, a escolha do modelo causal adequado para cada negócio deve ser cuidadosamente estudada, de modo a garantir resultados satisfatórios.
2.4.1.1 Análise de Regressão
Dentre os principais modelos causais, destaca-se a análise de regressão, que se baseia em analisar a relação entre a demanda e as variáveis independentes, como preço, tendências sociais e econômicas, entre outras. Segundo Moreira (2017), a análise de regressão é um dos métodos mais utilizados, pois permite identificar melhor o grau de influência de cada variável. Um fator relevante no estudo de regressão é a tendência.
2.4.2 Tendência
Segundo Tubino (2000), a tendência é caracterizada pelo movimento gradual de longo prazo da demanda, e sua estimativa é obtida ao identificar uma equação que descreva esse padrão. Analisando os dados históricos, é possível identificar essa equação, que pode ser linear ou não-linear (exponencial, parabólica, logarítmica, etc.).
Existem duas técnicas amplamente utilizadas para lidar com previsões de demanda que apresentam tendência. Uma delas é baseada em uma equação linear, enquanto a outra envolve o uso de ajustamento para obter o componente de tendência. A equação (1) representa uma equação linear.

Onde:
Y: é a previsão da demanda para o período X;
a: ordenada à origem ou intersecção no eixo dos Y;
b: o coeficiente angular e X o período (partindo de X = 0) para previsão.
Com os dados históricos da demanda, obtêm se os coeficientes a e b pelas equações (2) e (3).
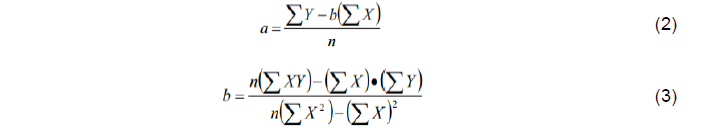
Onde:
n: é o número de períodos observados
De acordo com Martins et al. (2004) ajustamento de tendência consiste no tratamento de demandas que apresentam tendência e visa garantir que os dados resultantes da previsão considerem essa variação. Isso pode ser realizado através da plotagem de dados passados, identificando uma equação que pode ser linear ou não-linear (exponencial, polinomial, logarítmica, etc.). Essa plotagem pode ser feita utilizando cálculos matemáticos ou softwares computacionais que determinam uma equação de ajustamento para a tendência.
O ajustamento indica maior confiabilidade quando seu valor de R-quadrado é próximo ou o próprio 1. Quando se ajusta uma linha de tendência a seus dados. Trazendo as equações não-lineares, temos:
Polinomial: a linha de tendência polinomial é uma linha curva utilizada para analisar ganhos e perdas em um conjunto de dados grande, quando os dados flutuam. A ordem da curva polinomial pode ser determinada pelo número de flutuações nos dados ou pelo número de picos e vales na curva. A equação para calcular a linha de tendência polinomial é obtida por meio do método dos mínimos quadrados, utilizando pontos de dados e está representada na equação (4).
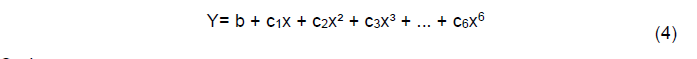
Onde:
b e c: são constantes
Logarítmica: a linha de tendência logarítmica é uma linha curva que se ajusta melhor aos dados, sendo particularmente útil quando a taxa de alteração nos dados aumenta ou diminui rapidamente e depois se estabiliza. Essa linha pode utilizar valores negativos e/ou positivos. Seu cálculo é obtido por meio do método dos mínimos quadrados, utilizando pontos de dados, conforme expresso na equação (5).
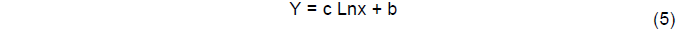
Onde:
c: é constante;
Ln: função do logaritmo natural;
b: é constante.
Exponencial: a linha de tendência exponencial é uma curva muito útil para analisar dados que estão crescendo ou diminuindo com taxas cada vez mais elevadas. No entanto, é importante destacar que não é possível criar essa linha se os dados contiverem valores nulos ou negativos. O cálculo da linha de tendência exponencial é realizado utilizando o método dos mínimos quadrados através de pontos, conforme expresso na equação (6):
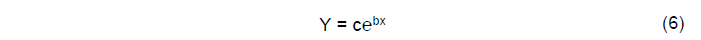
Onde:
c: é constante;
e: é a base do logaritmo natural;
b: é constante.
2.4.3 Séries Temporais
A análise de séries temporais utiliza o histórico de demanda para prever o futuro, já que segundo Calsing (2015) pressupõe que os padrões de dados passados, como tendência e sazonalidade, permanecerão inalterados.
De acordo com Moreira (1996) uma série temporal é definida a partir de um conjunto de valores a partir de momentos específicos em intervalos, geralmente, de mesmo período, sobre a demanda ou qualquer outra variável que se deseja prever, na expectativa dos valores passados possam fornecer informações adequadas para uma previsão futura. Dois fatores relevantes na análise de série temporal são tendência e sazonalidade. O item 2.4.2 coloca, de forma simplificada, a tendência.
2.4.3.1 Sazonalidade
De acordo com Wallis et al. (1971) a definição de sazonalidade envolve os movimentos ou flutuações que ocorrem em um período igual ou inferior a um ano, sendo sistemáticos, mas não necessariamente regulares, em uma série temporal. Esses movimentos são resultado de diversas causas, tais como naturais, econômicas, sociais e institucionais. O ajuste de séries temporais para variação sazonal tem dois objetivos principais: o estudo da sazonalidade em si e a remoção da sazonalidade da série para analisar outros aspectos.
A sazonalidade também pode ser classificada como aditiva ou multiplicativa. No caso aditivo, a série apresenta uma flutuação sazonal constante, independentemente do nível médio da série. Já no caso multiplicativo, o tamanho da flutuação sazonal varia de acordo com o nível médio da série.
2.4.3.2 Média Móvel Simples
A Média Móvel Simples (MMS) representa um alicerce estatístico fundamental na análise técnica aplicada a dados financeiros e séries temporais. Segundo Benson (2022) é uma ferramenta de medida que ajuda a suavizar flutuações de curto prazo em um conjunto de dados com outras análises e indicadores, simplificando assim a detecção de padrões e tendências de longo prazo, resultando em uma melhor tomada de decisão.
Sua fórmula expressa na equação (7), consiste em somar os valores de um conjunto de dados em um determinado período e, em seguida, dividir essa soma pelo número de pontos no período.
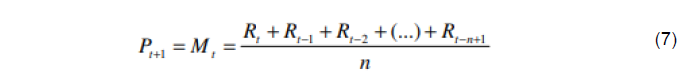
Onde:
Pt+1: Previsão para o período t+1;
Mt: Média Móvel para o período t;
Rt: Demanda real ocorrida em t;
n: Número de dados que deverão ser considerados para o cálculo.
Por meio dessa fórmula, a MMS mostra as tendências subjacentes ao eliminar as características das oscilações de curto prazo. No entanto, é importante ressaltar que a ferramenta se baseia em dados históricos, e por isso, sua aplicação mais eficaz reside na conjunção com outras abordagens analíticas e informações atuais de dados.
2.4.3.3 Média Móvel Ponderada
De acordo com Benson (2022), a Média Móvel Ponderada (MMP) é um conceito utilizado em estatísticas e análise de dados para suavizar variações temporais em uma série de valores. É uma técnica que atribui pesos diferentes aos valores da série, dando mais importância àqueles mais recentes e menos importância aos mais antigos, resultando então em uma média que se adapta às mudanças nos dados, refletindo melhor as tendências atuais.
É frequentemente usada em análises financeiras, previsões de vendas, análise de séries temporais e em qualquer situação em que seja importante considerar tanto os padrões passados quanto os recentes.
A fórmula da média móvel ponderada enfatiza valores atuais, multiplicando-os por pesos específicos, somando esses resultados e dividindo pela soma dos pesos (geralmente 1). Isso é útil para reconhecer mudanças recentes em conjuntos de dados que evoluem ao longo do tempo, acompanhando tendências em constante evolução.
A média móvel ponderada está definida pela equação (8).
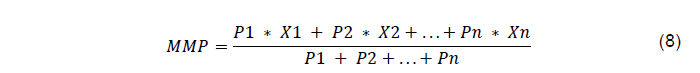
Onde:
MMP: é a Média Móvel Ponderada;
Xn: são os valores da série;
Pn: são os pesos correspondentes a cada valor, onde a soma é igual a 1.
2.4.3.4 Método Suavização Exponencial Simples
Este método é o tipo mais simples de série temporal, onde os valores da série temporal flutuam aleatoriamente em torno de um valor fixo sem qualquer tendência. Brown (1959, 1963) propôs que se os dados permanecerem constantes em relação a algum nível médio, a suavização exponencial simples pode ser usada para prever os valores futuros da série. Sendo representada matematicamente pela equação (9).
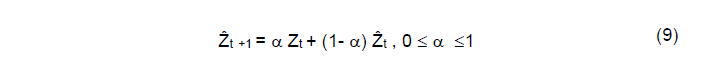
Onde:

O valor da constante de suavização α é arbitrário, sendo que a escolha de seu melhor valor pode ser feita iterativamente, utilizando algum método de comparação. Assim, os valores iniciais das constantes são escolhidos aleatoriamente para gerar estimativas. Comparam-se os valores previstos com os reais, e calcula-se a média do quadrado das diferenças entre eles; o parâmetro que minimiza essa média é utilizado no modelo final (PELLEGRINI e FOGLIATTO, 2001).
2.4.3.5 Método de Holt (Suavização Exponencial Dupla)
O método de Holt é uma ferramenta eficaz de previsão proposta por Holt (1957) que ampliou a suavização exponencial simples para dados de séries temporais que demonstram uma tendência linear. Este método coloca uma constante de suavização que afeta a tendência da série. A equação (10) representa o método de Holt.
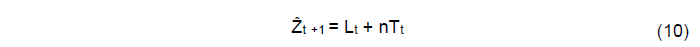
Onde:
Ẑt+n: é a previsão para o período t+n;
Lt: é igual estimativa do nível esperado da série temporal no período t;
nT: é a influência esperada da tendência (taxa de aumento ou redução) durante os próximos n períodos.
O método de Holt utiliza os parâmetros α e β chamados constantes de suavização. Além da função (10) que calcula a previsão duas outras funções são usadas para estimar o nível de tendência da série temporal, representadas nas equações (11) e (12), respectivamente.
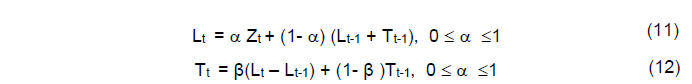
Onde:
Lt: é a estimação para o nível da série no período t;
Tt: é a estimação da inclinação (tendência) da série no mesmo período t.
A equação (10) ajusta diretamente Lt para a tendência do período anterior T t−1, adicionando o último valor suavizado L t−1.
O ideal é encontrar valores de α e β que minimizam o erro quadrático médio, eles são encontrados através de testes sobre a série histórica. Na hora de escolher os parâmetros (α e β) são utilizadas algumas medidas como, erro médio (ME), erro absoluto médio (MAE) e erro quadrático médio (MSE), para enfrentar o problema da subjetividade na seleção dos parâmetros. (BILLAH et al, 2006; GELPER, FRIED e CROUX, 2010)
2.4.3.6 Método de Holt-Winters (Suavização Exponencial Tripla)
Os métodos estatísticos de séries temporais são técnicas quantitativas comumente colocadas para predizer variáveis, incluindo métodos de suavização exponencial, especialmente o método Holt-Winters, uma extensão do método Holt (1957) desenvolvido por Winter (1960) com intuito de utilizar em séries temporais que exibem tendência e sazonalidade.
É um dos métodos de previsão de demanda de curto prazo mais aplicados, devido à sua simplicidade, baixo custo operacional, boa precisão e capacidade de ajuste automático e veloz a mudanças na série analisada. Determinadas séries possuem um fator sazonal, além do nível e tendência demonstrando características da série que se repetem a intervalos regulares de tempo, Winter oferece uma maneira de exibir essas séries. Considera dois tipos de efeitos sazonais: multiplicativo e aditivo.
2.4.3.7 Modelo autorregressivo integrado de médias móveis (ARIMA)
Os modelos ARIMA visam encontrar o comportamento da correlação seriada entre os valores da série temporal e assim realizar as previsões futuras. Portanto, quanto melhor a estrutura de correlação, melhor será os valores da previsão (CONSUL; WERNER, 2010).
Para Fava (2000), os modelos ARIMA são compostos da combinação de três componentes: o componente autorregressivo (AR), o filtro de integração (I) e o componente de médias móveis (MA). Onde a parte AR é uma combinação linear de p valores anteriores da variável, MA é uma combinação linear de q erros de previsões anteriores, e a parte integrada (I) pois os valores são diferenciados d vezes para atender a um requisito de estacionariedade.
Estes modelos são construídos através de um processo interativo, visando identificar o comportamento de autocorrelação entre os valores da série temporal (BALLOU, 2005).
2.4.3.8 Modelo sazonal autorregressivo integrado de médias móveis (SARIMA)
Quando a frequência de uma série é inferior a um ano (como nas séries mensais e trimestrais), a correlação entre momentos de tempo separados por s ou múltiplos de s ganha importância, onde s é o número de observações feitas em um ano (VASCONCELLOS; ALVES, 2000).
O modelo SARIMA significa Sazonal-ARIMA e contém a contribuição da sazonalidade para a previsão. Assim, este modelo possui mais robustez e é representado no modelo (13).
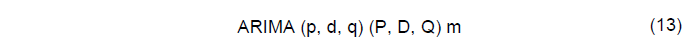
Onde:
p: é a ordem (número de defasagens) do modelo autorregressivo (AR);
d: é o grau de diferenciação, quantidade em que os dados tiveram valores subtraídos no passado (I);
q: é a ordem do modelo de média móvel (MA);
m: é o número de observações por ano.
A notação maiúscula representa as partes sazonais do modelo e a notação minúscula as partes não sazonais.
2.5 Critérios para escolha do modelo de previsão adequado
Uma empresa pode utilizar quantos modelos de previsão de demanda achar necessário, isso para antecipar os números de suas atividades. Possa ser que essa mesma empresa use métodos distintos durante o ciclo de vida de um mesmo produto. Segundo Riggs (1987), a escolha do modelo de previsão adequado dependerá de alguns, senão todos os seguintes fatores:
a) Disponibilidade e precisão de dados históricos;
b) Grau de precisão esperado da previsão;
c) Custo de desenvolvimento da previsão;
d) Tamanho do período da previsão;
e) Tempo disponível para fazer a análise;
f) Complexidade de fatores que afetam futuras operações.
2.5.1 Disponibilidade e precisão de dados históricos
A disponibilidade e a precisão dos dados históricos são fundamentais para realizar previsões de uma demanda. De acordo com Santos et al. (2018), a qualidade desses dados pode influenciar diretamente a precisão das previsões e a falta de dados ou lacunas podem levar a conclusões equivocadas e a previsões imprecisas. Portanto, é importante que as empresas coletem e mantenham um histórico de dados abrangente e consistente para embasar suas análises de previsão.
Além da disponibilidade, a precisão dos dados históricos também é um elemento crítico a ser considerado. Conforme afirma Machado et al. (2019), é essencial que os dados sejam livres de erros, anomalias ou inconsistências, uma vez que dados imprecisos podem distorcer as análises estatísticas e dificultar a identificação de tendências na demanda.
A precisão dos dados também está relacionada à sua especificidade. Segundo Lima et al. (2015), é importante que os dados históricos sejam registrados em níveis de desintegração adequados. É possível citar como exemplo, a empresa abordada em nosso estudo de caso, que possui diferentes linhas de produtos, fazendo-se necessário registrar as vendas de cada produto individualmente, em vez de apenas um valor agregado para todos os produtos. Isso permite uma análise mais detalhada e precisa da demanda.
2.5.2 Grau de precisão esperado da previsão
O grau de precisão esperado da previsão da demanda influencia diretamente sua capacidade de planejamento, estoque e produção. Porém, determinar o nível de precisão desejado pode ser difícil, uma vez que está sujeito a diversos fatores, como a natureza dos produtos, o mercado em que a empresa está inserida e o tipo de processo produtivo adotado.
Segundo Bonfa et al. (2017), o grau de precisão esperado da previsão da demanda pode variar de acordo com os objetivos da empresa e o contexto que a enquadra. Em alguns setores, como o de bens de consumo, onde a demanda tende ser mais volátil e imprevisível, espera-se que as previsões apresentem um grau de precisão mais conservador, visando reduzir riscos de estoque excessivo ou até mesmo a escassez de produtos. Já em setores de maior estabilidade, como alguns segmentos industriais, as previsões podem ter um grau de precisão menos rigoroso.
De acordo com Ribeiro et al. (2018), o grau de precisão esperado da previsão da demanda deve ser definido levando em consideração o trade-off entre custos associados à imprecisão e custos associados ao excesso de precisão. É importante realizar uma análise cautelosa dos custos de falta ou excesso de estoque, além dos custos de alterações na produção, para determinar o nível ótimo de precisão desejado.
Também é pertinente considerar a acurácia histórica das previsões, conforme ressaltam Tottoli e Abreu (2016). Ao analisar a precisão das previsões feitas no passado, é possível identificar tendências e padrões que podem ser utilizados como base para definir o grau de precisão esperado. Caso as previsões anteriores tenham sido consistentemente imprecisas, é necessário reavaliar e aferir o nível esperado de precisão.
2.5.3 Custo de desenvolvimento da previsão
Os custos para desenvolver uma previsão de demanda devem ser levados em conta pelas empresas ao realizar um sistema de previsão. O processo de desenvolvimento de uma previsão eficiente carece de investimentos que podem ter impactos diretos nos resultados financeiros da companhia.
Conforme Santos e Figueiredo (2018), os custos de desenvolvimento de uma previsão da demanda envolve três principais itens, sendo eles, os custos de contratação e capacitação de profissionais, os custos de implementação de sistemas de previsão e suas tecnologias e os custos regulares de manutenção e atualização dos modelos de previsão.
É de suma importância que as empresas considerem esses custos ao avaliar a viabilidade e o retorno sobre o investimento de um sistema de previsão da demanda.
2.5.4 Tamanho do período da previsão
O período escolhido para uma previsão pode variar de curto à longo prazo. Segundo Silva e Pereira (2019), para definir o tamanho adequado do período de previsão, é necessário levar em consideração três principais elementos, como, a estabilidade do mercado, a taxa de variação da demanda e a disponibilidade de dados históricos confiáveis. É importante que as empresas analisem esses fatores cuidadosamente para determinar o período mais adequado à sua realidade e necessidades.
2.5.5 Tempo disponível para fazer a análise
De acordo com Carvalho e Abreu (2018), o tempo disponível para fazer uma previsão da demanda deve ser suficiente para garantir a qualidade e a precisão do resultado. Em situações em que há um prazo mais longo para realizar a previsão, é possível utilizar métodos mais elaborados e complexos, como modelos estatísticos avançados ou técnicas de análise de séries temporais. No entanto, em cenários em que há uma restrição de tempo, é necessário buscar alternativas mais ágeis e simplificadas para realizar a previsão. É fundamental escolher as técnicas mais adequadas e contar com uma equipe capacitada para garantir a qualidade e a precisão da previsão.
2.5.6 Complexidade de fatores que afetam futuras operações
Segundo Silva e Araújo (2019), a complexidade dos fatores que influenciam a demanda pode envolver uma série de variáveis, tais como sazonalidades, tendências, comportamento do consumidor, condições econômicas, concorrência, entre outros. O que torna a previsão da demanda um processo dinâmico. Nesse caso, o ideal é considerar a interdependência entre esses fatores, uma vez que eles podem se influenciar mutuamente. O uso de métodos avançados, como o de séries temporais, e o suporte de sistemas de informação adequados contribuem para a minimizar riscos e para uma gestão mais eficiente da demanda.
2.6 Modelos de erros
As medidas e modelos de erro são ferramentas essenciais na avaliação e comparação de modelos estatísticos e de aprendizado. Estes modelos desempenham um papel fundamental na avaliação, seleção de modelos, ajuste de hiperparâmetros, comparação de métodos e otimização de modelos estatísticos e de aprendizado de máquina, fornecendo métricas quantitativas para avaliar o desempenho dos modelos e guiar a tomada de decisões durante o processo de modelagem.
O Desvio Médio Absoluto (MAD – Mean Absolute Deviation) é uma medida de dispersão dos erros em relação a um valor médio. Ele é usado para avaliar a precisão ou a acurácia de um modelo ou previsão.
O desvio médio absoluto é calculado tomando-se a média dos valores absolutos das diferenças entre os valores observados e os valores previstos. Essa medida captura o tamanho médio das diferenças entre os valores reais e os valores previstos, independentemente de sua direção.
A fórmula (14) é usada para calcular o desvio médio absoluto.
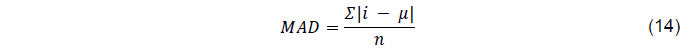
Onde:
MAD: é o Desvio Médio Absoluto;
n: é o número total de observações ou amostras; Σ: representa a soma;
I: é o valor individual;
μ: é a média dos valores.
Uma vez calculado o MAD, um valor maior indica que as previsões têm uma maior dispersão em relação aos valores observados, enquanto um valor menor indica uma maior precisão nas previsões.
O desvio médio absoluto é uma medida eficaz para avaliar a precisão de modelos de previsão ou estimativas em várias áreas da engenharia, como análise de projetos, análise de risco e planejamento financeiro.
Outras diferentes medidas de erro utilizadas para avaliar modelos são o erro médio absoluto (MAE), o qual tem a mesma fórmula de cálculo do MAD, porém com dados distintos, erro quadrático médio (RMSE), erro médio absoluto percentual (MAPE). Segundo Géron (2019) o Erro Médio Absoluto (MAE – Mean Absolute Error) é uma medida de erro que quantifica a média das diferenças absolutas entre os valores previstos e os valores reais. Por ser uma medida intuitiva é bastante útil na avaliação da magnitude média dos erros de previsão, análise de séries temporais e regressão, independentemente da direção. Quanto menor o valor do MAE, melhor é a precisão do modelo.
A equação (15) é usada para o cálculo do Erro Médio Absoluto.
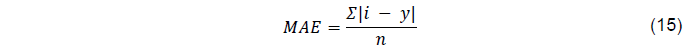
Onde:
MAE: é o Erro Médio Absoluto;
n: é o número total de observações ou amostras; Σ: representa a soma;
i: é o valor predito ou estimado;
y: é o valor real ou observado;
|i – y|: representa o valor absoluto da diferença entre i e y.
E com isso, no contexto da avaliação, o MAE é usado para comparar o desempenho de diferentes modelos, selecionar aquele com o menor Erro Médio Absoluto e verificar a melhoria do desempenho ao ajustar hiperparâmetros ou introduzir novas variáveis. Enquanto o Erro Quadrático Médio da Raiz (RMSE – Root Mean Squared Error) é uma medida de erro que calcula a raiz quadrada da média dos quadrados das diferenças entre os valores previstos e os valores reais, sendo mais sensível a erros grandes, devido à sua natureza de elevar ao quadrado as diferenças. Mas, assim como o MAE, quanto menor o valor do RMSE, melhor é a precisão do modelo, porém, ele é uma medida de erro que considera tanto a magnitude do erro em relação à escala dos dados quanto a direção dos erros de previsão.
Para cada observação ou exemplo no conjunto de dados, o RMSE calcula a diferença entre o valor previsto e o valor real do modelo pela equação (16).
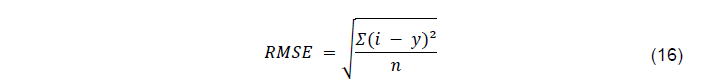
Onde:
RMSE: é o Erro Quadrático Médio da Raiz;
n: é o número total de observações ou amostras;
Σ: representa a soma;
i: é o valor predito ou estimado;
y: é o valor real ou observado;
(i – y)²: representa o quadrado da diferença entre i e y.
O RMSE tem como vantagem que sua unidade de medida é a mesma dos valores observados, o que facilita a interpretação em relação ao contexto do problema. E o Erro Médio Absoluto Percentual (MAPE – Mean Absolute Percentage Error) é uma medida de erro utilizada para avaliar a precisão de modelos de previsão, selecionar aquele com o menor Erro Médio Absoluto Percentual e verificar a melhoria do desempenho. O MAPE calcula a média das porcentagens absolutas das diferenças entre os valores previstos e os valores reais, expressando o erro como uma porcentagem do valor real e permitindo então uma comparação relativa entre eles. Com isso, é importante notar que o MAPE não é adequado quando os valores reais são próximos ou iguais a zero, pois podem levar a divisões por zero ou a valores infinitos.
A diferença percentual absoluta é dada pela equação (17).
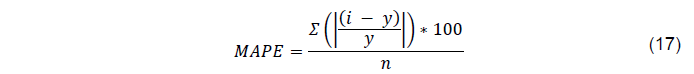
Onde:
MAPE: é o Erro Médio Absoluto Percentual;
n: é o número total de observações ou amostras;
Σ: representa a soma;
i: é o valor predito ou estimado;
y: é o valor real ou observado;
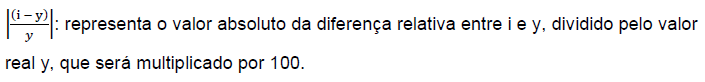
2.7 Crystal Ball
O software Crystal Ball é uma ferramenta desenvolvida e comercializada pela empresa Oracle, sendo um programa que auxilia na previsão de resultados incertos, baseia-se em planilha para modelagem preditiva, previsão, simulação e otimização, oferecendo percepções valiosas sobre os fatores mais importantes que afetam os riscos e contribuindo para a tomada de decisões táticas mais assertivas com vistas ao alcance dos objetivos (ORACLE, 2008).
Em relação a previsão de demanda, o software possibilita a identificação e redução das principais entradas que geram riscos, além de proporcionar a otimização das decisões ao considerar as variações e restrições existentes, indicando onde se deve concentrar os esforços.
2.7.1 Métrica U de Theil
A métrica U de Theil, utilizada para avaliar o desempenho de um modelo de previsão para séries temporais, foi desenvolvida pelo econometrista holandês Henri Theil e está presente no software Crystal Ball para indicar ao usuário se determinada previsão é promissora ou não, conforme nos diz Pinheiro (2021). A equação (18) representa essa métrica.
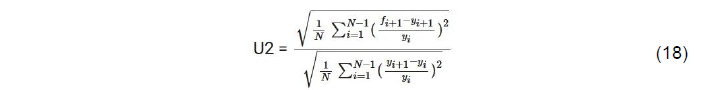
Onde:
yᵢ: corresponde ao valor observado no instante i;
fᵢ: consiste na predição para o mesmo instante;
fᵢ+1 e yᵢ+1: correspondem ao valor predito e observado no momento imediatamente posterior ao instante i;
N: é o número de valores observados/preditos.
A equação U2 examina a qualidade das predições, comparando seu resultado com o método ingênuo, que assume que a próxima medição em uma série temporal é igual ao último valor observado. Assim um modelo de previsão minimamente promissor deve superar o desempenho do procedimento ingênuo, onde:
Se U2 for menor que 1, o modelo analisado é superior ao método ingênuo;
Se U2 for maior que 1, o modelo analisado é inferior ao método ingênuo;
Se U2 for igual a 1, o modelo analisado apresenta desempenho idêntico ao método ingênuo.
2.7.2 Teste Durbin-Watson
O teste Durbin-Watson (DW), de acordo com Kotaiah (2021) é uma métrica estatística utilizada para testar a presença de autocorrelação nos erros de um modelo de regressão, foi criada pelos professores estatísticos James Durbin e Geoffrey Stuart Watson e foi incluída na ferramenta Crystal Ball para validar se os preditores realmente são significativos ou não. A equação (19) é usada para este teste.
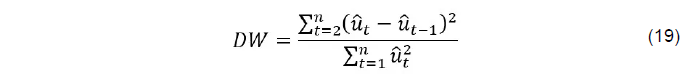
Onde:
n: é o número total de observações;
t: é o resíduo do modelo de regressão;
û: é a autocorrelação amostral dos resíduos.
3. Metodologia
O método aplicado para o desenvolvimento desse artigo é o estudo de caso, considerando a abordagem quantitativa para analisar os dados com base nos conceitos já descritos. Segundo Yin (1994), o estudo de caso é considerado uma estratégia de pesquisa onde são respondidas perguntas “como” e “por que”, com foco em assuntos da vida real de casos atuais. Através de uma investigação empírica com coleta e análise de dados.
A empresa escolhida é um grande laboratório farmacêutico localizado na cidade de Curitiba e que atua em todo o Brasil. Os dados fornecidos referem-se à quantidade de vendas de 20 produtos nos meses de janeiro/2022 a março/2023, juntamente com as previsões que a própria empresa desenvolveu para o mesmo período. Além disso, há dois modelos de vendas utilizados pela organização, que são Sell In e Sell Out, sendo o primeiro as vendas diretamente aos fornecedores e o segundo as vendas ao cliente final.
Para determinar quais produtos seriam usados no estudo de caso foi feita uma curva ABC com base nas vendas totais do período fornecido. De acordo com Dias (2010), a curva ABC é uma ferramenta importante para os gestores na tomada de decisão. Ela ajuda os mesmos a identificarem os elementos que requererem cuidados especiais e gestão adequada. Após a classificação dos produtos, foi determinado que apenas os itens da classe A e B seriam utilizados no software de previsão de demanda.
Para realizar a previsão da demanda foi utilizado o software Crystal Ball, onde foi inserido as vendas dos 13 primeiros meses, solicitando ao programa a previsão dos próximos dois meses (fevereiro e março/2023). Desta forma seria possível comparar a previsão obtida nos testes com a previsão da empresa e as vendas reais nesse período permitindo posterior análise e discussão dos resultados obtidos. A fim de avaliar as previsões apresentadas pelo software, foram utilizados métodos de avaliações de erro (RMSE e MAPE).
4. Resultados e discussão
O estudo teve como base dados históricos de vendas, informações internas e externas do mercado farmacêutico, e a aplicação de métodos estatísticos e modelos de previsão.
Neste capítulo, serão discutidos os principais achados, comparando as previsões realizadas pelos modelos com os valores obtidos pelos métodos da empresa e os valores reais de demanda, visando identificar a eficácia dos métodos utilizados e suas contribuições para o processo de tomada de decisões na empresa.
Além disso, serão exploradas possíveis razões para eventuais desvios e variações identificados entre as previsões e a demanda efetiva, bem como sugestões de melhorias para aprimorar o sistema de previsão utilizado pela fabricante de medicamentos.
4.1 Aplicação da curva ABC
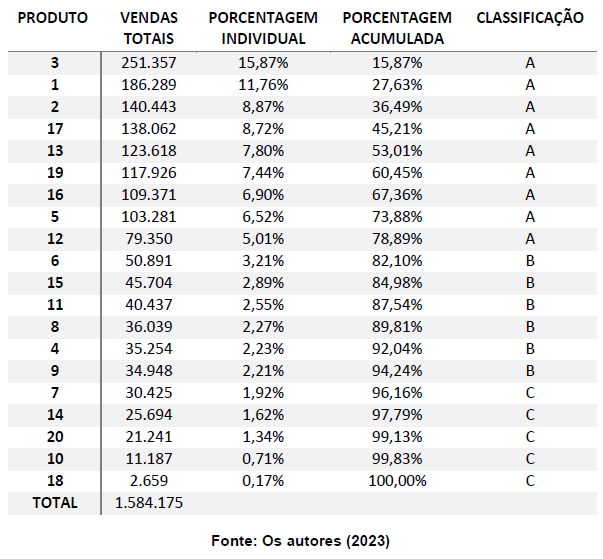
A fim de identificar quais produtos possuem maior nível de importância, requerendo assim mais atenção para serem objetos desse estudo, foi aplicado a curva ABC com base nas vendas totais do período disponibilizado pela empresa. Na tabela 1 consta a classificação ABC:
Tabela 1: Tabela de classificação ABC dos produtos
Na tabela 2 é apresentada as proporções entre a quantidade de itens e de vendas em cada classe.
Tabela 2 – Resumo das proporções por classe
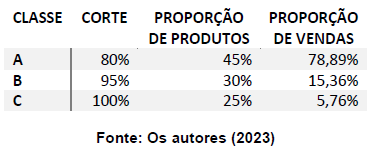
Percebe-se uma uniformidade na distribuição nas vendas dos produtos, dado que 9 itens se enquadraram na classe A, 6 na classe B e 5 na classe C. Isso se deve ao tipo de demanda existente no setor em que a empresa está inserida, onde não há grandes discrepâncias nas vendas dos produtos.
4.2 Análise dos resultados obtidos no Crystal Ball
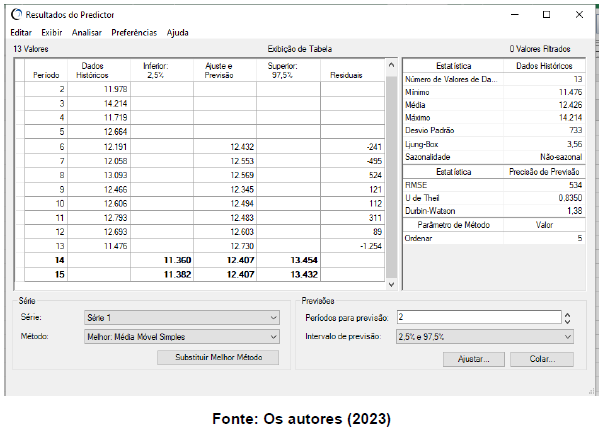
Conforme as figuras 1 e 2 apresentam, ao inserir os dados no Crystal Ball, é possível verificar alguns dados importantes como: a previsão para os próximos meses, o valor do MAPE, o valor do RMSE, U de Theil, Durbin-Watson e o melhor método de previsão encontrado para cada produto.
Figura 1: Gráfico gerado pelo Software Crystal Ball
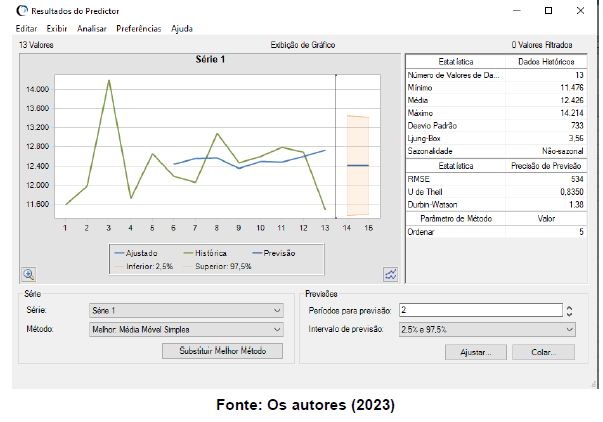
Figura 2: Tabela gerada pelo Software Crystal Ball
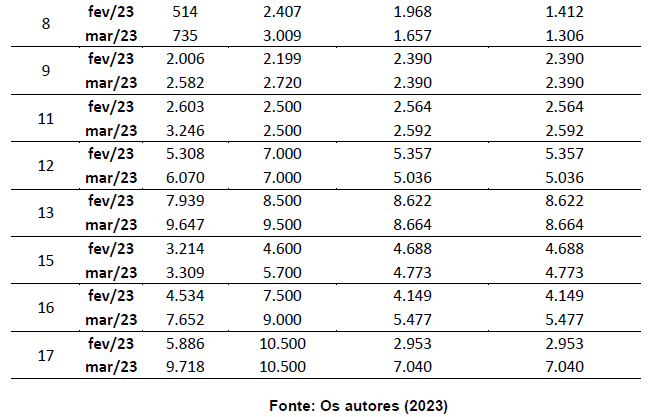
A tabela 3 apresenta o valor real e a previsão realizada pela empresa, que aplicou a sua própria metodologia para realização do cálculo (fórmula não informada), e as previsões calculas pelo software Crystal Ball, pelas metodologias RMSE e MAPE. Todas se referem aos meses de fevereiro e março de 2023 dos 14 produtos selecionados para o estudo após a realização da curva ABC (classe A e B).
Tabela 3 – Valor real e previsões para os meses de 14 e 15

Com vistas a avaliar a assertividade das previsões do software em relação a previsão da empresa, foram aplicadas as fórmulas estatísticas Erro Quadrático Médio e Erro Percentual, a fim de compreender qual previsão mais se aproxima do valor de real de vendas dos produtos. Para isso, foi calculado o RMSE de todas as previsões, sendo apresentado os resultados na última linha da tabela 4.
Tabela 4 – Erros Quadrático e Percentual sobre as previsões obtidas
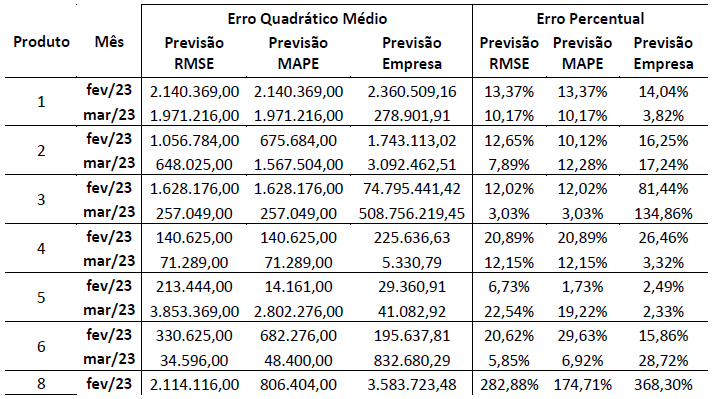
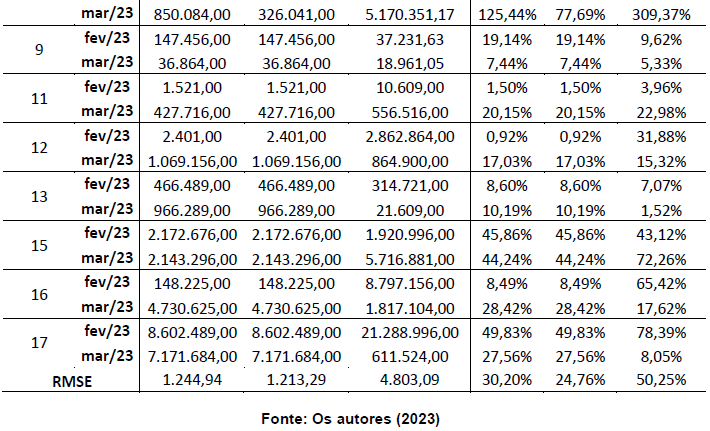
Percebe-se que, no geral, as previsões realizadas pelo software Crystal Ball se aproximam mais do valor real se comparado com as previsões feitas pela empresa, tanto na comparação feita pelo Erro Quadrático como pelo Erro Percentual.
4.3 Comparação da previsão do estudo com a previsão da empresa
Para facilitar a visualização dos resultados obtidos nas previsões, na tabela 5 é apresentado um placar de assertividade, onde é possível comparar a quantidade de acertos das previsões feitas nesse estudo com a previsão da empresa.
Tabela 5 – Placar geral de acertos

Das 28 previsões realizadas, os resultados adquiridos nesse estudo se mostraram mais assertivos em 15 vezes, em comparação a empresa que foi mais assertiva 13 vezes. É possível considerar essa comparação como positiva, já que está sendo comparado previsões de um software com os dados previstos por uma empresa conceituada em seu setor de atuação.
4.4 Modelos de previsão que mais aparecem
É interessante mencionar que o modelo de previsão que mais vezes foi considerada pelo software Crystal Ball como mais adequada foi a Arima. Porém, outros modelos de previsão foram considerados, como a Média Móvel Simples, Média Móvel Dupla, Suavização Exponencial Simples, Suavização Exponencial Dupla, Tendência de Amortecida Não Sazonal e Sarima.
4.5 Possíveis causas para previsão da empresa ser melhor
Ao comparar as previsões realizadas pelo software e as previsões/dados reais da empresa percebe-se que em alguns casos “perdemos”, esse erro se dá porque existem alguns fatores que influenciam a assertividade das previsões. Os principais são:
a) Número de dados: A empresa possui o histórico de venda de um período maior que o disponibilizado para o estudo, influenciando nas previsões.
b) Pandemia: Os dados utilizados no estudo são do período de pandemia, onde as vendas principalmente no setor farmacêutico tiveram variações imprevisíveis, com vendas muito acima ou abaixo do esperado.
4.6 Dificuldade em conseguir dados e a influência na previsão
Uma das principais dificuldades encontradas para realizar este estudo de caso foi a dificuldade em obter dados. Quando falamos de previsão da demanda a quantidade de informações é essencial, já que normalmente quanto mais dados melhores serão as previsões.
4.7 Séries Temporais x Causalidades
Este estudo foi realizado por meio de séries temporais, sendo assim não foram consideradas as causalidades que poderiam também impactar nos resultados.
5. Considerações Finais
Este trabalho apresentou através da pesquisa da literatura cientifica e técnica junto a um estudo de caso a aplicação dos métodos de previsão da demanda, abordando as principais ferramentas, os benefícios e os desafios em realizar previsões. O comportamento dos consumidores evolui rapidamente gerando um cenário cada vez mais complexo e volátil, que por sua vez exige que as empresas otimizem cada vez mais suas ferramentas de previsão. A previsão da demanda é essencial em qualquer tipo de negócio e traz diversos benefícios, entre eles destacam-se: planejamento de recursos, logística de entrada, planejamento financeiro, avaliação de risco e gestão de estoque.
O objetivo desse trabalho foi o de analisar o uso das ferramentas de previsão de demanda em um estudo de caso, nele foi possível identificar a importância de uma previsão e os principais fatores que a influenciam, como também determinar os melhores métodos para o caso estudado. A utilização do software Crystal Ball para realizar previsões possibilitou que fossem identificadas ferramentas que geram melhores soluções do que as usadas atualmente pela empresa. As propostas de melhorias foram apresentadas para a empresa, ficando a critério da mesma adotá-las. Como sugestões futuras propõe-se analisar outros fatores da empresa que podem ser levados em consideração nas previsões e adotar outras ferramentas/métodos de previsão de demanda afim de manter a competitividade da empresa.
6. Referências Bibliográficas
ARVAN, M., FAHIMNIA, B., REISI, M., & SIEMSEN, E..Integrating human judgement into quantitative forecasting methods: A review. Omega, 86, 237- 252. 2019.
BALLOU, Ronald H. Gerenciamento da cadeia de suprimentos: logística empresarial. 5. ed.. Porto Alegre: Bookman, 2005.
BENSON, Mark. Média Móvel Simples – O que é a MMS e como ela funciona? 2022. Disponível em: https://www.earn2trade.com/blog/pt/media-movel-simples mms/. Acesso em: 27 jul. 2023.
BILLAH, B.; KING, M. L.; SNYDER, R. D.; KOEHLE, A. B. (2006). Exponential smoothing model selection for forecasting. International Journal of Forecasting, v.22, n. 2, p. 239-247, 2006.
BONFA, F., SOUZA, M., & ALBINO, V. Análise comparativa dos métodos de previsão de demanda para auxiliar a gestão de estoques: um estudo de caso. Revista Científica do ITESCS, v.10, n.1, p.12-27. 2017.
BROWN, R. G. Smoothing, forecasting, and prediction. Englewood Cliffs, N.J.: Prentice Hall, 1963.
BROWN, R.G. Statistical Forecasting for Inventory Control. McGraw-Hill, New York, NY, 1959.
CALSING, L. C. Previsão de demanda combinada a partir de métodos quantitativos e opinião de especialistas. Porto Alegre: UFRGS, 2015. Dissertação (Mestrado em Engenharia) – Universidade Federal do Rio Grande do Sul, Brasil, Porto Alegre, 2015.
CARVALHO, J., & ABREU, T. Planejamento da demanda utilizando modelos de previsão em uma empresa de soluções tecnológicas. Revista de Administração da UNIFATEA, v.7, n.2, p.11-25. 2018.
CHING, Hong Yuh. Gestão de estoques na cadeia de logística integrada. São Paulo: Atlas S.A. 3. ed. p.220. 2027.
CONSUL, B. Fabrício; WERNER, Liane. Avaliação de técnicas de previsão de demanda utilizadas por um software de gerenciamento de estoques no setor farmacêutico. Porto Alegre: UFRGS, 2010.
DIAS, G. P. P. Proposta de processo de previsão de vendas para bens de consumo. XIX Encontro Nacional de Engenharia de Produção, Rio de Janeiro: ABEPRO,1999.
DIAS, Marco Aurélio P.. Administração de Materiais: uma abordagem logística. 5. ed. São Paulo: Atlas, 2010.
ECONOMY-PEDIA. Durbin Watson Contrast – O que é, definição e conceito. Disponível em: <https://pt.economy-pedia.com/11031150-durbin-watson-contrast> Acesso em: 11 jul. 2023.
FAVA, V. L. Análise de Séries de Tempo. In: VASCONCELLOS, M. A. S.; ALVES, D. Manual de econometria: nível intermediário. São Paulo: Atlas, 2000. GERBER, J. Z.; MIRANDA, R. G. de,; BORNIA, A. C.; FREIRES, F. G. M. Organização de Referenciais Teóricos sobre Diagnóstico para a Previsão de Demanda. Revista Eletrônica de Gestão Organizacional, Recife, v. 11, n. 1, p. 160- 185, jan./abr. 2013.
GÉRON, Aurélien. Mãos à obra: aprendizado de máquina com Scikit-Learn & TensorFlow. Rio de Janeiro: Alta Books, p.42-45. 2019.
HOLT, C.E. Forecasting Trends and Seasonal by Exponentially Weighted Averages. ONR Memorandum No. 52, Carnegie Institute of Technology, Pittsburgh, USA, 1957.
KOTAIAH, Shristi V. Teste Durbin Watson. 2021. Disponível em: https://acervolima.com/teste-durbin-watson/. Acesso em: 11 jul. 2023. LIMA, V., PINTO, A., & BRAGANÇA, L. Análise de demanda de produtos: um estudo de caso no segmento hoteleiro. Revista Científica do ITPAC, v.8, n.1, p.95- 112. 2015
MACHADO, C., BORGES, P., & FERREIRA, B. Análise de previsão de demanda: um estudo de caso em uma empresa de confecções. Revista de Gestão e Planejamento, v.20, n.2, p.268-285. 2019
MARTINS, Fernanda Roberta Gomes da Silva Pinto & LOUREIRO, Lorena Drumond. Previsão de demanda de um produto classe A de uma Empresa de Perfumes e Cosméticos visando otimizar o estoque de segurança desse produto. Belém, 2004. 63 f. Trabalho de Conclusão de Curso em Engenharia de Produção (Gerência de Produção) – Universidade do Estado do Pará (UEPA), Belém.
MARTINS, P. G.; ALT. P. R. C. Administração de Materiais e Recursos Patrimoniais. São Paulo: Saraiva, 2005.
MOREIRA, Daniel Augusto. Previsão de demanda: modelos e técnicas para sua aplicação. São Paulo: Atlas, 2017.
NIKOLAEV, Kiril. Média Móvel Ponderada – O que é e como calcular? 2022. Disponível em: https://www.earn2trade.com/blog/pt/media-movel-ponderada/. Acesso em: 27 jul. 2023.
ORACLE. Crystal Ball. 2008. Disponível em: <https://www.oracle.com/br/applications/crystalball/#rc30p3>. Acesso em: 11 jul. 2023.
PELLEGRINI, F.R.; FOLIATTO, F.S. Passos para Implantação de Sistemas de Previsão de Demanda -Técnicas e Estudo de Caso. Revista Produção, v. 11, n. 1, p. 43-64, 2001.
PINHEIRO, Janael. Como usar a métrica U de Theil. 2021. Disponível em: <https://janaelpinheiro.medium.com/como-usar-a-m%C3%A9trica-u-de-theil 913eb5ba9512>. Acesso em: 11 jul. 2023.
PINTO, K. A. da C. O desafio do planejamento de compra em um hospital oncológico com foco em sua previsão de demanda: estudo de caso. Simpósio de Engenharia de Produção, 21, 2014. Bauru, SP, Brasil, 10 a 12 de Novembro de 2014. Anais… XXI SIMPEP, 2014.
POZO, Hamilton. Administração de recursos materiais e patrimoniais: uma abordagem logística. 6. ed. São Paulo: Atlas, 2010.
RIBEIRO, G., ALMEIDA, J., & ARAÚJO, G. Avaliação da precisão das previsões da demanda em uma indústria siderúrgica. Revista Eletrônica de Administração e Turismo, v.12, n.2, p.202-219. 2018.
RIGGS, James L. Production Systems: Planning, Analysis, and Control. New York: John Wiley, Inc., 1987.
SANTOS, A., & FIGUEIREDO, J. Previsão de demanda em empresas do setor industrial: um estudo de caso. Revista de Gestão Industrial, v.14, n.2, p.12-31. 2018
SANTOS, T., ALVARENGA, A., & ALBINO, V. Previsão de demanda: estudo comparativo entre métodos generalizados. Revista Científica do ITPAC, v.11, n.1, p.107-128. 2018.
SILVA, J., & PEREIRA, G. Análise de previsão da demanda para tomada de decisão em uma indústria de alimentos. Congresso de Pesquisa, Ensino e Extensão, v.5, n.1, p.7. 2019.
SILVA, M. R., & ARAÚJO, A. M. Previsão de demanda: fatores que influenciam a tomada de decisão nas empresas de Vestuário no município de Guaíba/RS. Revista Eletrônica de Administração e Turismo – REAT, v.13, n.2, p.414-433. 2019.
SLACK, Nigel et al. Administração da produção. São Paulo: Atlas, 2013. TOTTOLI, G., & ABREU, A. Previsão de demanda em empresas do setor de tecnologia por meio do método Holt-Winters. Revista Tecnologia & Sociedade, v. 12, n.27, p.55-67. 2016.
TUBINO, D.F. Planejamento e controle da produção. São Paulo: Atlas, 2000. VASCONCELLOS, M. A. S.; ALVES, D. Manual de econometria: nível intermediário. São Paulo: Atlas, 2000.
WALLIS, K. F.; THOMAS, J. J. Seasonal variation in regression analysis. Journal of the Royal Statistical Society, Ser. A, v. 134, n. 1, p. 57-72. 1971. WINTERS, P. R. Forecasting sales by exponentially weighted moving averages. Management Science, v. 6, n. 3, p. 324-342, 1960.
YIN, Robert K.. Estudo de Caso: Planejamento e Métodos. 2. ed. Porto Alegre: Bookman, 2001. Tradução de Daniel Grassi.
