PLATFORM STABILIZATION USING SENSORS: CONCEPT STUDY
REGISTRO DOI: 10.5281/zenodo.7347362
Giovanni Santos Guimarães
Jefferson Delgado Bezerra
Matheus do Santos Bueno
Pedro Augusto Calixto Ferreira
Orientador: Prof(a). Dra.: Thaís Cavalheri dos Santos
Resumo: O trabalho buscou utilizar ferramentas já conhecidas na academia e na indústria, tais como sensores, servomotores, programação C++, Python e as transformadas de Fourier. Para isso, desenvolve-se uma superfície auto estabilizadora, a fim de manter e equilibrar um objeto esférico no meio da superfície, habilidade muito usada para diversos fins industriais, principalmente aquelas que envolvem a centralização do objeto em referência ao maquinário que o produz.
Palavras-chave: Estabilização, Sensores, Sinais, Transformada de Fourier.
Abstract: The work sought to use tools already known in the Academy and in the industry such as sensors, servomotors, C++, and Python programming and as FFT. For this to develop a self-stabilizing surface, in order to maintain and balance a spherical object in the middle of the surface, a skill widely used for various industrial purposes, mainly, centralization of the object in reference to the machinery that produces it.
Keywords: Stabilization, Sensors, Signals, FourierTransform
1. Introdução
Com o avanço da competição no meio industrial, a busca cotidianamente por sistemas com alto grau de precisão é cada vez maior. Para atingir tal obejtivo é necessario o desenvolvimento de sensores mais precisos, aperfeiçoamento de tecnicas de escaneamento de área e criação de novas tecnologias de controle de sistemas de poscionamento. (JESUS,2019).
Com isso, esse artigo busca a exposição de conceitos, apresentando a criação de uma mesa estabilizadora. A mesa tem por objetivo estabilizar o objeto que se encontra sob sua superfície, levando-o para o centro dela. Tal movimentação é executada através da mudança de ângulo da superfície em referência a sua posição inicial, ou seja, mudando a sua própria inclinação e corrigindo-a, quando necessário.
A análise de correção de rota é feita por meio de sensores que mandam sinais para os motores que inclinam o tampo, fazendo um objeto esférico se mover até o centro da superfície (JESUS,2019).
Em suma, o estudo busca mover um objeto esférico em uma superfície que pode ser inclinada via um Controlador Proporcional Integral Derivativo (PID), tal mudança na angulação desta mesa será corrigida pelo sensor correspondente a uma câmera e dois servomotores. O projeto visa estabilizar e levar a esfera para o centro da plataforma. Como já é de conhecimento da academia e indústria o uso de sensores, com isso nosso estudo busca ampliar, explorar e aplicar as utilidades, assim como os conceitos de realimentação para a realização de controle.
1.1 Justificativa
Essas funcionalidades aprimoram o uso na indústria e no cotidiano, a fim de melhorar os processos que envolvem o afunilamento ou centralização de etapas, podendo ser usada em diversas áreas, tais como nas indústrias, em etapas de pesagem, envasamento, embalagem, entre outros.
Também há usos no cotidiano cívico, melhorando a vida das pessoas, principalmente as com dificuldades motoras, tais como Mal de Parkinson, Esclerose múltipla e paralisias de tronco. (MARQUES, 2022, p. 23)
1.2 Objetivos (Geral e específicos)
Este sistema tem como objetivo primário manter uma bola em equilíbrio no centro de uma plataforma, independentemente da posição inicial da esfera. Para isso, recorre-se a uma serie de metas menores para facilitar a obtenção do resultado, entre elas temos:
– Configurar um smartphone com função de webcam, a fim de escanear a estrutura, informando a velocidade e posição da esfera.
– Programar um Giroscópio para melhor localização do objeto sobre a superfície e para melhorar a precisão da aquisição das variáveis de referência da plataforma, conseguindo ter movimentos mais precisos e delicados com o controlador;
– Aplicar um regulador proporcional-integral-derivado (PID) e usá-lo para compensar os movimentos da bola;
– Automatizar, via a linguagem Python para a obtenção de informações recolhidas dos sensores, encontrando a posição da bola, assim calculando a inclinação da bandeja.
– Controlar a movimentação da plataforma usando dois servomotores;
– Confeccionar a plataforma estabilizadora com uma carcaça e tampo manufaturados de Medium Density Fiberboard (MDF), em português, chapa de fibra de madeira de média densidade.
2.1. Conceitos do Controlador PID
Os controladores PID são muito usados tanto dentro quanto fora das indústrias, nos casos em que se demanda utilização e um sistema de controle em malha fechada. (NISE, 2017 p.4)
O controle proporcional integral e derivativo (PID), é um controle que une uma ação de controle integral, derivativa e proporcional, ocasionando assim que o erro em regime permanente seja minimizado pela parte proporcional, zerado pela parte integral e corrigido antecipadamente pela parte derivativa.
Na figura 1 podemos visualizar a representação de blocos de uma planta em série com um controlador.
2.2. Visão geral do PID
Figura 1 – Planta sendo controlada: Chegg, Controller Plant C(S) P(S)
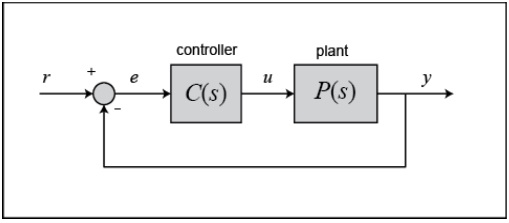
Como visto acima, a saída do controlador PID, que é a entrada de controle da planta, é calculada a partir do erro de regime permanente no domínio do tempo pela seguinte fórmula:
Onde:
: Ganho Proporcional
: Ganho Integral
: Ganho Derivativo
: Erro de realimentação
: Tempo
: Tempo de integração
O sinal de controle (u) é alimentado à planta e a saída (y) é obtida. Essa saída (y) é então realimentada e comparada com o setpoint(referência) para encontrar o novo erro (). Esse processo continua enquanto o controlador está em funcionamento. (MESSNER; TILBURY, 2020)
A função de transferência do controlador PID é dada pela transformada de Laplace da equação (1):
eq.(1)
2.3 – Características das ações Proporcionais, Integrativas e Derivativas
2.3.1. Ação Proporcional
Aumentar o ganho proporcional (Kp) tem o resultado de aumentar proporcionalmente o sinal de controle para o mesmo nível do erro (e(t)).
eq.(2)
Esse ganho faz com que o sistema de malha fechada reaja mais rapidamente, porém a saída é proporcional ao ganho, um sinal alto de saída é consequência de uma alta entrada, podendo acarretar na desestabilização do sistema e, se o ganho proporcional é muito baixo, o sistema falha em aplicar a ação necessária para corrigir os distúrbios. Além de que o aumento do Kp tende a reduzir, mas não elimina o erro em estado estacionário. (DORF; BISHOP; 2018, p.23)
2.3.2. Ação Derivativa
A adição de um termo derivativo (Kd) ao controlador fornece uma correção antecipada do erro, diminuindo o tempo de resposta e melhorando a estabilidade do sistema.
eq.(3)
E essa antecipação tende a adicionar amortecimento no sistema, diminuindo o sobressinal, com isso, a adição de um termo derivativo não é indicada para processos em que o sistema precise de uma resposta rápida a algum tipo de perturbação, nem em processos que apresentem muito ruído, pois levaria o sistema à instabilidade (MESSNER; TILBURY, 2020).
2.3.3. Ação Integral
A adição de um termo integrativo (Ki) ao controlador ajuda a reduzir o erro em regime permanente, permitindo que o sistema chegue ao valor de referência mais rapidamente.
Se houver um erro constante o integrador aumenta o sinal de controle reduzindo esse erro.
eq.(4)
Se o ganho do termo integrador é pequeno, o sistema pode levar um tempo maior para atingir o valor de referência, entretanto, se o ganho do termo integrador for muito alto, o sistema pode ficar instável. (MESSNER; TILBURY, 2020)
A desvantagem do termo integrador é que ele pode tornar o sistema mais lento e oscilatório, pois quando o sinal de erro muda de intensidade, pode demorar um pouco para o integrador se adaptar. (MESSNER; TILBURY, 2020)
Podemos resumir então os efeitos gerais de cada parâmetro do controlador (Ki, Kp, Kd) na tabela 1.
Tabela 1- Respostas de controle PID
Resposta do controle Tempo de subida Sobressinal Tempo de acomodação Erro estado estacionário Kp Diminuir Aumentar Pequena mudança Diminuir Ki Diminuir Aumentar Aumentar Diminuir Kd Pequena mudança Diminuir Diminuir Sem alteração
2.3.4 – Discretização do controle PID
2.3.4.1 – Ação proporcional discreta
A ação proporcional do controlador PID discreto se faz idêntica a do PID contínuo, onde efetuamos uma multiplicação proporcional Kp com o valor de erro u(t) obtido na amostragem atual. Na figura 2 podemos verificar um erro em vermelho, esse erro em questão será multiplicado pelo fator Kp, resultando em um sinal de saída para alcançar o valor de referência solicitado.
Figura 2 – Erro sinal de erro atual
A fórmula para o cálculo da ação proporcional pode ser feita a partir da seguinte formula.
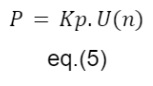
2.3.4.2 – Ação Integral Discreta
A ação integrativa de um controlador PID discreto possui o mesmo princípio do contínuo, todavia, o seu cálculo se dá de forma distinta. Se no sinal contínuo a ação integrativa se relaciona por meio de uma integral, que proporciona uma taxa acumulativa da área embaixo dos erros obtidos ao longo do compensador, no sinal discreto obtemos uma área aproximada, usando um somatório dos erros obtidos e multiplicando-os pelo tempo de amostragem. Após a finalização dos cálculos é necessário realizar a multiplicação dos elementos integrativos por um proporcional correspondente Ki, a fim de minimizar ou maximizar seus efeitos no compensador. Na figura 3 podemos verificar uma representação gráfica da obtenção de um valor integrativo de controle para uma amostra de erro. (DORF; BISHOP, 2018, p.194)
Figura 3 – Erro integrativo
Podemos expressar o cálculo do elemento integrativo do controlador por meio da seguinte formula.
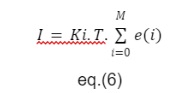
Onde “t” é o tempo de amostragem e e(i) corresponde aos erros obtidos ao longo das amostras.
2.3.4.3 – Ação Derivativa Discreta
Assim como a ação integrativa discreta, a derivativa também possui uma diferença em comparação ao controlador contínuo, ao invés de realizar a derivada da função e com isso obter a reta tangente, se faz necessário a obtenção da tangente do ângulo entre o erro da amostra atual e o erro identificado anteriormente, para isso, é necessário encontrar a diferença dos erros obtidos anteriormente e dividir pelo espaço de tempo entre ambas as amostras. Na figura 4 podemos verificar a reta tangente entre os erros em vermelho, para esse cálculo se faz necessário realizar a diferença entre o erro obtido na amostra atual u(n) e o erro obtido na amostra anterior u(n-1), após realizar a diferença entre ambos os dados, é necessário dividir pelo tempo “t” que demorou entre a amostra atual e a anterior, esse processo se dá pois a tangente de um ângulo é calculado pelo cateto oposto (u(n) – u(n-1)) sobre o cateto adjacente (t). Com todos os cálculos realizados basta efetuar a multiplicação desta derivada por um proporcional derivativo Kd, que visa minimizar ou maximizar os efeitos do compensador derivativo (DORF; BISHOP, 2018, p.324).
Figura 4 – Erro derivativo
A seguir podemos verificar uma fórmula que expressa o cálculo do elemento derivativo do sistema.
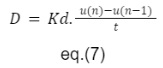
Após a realização dos cálculos dos elementos P, I e D o controle PID efetivamente se dá pela soma algébrica dos compensadores, obtemos assim a seguinte formula.
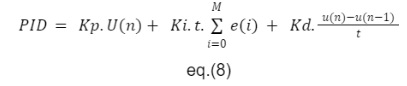
2.4. ESP32
O ESP 32 é uma placa de desenvolvimento que para o seu funcionamento utiliza o microcontrolador ESP32-WROOM-32D. Este módulo foi desenvolvido pela empresa Espressif e possui integrado ao mesmo WiFi e o Bluetooth BLE. O ESP 32 é amplamente utilizado em soluções de internet das coisas (IOT), todavia, para este projeto, será implementada apenas a funcionalidade de Bluetooth a fim de se comunicar com um servidor Python contido em um notebook. (ESPRESSIF). Na figura 5 podemos visualizar as funcionalidades de suas portas.
Figura 5 – Pinos da placa ESP32
2.5. Servomotor
Os servomotores são dispositivos eletromecânicos capazes de se movimentar com relativa precisão e velocidade. Eles são motores elétricos rotativos, com os quais é possível estipular um ângulo a qual ele deve se mover, assim como a velocidade até que se alcance o valor estipulado. Uma observação é que os servomotores possuem esse nome pois não são capazes de passar um ângulo máximo, ou seja, não possuem uma rotação livre de maneira contínua. Este dispositivo é amplamente utilizado em soluções de robótica e de automação industrial, pois, além da precisão de ângulo e velocidade, são capazes de manter o seu torque elevado. (BRITO,2017).
Torna-se possível o controle do servomotor por meio de pulsos PWM (Pulse-Width Modulation), em português “modulação por largura de pulso”, que devem, por sua vez, possuir um período contínuo de 20-25ms, do contrário, o servomotor pode voltar à posição central. Além do período contínuo do PWM, o controle preciso do ângulo se dá pelo tamanho do pulso positivo, quando o pulso positivo possui 1ms de largura, o servomotor se desloca para 0º, e quando o pulso é de 2ms, o mesmo se move para 180º. Valores proporcionais entre esta faixa corresponde à uma angulação de 0 a 180º (BRITO,2017). Na figura 6 podemos visualizar as larguras de pulso PWM para obtenção de um valor angular.
Figuras 6 – Pulsos PWM para o servomotor
2.6. Giroscópio e Acelerômetro
O Acelerômetro usa as duas principais leis da física em sua atuação, ele usa os conceitos da primeira lei de Newton, que definem que um corpo deve permanecer em repouso até o momento em que uma força externa seja exercida sobre ele, e usa também os conceitos da segunda lei de Newton, que definem a força como o produto da massa de um objeto por sua aceleração. Com essas características, ele consegue determinar a velocidade de um objeto e qual direção ele está tomando.
O Giroscópio tem a capacidade de se auto estabilizar em seus eixos, logo, com essa capacidade, esse sensor é capas de parametrizar a angulação precisa das superfícies em que ele está apoiado.
No nosso projeto, esses sensores têm funções bem importantes. Com o acelerômetro, nós conseguimos medir a variação do angulo na plataforma que é exercida pela força externa, “a bolinha”, já com o giroscópio, nós conseguimos medir precisamente a angulação da mesa, fazendo com que nosso programa execute os comandos de forma precisa e se autoajuste, caso seja necessário.
Usamos essas informações para suavizar os comandos e aumentar a eficiência da plataforma. Na figura 7 podemos visualizar uma representação do acelerômetro.
Figura 7 – Giroscópio
2.7. IP Webcam
IP Webcam é um aplicativo cuja finalidade é a conversão de um celular para uma webcam que possa enviar as imagens e os sons para uma rede de internet, possibilitando assim a análise de objetos por meio de servidores externos. O aplicativo possibilita diversas opções de visualização do vídeo transmitido, e o vídeo pode ser recuperado por meio de uma URL informada pelo APP. (Pavel Khlebovich,2021).
2.8 Biblioteca Python Opencv
Para a programação, aderimos a acervos grátis de Python. O Open Source Computer Vision OpenCV é uma biblioteca que possui a finalidade de solucionar problemas que necessitem de visão computacional. A princípio, o OpenCV foi desenvolvido pela Intel a fim de tornar a visão computacional mais acessível. Esta biblioteca possui um código fonte aberto para os desenvolvedores e está disponível em diversas linguagens de programação tais como C++, Python, Ruby, Java e muito mais. (ANTONELLO,2017, p.6).
Esta ferramenta permite realizar ações simples como segmentação de imagens ou, até mesmo, aplicações mais complexas como reconhecimento facial, detecção de objetos e detecção e análise de textos etc. (ANTONELLO,2017, p.63)
2.8.1 Processamento de imagens
O processamento de imagens será um dos processos mais importantes para a realização da detecção de objetos. Neste processo será realizado por meio do openCV a filtragem de certos atributos contidos nas imagens de cada frame.
Os filtros de imagens podem ser executados por meio da passagem de um kernel em convolução, que permite a manipulação dos pixels. Este kernel é uma matriz de tamanho e valores escolhidos a fim de desempenhar uma filtragem específica. Na figura 8 podemos visualiza a filtragem por meio de um kernel 3×3 pixels que transcorre por uma imagem de 7×7 pixels, note que o retorno possui dimensões de 5×5 pois o filtro só consegue englobar 5 posições dentro da janela. (RODRIGUES, 2019)
Figura 8 – Aplicação de filtro convolucional em uma imagem
Uma maneira de se evitar o redimensionamento da imagem, após a aplicação de um filtro, seria submetê-la a um padding zero, que consiste em preencher os contornos da imagem com pixels zerados, desse modo, o retorno do elemento após a aplicação do filtro permanece com as mesmas dimensões que o original. Na figura 9 podemos visualizar a aplicação de um padding zero a uma representação de uma imagem, note que o pedding pode possuir uma espessura maior, o tamanho do recuo irá depender do tamanho do kernel empregado à filtragem. (RODRIGUES, 2019)
Figura 9 – Aplicação de um padding zero em uma imagem
Outro processamento que será de suma importância para a detecção dos objetos é a aplicação de uma máscara que consiste em filtrar uma faixa de cores da imagem, com esta técnica podemos subtrair o fundo de um objeto com uma cor específica, e com isso realizar a detecção (LIMA, 2021)
Para facilitar a obtenção da faixa de cores é comum utilizar o padrão de cores HSV (hue, saturation and value ou matriz, saturação e brilho). A componente Hue ou matriz indica os tipos de cores em forma circular, do vermelho ao violeta, normalmente pode ser dividida de 0 a 360 tipos. A saturação permite definir a “pureza” da cor, quanto menor seu valor, mais escura a cor fica, entretanto se for definida no máximo obtemos uma cor “pura”, esta componente atinge valores entre 0 e 100%. Por fim temos a componente de brilho que pode possuir valores entre 0 e 100%. Na figura 10 podemos visualizar uma representação do padrão de cor HSV. (CHÁVEZ, 2018)
Figura 10 – Representação HSV de cores
3. Materiais e Métodos
3.1. Modelagem 3D e simulação dinâmica
3.1.1 Resumo de Montagem
Para a modelagem e simulação do nosso projeto foi utilizado o software de modelagem 3D Inventor da Autodesk, nele nós usamos as ferramentas disponíveis para modelar e otimizar a área da placa, para posteriormente fazer os cortes no equipamento a laser gastando a menor quantidade de material possível. Com ele nós verificamos qual seria o melhor tamanho, tanto para a produção e execução da montagem, quanto um tamanho que nos atendesse para conseguirmos atingir nosso objetivo de estabilizar o objeto esférico no centro da plataforma, usamos também, a ferramenta de animação para fazermos um pequeno vídeo de como nosso projeto ficaria, nos dando uma base de qual seria a melhor maneira de começarmos a montagem.
3.1.2 Modelagem 3D do projeto
Com base na modelagem da mesa estabilizadora podemos dividi-la em 4 principais partes, são elas, a base da mesa, os suportes do servomotores, a plataforma estabilizadora e por fim o suporte da câmera.
A base da mesa é a parte responsável por armazenar a estrutura do sistema de controle composto pelo ESP32, assim como aguentar o suporte dos servomotores a própria mesa estabilizadora. No seu interior será projetado duas peças de MDF a fim de estabilizar a protoboard em seu interior, ambas as peças permitem um espaço para a passagem da fiação que advém dos servomotores, oled e por fim do MPU6050. Na superficie da base será adicionado aberturas para o acoplamento do oled, interruptor, led, suportes de servomotor e cano pvc para a junção da base com a plataforma estabilizadora propriamente dita, note que o led será responsável por indicar se a plataforma se encontra ou não ligada.
Na figura 11 podemos verificar o modelo 3D da base, com suas furações para o acoplamento dos elementos necessários para o funcionamento do projeto, além de suas cotas para um entendimento da escala, note que as cotas estão em milimetros.
Figura 11 – Modelo Base do projeto
Os suportes dos servomotores ficam logo acima da base e serão responsáveis por alterar os angulos da plataforma estabilizadora na frente de sua estrutura, existe uma abertura para o acoplamento com o servomotor e em sua base 5 outras furações que serão responsáveis por conectar com a base citada anteriormente, uma dessas furações se da para a passagem da fiação. Na figura 12 podemos verificar uma representação em 3D dos suportes assim como o primeiro braço do servomotor.
Figura 12 – Modelo Suporte do servomotor
Já a plataforma estabilizadora, propriamente dita, será acoplata junto a uma junção universal que irá permitir dois graus de liberdade para que a mesma possa se movimentar apenas nos eixos X e Y, evitando assim uma torção. Em duas laterais da plataforma serão adicionadas peças de madeira com uma furação que irá realizar a junção entre a plataforma e o segundo braço dos servomotores, os membros dos servos terão suas juntas acoplatas por meio de abraçadeiras de poliamida (Enforca gato), que permite também dois graus de liberdade para o sistema. A junta universal será acoplada a um cano PVC de 153mm para aumentar a altura da plataforma e não haver interferência entre a plataforma e os suportes dos servos, o cano possui 2 furos a fim de permitir a passagem da fiação do mpu6050 que permite um auxilio na estabiliação angular da plataforma na figura 13 podemos visualizar uma representação 3D da plataforma, assim como suas medidas para auxiliar na interpretação da escala.
Figura 13 – Modelo Plataforma
Para a realização da análise de posição do objeto esférico havia a necessidade de acomodar uma câmera de forma a conseguir visualizar a plataforma pela vista superior, optamos por utilizar um celular como sensor de imagens, com este objetivo em vista, iniciamos a modelagem do suporte da câmera, que deveria possuir altura suficiente para englobar e centralizar toda a plataforma na imagem. No apoio, adicionamos uma abertura para a câmera do celular e, no fundo, duas estruturas a fim de limitar a posição do sensor e permitir a passagem do cabo USB, para deixar nosso projeto esteticamente mais agradavel colocamos uma tampa para que os circuitos e fiações não ficassem a mostra. Nota-se, também, que no fundo do suporte existe um espaço vazio que irá receber um peso a fim de modificar o centro de massa do suporte, impedindo sua queda. Na figura 14 podemos visualizar um modelo 3D da estrutura do suporte da câmera, assim como suas cotas para auxiliar o entendimento de escala, note que a escala representada pelas cotas está em milimetros.
Figura 14 – Modelo suporte da câmera
Após a finalização da modelagem de todos os elementos que compôem a plataforma estabilizadora realizamos a junção entre a plataforma e a base responsável por armazenar o controlador. Neste processo o cano PVC, mostrado anteriormente, fora alocado até o fundo da base para auxiliar as propriedades estruturais da tampa, com isso o cano funciona como uma forma de pilar para a base. Após conectar a plataforma com a base, foi necessario que conectássemos o servomotor com a plataforma, de forma que o braço principal do servomotor fique conectado com o braço secundario da plataforma, por meio de uma abraçadeiras de poliamida (Enforca gato). Em lados opostos de cada servomotor foram adicionados elasticos para aumentar a confiabilidade da repetibilidade dos angulos inseridos pelos servomotores. Após realizar a junção entre a plataforma e a base, iniciamos a conexão com o suporte da câmera. Na figura 15 podemos visualizar a junção entre todas as partes e com isso a estrutura do projeto finalizado.
Figura 15 – Modelo do projeto finalizado
3.2. Captura e envio do vídeo via APP IP Webcam
Para a identificação da posição em que o objeto esférico se encontra na plataforma, optamos por utilizar uma câmera de celular e enviar os dados para uma janela web. A maneira que encontramos para realizar essa transferência era a utilização de um app conhecido como IP Webcam. Para que as imagens obtidas pelo app fossem enviadas com uma velocidade mais elevada, optamos por utilizar uma resolução de vídeo com 352×288 px. Caso a resolução fosse muito elevada, os frames do vídeo poderiam demorar a chegar no navegador, proporcionando, assim, maiores erros na identificação real da posição da bolinha, adicionamos, também, um cabo para a comunicação entre a câmera e o software, pois caso a comunicação fosse realizada por meio do Wi-Fi, haveria uma maior variabilidade entre o tempo de obtenção de cada frame, com uma variância elevada surge um problema para os cálculos das partes integrativas e derivativa do controle PID. (Pavel Khlebovich,2021)
3.3 Captura do vídeo do APP IP Webcam e o processamento das imagens via Python
Com o APP IP Webcam enviando as imagens do celular para uma rede web por meio de um cabo USB, basta realizar uma codificação com a biblioteca OpenCV, a fim de recuperar essas imagens. O software Python vai recuperando e realizando um tratamento em um frame por vez, o tratamento dos frames consiste em 6 etapas, são elas:
1) Aplicar um filtro do tipo Blur na imagem, com o intuito de borrá-la e, com isso, minimizar erros de cores decorrentes da variação de iluminação. Na figura 16 podemos visualizar a transição da imagem com o filtro blur de kernel 10×10.
Figura 16 – Aplicação de filtro Blur no frame normal
2) Aplicar uma máscara na imagem, a fim de converter uma faixa de cor HSV para branco e o restante se tornar preto. Esse filtro permitirá escolher apenas a cor correspondente ao objeto esférico e dividí-lo do restante da imagem. Na figura 17 podemos visualizar a transição do blur para a máscara binária, neste processa o filtro se deu por meio do tratamento individual dos pixels, caso o pixel estiver dentro de uma faixa estipulada a sua cor é colocado para branco, caso contrário a cor do pixel se torna preto.
Figura 17 – Aplicação da máscara
3) Aplicar um filtro de fechamento, que consiste em afinar as detecções que foram convertidas para a tonalidade branca. Esse processo é realizado para filtrar erros pequenos de detecção da cor especificada fora do objeto desejado. Na figura 18 podemos observar a aplicação do filtro de fechamento com kernel 5×5.
Figura 18 – Aplicação filtro de fechamento
4) Aplicar um filtro de abertura, a fim de recuperar o tamanho original do objeto esférico. Esse filtro permite engrossar as detecções da cor branca. Na figura 19 podemos visualizar a aplicação do filtro de abertura de kernel 5×5.
Figura 19 – Aplicação do filtro de abertura
5) Aplicar um filtro de elipse a fim de melhorar a detecção branca do objeto. Na figura 20 podemos visualizar a imagem já processada com o filtro de elipse.
Figura 20 – Aplicação do filtro de Elipse
6) Aplicar um código que é capaz de identificar os contornos externos de uma imagem. Como o frame que acabou de ser filtrado se tornou uma imagem binária (preto e branco), os contornos obtidos por este código correspondem apenas aos contornos da própria bolinha, desse modo, a partir dos contornos, é possível identificar a posição da bolinha em relação à imagem.
Com a finalização destas 6 etapas, somos capazes de identificar a posição relativa da bolinha alocada acima da plataforma, portanto, temos assim um sensor de posição que será utilizada para realizar o controle do projeto.
3.4. Desenvolvimento da interface gráfica do software Python
Para que o projeto se torne mais dinâmico, podendo assim escolher a faixa de cor, e os setpoints, optamos por desenvolver uma interface gráfica no software, para isso, adicionamos alguns botões e permitimos a visualização do conteúdo da câmera e do fragmento em que o software realiza o processamento dos frames. Ao iniciar o programa, o software solicita que seja selecionado uma região onde se encontra a plataforma, é nessa região que todo o processamento de imagem será realizado. Na figura 21 podemos visualizar o formato da interface gráfica desenvolvida no software.
Figura 21 – Software Python
Os botões “Iniciar Plataforma” e “Resetar Pontos” são capazes de adicionar ou remover, respectivamente, os setpoints. Note que é possível adicionar mais de um ponto de referência, todavia, o software vai oscilar entre estes pontos, alternando entre eles por um tempo indeterminado. Podemos alterar este tempo por meio dos botões +, – e Aguardar.
Também possuímos botões responsáveis por alterar a faixa de cor em que o software irá realizar o processamento da imagem, e, com isso, identificar a posição relativa da bolinha.
Por fim, podemos identificar que o software exibe abaixo dos botões dois tipos de erros, um erro relativo à distância em que a bolinha se encontra em relação ao setpoint e um erro derivativo, que indica a velocidade da bolinha. Note que tanto a distância quanto a velocidade estão sendo mensuradas em pixels.
3.5. Identificando a função de transferência experimentalmente
Podemos identificar uma função de transferência correspondente ao sistema por meio experimental, para isso, realizamos 10 testes e coletamos os dados de cada um deles a fim de traçar uma curva característica do sistema e, com isso, identificar uma função de transferência correspondente. Na figura 22 podemos visualizar os dados que foram coletados experimentalmente. Note que o teste fora realizado a partir da aplicação de um degrau unitário nos servomotores de 60º e que os dados constantes indicam que o objeto esférico chegou no limite da plataforma, entretanto, o mesmo poderia continuar crescendo indefinidamente. (NORMAN, 2017)
Figura 22. Dados obtidos experimentalmente
Após a realização desse experimento, podemos traçar uma linha média imaginária entre os dados, estipulando uma função de transferência correspondente. Note que os dados possuem uma forma muito similar a uma parábola antes de alcançarem o limite da plataforma, desse modo, podemos criar uma função de segundo grau similar aos dados encontrados experimentalmente, como mostrado na figura 23.(NORMAN, 2017)
Figura 23. Parábola C(t)
Na imagem 16, podemos verificar uma função similar aos dados, essa função foi obtida através da seguinte formula.
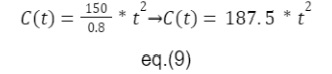
Aplicando uma transformada de Laplace podemos obter uma função de saída de terceira ordem, como mostrado a seguir.
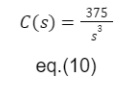
Como na função fora aplicada um degrau unitário temos que a saída pode ser representada da seguinte maneira.
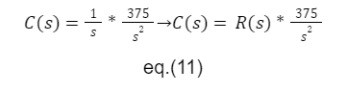
Com esses cálculos realizados temos a seguinte função de transferência.
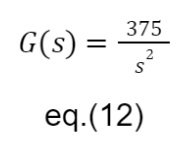
A fim de confirmar a veracidade dos cálculos, realizamos uma breve simulação no scilab da função de transferência obtida e verificamos se a saída era similar a estipulada, a figura 24 mostra a simulação da função de transferência.
Figura 24. Simulação da função de transferência
Após a obtenção da função de transferência, podemos realizar a análise da estabilidade deste sistema por meio da tabela de Routh, para isso, devemos realizar uma realimentação na função de transferência obtendo a seguinte equação:
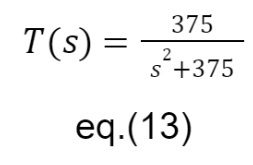
Aplicando a tabela, temos:
Tabela 2- Tabela de Routh
S^3 0 0 S^2 1 375 S^1 A1 0 S^0 B1 0
Com a tabela de Routh, podemos verificar a impossibilidade de realizar a análise de estabilidade deste sistema, pois o mesmo possui uma linha inteira zerada.
3.6. Criando o controlador PID
Para o desenvolvimento do controle PID devemos realizar a coleta do erro do sistema, neste projeto o erro consiste na distância relativa do objeto esférico ao ponto de referência, localizado, por padrão, no centro da plataforma. O erro máximo que a bolinha consegue alcançar, até sua queda da plataforma, é de ± 130 pixels, tanto no eixo X quanto no eixo Y.
A amostragem máxima que a câmera consegue fornecer ao software Python é de aproximadamente 25 frames por segundo, todavia, os servomotores conseguem se mover por completo com relação ao menor e ao maior ângulo estabelecido em aproximadamente 0.1 segundos. Tendo esta informação em mente, optamos por realizar uma amostragem de aproximadamente 0.04 segundos, observe que a amostragem nunca será exatamente esta pois o programa possui um tempo de execução relativamente mais elevado, a fim de solucionar este problema. Codificamos uma variável capaz de coletar o tempo que o software demora para a próxima rodada, e, com isso, calcular a variação do tempo anterior e o tempo atual. O cálculo da variação dos tempos é importante para a realização dos efeitos derivativos e integrativos, como visto no tópico de discretização do controle PID.
Após realizar a coleta do erro e obter a variação do tempo entre o erro anterior e o atual é possível realizar os cálculos de derivação e integração do controle PID, para isso usamos a mesma formula do controlador PID discreto, tendo assim as seguintes fórmulas para obter a derivada e a integral.

Após realizar os cálculos de derivada e integral dos erros no frame atual, é necessário realizar a multiplicação Kd e Ki nos valores obtidos, também é necessário multiplicar uma constante proporcional (Kp) ao próprio erro.
Os valores Kd, Ki e Kp foram inicializados randomicamente, e por meio de diversas tentativas eles foram sendo ajustados, ao final dos ajustes obtemos os seguintes valores das constantes para ambos os eixos.
Tabela 3– Valores de KD, KI E KP
Constantes Eixo X – Direita Eixo X – Esquerda Eixo Y – Cima Eixo Y – Baixo Kp 0.05 0.1 0.05 0.1 Ki 0 0 0 0 Kd 0.8 0.6 0.8 0.6
Podemos notar que o controlador PID calculado se tornou apenas um controlador PD (Proporcional e Derivativo).
Feita a identificação dos valores Proporcional e Derivativo, o software Python irá realizar uma limitação em cada um dos valores, a fim de estabilizar o sistema. Após a limitação, basta realizar a soma entre os fatores, obtendo um ângulo positivo ou negativo, por meio do PD. Este ângulo calculado, tanto para o eixo X, quanto para o eixo Y, será enviado para o ESP32 por meio do protocolo Bluetooth BLE. Após o envio do ângulo o processo volta ao início continuando assim o ciclo.
3.7. Comunicação Python e ESP32 via Bluetooth BLE
A última etapa do ciclo do projeto consiste na obtenção do ESP32 dos ângulos gerados pelo controlador PD. Nesta etapa, o ESP32 apenas coleta o ângulo e vai movimento os servomotores a fim de inclinar a plataforma. O ciclo continua até a finalização do software Python.
4. Resultados e Discussão
Ao decorrer do desenvolvimento do projeto foram surgindo diversas problemáticas. O primeiro problema identificado fora os graus de liberdade do sistema. Inicialmente, estávamos utilizando uma esfera entre a conexão da plataforma e a caixa, todavia, a bolinha permitia 3 graus de liberdade em um sistema que só devia conter 2 graus, a fim de solucionar este problema, substituímos a esfera por uma junção universal e limitamos a dinâmica da plataforma para apenas 2 graus de liberdade.
Outro problema mecânico identificado ao decorrer da elaboração do projeto consiste na junção dos servomotores com a plataforma. Pretendíamos utilizar apenas um arame, entretanto, o mesmo se deformava, impossibilitando uma confiabilidade mais precisa dos ângulos que os servomotores poderiam fornecer à plataforma. Para resolver este problema utilizamos um objeto de madeira mais resistente e o enrolamos com o arame, com isso, a precisão dos ângulos teve um aumento relevante.
Também tivemos certos problemas no desenvolvimento do software voltado à aplicação do controle PID. Uma vez que não havíamos identificado como encontrar o ângulo correspondente do servomotor a partir dos erros em distância, só posteriormente percebemos não era sumariamente necessário fazer uma conversão, e que o PID já estava por si só retornando os valores do ângulo. Para conseguir identificar os melhores valores possíveis de ganho para cada componente do controlador PID, fizemos uma limitação provisória de cada grau de liberdade, com isso, quando o PID conseguia realizar um ajuste eficiente do erro, em um dos eixos específicos, parávamos esta limitação e analizávamos o outro eixo para encontrar seus valores mais efetivos.
O objetivo final do projeto era realizar uma estabilização no setpoint solicitado pelo software, todavia, um eixo acabava por interferir no outro. Desse modo, o sistema não consegue estabilizar o objeto rapidamente, ficando um tempo mais elevado no estado marginalmente estável, de tempos em tempos ele consegue se estabilizar. Note que quando o sistema se estabiliza, o mesmo não consegue zerar o erro, pois o fator integrativo é 0. Optamos por não usar o integrativo pois, caso utilizado, o sistema tendia a nunca se estabilizar, ficando marginalmente estável, indeterminadamente, até que o software Python fosse finalizado.
5. Arquivos do projeto
Figura 25. Qrcode dos arquivos utilizados no projeto
Link para os arquivos utilizados no projeto: < https://drive.google.com/drive/folders/1CoJxvMonvQBP7pzVrH_kj2_7xo58R2ia?usp=share_link>
6. Referências Bibliográficas
Acervo Lima. IDENTIFICAÇÃO DE CORES EM IMAGENS USANDO PYTHON – OPENCV. Disponível em: < https://acervolima.com/identificacao-de-cores-em-imagens-usando-python-opencv/#:~:text=Para%20encontrar%20a%20cor%20especificada,a%20cor%20verde%20como%20segue.> Acesso em: 02 nov. 2022
Acelerômetro e Giroscópio 3 Eixos 6 DOF MPU-6050, Disponível em: < https://www.filipeflop.com/produto/acelerometro-e-giroscopio-3-eixos-6-dof-mpu-6050/ >, Acessado em 23 de out de 2022.
ANTONELLO, Ricardo. Introdução a Visão Computacional com Python e OpenCV. Santa Catarina, 2018 Disponível em: <https://professor.luzerna.ifc.edu.br/ricardo-antonello/wp-content/uploads/sites/8/2017/02/Livro-Introdução-a-Visão-Computacional-com-Python-e-OpenCV-3.pdf> Acessado em 24 de out de 2022.
BRITO, Fábio. Sensores e Atuadores. Segunda Edição. São Paulo: Editora Érica, 2019.
CARRARA, Valdemir. INTRODUÇÃO À ROBÓTICA INDUSTRIAL. Repositório INPE São José dos Campos, 2015. Dissertação (Mestrado). Disponível em:<http://mtc-m21b.sid.inpe.br/col/sid.inpe.br/mtc-m21b/2015/08.25.14.16/doc/publicacao.pdf?metadatarepository=&mirror=iconet.com.br/banon/2006/11.26.21.31> Acessado em 24 de out de 2022.
CHÁVEZ, Guillermo Cámara. Sistema de Cores. Disponível em: < http://www.decom.ufop.br/guillermo/BCC326/slides/Processamento%20de%20Imagens%20-%20Sistema%20de%20Cores.pdf> Acesso em: 02 nov. 2022
CEDRO Technologies. OpenCV: Uma breve introdução à visão computacional com python. Blog Cedrotech, São Paulo, 2018. Disponível em: < https://blog.cedrotech.com/opencv-uma-breve-introducao-visao-computacional-com-python>. Acessado em 24 de out de 2022.
DANIEL, Luciano Teoria de Controle – Controlador PID discreto simulado no Python – Parte 1. Youtube, São Paulo, 2022. Disponível em: < https://www.youtube.com/watch?v=-C4YYNX0Q2k&ab_channel=ProfLucianoDaniel> Acessado em 24 de out de 2022.
DANIEL, Luciano; Teoria de Controle – Controlador PID discreto simulado no Python – Parte 2. Youtube, São Paulo, 2022. Disponível em: <https://www.youtube.com/watch?v=HdQ1HMhWQV8&ab_channel=ProfLucianoDaniel> Acessado em 24 de out de 2022.
DORF, Richard.C.; BISHOP, Robert.H. Sistemas de Controle Modernos. Rio de Janeiro. Editora: LTC, 2018. 13ª edição
ESPRESSIF. ESP-WROOM-32 Datasheet (PDF) – ESPRESSIF SYSTEMS (SHANGHAI) CO., LTD. Shanghai. Disponível em: <https://pdf1.alldatasheet.com/datasheet-pdf/view/1179101/ESPRESSIF/ESP-WROOM-32.html> Acessado em 24 de out de 2022.
FRANK, Caron. Of gyroscopes and gaming: the tech behind the Wii MotionPlus, Arstechnica , California, Agosto 2008 Disponível em: https://arstechnica.com/gaming/2008/08/wii-motion-sensor/https://arstechnica.com/gaming/2008/08/wii-motion-sensor/ Acessado em 23 de out de 2022.
JESUS, Gilva Altair Rossi de; Uma contribuição para o desenvolvimento e controle de sistemas de posicionamento submicrométricos. Repositório Institucional USFC, Santa Catarina, 1999. Dissertação (Mestrado). Disponível em: < http://repositorio.ufsc.br/xmlui/handle/123456789/80866>
LANDIM, Wikerson. Como funcionam acelerômetros e giroscópios? , São Paulo – SP, Junho 2010 Disponível em : https://www.tecmundo.com.br/celular/4406-como-funcionam-acelerometros-e-giroscopios-.htm Acessado em 23 de out de 2022.
MARQUES, Larissa. R. F; A EXPERIÊNCIA DO USUÁRIO EM PRODUTOS DE TECNOLOGIAASSISTIVA:INVESTIGAÇÃO ENTRE COLHERES DESTINADAS ÀS PESSOASCOMDOENÇA DE PARKINSON E TREMOR ESSENCIAL. Repositório Institucional Unesp, São Paulo, 24/02/2022. Dissertação (Mestrado). Disponível em: < https://repositorio.unesp.br/handle/11449/217991>
MESSNER, Bill; TILBURY, Dawn. Introduction: PID Controller Design. Control Tutorials for MATLAB and Simulink, Michigan (EUA), 2017. Disponível em: <https://ctms.engin.umich.edu/CTMS/index.php?example=Introduction§ion=ControlPID > Acessado em 24 de out de 2022.
MARTOUZ, Nuno. Modelos de cor RGB, CMYK, HSV, YUV Disponível em: < http://martinhoecardoso.blogspot.com/2017/11/modelos-de-cor-rgb-cmyk-hsv-yuv.htmlAcesso em: 02 nov. 2022
NORMAN, S.Nise. Engenharia de Sistemas de Controle. São Paulo. Editora LTC. 2017. 7ª Edição.
PRADA, Rodrigo. O que é um acelerômetro? , São Paulo – SP, 26 de agosto de 2009. Disponível em: https://www.tecmundo.com.br/curiosidade/2652-o-que-e-um-acelerometro-.htm Acessado em 23 de outubro de 2022
Pavel Khlebovich. IP Webcam, Google Play 10 de dez. de 2021. Disponível em: <https://play.google.com/store/apps/details?id=com.pas.webcam&hl=pt_BR&gl=US> Acessado em 24 de out de 2022.
ROMANO, Vitor Ferreira Romano; DUTRA, Max Suell. INTRODUÇÃO À ROBÓTICA INDUSTRIAL. Primeira Edição. São Paulo: Editora Blucher. 2002.
SHIRAHIGE, Alessandro. METODOLOGIA PARA AFERIÇÃO DA AÇÃO DE CONTROLE PROPORCIONAL INTEGRAL DERIVATIVA IMPLEMENTADA EM CONTROLADORES INDUSTRIAIS. Repositório USP, São Paulo, 2007 Dissertação (Mestrado). Disponível em: <https://www.teses.usp.br/teses/disponiveis/3/3143/tde-17012008-120856/publico/DissertacaoMAFPID.pdf> Acessado em 24 de out de 2022.
Sistemas de Controle I/Roteiro de Laboratório Repositório USP, São Paulo, 2014. Disponível em: <https://edisciplinas.usp.br/pluginfile.php/1166397/mod_resource/content/1/Pratica1_SCII_2016.pdf> Acessado em 24 de out de 2022.
SNURMACHER, Antonio. Tutorial teórico prático com servos y Arduino. Dronprofesional.com, Espanha, 2019. Disponível em: <https://dronprofesional.com/blog/tutorial-teorico-practico-con-servos-y-arduino/> Acessado em 24 de out de 2022.
SILVA, Rafael. Acelerômetros: para que servem e como funcionam?, São Paulo, 2011. Disponível em: <https://tecnoblog.net/responde/acelerometro-notebooks/>Acessado em 23 de outubro de 2022
RODRIGUES, Vitor. Conhecendo a visão do computador: Redes Neurais Convolucionais. Disponivel em: < https://vitorborbarodrigues.medium.com/conhecendo-a-vis%C3%A3o-do-computador-redes-neurais-convolucionais-e1c2b14bf426Acesso em: 02 nov. 2022
