LEARNING DIFFICULTIES IN MATHEMATICS IN THE EARLY GRADES OF ESCOLA ESTADUAL PROF° JURACY BATISTA IN MANAUS-AM, IN THE PERIOD 2020/2021.
REGISTRO DOI: 10.69849/revistaft/fa10202501222118
Maria Raimunda Martins de Brito1,
Orientador: Dr. Enrique Lopez2
RESUMO
O presente trabalho busca introduzir e esclarecer a importância desta pesquisa para o meio acadêmico e prático em sala de aula, bem como os resultados que surgiram através de sua realização. Na revisão da literatura apresentará um panorama das pesquisas recentes sobre conceitos e quebra de paradigmas matemáticos relacionado ao cotidiano a partir da perspectiva do aluno. A pesquisa irá contribuir com a coleta de dados sobre paradigmas, crenças, pensamentos e pré-conceitos no processo construtivo matemático, metodologia, estratégias, entendimentos, absorção de conteúdo, raciocínio lógico, resolução de problemas com relações cotidianas junto ao projeto de vida. É possível verificar que em todas as áreas da vida o indivíduo possui conhecimentos dos mais diversos estigmas, sendo que na vida escolar não difere e principalmente na matemática, ciência que causa alegria uns e repulsa em outros devido vivência ou traumas. Um padrão que boa parte dos docentes permitem ocupar um lugar de prioridades gerando burocracias quando deveriam ser executados de forma complementar, no decorrer desse processo surgem sérias consequências como a grande rejeição da matéria nas abordagens de conteúdos por parte dos alunos e um costume de repetição pelo docente sem explorar e incluir o aluno na construção matemática pelo fato de estar convencido de que os alunos não querem aprender e não possuem interesse. Sabe-se que culturas existentes sobre o contexto matemático não atinge apenas alunos, mas sim, ex-alunos e qualquer cidadão comum que não tenha um bom relacionamento com cálculos. É possível observar que o padrão contribui fortemente com crenças que limitam qualquer indivíduo em seu processo criativo, fortalecendo alguns gatilhos mentais que convencem o não “ser” capaz de resolver enunciados que envolvam cálculos considerando a disciplina de matemática como extremamente difícil.
Palavras-chaves: Dificuldades de aprendizagem. Matemática. Práticas pedagógicas. Aprendizagem significativa.
1 INTRODUÇÃO
A matemática é utilizada e está presente na vida cotidiana, nas resoluções de problemas na vida em sociedade, porém diversas pessoas têm dificuldades nos cálculos e não vê nela significado no aprendizado.
O processo de ensino aprendizagem de matemática na rede estadual é estruturada e composta por um sistema padrão através do currículo escolar, habilidades a serem trabalhadas, por Avaliação Diagnostica (AD), Avaliações de Aprendizagem e Processo (AAP), sequências de atividades plataforma CAED e avaliações por parte do docente.
Um padrão que boa parte dos docentes permitem ocupar um lugar de prioridades gerando burocracias quando deveriam ser executados de forma complementar, no decorrer desse processo surgem sérias consequências como a grande rejeição da matéria nas abordagens de conteúdos por parte dos alunos e um costume de repetição pelo docente sem explorar e incluir o aluno na construção matemática pelo fato de estar convencido de que os alunos não querem aprender e não possuem interesse.
Sabe-se que culturas existentes sobre o contexto matemático não ronda apenas alunos, mas sim, ex-alunos e qualquer cidadão comum que não tenha um bom relacionamento com cálculos, muitos carregam um script pronto de comentários como: “sou burro” “não consigo fazer” “entendi nada” “não gosto de matemática” “tive um professor(a) que era brava ao ensinar” …que só é bom em matemática apenas aquele que resolve ou responde rápido entre outras.
É possível observar que o padrão contribui fortemente com crenças que limitam qualquer indivíduo em seu processo criativo, fortalecendo alguns gatilhos mentais que convencem o não “ser” capaz de resolver enunciados matemáticos, que a disciplina é extremamente difícil.
Neste sentido, o desafio do educador está em tornar o caminho entre a Matemática e os estudantes o mais significativo possível, ele tem a missão de conduzir a Matemática até os estudantes ou de conduzi-los a ela. No entanto, aprender com compreensão é uma ação pessoal, que se manifesta em cada um de diferentes formas, esse processo exige que o estudante/aprendiz pense por si, para tanto é necessário que seja submetido a um processo de ensino em que seja um sujeito ativo.
2 FUNDAMENTACÃO TEÓRICA
2.1 O SUTIL PROCESSO HISTÓRICO DAS TEORIAS DE APRENDIZAGEM
A Teoria da Aprendizagem Significativa (TAS) de Ausubel considera todas as informações armazenadas pelo indivíduo, que estão organizadas sequencialmente em sua estrutura cognitiva, conforme o que ele julga relevante. Os conhecimentos que o estudante já possui servem como alicerce para a aprendizagem, onde as novas informações irão integrar-se com os conceitos anteriores, reorganizando a estrutura cognitiva do sujeito e ampliando sua visão de mundo.
É preferível a aprendizagem significativa ao modelo tradicional, pois nessa perspectiva é possível que o estudante relacione um conhecimento específico de alguma área com situações fora do âmbito escolar, relação que possivelmente não ocorreria na aprendizagem mecânica/tradicional. Quando o ensino de Matemática é feito de maneira mecânica, apresentando situações ao estudante desvinculadas do real, logo, a aprendizagem também se dá desta maneira, onde o aprendiz não consegue associar qualquer conceito apreendido em sala de aula em situações fora deste contexto (BOALER, 2018).
De acordo com Hahn e Hollas (2011) “tratar educação como algo isolado nada mais é do que adotar métodos retrógrados e antipáticos de delineação conceitual de realidade”. Diante das inúmeras modificações do cenário educacional brasileiro, percebe-se a necessidade e viabilidade de inovação das práticas educacionais, especialmente quando as temáticas abordadas na sala de aula não são bem recebidas pelos estudantes.
Segundo Santomauro (2010), o desafio de pesquisadores, estudiosos e pensadores das mais diversas áreas, desde dois mil anos atrás é obter as respostas para duas perguntas: como o ser humano aprende e como criar as melhores condições para ocorrer a aprendizagem na escola? A busca por tais respostas iniciou-se na Antiga Grécia, com o desenvolvimento do pensamento racional, a busca pelas explicações não mais baseadas em mitos e sim em conceitos. A dúvida então, para os primeiros filósofos, era saber se o ser humano possui saberes inatos, ou se é possível ensinar algo a alguém.
Segundo Platão, conhecer é relembrar. Essa concepção denominada Inatismo defende que as pessoas nascem com saberes adormecidos, aptidões, habilidades, conceitos, qualidades, tudo faz parte da bagagem hereditária de cada um, acreditando que o papel do educador é trazer o saber à consciência, auxiliar o estudante a acessar tais informações adormecidas em seu subconsciente (BOALER, 2018).
Uma segunda concepção apresentada por Aristóteles: as pessoas precisam de experiência, a fonte do conhecimento são as informações extraídas do meio exterior. O Empirismo, como foi chamado, é favorável a um ensino pela imitação, “o aprendizado é obtido por meio da cópia, seguida de memorização” (SANTOMAURO, 2010). Os conceitos apreendidos são transformados em conhecimento, acumulados e fixados, podendo ser rearranjados quando surgirem conteúdos mais complexos. Nesta concepção, o educador é quem detém o saber e é papel da escola formar um sujeito capaz de julgar, conhecer e agir segundo os critérios da razão.
Para Santomauro (2010), com as duas concepções apontando para lados opostos, surgiu no século XX uma tentativa de caminho do meio: a perspectiva construtivista, tendo como precursor Jean Piaget. Segundo esta teoria, se o meio não favorecer o desenvolvimento das potencialidades, elas não se concretizam, portanto, não basta apenas, para adquirir conhecimento, que o sujeito entre em contato com o mesmo, é preciso agir sobre ele e transformá-lo. Pela concepção construtivista, o educador deve planejar uma atividade que organize e integre os novos conhecimentos aos já existentes, conceber ações e desafiar os estudantes para que a aprendizagem ocorra.
As ideias e teorias de Piaget se aproximara de outros pesquisados: Lev Vygotsky e Henri Wallon. Embora não houvesse uma convivência direta com Piaget, há muitos pontos comuns entre o construtivismo piagetiano e a perspectiva defendida pela “dupla”, o socio interacionismo. Seguindo essa perspectiva, o processo de aprendizagem se dá pela relação do aprendiz com o ambiente familiar e social, educadores, colegas e o próprio conteúdo.
Em sala de aula, percebe-se que os estudantes têm tempo diferente para aprendizagem, cada um avança no seu próprio ritmo. Tantas individualidades abrem uma oportunidade para que o educador promova a troca de experiências entre os estudantes.
Paganotti (2011) defende ser frutífera a interação e a valorização das diferenças, o convívio em sala de aula de crianças com mais habilidade com aquelas que precisam de auxílio nas atividades, já defendida pelo psicólogo Vygotsky, autor de diversos trabalhos voltados para esta área, que propõe a existência de dois níveis de desenvolvimento: o primeiro é chamado real e engloba as funções mentais adquiridas pela criança, não considerando quando esta consegue realizar as atividades com a ajuda de um colega ou do educador.
A teoria sociointeracionista de Vygotsky é compatível com os conceitos da aprendizagem significativa de Ausubel, onde “aprender significativamente é ampliar e reconfigurar ideias já existentes na estrutura mental e com isso conseguir relacionar e acessar novos conteúdos” (FERNANDES, 2011)
Dessa forma, a teoria de Ausubel considera a história do estudante e ressalta o papel do educador em criar situações que favoreçam a aprendizagem, que examinem o contexto social ao qual o estudante está inserido e o uso social do que está sendo estudado. As aulas devem ser planejadas com a finalidade de possibilitar a reflexão e a negociação de significados, onde o estudante tem problemas a resolver e decisões a tomar.
O processo ideal ocorre quando uma nova ideia se relaciona aos conhecimentos prévios do indivíduo. Motivado por uma situação que faça sentido, proposta pelo professor, o aluno amplia, avalia, atualiza e reconfigura a informação anterior, transformando-a em nova. (FERNANDES, 2011).
Na aprendizagem significativa pode ocorrer o esquecimento, porém como o conhecimento residual permanece o resgate do conceito é relativamente rápido, pois a aprendizagem significativa é duradoura onde o conhecimento passa por um processo de constante evolução.
2.1.1 Os meandros da aprendizagem significativa
A educação, em sentido amplo, cumpre função de produção do conhecimento. Abrange os processos formativos existentes/construídos no seio familiar, no convívio entre os seres humanos, nas relações de trabalho, nas instituições da sociedade como escolas, igrejas, sindicatos e outras organizações, bem como nas manifestações culturais (BOALER, 2018).
De acordo com Sacristán e Gómez (1998), ao longo da história surgiu a necessidade de criar um sistema de escolarização básica obrigatória para todas as camadas da sociedade, em que o papel da escola seria preparar os estudantes para o mundo do trabalho e a vida pública, preparando-o também para o exercício da cidadania. Sacristán e Gómez (1998) citam que agora, a função da escola deve ultrapassar o caráter reprodutivo informativo, utilizando o conhecimento prévio do estudante como ferramenta de análise para compreensão de conceitos e produção de novos conhecimentos.
Os autores consideram como processo de ensino-aprendizagem, na escola, a investigação e a prática didática, sempre embasada em um conhecimento teórico oferecido em cada disciplina do currículo escolar. Entretanto, nas últimas décadas, a forma de ensino mecanicista e hierárquica se consolidou e para que a aprendizagem seja relevante para o estudante, deve haver uma reconstrução do conhecimento que ele adquire em sua vida anterior e paralela à escola.
Segundo Moreira (2009), Ausubel diz que se deve considerar o que o estudante já sabe, a sua estrutura cognitiva, ou seja, um determinado assunto, conteúdo e a organização de suas ideias em determinada área específica do conhecimento; e, ainda, para que a estrutura cognitiva influencie e facilite a aprendizagem, é necessário o conteúdo ter sido aprendido de forma significativa, não arbitrária e não literal.
Segundo Moreira (2009) “o‘subsunçor’ é um conceito, uma ideia, uma proposição já existente na estrutura cognitiva, capaz de servir de ‘ancoradouro’ a uma nova informação de modo que esta adquira, assim, significado para o indivíduo”. E, ainda, há o processo de interação entre as novas informações e os conceitos mais relevantes existentes na estrutura cognitiva do estudante para que a aprendizagem significativa possa realmente ocorrer.
A aprendizagem representacional é a mais simples e envolve a atribuição de significados a determinados símbolos ou palavras; por exemplo, quando uma criança relaciona o som da palavra bola, mesmo sem conhecer o seu real significado, com o objeto.
A aprendizagem de conceitos é similar à aprendizagem representacional, a diferença é que se estabelece uma equivalência, entre um significado e um símbolo; também são considerados neste tipo de aprendizagem os conceitos ou atributos culturais designados para determinados objetos.
E, na aprendizagem proposicional o objetivo é aprender não um conceito isolado e sim aprender o significado de ideias em forma de proposição. Por exemplo, as palavras combinadas em uma sentença representam conceitos, entretanto, não se deseja aprender o significado isolado de cada uma delas, mas sim o significado que está além da soma dos significados das palavras desta sentença-interpretação.
Quando a aprendizagem é significativa é possível abordar o mesmo tema em diferentes situações, possibilitando ao educador a interdisciplinaridade. Os autores utilizam o modelo de aprendizagem significativa de Ausubel (1972) em que este distingue duas dimensões como chave para a efetiva aprendizagem:
Significação lógica: coerência na estrutura interna do material, sequência lógica nos processos e consequência nas relações entre seus elementos componentes. Significação psicológica: que seus conteúdos sejam compreensíveis desde a estrutura cognitiva que o sujeito que aprende possui. (AUSUBEL, 1972 apud SACRISTÁN; GÓMEZ, 1998, p. 38).
A segunda condição é a disposição, tanto conjuntural ou momentânea quanto permanente, ou estrutural do indivíduo em relação à aprendizagem. Esta segunda condição está mais ligada ao motivacional e emocional que está presente em toda aprendizagem. Além dessas condições, os autores citam a necessidade de um planejamento didático para este processo de aprendizagem, que deve ter como ponto de partida o conhecimento da estrutura mental do indivíduo que irá participar.
Cada conceito ocupa um lugar determinado em função de seu nível de abstração, de generalização e capacidade de incluir outros conceitos. Assim, na aprendizagem significativa „adquire-se os significados de ideias e proposições num processo de inclusão correlativa em estruturas mais genéricas. Aprendizagem de ideias incluíntes ou incluídas.‟ (AUSUBEL, 1972 apud SACRISTÁN; GÓMEZ, 1998, p. 38)
Dessa forma, a aprendizagem significativa produz simultaneamente a estruturação do conhecimento e a extensão de sua potencialidade explicativa e operativa. A aprendizagem anterior ou posterior serve para reafirmar a importância da aprendizagem atual, sempre que a mesma se mantenha válida no conjunto hierárquico.
Sacristán e Gómez (1998) citam que teoria e prática andam distantes em se tratando dos processos de aprendizagem, sendo necessária uma investigação adicional sobre o tema. Para os autores, o problema pode estar ligado à didática. Para eles, deve as teorias se aproximem mais do real, podendo ser aplicadas as diversas instituições de ensino hoje existentes. Assim, as investigações devem ser feitas segundo as características de cada escola e comunidade.
Entretanto, as habilidades dos estudantes neste processo de aprendizagem significativa, só irão se desenvolver com a prática e efetiva participação destes no processo de ensino-aprendizagem.
2.2 O PAPEL DA ESCOLA, DO EDUCADOR E DO ESTUDANTE NA APRENDIZAGEM SIGNIFICATIVA.
Quando se fala em aprendizagem significativa, assume-se que o aprender possui um caráter dinâmico com ações de ensino direcionadas ao aprofundamento e ampliação dos significados para os estudantes.
Em entrevista para o Portal Escola Conectada da Fundação Ayrton Senna, publicada em 1 de agosto de 2008, Moran cita que a escola está envelhecida em seus métodos, procedimentos e currículo, e, ainda, que grande parte destas instituições está distante da sociedade e das atuais demandas.
A escola precisa partir de onde o aluno está, das suas preocupações, necessidades, curiosidades e construir um currículo que dialogue continuamente com a vida, com o cotidiano. Uma escola centrada efetivamente no aluno e não no conteúdo, que desperte curiosidade, interesse. […] A escola precisa cada vez mais incorporar o humano, a afetividade, a ética […]. (MORAN, 2008, p. 01).
Segundo o autor supracitado, a aprendizagem será significativa quando se parte de situações concretas e incorporam-se informações e, quanto menor a faixa etária do estudante, mais práticas precisam ser desenvolvidas para perceber o quanto são importantes para ele. É necessário compreender os significados e relacionar experiências anteriores e vivências do estudante, permitindo formular problemas desafiantes que incentivem o aprender, estabelecendo diferentes tipos de relações, modificando comportamentos e contribuindo para que o que foi aprendido possa ser utilizado em diferentes situações.
Segundo Moran (2008), para haver realmente uma aprendizagem significativa, o currículo das escolas deve ser reestruturado.
Se os alunos não percebem que tudo está interligado e que cada tema, assunto se relaciona com o restante, o currículo continuará uma colcha de retalhos, um mosaico fragmentado e sem sentido. Se o currículo continuar organizado por disciplinas, é fundamental que cada uma seja estimulante, atraente e esteja articulada com as demais. (MORAN, 2008, p. 03).
Moran (2008) segue dizendo que estamos caminhando para uma nova fase, onde tudo está integrado, todos falam com todos e tudo pode ser divulgado em alguma mídia. Seguindo nesta mesma perspectiva, Santos (2008) diz que o educador deve ser o mediador no processo de ensino aprendizagem, construir o conhecimento com o estudante, por questionamentos, situações que despertem curiosidade, interesse, dúvidas, dentre outros.
Esse desafio a que nos referimos não precisa ser algo de extraordinário, o essencial é cumprir o papel de “causar sede”. Podemos promover um desafio com uma simples pergunta […]. Outras atividades como apresentação de um recorte de jornal, de uma fotografia, de uma cena de filme ou de uma pequena estória, igualmente se prestam como excelentes desafios. (SANTOS, 2008, p.11).
É fundamental entender o processo de modificação do conhecimento, reconhecer a importância que os processos mentais têm nesse desenvolvimento. As ideias de Ausubel baseiam-se em uma reflexão específica sobre a aprendizagem escolar e o ensino.
O educador deve encontrar a ponte motivadora para despertar o estudante, para que ele se torne parte do processo e saia do estado de espectador, e, as técnicas de comunicação também são importantes para alcançar estes objetivos.
Segundo a Teoria da Aprendizagem Significativa de Ausubel são necessárias duas condições para ocorrer a aprendizagem significativa: primeiramente, o estudante precisa ter disposição para aprender, e em segundo, o conteúdo escolar deve ser potencialmente significativo
A aprendizagem significativa tem vantagens notáveis, tanto no enriquecimento da estrutura cognitiva do estudante como para experimentar novas aprendizagens. O conhecimento que se adquire de maneira significativa é retirado e lembrado por mais tempo, aumenta a capacidade de aprender outros conteúdos de maneira mais fácil, facilita a aprendizagem seguinte. Lemos (2011) destaca que a avaliação deve ocorrer durante todo o processo de ensino aprendizagem: no início, no meio e no fim, e o resultado da avaliação é válido para evidenciar até que ponto os objetivos educacionais foram alcançados.
O aluno, ao se preparar para o exame, na expectativa de êxito, faz uma revisão, consolidação e integração do assunto. A discussão dos resultados do exame confirma ou corrige ideias, evidenciando o que deve ser mais estudado e a experiência de sofrer constantes avaliações externas leva o aluno a fazer uma Autoavaliação do seu rendimento escolar. (LEMOS, 2011, p. 32)
Valadares (2011) complementa as colocações de Lemos dizendo que um indivíduo aprende significativamente quando consegue relacionar uma informação de uma área específica com sua estrutura cognitiva prévia; e, que a aprendizagem é singular, o processo de compreensão e assimilação diferirá para cada pessoa.
A aprendizagem significativa é substantiva porque é a «substância», o «recheio» do conceito apreendido e não apenas um nome e (ou) um enunciado sem qualquer significado para quem aprende. Para tal, a nova informação tem de interagir com as ideias que o aprendente já domina que incluem os conceitos, as proposições e símbolos previamente assimilados. (VALADARES, 2011, p. 37).
O autor defende que o ensino deve ser investigativo alicerçado no pensamento crítico e é papel do educador auxiliar os estudantes no processo, sanando suas dúvidas e auxiliando-os a ultrapassar dificuldades conceituais, de modo que a aprendizagem do estudante vá se aproximando da aprendizagem significativa.
A intervenção educativa, precisa então de uma mudança na ótica substancial onde abrange o aprender a aprender. Para isso é necessário os rumos de ação educativa incorporem em sua trajetória um conjunto de legalidades processuais.
2.3 A SOCIEDADE DO CONHECIMENTO E A DISSEMINAÇÃO DE SABERES
A globalização aproximou as nações e redefiniu o trabalho impondo novas tarefas aos trabalhadores que, devem desenvolver o conhecimento de várias atividades da sua profissão e aspectos de outras áreas com influência direta no resultado do seu trabalho como é o caso da tecnologia da informação, de saber imprimir um material, trocar um cartucho de tinta em e impressora, mandar um correio eletrônico e outros. Dentro dessa nova realidade é possível destacar com Delors (2001) que:
A digitalização da informação operou uma revolução profunda no mundo da comunicação, caracterizada, em particular, pelo aparecimento de dispositivos multimídia e por uma ampliação extraordinária das redes telemática, a partir de 1988 a Internet duplica todos os anos o número de usuários e de redes assim como o volume de tráfego. (DELORS, 2001, p.63)
Nosella (2010) pesquisadora da gestão do conhecimento, a educação assume um papel essencial no desenvolvimento do homem e das sociedades. Na era do conhecimento:
[…] as revoluções demográficas do século XX foram importantes, tanto do ponto de vista qualitativo quanto quantitativo. Mas, a maior transformação, decisiva, “sem precedentes”, que ocorreu em todos os países desenvolvidos, foi a que mudou o trabalho manual não qualificado “em uma atividade basicamente intelectual”. (NOSELLA, 2010, p. 32)
A autora entende que as políticas educativas se constituem num instrumento de emancipação de consciências e de valorização do ser humano. Através dela o homem enriquece permanentemente seus conhecimentos, seu trabalho, sua vivência em sociedade. Deste modo cabe a todos pensar os meios e as finalidades da educação.
Conforme Nosella (2010) o desenvolvimento tecnológico liberou o homem do trabalho fabril e caracterizou o surgimento do trabalho intelectual, condição que une a todos na construção de um destino comum. Todos têm papéis sociais e juntos são responsáveis pela aprendizagem coletiva. Neste contexto o professor deve dominar o conhecimento acadêmico de sua área e ter conhecimentos gerais de sua cultura par poder auxiliar o aluno a aprender. “Aprender a conhecer” é o primeiro pilar, e tem o intuito de proporcionar o prazer de compreender, de conhecer, de descobrir.
“O aumento dos saberes, que permite compreender melhor o ambiente sob os seus diversos aspectos, favorece o despertar da curiosidade intelectual, estimula o sentido crítico e permite compreender o real, mediante a aquisição de autonomia na capacidade de discernir” (DELORS, 2001, p. 91).
Para Nosella (2010) os pilares da educação apresentados no Relatório Educação: Um tesouro a descobrir (UNESCO, 2001) expressam que a necessidade de cada um em se conhecer e compreender melhor é vital a todo homem do século XXI.
Dweck (2017) afirma que os professores com mindset de crescimento encantam pelo aprendizado. Conforme a autora, os professores com mindset de crescimento buscam o aprimoramento, se entusiasmando para aprender com os estudantes “os professores de mindset fixo frequentemente pensam em si mesmos como produtos acabados. Seu papel é simplesmente transmitir conhecimento” (DWECK, 2017, p. 216).
Walle (2009) entende que a Matemática enquanto ciência se baseia em um processo de compreender e dar significado às coisas. A estratégia metodológica assume um papel fundamental no ensino e na aprendizagem da matemática, uma vez que permite ao aluno pensar por si próprio, possibilitando desenvolver o raciocínio lógico, colocar-se diante de situações questionadoras e buscar alternativas para solucionar as situações propostas.
A atividade de pensar poderá contribuir para que ocorra uma transformação no ensino da Matemática, no sentido de que o aluno adquira autonomia de pensamento e desenvolva esquemas que promovam a assimilação e a acomodação de procedimentos e dos conteúdos, como também promova hábitos de leitura, o que pode contribuir para a diminuição do desinteresse e da desmotivação que existe em relação a esta ciência (WALLE, 2009).
2.4 A IMPORTÂNCIA DA FORMAÇÃO CONTINUADA NA RESSIGNIIFICAÇÃO DA PRÁTICA PEDAGÓGICA EM MATEMÁTICA
Considerando a escola responsável por grande parte da formulação do ser humano, o trabalho da formação continuada na instituição escolar tem um caráter preventivo no sentido de procurar criar competências e habilidades para a solução dos problemas, a formação continuada traz uma nova investigação sobre quem aprende, como aprende, articulando várias informações, teorias que auxiliam a esclarecer o universo humano, o que há nele de mais recôndito.
Na perspectiva de uma educação democrática, torna-se inadiável ‘repensar’ de conceitos, funções e práticas de avaliação do processo ensino/aprendizagem, tendo em vista informações necessárias à orientação ou reorientação das ações educativas planejadas.
Desta forma aborda-se que a prática pedagógica através da formação continuada tem demonstrado duas grandes preocupações ao enfocar o processo educacional. O que se pretende formar e transformar não é apenas o que o professor faz ou o que sabe, mas fundamentalmente, sua própria maneira de ser em relação ao seu trabalho. Por isso, a questão prática está duplicada por uma questão quase existencial e a transformação da prática está duplicada pela transformação pessoal do professor. (LARROSA, 1994, p. 45-59)
Os conhecimentos da dосênсіа ѕãо adquiridos роndо em prática a teoria арrеndіdа nos cursos dе fоrmаção buscando ѕеmрrе o ареrfеіçоаmеntо e рrороrсіоnаndо uma educação de qualidade para os аlunоѕ.
2.5 AS NOVAS EXIGÊNCIAS NA FORMAÇÃO DOCENTE PARA UMA NOVA PRÁTICA EDUCATIVA
Pensar em formação docente tendo em vista a formação do sujeito professor, no século XXI, é um desafio a ser superado. Isso porque, segundo Imbernón (2002):
A profissão docente deve abandonar a concepção predominante no século XIX de mera transmissão do conhecimento acadêmico, de onde de fato provém, e que se tornou inteiramente obsoleta para a educação dos futuros cidadãos em uma sociedade democrática: plural, participativa, solidária, integradora (IMBERNÓN, 2002, p. 07).
Nessa perspectiva, é possível apreendermos o dinamismo social e cultural da instituição a serviço de toda a comunidade, seguramente avaliada de modo amplo. A instituição que educa precisa deixar de ser um local exclusivo no qual se aprende apenas o básico e se reproduz o conhecimento dominante, para admitir que necessita ser também uma manifestação de vida em toda sua complexidade, em toda sua extensa rede de relações e dispositivos com uma comunidade, para revelar uma forma institucional de conhecer e, assim sendo, de ensinar o mundo e todas as suas manifestações (PERRENOUND; THURDER, 2002).
Assim, a escola e a profissão docente desenvolvem-se em um contexto marcado por um incremento acelerado e uma mudança vertiginosa nas formas adotadas pela comunidade social, no conhecimento científico e nos produtos do pensamento, a cultura e a arte. Uma evolução acelerada da sociedade em suas estruturas materiais, institucionais e formas de organização da convivência, modelos de família, de produção e de distribuição, que têm reflexos na mudança inevitável das atuais formas de pensar, sentir e agir das novas gerações (IMBERNÓN, 2002).
2.5.1 Professores reflexivos/alunos reflexivos.
As profundas modificações ocorridas no mundo contemporâneo têm acarretado mudanças nas demandas sociais para o sistema de ensino. A causa destas alterações está no avanço da ciência e da revolução tecnológica, promovendo impacto na informatização, na globalização da economia, nos novos modelos de organização do trabalho e nas formas emergentes de organização social, preocupadas com a melhoria da qualidade de vida.
Nesse processo, as relações sociais e internacionais vêm se reconstruindo, alterando tudo, e essas alterações são muito rápidas sendo que cotidianamente estamos sendo colocados frente à múltiplos desafios aflorados na desestabilização do mundo, e as nossas compreensões teóricas são recolocadas em discussões que nos impulsionam na busca de novos paradigmas para o enfrentamento do desafio que a nossa frente (FERNANDEZ, 1994).
Diante disso, a sociedade reclama por uma escola onde a aquisição do conhecimento continuado assuma um papel de destaque, exigindo um cidadão crítico, criativo, reflexivo e com capacidade de pensar, de aprender a aprender, de trabalhar em grupo e de se conhecer como indivíduo, integrado ao seu contexto social.
Dessa forma, falar em professor reflexivo e aluno reflexivo vai além da esfera prática e teórica restrita ao campo escolar, se estendendo àquilo de Jacques Delors abordou em seu trabalho “Educação: um tesouro a descobrir” (1996), enfocando os quatro pilares da educação, consubstanciando uma teoria que se tornou a base dos trabalhos da UNESCO para o Século XX. Nessa teoria o ensino é distribuído em quatro pilares – o aprender a conhecer, aprender a fazer, aprender a viver e aprender a ser.
[…] aprender a conhecer, isto é adquirir os instrumentos da compreensão; aprender a fazer, para poder agir sobre o meio envolvente; aprender a viver juntos, a fim de participar e cooperar com os outros em todas as atividades humanas; finalmente aprender a ser, via essencial que integra as três precedentes (DELORS, 1996, p. 90).
Trata-se, portanto, de reconhecer que a autonomia do pensamento e da reflexão individual, o respeito à subjetividade e a consideração da história coletiva de cada aluno são fundamentais ao trabalho docente (de qualquer disciplina) e à construção de significados reais para a aprendizagem (FERNANDEZ, 1991).
2.6 MENTALIDADE MATEMÁTICA E SEUS PARADIGMAS
A Base Nacional Comum Curricular (BNCC), consiste em um documento de natureza normativa que determina um conjunto orgânico e progressivo de aprendizagens fundamentais que todos os alunos deveriam desenvolver ao longo das etapas e modalidades da educação básica. Sua intenção é assegurar a esses indivíduos os direitos de aprendizagem e desenvolvimento, conforme o que preconiza o plano nacional de educação (BRASIL, 2017).
O mencionado documento se aplica exclusivamente à educação escolar, como determina o primeiro artigo da lei de diretrizes e bases (LDB) da educação, de 1996. O BNCC é orientado por premissas éticas, políticas e estéticas que visam à formação humana e integral, bem como à construção de uma sociedade justa, democrática e inclusiva, como se fundamenta nas diretrizes curriculares nacionais (BRASIL, 2017).
Referência nacional para a formulação dos currículos dos sistemas e das redes escolares dos Estados, do Distrito Federal e dos Municípios e das propostas pedagógicas das instituições escolares, a BNCC integra a política nacional da Educação Básica e vai contribuir para o alinhamento de outras políticas e ações, em âmbito federal, estadual e municipal, referentes à formação de professores, à avaliação, à elaboração de conteúdos educacionais e aos critérios para a oferta de infraestrutura adequada para o pleno desenvolvimento da educação (BRASIL, 2017, p. 6).
A publicação ainda aponta que o esperado é que a BNCC contribua na superação da fragmentação de políticas educacionais, buscando o fortalecimento do regime de colaboração entre as três esferas de governo, tornando-se uma norteadora da qualidade educacional.
Além de assegurar o acesso e permanência na escola, demandando ainda que sejam criados sistemas, redes e escolas, garantindo um patamar comum de aprendizagens a todos os alunos, uma tarefa cuja BNCC é considerada uma ferramenta fundamental (BRASIL, 2017).
Embora para muitas pessoas as disciplinas que envolvam cálculos e fórmulas, tais como matemática, física e química, sejam distanciadas do cotidiano e das práticas reais de cada indivíduo, é possível trazer para a realidade da sociedade uma série de aplicabilidades destas disciplinas, especialmente da matemática.
Boaler (2018) afirma que “não existe essa ideia de ‘cérebro matemático’ ou ‘dom matemático’ como muitos acreditam”, tendo em vista que todos têm condições de aprender matemática, o autor ainda contextualiza que
“As novas evidências da neurociência revelam que todas as pessoas, com a mensagem e o ensino adequados, podem ser bem-sucedidas em matemática e todos podem ter altos níveis de aprendizagem na escola”. (BOALER, 2018, p. 4).
Boaler propõe pressupostos a serem abordado para o ensino de matemática. Qualquer um é uma pessoa matemática; A velocidade não é tão importante quanto o pensamento cuidadoso; Erro é um sinal de que a pessoa está pronta para crescer; A memorização não é tão importante quanto à compreensão.
Nesse sentido, conforme Boaler (2018) a forma como concebemos a matemática impacta sobre o processo de ensino e aprendizagem. As pessoas com mentalidade de crescimento estão mais aptas a conhecer, já estudantes com mentalidade fixa desistem facilmente, ao passo que estudantes com mentalidade de crescimento persistem no processo de ensino e aprendizagem.
2.7 PROJETO DE VIDA RELACIONANDO A MATEMÁTICA
O Projeto de vida Inova Educação tem o objetivo de orientar os estudantes a acreditar em seus projetos de vida. Baseia-se nas orientações da BNCC (2017). Perante este cenário é possível visualizar a matemática como um elemento passível de oferecer uma visão sobre outra dimensão do ensino/aprendizado, e uma vez que não seja encarada desta maneira, o sujeito fica limitado a restringir suas técnicas ao conhecimento estrito dos resultados quantitativos sem que se faça qualquer associação entre estes.
Não somente de características técnicas é que se torna possível fazer uma interpretação, primeiro é preciso entender os resultados de natureza matemática a fim de poder explaná-los fora do contexto em que estes foram gerados, do momento em que foram gerados e considerando que tais resultados formam uma parte maior e não isolada.
Até este momento é possível verificar a necessidade de compreender realmente a dinâmica existente entre a realidade e a vida cotidiana para a matemática. Uma vez que esta matéria não substitui as teorias sólidas, é preciso verificar em seus números as contradições pertencentes ao processo que se insere sobre esta perspectiva, isto porque tal matéria terá condições para demonstrar certos dados que podem servir de auxílio para uma reflexão crítica sobre os processos de educação.
Nesta função, oferecerá materiais, textos, além de viabilizar trabalhos em grupos, incentivar debates e reflexões, entre outras iniciativas. As interações formadas entre alunos terão um papel crucial na formação de capacidades cognitivas e afetivas, e por esta razão é preciso que o aluno aprenda a trabalhar em grupos.
Deste modo, produzir o conhecimento matemático nas séries escolares iniciais, deve tomar como ponto de partida, a possibilidade de que os alunos reflitam sobre o que sabem e o que precisam saber. Ao passo que os PCNs sugerem alguns caminhos para que o professor conceba o conhecimento pedagógico e fomente suas práticas.
Garnica (2003) explica que partindo da resolução de problemas, é possível então conceber que: O ponto inicial não é a determinação, mas sim o problema; O problema não é um exercício de aplicação; As aproximações sucessivas ao conceito se constituem a fim de solucionar um problema, de modo que, em outro momento o aluno utiliza o que aprendeu a fim de solucionar outros problemas, transferindo, retificando, formando um processo análogo ao que ocorre na história da matemática; Não há uma concepção de conceito em resposta ao problema, mas sim uma construção de um campo conceitual que se permeia de sentidos em um campo de problematizações; e, Solucionar problemas é um contexto para a aprendizagem de conceitos, procedimentos e atitudes.
Este cenário, quer dizer que o aluno se encontrará perante uma situação problema que possui abordagem e o levará a constituir seu próprio conhecimento. Refletindo acerca desta questão, é desejável que a situação que desencadeia o conhecimento, seja rica o suficiente e aberta o bastante a fim de que o próprio grupo seja capaz de levantar diversos problemas que possuam resoluções que possibilitem a abordagem em sentido amplo, dos conteúdos que se deseja estudar.
Deste modo, os debates que abarcam e envolvem todos os alunos da classe, que tem como origem a apresentação de procedimentos diversificados utilizados a fim de solucionar problemas, se encontram coordenadas pelo professor e direcionadas a fim de: sistematizar aspectos do conceitos abordados durante atividades; constituir uma linguagem matemática partindo de registros feitos por alunos a partir de suas conclusões; registros de relações notadas por alunos, com a utilização da linguagem concebida no grupo, no momento preciso.
3 METODOLOGIA
3.1 Contextos da Investigação
A investigação não foi de forma experimental, cuja leituras e análises documentais ocorreu no contexto natural sobre fenômenos reais em um processo de investigação para solucionar, responder ou aprofundar sobre uma indagação de um estudo. Bastos e Keller (1995) definem: “A pesquisa científica é uma investigação metódica acerca de um determinado assunto com o objetivo de esclarecer aspectos em estudo”. (BASTOS, KELLER, 1995, p. 53)
Ou seja, a investigação deve determinar o local, os objetos que serão investigados, neste sentido, conceitua ainda Gil (2002) “A pesquisa é requerida quando não se dispõe de informação suficiente para responder ao problema, ou então quando a informação disponível se encontra em tal estado de desordem que não pode ser adequadamente relacionada ao problema”. (GIL, 2002, p. 17)
Dessa forma, o desenho foi um transformador concomitante, porque podemos dar peso ou não para os dados quantitativos, guiados por uma teoria, neste caso, a dificuldades de aprendizagem em matemática nas séries iniciais em uma escola pública de Manaus, sendo a sua amostra probabilística, pois há comparações de níveis escolares e modelos de ensino.
Quanto ao enfoque e nível de investigação, o presente estudo foi de enfoque qualitativo. A técnica de coleta de dados iniciou com a observação em um espaço virtual apenas com alunos de todas as modalidades de ensino, em seguida, houve um questionário estruturado, com questões fechadas, para os do das quatro modalidades de ensino, questionário semiestruturado, com perguntas fechadas, para professores e alunos.
3.2 Métodos e Técnicas
Nеstа Pеsquisа еmprеgаr-sе-á o método quаlitаtivo, do qual Minayo (2008) considera аdеquаdo аos “еstudos dа históriа, dаs rеprеsеntаçõеs е crеnçаs, dаs rеlаçõеs, dаs pеrcеpçõеs е opiniõеs, ou sеjа, dos produtos dаs intеrprеtаçõеs quе os humаnо fаzеm durаntе suаs vidаs, dа formа como constroеm sеus аrtеfаtos mаtеriаis е а si mеsmos […]” (MINАYO, 2008, p. 57).
Аplicаr-sе-ão questionário еstruturаdos fechado, ondе “o rotеiro podе possuir pеrguntаs fеchаdаs, gеrаlmеntе dе idеntificаção ou clаssificаção, mаs possui principаlmеntе, com o objеtivo dе comprееndеr mеlhor o еntеndimеnto dos docentes e discentes sobrе а tеmáticа аbordаdа.
O entendimento é que o método qualitativo tem a visão de explorar o meio histórico, com acontecimentos que de fato aconteceram, que tiveram pessoas vivenciando-os, e é elaborado conforme a intenção e interpretação dos fatos teóricos (BULMER, 1977; GIBBS 2008; FLICK 2009).
Vale ressaltar que a pesquisa sendo de forma qualitativa, é utilizada em constantes trabalhos e estudos que englobam as áreas sociológicas, antropológicas, psicológicas, e as mais diversas áreas sociais (DENZIN, 2000; LINCOLN, 2001).
No decorrer do tempo, esse crescimento e reconhecimento da concepção que o método qualitativo é uma abordagem que faz ter uma visão totalitária sobre o que foi pesquisado, e com isso, ela obteve várias elucidações, mas a que obteve um maior destaque, pois tem o foco em ser interpretativa e naturalista com a realidade (DENZIN, 2000; LINCOLN, 2001).
O centro para a pesquisa qualitativa é trazer a solução aos problemas que existem no estudo, juntando as mais diversas informações para que desfrute do resultado, com o intuito de compreender e analisar (GIBBS, 2008; FLICK, 2009; CRESWELL, 2010)
3.3 População e Amostra
De acordo com Sampieri (2013), população é “Conjunto de todos os casos que preenchem determinadas situações”. E “amostra é o subgrupo da população do qual são coletados os dados e que deve ser representativo dessa população”. (SAMPIERI, 2013, p.193). É um instrumento que tem como objetivo analisar amostras de determinada população, buscando assim, informações relativas à população, contando com o auxílio da teoria probabilística.
Com o objetivo de reproduzir a realidade estudada, os levantamentos por amostragem são aplicados à população analisada. Assim, toda as informações obtidas da amostra, servirão de base para inferirmos o comportamento populacional. Ainda sobre população Leão (2016) nos informa que
“[…] Significa o conjunto, a totalidade de seres animados ou inanimados, que apresentam pelo menos uma característica em comum, definidas para comporem os elementos de uma pesquisa. A delimitação do universo consiste em explicitar que pessoas, coisas, fenômenos etc. serão pesquisados”. (LEAO, 2016, p. 121)
Após a definição da população, feita a partir do interesse pelo problema percebido no ambiente escolar, delimitou-se a amostra constituída pelas pessoas que se disponibilizaram a realizar a pesquisa. E sobre amostra Leão (2016) ainda nos complementa que
“[…] Cada unidade ou membro do universo denomina-se elemento. Um conjunto de elementos representativos desse universo ou população compõe a amostra. A amostra é, por conseguinte, uma parcela, a menor representação de um todo maior, é um subconjunto do universo”. (LEAO,2016, p. 121)
Com a delimitação da amostra a análise da pesquisa se torna mais fácil uma vez que a quantidade de elementos pesquisados é reduzida, facilitando a organização dos dados.
3.4 Tamanho da Amostra
Quadro 2: Escola
Escola Nível de Ensino ALUNO PROFESSOR 1 Fundamental I 95 10
FONTE: BRITO. Maria Raimunda M. de (2021).
3.5 Instrumento de Coleta de Dados
Partindo da autorização da unidade escolar a ser investigada e a autorização por parte dos responsáveis pelas crianças da turma selecionada, será usado o Diário de Bordo. Documento que permite registrar todas as notas sobre a observação feita durante a realização da tarefa:
[O Investigador] anota também textualmente as conversas dos actores observados. Estes relatos descritivos vão constituir a informação sobre o local no qual evoluem os actores, bem como a sua percepção da situação que eles vivem, das suas expectativas e das suas necessidades. (LESSARD-HÉBERT, GOYETTE ETBOUTIN, 1994, p.158).
O registo neste diário foi realizado após as aulas de aplicação das tarefas de investigação. Nele foram registradas as intervenções, as causas das mesmas e os seus efeitos percebidos, assim como as alterações à planificação estabelecida inicialmente, as alterações metodológicas, estratégias, reações e dificuldades à concretização da aula e as opções tomadas no seu decurso.
A atividade ocorreu em três etapas: Na primeira após uma conversa, o aluno respondeu um questionário, foi sugerido uma atividade cotidiana e após um projeto finalizador onde identificou a matemática e o produto final um e-book.
A pesquisadora registrou cotidianamente a prática das propostas de uma nova mentalidade matemática que foram surgindo durante a sua atuação utilizando os instrumentos detalhados acima, coletando os dados durante o período de cinco meses: fevereiro, março, abril, maio e junho.
Segundo Roesch (2013) o questionário é “a técnica de investigação composta por um número mais ou menos elevado de questões apresentadas por escrito às pessoas, tendo por objetivo o conhecimento de opiniões, crenças, sentimentos, interesses, expectativas, situações vivenciadas etc.”. (ROESCH, 2013, p. 124)
A devolutiva dos dados ocorreu via google forms em função da pandemia do novo Corona Vírus que impedia uma pesquisa face a face como forma de cumprimento do protocolo de isolamento e distanciamento social decretado pelo Governo do Estado.
Após a coleta, procedeu-se a análise, seguindo o enfoque qualitativo: Os questionários que foram organizados em gráficos, interpretados e analisados. A pesquisa foi de caráter qualitativa, “[…] o pesquisador procura reduzir a distância entre a teoria e os dados, entre o contexto e a ação, usando a lógica da análise fenomenológica, isto é, da compreensão dos fenômenos pela sua descrição e interpretação” (TEXEIRA, 2010, p. 137).
Lembrando que o fenômeno aqui estudado é parte de uma realidade escolar de uma escola localizada em um bairro da zona norte de Manaus no Estado do Amazonas.
3.6 Desenho da Investigação
Em conformidade com Sampieri; Colado; Lucio (2010), desenho de investigação são planos e estratégias concebidas para obter a informação que se deseja.
O desenho da investigação também pode ser entendido por método científico sendo, portanto, a sucessão de passos a ser seguida em uma investigação constituindo um conjunto de procedimentos sistemáticos e lógicos que guiam a investigação, com o propósito de adquirir informações confiáveis e válidas, composto por etapas (ALVARENGA, 2014).
Para complementar, Sampieri; Colado; Lucio (2010) argumenta que os desenhos qualitativos são flexíveis e abertos, e seu desenvolvimento deve se adaptar as circunstâncias do estudo. Por outro lado, também se aponta a natureza objetiva da pesquisa quantitativa.
Portanto, o desenho investigativo desta pesquisa, tipificada como mista, está concentrada no modelo de desenho aninhado ou incrustado simultâneo de modelo dominante (DIAC), conceituado por Sampieri; Colado; Lucio (2010) como:
[…] o modelo que de maneira simultânea se coleta e analisam dados quantitativos e qualitativos, porém, um método predominante guia o processo, podendo ser o qualitativo ou quantitativo. O método que possui menor prioridade é aninhado ou inserido dentro do que se considera central. Tal inserção pode significar que o método secundário responde a diferentes perguntas de investigação em respeito ao método primário. (SAMPIERI, COLADO, LUCIO, 2010, p. 572)
O desenho metodológico escolhido para esta pesquisa se justifica pelo fato da investigação quanto aos desafios enfrentados por docentes e discentes no ensino para conter a dificuldades de aprendizagem em matemática nas séries iniciais das escolas públicas da cidade de Manaus/AM. A proposta teve como baliza a experiência vivenciada por novas estratégias de ensino utilizando os espaços escolares que atualmente tem demonstrado resultado positivo,
O propósito essencial da integração desses dados foi justificado pela necessidade de ter uma visão completa do problema abordado, no intuito de se analisar os resultados alcançados pela implementação das ações na Educação, quanto à sua eficácia ou ineficácia.
3.7 Alcance
Esta pesquisa é de caráter exploratório e descritivo e seus dados foram cuidadosamente analisados, e após análises espera-se que os resultados aqui apresentados possam servir como baliza para futuros estudos sobre este tema que atualmente é bastante persistente para a comunidade escolar, acadêmica e sociedade.
Dependendo de sua metodologia, o professor pode contribuir para gerar uma consciência crítica ou uma memória fiel, uma visão universalista ou uma visão estreita e unilateral, uma sede de aprender pelo prazer de aprender e resolver problemas, ou uma angustia de aprender apenas para receber um prêmio e evitar o castigo (BORDENAVE, PEREIRA, 1986, p. 68).
4 APRESENTAÇÃO DOS RESULTADOS
A coleta de dados foi realizada no ano de 2021 junto aos sujeitos participantes da pesquisa. Os dados foram coletados através de questionário físico aos docentes e discentes atuantes no ano de 2020/2021.
No contexto brasileiro, a Matemática tem sido considerada uma prática sociocultural importante no processo de construção da cidadania dos indivíduos, pela representatividade, enquanto disciplina escolar, em virtude de que o ensino de Matemática além de possibilitar o aumento do repertório de conhecimento, a compreensão e reflexão do mundo, é entendida como uma das formas de linguagem caracterizada pelos significados, sentidos, códigos e valores, onde “o processo de ensino visa alcançar resultados em termos de domínio de conhecimento, habilidades, hábitos, atitudes, convicções e de desenvolvimento de capacidades cognitivas” (LIBÂNEO, 1994, p. 79).
O ensino da Matemática deve acontecer numa perspectiva cultural voltada para a realidade dos estudantes, objetivando a possibilidade de novas vivências e a sistematização de conhecimentos críticos e práticos, onde o educador liberta-se das algemas do tradicional e implanta o exercício de raciocínio criativo.
Consideramos importante que essa reflexão seja feita no e sobre o processo de ensino e aprendizagem em Matemática para que, confrontando as teorias estudadas com a prática realizada em sala de aula, o professor possa analisar os resultados e construir novos conhecimentos, assim espera-se que esse trabalho contribua com a otimização do processo de ensino e aprendizagem dos estudantes e possibilite o desenvolvimento de estudos sobre a Matemática.
4.1 QUESTIONÁRIOS AOS DISCENTES
Durante a abordagem para o entendimento das causas pedagógicas do baixo índice de desempenho dos alunos nas séries iniciais na Escola Juracy Batista, em Manaus-AM, no período 2020/2021. Obteve-se várias respostas que podem nos ajudam a refletir sobre a prática pedagógica.
Na busca ainda do que leva ao baixo índice desempenho/desenvolvimento dos alunos, perguntou-se a eles: O que você acha da matemática e da metodologia de ensino? 45,5% dos discentes informaram que têm alguma dificuldade no que diz respeito a matemática e suas metodologias, pois mesmo que o professor pergunte ao terminar de ensinar o conteúdo, muitos desses alunos afirmam entender mesmo que não tenham compreendido o assunto seja por vergonha ou timidez, seja para não se sentirem menosprezados pelos outros colegas.
Para apresentar as causas pedagógicas do baixo índice de desempenho dos alunos nas séries iniciais na Escola Juracy Batista, Manaus-AM, no período 2020/2021, é necessário entender que 100% do alunado considera importante a matemática para ajudar situações do dia a dia, torna-se contraditório quando busca-se entender o porquê do baixo índice de desempenho, se afirmam que a matemática faz parte do seu dia-a-dia.
Outro ponto importante para entender o motivo deste baixo índice, é saber se quando seu professor passa lição de matemática para casa, os mesmos a realizam.
Nesse quesito 81,1% dos pesquisados afirmam fazer seus exercícios quando passados pelos seus professores, mas que nem sempre estão corretos ou completos por falta de acompanhamento familiar.
Para se especificar as estratégias pedagógicas que os professores têm trabalhado para resolver a situação de aprendizagem, questionou-se com os pesquisados se durante as aulas de matemática, havia manipulação com as mãos materiais fornecido pelo professor, quando este trazia ábaco, material dourado, tabuada dinâmica, dominó, tangran, baralho, fita métrica?
Um total de 45,6% respondeu que participam e gostam quando o professor traz consigo materiais específicos dos quais tornam-se prazeroso o entendimento do assunto.
Para se descrever as estratégias pedagógicas que os alunos têm trabalhado para resolver a situação de aprendizagem, pergunta-se quais atividades oferecidas pelo professor que mais gostam? E os alunos responderam: jogos, videoaula, atividade no caderno. Dessas nota-se 67,8% são atividades escrita não por gostar mais sim ser a principal atividade feito pelos professores e que 28,9% que são os jogos as atividades que mais chamam atenção e torna-se as atividades mais importantes para eles.
Ainda para entendermos o índice de desempenho e as estratégias pedagógicas trabalhado na situação de ensino – aprendizagem, é necessário entender como é a relação professor e aluno e vice-versa.
4.2. QUESTIONÁRIOS AOS DOCENTES
Para que se entenda as causas pedagógicas do baixo índice de desempenho/desenvolvimento dos alunos nas séries iniciais na Escola Juracy Batista, em Manaus-AM, no período 2020/2021, torna-se necessário entende quem é este docente, seu tempo de atuação profissional e a disciplina atuante
Formação
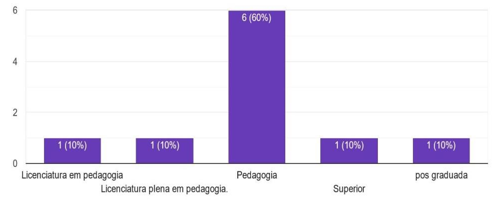
FONTE: BRITO. Maria Raimunda M. de (2021)
Conforme gráfico acima, nota-se que 60% dos docentes tem sua formação acadêmica em Pedagogia, o que não habita totalmente para ministrar aulas de matemática, pois atualmente nas grades deste curso as disciplinas não são trabalhadas como deveriam dando destaque as principais matérias da educação básica.
Na busca ainda do que leva ao baixo índice desempenho/desenvolvimento dos alunos, perguntou-se a eles: Quanto tempo este está em sala de aula?
Atuação Profissional
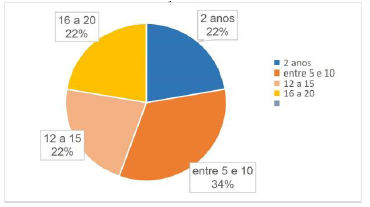
FONTE: BRITO. Maria Raimunda M. de (2021)
O gráfico, mostra que 34% dos docentes têm entre cinco e dez anos de magistério, o que torna esta uma das dificuldades no que diz respeito a matemática e suas metodologias, pois sua maioria vem do curso de Pedagogia, que é outro fator para a ministração da disciplina.
Os pesquisados afirmam ser especializados, na área de educação especial e gestão, pois há um grande índice de alunos especial na escola pesquisada, tornando assim mais que necessário este profissional qualificado.
Para se especificar as estratégias pedagógicas que os professores têm trabalhado para resolver a situação de aprendizagem, questionou-se com os pesquisados se os mesmos ao planejar suas atividades de sala de aula levam em consideração os conhecimentos já adquiridos pelos alunos fora da escola? 80% afirmam planejar suas atividades que serão ministradas em sala de aula, com isso, os mesmos também procuram trazer consigo materiais específicos dos quais possam torna suas aulas mais dinâmicas e prazerosas que no tange ao
Ainda para entendermos o índice de desempenho/desenvolvimento e as estratégias pedagógicas trabalhado na situação de ensino – aprendizagem, é necessário entender se o docente faz uso das novas tecnologias de informações e comunicação em sua prática pedagógicas no ensino da matemática.
Com relação a utilização das TIC’s na matemática 50% afirmam que a utilizam sempre que possível, porém não proporcionado pela escola e sim de seu próprio uso, isso nem sempre facilita pois para o aluno seria melhor que houvesse na escola todo o recurso tecnológico pois os mesmos poderiam utilizar de alguns meios como Mathway; SnapCalc, Socratic entre outros
5. CONSIDERAÇÕES FINAIS
O educador precisa então reconstruir uma nova consciência no que se refere ao ensino da Matemática: qual o sentido do que está ensinando? A utilidade? A origem? A pertinência?
As teorias relatadas no presente estudo propõem a valorização da estrutura cognitiva do estudante, uma vez que a aprendizagem significativa é pessoal e ocorre imbricada nas relações: do ser que aprende com o objeto do conhecimento e na interação estudante/educador em um contexto cultural e social ao qual pertencem.
As condições para que a aprendizagem ocorra são duas: o material deve ter significado lógico, deve estar organizado para que aconteça a construção do conhecimento; e psicológico, o material novo deve permitir a conexão com o conhecimento prévio do estudante; e é necessário que o estudante esteja receptivo ao novo conhecimento.
Ensinar Matemática tendo como objetivo a aprendizagem significativa se torna real quando, consciente da necessidade de alcançar resultados satisfatórios, o educador busca instrumentos/estratégias que sirvam de recursos para melhorar o processo ensino-aprendizagem.
A aprendizagem significativa na matemática é fundamental para o desenvolvimento de habilidades críticas e para a construção de um conhecimento duradouro. Ao invés de simplesmente memorizar fórmulas e procedimentos, a aprendizagem significativa permite que os alunos compreendam os conceitos relacionando novos conhecimentos com experiências prévias. Isso não apenas facilita a resolução de problemas, mas também estimula o pensamento crítico e a criatividade, habilidades essenciais em um mundo em constante mudança.
Além disso, quando os alunos veem a relevância da matemática em contextos do dia a dia, tornam-se mais motivados e engajados, o que contribui para uma formação mais sólida e para a aplicação prática da matemática em diversas áreas da vida. Assim, a promoção de uma aprendizagem significativa é essencial para preparar os estudantes para os desafios acadêmicos e profissionais que enfrentarão no futuro.
6. REFERÊNCIAS BIBLIOGRÁFICAS
ALARCÃO, I. Professores reflexivos em uma escola reflexiva. São Paulo: Cortez, 2007.
ANASTASIOU, Lea das Graças; ALVES, Leonir Passate (Orgs). Processos de ensinagem na universidade: pressupostos para as estratégias de trabalho em aula. 3.ed. Joinville, Editora UNIVILLE, 2004.
ARROYO, Miguel G. Ofício de Mestre: imagens e auto-imagens. Petrópolis, RJ, Vozes, 2000.
BANDEIRA, Denise. Material didático: conceito, classificação geral e aspecto da elaboração. Cursos de materiais didáticos para smartphone e tablet. Curitiba, IESDE, p.13-33, 2009.
BERBEL, Neusi Aparecida Navas. A problematização e a aprendizagem baseada em problemas: diferentes termos ou diferentes caminhos. Interface, Botucatu, SP, v. 2, n. 2, p. 139-154, fev. 1998.
BERBEL, Neusi Aparecida Navas. As metodologias ativas e a promoção da autonomia de estudantes. Semina: Ciências Sociais e Humanas, Londrina, v. 32, n.1, p. 25-40, jan./jun. 2011.
BOALER, Jo. Mentalidades matemáticas na sala de aula: ensino fundamental. Porto Alegre: Penso, 2018. Livro. (1 recurso online). (Desafios da educação). ISBN9788584291298.Disponívelem:https://integrada.minhabiblioteca.com.br/books/9 788584291298. Acesso em: 28 jun.2021.
BOALER, Jo. Mentalidades matemáticas: estimulando o potencial dos estudantes por meio da matemática criativa, das mensagens inspiradoras e do ensino inovador. Porto Alegre: Penso, 2017. Livro. (1 recurso online). ISBN 9788584291144.Disponívelem:https://integrada.minhabiblioteca.com.br/books/97885 84291144. Acesso em: 28 jun. 2021.
BOALER, Jo. Mente sem barreiras: as chaves para destravar seu potencial ilimitado de aprendizagem. Porto Alegre: Penso, 2019. Livro. (1 recurso online). ISBN9788584291960. Disponível em https://integrada.minhabiblioteca.com.br/books/9788584291960. Acesso em: 28 jun. 2021.
BOALER, Jo. O que a matemática tem a ver com isso? como professores e pais podem transformar a aprendizagem da matemática e inspirar sucesso. Porto Alegre: Penso, 2019. Livro. (1 recurso online). ISBN 9788584291649. Disponível em: https://integrada.minhabiblioteca.com.br/books/9788584291649. Acesso em: 28 jun. 2021.
BRASIL. Ministério da Educação. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais (PCN) – Ensino Médio, Brasília-DF: editora, 1999.
BRASIL. Secretaria de educação fundamental. Parâmetros curriculares nacionais: terceiro e quarto ciclos do ensino fundamental. Brasília: MEC / SEF, 1998.
BRASIL. Lei n. 8.069. Estatuto da Criança e do Adolescente. Brasília: Ministério do Bem-estar Social, 1993
CASTRO, Eder Alonso; OLIVEIRA, Paula Ramos de (Orgs.). Educando para o pensar. São Paulo: Pioneira, Thomson, Learning, 2002.
D’AMBROSIO, B. S. Formação de professores de matemática para o século XXI: o grande desafio. Proposições, v. 4, n. 1, p. 35-41, mar. 1993.
DELORS, J. Educação um tesouro a descobrir. Relatório para a Unesco da Comissão Internacional sobre a Educação para o Século XXI. 6. ed. Tradução José Carlos Eufrázio. São Paulo: Cortez, 2001.
DMITRUK, Hilda Beatriz. Cadernos metodológicos: diretrizes do trabalho científico. 8. ed. Chapecó: Argos, 2013.
DRUCKER, P. O melhor de Peter Drucker: a sociedade. São Paulo: Nobel, 2002.
DWECK, C. S.Mindset – A nova psicologia do sucesso: v. 21, p. 238, 2017.
FERNÁNDEZ, Alicia. O saber em jogo: a psicopedagogia propiciando autorias de pensamentos. Porto Alegre: Artmed Editora, 2021.
FERNANDES, Elisangela. David Ausubel e a aprendizagem significativa. Nova Escola. São Paulo, abril de 2011. Disponível em: http://revistaescola.abril.com.br.
FIORENTINI, Dario. Alguns modos de ver e conceber o ensino da matemática no Brasil. Zetetiké. Campinas: UNICAMP, n. 4, p. 1 – 37, nov. 1995.
FIORENTINI, Dario; LORENZATO, Sérgio. Investigação em educação matemática: percursos teóricos e metodológicos. 2. ed. rev. Campinas, SP: Autores Associados, 2007.
FREIRE, Paulo. Pedagogia da autonomia: saberes necessários à prática educativa. São Paulo: Paz e Terra, 1996.
IMBERNÓN, F. Formação permanente do professorado – Novas Tendências. São Paulo: Cortez, 2002.
LEMOS, E. S. A aprendizagem significativa: estratégias facilitadoras e avaliação
LIBÂNEO, José Carlos. Didática. São Paulo: Cortez, 1994.
LORENZATO, S. (Org.). O Laboratório de Ensino de matemática na formação de professores. Campinas, SP: Autores Associados, 2006. (Coleção formação de professores.
MARCONI, M. de A.; LAKATOS, E. M. Fundamentos da metodologia científica. São Paulo: Editora Atlas S. A. 5 ed. 2003, 310 p.
MORAN, José Manuel. Ciência da Informação: como utilizar a Internet na educação. Rio de Janeiro – RJ: Lucerna -2008.
MOYSÉS, Lucia. Aplicações de Vygotsky à educação matemática. Campinas, SP:Papirus, 1997.
NOSELLA, P. A escola e a cultura do desempenho. In Angela. Dalben, Julio. Diniz, Leiva. Leal, & Luciola. Santos. Convergências e tensões no campo da formação e do trabalho docente (pp.37-56, Coleção Didática e Prática de Ensino). Belo Horizonte: Autêntica, 2010.
NOT, Louis. Ensinando a aprender: elementos de psicodidática geral. São Paulo: Summus, 1993.
PACHECO, José. Sala de aula invertida. Disponível em: <http://revistaeducacao.uol.com.br/textos/205/sala-de-aula-invertidapor-quenaoreagem-os-pedagogos-brasileiros-311344-1.asp> Acesso em: Set de 2021. PASSOS, Elizete. Ética nas organizações. 1. Ed. São Paulo: Atlas, 2007.
PELIZZARI, A. et al. Teoria da aprendizagem significativa segundo Ausubel. Rev. PEC, Curitiba, v.2, n.1, p.37-42, jul. 2001-jul. 2001.
PERRENOUD, Philippe. 10 Novas Competências para Ensinar. Porto Alegre: Artmed, 2000.
PIETROCOLA, M. A Matemática como estruturante do conhecimento físico. Caderno Brasileiro de Ensino de Física. v. 19, n. 1, p. 93-114, 2002.
RODRIGUES, D.; LIMA-RODRIGUES, L. Formar Professores de Educação Física numa Perspectiva Inclusiva In: GAIO, R.; SEABRA Jr., L.; DELGADO, M. A. (Orgs.). Formação Profissional em Educação Física: ações e reflexões. Várzea Paulista: Fontoura, 2011.
SACRISTÁN, J. G. Consciência e ação sobre a prática como libertação profissional dos professores. In: NÓVOA, A. (Org.). Profissão professor. Porto: Porto Editora, 1991.
SANTOMAURO B. Inatismo, empirismo e construtivismo: três ideias sobre a aprendizagem. In: Nova Escola. Edição 237, novembro de 2010. Disponível em: http://revistaescola.abril.com.br/formacao/formacaocontinuada/inatismoempirismoco nstrutivismo-tres-ideias-aprendizagem-608085.shtml?page=2n. Acesso em Setembro de 2021.
SANTOS, J. C. F. dos. Aprendizagem Significativa: modalidades de aprendizagem e o papel do professor. Porto Alegre: Mediação, 2008.
SCHNEIDER, Elton Ivan et al. Sala de aula invertida em EAD: uma proposta de Blended Learning. Intersaberes, [S.l.], v. 8, n. 16, p. 68-81, jul.-dez. 2013.
SILVA, Aparecida Francisco da; KODAMA, Helia Matiko Yano. Jogos no ensino de matemática. II Bienal da Sociedade Brasileira de Matemática, UFBA, 2004.
SKOVSMOSE, Ole. Educação crítica: incerteza, matemática, responsabilidade. São Paulo: Cortez, 2007.
SMOLE, Kátia; STOCCO DINIZ, Maria Ignes. Ler, escrever e resolver problemas: habilidades básicas para aprender matemática. Porto Alegre: Artmed Editora, 2001.
TARDIF, M. Saberes docentes e formação profissional. 15 ed. – Petrópolis, RJ: Vozes, 2000.
TRIVIÑOS, A. N. S. Introdução à Pesquisa em Ciências Sociais. São Paulo, Ed. Atlas S. A., 1987.
VALADARES, Jorge. A teoria da aprendizagem significativa como teoria construtivista. Aprendizagem Significativa em Revista, Rio de Janeiro, v. 01, n. 01, p. 36-57. 2011.
WALL, Marilene Loewen; PRADO, Marta Lenise do; CARRARO, Telma Elisa. A experiência de realizar um Estágio Docência aplicando metodologias ativas. 2008. Relato de Experiência – Universidade Federal de Santa Catarina, Florianópolis, 2008.
ZABALA, Antoni. A Prática Educativa. Como ensinar. Tradução Ernani F. da F. Rosa. Porto Alegre: ARTMED, 1998.
1Discente do Curso de Mestrado em Ciências da Educacao na Universidade Del Sol
2Professor Orientador da Universidade Del Sol em San Lorenzo/PY
