CARDIO JUNCTION: COMPUTATIONAL TOOL IMPLEMENTED FROM A MODEL OF COMPARTMENTS FOR THE RAT VENTRICULAR MYOCYTE
REGISTRO DOI: 10.5281/zenodo.7934209
Ricardo Agostinho de Rezende Junior1
Daniel Gustavo Goroso2
José Luis Puglisi3
Robson Rodrigues da Silva4
RESUMO
O cálcio (Ca2+), um dos íons envolvidos no complexo funcionamento do coração, é também considerado o mais importante pelo fato de ser o ativador direto dos miofilamentos que causam a contração. O seu fluxo irregular é uma das principais causas de arritmias cardíacas e disfunção contráctil. Nesse sentido, a formulação de novos modelos matemáticos e computacionais de miócito ventricular de mamífero aporta ferramentas importantes para entender os mecanismos de liberação de Ca2+ e analisar de forma detalhada as causas dos diversos tipos de arritmia cardíaca. O objetivo desse trabalho é apresentar um modelo de compartimentos para o miócito ventricular de rato, fundamentado no modelo de Shannon et al. (2004) e a partir desse modelo desenvolver a ferramenta computacional Cardio Junction que pode ser acessada no endereço: https://cardiolab.ifspguarulhos.edu.br/, uma plataforma online para simulação, desenvolvida na linguagem de programação Python. Para avaliação da plataforma foram realizados testes de validação do modelo para o transiente de Ca2+ e força de contração, além de simulações envolvendo a aplicação do fármaco (SS-68). O modelo e a aplicação WEB foram ajustados para uma melhor reprodução do fenômeno em estudo, e o sistema deve contribuir com as pesquisas dessa área bem como servir de base para complementar o ensino dos princípios básicos da eletrofisiologia cardíaca.
Palavras-chave: Ferramenta Computacional. Python.
ABSTRACT
The calcium (Ca2+), one of the ions involved in the complex functioning of the heart, it is also considered the most important due to its role in activation of the myofilaments, resulting in contraction. The irregular flow of calcium is one of the main causes of cardiac arrhythmias and contractile dysfunction. In this sense, new mathematical and computational models of mammalian ventricular myocytes formulations have become an important tool for understand the mechanisms of Ca2+ release and to analyze in detail the causes of different types of cardiac arrhythmia. The objective of this work is to apply a rat ventricular myocyte compartment model, proposed by Shannon et al. 2004, on an implementation, using the computational tool Cardio Junction (https://cardiolab.ifspguarulhos.edu.br/), which consists of an online simulation platform, developed using of Python programming language. To evaluate the platform, model validation tests were performed for the Ca2+ transient and contraction force, in addition to simulations involving the application of drugs (SS-68). The WEB model and application were adjusted for a better reproduction of the phenomenon under study, the system should contribute to research in this area as well as serve as a basis to complement the teaching of the basic principles of cardiac electrophysiology.
Keywords: Computational Tool. Python.
1 INTRODUÇÃO
Segundo dados da Organização Mundial de Saúde (OPAS, 2019), o número de casos de doenças cardiovasculares (DCV) cresceu, e essas acarretaram cerca de 17,7 milhões de óbitos em 2017, representando mais de 30% de todos os casos de mortes no mundo. Por outro lado, nos países subdesenvolvidos e emergentes, a situação é ainda mais grave, pois esse percentual é de 75%, o que eleva o patamar de mortes em decorrência dessas doenças.
Nesse contexto, a formulação de modelos matemáticos e computacionais da eletrofisiologia cardíaca e a comparação entre os resultados das simulações com os experimentos “in vitro” ou “in vivo” já foram capazes de produzir importantes informações, não apenas sobre os mecanismos da dinâmica de cálcio (Ca2+) intracelular, mas principalmente sobre as características e funções das correntes iônicas e sua influência em problemas relacionados com a força de contração e arritmias cardíacas (MIRAMS et al., 2012).
Existem na literatura alguns modelos matemáticos que descreveram a eletrofisiologia e a contração do miócito ventricular, tendo como destaque o modelo desenvolvido por Shannon et al. (2004) que implementa as correntes iônicas de sódio (Na+), potássio (K+) e Ca2+ para o miócito ventricular de coelho. Já o modelo desenvolvido por Negroni e Lascano (2008) permite o cálculo da força de contração no miócito ventricular em função do curso temporal da concentração de Ca2+. Outro modelo de grande destaque é o que descreve a eletrofisiologia para o miócito ventricular de camundongos, desenvolvido por Bondarenko et al. (2004) e que em 2013 foi atualizado com a implementação do modelo de contração proposto por Rice et al. (1999).
O objetivo desse projeto trabalho é apresentar um modelo de compartimentos para o miócito ventricular de rato, fundamentado no modelo de Shannon et al. (2004) e a partir desse modelo desenvolver a ferramenta computacional, Cardio Junction, uma plataforma online para simulação, desenvolvida na linguagem de programação Python. Para avaliação da plataforma foram realizados testes de validação do modelo para o transiente de Ca2+ e força de contração, além de simulações envolvendo a aplicação do fármaco (SS-68). O modelo final é descrito por um sistema de 113 equações diferenciais, acopladas, resolvidas utilizando-se o método de Runge-Kutta de 4a ordem com passo de integração de 10−5 segundos. Toda interface e arquitetura da plataforma foi desenvolvida utilizando a linguagem de programação Python com a biblioteca “SciPy”, desenvolvida com o objetivo de ser utilizado nas aplicações cientificas. Os gráficos foram desenvolvidos utilizando “Java Script”. Para acessar a plataforma é preciso realizar um breve cadastro no endereço <http://cardiolab.ifspguarulhos.edu.br/>.
2 DESENVOLVIMENTO
2.1 Implementações do modelo matemático
A literatura base para o desenvolvimento da pesquisa foi o modelo de compartimentos apresentado por Shannon et al. (2004). A partir desse modelo foram realizadas as seguintes modificações e atualizações:
a)Implementação do canal de vazamento do Retículo Sarcoplasmático (RS) em direção ao citosol;
b)Implementação do canal de Ca2+ do tipo L segundo modelo proposto por Mahajan et al. (2008);
c)Implementação dos canais de Na+ e K+ (IKur e IKss) segundo modelo proposto por Winslow et al. (2004);
d)Implementação dos canais de K+ (Itof e Itos) segundo modelo proposto por Winslow et al. (2004);
e)Possibilidade de seleção dos principais canais Ca2+, Na+ e K+ segundo a modelagem proposta por Hodgkin e Huxley (HH) ou Modelos de Markov (MM);
f)Implementação do modelo de contração proposto por Negroni e Lascano (2008).
Nesse modelo, a concentração de Ca2+ livre no citosol é dada pela seguinte Equação Diferencial:
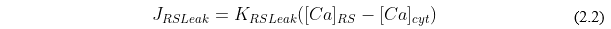
Já, a força de contração gerada pelas pontes cruzadas é fundamentada no modelo proposto por Negroni & Lascano (2008):
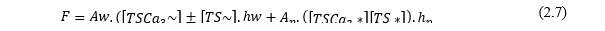
Sendo que Aw e Ap são, respectivamente, constantes elásticas para os estados de ligação fraca (weak) e forte (power) das pontes cruzadas. Já, hw e hp indicam o comprimento médio das pontes cruzadas nos seus respectivos estados.
A partir do novos modelo matemático, iniciou-se o desenvolvimento da ferramenta computacional Cardio Junction, uma plataforma online para simular o curso temporal das principais correntes iônicas e força contrátil no miócito ventricular de rato.
2.2 Implementações da ferramenta computacional
Para desenvolver a aplicação através de uma linguagem simples e apresentar o comportamento do sistema, onde é possível apresentar por uma perspectiva do usuário, conforme (WAZLAWICK, 2011), foi desenvolvido o diagrama de caso de uso (Figura 1), onde é possível observar uma descrição detalhada e estruturada sobre as principais funcionalidades da ferramenta.
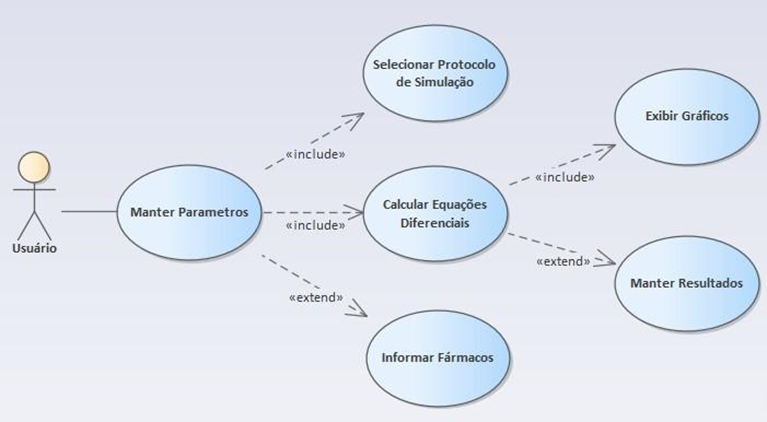
Figura 1 – Diagrama de Caso de Uso da Ferramenta.
O diagrama de atividades permite representar a aplicação esquematicamente de forma encadeada (WAZLAWICK, 2011). A Figura 2 apresenta o fluxo inicial da aplicação e como os módulos interagem com o usuário e entre si.
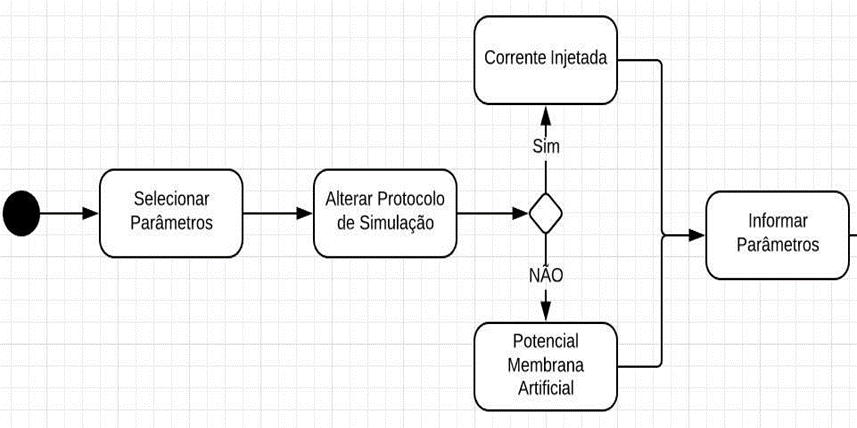
Figura 2 – Diagrama de atividades: início do fluxo
A Figura 3 apresenta o fluxo final da aplicação, onde pode-se observar a possibilidade da aplicação de fármacos.
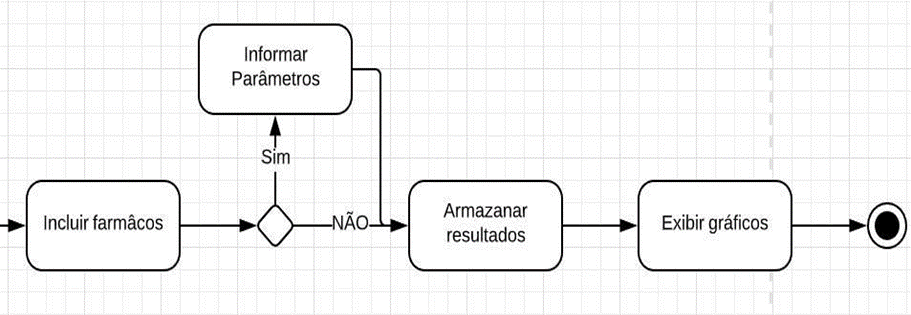
Figura 3 – Diagrama de atividades: final do fluxo.
O sistema foi desenvolvido através de uma plataforma Web (modelo cliente-servidor, apresentado na Figura 4), onde a comunicação é realizada através da Rede Mundial de Computadores, que pode ser acessado através de um navegador de internet, isto possibilita maior facilidade de interação com os usuários (MARINI, 2012).
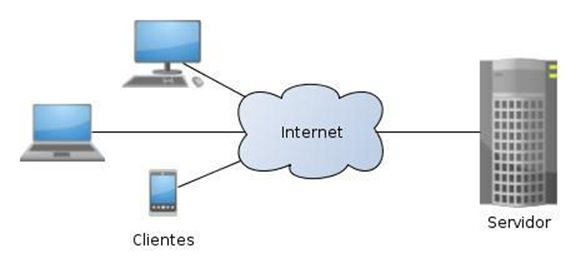
Figura 4 – Modelo Cliente Servidor na Internet.
Devido ao uso do modelo cliente/servidor a aplicação foi dividida em módulos para ter seu desenvolvimento plenamente integrado. Para a interação do usuário com o sistema foi utilizada a linguagem de marcação HTML (Hyper Text Markup Language) com a linguagem de estilo CSS (Folhas de Estilo em Cascata). O módulo de processamento do sistema foi desenvolvido com a linguagem de programação Python e com um arcabouço Flask. Os gráficos foram gerados com o uso da ferramenta Plotly, biblioteca de plotagem que permite criar gráficos interativos. A Figura 5 apresenta a arquitetura de desenvolvimento utilizada para esta aplicação.
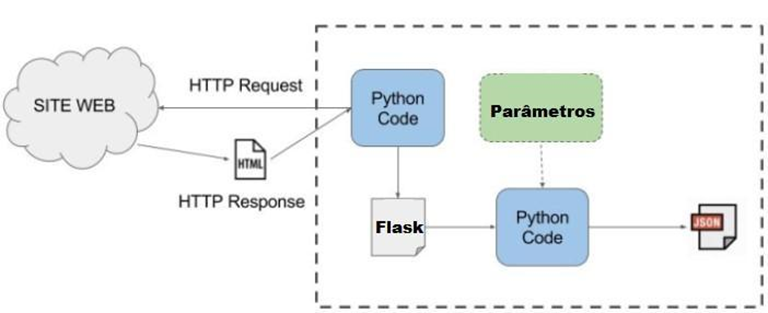
Figura 5 – Arquitetura da Aplicação.
A aplicação está hospedada em um servidor Web com a seguinte configuração: Processador Intel(R) Xeon(R) Silver 4114 CPU @ 2.20GHz – 20 core, memória RAM de 30GB e com capacidade de armazenamento de 6x2TB (raid 6).
2.3 VALIDAÇÃO DO MODELO
Nesta seção tem-se uma breve descrição da metodologia utilizada para a validação do modelo matemático. Dados experimentais, relativos ao transiente de Ca2+ e força de contração, reportados na literatura, foram transcritos a partir da ferramenta computacional Web Ploter Digitizer (https://apps.automeris.io/wpd/) onde foi possível gerar um arquivo *txt para extração das principais variáveis descritas nas Figuras 6 e 7 e que serão analisadas e comparadas posteriormente com os resultados das simulações.
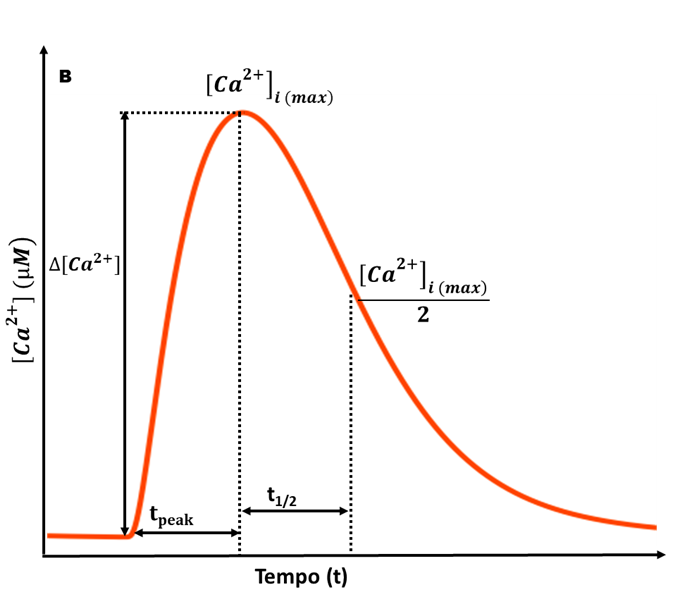
Figura 6 – Principais variáveis analisadas para o Transiente de Ca2+.
Fonte: (FILHO, 2020)
Legenda: [Ca2+](max) representa a maior concentração de Ca2+ observada na célula, [Ca2+](max)/2 representa quando que a concentração de Ca2+, após seu pico, estava na metade do ciclo, ∆[Ca2+] representa o valor entre o último momento da fase sistólica até o pico da concentração de Ca2+, o tpeak representa o tempo para alcançar o pico da concentração e o t1/2 é o momento em que alcança a metade do pico.
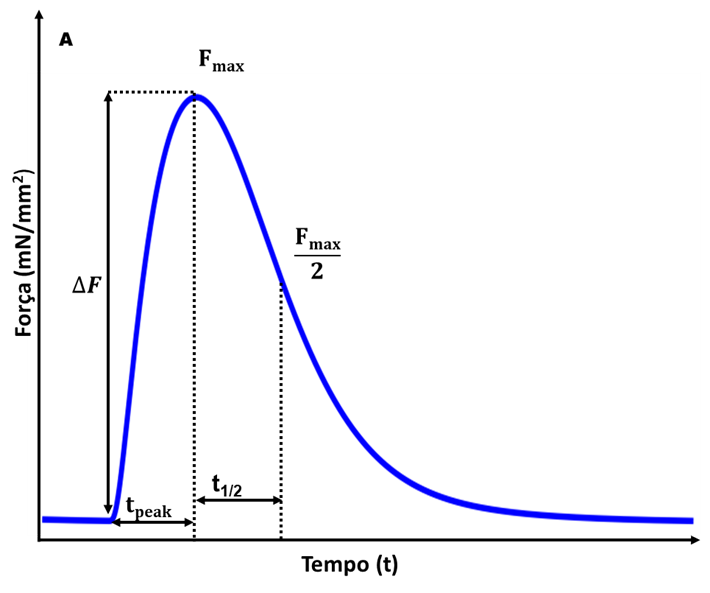
Figura 7 – Principais variáveis analisadas na Força de Contração.
Fonte: (FILHO, 2020)
Legenda: Fmax representa a força máxima de contração observada, Fmax/2 representa quando que a força de contração, após seu pico, estava na metade do ciclo da força, ∆F representa o valor entre a último momento da fase sistólica até o pico da força de contração, o tpeak representa o tempo para alcançar o pico da força de contração e o t1/2 é o momento em que alcança a metade do pico.
2.3.1 Dados experimentais para validação do transiente de Ca2+
A validação do transiente de Ca2+ foi obtida através da comparação dos resultados das simulações com dados experimentais obtidos por Jones et al. (1998), Gao et al. (1999), Kogler et al. (2001) e McCloskev et al. (2003) e reportados por Bondarenko et al. (2013) e ilustrados na Figura 8.
Os dados quantitativos referentes aos dados experimentais são apresentados na Tabela 1.
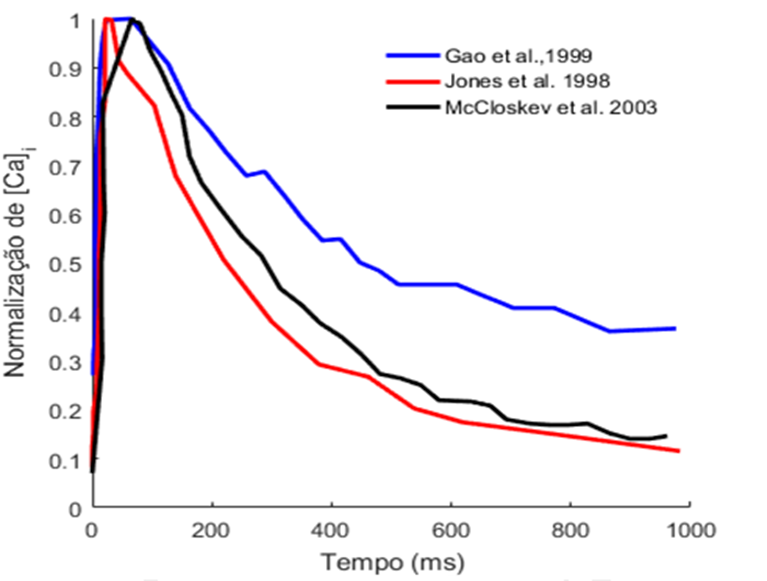
Figura 8 – Dados experimentais do transiente de Ca2+ (adaptado de Bondarenko et al. (2013))
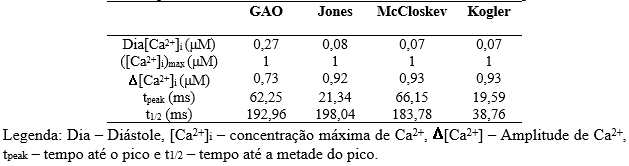
Tabela 1 – Dados quantitativos do transiente de Ca2+ extraídos dos dados experimentais
2.3.2 Dados experimentais para validação da força de contração
A validação da força de contração foi obtida através da comparação dos resultados das simulações com dados experimentais obtidos por Gao et al. (1999), Kogler et al. (2001), McCloskev et al. (2003) e Stuyvers et al. (2002). Esses dados foram reportados no artigo de Bondarenko et al. (2013) e estão ilustrados na Figura 10.

Figura 10 – Dados experimentais da força de contração (adaptado de Bondarenko et al. (2013))
A Tabela 2 apresenta os dados quantitativos dos dados experimentais ilustrados anteriormente.
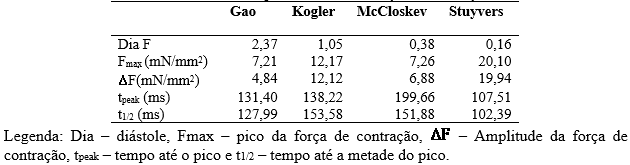
Tabela 2 – Dados quantitativos da Força de Contração
3 EXPERIMENTOS IN SILICO
Para testar a funcionalidade de aplicação de fármacos, proposta no modelo e na plataforma, o seguinte experimento “in silico” foi realizado:
3.1 Efeitos do fármaco SS-68 no transiente de Ca2+ e força de contração
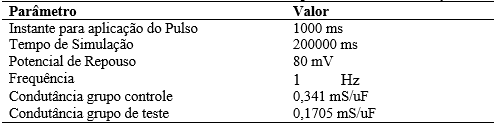
O fármaco SS-68 é do grupo dos antiarrítmicos, tem sido estudado com bons resultados pelo Institute of Physical and Organic Chemistry na Soyth Federal University da Russia (BOGUS, 2015). O estudo realizado por Leonardo (2019) implementou no modelo de Bondarenko et al. (2013) o fármaco SS-68 para verificar sua atuação nas correntes de Ca2+ e no Potencial de Ação (PA). Este fármaco inibe o fluxo do canal de Ca2+ do tipo L em 50%, isto é possível dimensionar a atuação da droga em teste computacional. Os protocolos de simulação utilizados para replicar a simulação descrita por Leonardo (2019) são apresentados na Tabela 3.
Tabela 3 – Parâmetros iniciais utilizados para realizar a simulação.
4 RESULTADOS
Nesta seção serão apresentados os principais resultados obtidos com o desenvolvimento dessa pesquisa.
4.1 NOVO MODELO MATEMÁTICO
A partir do método e equações descritas na seção 2, o novo modelo matemático é constituído de cento e treze (113) equações diferenciais acopladas e noventa e quatro (94) parâmetros biofísicos. O sistema de Equações Diferenciais foi resolvido pelo método de Runge-Kutta de 4a ordem, utilizando passo de integração de 10−5.
O novo modelo implementado possibilita a utilização de dois tipos de modelagem para os canais iônicos: a modelagem de Hodgkin-Huxley (HH), que descreve aberturas e fechamentos dos canais de Ca2+, Na+ e K+ e os modelos de Markov (MM), com base nas transições de estados dos canais. Além dos dois tipos de modelagem para os canais iônicos, o novo modelo proposto também passa contemplar a difusão do Ca2+ entre quatro compartimentos: o cleft (junção localizada entre o canal de Ca2+ do tipo L e os receptores RyRs); o espaço do subsarcomela; o citosol e RS. Esses compartimentos estão ilustrados na Figura 11.
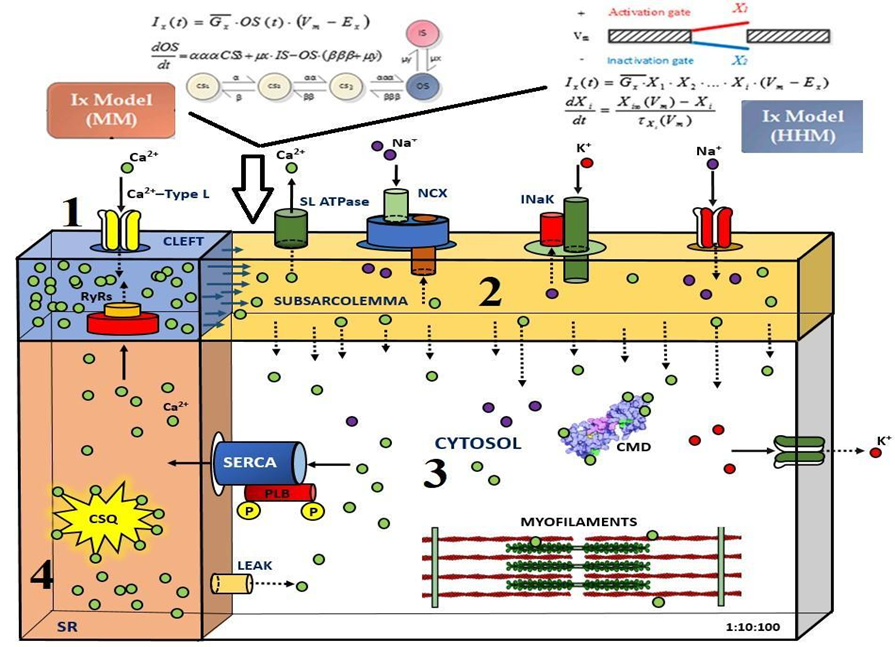
Figura 11 – Modelo de quatro compartimentos do miócito ventricular de rato.
Legenda: O modelo considera equações de HH e MM. 1 é o Cleft, 2 o subsarcolema, 3 o Citosol e 4 o RS.
Todas as equações e parâmetros utilizados no novo modelo proposto podem ser localizados no endereço: https://github.com/ricardoagostinho10/Doutorado/
4.2 O SIMULADOR CARDIO JUNCTION
A partir do modelo matemático descrito no capítulo anterior e utilizando as ferramentas computacionais descritas na seção 1.3.4, foi desenvolvido o sistema Cardio Junction. O sistema pode ser acessado (https://cardiolab.ifspguarulhos.edu.br/) de qualquer dispositivo conectado à internet, através de um navegador. O simulador, possui uma tela principal, Figura 12 que permite acesso a telas secundárias do programa.
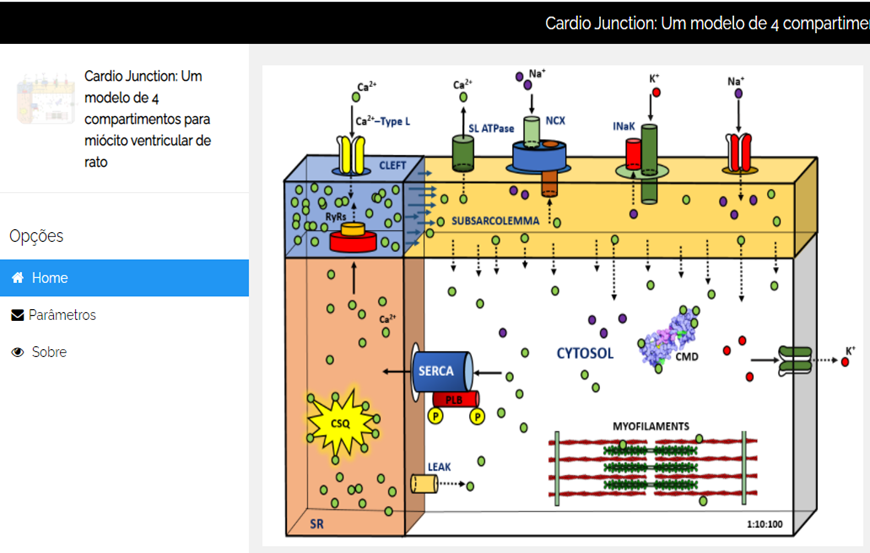
Figura 12 – Tela principal do simulador Cardio Junction.
A seguir tem-se uma apresentação das telas secundárias do simulador.
Na Figura 13 é possível acessar o tipo de modelagem para os principais canais iônicos, bem como alterar os valores de parâmetros relativos à aplicação de fármacos, protocolos iniciais para executar a simulação (corrente injetada ou PA artificial) e os parâmetros iniciais para executar uma simulação. Também é possível aceitar os valores que foram definidos previamente. Após isso, o usuário seleciona a opção “Executar” e neste momento o sistema passa a resolver o sistema de equações diferenciais acopladas e encaminhará para a tela de resultados que será apresentada no decorrer do capítulo.
Figura 13 – Tela para seleção de parâmetros e execução dos cálculos.
Na Figura 14 são apresentados os parâmetros gerais e que podem ser alterados pelo usuário. É possível a definição de qual modelo será aplicado para os diferentes canais iônicos, onde pode-se optar pelo MM ou HH (Figura 14 A). Na Figura 14 B é possível realizar a aplicação de fármacos, sempre considerando em termos percentuais e a simulação de cafeína.
Já na Figura 14 C é possível selecionar o protocolo de simulação, podendo ser o PA artificial ou injeção de corrente. Ao selecionar uma destas opções os parâmetros são ajustados para atender estes critérios. Na Figura 14 D pode-se informar parâmetros gerais para cada protocolo de simulação, inclusive o tempo de simulação.

Figura 14 – Interfaces secundárias do simulador.
Legenda: A) Tipo de modelagem para os canais iônicos; B) Aplicação de fármacos; C) Seleção do protocolo de simulação; D) Parâmetros de entrada.
Na Figura 15 apresentam as possíveis visualizações gráficas que foram divididas em 5 categorias. Ao selecionar uma das categorias o sistema exibirá todos os gráficos relacionados em um carrossel de imagens. Descreve a seguir as 5 categorias de gráficos que são passíveis de exibição:
Figura 15 – Interface para selecionar a visualização dos resultados.
A seguir temos uma breve descrição de cada categoria.

A Figura 16 ilustra a representação gráfica da Categoria 2.
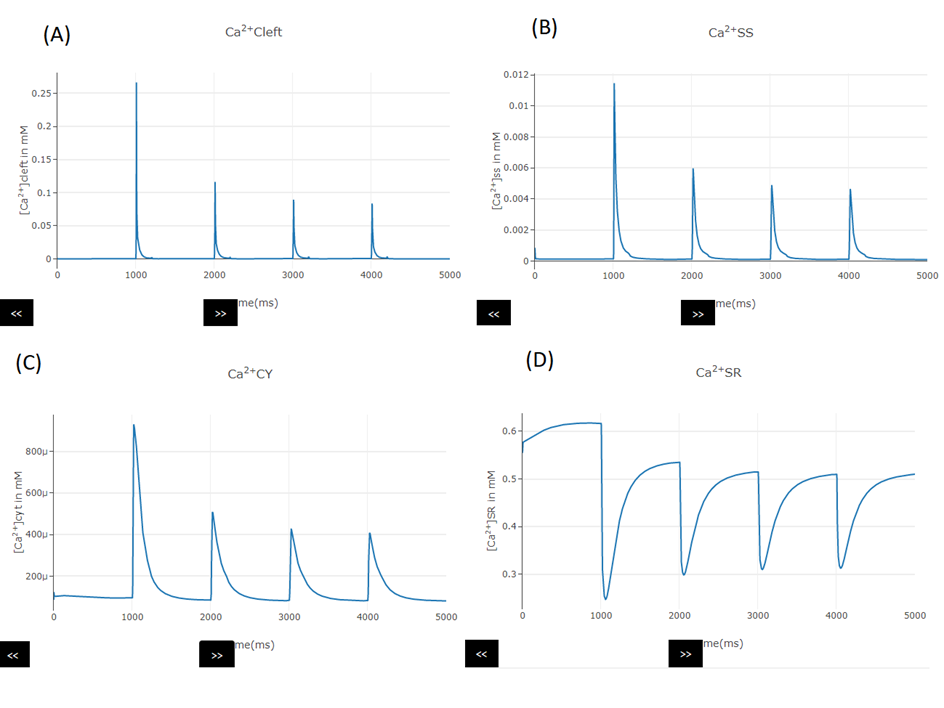
Figura 16 – Interface de visualização dos gráficos.
Fonte: (A) gráfico da concentração Ca2+ no cleft (B) gráfico da concentração de Ca2+ no SS. (C) gráfico da concentração Ca2+ no citosol e (D) concentração Ca2+ no RS.
Para verificar o tempo de resposta do servidor em relação ao protocolo selecionado e o tempo de simulação, foram realizados testes cujos resultados estão descritos na Tabela 4.
Tabela 4 – Tempo de resposta para simulações com Corrente Injetada (C.I) e Potencial da Membrana Artificial (P.A)

4.3 VALIDAÇÃO DO MODELO
4.3.1 Validação do transiente de Ca2+
Para validação do transiente de Ca2+ obtido com o novo modelo proposto, os resultados das simulações foram comparados com os dados experimentais descritos na seção 2.
O resultado da comparação é ilustrado na Figura 17 e os dados quantitativos dessa comparação estão descritos na Tabela 5.
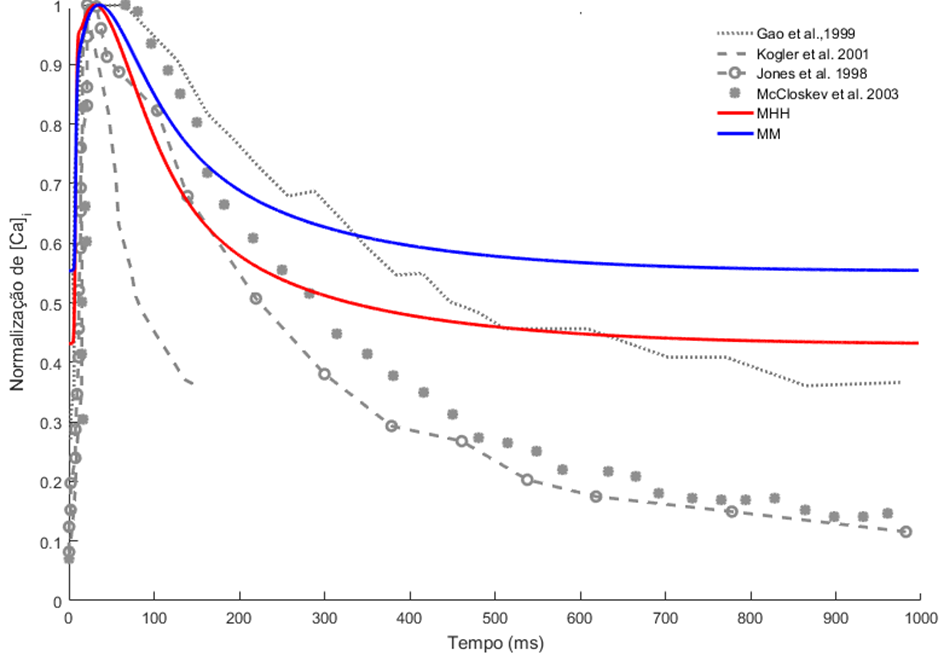
Figura 17 – Transiente de Ca2+: Simulação versus Experimentos
Legenda: MHH – Modelo de HH; MM – Modelo de Markov.
Tabela 5 – Transiente de Ca2+: simulação vs dados experimentais
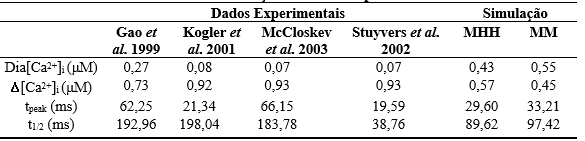
Legenda: MHH – Modelo de HH; MM – Modelo de Markov
Utilizando o novo modelo proposto e selecionando a modelagem de HH para os principais canais iônicos, quando comparamos o transiente de Ca2+ simulado com os dados experimentais obtemos os seguintes resultados: a maior diferença entre o valor diastólico ocorreu com os dados experimentais de McCloskev et al. 2003 e Stuyvers et al. 2002 (87,27%). Já a menor diferença foi obtida comparando a simulação com Gao et al. 1999 (50,91%). A maior diferença entre o valor da ∆[Ca2+]i ocorreu com os dados experimentais McCloskev et al. 2003 e Stuyvers et al. 2002 (51,61%) e a menor diferença foi obtida na comparação com o Gao et al. 1999 (38,36%). Para o tpeak a maior diferença ocorreu com os dados experimentais do McCloskev et al. 2003 (49,80%) e a menor diferença foi obtida com os dados do Kogler et al. 2001 (35,74%). Com relação ao t1/2 a maior diferença foi obtida Stuyvers et al. 2002 (60,21%) e a menor foi de McCloskev et al. 2003 (46,99%).
Já, selecionando a modelagem de MM para os principais canais iônicos, quando comparamos o transiente de Ca2+ simulado com os dados experimentais obtemos os seguintes resultados: a maior diferença entre o valor diastólico ocorreu com os dados experimentais de McCloskev et al. 2003 e Stuyvers et al. 2002 (83,72%). Já a menor diferença foi obtida comparando a simulação com Gao et al. 1999 (37,21%). A maior diferença entre o valor da ∆[Ca2+]i ocorreu com os dados experimentais McCloskev et al. 2003 e Stuyvers et al. 2002 (38,71%) e a menor diferença foi obtida na comparação com o Gao et al. 1999 (21,92%). Para o tpeak a maior diferença ocorreu com os dados experimentais do McCloskev et al. 2003 (55,25%) e a menor diferença foi obtida com os dados do Kogler et al. 2001 (27,91%). Com relação ao t1/2 a maior diferença foi obtida Stuyvers et al. 2002 (56,75%) e a menor foi de McCloskev et al. 2003 (51,24%).
4.3.2 Validação da força de contração
Para validação da força de contração obtido com o novo modelo proposto, os resultados das simulações foram comparados com os dados experimentais descritos na seção 2. O resultado da comparação é ilustrado na Figura 18 e os dados quantitativos dessa comparação estão descritos na Tabela 6.
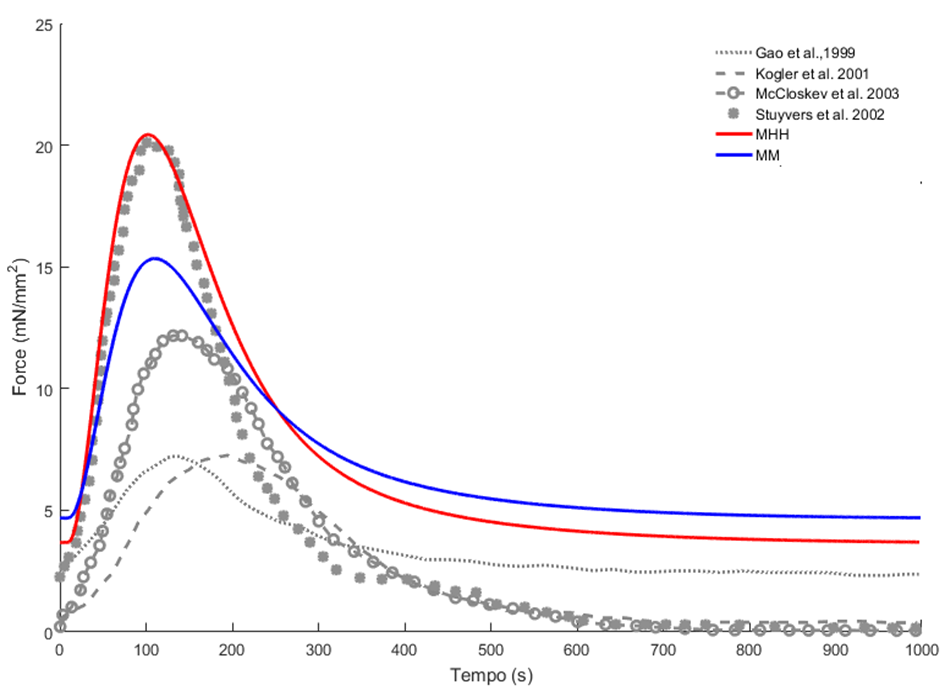
Figura 18 – Força de contração: simulação versus experimentos
Legenda: MHH – Modelo de HH; MM – Modelo de Markov.
Tabela 6 – Força de contração: simulação versus dados experimentais
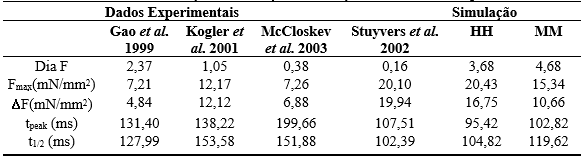
Utilizando o novo modelo proposto e selecionando a modelagem de HH para os principais canais iônicos, quando comparamos a força de contração simulado com os dados experimentais obtemos os seguintes resultados: a maior diferença entre o valor diastólico ocorreu com os dados experimentais de Stuyvers et al. 2002 (95,65%). Já a menor diferença foi obtida comparando a simulação com Gao et al. 1999 (35,60%). Para o pico da força a maior diferença ocorreu com os dados experimentais de Gao et al. 1999 (64,71%) e a menor foi com Stuyvers et al. 2002 (1,62%). Para a ∆F a maior diferençaocorreu com os dados experimentais de Gao et al. 1999 (71,10%) e a menor foi de Stuyvers et al. 2002 (16%). Para o tpeak a maior diferença ocorreu com os dados experimentais do McCloskev et al. 2003 (52,21%) e a menor diferença foi obtida com os dados do Stuyvers et al. 2002 (11,25%). Com relação ao t1/2 a maior diferença foi obtida Kogler et al. 2001 (31,75%) e a menor foi de Stuyvers et al. 2002 (2,32%).
Utilizando o novo modelo proposto e selecionando a modelagem de MM para os principais canais iônicos, quando comparamos a força de contração simulado com os dados experimentais obtemos os seguintes resultados: a maior diferença entre o valor diastólico ocorreu com os dados experimentais de Stuyvers et al. 2002 (96,58%). Já a menor diferença foi obtida comparando a simulação com Gao et al. 1999 (49,36%). Para o pico da força a maior diferença ocorreu com os dados experimentais de Gao et al. 1999 (53,00%) e a menor foi com Kogler et al. 2001 (20,66%). Para a amplitude da força a maior diferençaocorreu com os dados experimentais de Gao et al. 1999 (54,60%) e a menor foi de Kogler et al. 2001 (12,05%). Para o tpeak a maior diferença ocorreu com os dados experimentais do McCloskev et al. 2003 (48,50%) e a menor diferença foi obtida com os dados do Stuyvers et al. 2002 (11,25%). Com relação ao t1/2 a maior diferença foi obtida Kogler et al. 2001 (31,75%) e a menor foi de Stuyvers et al. 2002 (4,36%).
4.4 RESULTADOS DOS EXPERIMENTOS IN SILICO
4.4.1 Efeitos da aplicação do fármaco SS-68
Para aplicação do fármaco SS-68 os dados experimentais foram estabelecidos conforme a pesquisa do Leonardo (2019), os resultados das simulações foram comparados com os dados experimentais descritos na seção 2. As Figuras 19 e 20 apresentam os resultados das simulações da aplicação do fármaco SS-68 para cada um dos modelos. As Tabelas 7 e 8 apresentam os resultados da diástole, pico da força, amplitude da força, o pico do tempo e a metade do pico.
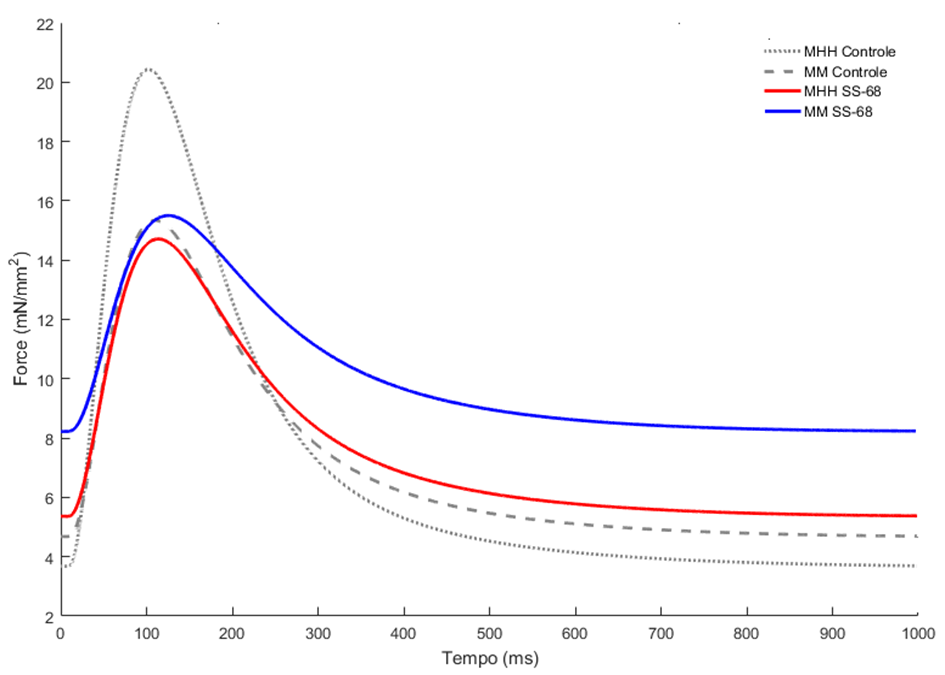
Figura 19 – Força de contratação: Controle versus aplicação do fármaco SS-68.
Legenda: MHH – Modelo HH; MM – Modelo de Markov.
Tabela 7 – Dados quantitativos da força de contração: de controle vesus SS-68
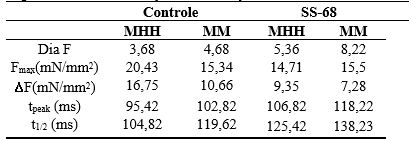
Legenda: MHH – Modelo HH; MM – Modelo de Markov.
Utilizando o novo modelo proposto e selecionando a modelagem de MM e MHH para os principais canais iônicos, quando comparamos a força de contração simulado com os dados experimentais obtemos os seguintes resultados: a maior diferença entre o valor diastólico ocorreu com os dados experimentais de MM (43,07%). Para o pico da força a maior diferença ocorreu com os dados experimentais de MHH (28%). Para a amplitude da força a maior diferençaocorreu com os dados experimentais MHH (44,18%). Para o tpeak a maior diferença ocorreu com os dados experimentais MM (13,03%). Com relação ao t1/2 a maior diferença foi obtida MHH (16,42%).
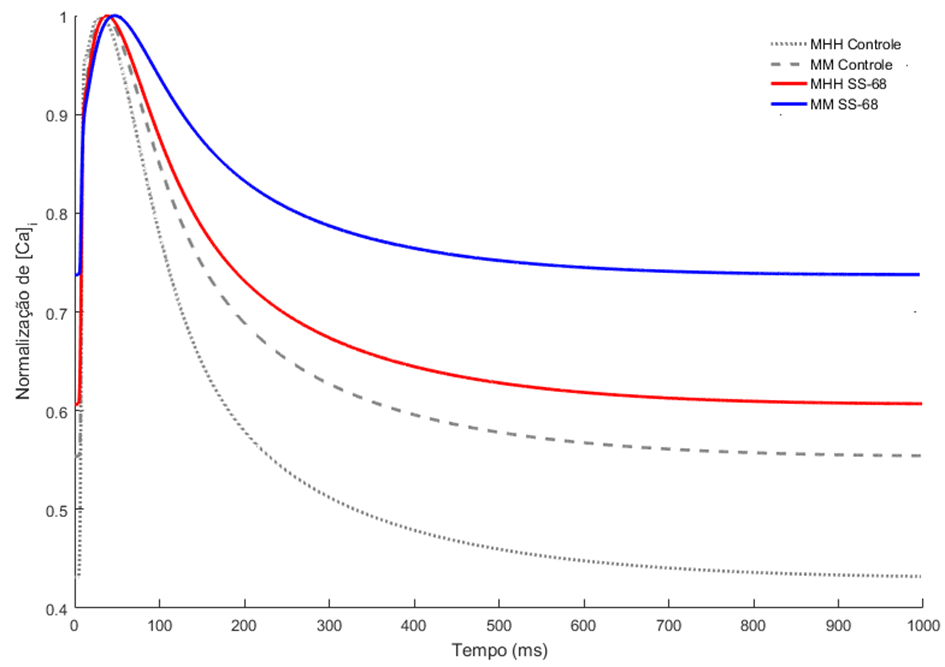
Figura 20 – Transiente de Ca2+ normalizado: controle versus SS-68.
Legenda: MHH – Modelo HH; MM – Modelo de Markov.
Tabela 8 – Dados quantitativos do transiente de Ca2+ normalizado: controle versus SS-68
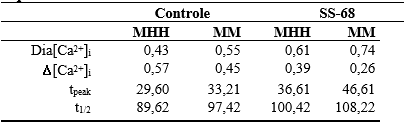
Legenda: MHH – Modelo HH; MM – Modelo de Markov.
Utilizando o novo modelo proposto e selecionando a modelagem de MM e MHH para os principais canais iônicos, quando comparamos o transiente de Ca2+ simulado com os dados experimentais obtemos os seguintes resultados: a maior diferença entre o valor diastólico ocorreu com os dados experimentais de MHH (29,51%). Para a amplitude a maior diferença ocorreu com os dados experimentais de MM (42,22%). Para o tpeak a maior diferença ocorreu com os dados experimentais MM (28,75%). Com relação ao t1/2 a maior diferença foi obtida MHH (10,75%).
5 DISCUSSÃO
Como resultado principal desse projeto de pesquisa temos a implementação de um modelo biofísico de miócito ventricular de rato para simulação, através de uma plataforma WEB e acessível de qualquer equipamento com navegador de acesso à internet. O sistema possui aspectos didáticos por permitir que estudantes simulem determinados fenômenos relacionados ao miócito ventricular de rato.
As telas do sistema estão detalhadas no capítulo 2.4, inclusive com o endereço de acesso (http://cardiolab.ifspguarulhos.edu.br/). No capítulo 3 são apresentados alguns resultados obtidos com o uso do simulador e a estrutura do modelo, mostrando os 4 compartimentos enfatizados neste trabalho.
A ferramenta computacional apresenta o complexo processo de acoplamento, excitação, contração e relaxamento do miócito cardíaco de rato implementando a divisão em 4 compartimentos: subsarcolema, citosol, cleft e RS.
As implementações realizadas no modelo de Shannon et al. (2004), como por exemplo a inserção do modelo de contração descrito por Negroni e Lascano (2008) e as modelagens dos canais iônicos possibilitando a seleção de modelos de Markov ou HH, permitem uma ampla opção para realização de experimentos “in silico” e a aplicação de fármacos.
5.1 NOVO MODELO MATEMÁTICO E o SIMULADOR CARDIO JUNCTION
O simulador permite resolver 113 equações diferenciais com performance adequada, conforme apresentado por Junior (2016).
Outro diferencial do simulador é por permitir a utilização de dois tipos de modelagem para os canais iônicos: a modelagem de HH (CLANCY E RUDY, 2002; CARBONELL-PASCUAL et al., 2016) e o modelo de Markov (CARBONELL-PASCUAL et al., 2016) implementando ainda a difusão do Ca2+ em quatro compartimentos.
A interface gráfica do simulador seguiu todos os padrões estabelecidos pela W3C (World Wide Web Consortium), sendo ajustável a qualquer equipamento, inclusive smartphones, possibilitando livre acesso.
5.2 VALIDAÇÃO DO MODELO
Para validar o modelo foram utilizados dados experimentais que são referência na literatura (NEGRONI e LASCANO, 2008; SHANNON, 2004).
Pode-se constatar, na Tabela 15, que o modelo HH reproduziu de forma satisfatória a diástole, a amplitude do pico e o tempo de subida do transiente de Ca2+. Por exemplo: para a diástole a diferença maior foi de 0,46 ms para os dados experimentais de McCloskev et al. (2003), para a amplitude a maior diferença foi de 0,16 ms quando comparado com dados experimentais de Gao et al. (1999). Já, para o tempo de subida a maior diferença de 36,50 ms e para o tempo de descida a maior diferença foi de 108,42 ms. O resultado dessa última comparação permite concluir que o modelo necessita de ajustes, fator de estudos constantes nos trabalhos do Shannon (2004) e Negroni e Lascano (2008). A modelagem por MM também reproduziu resultados aproximados como a modelagem por HH.
A Tabela 16 apresenta os dados experimentais da força de contração e destaca-se o MM têm uma diferença maior da diástole com os dados experimentais de Stuyvers et al. 2002, sendo de 4,52 mN/mm2. Para o pico da força de contração a maior diferença está com projeto de Gao et al. 1999 de 8,13 mN/mm2. Na amplitude da força de contração a maior diferença está no projeto do Stuyvers et al. 2002, onde observa-se 9,28 mN/mm2. Para o tempo para alcançar o pico a maior diferença está com McCloskey et al. 2003 com 96,84 mN/mm2. Os valores apresentados são próximos do modelo HH.
5.3 Efeitos da aplicação do fármaco SS-68
Para os dados experimentais do efeito do fármaco SS-68 foi utilizado como parâmetro a pesquisa de Leonardo et al. 2019. A Tabela 22 apresenta o percentual de diferença os dados de controle e com aplicação do fármaco e percebe-se que o pico da força a diferença mais representativa foi no modelo HH de 28%, isto representa um resultado próximo ao obtido na literatura, onde no projeto de Leonardo et al. (2019), houve uma queda de 63,45%, mas os valores alcançados pela força de contração máximo foi de 3,94 e neste projeto de pesquisa foi de 20,43, valor mais próximo das literaturas que estão entre 12 e 25. O fármaco gerou curvas mais suavizadas com períodos de descida e subida mais longos, comportamento observado na literatura.
Na Tabela 24 pode-se observar a diferença percentual com a aplicação do fármaco SS-68 no transiente de Ca2+. Houve uma suavização nos índices das curvas para os dois modelos, inclusive o tempo para atingir a diminuição da concentração de Ca2+ foi alongado. Resultado que também foi observado no projeto de Leonardo et al. 2019.
6 CONCLUSÃO
O simulador CARDIO JUNCTION possibilitou a realização de estudos dos sobre eletrofisiologia do miócito ventricular, permitindo ainda a aplicação de fármacos, A plataforma possui uma interface gráfica que seguiu as recomendações da W3C (World Wide Web Consortium) e mecanismos que possibilitam as mais diversas combinações, tudo através da internet, utilizando qualquer aparelho conectado à internet. A linguagem de programação Python possibilitou ter todo o desenvolvimento dentro de um mesmo ambiente, possibilitando incrementos no sistema a curto, médio e longo prazo.
O sistema foi desenvolvido utilizando diversos estudos encontrados na literatura e permite que sejam combinados. Como exemplo, o modelo de Markov e HH, esta versatilidade e facilidade de acesso produzem elementos necessários para a expansão e atratividade da plataforma. A ferramenta atende uma lacuna quando concentra em uma mesma plataforma e ambiente todas as possibilidades de simulação, que antes tinham que ser realizadas em diversas plataformas ou que necessitavam de conhecimento avançado do usuário em informática.
A plataforma foi desenvolvida tendo como modelo a plataforma de Silva (2013) que é um aplicativo do tipo Desktop e que requer instalação em computadores para ser utilizada, além disso outras funcionalidades foram implementadas com o objetivo de tornar o simulador mais robusto e usual.
O usuário pode escolher o formato que deseja gravar os resultados, todos gerados em um servidor de internet, além de interagir com a plataforma, isso é possível através do próprio navegador de internet, por este motivo o sítio foi desenvolvido para se adaptar a qualquer tamanho de tela.
Para validar o novo modelo proposto foram realizadas simulações com os modelos de HH e Markov e os resultados foram comparados com dados experimentais descritos em Bondarenko (2013). O resultado da comparação mostrou que o modelo necessita de novos ajustes em seus parâmetros.
Já, a ferramenta computacional Cardio Junction, que pode ser acessada no endereço: http://cardiolab.ifspguarulhos.edu.br/ permite a realização de simulações sobre o complexo fenômeno da excitação – contração no miócito ventricular de rato, tudo de forma online. Novos ajustes nas interfaces podem ser realizados à medida que forem surgindo sugestões de novos usuários.
AGRADECIMENTOS
Os autores são gratos pelo apoio do Instituto Federal de Educação, Ciência e Tecnologia de São Paulo (IFSP) e a Universidade de Mogi das Cruzes (UMC).
REFERENCIAS
BONDARENKO, V. E. et al. Computer model of action potential of mouse ventricular myocytes. American Journal of Physiology-Heart and Circulatory Physiology, American Physiological Society, v. 287, n. 3, p. H1378–H1403, 2004.
CARBONELL-PASCUAL, B. et al. Comparison between hodgkin–huxley and markov formulations of cardiac ion channels. Journal of theoretical biology, Elsevier, v. 399, p. 92–102, 2016.
COOPER, J.; SCHARM, M.; MIRAMS, G. R. The cardiac electrophysiology web lab. Biophysical journal, Elsevier, v. 110, n. 2, p. 292–300, 2016.
GAO, Wei Dong et al. Altered cardiac excitation–contraction coupling in mutant mice with familial hypertrophic cardiomyopathy. The Journal of clinical investigation, v. 103, n. 5, p. 661-666, 1999.
GUO, W.; CAMPBELL, K. P. Association of triadin with the ryanodine receptor and calsequestrin in the lumen of the sarcoplasmic reticulum. Journal of Biological Chemistry, ASBMB, v. 270, n. 16, p. 9027–9030, 1995.
IYER, V.; MAZHARI, R.; WINSLOW, R. L. A computational model of the human left-ventricular epicardial myocyte. Biophysical journal, Elsevier, v. 87, n. 3, p. 1507–1525, 2004.
JÚNIOR, R.A.R. & Goroso, Daniel & Puglisi, Jose & Rodrigues da Silva, Robson. (2016). Ferramentas computacionais para estudo dos canais iônicos utilizando diagramas de estados: matlab vs python. CBEB, p.305-308, 2016.
LEONARDO, M. et al. Aplicação do fármaco ss-68 no miócito ventricular de camundongo: um experimento “in silico”. In: . [S.l.: s.n.], 2019.
LUO, C.-h.; RUDY, Y. A model of the ventricular cardiac action potential. depolarization, repolarization, and their interaction. Circulation research, Am Heart Assoc, v. 68, n. 6, p. 1501–1526, 1991.
MAHAJAN, A. et al. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophysical journal, Elsevier, v. 94, n. 2, p. 392–410, 2008.
MOROTTI, S. et al. Theoretical study of l-type Ca2+ current inactivation kinetics during action potential repolarization and early afterdepolarizations. The Journal of physiology, Wiley Online Library, v. 590, n. 18, p. 4465–4481, 2012.
NEGRONI, J. A.; LASCANO, E. C. A cardiac muscle model relating sarcomere dynamics to calcium kinetics. Journal of molecular and cellular cardiology, Elsevier, v. 28, n. 5, p.915–929, 1996.
NEGRONI, J. A.; LASCANO, E. C. Simulation of steady state and transient cardiac muscle response experiments with a huxley-based contraction model. Journal of molécular and cellular cardiology, Elsevier, v. 45, n. 2, p. 300–312, 2008.
OPAS. Doenças cardiovasculares. 2019. Disponível em:
<https://www.paho.org/bra/index.php?option=com\_content&view=article&id=5253:doencas-cardiovasculares&Itemid=839>. Acesso em: 09 fev. 2019.
PERIASAMY, M.; BHUPATHY, P.; BABU, G. J. Regulation of sarcoplasmic reticulum Ca2+ atpase pump expression and its relevance to cardiac muscle physiology and pathology. Cardiovascular research, Oxford University Press, v. 77, n. 2, p. 265–273, 2008.
PESSOA, C. A. et al. Markolab web: Uma plataforma online para estudo do comportamento estocástico dos canais iônicos. In: COBECSEB. V Congresso Brasileiro de Eletromiografia e Cinesiologia e X Simpósio de Engenharia Biomédica. [S.l.], 2017. p.709–717.
PUGLISI, J. L.; BERS, D. M. Labheart: an interactive computer model of rabbit ventricular myocyte ion channels and Ca transport. American Journal of Physiology-Cell Physiology, American Physiological Society Bethesda, MD, v. 281, n. 6, p. C2049–C2060, 2001.
RICE, J. J.; JAFRI, M. S.; WINSLOW, R. L. Modeling gain and gradedness of Ca2+ release in the functional unit of the cardiac diadic space. Biophysical journal, Elsevier, v. 77, n. 4, p. 1871–1884, 1999.
SHANNON, T. R. et al. A mathematical treatment of integrated ca dynamics within the ventricular myocyte. Biophysical journal, Elsevier, v. 87, n. 5, p. 3351–3371, 2004.
SILVA, R. R.; GOROSO, D. G.; BISSACO, M. A. Miolab: Simulator for cardiac myocyte contractile force of rat based on the dynamics of calcium. Medical engineering & physics, Elsevier, v. 35, n. 3, p. 338–349, 2013.
WINSLOW, R. L. et al. Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, ii: model studies. Circulation research, Am Heart Assoc, v. 84, n. 5, p. 571–586, 1999.
1Doutorado em Engenharia Biomédica IFSP
2Núcleo de Pesquisas Tecnológicas Universidade de Mogi das Cruzes
3College of Medicine California Northstate University
4Núcleo de Pesquisas Tecnológicas / Universidade de Mogi das Cruzes LabNECC – Laboratório Nacional para Estudo do Cálcio Celular Centro de Engenharia Biomédica / Universidade Estadual de Campinas
