REGISTRO DOI: 10.5281/zenodo.10699274
George Forte da Guia; Jhones Wendel Silva de Lima; Abraão Lucas Silva dos Santos; Yarlei dos Santos Barbosa; Erika Campos Saldanha Granja; Johana Lima Gomes; Arthur Feitosa Moreira; Josy Kelly Almeida Silva; Thácyla Oliveira Souza; Werbeson da Silva Freitas; Alex Soares da Silva; Daiane Fabrício dos Santos; Ícaro Jael Mendonça Moura
RESUMO
O GeoGebra é um software matemático interativo com diversas aplicações: construção de gráficos, análise geométrica, cálculo diferencial e integral e estatística. Esse software pode ser utilizado para estudo de problemas matemáticos ou para o ensino de matemática. O presente trabalho teve como objetivo apresentar a utilização do Geogebra como instrumento para o cálculo da rotação diferencial do Sol. A partir da observação das manchas solares – utilizando imagens do satélite SDO – e de conceitos da trigonometria, demonstra-se a possibilidade de aplicações desta tecnologia digital para a resolução do problema proposto ou no ensino dos conceitos envolvidos na sua resolução. O resultado calculado com o uso do GeoGebra foi considerado coerente e o software mostrou-se eficaz para demonstrar os valores da rotação diferencial do Sol, além de permitir uma abordagem prática para o ensino de trigonometria.
Palavras-chave: Geogebra. Ensino de Matemática. Trigonometria. Rotação solar. Manchas solares.
ABSTRACT
GeoGebra is an interactive mathematical software with several applications: graph construction, geometric analysis, differential and integral calculus and statistics. This software can be used to study mathematical problems or to teach mathematics. The present work aimed at presenting the use of Geogebra as an instrument to calculate the differential rotation of the Sun. From the observation of sunspots – using images from the SDO satellite – and trigonometry concepts, the possibility of application of this digital technology to solve the proposed problem or in teaching the concepts involved in its solution. The result calculated using GeoGebra was considered coherent and the software proved to be effective in demonstrating the values of the Sun’s differential rotation, in addition to allowing a practical approach to teaching trigonometry.
Keywords: Geogebra. Teaching Mathematics. Trigonometry. Solar rotation. Sunspots.
INTRODUÇÃO
É muito comum apontar que a utilização de softwares educacionais como recursos pedagógicos pode auxiliar os professores a tornar as aulas mais atraentes. Conteúdos mais abstratos, como a Física e a Matemática, podem ser mais facilmente apresentados através da utilização desse tipo de ferramenta. Um ambiente interativo, que apresenta imagens, sons ou animação é considerado positivo para o processo de aprendizagem, pois torna o estudo mais dinâmico e permite que o aluno visualize, construa e experimente por si mesmo, buscando as soluções para os problemas propostos e, dessa maneira, fomentando a construção do conhecimento pelos próprios alunos (SILVEIRA; BISOGNIN, 2018).
O GeoGebra é uma ferramenta matemática abrangente com ênfase em geometria e álgebra. Ele consiste em uma plataforma que permite não apenas o estudo de equações algébricas, mas também a análise de gráficos, estruturas geométricas e estatística. Essa característica torna o software não apenas um recurso técnico, mas também um instrumento de análise em contextos que demandam a aplicação de elementos matemáticos mais elaborados (FREIRES; SANTOS; SALES; 2023). Ademais, o GeoGebra é bastante acessível por ser gratuito e dispor de várias versões para diferentes sistemas operacionais, incluindo Android e Windows, além de uma versão online para navegador.
Este trabalho propõe apresentar a utilização do GeoGebra como ferramenta para calcular a rotação diferencial do Sol, aplicando os princípios fundamentais da trigonometria. Resolver esse tipo de problema destaca não apenas a efetividade do GeoGebra, mas também ressalta a aplicabilidade do software como ferramenta de ensino de matemática, em particular de trigonometria, em um contexto de aplicação prática na solução de um problema fundamentalmente físico: a rotação de uma estrela. Adicionalmente, isto evidencia o papel crucial e o amplo uso da trigonometria nos estudos astronômicos, uma tradição que remonta à antiguidade, como exemplificado pelo cálculo da circunferência da Terra realizado por Eratóstenes e outras contribuições dos estudiosos da época (SILVA, 2005).
O Sol é uma estrela (a mais próxima da Terra) e, assim, é constituído de plasma, não possuindo uma formação sólida. Essa característica dificulta a observação do seu movimento de rotação, pois sua superfície apresenta-se homogênea em forma e cores quando observada em baixas resoluções (SILVA et al, 2015). Porém, devido às atividades magnéticas do astro e de sua estrutura interna, ocorre na sua superfície o fenômeno das manchas solares. Manchas solares são regiões na superfície do Sol com uma temperatura menor que o seu entorno, o que as torna mais escuras, possibilitando diferenciá-las do resto da superfície. Essas manchas podem aparecer em zonas diferentes, por exemplo, próximas aos pólos ou ao equador do astro, e, é possível perceber que elas se movimentam no decorrer do tempo. Isso evidencia a rotação do Sol e, para além disso, é possível verificar que a velocidade dessa rotação muda de acordo com a distância ao equador do astro (MENEZES, 2021).
Assim, neste contexto, o presente trabalho objetivou especificamente apresentar uma maneira de calcular a velocidade (ou, de forma equivalente, o período) de rotação do Sol a partir da observação de manchas solares e utilizando o GeoGebra como ferramenta matemática para a realização dos cálculos. Dessa forma, objetivou-se proporcionar uma compreensão contextualizada da trigonometria, que pode ser utilizada para enriquecer o desenvolvimento desses conceitos a partir da sua aplicação em problemas reais.
FUNDAMENTAÇÃO TEÓRICA
O Sol
Devido a sua grande massa, as estrelas exercem uma grande força gravitacional sobre o plasma que as constitui. Isso faz com que as partículas em seu interior estejam sujeitas a uma grande pressão que as confina em um formato aproximadamente esférico (dada a simetria radial da força gravitacional). Submetido a elevadas pressão e temperatura, o gás no interior da estrela é fundido em novos elementos mais pesados, produzindo grande quantidade de energia e pressão que se opõe à força gravitacional e evita um colapso gravitacional (SILVA; BINOTI; DILEM,2023). É possível ainda delimitar uma estrutura bem definida para as estrelas (Figura 1). Seu interior é composto por camadas com características distintas, sendo elas: núcleo, camada radiativa, camada convectiva, enquanto a sua atmosfera é dividida em fotosfera, cromosfera e coroa (SILVA; et al, 2015).
Como toda estrela, o Sol é uma fonte primária de luz dotada de altas temperaturas e alimentada por reações de fusão nuclear que ocorrem no seu núcleo. Na região da atmosfera solar, ocorrem as manchas solares.
Figura 1 – Estrutura geral de uma estrela, como o Sol.
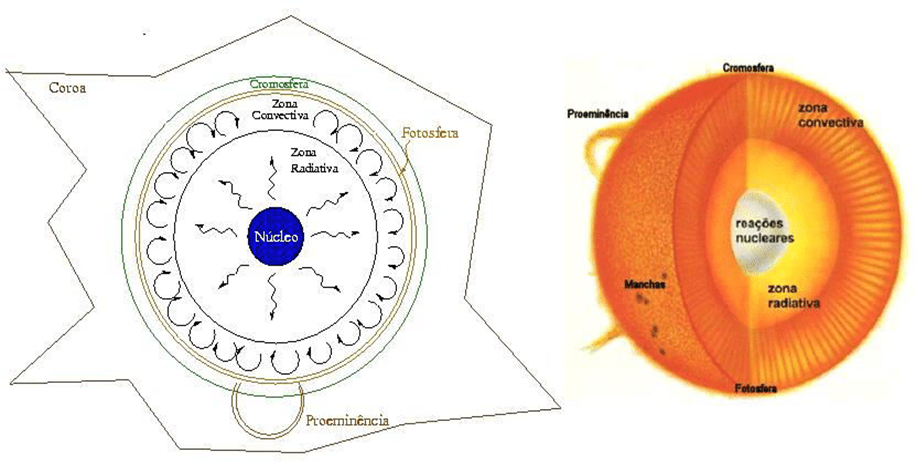
Fonte: SILVA et al. (2015)
Assim, por não ser sólido, o Sol apresenta uma rotação diferencial, ou seja, a velocidade de sua rotação em torno do próprio eixo varia de acordo com a região da superfície. Uma das formas de realizar essa aferição é através da observação do movimento das manchas solares em sua superfície. O mecanismo de formação das manchas solares tem relação com o campo magnético na superfície do Sol e, dependendo do estado de atividade magnética, essas manchas podem permanecer na fotosfera solar por vários dias.
Na fotosfera solar, a força do campo magnético solar é tipicamente cerca de 1 Gauss, enquanto nas manchas a medida pode alcançar milhares de Gauss. Isso acontece quando os tubos magnéticos (conjuntos de linhas de campo) se formam na tacoclina (região entre a zona radiativa e convectiva), devido à alta densidade da região convectiva e ao movimento de rotação diferencial, ilustrado na Figura 2. Quando isso ocorre, essas regiões com campo magnético acumulado se apresentam como manchas solares. As manchas também podem ser divididas em duas regiões: a umbra, a parte central e mais escura, e a penumbra, uma região um pouco mais clara envolvendo a umbra (MENEZES, 2021).
Figura 2 – Formato das linhas de campo solar ao decorrer do tempo.
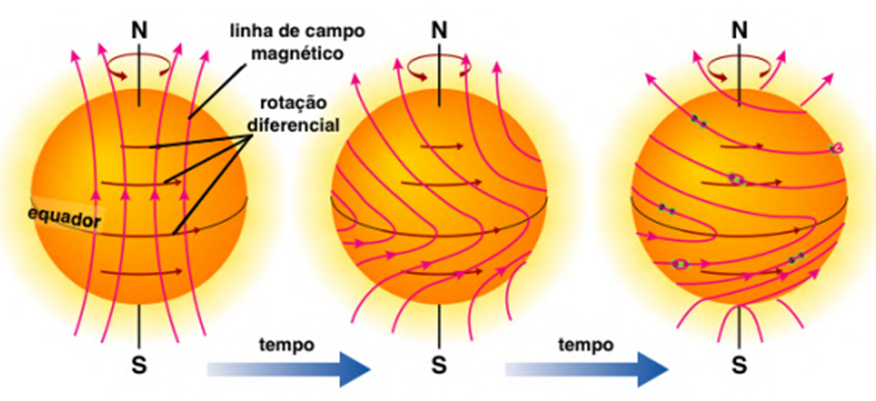
Fonte: MENEZES (2021).
Aspectos básicos de trigonometria
A trigonometria pode ser entendida como o estudo matemático, algébrico ou geométrico, do triângulo retângulo. O triângulo retângulo é aquele que apresenta um ângulo reto, ou seja, dois de seus lados (chamados catetos) são perpendiculares; o terceiro lado é chamado hipotenusa. Na mensuração dos ângulos de um triângulo retângulo, e usando o grau como unidade de medida, observa-se que, dado que o ângulo reto tem uma medida de 90°, os outros dois ângulos do triângulo retângulo são agudos e somam 90° em suas medidas (MARQUES 2014). Ao longo da história humana, a trigonometria tem sido empregada para cálculos relacionados a diversas medições, inclusive astronômicas.
Na Grécia antiga, no Século VI a.C., Pitágoras demonstrou uma das relações fundamentais dessa área de estudo, que ficou conhecida como o Teorema de Pitágoras. Esse teorema estabelece a relação matemática entre os três lados de qualquer triângulo retângulo. Em sua essência, o teorema afirma que, se e somente se um triângulo é retângulo, a soma das áreas dos quadrados cujo lado tem medida igual a dos catetos é igual à área do quadrado cujo lado tem medida igual a da hipotenusa. Embora o teorema seja associado ao nome de Pitágoras, registros históricos indicam que algumas civilizações antigas já possuíam conhecimentos relevantes sobre essa relação, sendo Pitágoras o primeiro a formalizar sua demonstração (SAMPAIO, 2021).
O mais antigo registro escrito no Egito, em grego, que aborda o Teorema de Pitágoras é encontrado nos “Elementos” de Euclides. A incerteza persiste sobre a demonstração empregada por Pitágoras, uma vez que não há registros de como ele provou seu teorema. Atualmente, sabe-se de mais de 400 demonstrações distintas do Teorema de Pitágoras, elaboradas por figuras proeminentes como Bháskara, Leonardo da Vinci e até mesmo por um dos presidente dos Estados Unidos, James Abram Garfield (1831-1881), em 1871 (SAMPAIO, 2021).
Conforme destacado anteriormente, as observações astronômicas e os problemas ligados a essas observações – como a determinação das distâncias entre a Terra e a Lua, e entre a Terra e o Sol, e a estimativa dos seus tamanhos – deram origem a aplicações do conceito de ângulo na resolução de problemas relacionados a triângulos. Entre essas expressões, merecem destaque as contribuições de Aristarco de Samos Século III a.C. e Eratóstenes de Cirene Século III a.C. (SILVA, 2005).
Os gregos mantiveram um foco significativo no progresso da astronomia ao longo de diversas gerações. Os elementos matemáticos associados a essa área eram principalmente a semelhança e a razão entre segmentos. Pode-se afirmar que, desde Hipócrates até Eratóstenes, os gregos exploraram as conexões entre retas e círculos, aplicando esses conceitos na astronomia. No entanto, esse empenho não resultou em uma formulação sistemática da trigonometria (BOYER, 2006).
Hiparco, do Século II a.C., é creditado por iniciar a trigonometria, ou mais precisamente, por introduzir de maneira indireta o conceito de seno de um ângulo. Ele desempenhou a função de pesquisador no Museu de Alexandria, considerado como a primeira instituição científica financiada pelo poder público, e tornou-se um dos maiores astrônomos da antiguidade. Sua contribuição matemática foi profundamente influenciada pela abordagem dos babilônios. A ele é atribuída a introdução, nos meios científicos relevantes da época, da medida de ângulo proposta pelos babilônios. Além disso, Hiparco também introduziu a função seno, utilizando a base numérica 60 (MARQUES, 2014).
Na segunda metade do Século II a.C., Hiparco elaborou um tratado em doze livros, abordando a construção do que provavelmente foi a primeira tabela trigonométrica, incluindo uma tábua de cordas. A abordagem de Hiparco na época fundamentava-se no estudo da relação entre um arco arbitrário e sua corda. Embora não se tenha certeza sobre quando se popularizou a divisão da circunferência em 360 partes, Hiparco parece ter desempenhado um papel significativo nisso, assim como na atribuição do nome “arco de 1 grau” a cada divisão da circunferência. Ele subdividiu cada arco de um grau em 60 partes, resultando no arco de 1 minuto. Hiparco detalhou o cálculo dos comprimentos das cordas e, apesar de a corda de um arco não ser diretamente o seno, uma vez conhecido o comprimento da corda, era possível calcular o seno da metade do arco, pois, para um círculo de raio unitário, o comprimento da corda subtendida por um ângulo x é 2sen(x/2).
Após a obra de Hiparco, a Syntaxis Mathematica, escrita por Ptolomeu de Alexandria por volta da segunda metade do Século II d,C, destacou-se como a obra trigonométrica mais influente e significativa da Antiguidade e trazia consigo uma influência babilônica semelhante à de Hiparco. Ptolomeu subdividiu a circunferência em 360 partes e o diâmetro em 120 partes. Ele aproximou o número π usando a razão 120/377. Mesmo sem fazer referência direta aos termos seno e cosseno, ele empregou as cordas e utilizou o que pode ser interpretado como um precursor da conhecida relação fundamental Sen2(x)+Cos2(x)= 1 (SILVA, 2005).
Como mencionado anteriormente, uma das formas para determinar os lados de um triângulo retângulo é com a aplicação do teorema de Pitágoras, que afirma que o quadrado da medida da hipotenusa é igual à soma dos quadrados das medida dos catetos. Essa relação pode ser expressa matematicamente pela fórmula a2+b2= c2. No entanto, para determinar a medida de todos os lados desse triângulo, é necessário conhecer pelo menos dois valores de lados ou possuir a medida de um lado e o valor de um dos ângulos agudos. Nesse último caso, pode-se recorrer às funções trigonométricas seno, cosseno e tangente (SANTOS, 2011).
Em um triângulo retângulo ABC, tomemos o ângulo A como exemplo. O lado oposto a ele, BC, é chamado de cateto oposto, com medida representada por a, enquanto o cateto adjacente, AC, tem medida representada por b. Vale ressaltar que, ao considerar o ângulo B, o lado AC torna-se o cateto oposto, enquanto o lado BC é designado como cateto adjacente (SOUZA, 2013).
Nesse contexto, as definições das relações seno, cosseno e tangente são aplicadas para determinar os valores dos lados ou até mesmo dos ângulos, e são dadas pelas equações 1, 2 e 3.

A ferramenta GeoGebra
O GeoGebra é uma ferramenta digital que pode ser aplicada no processo de ensino, aprendizagem e em pesquisa, pois é um software matemático com caráter multidisciplinar, sendo possível trabalhar de forma gráfica com álgebra, geometria, estatística, cálculo, tabelas e imagens (OLIVEIRA; SILVA; LIMA, 2021). O software GeoGebra foi criado por Markus Hohenwarter, em 2001, como tema de sua tese de doutorado. Desde então, o software tem sido utilizado em vários países e traduzido para diversos idiomas, sendo mantido pela Universidade Atlântica da Flórida (SOUSA, 2018).
O Geogebra pode ser utilizado em celulares, computadores, ou nos principais navegadores, sendo facilmente encontrado no endereço eletrônico http://www.geogebra.org. O Geogebra tem registro nos termos da GNU General Public License, o que garante ao usuário a possibilidade de utilizá-lo, estudá-lo ou mesmo modificá-lo de acordo com suas necessidades. Além disso, sua boa compatibilidade com várias plataformas se deve à linguagem de programação em que foi desenvolvido, a JAVA (CARDOSO, 2019).
O Software tem uma interface bem intuitiva. Sua janela principal é dividida em barras de funções, de ferramentas e de menu, além de campo de entrada, teclado virtual, janela de álgebra e janela de visualização (Figura 3).
Figura 3 – Interface do Geogebra.
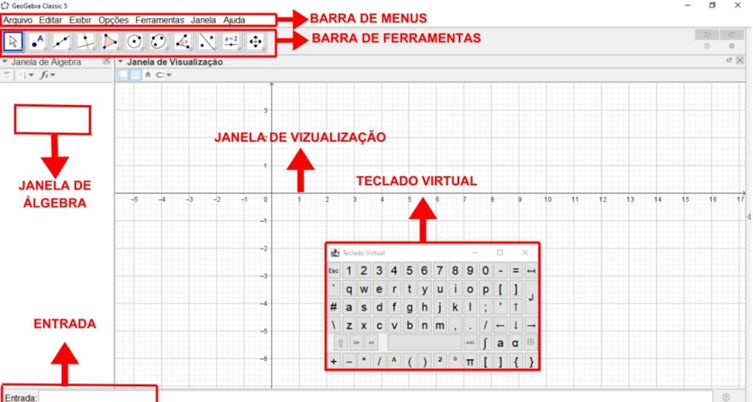
Fonte: adaptada de Silva (2019)
Na barra de ferramentas encontram-se os recursos para trabalhar nas áreas da matemática (Figura 4).
Figura 4 – Barra ferramentas do GeoGebra.
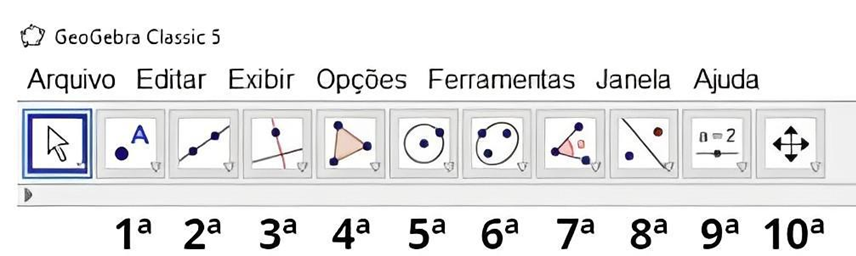
Fonte: adaptada de Silva (2019)
A barra de ferramentas apresenta 10 opções, incluindo o ícone do mouse, que só tem a utilidade de seleção. De acordo com a ordenação da Figura 4, as funções são: (1ª) ferramenta ponto, utilizada para criar pontos no plano cartesiano, vincular ou desvincular pontos de objetos, encontrar interseções entre dois objetos, calcular pontos médios ou centros, representar números complexos, realizar otimizações e encontrar raízes de equações; (2ª) ferramenta reta, usada para desenhar retas, segmentos de retas, segmentos com comprimento fixo, semirretas, caminhos poligonais, vetores e vetores a partir de um ponto; (3ª) ferramenta reta perpendicular, que permite desenhar retas perpendiculares, retas paralelas, mediatrizes, bissetrizes, retas tangentes, retas polares ou diametrais, retas de regressão linear e lugares geométricos; (4ª) ferramenta polígono, utilizada para criar polígonos, polígonos regulares, polígonos rígidos e polígonos semideformáveis; (5ª) ferramenta círculo com centro passando pelo ponto, usada para desenhar círculos com centro em um ponto específico, círculos definidos por centro e raio, compassos, círculos definidos por três pontos, semicírculos, arcos circulares, arcos circuncirculares, setores circulares e setores circuncirculares; (6ª) ferramenta elipse, utilizada para criar elipses, hipérboles, parábolas e cônicas a partir de cinco pontos, (7ª) ferramenta ângulo, que permite desenhar ângulos com amplitude fixas, calcular distâncias, comprimentos ou perímetros, áreas, inclinações, listas, relações e inspecionar funções; (8ª) ferramenta reflexão em relação a uma reta, que é usada para realizar reflexões em relação a uma reta, reflexões em relação ao ponto, inversões, rotações em torno de um ponto, translações por um vetor e homotetias; (9ª) ferramenta controle deslizante, utilizada para criar controles deslizantes, inserir texto, imagens, botões, caixas para exibir ou esconder objetos e campos de entrada; e (10ª) ferramenta mover janela de visualização, que permite mover a janela de visualização, ampliar ou reduzir a visualização, exibir/ocultar objetos ou rótulos, copiar estilos visuais e apagar elementos.
O campo de entrada do aplicativo é o mais usual para tarefas rápidas, como trabalhar com equações, por exemplo. Nesse campo é possível simplesmente digitar uma equação que será utilizada pelo software para criar um gráfico. Pode-se ainda adicionar várias equações e destacá-las em cores diferentes, como apresentado na Figura 5.
Figura 5 – Gráfico das equações inseridas no campo de entrada
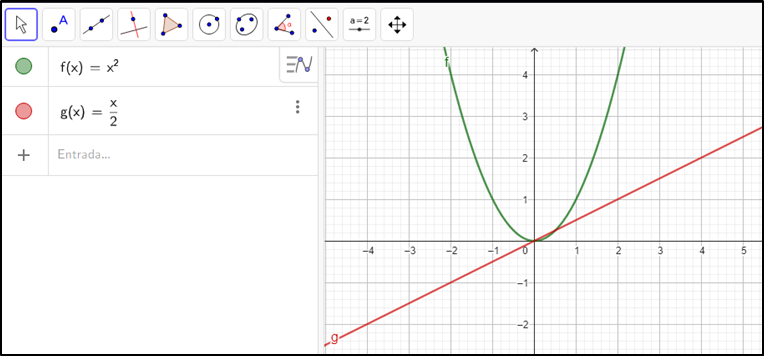
Fonte: Próprios autores
MATERIAIS E MÉTODOS
Coleta de Dados
O cálculo da rotação diferencial seguiu metodologia semelhante à feita por Carrington (1859). O Solar Dynamics Observatory, da National Aeronautics and Space Administration (NASA), disponibiliza imagens do Sol coletadas periodicamente no endereço eletrônico do projeto (http://sohodata.nascom.nasa.gov) com o propósito de facilitar e divulgar o estudo da estrela.
Foram escolhidas imagens captadas pelo instrumento Helioseismic and Magnetic Imager (HMI), que mede as oscilações na luz solar (dimensões de 512 por 512 pixels). Os critérios de escolha foram: apresentar o mínimo de interferências na superfície solar além das próprias manchas solares, consistência no movimento das mesmas e aparência geométrica próxima a de um círculo, além de terem sido coletadas em dias sequenciais. As imagens escolhidas foram as seguintes: SDO HMI 28-Set-2017, SDO HMI 29-Set-2017, SDO HMI 30-Set-2017 e SDO HMI 01-Out-2017. Além dessas, foram selecionadas mais 4 imagens datadas de 28 setembro a 01 de outubro de 2022, com o objetivo de acompanhar a trajetória da mancha 2941 durante esses 4 dias. A escolha se deu devido aos efeitos mais perceptíveis em seus movimentos, uma vez que esta mancha estava consideravelmente afastada da região equatorial do Sol. A Figura 6 apresenta uma dessas imagens na qual é possível visualizar três manchas solares, em que apenas duas manchas enumeradas com 2683 e 2682, foram selecionadas para o estudo, além da mancha 2941 que ocorreu apenas em 2022.
Figura 6 – Fotografia capturada pelo telescópio SDO no dia 28/09/2017 às 17:00 horas.

Fonte: Telescópio SDO
Processamento de imagens no GIMP
As figuras selecionadas foram processadas utilizando o GNU Image Manipulation Program (GIMP). Cada arquivo de imagem foi aberto individualmente e a temperatura da cor original foi corrigida para 1500K. A imagem SDO HMI 01-Out-2017, que é a última imagem da movimentação das manchas solares 2683 e 2682, foi escolhida entre as oito imagens por conter duas das três manchas utilizadas para o estudo e adicionada como imagem base.
Em seguida, a ferramenta de seleção elíptica foi utilizada nas outras imagens para recortar as manchas solares, englobando suas respectivas áreas (isso foi feito com um zoom de 400%, para recortar com o máximo de confiança apenas os pixels pertencentes às manchas solares). Posteriormente, o comando “colar na seleção no lugar” foi aplicado, fazendo com que as manchas ocupassem seu local de origem na imagem base, que havia sido escolhida anteriormente.
O resultado desta etapa de processamento é apresentado na Figura 7.
Figura 7 – Empilhamento das 8 imagens SDO HMI em uma imagem única, com a nomenclatura de identificação das manchas solares.

Fonte: próprios autores.
Procedimento de Cálculo da Velocidade de Rotação
Analisando as fotografias, é possível observar que as manchas solares movimentam-se na superfície do Sol, perfazendo movimento no sentido da esquerda para a direita. Um exemplo desse movimento é apresentado na Figura 8.
Figura 8 – Fotografias do Sol de 28/09/2017 a 01/10/2017, com periodicidade de 24 horas, capturadas pelo telescópio SDO.
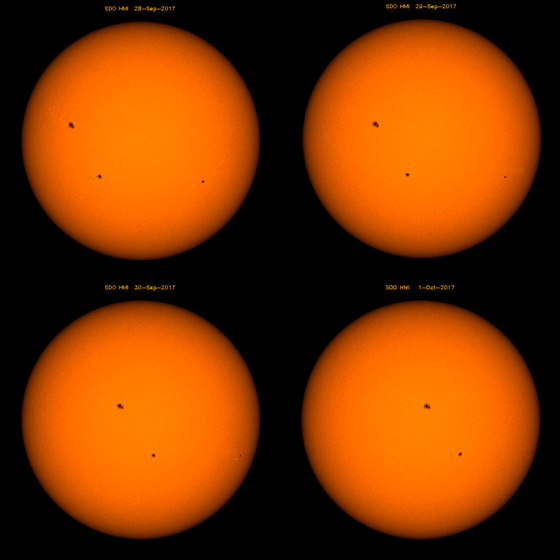
Fonte: Adaptado telescópio SDO.
Após o empilhamento das manchas solares em uma só imagem e a importação da mesma para o plano cartesiano do Geogebra (o centro do disco solar foi posicionado na origem do sistema de coordenadas), as manchas solares foram nomeadas (G, F e J, nomenclatura arbitrária) e suas posições registradas.
Usando o comando “ponto”, marcou-se próximo ao centro de cada mancha. Em cada mancha G, o valor das coordenadas y é aproximadamente igual a 7,13, aproximando a uma trajeto retilíneo, pois os pontos G1 e G2 estavam em um y superior às das outras manchas subsequentes. No caso da mancha F, apenas no último registro não foi observada uma trajetória retilínea; por isso, o ponto F4 teve sua coordenada x preservada, e y tornadas iguais a de F1, F2 e F3, -18,40, enquanto a mancha J teve todos seus valores em y iguais sem necessidade de alteração. Na movimentação das manchas solares, considerou-se seu movimento em uma superfície esférica, portanto, sua trajetória percorre uma região em uma circunferência teórica com o diâmetro sendo função da região onde se deslocam.
Para cada mancha, foram criados círculos com o auxílio do GeoGebra. Nomeou-se o círculo superior L, o círculo médio de A e o inferior de B. Na posição vertical da mancha, determina-se os pontos limiares nas extremidades esquerda e direita do disco solar. Em seguida, com o auxílio da ferramenta “ponto médio”, determinou-se o ponto central entre os pontos criados nos extremos do Sol na altura da mancha G. Isso permitiu a criação do círculo A com a ferramenta “círculo”, arrastando do ponto médio da mancha média até que as extremidades do círculo atingissem o limite imposto pelos dois pontos nos extremos. O procedimento análogo foi seguido para a determinação do círculo B e L.
Após a demarcação dos círculos, utilizou-se o comando de segmento de reta que partiu do ponto de origem de cada mancha até a origem do círculo correspondente (à da mancha G, B da mancha F e L da mancha J), repetindo isso para cada ponto (de G1 a G4, F1 a F4 e de J1 a J4). Com isso, construíram-se os triângulos retângulos. Através dos valores de altura e hipotenusa já conhecidos, medidos com a ferramenta distância/comprimento, aplicou-se o teorema de Pitágoras para a obtenção da base de cada triângulo retângulo formado. Posteriormente, realizou-se uma relação entre as bases que permitiu obter a distância percorrida dos pontos G1, F1 e J1, considerados como pontos iniciais, até G4, F4 e J4, respectivamente. Esses resultados estão apresentados na Figura 9.
Além disso, para se aproximar dos reais valores de deslocamentos, levou-se o ângulo de captura das imagens do Sol por meio do telescópio SDO, considerando a latitude para a obtenção dos raios reais que o círculo teórico deveria apresentar. Para isto, foi estimado o ângulo da latitude por meio da superposição à imagem de uma superfície esférica contendo uma grade de ângulos de latitude e longitude (e eixo central coincidente com o do disco solar, 7,5º), adequando-a à imagem do disco solar. O espaçamento entre as linhas de latitude na grade (representada na Figura 9) é de 10°. Após a determinação do ângulo de latitude , utilizou-se a equação abaixo para encontrar os raios médios R para cada mancha em sua respectiva latitude nos círculos A, B e L:

Após relacionar Rm(raio médio do Sol) com o ângulo da longitude, com o auxílio do Geogebra, foram obtidas as medidas em escala real dos deslocamento das manchas em quilômetros x, possibilitando calcular a variação do ângulo () nesse deslocamento a partir da equação 5, e com isso, foi permitido montar novas relações, assim obtendo as velocidades médias de deslocamentos das manchas e o período de translação.

Figura 9 – Imagem da grade esférica utilizada, com eixo de inclinação de 7.5 °. O “equador” é destacado em vermelho, as linhas horizontais representam a latitude e as verticais, a longitude.
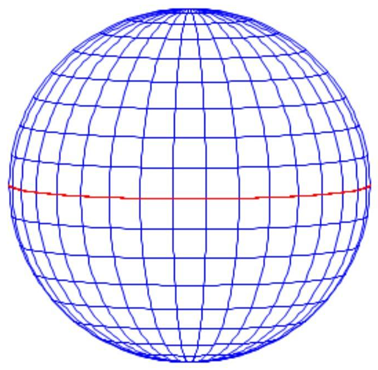
Fonte: Próprios autores.
Por conseguinte, para o cálculo do período de rotação foi realizado a partir da determinação da velocidade média em rad/dia, e da Equação 6. Esse processo foi repetido para as manchas nos círculos B e L.

Figura 10 – Projeção do trajeto das manchas J, G e F e extensões para a transposição do caminho reto no disco solar para um arco sobre os círculos L, A e B, respectivamente apresentado de cima para baixo na figura.
Fonte: Próprios autores.
Com os valores das bases dos triângulos que correspondiam a trajetória percorrida do ponto considerado inicial, para mancha G, G1, enquanto para mancha F, F1, até a distância máxima percorrida, relacionando estes dois ponto em uma soma, por se tratarem de triângulos retângulos em quadrantes adjacentes, com isso obteve-se a distância total percorrida pelas manchas G e F, essa relação específica para o cálculo é dado na Equação 7.

Essa relação entre as bases desses dois triângulos permite determinar aproximadamente a distância total que a mancha G e F percorreu no disco solar.
RESULTADOS
Na Tabela 1 são apresentados os resultados obtidos para a distância percorrida pela mancha G, utilizando o GeoGebra.
Tabela 1 – Distância percorrida pela mancha G.
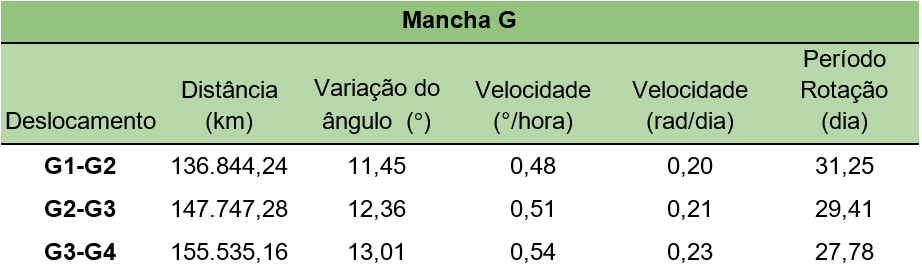
Fonte: Próprios autores.
Para o resultado foi considerado o deslocamento G3-G4, para isso foi levado em conta a figura 10. Como a captura da imagem é 2D, foi estipulado que a região perpendicular à visão, ou seja as regiões longitudinais mais centrais ao Sol, por aparentemente serem mais planas ao observador, apresentando pouca curvatura, evitando assim o aumento de erros ao medir o deslocamento aparente. Com isso os valores adotados para G será o raio de 6,851053,4799104 km, levando em conta a Equação 4 e a Figura 9, para estimar a latitude na região do movimento da mancha. A variação de ângulo em 13,010,67 °, de uma mancha a outra no período de 24 horas, com o movimento de 0,540,028 °/hora. A velocidade da mancha foi de 0,230,012 raddia e o período de rotação calculado para a região foi de 27,780,33 dias.
Na Tabela 2 são apresentados os resultados obtidos para a distância percorrida pela mancha F, utilizando o GeoGebra.
Tabela 2 – Distância percorrida pela mancha F.
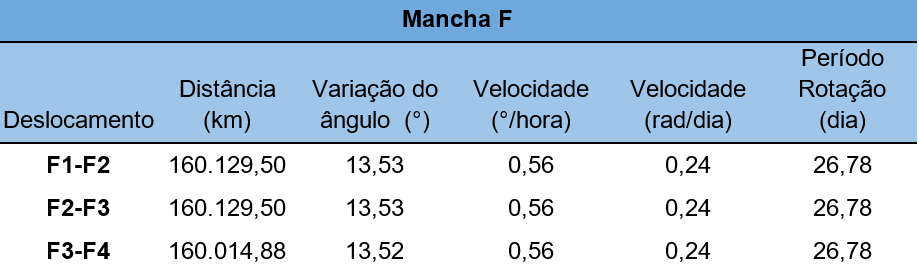
Utilizando de recursos adotados na consideração de resultado para a mancha G. Para a mancha F, foi escolhido o deslocamento da mancha F2 para a F3. A partir disto o raio calculado na região foi de 6,781053,4789104 km, para a latitude de 13 °, a variação do ângulo obtida foi de 13,530,70 °, de uma mancha a outra no período de 24 horas, com alteração de 0,56 0,029°/hora. A velocidade da mancha foi de 0,240,012 raddia e o período de rotação calculado para região foi de 26,780,31 dias.
Tabela 3 – Distância percorrida pela mancha J.
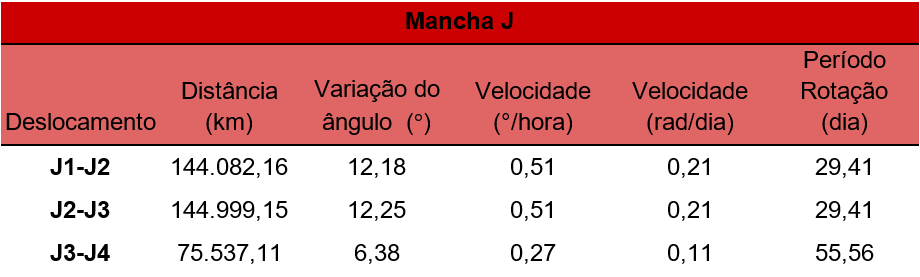
Partindo de processos análogos nas manchas anteriores, foi escolhido o deslocamento da mancha J2 para a J3. Com isso, foi calculado um raio de 5,701053,4798104 km, para a latitude aparente da mancha de 35 º, a variação do ângulo obtida foi de 12,250,95 °, de uma mancha a outra no período de 24 horas, com alteração de 0,51 0,039 °/hora. A velocidade da mancha foi de 0,210,016 raddia e o período de rotação calculado para a região foi de 29,380,48 dias.
É notório que a distância percorrida pela mancha G foi menor que pela mancha F, e a por J, menor que ambas. Também nota-se em uma análise individual das manchas que as distâncias percorridas variam nos períodos de 24 horas, onde a mancha G nas primeiras 24 percorreu uma distância menor do que nas 24 horas seguintes, enquanto na mancha F o deslocamento se mantém constante. A maior discrepância é observada no movimento da mancha J, que contém uma movimentação quase constante nas primeiras 48 horas, enquanto nas 24 horas seguintes, seu deslocamento cai quase para metade se comparada aos períodos anteriores. Isto se deve a vários fatores como, por exemplo, a distorção gerada pela projeção da superfície solar, esférica, no plano circular de captura da fotografia, e à não uniformidade no movimento do gás na superfície solar.
Pode-se apontar que o emprego do GeoGebra foi um elemento facilitador da execução dos cálculos necessários para a resolução do problema proposto neste trabalho. O software proporcionou uma abordagem visual e interativa, permitindo uma representação gráfica clara e precisa dos dados, como os círculos e os triângulos formados. Ademais, a facilidade de manipulação das figuras no GeoGebra simplificou a demarcação dos círculos e na criação dos triângulos retângulos associados. A identificação do cateto adjacente, base do triângulo retângulo, a aplicação do Teorema de Pitágoras e a compreensão das demais razões trigonométricas necessárias para o cálculo das velocidades de rotação foram conceitos primários mobilizados para a utilização eficaz desse instrumento nesse contexto.
CONSIDERAÇÕES FINAIS
O software GeoGebra se mostrou uma ferramenta eficaz para a análise e cálculo da rotação diferencial solar, a partir dos conceitos aplicados sobre a trigonometria. Os valores obtidos para o período de rotação, principalmente para a mancha F, que está próxima ao equador do astro, e cujo período calculado de 26,60,31 dias é similar aos valores encontrados na literatura, por exemplo NASA (2023). Da mesma forma, a mancha com latitude mais elevada terá um período maior, resultado já esperado segundo a literatura.
Esta aplicação demonstra o potencial do software ao empregar conceitos fundamentais da trigonometria, tais como os elementos e as relações estabelecidas entre as medidas e ângulos em um triângulo retângulo. Além disso, é possível explorar conceitos de astronomia, incluindo principalmente mensuração de astros ou distâncias. Desta forma, é possível abrir um leque de possibilidades, não somente para o uso na área da pesquisa, mas também para a aplicação no ensino.
No caso, o conteúdo apresentado no trabalho pode ser facilmente adaptado para uma aula de ensino médio, por exemplo, trazendo o uso da trigonometria em situações ou necessidades práticas e na resolução de problemas reais, que tendem a motivar o aluno muito mais do que problemas artificiais e muitas vezes surreais ou demasiadamente abstratos.
Por fim, destaca-se que o GeoGebra pode ser uma importante ferramenta para a aprendizagem ativa, pois o software é de acesso gratuito e possui uma interface de fácil compreensão, estimulando inclusive a utilização de outras tecnologias digitais auxiliares como o GIMP.
REFERÊNCIAS BIBLIOGRÁFICAS
BOYER, Carl B.. História da matemática. 2. ed. São Paulo: Blucher, 2006. ISBN 8521200234.
FREIRES, Kevin Cristian Paulino; SANTOS, Mateus Abreu; SALES, Francisco Odécio. O uso da teoria dos números na computação: uma visão metodológica. In: COSTA, Allan Júnior da Silva et al. (Org.). Matemática e suas possibilidades: ensino, pesquisa, formação docente e práticas pedagógicas*. Iguatu, CE: Quipá Editora, 2023. p. 7-17.
MARQUES, Gil da Costa. Fundamentos de matemática I. São Paulo: USP/Univesp/Edusp. Acesso em: 15 jan. 2024.
MENEZES, F. M. Influência da atividade magnética na atmosfera solar e na propagação de ejeções de massa coronal de estrelas do tipo-solar. Tese de doutorado, São Paulo, SP: Universidade Presbiteriana Mackenzie, 2021.
NASA. “Sun: Facts – NASA Science.” Science.nasa.gov, Dec. 2023, Disponível em: science.nasa.gov/sun/facts/. Acesso em: 13 Jan. 2024.
OLIVEIRA, T. S. P. de; SILVA, D. C. S.; LIMA, A. C. D. S. O software GeoGebra no ensino da Função Quadrática . Boletim Cearense de Educação e História da Matemática, [S. l.], v. 8, n. 23, p. 861–876, 2021. DOI: 10.30938/bocehm.v8i23.4954. Disponível em: https://revistas.uece.br/index.php/BOCEHM/article/view/4954. Acesso em: 6 fev. 2024.
SAMPAIO, L. O. Teorema de Pitágoras a partir da história da matemática. 2021. Trabalho de Conclusão de Curso (Graduação em Licenciatura em Matemática) – Faculdade de Engenharia, Campus de Guaratinguetá, Universidade Estadual Paulista, São Paulo, março de 2021.
SANTOS, Marconi Coelho dos. Teorema de Pitágoras: Suas Diversas Demonstrações. 2011. Monografia de Especialização em Educação Matemática para Professores do Ensino Médio – Universidade Estadual da Paraíba, Campina Grande, PB, outubro de 2011.
SILVA, C. D. C.; BINOTI, V. H. N.; DILEM, B. B. Estrelas: propriedades e ciclo de vida. Cadernos de Astronomia, v. 4, n. 1, p. 143–155, 10 mar. 2023.
SILVA, P. L. N. FUNÇÃO AFIM VIA SOFTWARE GEOGEBRA: UMA PROPOSTA PARA O ENSINO MÉDIO. 2019. 54 f. Trabalho de Conclusão de Curso (Graduação em 2019) – Universidade Estadual do Ceará, , 2019. Disponível em: <http://siduece.uece.br/siduece/trabalhoAcademicoPublico.jsf?id=94316> Acesso em: 6 de fevereiro de 2024
SILVA, R.; MACHADO, P.; ROCHA, R.; SILVA, S. A Luz e os Filtros Solares: Uma Temática Sociocientífica. Revista Virtual de Química, v. 7, jan. 2015. DOI: 10.5935/1984-6835.20150011.
SILVA, Sílvio Alves da. Trigonometria no Triângulo Retângulo: Construindo uma Aprendizagem Significativa. 2005. Dissertação (Mestrado em Educação Matemática) – Pontifícia Universidade Católica de São Paulo, São Paulo, 2005.
SOUSA, J. F. Uso do Geogebra no ensino da Matemática. 2018. Dissertação (Mestrado) – Curso de Ensino, Universidade do Vale do Taquari – Univates, Lajeado, 12 dez. 2018. Disponível em: http://hdl.handle.net/10737/2482
SILVEIRA, E. M.; BISOGNIN, E. O uso de programas computacionais como recurso auxiliar para o ensino de geometria espacial. UNIFRA, 2008.
SOUZA, Thuysa Schlichting de. Um Estudo da Extensão do Seno, Cosseno e Tangente no Triângulo Retângulo para Funções de Domínio Real. 2013. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Universidade Federal de Santa Catarina, Florianópolis, 2013.
