REGISTRO DOI: 10.5281/zenodo.7311703
Fábio Marcos Fonseca Boiani1
Felipe Barbato de Biaggio2
Luciene Figueiredo Batista3
Roberto Bernardes Junior4
Valéria de Lima Tozzi5
RESUMO
O objetivo deste projeto foi verificar quais são as principais dificuldades no aprendizado do ensino de Matemática para o Ensino Fundamental – Anos Iniciais e realizar uma proposta de aula para um dos conteúdos que gerem maior dificuldade, utilizando nesta aula uma metodologia que aborde aspectos lúdicos do ensino. Diversos autores têm ressaltado que o ensino de Matemática é o que traz o maior nível de dificuldade no aprendizado dos alunos, principalmente pelo fato dos mesmos não sentirem afinidade pela disciplina. Iniciamos o projeto analisando os dados de uma AAP (Avaliação de Aprendizagem em Processo) aplicada nos 5ºs Anos do Ensino Fundamental – Anos Iniciais no 2º bimestre de 2018. Analisamos o percentual de acertos das questões da prova de Matemática de nove turmas, de duas escolas diferentes, bem como o Currículo Paulista para o 5º ano – Matemática, e identificamos que a maior dificuldade desses alunos se refere às questões relacionadas a Frações e Números Decimais. Com base nisso, realizamos uma pesquisa buscando o referencial teórico sobre o estudo dos Números Racionais, Frações e metodologias de avaliação – Somativa e Formativa – e aspectos lúdicos do ensino de Matemática e apresentamos, ao final, uma proposta de aula sobre o tema incluindo o aspecto lúdico do ensino de Frações para o 5º Ano do Ensino Fundamental – Anos Iniciais, a fim de atrair o interesse dos alunos e melhorar o aprendizado deles.
Palavras-Chave: Plano de Ensino; Frações; Números Racionais; Ensino Lúdico, Avaliação Somativa e Formativa.
1. INTRODUÇÃO
O MEC (Ministério da Educação e Cultura), por meio do SAEB (Sistema Nacional de Avaliação da Educação Básica) e da Prova Brasil, busca avaliar a qualidade da educação no Brasil, e identifica que há uma defasagem no aprendizado da Matemática. Este tema tornou-se objeto de estudo e há ampla bibliografia sobre ele, como observamos através de nossas pesquisas, como, por exemplo, a reportagem “Por que 89% dos estudantes chegam ao final do Ensino Médio sem aprender o esperado em matemática?”, publicada em 27/10/2012 na versão online do jornal Gaúcha ZH, que procura, através de pesquisas e entrevistas, encontrar as causas deste problema, ou o artigo “Matemática: por que o nível elevado de rejeição?”, de autoria de Franciele Tatto e Ivone José Scapin, publicado em junho de 2004, que também busca algumas causas, recorrendo até mesmo à psicologia.
Partindo destas leituras, identificamos algumas causas e optamos por direcionar nosso Projeto Integrador para Licenciatura I na dificuldade que os estudantes têm em associar o conteúdo ao cotidiano; isso os distancia da disciplina, pois, na visão deles, não há uso efetivo da matemática em suas vidas e seu estudo se limita a “decorar fórmulas burocraticamente”.
Para melhor entendimento do objeto de que trata este Projeto Integrador, é importante que iniciemos com uma reflexão sobre os modelos de avaliação praticados nas escolas, dos quais destacamos dois, Avaliação Somativa e Avaliação Formativa.
Comecemos pela Avaliação Somativa. Trata-se de uma modalidade que ocorre ao fim de um processo educacional, que pode ser um ciclo, ano, semestre, bimestre ou curso, sendo o objeto desta os resultados obtidos. Diz-se Somativa, por compilar as aprendizagens dos alunos em uma síntese de resultados, tendo estes resultados caráter classificatório.
A Avaliação Somativa, na perspectiva de muitos teóricos, estudiosos sobre o assunto e professores, é pontual, classificatória e excludente. Classificatória porque que se restringe ao desempenho obtido por meio de um único documento, a(s) prova(s), classificando o aluno em aprovado ou reprovado, promovido ou retido, atende ou não atende; e excludente na medida em que os que não atendem ao resultado esperado ficam de fora. Em uma Avaliação Somativa, somente o aluno é avaliado, nunca o processo, o método, as práticas dos formadores. Não se leva em conta o histórico do aluno, sua subjetividade, individualidade, seus saberes trazidos na bagagem.
Já a Avaliação Formativa, ou como nas palavras de Cipriano C. Luckesi, Diagnóstica ou Inclusiva, ou Dialética, se detém no caminho percorrido pelo aluno, seus conhecimentos prévios, na avaliação de erros e acertos, sendo o erro não alvo de punição, mas objeto de análise e de reavaliação de métodos e prática docente.
A Avaliação Formativa, por ter no seu bojo o aspecto investigativo, possibilita que o método de ensino e práticas sejam revistos durante o processo e não ao término deste, quando os resultados já estão consolidados, com vencedores e perdedores.
É esta possibilidade de se debruçar sobre o problema identificado – dificuldade de aprendizado do conteúdo de frações em matemática, com foco na investigação, análise e proposição de novos formatos objetivando o aprendizado, que significa o ensino, que faz da Avaliação Formativa o modelo ideal a ser seguido.
E é sobre novos formatos que este grupo vai tratar neste projeto ao propor um Plano de Aula para a aprendizagem de Frações para o 5º Ano do Ensino Fundamental – Anos Iniciais de forma agradável e lúdica.
2. DESENVOLVIMENTO
2.1 Problema e objetivos
De que maneira alunos do 5º Ano do Ensino Fundamental – Anos Iniciais podem aprender o conceito e a utilização de Frações de forma atrativa?
2.1.1. Objetivo Geral:
Facilitar a aprendizagem de Frações pelos educandos de forma divertida e significativa.
2.1.2. Objetivos Específicos:
Fomentar a percepção da importância da Matemática no cotidiano.
Trabalhar a cooperação entre os alunos.
Promover a interdisciplinaridade.
Desmistificar a Matemática como “algo difícil”.
2.2. Justificativa
A disciplina de Matemática é encarada como um grande desafio por muitos. Esse projeto visa destacar que a aprendizagem não precisa ser encarada de forma maçante pelos docentes e discentes, mas sim que conteúdos desta disciplina, como Frações, devem ser aplicados no dia a dia do aluno, como forma de facilitar o entendimento e utilização. Afinal, é um conteúdo relevante que será usado em diversas situações corriqueiras, seja uma receita culinária, a repartição de uma pizza, para lidar com o dinheiro e os próprios problemas matemáticos futuros que serão muito facilitados com essa aprendizagem ao gerar autonomia dos alunos.
2. 3. Fundamentação teórica
2.3.1 A matemática e os números racionais
A arte de contar e registrar números é uma das mais antigas habilidades matemáticas de que temos notícia. Na verdade, há algumas evidências de que ela antecedeu a linguagem escrita. (WALL, 2014, P. 27). Para realizar a contagem das coisas e objetos utilizamos os números inteiros.
De acordo com SILVA (2020):
“O conjunto dos números inteiros é formado por todos os números que não são decimais. Em outras palavras, o conjunto dos números inteiros é formado pelo conjunto dos números naturais e seus opostos aditivos. Por exemplo: o número 1 pertence ao conjunto dos números naturais e dos números inteiros. Já o número – 1 pertence apenas ao conjunto dos números inteiros, pois é o oposto aditivo do natural (SILVA, 2020).”
Os números inteiros surgem como abstrações do processo de contar as coisas. No entanto, na vida diária, precisamos não apenas contar objetos individuais, mas também medir quantidades tais como comprimentos, áreas, pesos e tempos. Para a medição, os números inteiros já não são os mais adequados e torna-se necessária outra categoria de números, que possibilite uma maior precisão. Conforme afirma Courante e Robbins (2000, p 61),
“Se desejamos operar livremente com as medidas destas quantidades, que são capazes de subdivisões arbitrariamente pequenas, é necessário ampliar o domínio da Aritmética para além dos números inteiros. O primeiro passo consiste em reduzir o problema de medir ao problema de contar.”
Portanto, quando trabalhamos com medidas de quantidades, torna-se mais adequado a utilização de números racionais. Definimos os números racionais como
“aqueles que são formados por todos os elementos que podem ser escritos na forma de fração. Portanto, se o número pode ser representado por uma fração, então ele é um número racional. Uma fração, por sua vez, é uma divisão entre números inteiros, representada da seguinte maneira” (SILVA, 2020):
a/b
“Assim, para que seja uma fração, os números “a” e “b” precisam ser inteiros e o número “b” sempre será diferente de zero.” (SILVA, 2020).
Podemos concluir que o conjunto dos racionais é formado por todos os números que podem ser escritos na forma de fração; assim, para mostrar que um número é racional, basta mostrar que existe uma maneira de escrevê-lo nessa forma. Portanto, qualquer fração é um número racional. Os números racionais são fundamentais para o entendimento dos conceitos de razão e proporcionalidade.
2.3.2. Razão e Proporcionalidade
Conforme Wall (2014, p. 125) as noções sobre razões e proporções remontam à época de Euclides, onde “expressões do tipo a : b eram usadas para dar nome a razões. Hoje, usamos a representação para designar razões, bem como frações.”
Uma razão é um número relacional que possui duas propriedades: (1) relaciona duas quantidades em uma situação e (2) projeta essa relação sobre uma segunda situação, em que os valores relativos a duas quantidades permanecem os mesmos. (WALL, 2014, P. 125).
Para explicar o conceito, Edward Wall exemplifica:
“...suponha que um time de futebol faça 11 gols em 5 jogos. Alguém pode usar a razão “11 gols, cinco jogos” para estimar quantos gols a equipe marcaria em uma temporada de 15 jogos (ou seja, 33 gols, 15 jogos). A primeira propriedade é exemplificada por marcar em 5 jogos, e a segunda propriedade é exemplificada por marcar até o final do campeonato. Assim, pensar em uma razão é equivalente ao que muitas vezes se chama de raciocínio proporcional, com uma exceção importante. O raciocínio proporcional é um tipo de pensamento; não é uma questão de escrever uma determinada expressão no papel.” (WALL, 2014, p 125)
Alguns precursores da razão aparecem nos primeiros anos do Ensino Fundamental. Parece que as crianças desses anos têm noções intuitivas de escala (dois objetos grandes sobre a mesa pertencem ao mesmo grupo) e de covariação (se um dos dois objetos associados mudar de tamanho, o outro também deve mudar). Esses precursores parecem sustentar o desenvolvimento posterior das estratégias sensíveis em situações proporcionais (WALL, 2014, P. 126).
2.3.3 Números decimais
Na maioria das escolas, as crianças se deparam com os números decimais pela primeira vez no 4º ano do Ensino Fundamental – Anos Iniciais, embora seu uso em cálculos extensos comece no ano seguinte, 5º ano. A essa altura, a maioria das crianças é proficiente em cálculos simples, envolvendo números inteiros, e possui um conhecimento conceitual e processual significativo, o qual pode, com instrução adequada, contribuir para a sua aprendizagem da aritmética decimal. De acordo com Edwar Wall:
“Os números decimais são parte de um sistema complexo de representação. Os sistemas anteriores de números inteiros e frações comuns, (…) foram subsumidos em um sistema único, que é muito elegante e eficiente. Algumas vantagens são que a aritmética com números decimais é construída, até certo ponto, sobre os conceitos e procedimentos já encontrados dentro do sistema de numerador de base 10. Evita também um pouco da complicação percebida em relação aos racionais”.
Qualquer decimal finito, ou seja, que possui um número limitado de casas decimais, pode ser escrito na forma de fração. Para isso, basta lembrar que todo decimal finito é resultado de uma divisão por alguma potência de base 10. (SILVA, 2020)
Exemplo: 2,455 é um decimal finito que possui três casas decimais.
Isso significa que uma das frações equivalentes a ele possui denominador igual a 103. Essa fração é:
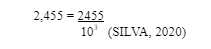
“Parece que as crianças muitas vezes reconhecem pouca ou nenhuma conexão entre seu conhecimento conceitual das frações decimais e os procedimentos que usam na aritmética decimal. A ausência dessas ligações pode ser tão ampla e profunda que é como se os dois tipos de conhecimento pertencessem a dois mundos mentais separados. Não é incomum, por exemplo, que as crianças erroneamente tentem exagerar a generalização das regras que memorizaram para operações aritméticas com números inteiros”. (WALL, 2014, p. 132)
O estudo das frações apresenta-se como conteúdo conceitual no Ensino Fundamental, em geral relacionando a ideia da parte de um todo, seja ele através do manuseio da reta, gráficos de áreas ou em alguns casos até mesmo uso de volumes sólidos. O domínio do conceito de fração está vinculado à relação entre quantidades e propriedades que não podem ser definidas por números inteiros e em alguns casos de forma indesejada por números reais, assim exigindo do estudante algumas habilidades para resolução de problemas específicos deste campo.
A dificuldade presente, tanto no ensino quanto na aprendizagem do assunto, induz a abordagens algorítmicas que focam na resolução dos problemas aritméticos levando o aluno muitas vezes a fazer uma manipulação correta dos números racionais, ainda que sem o total entendimento do conceito. Nunes & Bryant (1997, p.191):
“Com as frações as aparências enganam. Às vezes as crianças parecem ter uma compreensão completa das frações e ainda não a têm. Elas usam os termos fracionários certos; falam sobre frações coerentemente, resolvem alguns problemas fracionais; mas diversos aspectos cruciais das frações ainda lhes escapam. De fato, as aparências podem ser tão enganosas que é possível que alguns alunos passem pela escola sem dominar as dificuldades das frações, e sem que ninguém perceba”. (NUNES & BRYANT, 1997, p.191)
Tal cenário, além das implicações cotidianas, pode refletir-se posteriormente em campos mais avançados do estudo da matemática, como na álgebra onde com frequência se faz uso das propriedades e operações racionais como meio de manipulação dos seus elementos. Sendo assim, o entendimento dos números racionais se mostra essencial para o bom desenvolvimento das competências posteriores.
2.4. Aplicação das disciplinas estudadas no Projeto Integrador
Planejamento de Ensino é todo o processo até chegar ao Plano de Aula, toda a reflexão do trabalho pedagógico do professor com os alunos, toda a pesquisa e desenvolvimento, interações. É através desse planejamento e do diagnóstico de dificuldade dos alunos com frações analisadas na AAP que iremos desenvolver um Plano de Aula, que é o documento que resume, sintetiza as propostas de trabalho de determinada disciplina; é o produto do Planejamento de Ensino, que mostra as diretrizes do trabalho docente. Portanto, ao desenvolver esse documento estamos a discutir “o que”, “para que”, “como” e “com o que” ensinar, para que a proposta de Plano de Aula se mostre efetiva em seus objetivos.
2.5. Metodologia
Através de reuniões do grupo via aplicativos de reuniões online, analisamos uma AAP – Avaliação de Aprendizagem em Processo – de Matemática aplicada aos alunos do 5º Ano do Ensino Fundamental – Anos Iniciais no segundo bimestre de 2018, para identificarmos algumas dificuldades e selecionarmos uma para desenvolver nosso PI. A AAP trata-se de uma avaliação aplicada pela Secretaria da Educação do Estado de São Paulo, em todas as escolas do Estado para alunos a partir do 2º ano do Ensino Fundamental – Anos Iniciais, que visa diagnosticar as dificuldades de aprendizagem dos estudantes e direcionar as escolas nas habilidades que devem ser reforçadas, através de projetos, aulas de reforço, ou como cada unidade escolar, junto ao seu corpo docente e gestão definir, para que possam melhorar suas práticas pedagógicas. Esta avaliação a partir de 2020 é aplicada duas vezes ao ano (nos meses fevereiro e agosto), mas até 2019, época que engloba o material que pesquisamos, era aplicada ao final dos 2º, 3º e 4º bimestres.
Para termos uma base ampla de coleta de dados, consultamos os resultados da mesma avaliação em nove turmas de duas escolas diferentes. Na primeira escola, “Escola Estadual Professor Alípio de Barros”, consultamos os resultados dos 5ºs Anos A e B, do período da manhã, e C e D, do período da tarde; na segunda escola, “Escola Estadual Cacilda Becker”, analisamos os resultados dos 5º Anos A e B, do período da manhã e C, D e E, do período da tarde, totalizando 248 provas analisadas. Essa quantidade de turmas e diferença de escolas e períodos nos permitiu especificar algumas dificuldades comuns a muitos alunos, independentemente de escola, horário, turma ou professor, visto que na Educação Básica não há o professor especialista que atua em diversas salas, e sim o professor polivalente, que atua em uma única sala.
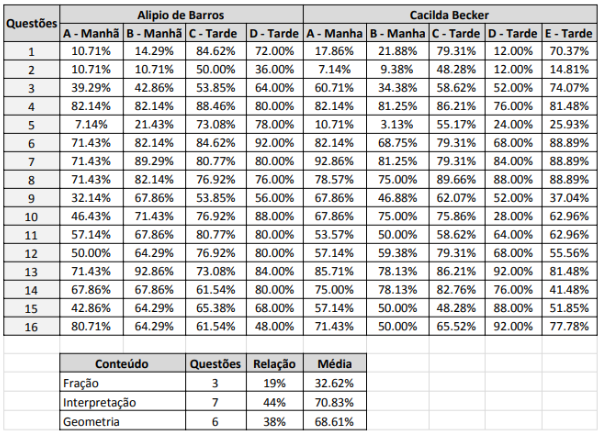
Assim, a partir da nossa análise, identificamos que há uma dificuldade recorrente em operação com Frações nos alunos do 5º Ano do Ensino Fundamental – Anos Iniciais. Conforme explicitado na tabela, houve grande disparidade no número de acertos das questões 1, 2 e 5, cujo tema foi Frações e operações com Frações, de forma que a média total de acertos foi de apenas 32,62%. Desta forma, decidimos focar nosso PI neste conteúdo, de modo a desenvolvermos um Plano de Aula que aborde esse tema de forma leve, divertida, inserindo-o na vida cotidiana do aluno a partir de situações práticas do dia a dia.
3. PROJETO
Identificada a principal dificuldade dos alunos nessa etapa do processo de ensino/aprendizagem, nos propusemos a criar uma atividade de reforço que trabalhasse este conteúdo de forma lúdica. Essa decisão se deu por, a partir das nossas leituras, entendermos que uma das barreiras que os alunos encontram no aprendizado da Matemática é a falta de percepção de sua utilidade no cotidiano, o que a faz parecer “difícil” e “sem propósito”. Assim, a partir da criação de um jogo que trabalhe as frações, pretendemos tornar este tema algo mais comum para estes estudantes. Além disso, acreditamos que o desenvolvimento desta atividade pode se tornar um projeto interdisciplinar, já que há todo um processo envolvido na criação de um jogo – como o desenho do tabuleiro, a criação de cartas de perguntas – que pode contar com a ajuda de professores de disciplinas como Artes e Língua Portuguesa, entre outras. A interdisciplinaridade e sua aplicação na educação hodierna são de extrema relevância e importância, pois a superação da fragmentação do conhecimento viabiliza uma formação integral e possibilita que os educandos desenvolvam um senso crítico mais apurado, podendo analisar situações e fatos com base em diferentes conhecimentos. Sobre a importância da formação integral, a BNCC, nos seus Fundamentos Pedagógicos, diz:
“...que a Educação Básica deve visar à formação e ao desenvolvimento humano global, o que implica compreender a complexidade e a não linearidade desse desenvolvimento, rompendo com visões reducionistas que privilegiam ou a dimensão intelectual (cognitiva) ou a dimensão afetiva. Significa, ainda, assumir uma visão plural, singular e integral da criança, do adolescente, do jovem e do adulto – considerando-os como sujeitos de aprendizagem – e promover uma educação voltada ao seu acolhimento, reconhecimento e desenvolvimento pleno, nas suas singularidades e diversidades. Além disso, a escola, como espaço de aprendizagem e de democracia inclusiva, deve se fortalecer na prática coercitiva de não discriminação, não preconceito e respeito às diferenças e diversidades.”
Assim, criamos o “Jogo das Frações”, que consiste em um jogo de tabuleiro com a finalidade de montar um Quebra-Cabeça a partir do cálculo de Frações pelos alunos de cada grupo.
3.1 Regras:
– Pode ser jogado em duplas ou trios;
– Eles deverão colocar o marcador na entrada (no caso está representado pelo trem);
Figura 1– Tabuleiro do jogo das frações
– O primeiro jogador pegará uma carta da pilha de “Perguntas” e sem deixar os outros verem, lê a pergunta e aguarda a resposta dos outros jogadores. Caso a resposta esteja correta, o jogador que respondeu deve pegar outra carta e repetir o processo, perguntando dessa vez para o último jogador que leu a pergunta;
– Eles só poderão avançar no tabuleiro quando todos já tiverem perguntado e respondido. Para isso, quem pergunta poderá ajudar quem responde, explicando e dando dicas para que o outro consiga responder e aprenda com a dinâmica, pois o jogo deve ser colaborativo;
– Quando avançarem para a próxima casa, terão o direito de virar uma carta da pilha de frações e todos devem posicionar a mesma na fração equivalente (por exemplo: ½ equivale a 5/10) no “quebra-cabeça”, e assim, recomeçar a fase de perguntas;
Figura 2 – Cards de perguntas
Figura 3 – Marcador na penúltima casa e quebra-cabeça quase finalizado.
– Para vencer, os grupos precisam alcançar a chegada e completar o quebra-cabeça antes de acabar o tempo da aula.
Ao criarmos este jogo, tivemos grande preocupação em fazê-lo de modo que fosse colaborativo, já que além de fomentar o aprendizado de Frações, também nos atentamos às competências socioemocionais que podem ser trabalhadas nesta atividade, como a empatia, tolerância à frustração, autoconfiança e curiosidade para aprender. Sobre essas competências, o Currículo Paulista diz:
“Competências como a comunicação, autogestão, criatividade, empatia, colaboração e autoconhecimento, entre outras, quando trabalhadas intencionalmente nas práticas escolares de modo articulado à construção do conhecimento, impactam de modo positivo a permanência e o sucesso dos estudantes na escola, têm relação direta com a continuidade dos estudos, com a empregabilidade e com outras variáveis ligadas ao bem-estar da pessoa, como a saúde e os relacionamentos interpessoais.”
Assim, o fortalecimento das competências socioemocionais auxilia na formação integral dos alunos, uma vez que se entende que o autoconhecimento faz com que os alunos reconheçam seus sonhos e projetos e compreendam a importância do estudo para alcançá-los. Além disso, o desenvolvimento das competências socioemocionais atua na percepção do estudante como parte integrante dos meios sociais em que está inserido, como a família, a escola, a comunidade, e o coloca como agente, às vezes protagonista, das mudanças nesses meios, quando necessário.
3.2 Plano de Aula
Nos termos do plano abaixo descrito, e pensando que o “Jogo das Frações” faz parte de um projeto, a ideia é que esta aula dupla seja aplicada após a confecção do jogo pelos próprios alunos e também após uma aula de revisão do conteúdo Frações. Assim, nesta aula será colocado em prática o trabalho realizado por professores e estudantes, como uma culminância, com os alunos jogando e o professor acompanhando esta atividade e observando o desenvolvimento da mesma, eventualmente prestando auxílio caso seja necessário.
Plano de aula
Data: Professor(a): Turma /Ano 5º Ano do Ensino Fundamental – Anos Iniciais Componente curricular: Matemática Habilidades a serem desenvolvidas – Identificar e representar frações (menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando a reta numérica como recurso.- Compreender, comparar e ordenar frações associadas às ideias de partes de inteiros e resultado de divisão, identificando frações equivalentes.- Compreender o significado das frações na representação de medidas não inteiras e da equivalência de frações.- Saber realizar as operações de adição e subtração de frações de modo significativo. Metodologia: – Trabalhar as frações de modo lúdico, através de jogos colaborativos nos quais os alunos precisarão retomar os conhecimentos adquiridos sobre o conteúdo para o desenvolvimento e conclusão dos mesmos. Situação de Aprendizagem – Potencializar a aprendizagem das frações e proporcionar aos alunos a percepção da aplicabilidade deste conteúdo na vida cotidiana deles.
Recursos Didáticos
– Aula expositiva;Formas de Avaliação – Contínua e diagnóstica:Será feita observação dos alunos durante o desenvolvimento da atividade para identificação de eventuais dificuldades de compreensão das regras dos jogos ou do conteúdo necessário ( Frações ) para praticá-los. Conteúdo Aulas 1 e 2 – Prática
Após aulas expositivas retomando as frações e o desenvolvimento do material, nestas aulas os alunos farão aulas práticas jogando os jogos produzidos por eles mesmos, e para isso colocarão em uso o conteúdo aprendido
4. CONSIDERAÇÕES FINAIS
É necessário todo um planejamento, análise e discussão acerca dos agentes envolvidos no processo de ensino/aprendizagem. É essencial investigar quais são as dificuldades dos alunos, que no caso identificado pelo grupo foi assimilar o conteúdo relacionado às Frações, na disciplina de Matemática, pelos do 5º Ano do Ensino Fundamental – Anos Iniciais. Esse diagnóstico se deu por meio da análise de uma avaliação externa e diagnóstica, usada por nós como ferramenta no processo de formação do aluno e como forma de revermos as práticas docentes, para assim criarmos um Plano de Aula que é a síntese de toda a elaboração, pesquisa e debates, buscando uma aula que seja interessante e atrativa a esse público-alvo, fazendo-os agentes ativos de sua prática de aprendizagem, correlacionando-a com problemáticas cotidianas.
É importante salientar que no processo de elaboração do referido plano houve grande preocupação em adequá-lo às competências e habilidades apontadas como essenciais para essa etapa da formação escolar pela BNCC – Base Nacional Comum Curricular – e pelo Currículo Paulista, que inclusive encontra-se já alinhado à primeira; além das habilidades e competências curriculares, com a criação e execução de um Plano de Aula nos termos do plano apresentado, que envolve jogos colaborativos como o proposto, também se espera o desenvolvimento de habilidades socioemocionais pelos alunos, como empatia, autoconfiança, curiosidade para aprender, foco, tão importantes quando pensamos na educação para a cidadania.
Houve também a intenção e o cuidado de criar um plano capaz de fazer parte de um projeto interdisciplinar, já que a criação e o desenvolvimento dos jogos pelos alunos possibilitam que professores de Língua Portuguesa e Artes, por exemplo, participem e dêem contribuições importantes para a atividade, superando a fragmentação entre as disciplinas e proporcionando um diálogo entre elas, fomentando uma aprendizagem global.
REFERÊNCIAS
BRASIL, MEC, Base Nacional Comum Curricular – BNCC, versão aprovada pelo CNE, novembro de 2017. Disponível em: < http://basenacionalcomum.mec.gov.br/abase/#introducao > Acesso em 01 de julho de 2020.
COURANT, R.; ROOBINS, H. O que é matemática? Rio de Janeiro: Editora Ciência Moderna Ltda., 2000.
GONZATTO, M. Por que 89% dos estudantes chegam ao final do Ensino Médio sem aprender o esperado em matemática?, jornal Gaúcha ZH, 2012. Disponível em < https://gauchazh.clicrbs.com.br/geral/noticia/2012/10/por-que-89-dos-estudantes-chegam-ao-final-do-ensino-medio-sem-aprender-o-esperado-em-matematica-3931330.html> Acesso em 14 de Maio de 2020.
KENSKI, V. M. Repensando a Avaliação da Aprendizagem. Repensando a Didática. 29 ed. Campinas: Papirus, p. 135-148, 2011.
NUNES, T. & BRYANT, P. Crianças fazendo matemática. Porto Alegre: ARTMED, 1997.
SÃO PAULO (ESTADO). Secretaria da educação. Currículo Paulista: Uma construção colaborativa. 2019. Diponível em: <http://www.escoladeformacao.sp.gov.br/portais/Portals/84/docs/pdf/curriculo_paulista_26_07_2019.pdf> Acesso em 01 de julho de 2020.
SILVA, L. P. M. O que são números racionais?; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-numeros-racionais.htm. Acesso em 14 de maio de 2020.
TATTO, F.; SCAPIN I. J. Matemática: por que o nível elevado de rejeição?. Rev. Ciênc. Hum. Educ., Frederico Westphalen – ISSN 1981-9250. 2004.
WALL, E. S. Teoria dos números para professores do ensino fundamental [recurso eletrônico]; tradução: Roberto Cataldo Costa ; revisão técnica: Katia Stocco Smole. – Dados eletrônicos. – Porto Alegre: AMGH, 2014.
