REGISTRO DOI: 10.5281/zenodo.7693018
A. R. da Cruz1
G. R. de Melo1
L. A. de Oliveira Silva1
R. S. Tito2
Abstract
In this paper, we use the Bäcklund transformations to construct the breather and wobble exact solutions for the Konno-Sanuki equation. Moreover, we present these solutions through graphics.
1. Introduction
Nonlinear Partial Differential Equations (NPDEs) and their solutions can describe many natural phenomena. Important methods exist to seek soliton solutions, such as the inverse scattering method, Hirota bilinear method, Bäcklund transformations, among others. The eigenvalue problem associated is frequently used on the underlying structure of some solutions methods, for example, the inverse scattering method. One can explain solution solutions methods by using algebraic or geometric perspectives.
Sasaki has shown that nonlinear equations illustrated by the inverse scattering method describe pseudo spherical surfaces, presented some geometric interpretations of Bäcklund transformation and conservation laws to solitons equations [17]. On the other hand, Chern and Tenenblat [8] introduced the Bäcklund transformations for the Korteweg-de Vries (KdV), modi ed Korteweg-de Vries (mKdV) and sine-Gordon equations through a systematic geometric method, thus enabling a more organized study for the pseudospherical equations.
In [13] Konno et al obtained the equation of the motion for the nonlinear lattice under the in uence of the weak dislocation potential,
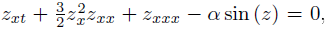
well known as Konno-Sanuki equation, furthermore, they discovered that the equation considered has N-kink solution. In [12] the Bäcklund trans formations and non-linear superposition formula for the Konno-Sanuki equation were obtained by Konno and Sanuki.
The breather solution is a particular 2-soliton solution, which is a periodic in time, spatially localized real function. The breather solutions were previously studied for the sine-Gordon [4], mKdV equation [1, 2], and Gardner equation [3]. The wobble solution for the sine-Gordon equation was rst obtained by Segur [18]. Kälberman [11] gave an analytical form of this solution using the inverse scattering method. Ferreira et al [9] obtained the wobble through the Hirota method and they showed that the wobble was a 3-soliton solution, where two solitons combined to form the breather and the third soliton as a kink. More recently, Cuenda et al [7] constructed the wobble solution for the sine-Gordon equation via Bäcklund transformation; they found the parameters of the transformation corresponding to the Bianchi diagram to obtain the wobble as a special case of a 3-soliton solution.
Our work aims to obtain the breather and wobble solution for the Konno-Sanuki equation via Bäcklund transformation. The paper is organized as follows. Section 2, we collect some preliminaries on differential equations that describe pseudospherical surfaces. We observe that the Konno-Sanuki equation is a known example that belongs to this class and use this fact to present its Bäcklund transformation and non-linear superposition formula. Section 3, we construct the breather and wobble exact solutions for the Konno-Sanuki equation through Bäcklund transformation and illustrate these solutions through graphics. Finally, in Section 4, the conclusions are presented.
2. Preliminaries
In this section, we collect some preliminaries on differential equations that describe pseudospherical surfaces. Moreover, we observe that the Konno-Sanuki equation is a known example that belongs to this class and use this fact to present its Bäcklund transformation and non-linear superposition formula.
2.1 Equations which describe pseudospherical surfaces
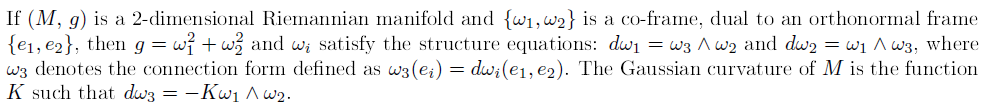

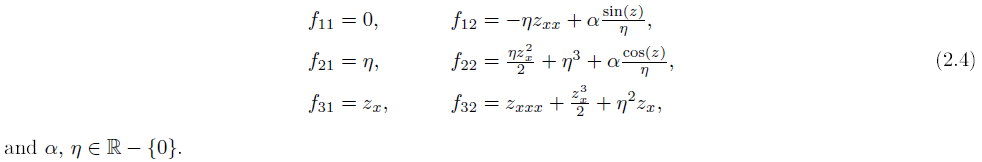
Equations that describe pseudospherical surfaces can also be characterized in a few alternative ways. For instance, the system of equations (2.1) is equivalent to the integrability condition of the linear system


2.2 Bäcklund transformation and superposition fórmula

3. Breather and wobble solutions for Konno-Sanuki equation
In section, we construct the breather and wobble exact solutions for the Konno-Sanuki equation (2.3) through Bäcklund transformation (2.12) and illustrate these solutions through graphics.
3.1 Breather solution
The breather solution is a particular 2-soliton solution. However, to get this type of solution, we consider the initial solution z0 = 0, and the parameters complex conjugates with unitary norms (see Figure 1), as follows the
Theorem 3.1. The breather solution for the Konno-Sanuki equation (2.3), via Bäcklund transformations, is given by
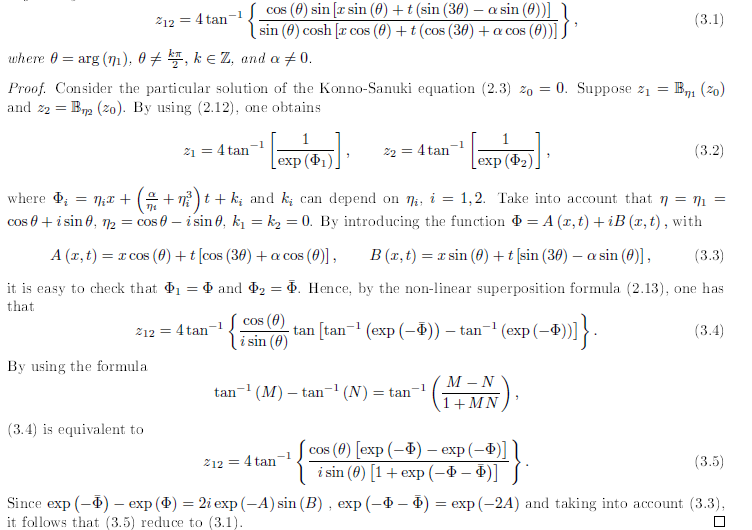
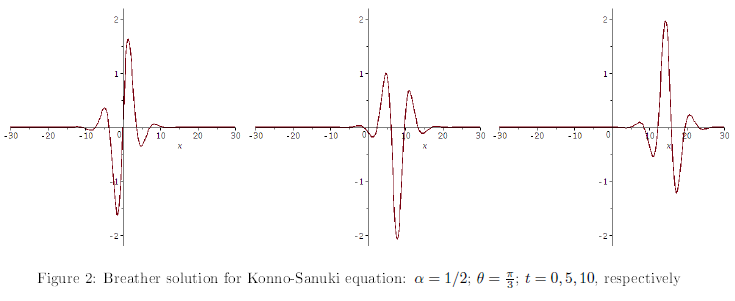
3.2 Wobble solution
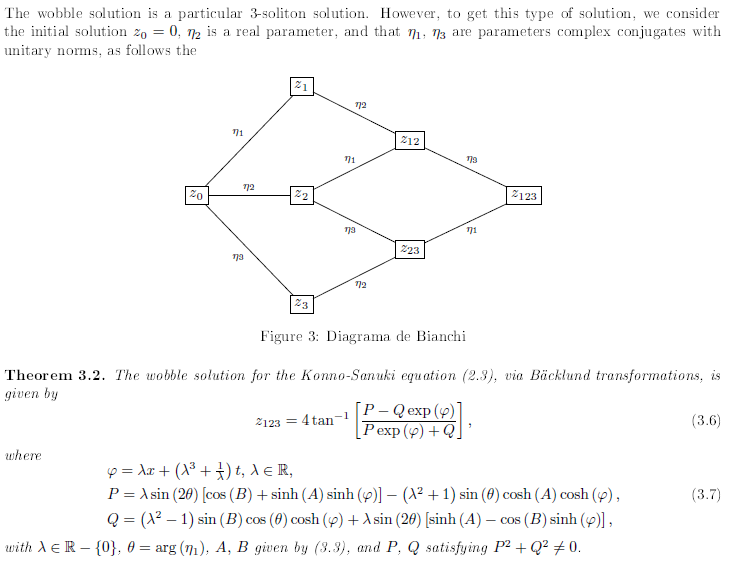

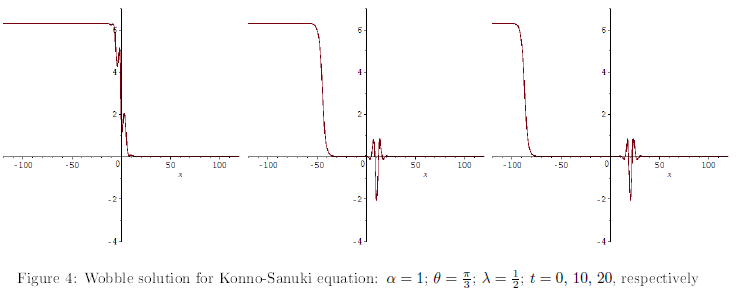
4. Conclusions
In this paper, we have used the Bäcklund transformation to end the breather and wobble solutions for the Konno-Sanuki equation (2.3). The breather solution is represented by the formula (3.1), whereas the wobble solution is represented by relation (3.6), satisfying (3.3), and (3.7). In the construction of the breather solution, we have used the Bianchi diagram (see Figure 1) with the initial solution z0 = 0, and the parameters complex conjugates with unitary norms, whereas in the construction of the wobble solution, we have used the Bianchi diagram (see Figure 3) with the initial solution z0 = 0, η2 a real parameter, and η1, η3 parameters complex conjugates with unitary norms. The solutions considered were represented graphically.
References
[1] M. A. Alejo, C. Muñoz, Nonlinear stability of mKdV breathers, Comm. Math. Phys. 37 (2013) 2050 2080.
[2] M. A. Alejo, C. Muñoz, Dynamics of complex-valued modi ed KdV solitons with applications to the stability of breathers, Analysis and PDE 8-3 (2015) 629 674.
[3] M.A. Alejo, Nonlinear Stability of Gardner Breathers, Jour. Di . Equat. 264 n.2 (2018) 1192- 1230 .
[4] M.A. Alejo, C. Muñoz, J.M. Palacios, On the variational structure of breather solutions I: the Sine-Gordon case, Jour. Math. Anal. Appl. Vol.453/2 (2017) 1111- 1138.
[5] R. Beals, R. Coifman, Scattering and inverse scattering for rst order systems, Commun. Pure Appl. Math. 37 (1984) 39 90.
[6] R. Beals, R. Coifman, Scattering and inverse scattering for rst order systems, II. Inverse Prob. 3 (1987) 577 593.
[7] S. Cuenda, N. R. Quintero, A. Sánches, Sine-Gordon wobbles through Bäcklund transformations, Discrete and Continuous Dynamical system series S. 4 n. 5 (2011) 1047-1056.
[8] S. S. Chern, K. Tenenblat, Pseudo-spherical surfaces and evolution equations, Stud. Appl. Math. 74 (1986) 55 83.
[9] L. A. Ferreira, B. Piette, W. Zakrzewski, Wobbles and other kink-breather solutions of the sine-Gordon model, Phys. Rev. E. 77 (2008) 036613-1 036613-9.
[10] C.S. Gardner, J.M. Greene, M.D. Kruskal, R.M. Miura, Method for solving the Korteweg-de Vries equation, Phys. Rev. Lett. 19 (1967) 1095-1097.
[11] G. Kälbermann, The sine-Gordon wobble, J. Phys. A: Math. Gen. 37 (2004) 11603 11612.
[12] K. Konno, H. Sanuki, Bäcklund transformation for equation of motion for non-linear lattice under weak dislocation potential, J. Phys. Soc. Japan 39 (1975) 22 24 .
[13] K. Konno, W. Kameyama, H. Sanuki, E ect of weak dislocation potential on nonlinear wave equation in an anharmonic crystal, J. Phys. Soc. Japan 37, 171 176 (1974).
[14] K. Konno, M. WADATI, Simple Derivation of Bäcklund Transformation from Riccati Form of Inverse Method, Progress of Theoretical Physics. Japan, Vol.53, No.6, (Jun 1975)
[15] C. Rogers, W. K. Schief, Bäcklund and Darboux transformations. Geometry and Modern Applications in Soliton Theory. Cambridge University Press, Cambridge (2002)
[16] C. Rogers, W. F. Shadwick, CHAPTER 1 Bäcklund Transformations and Their Applications to Nonlinear Equations of Mathematical Physics, Mathematics in Science and Engineering, 162 (1982), 12-122
[17] R. Sasaki, Soliton equations and pseudo-spherical surfaces, Phys. B 154 (1979) 343 357
[18] H. Segur, Wobbling kinks in ϕ4 and sine-Gordon theory, J. Math. Phys. 24 (1983) 1439 1443.
1Centro de Ciências Exatas e Tecnológicas, Universidade Federal do Recôncavo da Bahia, Rua Rui Barbosa, 710 Centro, CEP 44.380.000, Cruz das Almas, BA, Brazil
2Centro de Matemática, Computação e Cognição, Universidade Federal do ABC, Avenida dos Estados, 5001, Bairro Bangu, 09.210-580, Santo André, SP, Brazil
