REGISTRO DOI: 10.5281/zenodo.7829821
Gabriel Gomes de Souza¹
Profa. Dra. Rosenda Valdes Arencibia²
RESUMO
O presente documento visa a exposição do desenvolvimento do projeto de iniciação científica sobre o tema de “Avaliação da incerteza associada à tenacidade à fratura obtida via indentação instrumentada”. Ao longo do expresso no documento será possível identificar as etapas do projeto que já foram desenvolvidas, análises e conclusões acerca do projeto. O estudo visa a avaliação da incerteza associada ao módulo de elasticidade a partir do ensaio de tração realizado na máquina de teste universal da fabricante Instron® modelo 8801. Nos ensaios foram utilizados corpos de prova com duas geometrias diferentes, um deles sendo de secção transversal cilíndrica, fabricado em aço 4340 e um de secção transversal retangular, fabricado em aço 304. Os procedimentos de cálculo da incerteza foram implementados em dois códigos utilizando o Matlab®R2021a para evitar erros de cálculo e realizar a leitura direta do arquivo Excel® gerado pela máquina de teste. Desta forma todos aqueles que no LTAD determinam o módulo de elasticidade dos materiais têm a disposição esses dois códigos para determinação da incerteza de medição. Se espera com isto contribuir para a rastreabilidade dos valores de módulo de elasticidade, bem como o atendimento às normas técnicas em vigor, principalmente a NBR ISO/IEC 17025 (ISO, 2016).
1 INTRODUÇÃO
As fraturas são objetos de estudo desde o início das construções estruturais no mundo e se tornou um desafio econômico. De acordo com Anderson (2005), um estudo econômico estimou que em 1978 o custo oriundo de fraturas nas estruturas fabricadas nos Estados Unidos era de $119 bilhões de dólares, o que naquela época correspondia a aproximadamente 4 % do produto interno bruto do país. Esse autor mostrou que somente com os estudos existentes sobre a mecânica da fratura, seria possível minimizar o valor de custo com fraturas em $28 bilhões. Este autor destacou as causas principais da maioria das fraturas estruturais, quais sejam: negligência durante o projeto, construção ou operação da estrutura; e aplicação de um processo ou material novo, o que implica em comportamentos imprevisíveis ou até mesmo indesejáveis. A negligência durante o projeto é frequente, sabendo que existem alguns processos de fabricação, que são muito complexos e que facilmente resultam em microestruturas não previstas nos componentes fabricados. Além disso, as simulações durante o projeto e construção das estruturas nem sempre conseguem reproduzir de forma completa as condições de serviço. Em muitos casos, parte-se de pressupostos e aproximações que podem implicar em erros. Já a segunda causa tem se tornado habitual, pois a inovação tecnológica e o desenvolvimento de novos materiais têm propiciado comportamentos estruturais complexos e difíceis de serem estimados.
As falhas estruturais são estudadas pela mecânica da fratura. Esse estudo se dá, principalmente, em função da tenacidade à fratura, uma importante propriedade mecânica do material. A tenacidade à fratura representa a resistência de um material à propagação de trinca, sendo considerada um dos aspectos mais importantes na avaliação da integridade estrutural (JEON et al., 2017). Diferentes parâmetros são propostos para avaliar a tenacidade à fratura do material, sendo eles: o fator de intensidade de tensão (K); a integral J e o deslocamento de abertura na ponta da trinca (CTOD-Crack Tip Opening Displacement). O fator K é o parâmetro capaz de descrever a intensidade dos campos elásticos desenvolvidos na ponta de uma trinca, e sua utilização simboliza a mecânica da fratura linear (IRWIN, 1957). A integral J foi proposta por Rice (1968) e, diferentemente do que Irwin (1957) propôs, esse parâmetro descreve a intensidade dos campos elastoplásticos que se desenvolvem na ponta de uma trinca. Esse conceito está diretamente relacionado à mecânica da fratura elastoplástica. Wells (1963) foi o primeiro a propor o conceito do CTOD, o qual é normalmente utilizado como parâmetro de fratura, e em prática, pode ser utilizado como um correspondente do fator K ou da integral J. Métodos experimentais distintos foram desenvolvidos para cada um desses parâmetros capazes de descrever a tenacidade à fratura.
Vale ressaltar que o desempenho do material durante a realização de um ensaio de tenacidade à fratura depende de três fatores relacionados ao material: o comportamento de fratura, o comportamento da deformação e o efeito da restrição da geometria (ZHU e JOYCE, 2012). O comportamento de fratura remete aos micro-mecanismos de fratura do material, sendo normalmente descritos como frágil ou dúctil. Uma fratura considerada frágil é identificada por uma separação normal à tensão de aplicação e sua superfície é lisa com quase nenhuma deformação plástica macroscópica e pouca microdeformação. Nesse tipo de fratura, na ponta da trinca há o desenvolvimento de uma zona de deformação elástica linear, e a tenacidade de iniciação da trinca domina a resistência à fratura do material, com apenas uma pequena contribuição da resistência à propagação da trinca além da iniciação. Em geral, a quantidade de energia que se faz necessária para propagar a trinca além de sua iniciação é baixa, levando à uma falha instável e instantânea. Dessa forma, a tenacidade medida é, normalmente, um valor pontual e caracterizado pelo fator K ou pela taxa de liberação de energia G no início da trinca. O primeiro método de determinar valores do fator de intensidade de tensão em um estado plano de deformação para pontos no início ou próximo do início da trinca (KIC) é descrito pela norma ASTM E399 (ASTM, 2020).
A fratura dúctil é caracterizada pela propagação da trinca devido ao crescimento e coalescência de microvazios. Durante esse processo, uma maior quantidade de energia é absorvida, resultando em uma extensão de trinca lenta e estável. Diferentemente do observado na fratura frágil, a dominância na ponta da trinca deixa de ser elástica e passa a ser plástica. Em resumo, a resistência do material à fratura se eleva à proporção que há o crescimento da trinca. Consequentemente, a tenacidade descrita não é pontual e sim uma curva de resistência, denominada curva-R, a qual pode ser avaliada tanto pela integral J quanto pelo CTOD (δ).
A integral J quantifica uma energia elástica não-linear, e seu uso para determinar a tenacidade à fratura elastoplástica requer cuidados. Normalmente, uma curva J-R é construída, representando a resistência do material à propagação estável da trinca em termos de J. A norma ASTM E1820 (ASTM, 2018) foi desenvolvida com o objetivo de regulamentar a determinação das curvas de tenacidade de iniciação elastoplástica (JIC), assim como a curva J-R.
O uso desses métodos da mecânica da fratura, além de outros aqui não citados, como CTOA, permite a utilização da tenacidade à fratura como um parâmetro de projeto para um componente mecânico ou estrutural. Porém, as dimensões dos corpos de prova avaliados nos ensaios podem influenciar fortemente as condições de tensão na ponta da trinca, resultando em valores errados (ZHU e JOYCE, 2012). Caso haja elevada restrição geométrica, as tensões atuantes na ponta da trinca são mais altas o que pode promover uma fratura mais frágil, ou, ainda, diminuir a área sob a curva de tenacidade à fratura dúctil do material. Por outro lado, caso haja baixa restrição, menores tensões podem ser observadas na ponta da trinca, o que tende a minimizar a possibilidade de ocorrer fratura frágil, bem como, aumentar a área sob a curva de tenacidade à fratura dúctil do material.
Essa restrição geométrica, geralmente, é especificada em função do estado de tensão que esta gera na ponta da trinca, quais sejam: plano de deformação e plano de tensão, sendo o primeiro aquele com menor valor de tenacidade à fratura associado. Normalmente, a fim de reduzir os efeitos das dimensões do corpo de prova, as normas ASTM E399 (ASTM, 2020) e ASTM E1820 (ASTM, 2018) definem faixas limites para as dimensões da trinca inicial, ligamento e espessura. Entretanto, essa restrição geométrica limita o campo de aplicação destes métodos. Uma alternativa bastante promissora para superar as limitações dos métodos convencionais é a indentação instrumentada, que permite realizar ensaios mais simples, rápidos, não destrutivos e podem ser realizados in situ (HAGGAG et al, 1990; LEE et al., 2006).
1.1 Indentação Instrumentada
Um ensaio de indentação pode ser considerado como uma versão avançada de um teste de dureza convencional, e tem sido amplamente utilizado em aplicações estruturais e campos de pesquisa de engenharia (AMIRI et al., 2014). Muitas teorias e modelos foram desenvolvidos para medir as propriedades mecânicas de materiais utilizando técnicas de indentação. Utilizando desses modelos pode-se obter curvas tensão-deformação e algumas propriedades mecânicas fundamentais, como limite de escoamento e limite de resistência (BYUN et al., 1997). Para estimar a tenacidade à fratura estes ensaios requerem apenas uma área mínima da qualidade do polimento podendo ser realizado em um testador de dureza padrão. Dessa forma, elimina-se o uso de máquinas pesadas, geometrias complexas de amostras e procedimentos experimentais complexos (HE et al., 2011). São realizados sem remoção de material da superfície de teste no material e, portanto, sem interrupção da produção (MATHEW et al., 1999). Essa técnica pode ser utilizada para a análise das propriedades dos materiais sem a necessidade de realizar paradas devido aos custos altos que isto envolve, como a indústria de óleo e gás (NICOLOSI, 2015). Ainda, usando um equipamento de campo, a técnica pode avaliar componentes deformados e componentes estruturais envelhecidos e fragilizados, podendo resultar em prolongar sua vida útil. Além disso, por utilizar um volume muito pequeno de material de teste, poderia ser útil no desenvolvimento de novas ligas e quando quantidades limitadas de material estiverem disponíveis (HAGGAG et al, 1990).
A técnica de fratura por indentação tem sido amplamente aceita e relatada na literatura na avaliação da tenacidade à fratura em materiais frágeis, como cerâmica ou compósito, visto que, para esses materiais, obter a tenacidade à fratura por métodos convencionais pode ser uma tarefa árdua (RANGEL, 2011). A indentação instrumentada com sensor de profundidade tem sido um tópico de consideráveis estudos experimentais e teóricos nas últimas décadas. Nesses testes, é realizado o monitoramento contínuo da força de penetração do indentador em função da profundidade h de penetração em um corpo de prova durante o carregamento e o descarregamento (HE et al., 2011). Estes podem ser realizados com controle de força e controle de profundidade, e em ambos os modos, a força aplicada e a profundidade de indentação são monitorados e registrados durante o ensaio. Uma curva típica de indentação durante a carga-descarga é mostrada na Fig. 1, no qual S é a rigidez de descarga (AMIRI et al., 2014). Onde: hp e hm são a profundidade plástica e máxima de indentação, respectivamente.
Figura 1.1: Curva de indentação versus de profundidade de indentação
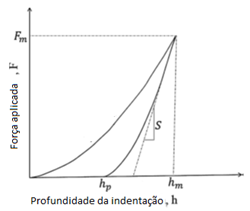
A determinação da tenacidade à fratura utilizando indentação instrumentada tem apresentado bons resultados. Haggag et al. (1990) obtiveram os valores tenacidade à fratura dentro de -11 % em comparação aos valores de literatura para os aços utilizados. Lee et al. (2006) obtiveram aproximadamente 10 % de diferença nos valores entre os testes de indentação e os testes CTOD. Mohammadi et al. (2011) verificaram erros relativos de 17 % entre a tenacidade à fratura estimada pelo modelo utilizado e a calculada a partir das equações de Rolfe-Barsom com base nos resultados dos testes de impacto realizados pelos autores. Além desses, Jeon et al. (2017) alcançaram boa concordância entre os valores de tenacidade à fratura obtidos nos testes de indentação e os obtidos nos testes padrão. Zhang et al. (2019) obtiveram erro máximo inferior a 10 %, em quatro aços utilizados, a partir do modelo baseado na taxa de liberação de energia proposto, concluindo que o modelo pode atender aos requisitos de precisão em aplicações de engenharia. Portanto, a partir dos bons resultados obtidos, muitos autores demonstram que o método de indentação é eficiente para estimar a tenacidade à fratura dos materiais (HE et al., 2011). Entretanto, para que o ensaio de indentação instrumentada possa ser utilizado para determinação da tenacidade à fratura resulta necessário validar os resultados obtidos. Esta validação requer entre outros aspectos o cálculo da incerteza associada aos resultados e a comparação desta incerteza com aquela obtida para os métodos convencionais.
2 OBJETIVOS
2.1 Objetivo principal
O objetivo principal desta Iniciação Científica é avaliar a incerteza associada à tenacidade à fratura obtida via ensaios de indentação instrumentada.
2.2 Objetivos específicos
a) Desenvolver, validar e documentar uma metodologia para cálculo da incerteza de medição associada à tenacidade à fratura obtida via ensaios de indentação instrumentada.
b) Identificar os fatores que contribuem para a incerteza associada à tenacidade à fratura.
c) Determinar a contribuição dos fatores de influência na incerteza final e propor boas práticas de medição para reduzir seus efeitos.
d) Comparar os valores de incerteza associada à tenacidade à fratura obtida via indentação instrumentada com aqueles obtidos via ensaios normatizados, Integral J, visando validar a técnica de indentação instrumentada.
e) Contribuir para a rastreabilidade metrológica dos valores de tenacidade à fratura, visando o atendimento da NBR ISO/IEC 17025 (2017).
3 ATIVIDADES DESENVOLVIDAS
De acordo com o cronograma proposto, Tab. 1, as seguintes atividades foram desenvolvidas e finalizadas de acordo com os prazos estipulados.
Tabela 1: Cronograma proposto, com destaque das atividades desenvolvidas.
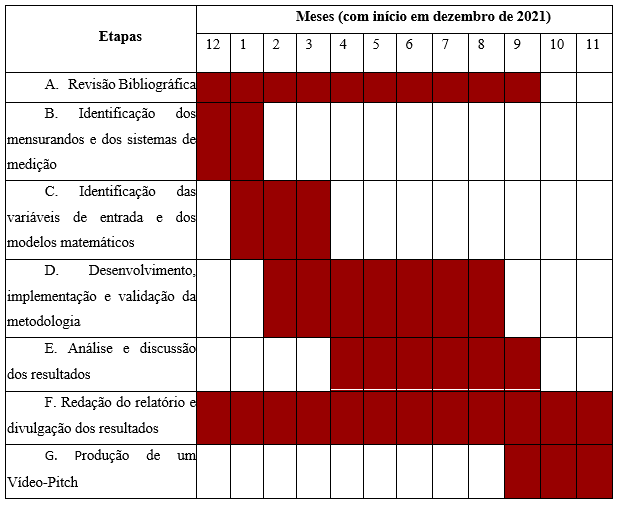
3.1 Revisão bibliográfica
Foi realizada uma ampla revisão bibliográfica sobre: tenacidade à fratura, incerteza de medição, enfatizando o guia para a expressão de incerteza de medição (GUM) e o de Monte Carlo.
3.1.1 Incerteza de medição
Quando relatado o resultado de medição de uma grandeza física deve-se sempre dar alguma indicação quantitativa da qualidade do resultado, de forma que aqueles que o utilizam possam avaliar sua confiabilidade. Sem essa indicação, resultados de medição não podem ser comparados, seja entre eles mesmos ou com valores de referência fornecidos numa especificação ou numa norma (BIPM et al., 2008a). Desta forma é evidente que a necessidade da existência de um método que seja capaz de caracterizar a qualidade de um resultado de medição, isto é, que seja ideal para avaliação e expressão da incerteza do resultado de medição. Assim, atendo-se a fácil compreensão e ampla aceitação, deu-se a formulação do método GUM.
Aceito a nível internacional, sua facilidade de compreensão e utilização permitem seu desmembramento, o que facilita em casos de primeiro contato, ou até mesmo de organização, o estudo do mensurando. Assim, a seguir é desenvolvido e explicado as etapas e análises da aplicação do método GUM.
Toda medição tem como objetivo a determinação do valor do mensurando (LEAL, J.E.S., 2016), este é definido como uma grandeza específica submetida a ação de medição. O mensurando pode ser obtido de duas formas, a primeira, obtenção direta, como por exemplo medidas de comprimento, e a segunda, obtenção indireta, como áreas de superfícies e volumes. No caso da segunda forma, o mensurando é determinado a partir de outras a partir de N outras grandezas X1, X2,…,XN por uma relação funcional f, como descrito na Eq. (1).

As grandezas de entrada X1, X2,…,XN das quais a grandeza de saída Y depende estão suscetíveis as grandezas de influência. O INMETRO (2010a) define grandeza de influência como aquela grandeza que, em uma medição direta, não afeta o mensurando, mas a relação entre a indicação e o resultado de medição.
Há diversas grandezas de influência que podem ser citadas, dentre elas, as mais comuns são: variabilidade das leituras (desvio padrão); resolução finita do instrumento; incerteza associada à calibração do sistema de medição ou dos equipamentos que compõem o sistema de medição, efeitos das condições ambientais, como por exemplo temperatura, umidade, vibração mecânica, etc… A quantidade e os tipos encontrados variam, assim, o operador deve conhecer e realizar uma sondagem quanto ao princípio de funcionamento do sistema de medição utilizado, as principais fontes de erros que podem estar presentes e o procedimento de medição.
Definida esta primeira etapa, a variável de saída pode enfim ser descrita por meio de um modelo matemático. Uma vez descrito, neste deve ser aplicado a lei de propagação de incertezas de acordo com a Eq. (2), que permitirá calcular a incerteza-padrão combinada associada ao mensurando em questão.
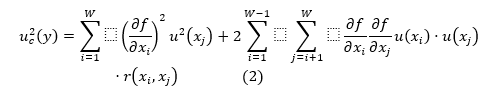
Na Eq. (2), o valor de y é a estimativa da variável de saída Y, xi é a estimativa da variável Xi, u2(xi) é a variância associada à xi, para i variando de 1 a W, W é o número de variáveis que afetam o resultado da medição de Y, u(xi) é a incerteza-padrão associada à estimativa xi e r(xi,xj)é o coeficiente de correlação entre a estimativa xi e xj. O segundo termo da equação expressa a correlação entre as duas fontes de incerteza xi e xj, i ≠ j. Quando não houver correlação (r = 0)a Eq. (2) reduz-se a Eq. (3)

Sobrando apenas o primeiro termo que diz respeito ao cálculo das derivadas parciais e da incerteza-padrão. Quando utilizado estimativas das grandezas de entradax1, x2,…,xN é necessário destacar que cada estimativa de entrada xi e sua incerteza-padrão associada u(xi) são obtidas de uma distribuição de valores possíveis da grandeza de entrada Xi .
A distribuição de probabilidade pode ser dividida de duas formas, uma baseada na frequência, de série de observaçõesXi,k de Xi, e uma baseada na distribuição. Assim, foram definidos dois tipos de avaliação da incerteza-padrão, as avaliações do tipo A, para distribuições de frequência e avaliações do tipo B para distribuições.
As avaliações do tipo A se baseiam na frequência, logo para uma grandeza de entrada xi estimada a partir de n observações repetidas independentes Xi,k , a média aritmética (Eq. (4)) é usada como estimativa de entrada xi para determinar o resultado da medição y.

Variabilidade de leituras serão obtidas das n medições realizadas, dessa forma a variância experimental das observações é obtida pelo uso da Eq. (5).

A partir desta, extraindo-se sua raiz quadrada é possível obter o desvio padrão experimental que caracteriza a variabilidade das leituras da grandeza. No geral, pode-se dizer que os gráficos que representam as avaliações de incerteza-padrão do tipo A terão configuração de histogramas como exemplificado na Fig.1.
Figura 1.3 : Histograma
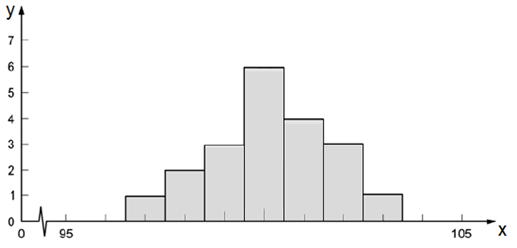
Caso a grandeza de entrada Xi não tenha sido obtida a partir de observações repetidas, a sua incerteza-padrão u(xi) é avaliada pelo tipo B. Neste tipo de avaliação, de acordo com BIPM et al., 2008ª, a base de avaliação se dá pelo julgamento científico baseando em todas as informações disponíveis sobre a possível variabilidade de Xi . Dentre essas informações é possível elencar dados de medições prévias, dados fornecidos em certificados de calibração e outros certificados, especificações do fabricante e entre outros. Assim é possível estimar a incerteza-padrão do tipo B para a grandeza e sua variância estimada.
Algumas observações devem ser realizadas quando analisado a incerteza-padrão do tipo B. A primeira delas diz que se incerteza da estimativa xi for declarada ser um determinado múltiplo de um desvio-padrão, a incerteza-padrão u(xi) é o valor mencionado dividido pelo multiplicador (Eq. (6)), e a variância estimada o quadrado desse quociente.

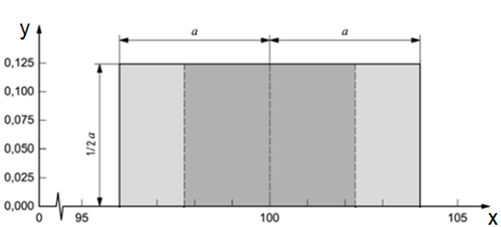
A segunda alerta ao caso em que com base nas informações disponíveis, podendo ser estabelecido que há uma chance de cinquenta por cento de que o valor da grandeza de entrada Xiesteja em um intervalo de a- até a+ pode ser suposto que a distribuição retangular (Fig. 2), dos valores possíveis da grandeza de entrada é aproximadamente normal e então a melhor estimativa xi de Xi pode ser representada pelo valor presente no ponto médio do intervalo. Admite-se o equacionamento desta como apresentado na Eq. (7).

Em outros casos onde se tem disponível o intervalo que ela pertence, entretanto, a chance de ela estar nesse intervalo é de dois em três, é possível assumir que a incerteza-padrão será dada pela Eq. (8).

Caso não se tenha conhecimento onde os valores possíveis de Xi possam estar dentro desse intervalo a incerteza-padrão passa a ser definida como descrito pela Eq. (9).

Figura 2.3 :Distribuição Retangular
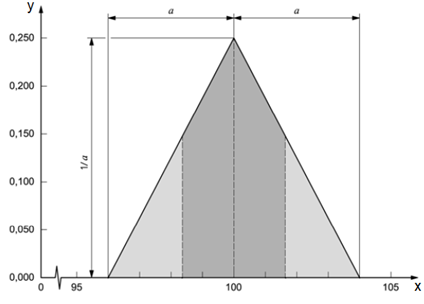
Em muitos casos, é mais realista esperar que valores perto dos limites sejam menos prováveis do que os que estejam perto do ponto médio (BIPM et al., 2008a). Assim, em relação a distribuição anterior, pode-se substituí-la por uma distribuição trapezoidal simétrica tendo lados inclinados iguais. Caso essa distribuição aproxime-se de uma distribuição triangular (Fig.3), a incerteza-padrão pode ser calculada por meio da Eq. (10).

Figura 3.3: Distribuição triangular
Caso a distribuição seja do tipo trapezoidal, a equação anterior modifica-se de tal forma como mostra a Eq. (11):

Pode-se definir três tipos de incerteza: a incerteza-padrão, a incerteza-padrão combinada e a incerteza expandida. Embora uc(y) possa ser universalmente usada para expressar a incerteza de um resultado de medição, em algumas aplicações comerciais, industriais e regulamentadoras, e quando a saúde e a segurança estão em questão, é muitas vezes necessário fornecer uma medida de incerteza que defina um intervalo em torno do resultado da medição […] (BIPM et al., 2008ª). É definido então incerteza expandida, uma medida adicional que satisfaz o requisito de fornecer este intervalo. Representada pela letra U , essa pode ser obtida pela multiplicação da incerteza-padrão combinada uc(y) por um fator de abrangência k (Eq. (12)).

O fator de abrangência k é escolhido em função do nível de confiança para o intervalo. No Anexo G da Recomendação INC-1 (1980) é discutido em G.6.6 que nos casos em que a distribuição é aproximadamente normal e os graus de liberdade efetivos são relativamente altos, o fator de abrangência é igual a 2,00 para um intervalo com um nível de confiança de 95,45 % e 3 para 99,73 % de confiança.
Para obter uma melhor aproximação do fator de abrangência outro método é proposto. Considerando que a variável e análise possua uma distribuição do tipo t-Student e seja do tipo aleatória normalmente distribuída, os graus de liberdade podem ser calculados pela Eq. (13).

Por fim, para que seja selecionado o fator de abrangência é necessário a utilização da tabela G.2 presente no Anexo G do documento da JCGM 2008. Caso o número de leituras n seja pequeno, caracterizando amostra pequena, não é verificado a distribuição t-Student e neste caso, deve ser utilizado o teorema do valor central junto com a tabela t-Student para definir o valor do fator de abrangência k baseado no grau de liberdade efetivo da incerteza-padrão combinada da medição. O cálculo do grau de liberdade efetivo é baseado na equação de Welch-Satterwaite e é expresso na Eq. (14).

Em que nesta equação tem-se: o número de variáveis de entrada (N), o número de graus de liberdade de cada variável de entrada ( veff ), incerteza-padrão combinada da variável de saída (uc(y)), incerteza-padrão de cada variável de entrada (u(xi)) e coeficiente de sensibilidade do mensurando em relação a cada variável de entrada yi (ci). O resultado de medição RM pode então ser expresso, como mostra a Eq. (14).

Na equação anterior, y é a estimativa de Y, mais especificadamente, seu valor médio e U(y) a incerteza expandida associada a y.
3.1.2 Métodos adicionais baseados no método GUM
Considerando o cenário atual de pandemia, o acesso a ambientes controlados e aos elementos necessários para ao estudo e aplicação do método GUM foram dificultados, assim, os métodos adicionais são introduzidos para resolver o caso em que um modelo de medição não pôde ser estabelecido, nesses casos entende-se que o modelo de medição não está disponível devido a dificuldades técnicas ou de restrições de custo. Nesta situação, um “modelo estatístico global” é usado representando uma simplificação do modelo de medição onde algumas grandezas de entrada foram combinadas. O desenvolvimento desses métodos adicionais não se restringe ao método GUM, seus desenvolvimentos levam em consideração outros métodos como os documentos internacionais e europeus EA 4/16 e a ISO 21748: 2010.
A justificativa destes métodos adicionais é exposta na seção 5.4.6.2 da ISO/IEC 17025 (ISO, 2016), em que afirmado que os laboratórios de teste devem ter e aplicar procedimentos para estimar a incerteza de medição e que em casos onde a natureza do método de teste pode impedir o cálculo rigoroso, metrologicamente e estatisticamente válido, da incerteza de medição, o laboratório deve pelo menos tentar identificar todos os componentes da incerteza e fazer uma estimativa razoável da incerteza. A estimativa razoável deve ser baseada no conhecimento do desempenho do método e no escopo da medição e deve fazer uso de, por exemplo, experiência anterior e dados de validação.
Com o intuito de simplificar os casos de aplicação destes métodos adicionais, faz-se uso da Fig. 4 para compreensão dos motivos aos quais são levados a sua aplicação, motivos esses que são resumidos nas situações distintas em que um modelo de medição está disponível e o caso em que um modelo de medição (modelo físico) não pode ser estabelecido.
Figura 4.3 : Fluxograma de métodos de avaliação da incerteza (ADAPTADO)
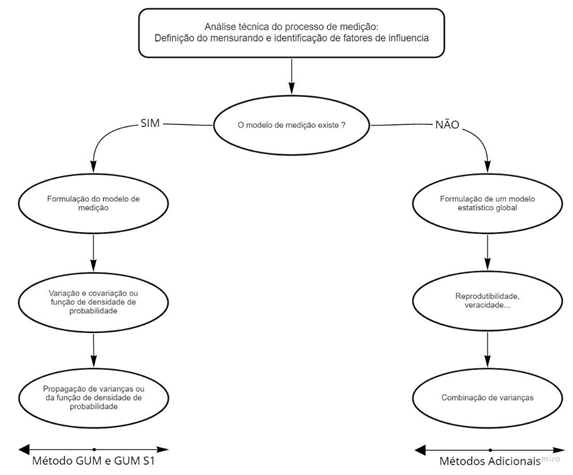
Desta forma, assumindo que não é possível estabelecer um modelo de medição para o mensurando, devido a dificuldades técnicas ou restrições de custo, o ‘modelo estatístico” é assumido e representa uma simplificação do modelo de medição onde algumas grandezas de entrada foram combinadas. O modelo (Eq. (15)), inspirado em um descrito na ISO 21748 (ISO, 2017), expressando o resultado da medição em função de um valor verdadeiro (desconhecido), correções para a compensação de diferentes efeitos sistemáticos e um erro residual pode ser estabelecido.

Em que na equação y representa o resultado calculado pela função definida apropriada, m o valor verdadeiro, δ a correção de tendência,cizi o fator de efeito de influencia e seus coeficientes de sensibilidade e e o erro aleatório das condições de repetibilidade. A função apropriada para o cálculo do resultado de medição (Eq. (16)) é escrita como:

Similar a equação descrita anteriormente com a diferença de que o valor verdadeiro é substituído pela indicação fornecida pelo sistema de medição l Conforme o fluxograma (Fig. 4) após definir o modelo estatístico global, faz-se necessário o estudo de elementos como variância, repetibilidade, confiabilidade e a combinação desses elementos. A estimativa da variância do resultado da medição é obtida pela aplicação da lei de propagação da incerteza (Eq. (17)).
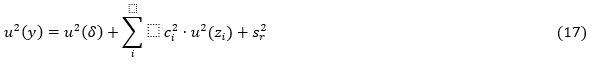
Onde seus termos representam respectivamente a incerteza devido a tendência(u(δ)) , incerteza devido ao fator de influência(u( zi)) e o valor estimado(sr 2)para a variança do erro aleatório e . Considerando que a variância da reprodutibilidade é a soma da variância da repetibilidade e das diferentes variâncias é assumido a equação 18.

Assim, agrupando as Eqs. (17) e (18), é obtido a Eq. (19) que representa a combinação de confiabilidade e reprodutibilidade de medição.

A avaliação da incerteza deve ser realizada considerando todas as informações disponíveis, assim recomenda-se as análises do design experimental para validação do método, testes de proficiência periódicos para checagem de performance do laboratório e estudos inter-laboratoriais conforme estabelecido na ISO 5725 (ISO,2018).
3.1.3 Incerteza de medição: Método Monte Carlo
É plausível afirmar a esse ponto que a aplicação do método GUM permite ao engenheiro poder estimar com maior assertividade o comportamento de um componente diante de esforços mecânicos, uma vez que pelo GUM é possível identificar e quantificar a qualidade do material do material utilizado.
O controle de qualidade do processo produtivo do material bruto ao produto acabado, é crítico no monitoramento de defeitos e permite a tomada de decisão e a qualidade do produto final (TREVISIAN e KAPPER, 2015). Dessa forma, quanto maior a quantidade de fatores considerados e maior a gama de análise realizada, mais confiável são os dados entregues.
Dependendo da complexibilidade, grau de não linearidade e a assimetria dos dados de entrada que serão analisados, a descrição da função matemática para cada fonte de incerteza se tornar cada vez mais complexa, tornando recomendável determinar a incerteza de medição através de outros métodos como o de Monte Carlo.
O método de Monte Carlo (MMC) pode ser descrito como um método estatístico, no qual se utiliza uma sequência de números aleatórios para a realização de uma simulação (GONÇALVES e PEIXOTO, 2015) ou, ainda, um método de amostragem artificial que opera numericamente sistemas complexos com valores de entrada independentes (BRUNI, 2008). A simulação de Monte Carlo é de fácil implantação e retorna informações completas sobre a distribuição de probabilidade. No entanto, possui algumas limitações: o tempo de simulação pode ser longo em alguns casos de maior complexidade e a seleção das distribuições de probabilidade para os dados de entrada pode ser difícil devido à inexatidão dos dados ou a um pouco entendimento do processo (KAPPER, 2018). O MMC pode ser descrito como um procedimento passo-a-passo e é mostrado esquematicamente na Fig. 5.
Figura 5.3 :Etapas de propagação e resumo de avaliação de incerteza usando o MMC para implementar a propagação de distribuições (fonte: JCGM 101:2008)
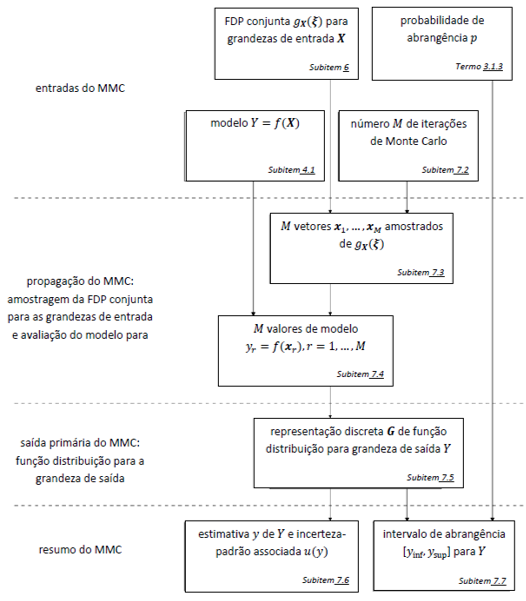
Partindo da primeira etapa do MMC, nota-se que um objetivo inicial é a formulação do modelo matemático de medição da grandeza estudada (Eq. (20)).

Nela Y representa a grandeza de saída (mensurando) e X representa as N grandezas de entrada(X1,…,XN)T das quais Y depende. Cada Xi é considerado uma variável aleatória com possíveis valores ξi e esperança xi.
É possível atribuir a essas variáveis aleatórias funções densidade de probabilidade (FDP’s), representadas por gxi(ξi) – gaussianas (normais), retangulares (uniformes), ou outras adequadas – que permitirão a obtenção da FDP da variável Y. A propagação das FDP’s (gxi(ξi), i=1,..,N) das grandezas de entrada Xi com o uso do modelo, para fornecer a FDP gy(n) para a grandeza de saída Y, está ilustrada na Fig. 6.
Figura 6.3: Ilustração da da propagação de distribuições das grandezas de entrada
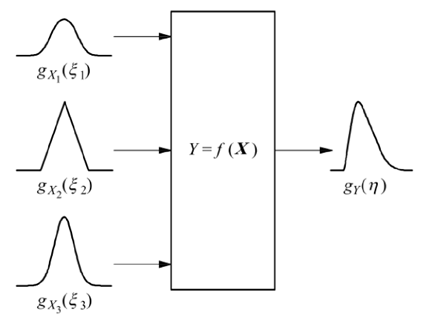
Uma variedade de FDP’s podem ser determinadas para as variáveis aleatórias e sua atribuição é realizada com base em uma análise de uma série de indicações ou em julgamento científico usando outras informações, como dados históricos, julgamento de especialistas e entre outros. Na Figura 7 é possível visualizar algumas dessas FPD’s, bem como as informações disponíveis quanto a distribuição. Destas será exposto de maneira resumida as FDP’s retangular e gaussiana.
Figura 7.3: Informação disponível e a FDP atribuída

Se as informações disponíveis da grandeza X forem apenas seus limites inferior a e superior b, com a < b, então, assume-se e atribui-se a X uma distribuição retangular R(a,b) com intervalo [a,b]. Nesta distribuição são definidos gx(ξ), esperança e variância de X como:
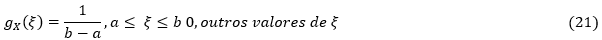

Para que a amostragem possa ser realizada é necessário utilizar valores aleatórios de r provenientes da distribuição retangular padronizada R(0,1). Com esses valores em mãos é possível obter:

Em distribuições do tipo gaussiana as únicas informações disponíveis a respeito de uma grandeza X são: uma melhor estimativa x e a incerteza-padrão associada u(x). Assim, a função gx(ξ), esperança e variância de X são atribuídas de tal forma que suas expressões são apresentadas como:
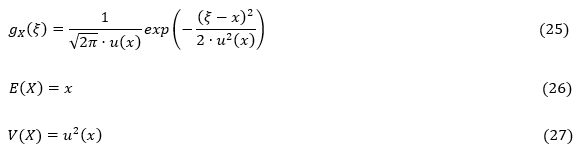
De acordo com o princípio da máxima entropia, é atribuído a destruições gaussianas uma distribuição de probabilidade N(x, u2(x)) que, a partir desta, é tomado aleatoriamente valores z provenientes da distribuição gaussiana padronizada N(0,1) para obtenção de ξ (Eq. (28)).

A implementação do MMC inicia-se com a definição do número M de iterações a serem executadas. A JCGM 101:2008 informa por meio de uma nota que um valor de 106 iterações já fornece em geral um alto intervalo de abrangência 95%. Ela ainda recomenda que a seleção do valor de M que seja pelo menos 104 vezes maior que 1/(1-p), onde p é a probabilidade de abrangência definida. Em seguida M vetores xr, r = 1,…,M são amostrados a partir das FDPs gx(ξi) das N grandezas de entrada Xi e assim obtém-se os valores do modelo yr = f(xr).
Uma vez definidos os valores, a representação discreta da função distribuição para a grandeza de saída é obtida por meio da organização dos valores do modelo em ordem crescente e, aplicando se necessário, uma perturbação numérica nos resultados para eventuais valores replicados. Assim é obtido a representação discreta G da função distribuição Gy(n). Alocando os valores do modelo em um histograma, adequadamente construindo, é possível visualizar uma distribuição de frequência que, quando normalizada, fornece uma aproximação para a FDP gy(n)de Y. Uma vez obtido os M valores da variável de saída é possível estimar sua média e desvio padrão.
3.2. Identificação dos mensurandos e dos sistemas de medição
Em virtude do estudo circundar a obtenção e análise dos resultados obtidos do módulo de elasticidade dos materiais ensaiados, exibe-se abaixo a Eq. (29) que descreve a expressão que permite a obtenção do módulo de elasticidade dos materiais.

Por meio da relação entre tensão e deformação presente na equação anterior, é possível compreender e identificar os mensurandos a serem estudados. Dessa forma é exposto através do desenvolvimento doas equações 30, 31, 32 e 33 as variáveis que deverão ser mensuradas e estudadas.

Dessa forma é evidente que as variáveis a serem mensuradas e estudadas para que o resultado final possa ser tratado são: o diâmetro D do corpo de prova cilíndrico, a altura Ca e o comprimento da base Cb do corpo de prova retangular, o comprimento de alongamento L que o material apresenta ao ser ensaiado, e as áreas, forças e módulo de elasticidade associadas aos corpos de prova cilíndrico e retangular.
Para que tais mensurandos possam ser avaliados, foiutilizado um paquímetro digital do fabricante Mitutoyo, com faixa nominal de 150 mm e resolução de 0,01 mm. No Anexo II deste presente neste documento é possível acessar o certificado de calibração e nele registrar sua incerteza expandida, incerteza expandida associada ao desvio de paralelismo das superfícies de medição externas (Ime), fator de abrangência e determinar a probabilidade de abrangência. Além do instrumento anteriormente citado também será utilizado uma célula de carga presente na máquina de testes universal Instron® que apresenta uma faixa nominal de 2 kN e resolução de 0,0001 kN. No Anexo III é possível visualizar seu certificado de calibração e registrar sua incerteza expandida. Por último, será também utilizado um extensômetro também presente na máquina de testes universal Instron® apresenta uma faixa nominal de 25 mm e resolução de 0,0001 mm. No Anexo IV é possível observar seu certificado de calibração e notar os erros relacionados ao deslocamento e à incerteza considerada. A máquina de testes universal da Instron® também conta com um certificado de calibração, este está disponível por meio do Anexo I.
3.3. Identificação das variáveis de entrada e dos modelos matemáticos
Para que as etapas futuras possam ser desenvolvidas faz-se necessário a identificação das variáveis de entrada e dos modelos matemáticos a serem utilizados. Dessa forma, analisando cada mensurando, nota-se que associadas à medição da altura, base e diâmetro com o paquímetro digital são: a resolução do paquímetro (R), a variabilidade das leituras (x̅) a incerteza associada à calibração do paquímetro (C) e a incerteza associada o desvio de paralelismo para medidas externas (Ime), declarado no certificado de calibração.
Relacionado a medição da força aplicada no ensaio, o certificado de calibração da célula de carga permite identificar variáveis como: a variabilidade das leituras (x_), a resolução da célula de carga (Rcc) e a incerteza associada à calibração da célula de carga (Ccc).
Por fim, relacionado ao extensômetro, o certificado de calibração permite identificar: a variabilidade das leituras (x_), a resolução do extensômetro (Re) e a incerteza associada à calibração do extensômetro (Ce).
3.4. Desenvolvimento, implementação e validação da metodologia
Em consequência do desenvolvimento dos itens anteriores foi possível aplicar a lei de propagação de incertezas no modelo matemático e com a utilização do software Matlab® desenvolver um código que permita calcular e obter os resultados de incerteza associados à obtenção do módulo de elasticidade dos corpos de prova ensaiados, sendo considerado ensaios que envolvem como resolução a obtenção da incerteza expandida média associada ao módulo de elasticidade de um corpo de prova e a incerteza expandida e módulo de elasticidade médio associado a um tipo de corpo de prova.
Nos Anexos V e VI é possível constatar os códigos desenvolvidos para ambos os corpos de prova. Justifica-se a produção de dois códigos diferentes para melhor identificação do cálculo realizado, melhor organização e separação das análises que envolvem o ensaio, e diminuição das linhas de códigos necessários para compilação.
Com a finalização dos códigos os mesmos foram testados, comparados com sua versão anterior e revisados pela professora orientadora para que os resultados obtidos pudessem ser validados e certificados.
3.5 Análise e discussão dos resultados
Dentre as análises de incerteza realizadas sobre o módulo de elasticidade dos corpos de prova analisados, constatou-se que as incertezas associadas às variáveis que compõem o cálculo do módulo de elasticidade foram pequenas, com as mesmas sendo menores que 1.
Seguindo essa tendência de comportamento, o mesmo foi observado no cálculo na incerteza associada aos módulos de elasticidade dos corpos de prova, onde em ambos foi identificado pequenos valores associados à incerteza, o que permite constatar que os valores obtidos são confiáveis e de alta qualidade.
3.6 Redação do relatório e divulgação dos resultados
Simultaneamente à revisão bibliográfica foi realizada a identificação dos mensurandos e dos sistemas de medição. Apresentando menos dificuldade que o citado anteriormente, esta etapa da pesquisa foi realizada de forma segura e confiável de modo a produzir ótimos resultados ao final de seu desenvolvimento. Relaciona-se a menor dificuldade de realização desta etapa com conhecimento anterior de metrologia que foram introduzidos pela orientadora que facilitam seu desenvolvimento.
Uma vez finalizado o item anterior, o próximo se mostrou mais complexo, dado sua natureza, mas não foi tanto quanto poderia. Dado a experiência na universidade com as aulas de metrologia e cálculo, a definição das variáveis de entrada e os modelos matemáticos a serem utilizados foi realizada com fluência e sem muitas adversidades.
O desenvolvimento, implementação e validação da metodologia mostrou-se o maior desafio sobre a pesquisa. A princípio determinou-se a necessidade de formular um código utilizando o software Matlab® para que o tratamento dos dados obtidos pudesse ser implementado e a validação dos resultados obtidos pudesse ser realizada. No software optou-se por utilizar o formato live script de código que permite a melhor visualização do tratamento dos dados e apresentação do obtido da análise metrológica. Alguns desafios foram encontrados com a inserção dos modelos matemáticos e leitura de dados previamente adquiridos, entretanto com a utilização dos fóruns e biblioteca virtual do próprio software foi possível desenvolvê-los.
Com o intuito de atingir o objetivo da pesquisa e apresentar um programa que permitisse a quem utilizá-lo fácil compreensão do que está sendo realizado, foi feito o refinamento do código com implementação de lógicas mais simples de programação e explicações acerca das etapas de análises presentes. Não somente isso, foram realizadas reuniões com a orientadora para que os resultados obtidos pudessem ser analisados em conjunto e discutidos caso estejam apresentando qualquer anormalidade.
Por fim concluiu-se que o projeto pode ser realizado de forma contundente e eficiente graças à orientação da professora e disponibilidade de recursos presentes na internet e universidade que permitiram tornar as etapas mais desafiadoras do projeto menos trabalhosas. Os resultados finais foram satisfatórios apresentando ao longo de seu desenvolvimento baixos valores de incertezas associadas às variáveis, o que indica precisão dos equipamentos e conhecimento de utilização destes por parte dos operadores.
4 RESULTADOS PARCIAIS
Referente a identificação dos mensurados, seu sistema de medição e a implementação de seus modelos matemáticos, foram elaboradas duas tabelas respectivamente, Tab. 1.4 e Tab. 2.4, com o intuito de facilitar seu reconhecimento e permitir uma melhor apresentação e organização destes.
Tabela 1.4 : Mensurandos e sistema de medição
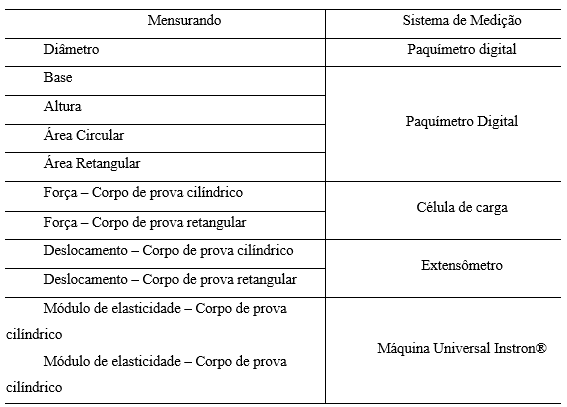
Tabela 2.4 : Modelos matemáticos de cada mensurando

A análise dos dados obtidos é realizada com o apoio do software Matlab®, uma vez que os códigos parciais são extensos e com diversas linhas de comando, os Anexos V e VI, presentes neste documento visam a facilitação e melhor apresentação destes. Por se tratar de um código parcial e não completo alguns erros de português podem ser identificados.
5 RESULTADOS FINAIS
Para que o código pudesse ser finalizado, aplicou-se a lei da propagação de incertezas para que fosse possível obter as expressões que possibilitaram o cálculo das incertezas padrão combinada das variáveis (Tab.1.5) obtidas.
Tabela 1.5 : Incertezas Padrão Combinadas

Com as equações definidas, as etapas seguintes do código puderam ser concluídas possibilitando o cálculo da incerteza padrão combinada associada ao módulo de elasticidade que permitiu posteriormente que fosse calculada a incerteza padrão expandida associado ao módulo de elasticidade do corpo de prova cilíndrico e retangular (Tab 2.5). Desta-se ainda que nessas etapas que foi implementado uma lógica que permitisse a obtenção simultânea de três conjunto de dados das variáveis de entrada e módulo de elasticidade para que fosse possível obter a médias de seus valores e incertezas para diferentes corpos de prova.
Tabela 2.5 : Módulo de Elasticidade
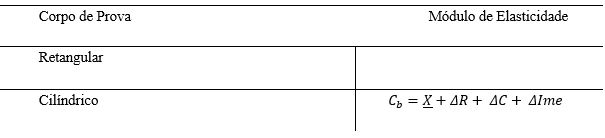
É possível concluir dos resultados que os dados associados às variáveis de entrada foram obtidos de forma confiável e que os instrumentos utilizados para tal são confiáveis para o objetivo proposto desse projeto. As incertezas padrão expandidas dos módulos de elasticidade apresentaram-se com valores baixo indicando precisão e exatidão dos dados obtidos e de seu tratamento. Nos Anexos V e IV é possível visualizar todo o código responsável pelo tratamento dos dados citados, bem como os valores obtidos de incerteza.
BIBLIOGRAFIA
ABNT – Associação Brasileira de Normas Técnicas, “NBR ISSO/IEC 17025 – Requisitos gerais para competência de laboratórios de ensaio e calibração”. Rio de Janeiro, 2017, 20p.
AMIRI, S.; LECIS, N.; MANES, A.; GIGLIO, M. “A study of a micro-indentation technique for estimating the fracture toughness of Al6061-T6”. Mechanics Research Communications, v. 58, p. 10-16, 2014.
ANDERSON, T. L., “Fracture Mechanics: Fundamentals and Applications”. 3ª Ed. New York: CRC Press, 2005.
ASTM E1820, “Standard Test Method for Measurement of Fracture Toughness”. ASTM International, West Conshohocken, 2018.
ASTM E399, “Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials”. ASTM International, West Conshohocken, 2019.
BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 100 – “Evaluation of Measurement Data – Guide to the Expression of Uncertainty in Measurement”. 2008a.
BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML. JCGM 101 – “Evaluation of measurement data — Supplement 1 to the “Guide to the expression of uncertainty in measurement” — Propagation of distributions using a Monte Carlo method”. JCGM 101, 2008b. 90 p.
BYUN, T. S.; KIM, J. W.; HONG, J. H. “A theoretical model for determination of fracture toughness of reactor pressure vessel steels in the transition region from automated ball indentation test”. Journal of Nuclear Materials, v. 252, n. 3, p. 187-194, 1997.
DÉSENFANT, M., PRIEL, M., “Reference and additional methods for measurement uncertainty evaluation”. Measurement 95:339–344. 2017. Disponível em: <https://doi.org/10.1016/j.measurement.2016.10.022>
HAGGAG, F. M.; NANSTAD, R. K.; HUTTON, J. T.; THOMAS, D. L.; SWAIN, R. L. “Use of automated ball indentation testing to measure flow properties and estimate fracture toughness in metallic materials. In: Applications of automation technology to fatigue and fracture testing”. ASTM International, 1990.
HE, M.; LI, F.; CAI, J.; CHEN, B. “An indentation technique for estimating the energy density as fracture toughness with Berkovich indenter for ductile bulk materials”. Theoretical and applied fracture mechanics, v. 56, n. 2, p. 104-111, 2011.
IRWIN, G.R., “Analysis of stresses and strains near the end of a crack traversing a plate”. J Appl Mech, 1957. 24:361-64.
JEON, S. W.; JEON, S. W.; LEE, K. W.; KIM, J. Y.; KIM, W. J.; PARK, C. P.; KWON, D. “Estimation of fracture toughness of metallic materials using instrumented indentation: critical indentation stress and strain model. Experimental Mechanics”. v. 57, n. 7, p. 1013-1025, 2017.
LEE, J. S.; JANG, J. I.; LEE, B. W.; CHOI, Y.; LEE, S. G.; KWON, D. “An instrumented indentation technique for estimating fracture toughness of ductile materials: A critical indentation energy model based on continuum damage mechanics”. Acta materialia, v. 54, n. 4, p. 1101-1109, 2006.
MATHEW, M. D.; MURTY, K. L.; RAO, K. B. S.; MANNAN, S. L. “Ball indentation studies on the effect of aging on mechanical behavior of alloy 625”. Materials Science and Engineering: A, v. 264, n. 1-2, p. 159-166, 1999.
MOHAMMADI, A. H.; NADERI, M.; IRANMANESH, M. “Fracture toughness evaluation of 3Cr-1Mo steel from Vickers indentation and tensile test data”. Procedia Engineering, v. 10, p. 228-235, 2011.
NICOLOSI, E. R. “Avaliação de Métodos Analíticos para Determinação de Propriedades Mecânicas de Aços Via Ensaio de Macroindentação Instrumentada”. 2015. 308 p. Dissertação de Mestrado, Universidade Federal de Uberlândia, Uberlândia.
RANGEL, E. R. “Fracture Toughness Determinations by Means of Indentation Fracture”. In: CUPPOLETTI, J. (Ed.). Nanocomposites with unique properties and applications in medicine and industry. Croatia, 2011. p. 21-38.
RICE, J. R., “A path independent integral and the approximate analysis of strain concentration by notches and cracks”. J Appl Mech, 1968. 35:379-86. Disponível em: <https://doi.org/10.1115/1.3601206>
WELLS, A. A., “Application of fracture mechanics at and beyond general yielding”. Br Weld J, 1963. 10:563-70.
ZHANG, T.; WANG, S.; WANG, W. “A unified energy release rate based model to determine the fracture toughness of ductile metals from unnotched specimens”. International Journal of Mechanical Sciences, v. 150, p. 35-50, 2019.
ZHU, X. K., JOYCE, J. A., “Review of fracture toughness (G, J, CTOD, CTOA) testing and standardization”. Engineering Fracture Mechanics, p. 1-42, 2012. Disponível em: <https://doi.org/10.1016/j.engfracmech.2012.02.001>
ANEXO I – Certificado de calibração máquina de teste universal instron®

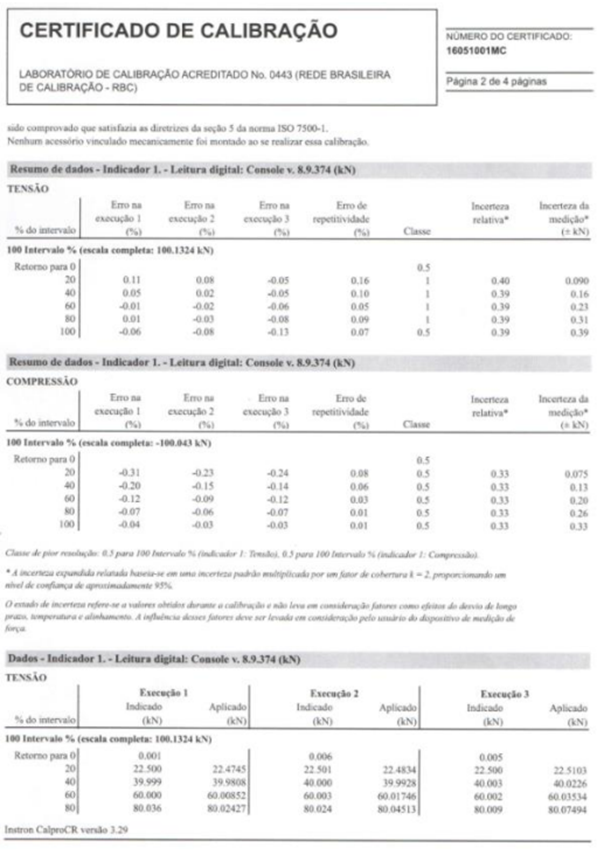
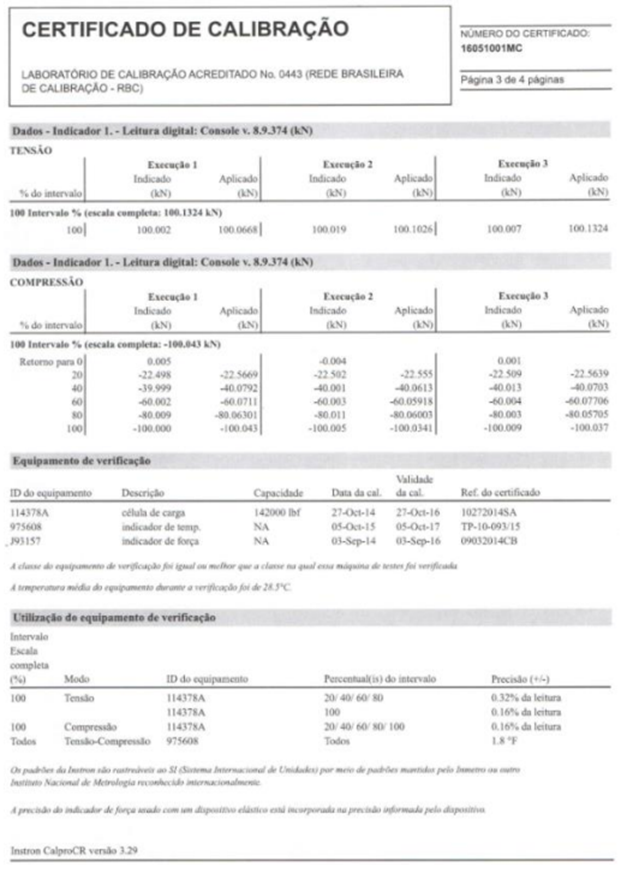

ANEXO II – Certificado de calibração paquímetro digital

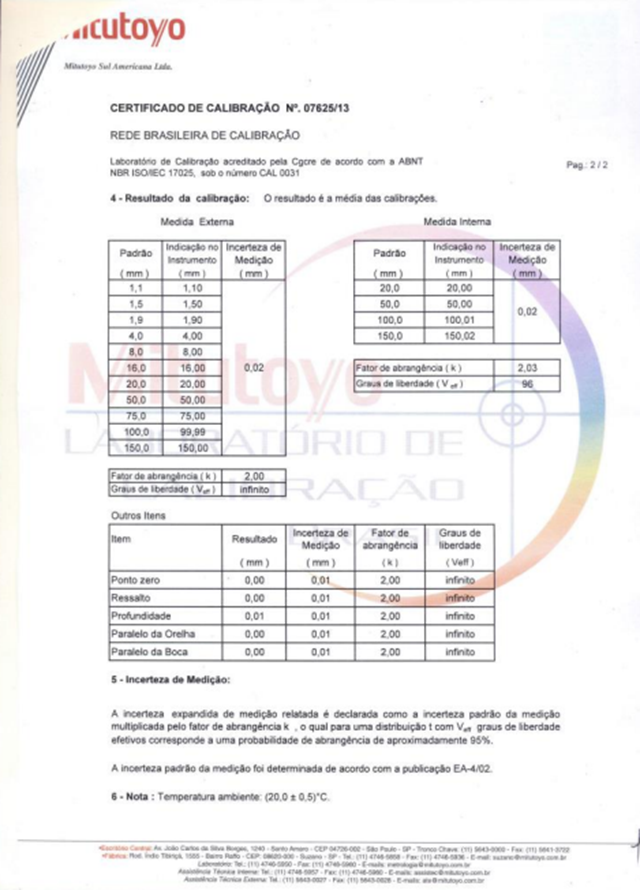
ANEXO III – Certificado de calibração extensômetro
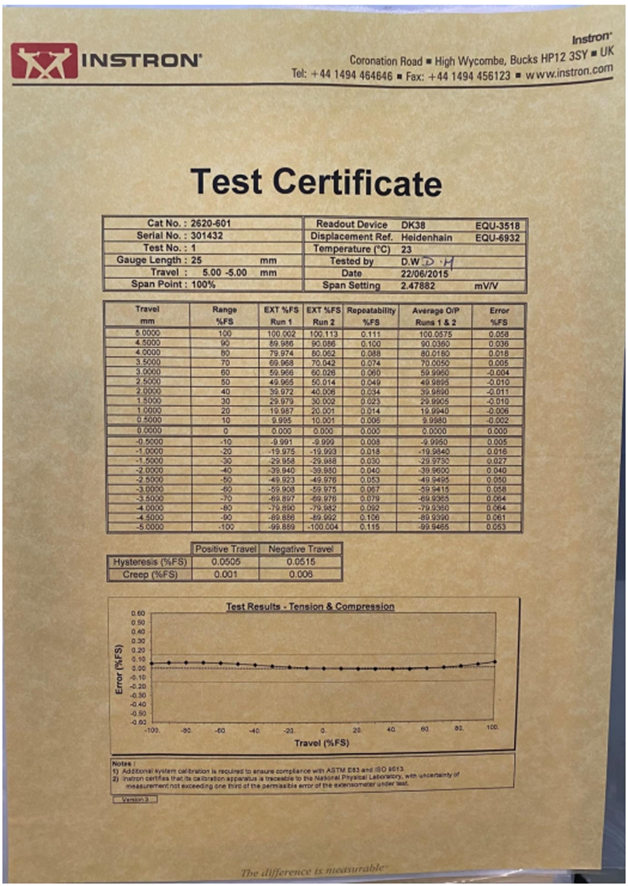
ANEXO IV – Certificado de calibração da célula de carga

ANEXO V – Código Matlab® de avaliação de incerteza do modulo de elasticidade do corpo de prova cilíndrico

Código responsável pela tratamento,cálculo e análise dos resultados obtidos do ensaio de Tencacidade à fratuta obtida via indentação instrumentada aplicado a um corpo de prova cilindrico
Inicialmemte faz-se necessário a inicialização do programa,dessa forma utiliza-se os comandos clc (Clear Command Window),clear all e close all. O primeiro comando responsável por limpar a janela Command Window ,o segundo por remover os itens da janela Workspace,e o terceiro por fechar as janelas abertas peloMatlab®2021a.
clc;clear all;close all;
1 Incerteza associada a medição do diâmetro do corpo de prova cilíndrico
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilha” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição do corpo de prova do diâmetro.
planilha = 2;
Uma vez expresso para o código a planilha que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados do diâmetro do corpo de prova utilizando o comando xlsread,e em seguida os dados são salvos na variável “diametros.medidas”. Para que em conjunto da variável “diametro.dados”,seja impresso a tabela com o titulo “Dados de medição”,é utilizado o comando table,para que por meio da variável “Tdiametrosmedidas” seja impresso a tabela contendo os dados adquiridos.
diametros.medidas = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha,’A:A’);
diametros.titulo.medidas = [“Dados de medição”];
T_diametros_medidas = table(diametros.medidas,’VariableNames’,diametros.titulo.medidas)
Após a leitura dos dados de medição presentes na planilha,é possivel atravez dos comandos mean,std e length é possivel apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “diametros.media”,”diametros.desvio_padrao” e “diametros.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
diametros.leituras = length(diametros.medidas);
diametros.media = mean(diametros.medidas);
diametros.desvio_padrao = std(diametros.medidas);
diametros.titulo.estatisticos = [“Média”,”Desvio Padrão”,”Tamanho da Amostra”];
T_diametros_estatisticos = table(diametros.media,diametros.desvio_padrao,diametros.leituras,’VariableNames’,diametros.titulo.estatisticos)
1.2 Incerteza Padrão Associada às Variáveis de Entrada
Utilizando os dados obtidos anteriormente é possivel calcular a incerteza padrão associada à variabilidade das leituras. Entretante,antes de realizar tal calculo,para que todas as incertezas padrão associadas às variaveis de entrada sejam calculadas,torna-se necessário a obtenção dos dados de resolução do equipamento de medição utilizado,a incerteza expandida associada a calibração do sistema de medição,o fator de abrangência,a incerteza expandida associada ao erro de paralelismo para medição externa e seu fator de abrangência correspondente. Todos os citados anterioremente estão disponiveis no certificado de calibração do equipamento.
diametros.resolucao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha,’B2′);
diametros.fator_de_abrangencia.calibracao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha,’C2′);
diametros.incerteza_expandida.calibracao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha,’D2′);
diametros.incerteza_expandida.paralelismo = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha,’E2′);
diametros.fator_de_abrangencia.medidas_externas = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha,’F2′);
diametros.titulo.sistema_de_medicao = [“Resolução”,”Fator de Abrangência para Calibração”,”Incerteza Expandida Associada à Calibração”,”Incerteza Expandida Associada ao Erro de Paralelismo”,”Fator de Abrangência para Medidas Externas”];
T_diametros_sistema_de_medicao = table(diametros.resolucao,diametros.fator_de_abrangencia.calibracao,diametros.incerteza_expandida.calibracao,diametros.incerteza_expandida.paralelismo,diametros.fator_de_abrangencia.medidas_externas,’VariableNames’,diametros.titulo.sistema_de_medicao)
Realizado a leitura dos dados citados anterioremente,é possivel calcular a incerteza padrão associada a variabilidade das leituras,a incerteza padrão associada à resolução do sistema de medição,a incerteza padrão associada à calibração do sistema de medição e a incerteza padrão associada ao desvio de paralelismo entre as superfícies de medição para externas do paquímetro. Cada um é obtido por meio da razão de dois elementos,o primeiro pela razão entre o desvio padrão das leituras e a raiz das “n” medições realizadas,o segundo pela resolução do sistema de medição e duas vezes o numero de leituras,o terceiro entre a a incerteza expandida e o fator de abrangência associados à calibração do sistema de medição e o ultimo pela incerteza expandida e o fator de abrangência associado ao erro de paralelismo para medição externa.
%Incertezas Padrão Associadas às Variáveis de Entrada
diametros.incerteza_padrao.variabilidade = diametros.desvio_padrao/sqrt(diametros.leituras);
diametros.incerteza_padrao.resolucao = diametros.resolucao/(2*sqrt(diametros.leituras));
diametros.incerteza_padrao.calibracao = diametros.incerteza_expandida.calibracao/diametros.fator_de_abrangencia.calibracao;
diametros.incerteza_padrao.paralelismo = diametros.incerteza_expandida.paralelismo/diametros.fator_de_abrangencia.medidas_externas;
diametros.titulo.incerteza_padrao = [“Incerteza Variabilidade das Leituras”,”Incerteza Resolução Do Sistema De Medição”,…
“Incerteza Calibração Do Sistema De Medição”,”Incerteza Desvio de Paralelismo Superfícies Externas”];
T_diametros_incerteza_padrao = table(diametros.incerteza_padrao.variabilidade ,diametros.incerteza_padrao.resolucao,…
diametros.incerteza_padrao.calibracao,diametros.incerteza_padrao.paralelismo,’VariableNames’,diametros.titulo.incerteza_padrao)
1.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
diametros.incerteza_padrao.saida = sqrt(diametros.incerteza_padrao.variabilidade ^2 + diametros.incerteza_padrao.resolucao^2 + diametros.incerteza_padrao.calibracao^2 + diametros.incerteza_padrao.paralelismo ^2);
diametros.titulo.saida = [“Incerteza Padrão Combinada Associada a Variável de Saida”];
T_diametros_incerteza_combinada_saida = table(diametros.incerteza_padrao.saida,’VariableNames’,diametros.titulo.saida)
Anteriormente a obtenção da incerteza expandida associada à vaiável de saída,é realizado os cálculos envolvendo os graus de liberdade efetivos e o fator de abrangência da medição. Dado a natureza de como foi realizado as medições,considera-se uma probabilidade de abrangência e é calculado em seguida o numero efetivo de graus de liberdade para que seja possivel a obtenção do fator de abrangência..
diametros.incerteza_combinada.probabilidade = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha,’G2′);
diametros.liberdade = (diametros.incerteza_padrao.saida^4)/(((diametros.incerteza_padrao.variabilidade )^4)/2);
diametros.fator_de_abrangencia.expandida = tinv(diametros.incerteza_combinada.probabilidade,diametros.liberdade);
diametros.titulo.incertezas.saida.liberdade = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
Tdiametros_liberdade = table(diametros.incerteza_combinada.probabilidade,diametros.liberdade,diametros.fator_de_abrangencia.expandida,’VariableNames’,diametros.titulo.incertezas.saida.liberdade)
Dessa forma,pelo produto entre o fator de abrangência associada a incerteza padrão associada a variável de saída com a incerteza padrão combinada asssociada a variável de saída,obtem-se a incerteza expandida associada a variável de saída.
diametros.incerteza_expandida.saida = diametros.fator_de_abrangencia.expandida*diametros.incerteza_padrao.saida;
diametros.titulo.contribuicao = [“Incerteza Expandida Associada à Variável de Saída”];
Tdiametros_liberdade = table(diametros.incerteza_expandida.saida,’VariableNames’,diametros.titulo.contribuicao)
1.3 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
diametros.contribuicao.variabilidade = (diametros.incerteza_padrao.variabilidade^2/diametros.incerteza_expandida.saida^2)*100;
diametros.contribuicao.resolucao = (diametros.incerteza_padrao.variabilidade^2/diametros.incerteza_expandida.saida^2)*100;
diametros.contribuicao.calibracao = (diametros.incerteza_padrao.calibracao^2/diametros.incerteza_expandida.saida^2)*100;
diametros.contribuicao.paralelismo = (diametros.incerteza_padrao.paralelismo^2/diametros.incerteza_expandida.saida^2)*100;
diametros.titulo.contribuicao = [“Contribuição Variável de Saída %”,”Contribuição Resolução %”,”Contribuição Calibração %”,”Contribuição Paralelismo %”];
Tdiametros_contribuicao = table(diametros.contribuicao.variabilidade,diametros.contribuicao.resolucao,diametros.contribuicao.calibracao,diametros.contribuicao.paralelismo,’VariableNames’,diametros.titulo.contribuicao)
1.4 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,diametros.media,diametros.incerteza_expandida.saida);
diametros.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_diametros_resultado = table(“RM =”,diametros.media,”+-“,diametros.incerteza_expandida.saida,’VariableNames’,diametros.titulo.resultado)
2. Incerteza Padrão Asssociada à Área do Corpo de Prova Cilíndrico
Referente a incerteza padrão associada à área,utiliza-se inicialmente o valor da média das medições do diâmetro para obtenção da área média e posteriormente para obtenção da incerteza padrão associada a área.
area.media = pi*diametros.media^2/4;
area.incerteza_padrao.area = sqrt(((pi*diametros.media/2)^2)*diametros.incerteza_padrao.saida^2);
area.titulo.area = [“Área Média”,”Incerteza Padrão Associada a Área”];
T_area_incerteza = table(area.media,area.incerteza_padrao.area,’VariableNames’,area.titulo.area)
2.1 Incerteza Expandida Associada à Variável de Saìda Àrea
Obtido o valor de incerteza padrão e utilizando a mesma probabilidade de abrangência utilizada anterioremnte,calcula-se os graus de liberdade efetivos e determina-se o fator de abrangência associado.
area.liberdade = (area.incerteza_padrao.area^4)/(((diametros.incerteza_padrao.saida*1)^4)/diametros.liberdade);
area.abrangencia = tinv(diametros.incerteza_combinada.probabilidade,area.liberdade);
area.titulo.liberdade = [“Graus de Liberdade Efetivos”,”Fator de Abregência Associado a Incerteza Expandida”];
Tarea_liberdade = table(area.liberdade,area.abrangencia,’VariableNames’,area.titulo.liberdade)
Por fim,com essas duas variáveis definidas,calcula-se a incerteza expandida associada a variável de saida.
area.incerteza_expandida.area = area.abrangencia*area.incerteza_padrao.area;
area.titulo.incerteza_expandida = [“Incerteza Expandida Associada a Área”];
Tarea_expandida = table(area.incerteza_expandida.area,’VariableNames’,area.titulo.incerteza_expandida)
2.2 Contribuições
Objetivando melhor compreender a contribuição da incerteza padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão com a incerteza expandida.
area.controbuicao.area = ((diametros.incerteza_padrao.saida^2)*100)/diametros.incerteza_padrao.saida^2;
area.titulo.incertezas.expandida = [“Contribuição Área %”];
Tarea_contribuicao = table(area.controbuicao.area,’VariableNames’,area.titulo.incertezas.expandida)
2.3 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,area.media,area.incerteza_expandida.area)
area.titulo.incertezas.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
Tarea_resultado = table(“RM =”,area.media,”+-“,area.incerteza_expandida.area,’VariableNames’,area.titulo.incertezas.resultado)
3 Incerteza Associada a Medição das Forças Aplicadas ao Corpo de Prova Cilíndrico
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilhacarga” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição das forças aplicadas ao corpo de prova cilindrico.
planilha_carga = 1;
Uma vez expresso para o código a planilha que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados de força aplicado ao corpo de prova utilizando o comando xlsread e em seguida os dados são salvos na variável “forcas.cargas”. Utilizando o comando table é criado uma tabela apresentando os dados adiquiridos.
forcas.cargas = xlsread(‘Specimen_RawData_3.xlsx’,planilha_carga,’C185:C205′);
forcas.titulo.cargas = [“Dados de medição (kN)”];
T_forcas_cargas = table(forcas.cargas,’VariableNames’,forcas.titulo.cargas)
Após a leitura dos dados de medição presentes na planilha,é possivel atravez dos comandos mean,std e length apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “forcas.media”,”forcas.desvio_padrao” e “forcas.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
forcas.media = mean(forcas.cargas);
forcas.desvio = std(forcas.cargas);
forcas.leituras = length(forcas.cargas);
forcas.titulo.estatisticos = [“Média”,”Desvio Padrão”,”Tamanho da Amostra”];
T_forcas_estatisticos = table(forcas.media,forcas.desvio,forcas.leituras,’VariableNames’,forcas.titulo.estatisticos)
3.2 Incerteza Padrão Associada às Variáveis de Entrada
Utilizando os dados obtidos anteriormente é possivel calcular a incerteza padrão associada à variabilidade das leituras. Entretanto,antes de realizar tal calculo,para que todas as incertezas padrão associadas às variaveis de entrada sejam calculadas,torna-se necessário a obtenção dos dados de resolução do equipamento de medição utilizado,a incerteza expandida associada a calibração do sistema de medição,o fator de abrangência,a incerteza expandida associada ao erro de paralelismo para medição externa e seu fator de abrangência correspondente. Todos os citados anterioremente estão disponiveis no certificado de calibração do equipamento.
planilha_carga_sistema_de_medicao = 1;
forcas.resolucao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_carga_sistema_de_medicao,’B2′);
forcas.fator_de_abrangencia.calibracao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_carga_sistema_de_medicao,’C2′);
forcas.incerteza_expandida.calibracao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_carga_sistema_de_medicao,’D2′);
forcas.titulo.sistema_de_medicao = [“Resolução”,”Fator de Abrangência para Calibração”,”Incerteza Expandida Associada à Calibração”];
T_forcas_sistema_de_medicao = table(forcas.resolucao,forcas.fator_de_abrangencia.calibracao,forcas.incerteza_expandida.calibracao,’VariableNames’,forcas.titulo.sistema_de_medicao)
Realizado a leitura dos dados citados anterioremente,é possivel calcular a incerteza padrão associada a variabilidade das leituras,a incerteza padrão associada à resolução do sistema de medição,a incerteza padrão associada à calibração do sistema de medição e a incerteza padrão associada ao desvio de paralelismo entre as superfícies de medição para externas do paquímetro. Cada um é obtido por meio da razão de dois elementos,o primeiro pela razão entre o desvio padrão das leituras e a raiz das “n” medições realizadas,o segundo pela resolução do sistema de medição e duas vezes o numero de leituras,o terceiro entre a a incerteza expandida e o fator de abrangência associados à calibração do sistema de medição e o ultimo pela incerteza expandida e o fator de abrangência associado ao erro de paralelismo para medição externa.
forcas.incerteza_padrao.variabilidade = forcas.desvio/sqrt(forcas.leituras);
forcas.incerteza_padrao.resolucao = forcas.resolucao/(2*sqrt(3));
forcas.incerteza_padrao.calibracao = forcas.incerteza_expandida.calibracao/forcas.fator_de_abrangencia.calibracao;
forcas.titulo.incerteza_padrao = [“Incerteza Variabilidade das Leituras”,”Incerteza Resolução Do Sistema De Medição”,”Incerteza Calibração Do Sistema De Medição”];
T_forcas_incerteza_padrao = table(forcas.incerteza_padrao.variabilidade,forcas.incerteza_padrao.resolucao,forcas.incerteza_padrao.calibracao,’VariableNames’,forcas.titulo.incerteza_padrao)
3.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
forcas.incerteza_padrao.saida = sqrt(forcas.incerteza_padrao.variabilidade^2 + forcas.incerteza_padrao.resolucao^2 + forcas.incerteza_padrao.calibracao^2);
forcas.titulo.saida = [“Incerteza Padrão Combinada Associada a Variável de Saida”];
T_forcas_incerteza_padrao_saida = table(forcas.incerteza_padrao.saida,’VariableNames’,forcas.titulo.saida)
Anteriormente a obtenção da incerteza expandida associada à vaiável de saída,é realizado os cálculos envolvendo os graus de liberdade efetivos e o fator de abrangência da medição. Dado a natureza de como foi realizado as medições,considera-se uma probabilidade de abrangência e é calculado em seguida o numero efetivo de graus de liberdade para que seja possivel a obtenção do fator de abrangência..
forcas.probabilidade.abrangencia = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_carga_sistema_de_medicao,’E2′);
forcas.liberdade = (forcas.incerteza_padrao.saida^4)/(((forcas.incerteza_padrao.variabilidade*1)^4)/(forcas.leituras-1));
forcas.fator_de_abrangencia.expandida.saida = tinv(forcas.probabilidade.abrangencia,forcas.liberdade);
forcas.titulo.saidas = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
T_forcas_incerteza_saida = table(forcas.probabilidade.abrangencia,forcas.liberdade,forcas.fator_de_abrangencia.expandida.saida,’VariableNames’,forcas.titulo.saidas)
Dessa forma,pelo produto entre o fator de abrangência associada a incerteza padrão associada a variável de saída com a incerteza padrão combinada asssociada a variável de saída,obtem-se a incerteza expandida associada a variável de saída.
forcas.incerteza_expandida.saida = forcas.fator_de_abrangencia.expandida.saida*forcas.incerteza_padrao.saida;
forcas.titulo.incerteza_expandida = [“Incerteza Expandida Associada à Variável de Saída”];
T_forca_incerteza_expandida_saida = table(forcas.incerteza_expandida.saida,’VariableNames’,forcas.titulo.incerteza_expandida)
3.3 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
forcas.contribuicao.leituras = ((forcas.incerteza_padrao.variabilidade^2)*100)/forcas.incerteza_padrao.saida^2;
forcas.contribuicao.resolucao = ((forcas.incerteza_padrao.resolucao^2)*100)/forcas.incerteza_padrao.saida^2;
forcas.contribuicao.calibracao = ((forcas.incerteza_padrao.calibracao^2)*100)/forcas.incerteza_padrao.saida^2;
forcas.titulo.contribuicao = [“Contribuição Variável de Saída %”,”Contribuição Resolução %”,”Contribuição Calibração %”];
T_forca_contribuicao = table(forcas.contribuicao.leituras,forcas.contribuicao.resolucao,forcas.contribuicao.calibracao,’VariableNames’,forcas.titulo.contribuicao)
3.4 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,diametros.media,diametros.incerteza_expandida.saida);
forcas.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_forca_resultado = table(“RM =”,forcas.media,”+-“,forcas.incerteza_expandida.saida,’VariableNames’,forcas.titulo.resultado)
4 Incerteza Associada a Variaçã do Deslocamento do Corpo de Prova Cilíndrico
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilhacarga” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição das forças aplicadas ao corpo de prova cilindrico.
planilha_carga = 1;
Uma vez expresso para o código a planilha que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados de força aplicado ao corpo de prova utilizando o comando xlsread e em seguida os dados são salvos na variável “forcas.cargas”. Utilizando o comando table é criado uma tabela apresentando os dados adiquiridos.
deslocamentos.mm = xlsread(‘Specimen_RawData_3.xlsx’,planilha_carga,’B185:B205′);
deslocamentos.titulo.mm = [“Dados de medição (kN)”];
T_deslocamentos_mm = table(deslocamentos.mm,’VariableNames’,deslocamentos.titulo.mm)
Após a leitura dos dados de medição presentes na planilha,é possivel atravez dos comandos mean,std e length apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “deslocamentos.media”,”deslocamentos.desvio_padrao” e “deslocamentos.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
deslocamentos.media = mean(deslocamentos.mm);
deslocamentos.desvio = std(deslocamentos.mm);
deslocamentos.leituras = length(deslocamentos.mm);
deslocamentos.titulo.estatisticos = [“Média”,”Desvio Padrão”,”Tamanho da Amostra”];
T_deslocamentos_estatisticos = table(deslocamentos.media,deslocamentos.desvio,deslocamentos.leituras,’VariableNames’,deslocamentos.titulo.estatisticos)
4.2 Incerteza Padrão Associada às Variáveis de Entrada
Utilizando os dados obtidos anteriormente é possivel calcular a incerteza padrão associada à variabilidade das leituras. Entretanto,antes de realizar tal calculo,para que todas as incertezas padrão associadas às variaveis de entrada sejam calculadas,torna-se necessário a obtenção dos dados de resolução do equipamento de medição utilizado,a incerteza expandida associada a calibração do sistema de medição,o fator de abrangência,a incerteza expandida associada ao erro de paralelismo para medição externa e seu fator de abrangência correspondente. Todos os citados anterioremente estão disponiveis no certificado de calibração do equipamento.
planilha_deslocamento_sistema_de_medicao = 3;
deslocamentos.resolucao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_deslocamento_sistema_de_medicao,’B2′);
deslocamentos.fator_de_abrangencia.resolucao = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_deslocamento_sistema_de_medicao,’C2′);
deslocamentos.referencia_incercial = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_deslocamento_sistema_de_medicao,’D2′);
deslocamentos.porcentagem_valor_medio = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_deslocamento_sistema_de_medicao,’F2′);
deslocamentos.titulo.sistema_de_medicao = [“Resolução”,”Fator de Abrangência para Resolução”,”Deslocamento Referencial Incercial”,”Porcentual do Valor Médio”];
T_deslocamentos_sistema_de_medicao = table(deslocamentos.resolucao,deslocamentos.fator_de_abrangencia.resolucao,deslocamentos.referencia_incercial,deslocamentos.porcentagem_valor_medio,’VariableNames’,deslocamentos.titulo.sistema_de_medicao)
Realizado a leitura dos dados citados anterioremente,é possivel calcular a incerteza padrão associada a variabilidade das leituras,a incerteza padrão associada à resolução do sistema de medição,a incerteza padrão associada à calibração do sistema de medição e a incerteza padrão associada ao desvio de paralelismo entre as superfícies de medição para externas do paquímetro. Cada um é obtido por meio da razão de dois elementos,o primeiro pela razão entre o desvio padrão das leituras e a raiz das “n” medições realizadas,o segundo pela resolução do sistema de medição e duas vezes o numero de leituras,o terceiro entre a a incerteza expandida e o fator de abrangência associados à calibração do sistema de medição e o ultimo pela incerteza expandida e o fator de abrangência associado ao erro de paralelismo para medição externa.
deslocamentos.incerteza_padrao.deslocamento_referencial = deslocamentos.referencia_incercial*deslocamentos.porcentagem_valor_medio/sqrt(3);
deslocamentos.incerteza_padrao.variabilidade = deslocamentos.desvio/sqrt(deslocamentos.leituras);
deslocamentos.incerteza_padrao.resolucao = deslocamentos.resolucao/(2*sqrt(3));
deslocamentos.titulo.incerteza_padrao = [“Incerteza Deslocamento Referencial”,”Incerteza Variabilidade das Leituras”,”Incerteza Resolução Do Sistema De Medição”];
T_deslocamentos_incerteza_padrao = table(deslocamentos.incerteza_padrao.variabilidade,deslocamentos.incerteza_padrao.resolucao,deslocamentos.incerteza_padrao.deslocamento_referencial,’VariableNames’,deslocamentos.titulo.incerteza_padrao)
4.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
deslocamentos.incerteza_padrao.saida = sqrt(deslocamentos.incerteza_padrao.deslocamento_referencial^2 + deslocamentos.incerteza_padrao.variabilidade^2 + deslocamentos.incerteza_padrao.resolucao^2);
deslocamentos.titulo.saida = [“Incerteza Padrão Combinada Associada a Variável de Saida”];
T_deslocamentos_incerteza_padrao_saida = table(deslocamentos.incerteza_padrao.saida,’VariableNames’,deslocamentos.titulo.saida)
Anteriormente a obtenção da incerteza expandida associada à vaiável de saída,é realizado os cálculos envolvendo os graus de liberdade efetivos e o fator de abrangência da medição. Dado a natureza de como foi realizado as medições,considera-se uma probabilidade de abrangência e é calculado em seguida o numero efetivo de graus de liberdade para que seja possivel a obtenção do fator de abrangência..
deslocamentos.probabilidade.abrangencia = xlsread(‘CORPOCILINDRICOO.xlsx’,planilha_deslocamento_sistema_de_medicao,’E2′);
deslocamentos.liberdade = (deslocamentos.incerteza_padrao.saida^4)/(((deslocamentos.incerteza_padrao.variabilidade*1)^4)/(deslocamentos.leituras-1));
deslocamentos.fator_de_abrangencia.expandida.saida = tinv(deslocamentos.probabilidade.abrangencia,deslocamentos.liberdade);
deslocamentos.titulo.saidas = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
T_deslocamentos_incerteza_saida = table(deslocamentos.probabilidade.abrangencia,deslocamentos.liberdade,deslocamentos.fator_de_abrangencia.expandida.saida,’VariableNames’,deslocamentos.titulo.saidas)
Dessa forma,pelo produto entre o fator de abrangência associada a incerteza padrão associada a variável de saída com a incerteza padrão combinada asssociada a variável de saída,obtem-se a incerteza expandida associada a variável de saída.
deslocamentos.incerteza_expandida.saida = deslocamentos.fator_de_abrangencia.expandida.saida*deslocamentos.incerteza_padrao.saida;
deslocamentos.titulo.incerteza_expandida = [“Incerteza Expandida Associada à Variável de Saída”];
T_forca_incerteza_expandida_saida = table(deslocamentos.incerteza_expandida.saida,’VariableNames’,deslocamentos.titulo.incerteza_expandida)
4.3 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
deslocamentos.contribuicao.leituras = ((deslocamentos.incerteza_padrao.variabilidade^2)*100)/deslocamentos.incerteza_padrao.saida^2;
deslocamentos.contribuicao.resolucao = ((deslocamentos.incerteza_padrao.resolucao^2)*100)/deslocamentos.incerteza_padrao.saida^2;
deslocamentos.contribuicao.deslocamento_referencial = ((deslocamentos.incerteza_padrao.deslocamento_referencial^2)*100)/deslocamentos.incerteza_padrao.saida^2;
deslocamentos.titulo.contribuicao = [“Contribuição Variável de Saída %”,”Contribuição Resolução %”,”Contribuição Deslocamento Referencial %”];
T_deslocamentos_contribuicao = table(deslocamentos.contribuicao.leituras,deslocamentos.contribuicao.resolucao,deslocamentos.contribuicao.deslocamento_referencial,’VariableNames’,deslocamentos.titulo.contribuicao)
4.4 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,diametros.media,diametros.incerteza_expandida.saida);
deslocamentos.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_forca_resultado = table(“RM =”,deslocamentos.media,”+-“,deslocamentos.incerteza_expandida.saida,’VariableNames’,deslocamentos.titulo.resultado)
5 Incerteza Associada ao Módulo de Elasticidade do Corpo de Prova Cilíndrico
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilhacarga” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição das forças aplicadas ao corpo de prova cilindrico.
planilha_elasticidade = 1;
Uma vez expresso para o código a planilha que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados de força aplicado ao corpo de prova utilizando o comando xlsread e em seguida os dados são salvos na variável “forcas.cargas”. Utilizando o comando table é criado uma tabela apresentando os dados adiquiridos.
elasticidade.dado = xlsread(‘Specimen_RawData_3.xlsx’,planilha_carga,’B1:B1′);
elasticidade.titulo.dados = [“Dados de medição (GPa)”];
T_elasticidade_dados = table(elasticidade.dado,’VariableNames’,elasticidade.titulo.dados)
Após a leitura dos dados de medição presentes na planilha,é possivel atravez dos comandos mean,std e length apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “elasticidade.media”,”elasticidade.desvio_padrao” e “elasticidade.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
elasticidade.media = mean(elasticidade.dado);
elasticidade.titulo.estatisticos = [“Média”];
T_elasticidade_estatisticos = table(elasticidade.media,’VariableNames’,elasticidade.titulo.estatisticos)
5.1 Incerteza Padrão Associada às Variáveis de Entrada
5.1.1 Coeficiente de Sensibilidade
[INSERIR TEXTO]
elasticidade.coeficiente_de_elasticidade.area = (forcas.media*deslocamentos.referencia_incercial)/(deslocamentos.media*area.media^2);
elasticidade.coeficiente_de_elasticidade.forcas = (deslocamentos.referencia_incercial*forcas.media^2)/(deslocamentos.media*area.media);
elasticidade.coeficiente_de_elasticidade.deslocamento = (forcas.media*deslocamentos.referencia_incercial^2)/(deslocamentos.media*area.media);
elasticidade.coeficiente_de_elasticidade.variacao_deslocamento = (forcas.media*deslocamentos.referencia_incercial)/((deslocamentos.media^2)*area.media);
elasticidade.titulo.coeficiente_sensibilidade = [“Coeficiente de Sensibilidade Area”,”Coeficiente de Sensibilidade Força”,”Coeficiente de Sensibilidade Deslocamento”,”Coeficiente de Sensibilidade Variacao Deslocamento”];
T_deslocamentos_sistema_de_medicao = table(elasticidade.coeficiente_de_elasticidade.area,elasticidade.coeficiente_de_elasticidade.forcas,elasticidade.coeficiente_de_elasticidade.deslocamento,elasticidade.coeficiente_de_elasticidade.variacao_deslocamento,’VariableNames’,elasticidade.titulo.coeficiente_sensibilidade)
5.1.2 Propagação de Incertezas na Área do Corpo Retangular
%Os tres sao usados para o calculo da incerteza
elasticidade.propagacao_incerteza.area = ((elasticidade.coeficiente_de_elasticidade.area^2)*(area.incerteza_padrao.area^2));
elasticidade.propagacao_incerteza.forca = ((elasticidade.coeficiente_de_elasticidade.forcas^2)*(forcas.incerteza_padrao.saida^2));
elasticidade.propagacao_incerteza.deslocamento = ((elasticidade.coeficiente_de_elasticidade.deslocamento^2)*(deslocamentos.incerteza_padrao.deslocamento_referencial^2));
elasticidade.propagacao_incerteza.deslocamento_variacao = ((elasticidade.coeficiente_de_elasticidade.variacao_deslocamento^2)*(deslocamentos.incerteza_padrao.saida^2));
elasticidade.titulo.incerteza_padrao.variaveis = [“Contribuicao Incerteza Padrao Area”,”Contribuicao Incerteza Padrao Força”,”Contribuicao Incerteza Padrao Deslocamento”,”Contribuicao Incerteza Padrao Variacao Deslocamento”];
T_deslocamentos_sistema_de_medicao = table(elasticidade.propagacao_incerteza.area,elasticidade.propagacao_incerteza.forca,elasticidade.propagacao_incerteza.deslocamento,elasticidade.propagacao_incerteza.deslocamento_variacao,’VariableNames’,elasticidade.titulo.incerteza_padrao.variaveis)
5.2 Incerteza Padrao Associada ao Modulo de Elasticidade
elasticidade.incerteza_padrao.saida = sqrt(elasticidade.propagacao_incerteza.area+elasticidade.propagacao_incerteza.forca+elasticidade.propagacao_incerteza.deslocamento+elasticidade.propagacao_incerteza.deslocamento_variacao);
elasticidade.titulo.incerteza_padrao.padrao = [“Incerteza Padrão Associada à Variável de Saída”];
T_forca_incerteza_padrao_saida = table(elasticidade.incerteza_padrao.saida,’VariableNames’,elasticidade.titulo.incerteza_padrao.padrao)
5.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
elasticidade.liberdade = (elasticidade.incerteza_padrao.saida^4) / ( (area.incerteza_padrao.area^4/diametros.liberdade) + (forcas.incerteza_padrao.saida^4/forcas.liberdade) + (deslocamentos.incerteza_padrao.saida^4/deslocamentos.liberdade));
elasticidade.fator_de_abrangencia.expandida = tinv(0.95,elasticidade.liberdade);
deslocamentos.titulo.saidas = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
T_deslocamentos_incerteza_saida = table(deslocamentos.probabilidade.abrangencia,deslocamentos.liberdade,deslocamentos.fator_de_abrangencia.expandida.saida,’VariableNames’,deslocamentos.titulo.saidas)
Assim, obtem-se a incerteza expandida associada a variavel de saida
elasticidade.incerteza_expandida_saida = elasticidade.fator_de_abrangencia.expandida*elasticidade.incerteza_padrao.saida;
elasticidade.titulo.incerteza_expandida = [“Incerteza Expandida Associada à Variável de Saída”];
T_elasticidade_incerteza_expandida_saida = table(elasticidade.incerteza_expandida_saida,’VariableNames’,elasticidade.titulo.incerteza_expandida)
5.4 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
elasticidade.contribuicao.area = ((area.incerteza_padrao.area^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.contribuicao.forca = ((forcas.incerteza_padrao.saida^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.contribuicao.deslocamento_inercial = ((deslocamentos.incerteza_padrao.deslocamento_referencial^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.contribuicao.deslocamento = ((deslocamentos.incerteza_padrao.saida^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.titulo.contribuicao = [“Contribuição Area %”,”Contribuição Força %”,”Contribuição Deslocamento Inercial %”,”Contribuição Deslocamento”];
T_deslocamentos_contribuicao = table(elasticidade.contribuicao.area,elasticidade.contribuicao.forca,elasticidade.contribuicao.deslocamento_inercial,elasticidade.contribuicao.deslocamento,’VariableNames’,elasticidade.titulo.contribuicao)
5.5 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
%disp(‘RM=’),disp(elasticidade.media),disp(‘+-‘),disp(elasticidade.incerteza_expandida_saida)
elasticidade.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_elasticidade_resultado = table(“RM =”,elasticidade.media,”+-“,elasticidade.incerteza_expandida_saida,’VariableNames’,elasticidade.titulo.resultado)
ANEXO VI – Código Matlab® de avaliação de incerteza do modulo de elasticidade do corpo de prova retangular

Código responsável pela tratamento,cálculo e análise dos resultados obtidos do ensaio de Tencacidade à fratuta obtida via indentação instrumentada aplicado a um corpo de prova cilindrico
Método GUM para Módulo de Elasticidade no Ensaio de Tração de um Corpo de Prova Retangular
Inicialmemte faz-se necessário a inicialização do programa,dessa forma utiliza-se os comandos clc (Clear Command Window),clear all e close all. O primeiro comando responsável por limpar a janela Command Window ,o segundo por remover os itens da janela Workspace,e o terceiro por fechar as janelas abertas peloMatlab®2021a.
clc;clear all;close all;
1 Incerteza associada a medição da altura do corpo de prova retangular
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha_transversal Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilha_transversal” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição do corpo de prova do diâmetro.
planilha_transversal_altura = 2;
Uma vez expresso para o código a planilha_transversal que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados do diâmetro do corpo de prova utilizando o comando xlsread,e em seguida os dados são salvos na variável “altura.medidas”. Para que em conjunto da variável “altura.dados”,seja impresso a tabela com o titulo “Dados de medição”,é utilizado o comando table,para que por meio da variável “T_altura_medidas” seja impresso a tabela contendo os dados adquiridos.
altura.medidas = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’A2:A4′);
altura.titulo.medidas = [“Dados de medição”];
T_altura_medidas = table(altura.medidas,’VariableNames’,altura.titulo.medidas)
T_altura_medidas = 3×1 table
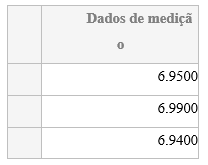
Após a leitura dos dados de medição presentes na planilha_transversal,é possivel atravez dos comandos mean,std e length é possivel apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “altura.media”,”altura.desvio_padrao” e “altura.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
altura.leituras = length(altura.medidas);
altura.media = mean(altura.medidas);
altura.desvio_padrao = std(altura.medidas);
altura.titulo.estatisticos = [“Média”,”Desvio Padrão”,”Tamanho da Amostra”];
T_altura_estatisticos = table(altura.media,altura.desvio_padrao,altura.leituras,’VariableNames’,altura.titulo.estatisticos)
T_altura_estatisticos = 1×3 table
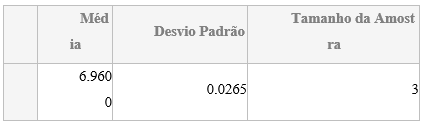
1.2 Incerteza Padrão Associada às Variáveis de Entrada
Utilizando os dados obtidos anteriormente é possivel calcular a incerteza padrão associada à variabilidade das leituras. Entretante,antes de realizar tal calculo,para que todas as incertezas padrão associadas às variaveis de entrada sejam calculadas,torna-se necessário a obtenção dos dados de resolução do equipamento de medição utilizado,a incerteza expandida associada a calibração do sistema de medição,o fator de abrangência,a incerteza expandida associada ao erro de paralelismo para medição externa e seu fator de abrangência correspondente. Todos os citados anterioremente estão disponiveis no certificado de calibração do equipamento.
altura.resolucao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’B2′);
altura.fator_de_abrangencia.calibracao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’C2′);
altura.incerteza_expandida.calibracao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’D2′);
altura.incerteza_expandida.medidas_externas = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’E2′);
altura.fator_de_abrangencia.paralelismo = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’G2′);
altura.incerteza_expandida.paralelismo = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’F2′);
altura.titulo.sistema_de_medicao = [“Resolução”,”Fator de Abrangência para Calibração”,”Incerteza Expandida Associada à Calibração”,”Incerteza Expandida Medidas Externas”,”Fator de Abrangência Paralelismo”,”Incerteza Expandida Paralelismo”];
T_altura_sistema_de_medicao = table(altura.resolucao,altura.fator_de_abrangencia.calibracao,altura.incerteza_expandida.calibracao,altura.incerteza_expandida.medidas_externas,altura.fator_de_abrangencia.paralelismo,altura.incerteza_expandida.paralelismo,’VariableNames’,altura.titulo.sistema_de_medicao)
T_altura_sistema_de_medicao = 1×6 table
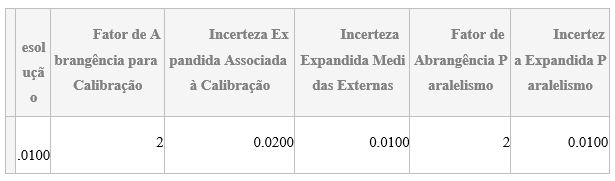
Realizado a leitura dos dados citados anterioremente,é possivel calcular a incerteza padrão associada a variabilidade das leituras,a incerteza padrão associada à resolução do sistema de medição,a incerteza padrão associada à calibração do sistema de medição e a incerteza padrão associada ao desvio de paralelismo entre as superfícies de medição para externas do paquímetro. Cada um é obtido por meio da razão de dois elementos,o primeiro pela razão entre o desvio padrão das leituras e a raiz das “n” medições realizadas,o segundo pela resolução do sistema de medição e duas vezes o numero de leituras,o terceiro entre a a incerteza expandida e o fator de abrangência associados à calibração do sistema de medição e o ultimo pela incerteza expandida e o fator de abrangência associado ao erro de paralelismo para medição externa.
altura.incerteza_padrao.variabilidade = altura.desvio_padrao/sqrt(altura.leituras);
altura.incerteza_padrao.resolucao = altura.resolucao/(2*sqrt(altura.leituras));
altura.incerteza_padrao.calibracao = altura.incerteza_expandida.calibracao/altura.fator_de_abrangencia.calibracao;
altura.incerteza_padrao.paralelismo = altura.incerteza_expandida.paralelismo/altura.fator_de_abrangencia.paralelismo;
altura.titulo.incerteza_padrao = [“Incerteza Variabilidade das Leituras”,”Incerteza Resolução Do Sistema De Medição”,…
“Incerteza Calibração Do Sistema De Medição”,”Incerteza Desvio de Paralelismo Superfícies Externas”];
T_altura_incerteza_padrao = table(altura.incerteza_padrao.variabilidade ,altura.incerteza_padrao.resolucao,…
altura.incerteza_padrao.calibracao,altura.incerteza_padrao.paralelismo,’VariableNames’,altura.titulo.incerteza_padrao)
T_altura_incerteza_padrao = 1×4 table

1.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
altura.incerteza_padrao.saida = sqrt(altura.incerteza_padrao.variabilidade^2 + altura.incerteza_padrao.resolucao^2 + altura.incerteza_padrao.calibracao^2 + altura.incerteza_padrao.paralelismo ^2);
altura.titulo.saida = [“Incerteza Padrão Combinada Associada a Variável de Saida”];
T_altura_incerteza_combinada_saida = table(altura.incerteza_padrao.saida,’VariableNames’,altura.titulo.saida)
T_altura_incerteza_combinada_saida = table table

Anteriormente a obtenção da incerteza expandida associada à vaiável de saída,é realizado os cálculos envolvendo os graus de liberdade efetivos e o fator de abrangência da medição. Dado a natureza de como foi realizado as medições,considera-se uma probabilidade de abrangência e é calculado em seguida o numero efetivo de graus de liberdade para que seja possivel a obtenção do fator de abrangência..
altura.incerteza_combinada.probabilidade = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal_altura,’H2′);
altura.liberdade = (altura.incerteza_padrao.saida^4)/(((altura.incerteza_padrao.variabilidade )^4)/2);
altura.fator_de_abrangencia.expandida = tinv(altura.incerteza_combinada.probabilidade,altura.liberdade);
altura.titulo.incertezas.saida.liberdade = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
Taltura_liberdade = table(altura.incerteza_combinada.probabilidade,altura.liberdade,altura.fator_de_abrangencia.expandida,’VariableNames’,altura.titulo.incertezas.saida.liberdade)
Taltura_liberdade = 1×3 table

Dessa forma,pelo produto entre o fator de abrangência associada a incerteza padrão associada a variável de saída com a incerteza padrão combinada asssociada a variável de saída,obtem-se a incerteza expandida associada a variável de saída.
altura.incerteza_expandida.saida = altura.fator_de_abrangencia.expandida*altura.incerteza_padrao.saida;
altura.titulo.contribuicao = [“Incerteza Expandida Associada à Variável de Saída”];
T_altura_liberdade = table(altura.incerteza_expandida.saida,’VariableNames’,altura.titulo.contribuicao)
T_altura_liberdade = table table

1.3 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
altura.contribuicao.variabilidade = (altura.incerteza_padrao.variabilidade^2/altura.incerteza_expandida.saida^2)*100;
altura.contribuicao.resolucao = (altura.incerteza_padrao.variabilidade^2/altura.incerteza_expandida.saida^2)*100;
altura.contribuicao.calibracao = (altura.incerteza_padrao.calibracao^2/altura.incerteza_expandida.saida^2)*100;
altura.contribuicao.paralelismo = (altura.incerteza_padrao.paralelismo^2/altura.incerteza_expandida.saida^2)*100;
altura.titulo.contribuicao = [“Contribuição Variável de Saída %”,”Contribuição Resolução %”,”Contribuição Calibração %”,”Contribuição Paralelismo %”];
T_altura_contribuicao = table(altura.contribuicao.variabilidade,altura.contribuicao.resolucao,altura.contribuicao.calibracao,altura.contribuicao.paralelismo,’VariableNames’,altura.titulo.contribuicao)
T_altura_contribuicao = 1×4 table

1.4 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,altura.media,altura.incerteza_expandida.saida);
altura.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_altura_resultado = table(“RM =”,altura.media,”+-“,altura.incerteza_expandida.saida,’VariableNames’,altura.titulo.resultado)
T_altura_resultado = 1×4 table

2 Incerteza Padrão Asssociada a Base da Secção Tranversal do Corpo de Prova Retangular
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha_transversal Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilha_transversal” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição do corpo de prova do diâmetro.
planilha_transversal = 1;
Uma vez expresso para o código a planilha_transversal que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados do diâmetro do corpo de prova utilizando o comando xlsread,e em seguida os dados são salvos na variável “seccao_transversal.medidas”. Para que em conjunto da variável “diametro.dados”,seja impresso a tabela com o titulo “Dados de medição”,é utilizado o comando table,para que por meio da variável “Tseccao_transversalmedidas” seja impresso a tabela contendo os dados adquiridos.
seccao_transversal.medidas = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal,’A2:A4′);
seccao_transversal.titulo.medidas = [“Dados de medição”];
T_seccao_transversal_medidas = table(seccao_transversal.medidas,’VariableNames’,seccao_transversal.titulo.medidas)
T_seccao_transversal_medidas = 3×1 table
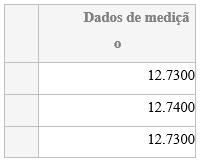
Após a leitura dos dados de medição presentes na planilha_transversal,é possivel atravez dos comandos mean,std e length é possivel apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “seccao_transversal.media”,”seccao_transversal.desvio_padrao” e “seccao_transversal.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
seccao_transversal.leituras = length(seccao_transversal.medidas);
seccao_transversal.media = mean(seccao_transversal.medidas);
seccao_transversal.desvio_padrao = std(seccao_transversal.medidas);
seccao_transversal.titulo.estatisticos = [“Média”,”Desvio Padrão”,”Tamanho da Amostra”];
T_seccao_transversal_estatisticos = table(seccao_transversal.media,seccao_transversal.desvio_padrao,seccao_transversal.leituras,’VariableNames’,seccao_transversal.titulo.estatisticos)
T_seccao_transversal_estatisticos = 1×3 table
Média Desvio Padrão Tamanho da Amostra 1 12.7333 0.0058 3
2.1 Incerteza Padrão Associada às Variáveis de Entrada
Utilizando os dados obtidos anteriormente é possivel calcular a incerteza padrão associada à variabilidade das leituras. Entretante,antes de realizar tal calculo,para que todas as incertezas padrão associadas às variaveis de entrada sejam calculadas,torna-se necessário a obtenção dos dados de resolução do equipamento de medição utilizado,a incerteza expandida associada a calibração do sistema de medição,o fator de abrangência,a incerteza expandida associada ao erro de paralelismo para medição externa e seu fator de abrangência correspondente. Todos os citados anterioremente estão disponiveis no certificado de calibração do equipamento.
seccao_transversal.resolucao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal,’B2′);
seccao_transversal.fator_de_abrangencia.calibracao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal,’C2′);
seccao_transversal.incerteza_expandida.calibracao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal,’D2′);
seccao_transversal.incerteza_expandida.paralelismo = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal,’F2′);
seccao_transversal.fator_de_abrangencia.paralelismo = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal,’H2′);
seccao_transversal.titulo.sistema_de_medicao = [“Resolução”,”Fator de Abrangência para Calibração”,”Incerteza Expandida Associada à Calibração”,”Incerteza Expandida Associada ao Erro de Paralelismo”,”Fator de Abrangência Paralelismo”];
T_seccao_transversal_sistema_de_medicao = table(seccao_transversal.resolucao,seccao_transversal.fator_de_abrangencia.calibracao,seccao_transversal.incerteza_expandida.calibracao,seccao_transversal.incerteza_expandida.paralelismo,seccao_transversal.fator_de_abrangencia.paralelismo,’VariableNames’,seccao_transversal.titulo.sistema_de_medicao)
T_seccao_transversal_sistema_de_medicao = 1×5 table
Resolução Fator de Abrangência para Calibração Incerteza Expandida Associada à Calibração Incerteza Expandida Associada ao Erro de Paralelismo Fator de Abrangência Paralelismo 1 0.0100 2 0.0200 0.0100 2
Realizado a leitura dos dados citados anterioremente,é possivel calcular a incerteza padrão associada a variabilidade das leituras,a incerteza padrão associada à resolução do sistema de medição,a incerteza padrão associada à calibração do sistema de medição e a incerteza padrão associada ao desvio de paralelismo entre as superfícies de medição para externas do paquímetro. Cada um é obtido por meio da razão de dois elementos,o primeiro pela razão entre o desvio padrão das leituras e a raiz das “n” medições realizadas,o segundo pela resolução do sistema de medição e duas vezes o numero de leituras,o terceiro entre a a incerteza expandida e o fator de abrangência associados à calibração do sistema de medição e o ultimo pela incerteza expandida e o fator de abrangência associado ao erro de paralelismo para medição externa.
%Incertezas Padrão Associadas às Variáveis de Entrada
seccao_transversal.incerteza_padrao.variabilidade = seccao_transversal.desvio_padrao/sqrt(seccao_transversal.leituras);
seccao_transversal.incerteza_padrao.resolucao = seccao_transversal.resolucao/(2*sqrt(seccao_transversal.leituras));
seccao_transversal.incerteza_padrao.calibracao = seccao_transversal.incerteza_expandida.calibracao/seccao_transversal.fator_de_abrangencia.calibracao;
seccao_transversal.incerteza_padrao.paralelismo = seccao_transversal.incerteza_expandida.paralelismo/seccao_transversal.fator_de_abrangencia.paralelismo;
seccao_transversal.titulo.incerteza_padrao = [“Incerteza Variabilidade das Leituras”,”Incerteza Resolução Do Sistema De Medição”,…
“Incerteza Calibração Do Sistema De Medição”,”Incerteza Desvio de Paralelismo Superfícies Externas”];
T_seccao_transversal_incerteza_padrao = table(seccao_transversal.incerteza_padrao.variabilidade ,seccao_transversal.incerteza_padrao.resolucao,…
seccao_transversal.incerteza_padrao.calibracao,seccao_transversal.incerteza_padrao.paralelismo,’VariableNames’,seccao_transversal.titulo.incerteza_padrao)
T_seccao_transversal_incerteza_padrao = 1×4 table
Incerteza Variabilidade das Leituras Incerteza Resolução Do Sistema De Medição Incerteza Calibração Do Sistema De Medição Incerteza Desvio de Paralelismo Superfícies Externas 1 0.0033 0.0029 0.0100 0.0050
2.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
seccao_transversal.incerteza_padrao.saida = sqrt(seccao_transversal.incerteza_padrao.variabilidade ^2 + seccao_transversal.incerteza_padrao.resolucao^2 + seccao_transversal.incerteza_padrao.calibracao^2 + seccao_transversal.incerteza_padrao.paralelismo ^2);
seccao_transversal.titulo.saida = [“Incerteza Padrão Combinada Associada a Variável de Saida”];
T_seccao_transversal_incerteza_combinada_saida = table(seccao_transversal.incerteza_padrao.saida,’VariableNames’,seccao_transversal.titulo.saida)
T_seccao_transversal_incerteza_combinada_saida = table table
Incerteza Padrão Combinada Associada a Variável de Saida 1 0.0120
Anteriormente a obtenção da incerteza expandida associada à vaiável de saída,é realizado os cálculos envolvendo os graus de liberdade efetivos e o fator de abrangência da medição. Dado a natureza de como foi realizado as medições,considera-se uma probabilidade de abrangência e é calculado em seguida o numero efetivo de graus de liberdade para que seja possivel a obtenção do fator de abrangência..
seccao_transversal.incerteza_combinada.probabilidade = xlsread(‘CORPORETANGULAR.xlsx’,planilha_transversal,’I2′);
seccao_transversal.liberdade = (seccao_transversal.incerteza_padrao.saida^4)/(((seccao_transversal.incerteza_padrao.variabilidade )^4)/2);
seccao_transversal.fator_de_abrangencia.expandida = tinv(seccao_transversal.incerteza_combinada.probabilidade,seccao_transversal.liberdade);
seccao_transversal.titulo.incertezas.saida.liberdade = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
Tseccao_transversal_liberdade = table(seccao_transversal.incerteza_combinada.probabilidade,seccao_transversal.liberdade,seccao_transversal.fator_de_abrangencia.expandida,’VariableNames’,seccao_transversal.titulo.incertezas.saida.liberdade)
Tseccao_transversal_liberdade = 1×3 table
Probabilidade de Abrangência Graus de Liberdade Efetivos Fator de Abrangência 1 0.9500 338 1.6494
Dessa forma,pelo produto entre o fator de abrangência associada a incerteza padrão associada a variável de saída com a incerteza padrão combinada asssociada a variável de saída,obtem-se a incerteza expandida associada a variável de saída.
seccao_transversal.incerteza_expandida.saida = seccao_transversal.fator_de_abrangencia.expandida*seccao_transversal.incerteza_padrao.saida;
seccao_transversal.titulo.contribuicao = [“Incerteza Expandida Associada à Variável de Saída”];
Tseccao_transversal_liberdade = table(seccao_transversal.incerteza_expandida.saida,’VariableNames’,seccao_transversal.titulo.contribuicao)
Tseccao_transversal_liberdade = table table
Incerteza Expandida Associada à Variável de Saída 1 0.0198
2.3 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
seccao_transversal.contribuicao.variabilidade = (seccao_transversal.incerteza_padrao.variabilidade^2/seccao_transversal.incerteza_expandida.saida^2)*100;
seccao_transversal.contribuicao.resolucao = (seccao_transversal.incerteza_padrao.variabilidade^2/seccao_transversal.incerteza_expandida.saida^2)*100;
seccao_transversal.contribuicao.calibracao = (seccao_transversal.incerteza_padrao.calibracao^2/seccao_transversal.incerteza_expandida.saida^2)*100;
seccao_transversal.contribuicao.paralelismo = (seccao_transversal.incerteza_padrao.paralelismo^2/seccao_transversal.incerteza_expandida.saida^2)*100;
seccao_transversal.titulo.contribuicao = [“Contribuição Variável de Saída %”,”Contribuição Resolução %”,”Contribuição Calibração %”,”Contribuição Paralelismo %”];
Tseccao_transversal_contribuicao = table(seccao_transversal.contribuicao.variabilidade,seccao_transversal.contribuicao.resolucao,seccao_transversal.contribuicao.calibracao,seccao_transversal.contribuicao.paralelismo,’VariableNames’,seccao_transversal.titulo.contribuicao)
Tseccao_transversal_contribuicao = 1×4 table
Contribuição Variável de Saída % Contribuição Resolução % Contribuição Calibração % Contribuição Paralelismo % 1 2.8276 2.8276 25.4484 6.3621
2.4 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,seccao_transversal.media,seccao_transversal.incerteza_expandida.saida);
seccao_transversal.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_seccao_transversal_resultado = table(“RM =”,seccao_transversal.media,”+-“,seccao_transversal.incerteza_expandida.saida,’VariableNames’,seccao_transversal.titulo.resultado)
T_seccao_transversal_resultado = 1×4 table
RM Média +- Incerteza 1 “RM =” 12.7333 “+-“ 0.0198
3 Incerteza Padrão Asssociada à Área do Corpo de Prova Retangular
Referente a incerteza padrão associada à área,utiliza-se inicialmente o valor da média das medições do diâmetro para obtenção da área média e posteriormente para obtenção da incerteza padrão associada a área.
area.media = altura.media*seccao_transversal.media;
area.incerteza_padrao.area = altura.incerteza_padrao.saida + seccao_transversal.incerteza_padrao.saida ;
area.titulo.area = [“Área Média”,”Incerteza Padrão Associada a Área”];
T_area_incerteza = table(area.media,area.incerteza_padrao.area,’VariableNames’,area.titulo.area)
T_area_incerteza = 1×2 table
Área Média Incerteza Padrão Associada a Área 1 88.6240 0.0312
3.1 Incerteza Padrão Asssociada à Área do Corpo de Prova Retangular
3.1.1 Propagação de Incertezas na Área do Corpo Retangular
Para que seja possivel obter a incerteza associada a àrea do corpo retangular, faz-se necessário a propagação das incertezas associadas a altura e a secção média para seu cálculo.
area.contribuicao.seccao_transversal = (((seccao_transversal.media)^2)*(altura.incerteza_padrao.saida)^2);
area.contribuicao.altura = (((altura.media)^2)*(seccao_transversal.incerteza_padrao.saida)^2);
area.titulo.incerteza_padrao.contribuicao = [“Contribuicao Incerteza Padrao Secção Transversal”,”Contribuicao Incerteza Padrao Altura”];
T_deslocamentos_sistema_de_medicao = table(area.contribuicao.seccao_transversal,area.contribuicao.altura,’VariableNames’,area.titulo.incerteza_padrao.contribuicao)
T_deslocamentos_sistema_de_medicao = 1×2 table
Contribuicao Incerteza Padrao Secção Transversal Contribuicao Incerteza Padrao Altura 1 0.0595 0.0070
Por fim calcula-se a incerteza padrão associada a area do corpo de prova retangular.
area.incerteza_padrao.area = sqrt(area.contribuicao.altura + area.contribuicao.seccao_transversal);
area.titulo.padrao = [“Incerteza Padrão Associada a Área”];
T_area_incerteza = table(area.incerteza_padrao.area,’VariableNames’,area.titulo.padrao)
T_area_incerteza = table table
Incerteza Padrão Associada a Área 1 0.2578
3.3 Incerteza Expandida Associada à Variável de Saìda Àrea
Obtido o valor de incerteza padrão e utilizando a mesma probabilidade de abrangência utilizada anterioremnte,calcula-se os graus de liberdade efetivos e determina-se o fator de abrangência associado.
area.liberdade = (area.incerteza_padrao.area^4)/((((altura.incerteza_padrao.saida*1)^4)/5)+(((seccao_transversal.incerteza_padrao.saida*1)^4)/338));
area.abrangencia = tinv(altura.incerteza_combinada.probabilidade,area.liberdade);
area.titulo.liberdade = [“Graus de Liberdade Efetivos”,”Fator de Abregência Associado a Incerteza Expandida”];
Tarea_liberdade = table(area.liberdade,area.abrangencia,’VariableNames’,area.titulo.liberdade)
Tarea_liberdade = 1×2 table
Graus de Liberdade Efetivos Fator de Abregência Associado a Incerteza Expandida 1 1.6383e+05 1.6449
Por fim,com essas duas variáveis definidas,calcula-se a incerteza expandida associada a variável de saida.
area.incerteza_expandida.area = area.abrangencia*area.incerteza_padrao.area;
area.titulo.incerteza_expandida = [“Incerteza Expandida Associada a Área”];
Tarea_expandida = table(area.incerteza_expandida.area,’VariableNames’,area.titulo.incerteza_expandida)
Tarea_expandida = table table
Incerteza Expandida Associada a Área 1 0.4240
3.4 Contribuições
Objetivando melhor compreender a contribuição da incerteza padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão com a incerteza expandida.
area.controbuicao.seccao_transversal = ((altura.incerteza_padrao.saida^2)*100)/area.incerteza_padrao.area;
area.controbuicao.altura = ((seccao_transversal.incerteza_padrao.saida^2)*100)/area.incerteza_padrao.area;
area.titulo.incertezas.expandida = [“Contribuição Seccao Transversal %”,”Contribuição Altura %”];
Tarea_contribuicao = table(area.controbuicao.seccao_transversal,area.controbuicao.altura,’VariableNames’,area.titulo.incertezas.expandida)
Tarea_contribuicao = 1×2 table
Contribuição Seccao Transversal % Contribuição Altura % 1 0.1422 0.0560
3.5 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,area.media,area.incerteza_expandida.area)
area.titulo.incertezas.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
Tarea_resultado = table(“RM =”,area.media,”+-“,area.incerteza_expandida.area,’VariableNames’,area.titulo.incertezas.resultado)
Tarea_resultado = 1×4 table
RM Média +- Incerteza 1 “RM =” 88.6240 “+-“ 0.4240
4 Incerteza Associada a Medição das Forças Aplicadas ao Corpo de Prova Retangular
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilhacarga” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição das forças aplicadas ao corpo de prova cilindrico.
planilha_carga = 1;
Uma vez expresso para o código a planilha que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados de força aplicado ao corpo de prova utilizando o comando xlsread e em seguida os dados são salvos na variável “forcas.cargas”. Utilizando o comando table é criado uma tabela apresentando os dados adiquiridos.
forcas.cargas = xlsread(‘Specimen_RawData_3.xlsx’,planilha_carga,’C144:C152′);
forcas.titulo.cargas = [“Dados de medição (kN)”];
T_forcas_cargas = table(forcas.cargas,’VariableNames’,forcas.titulo.cargas)
T_forcas_cargas = 9×1 table
Dados de medição (kN) 1 6.3380 2 6.3412 3 6.3337 4 6.3445 5 6.3869 6 6.4249 7 6.4769 8 6.5367 9 6.6059
Após a leitura dos dados de medição presentes na planilha,é possivel atravez dos comandos mean,std e length apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “forcas.media”,”forcas.desvio_padrao” e “forcas.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
forcas.media = mean(forcas.cargas);
forcas.desvio = std(forcas.cargas);
forcas.leituras = length(forcas.cargas);
forcas.titulo.estatisticos = [“Média”,”Desvio Padrão”,”Tamanho da Amostra”];
T_forcas_estatisticos = table(forcas.media,forcas.desvio,forcas.leituras,’VariableNames’,forcas.titulo.estatisticos)
T_forcas_estatisticos = 1×3 table
Média Desvio Padrão Tamanho da Amostra 1 6.4210 0.0991 9
4.2 Incerteza Padrão Associada às Variáveis de Entrada
Utilizando os dados obtidos anteriormente é possivel calcular a incerteza padrão associada à variabilidade das leituras. Entretanto,antes de realizar tal calculo,para que todas as incertezas padrão associadas às variaveis de entrada sejam calculadas,torna-se necessário a obtenção dos dados de resolução do equipamento de medição utilizado,a incerteza expandida associada a calibração do sistema de medição,o fator de abrangência,a incerteza expandida associada ao erro de paralelismo para medição externa e seu fator de abrangência correspondente. Todos os citados anterioremente estão disponiveis no certificado de calibração do equipamento.
planilha_carga_sistema_de_medicao = 4;
forcas.resolucao = xlsread(‘CORPOretangular.xlsx’,planilha_carga_sistema_de_medicao,’B2′);
forcas.fator_de_abrangencia.calibracao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_carga_sistema_de_medicao,’C2′);
forcas.incerteza_expandida.calibracao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_carga_sistema_de_medicao,’D2′);
forcas.titulo.sistema_de_medicao = [“Resolução”,”Fator de Abrangência para Calibração”,”Incerteza Expandida Associada à Calibração”];
T_forcas_sistema_de_medicao = table(forcas.resolucao,forcas.fator_de_abrangencia.calibracao,forcas.incerteza_expandida.calibracao,’VariableNames’,forcas.titulo.sistema_de_medicao)
T_forcas_sistema_de_medicao = 1×3 table
Resolução Fator de Abrangência para Calibração Incerteza Expandida Associada à Calibração 1 0.0100 2 0.0900
Realizado a leitura dos dados citados anterioremente,é possivel calcular a incerteza padrão associada a variabilidade das leituras,a incerteza padrão associada à resolução do sistema de medição,a incerteza padrão associada à calibração do sistema de medição e a incerteza padrão associada ao desvio de paralelismo entre as superfícies de medição para externas do paquímetro. Cada um é obtido por meio da razão de dois elementos,o primeiro pela razão entre o desvio padrão das leituras e a raiz das “n” medições realizadas,o segundo pela resolução do sistema de medição e duas vezes o numero de leituras,o terceiro entre a a incerteza expandida e o fator de abrangência associados à calibração do sistema de medição e o ultimo pela incerteza expandida e o fator de abrangência associado ao erro de paralelismo para medição externa.
forcas.incerteza_padrao.variabilidade = forcas.desvio/sqrt(forcas.leituras);
forcas.incerteza_padrao.resolucao = forcas.resolucao/(2*sqrt(3));
forcas.incerteza_padrao.calibracao = forcas.incerteza_expandida.calibracao/forcas.fator_de_abrangencia.calibracao;
forcas.titulo.incerteza_padrao = [“Incerteza Variabilidade das Leituras”,”Incerteza Resolução Do Sistema De Medição”,”Incerteza Calibração Do Sistema De Medição”];
T_forcas_incerteza_padrao = table(forcas.incerteza_padrao.variabilidade,forcas.incerteza_padrao.resolucao,forcas.incerteza_padrao.calibracao,’VariableNames’,forcas.titulo.incerteza_padrao)
T_forcas_incerteza_padrao = 1×3 table
Incerteza Variabilidade das Leituras Incerteza Resolução Do Sistema De Medição Incerteza Calibração Do Sistema De Medição 1 0.0330 0.0029 0.0450
4.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
forcas.incerteza_padrao.saida = sqrt(forcas.incerteza_padrao.variabilidade^2 + forcas.incerteza_padrao.resolucao^2 + forcas.incerteza_padrao.calibracao^2);
forcas.titulo.saida = [“Incerteza Padrão Combinada Associada a Variável de Saida”];
T_forcas_incerteza_padrao_saida = table(forcas.incerteza_padrao.saida,’VariableNames’,forcas.titulo.saida)
T_forcas_incerteza_padrao_saida = table table
Incerteza Padrão Combinada Associada a Variável de Saida 1 0.0559
Anteriormente a obtenção da incerteza expandida associada à vaiável de saída,é realizado os cálculos envolvendo os graus de liberdade efetivos e o fator de abrangência da medição. Dado a natureza de como foi realizado as medições,considera-se uma probabilidade de abrangência e é calculado em seguida o numero efetivo de graus de liberdade para que seja possivel a obtenção do fator de abrangência..
forcas.probabilidade.abrangencia = xlsread(‘CORPORETANGULAR.xlsx’,planilha_carga_sistema_de_medicao,’E2′);
forcas.liberdade = (forcas.incerteza_padrao.saida^4)/(((forcas.incerteza_padrao.variabilidade*1)^4)/(forcas.leituras-1));
forcas.fator_de_abrangencia.expandida.saida = tinv(forcas.probabilidade.abrangencia,forcas.liberdade);
forcas.titulo.saidas = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
T_forcas_incerteza_saida = table(forcas.probabilidade.abrangencia,forcas.liberdade,forcas.fator_de_abrangencia.expandida.saida,’VariableNames’,forcas.titulo.saidas)
T_forcas_incerteza_saida = 1×3 table
Probabilidade de Abrangência Graus de Liberdade Efetivos Fator de Abrangência 1 0.9500 65.5476 1.6684
Dessa forma,pelo produto entre o fator de abrangência associada a incerteza padrão associada a variável de saída com a incerteza padrão combinada asssociada a variável de saída,obtem-se a incerteza expandida associada a variável de saída.
forcas.incerteza_expandida.saida = forcas.fator_de_abrangencia.expandida.saida*forcas.incerteza_padrao.saida;
forcas.titulo.incerteza_expandida = [“Incerteza Expandida Associada à Variável de Saída”];
T_forca_incerteza_expandida_saida = table(forcas.incerteza_expandida.saida,’VariableNames’,forcas.titulo.incerteza_expandida)
T_forca_incerteza_expandida_saida = table table
Incerteza Expandida Associada à Variável de Saída 1 0.0933
4.3 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
forcas.contribuicao.leituras = ((forcas.incerteza_padrao.variabilidade^2)*100)/forcas.incerteza_padrao.saida^2;
forcas.contribuicao.resolucao = ((forcas.incerteza_padrao.resolucao^2)*100)/forcas.incerteza_padrao.saida^2;
forcas.contribuicao.calibracao = ((forcas.incerteza_padrao.calibracao^2)*100)/forcas.incerteza_padrao.saida^2;
forcas.titulo.contribuicao = [“Contribuição Variável de Saída %”,”Contribuição Resolução %”,”Contribuição Calibração %”];
T_forca_contribuicao = table(forcas.contribuicao.leituras,forcas.contribuicao.resolucao,forcas.contribuicao.calibracao,’VariableNames’,forcas.titulo.contribuicao)
T_forca_contribuicao = 1×3 table
Contribuição Variável de Saída % Contribuição Resolução % Contribuição Calibração % 1 34.9355 0.2667 64.7979
4.4 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,diametros.media,diametros.incerteza_expandida.saida);
forcas.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_forca_resultado = table(“RM =”,forcas.media,”+-“,forcas.incerteza_expandida.saida,’VariableNames’,forcas.titulo.resultado)
T_forca_resultado = 1×4 table
RM Média +- Incerteza 1 “RM =” 6.4210 “+-“ 0.0933
5 Incerteza Associada a Variaçã do Deslocamento do Corpo de Prova Retangular
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilhacarga” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição das forças aplicadas ao corpo de prova cilindrico.
planilha_carga = 1;
Uma vez expresso para o código a planilha que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados de força aplicado ao corpo de prova utilizando o comando xlsread e em seguida os dados são salvos na variável “forcas.cargas”. Utilizando o comando table é criado uma tabela apresentando os dados adiquiridos.
deslocamentos.mm = xlsread(‘Specimen_RawData_3.xlsx’,planilha_carga,’B116:B124′);
deslocamentos.titulo.mm = [“Dados de medição (kN)”];
T_deslocamentos_mm = table(deslocamentos.mm,’VariableNames’,deslocamentos.titulo.mm)
T_deslocamentos_mm = 9×1 table
Dados de medição (kN) 1 0.0696 2 0.0705 3 0.0711 4 0.0722 5 0.0736 6 0.0742 7 0.0746 8 0.0754 9 0.0768
Após a leitura dos dados de medição presentes na planilha,é possivel atravez dos comandos mean,std e length apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “deslocamentos.media”,”deslocamentos.desvio_padrao” e “deslocamentos.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
deslocamentos.media = mean(deslocamentos.mm);
deslocamentos.desvio = std(deslocamentos.mm);
deslocamentos.leituras = length(deslocamentos.mm);
deslocamentos.titulo.estatisticos = [“Média”,”Desvio Padrão”,”Tamanho da Amostra”];
T_deslocamentos_estatisticos = table(deslocamentos.media,deslocamentos.desvio,deslocamentos.leituras,’VariableNames’,deslocamentos.titulo.estatisticos)
T_deslocamentos_estatisticos = 1×3 table
Média Desvio Padrão Tamanho da Amostra 1 0.0731 0.0024 9
4.2 Incerteza Padrão Associada às Variáveis de Entrada
Utilizando os dados obtidos anteriormente é possivel calcular a incerteza padrão associada à variabilidade das leituras. Entretanto,antes de realizar tal calculo,para que todas as incertezas padrão associadas às variaveis de entrada sejam calculadas,torna-se necessário a obtenção dos dados de resolução do equipamento de medição utilizado,a incerteza expandida associada a calibração do sistema de medição,o fator de abrangência,a incerteza expandida associada ao erro de paralelismo para medição externa e seu fator de abrangência correspondente. Todos os citados anterioremente estão disponiveis no certificado de calibração do equipamento.
planilha_deslocamento_sistema_de_medicao = 5;
deslocamentos.resolucao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_deslocamento_sistema_de_medicao,’B2′);
deslocamentos.fator_de_abrangencia.resolucao = xlsread(‘CORPORETANGULAR.xlsx’,planilha_deslocamento_sistema_de_medicao,’C2′);
deslocamentos.referencia_incercial = xlsread(‘CORPORETANGULAR.xlsx’,planilha_deslocamento_sistema_de_medicao,’D2′);
deslocamentos.porcentagem_valor_medio = xlsread(‘CORPORETANGULAR.xlsx’,planilha_deslocamento_sistema_de_medicao,’F2′);
deslocamentos.titulo.sistema_de_medicao = [“Resolução”,”Fator de Abrangência para Resolução”,”Deslocamento Referencial Incercial”,”Porcentual do Valor Médio”];
T_deslocamentos_sistema_de_medicao = table(deslocamentos.resolucao,deslocamentos.fator_de_abrangencia.resolucao,deslocamentos.referencia_incercial,deslocamentos.porcentagem_valor_medio,’VariableNames’,deslocamentos.titulo.sistema_de_medicao)
T_deslocamentos_sistema_de_medicao = 1×4 table
Resolução Fator de Abrangência para Resolução Deslocamento Referencial Incercial Porcentual do Valor Médio 1 1.0000e-05 2 0.0850 0.0030
Realizado a leitura dos dados citados anterioremente,é possivel calcular a incerteza padrão associada a variabilidade das leituras,a incerteza padrão associada à resolução do sistema de medição,a incerteza padrão associada à calibração do sistema de medição e a incerteza padrão associada ao desvio de paralelismo entre as superfícies de medição para externas do paquímetro. Cada um é obtido por meio da razão de dois elementos,o primeiro pela razão entre o desvio padrão das leituras e a raiz das “n” medições realizadas,o segundo pela resolução do sistema de medição e duas vezes o numero de leituras,o terceiro entre a a incerteza expandida e o fator de abrangência associados à calibração do sistema de medição e o ultimo pela incerteza expandida e o fator de abrangência associado ao erro de paralelismo para medição externa.
deslocamentos.incerteza_padrao.deslocamento_referencial = deslocamentos.referencia_incercial*deslocamentos.porcentagem_valor_medio/sqrt(3);
%POR ALGUM MOTIVO ELE HAVIA CALCULADO O EXPANDIDO MAS COMO SEM VEFF ???
deslocamentos.incerteza_padrao.variabilidade = deslocamentos.desvio/sqrt(deslocamentos.leituras);
deslocamentos.incerteza_padrao.resolucao = deslocamentos.resolucao/(2*sqrt(3));
deslocamentos.titulo.incerteza_padrao = [“Incerteza Deslocamento Referencial”,”Incerteza Variabilidade das Leituras”,”Incerteza Resolução Do Sistema De Medição”];
T_deslocamentos_incerteza_padrao = table(deslocamentos.incerteza_padrao.variabilidade,deslocamentos.incerteza_padrao.resolucao,deslocamentos.incerteza_padrao.deslocamento_referencial,’VariableNames’,deslocamentos.titulo.incerteza_padrao)
T_deslocamentos_incerteza_padrao = 1×3 table
Incerteza Deslocamento Referencial Incerteza Variabilidade das Leituras Incerteza Resolução Do Sistema De Medição 1 7.9891e-04 2.8868e-06 1.4719e-04
5.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
deslocamentos.incerteza_padrao.saida = sqrt(deslocamentos.incerteza_padrao.deslocamento_referencial^2 + deslocamentos.incerteza_padrao.variabilidade^2 + deslocamentos.incerteza_padrao.resolucao^2);
deslocamentos.titulo.saida = [“Incerteza Padrão Combinada Associada a Variável de Saida”];
T_deslocamentos_incerteza_padrao_saida = table(deslocamentos.incerteza_padrao.saida,’VariableNames’,deslocamentos.titulo.saida)
T_deslocamentos_incerteza_padrao_saida = table table
Incerteza Padrão Combinada Associada a Variável de Saida 1 8.1236e-04
Anteriormente a obtenção da incerteza expandida associada à vaiável de saída,é realizado os cálculos envolvendo os graus de liberdade efetivos e o fator de abrangência da medição. Dado a natureza de como foi realizado as medições,considera-se uma probabilidade de abrangência e é calculado em seguida o numero efetivo de graus de liberdade para que seja possivel a obtenção do fator de abrangência..
deslocamentos.probabilidade.abrangencia = xlsread(‘CORPORETANGULAR.xlsx’,planilha_deslocamento_sistema_de_medicao,’E2′);
deslocamentos.liberdade = (deslocamentos.incerteza_padrao.saida^4)/(((deslocamentos.incerteza_padrao.variabilidade*1)^4)/(deslocamentos.leituras-1));
deslocamentos.fator_de_abrangencia.expandida.saida = tinv(deslocamentos.probabilidade.abrangencia,deslocamentos.liberdade);
deslocamentos.titulo.saidas = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
T_deslocamentos_incerteza_saida = table(deslocamentos.probabilidade.abrangencia,deslocamentos.liberdade,deslocamentos.fator_de_abrangencia.expandida.saida,’VariableNames’,deslocamentos.titulo.saidas)
T_deslocamentos_incerteza_saida = 1×3 table
Probabilidade de Abrangência Graus de Liberdade Efetivos Fator de Abrangência 1 0.9500 8.5525 1.8441
Dessa forma,pelo produto entre o fator de abrangência associada a incerteza padrão associada a variável de saída com a incerteza padrão combinada asssociada a variável de saída,obtem-se a incerteza expandida associada a variável de saída.
deslocamentos.incerteza_expandida.saida = deslocamentos.fator_de_abrangencia.expandida.saida*deslocamentos.incerteza_padrao.saida;
deslocamentos.titulo.incerteza_expandida = [“Incerteza Expandida Associada à Variável de Saída”];
T_forca_incerteza_expandida_saida = table(deslocamentos.incerteza_expandida.saida,’VariableNames’,deslocamentos.titulo.incerteza_expandida)
T_forca_incerteza_expandida_saida = table table
Incerteza Expandida Associada à Variável de Saída 1 0.0015
5.3 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
deslocamentos.contribuicao.leituras = ((deslocamentos.incerteza_padrao.variabilidade^2)*100)/deslocamentos.incerteza_padrao.saida^2;
deslocamentos.contribuicao.resolucao = ((deslocamentos.incerteza_padrao.resolucao^2)*100)/deslocamentos.incerteza_padrao.saida^2;
deslocamentos.contribuicao.deslocamento_referencial = ((deslocamentos.incerteza_padrao.deslocamento_referencial^2)*100)/deslocamentos.incerteza_padrao.saida^2;
deslocamentos.titulo.contribuicao = [“Contribuição Variável de Saída %”,”Contribuição Resolução %”,”Contribuição Deslocamento Referencial %”];
T_deslocamentos_contribuicao = table(deslocamentos.contribuicao.leituras,deslocamentos.contribuicao.resolucao,deslocamentos.contribuicao.deslocamento_referencial,’VariableNames’,deslocamentos.titulo.contribuicao)
T_deslocamentos_contribuicao = 1×3 table
Contribuição Variável de Saída % Contribuição Resolução % Contribuição Deslocamento Referencial % 1 96.7158 0.0013 3.2829
5.4 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
formatSpec = ‘RM = %.4f +- %.4f \n’;
%fprintf(formatSpec,diametros.media,diametros.incerteza_expandida.saida);
deslocamentos.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_forca_resultado = table(“RM =”,deslocamentos.media,”+-“,deslocamentos.incerteza_expandida.saida,’VariableNames’,deslocamentos.titulo.resultado)
T_forca_resultado = 1×4 table
RM Média +- Incerteza 1 “RM =” 0.0731 “+-“ 0.0015
6 Incerteza Associada ao Módulo de Elasticidade do Corpo de Prova Cilíndrico
Os dados obtidos do ensaio do corpo de prova são obtidos atravez da leitura da planilha Excel® gerada após o experimento,dessa forma,é utilizado a variável “planilhacarga” para indicar no código a localização dos dados utilizados para o calculo da incerteza associada a medição das forças aplicadas ao corpo de prova cilindrico.
planilha_elasticidade = 1;
Uma vez expresso para o código a planilha que contem as informações necessárias para o cálculo da incerteza,faz-se a leitura dos dados de força aplicado ao corpo de prova utilizando o comando xlsread e em seguida os dados são salvos na variável “forcas.cargas”. Utilizando o comando table é criado uma tabela apresentando os dados adiquiridos.
elasticidade.dado = xlsread(‘Specimen_RawData_3.xlsx’,planilha_carga,’B1:B1′);
elasticidade.titulo.dados = [“Dados de medição (GPa)”];
T_elasticidade_dados = table(elasticidade.dado,’VariableNames’,elasticidade.titulo.dados)
T_elasticidade_dados = table table
Dados de medição (GPa) 1 214.6550
Após a leitura dos dados de medição presentes na planilha,é possivel atravez dos comandos mean,std e length apresentar os dados de média,desvio padrão e tamanho da amostra,e salvar seus valores nas variáveis “elasticidade.media”,”elasticidade.desvio_padrao” e “elasticidade.leituras”. Utilizando novamento o comando table,é criado uma nova tabela apresentando os dados obtidos.
elasticidade.media = mean(elasticidade.dado);
elasticidade.titulo.estatisticos = [“Média”];
T_elasticidade_estatisticos = table(elasticidade.media,’VariableNames’,elasticidade.titulo.estatisticos)
T_elasticidade_estatisticos = table table
Média 1 214.6550
5.1 Incerteza Padrão Associada às Variáveis de Entrada
5.1.1 Coeficiente de Sensibilidade
[INSERIR TEXTO]
elasticidade.coeficiente_de_elasticidade.area = (forcas.media*deslocamentos.referencia_incercial)/(deslocamentos.media*area.media^2);
elasticidade.coeficiente_de_elasticidade.forcas = (deslocamentos.referencia_incercial*forcas.media^2)/(deslocamentos.media*area.media);
elasticidade.coeficiente_de_elasticidade.deslocamento = (forcas.media*deslocamentos.referencia_incercial^2)/(deslocamentos.media*area.media);
elasticidade.coeficiente_de_elasticidade.variacao_deslocamento = (forcas.media*deslocamentos.referencia_incercial)/((deslocamentos.media^2)*area.media);
elasticidade.titulo.coeficiente_sensibilidade = [“Coeficiente de Sensibilidade Area”,”Coeficiente de Sensibilidade Força”,”Coeficiente de Sensibilidade Deslocamento”,”Coeficiente de Sensibilidade Variacao Deslocamento”];
T_deslocamentos_sistema_de_medicao = table(elasticidade.coeficiente_de_elasticidade.area,elasticidade.coeficiente_de_elasticidade.forcas,elasticidade.coeficiente_de_elasticidade.deslocamento,elasticidade.coeficiente_de_elasticidade.variacao_deslocamento,’VariableNames’,elasticidade.titulo.coeficiente_sensibilidade)
T_deslocamentos_sistema_de_medicao = 1×4 table
Coeficiente de Sensibilidade Area Coeficiente de Sensibilidade Força Coeficiente de Sensibilidade Deslocamento Coeficiente de Sensibilidade Variacao Deslocamento 1 9.5004e-04 0.5406 0.0072 1.1514
5.1.2 Propagação de Incertezas na Área do Corpo Retangular
%Os tres sao usados para o calculo da incerteza
elasticidade.propagacao_incerteza.area = ((elasticidade.coeficiente_de_elasticidade.area^2)*(area.incerteza_padrao.area^2));
elasticidade.propagacao_incerteza.forca = ((elasticidade.coeficiente_de_elasticidade.forcas^2)*(forcas.incerteza_padrao.saida^2));
elasticidade.propagacao_incerteza.deslocamento = ((elasticidade.coeficiente_de_elasticidade.deslocamento^2)*(deslocamentos.incerteza_padrao.deslocamento_referencial^2));
elasticidade.propagacao_incerteza.deslocamento_variacao = ((elasticidade.coeficiente_de_elasticidade.variacao_deslocamento^2)*(deslocamentos.incerteza_padrao.saida^2));
elasticidade.titulo.incerteza_padrao.variaveis = [“Contribuicao Incerteza Padrao Area”,”Contribuicao Incerteza Padrao Força”,”Contribuicao Incerteza Padrao Deslocamento”,”Contribuicao Incerteza Padrao Variacao Deslocamento”];
T_deslocamentos_sistema_de_medicao = table(elasticidade.propagacao_incerteza.area,elasticidade.propagacao_incerteza.forca,elasticidade.propagacao_incerteza.deslocamento,elasticidade.propagacao_incerteza.deslocamento_variacao,’VariableNames’,elasticidade.titulo.incerteza_padrao.variaveis)
T_deslocamentos_sistema_de_medicao = 1×4 table
Contribuicao Incerteza Padrao Area Contribuicao Incerteza Padrao Força Contribuicao Incerteza Padrao Deslocamento Contribuicao Incerteza Padrao Variacao Deslocamento 1 5.9973e-08 9.1337e-04 1.1091e-12 8.7484e-07
5.2 Incerteza Padrao Associada ao Modulo de Elasticidade
elasticidade.incerteza_padrao.saida = sqrt(elasticidade.propagacao_incerteza.area+elasticidade.propagacao_incerteza.forca+elasticidade.propagacao_incerteza.deslocamento+elasticidade.propagacao_incerteza.deslocamento_variacao);
elasticidade.titulo.incerteza_padrao.padrao = [“Incerteza Padrão Associada à Variável de Saída”];
T_forca_incerteza_padrao_saida = table(elasticidade.incerteza_padrao.saida,’VariableNames’,elasticidade.titulo.incerteza_padrao.padrao)
T_forca_incerteza_padrao_saida = table table
Incerteza Padrão Associada à Variável de Saída 1 0.0302
5.2.1 Incerteza Parão Combinada Associada à Variável de Saída
Uma vez calculado todos os termos que compõem a incerteza padrão associada às variáveis de entrada,realizando a soma dos quadrados das incertezas encontradas anteriormente, é possivel cálcular a incerteza padrão combinada associada à variável de saída.
elasticidade.liberdade = (elasticidade.incerteza_padrao.saida^4) / ( (area.incerteza_padrao.area^4/area.liberdade) + (forcas.incerteza_padrao.saida^4/forcas.liberdade) + (deslocamentos.incerteza_padrao.saida^4/deslocamentos.liberdade));
elasticidade.fator_de_abrangencia.expandida = tinv(0.95,elasticidade.liberdade);
deslocamentos.titulo.saidas = [“Probabilidade de Abrangência”,”Graus de Liberdade Efetivos”,”Fator de Abrangência”];
T_deslocamentos_incerteza_saida = table(deslocamentos.probabilidade.abrangencia,deslocamentos.liberdade,deslocamentos.fator_de_abrangencia.expandida.saida,’VariableNames’,deslocamentos.titulo.saidas)
T_deslocamentos_incerteza_saida = 1×3 table
Probabilidade de Abrangência Graus de Liberdade Efetivos Fator de Abrangência 1 0.9500 8.5525 1.8441
Assim, obtem-se a incerteza expandida associada a variavel de saida
elasticidade.incerteza_expandida_saida = elasticidade.fator_de_abrangencia.expandida*elasticidade.incerteza_padrao.saida;
elasticidade.titulo.incerteza_expandida = [“Incerteza Expandida Associada à Variável de Saída”];
T_elasticidade_incerteza_expandida_saida = table(elasticidade.incerteza_expandida_saida,’VariableNames’,elasticidade.titulo.incerteza_expandida)
T_elasticidade_incerteza_expandida_saida = table table
Incerteza Expandida Associada à Variável de Saída 1 0.0616
5.4 Contribuição das Incertezas
Objetivando melhor compreender a contribuição das incertezas padrão no calculo da incerteza expandida associada a variável de saida,é realizado a operação de razão de cada incerteza com a incerteza expandida.
elasticidade.contribuicao.area = ((area.incerteza_padrao.area^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.contribuicao.forca = ((forcas.incerteza_padrao.saida^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.contribuicao.deslocamento_inercial = ((deslocamentos.incerteza_padrao.deslocamento_referencial^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.contribuicao.deslocamento = ((deslocamentos.incerteza_padrao.saida^2)*100)/elasticidade.incerteza_padrao.saida^2;
elasticidade.titulo.contribuicao = [“Contribuição Area %”,”Contribuição Força %”,”Contribuição Deslocamento Inercial %”,”Contribuição Deslocamento”];
T_deslocamentos_contribuicao = table(elasticidade.contribuicao.area,elasticidade.contribuicao.forca,elasticidade.contribuicao.deslocamento_inercial,elasticidade.contribuicao.deslocamento,’VariableNames’,elasticidade.titulo.contribuicao)
T_deslocamentos_contribuicao = 1×4 table
Contribuição Area % Contribuição Força % Contribuição Deslocamento Inercial %
7267.5 341.8 0.0023695
Contribuição Deslocamento
0.072178
5.5 Resultado de Medição
Por fim,com a incerteza expandida associada à variável de saida definida e a média dos valores de medição calculado,é possivel obter o resultado de medição.
%disp(‘RM=’),disp(elasticidade.media),disp(‘+-‘),disp(elasticidade.incerteza_expandida_saida)
elasticidade.titulo.resultado = [“RM”,”Média”,”+-“,”Incerteza”];
T_elasticidade_resultado = table(“RM =”,elasticidade.media,”+-“,elasticidade.incerteza_expandida_saida,’VariableNames’,elasticidade.titulo.resultado)
T_elasticidade_resultado = 1×4 table
RM Média +- Incerteza
______ ______ ____ _________
“RM =” 214.66 “+-” 0.061642
¹Discente do Programa Institucional de Bolsas de Iniciação Científica e Tecnológica (PIBIC) Engenharia Aeronáutica – UFU
²Orientadora
