AS DIFICULDADES NO PROCESSO DE ENSINO E APRENDIZAGEM EM MATEMÁTICA PARA OS ALUNOS DO 7º ANO ENSINO FUNDAMENTAL II DAS ESCOLAS ESTADUAIS WALDEMIRO PEREZ LUSTOZA E SÃO LUIZ DE GONZAGA, LOCALIZADAS NA ZONA OESTE DA CIDADE DE MANAUS-AM/BRASIL NO ANO DE 2022

REGISTRO DOI: 10.69849/revistaft/th102501250810

Francisca Claudia Fernandes De Souza
Orientador: Prof. Dr. José Amauri Siqueira da Silva
Coorientador: Prof. Ms. Willianderson Marinho da Silva

RESUMO

O processo de aprendizagem da matemática é muito complexo e a tarefa cognitiva pode ser muito imponente para os alunos uma vez que requer muito esforço deles. Consequentemente, esses alunos precisam de muita motivação para lidar com a disciplina. Portanto, é benéfico para a educação produzir estratégias de ensino que são interessantes e estimulantes. Os educadores agora estão apresentando mais e várias formas de uso de tecnologia da informação direcionadas para suas atividades em sala de aula. Desta forma, essa dissertação de mestrado tem por objetivo analisar quais as dificuldades no processo de ensino e aprendizagem em matemática para os alunos do 7º ano ensino fundamental II das escolas estaduais Waldemiro Perez Lustoza e São Luiz de Gonzaga, localizadas na zona oeste da cidade de Manaus- AM/Brasil no ano de 2022. Para se atingir o objetivo foi realizada um pesquisa descritiva exploratória com enfoque quali-quantitativo que ouviu 6 professores de matemática e 60 alunos do 7º ano ensino fundamental II das escolas estaduais Waldemiro Perez Lustoza e São Luiz de Gonzaga. Os participantes consistiram em apresentar todas as dificuldades de aprendizagem a partir da didática dos professorese a visão dos professores sobre o aprendizado matemático a partir de suas próprias impressões indicando que os alunos têm dificuldades no aprendizado de matemáticaa partir da definição do currículo que para eles não faz muito sentido As diferenças de opinião entre alunos e professores são desafiadoras e devem ser discutidas para informar e orientar possíveis intervenções corretivas. Os resultados demonstraram que a didática dos professores, na visão dos alunos, desabilita o aprendizado e para os professores não desabilita o aprendizado.

Palavras-chave: Matemática, Dificuldades de aprendizagem, Avaliação, Erros, Correção.

RESUMEN

El proceso de aprendizaje de las matemáticas es muy complejo y la tarea cognitiva puede ser muy imponente para los estudiantes, ya que requiere mucho esfuerzo por su parte. En consecuencia, estos estudiantes necesitan mucha motivación para hacerfrente a la disciplina. Por lo tanto, es beneficioso para la educación producir estrategias didácticas que sean interesantes y estimulantes. Los educadores a hora están ideandomás y más formas de usar la tecnología de la información para sus actividades en el aula. De esta manera, esta tesis de maestría tiene como objetivo analizar cuáles son las dificultades en el proceso de enseñanza y aprendizaje de las matemáticas para los alumnos del 7º año de la Enseñanza Fundamental II de las escuelas estatales Waldemiro Perez Lustoza y São Luiz de Gonzaga, ubicadas en la zona oeste de la ciudad de Manaus-AM/Brasil en el año 2022. Si se logró el objetivo, se realizó una investigación exploratoria descriptiva con enfoque cualitativo y cuantitativo, que escuchó a 6 profesores de matemáticas y 60 alumnos del 7º grado de la escuela primaria II de las escuelas estatales Waldemiro Pérez Lustoza y São Luis de Gonzaga.Los participantes consistieron en presentar todas las dificultades de aprendizaje desdela didáctica de los docentes y la visión de los docentes sobre el aprendizaje matemático desde sus propias impresiones, indicando que los estudiantes tienen dificultades en el aprendizaje de las matemáticas desde la definición del currículo quepara ellos no tiene mucho sentido Las diferencias de opinión entre estudiantes y maestros son un desafío y deben discutirse para informar y guiar posibles intervenciones correctivas. Los resultados mostraron que la didáctica de los docentes,en la visión de los estudiantes, inhabilita el aprendizaje y, para los docentes, no inhabilita el aprendizaje.

Palabras clave: Matemáticas, Dificultades de aprendizaje, Evaluación, Errores, Corrección..

ABSTRACT

The process of learning mathematics is very complex and the cognitive task can be very imposing for students since it requires a lot of effort from them. Consequently, these students need a lot of motivation to deal with the discipline. Therefore, it is beneficial for education to produce teaching strategies that are interesting and stimulating. Educators are now coming up with more and more ways to use information technology for their classroom activities. In this way, this master’s thesis aims to analyze what are the difficulties in the process of teaching and learning in mathematics for students in the 7th year of elementary school II of the state schools Waldemiro Perez Lustoza and São Luiz de Gonzaga, located in the west zone of the city of Manaus-AM/Brazil in the year 2022. if the objective was achieved, a descriptive exploratory research was carried out with a qualitative and quantitative approach, which heard 6 mathematics teachers and 60 students from the 7th grade of elementary school II from the state schools Waldemiro Perez Lustoza and São Luiz de Gonzaga. The participants consisted of presenting all the learning difficulties from the teachers’ didactics and the teachers’ view on mathematical learning from their own impressions, indicating that students have difficulties in learning mathematics from the definition of the curriculum that for them doesn’t make much sense Differences of opinion between students and teachers are challenging and should be discussed to inform and guide possible remedial interventions. The results showed that the teachers’ didactics, in thestudents’ view, disables learning and, for the teachers, it does not disable learning.

Keywords: Mathematics, Learning difficulties, Assessment, Errors, Correction.

CAPÍTULO I: MARCO INTRODUTÓRIO

1. INTRODUÇÃO

Hoje, existem novas ferramentas de que o professor deve utilizar como mais um instrumento didático com o objetivo de estimular e desenvolver, cada vez mais, culturais no ensino da matemática, que são as novas tecnologias, criando possibilidades aos alunos renovando as suas habilidades e atualizando os seus conhecimentos, sem anular as experiências já existentes. Essa modernidade não poderia ficar à margem do mundo do aluno, que vive constantemente em busca de construir mais conhecimento.

É necessário, portanto, que os educadores modifiquem suas atitudes, buscando atualização diante dos meios de comunicação (novas tecnologias), para os mesmos não serem engolidos por essas tecnologias, podendo oferecer aos seus alunos uma troca de conhecimentos. Infelizmente, muitos professores colocam a modernidade educacional como inútil e difícil de ser manuseado, entretanto esta modernidade encontra-se inserida no dia-a-dia do alunado e por isso, muitas vezes eles têm mais conhecimento do que os professores.

Frente à perspectiva de um processo de mudança, os educadores sentem-se inseguros e ansiosos devido à sua formação inadequada e, principalmente, por terem acesso apenas a um conjunto de propostas vagas e teorias pouco explicitadas, não fundamentadas em uma prática vivenciada, articulada com o real.

Assim este estudo tem por objetivo geral analisar quais as dificuldades no processo de ensino e aprendizagem em matemática para os alunos do 7º ano ensino fundamental II das escolas estaduais Waldemiro Perez Lustoza e São Luiz de Gonzaga, localizadas na zona oeste da cidade de Manaus-AM/Brasil no ano de 2022. Tem como objetivos específicos: Identificar as dificuldades metodológicas de aprendizagem do 7º ano ensino fundamental II das escolas estaduais Waldemiro Perez Lustoza e São Luiz de Gonzaga, localizadas na zona oeste da cidade de Manaus-AM/Brasil no ano de 2022; Analisar as dificuldades pessoais no processo de ensino e aprendizagem em matemática dos alunos 7º ano ensino fundamental II;

Verificar as dificuldades socias no processo de ensino e aprendizagem em matemática.

A fraca fluência de cálculo é uma característica-chave dos com dificuldades de aprendizagem matemática ao longo da escola. A fluência dos cálculos refere-se a cálculos rápidos, precisos e sem esforço, com operações básicas, além de aplicação apropriada e flexível.

O baixo “domínio de fato” interfere na solução de problemas para o aprendizado de matemática avançada. Os déficits de fluência de cálculo podem ser diagnosticados de maneira confiável no ensino fundamental e, se não forem abordados, podem continuar a ter impactos negativos no desempenho da matemática em todo o restante da vida acadêmica.

O fracasso em se tornar proficiente em matemática é um grande obstáculo à oportunidade da sociedade. Por exemplo, ser pouco habilidoso em matemática diminui muitas oportunidades futuras além de prejudicar outras disciplinas como a baixa capacidade de leitura, baixo QI e muitos outros fatores.

Mesmo os alunos que são leitores hábeis têm certa dificuldade em matemática. Por causa de sua importância para os alunos e para a sociedade como um todo, os formuladores de políticas agora exigem que todos os alunos se formem como matematicamente proficientes. No entanto, pesquisadores e profissionais têm conhecimento limitado sobre o início, trajetórias e fatores de risco para dificuldades de aprendizagem em matemática. Este é particularmente o caso durante os primeiros anos da escola e que segue por todo o ensino fundamental.

Menos ainda avaliaram quais fatores aumentam o risco de um aluno ter dificuldades de matemática. No entanto, esses estudos foram críticos para aumentar a compreensão das necessidades educacionais dos alunos com dificuldades em matemática. É razoável supor que investigar a ocorrência das dificuldades da aprendizagem em matemática a partir da didática dos professores deve informar os esforços para ajudar todas os alunos a se tornarem matematicamente competentes.

Assim a aprendizagem em matemática, sem dúvida, um campo de pesquisa que tem muito a ser explorado. Sendo assim, formar o aluno em matemática é um processo longo que exige do pesquisador um acompanhamento paulatino de um grupo de alunos que serão escolhidos de forma aleatória. Assim este estudo se justifica se constituir uma questão importante, que diz respeito a toda a sociedade, perceber quais são as competências matemáticas essenciais a todos os cidadãos. Situar a questão nas séries finais do ensino fundamental implica também perceber a evolução que se tem registrado neste nível de ensino nos últimos anos para se puder

contextualizar o problema que se pretende estudar. A pesquisa utilizou o método dedutivo de abordagem, o que de acordo com Marconi e Lakatos (2010) é aquele que, partindo das teorias e leis, na maioria das vezes prediz a ocorrência dos fenômenos particulares conexões descendentes. O enfoque qualitativo e, também quantitativo, pois houve uma análise de conteúdo das respostas, com uma sistematização e apresentação mediante a utilização de gráficos.

A pesquisa foi de campo e se transcreveu de forma descritiva, construindo um trabalho por meio de registros, análise, classificação e interpretação dos fatos coletados, sem interferência do resultado final e levantamentos bibliográficos, com a finalidade de evidenciar a qualidade das informações.

Também se utilizou de documentos das duas escolas focoda pesquisa, além de livros, site da internet e revistas especializadas com objetivo depossuir a base teórica que fundamentará o estudo de caso. Sua amostra se constituiude 6 professores e 48 alunos.

A tese está composta de: introdução (contexto da totalidade do estudo); marco teórico (base teórica do trabalho); marco metodológico ( percurso dométodo aplicado no estudo); marco analitico discussão e análises de resultados (análise, avaliação e descrição dos resultados da pesquisa); conclusão (impressões finais do estudo); recomendações (indicações que o estudo apontou ou seja qual o direcionamento que a pesquisa indica).

ABORDAGEM DO PROBLEMA

Problema

O problema que trata esta tese se refere nas dificuldades no processo de ensino e aprendizagem em matemática do ensino fundamental II dos alunos 7º anos das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022.

Descrição do Problema

O problema de que se trata esta tese vem discorrer acerca das dificuldade do processo de ensino e aprendizagem em matemática dos alunos do 7 ano do ensino fundamental II das Escolas Estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus, Amazonas, no ano de 2022.

As dificuldades no processo de ensino e aprendizagem em matemática no ensino fundamental II, não são problemas novos, e atravessam por proporções metodológicas, fatores familiares, sociocultural e até á formação dos professores. Essas problemáticas tem sido cada vez mais pesquisada porque possui grandes destaque no estudo sobre a matemática. Bem como por uma conjuntos de autores especialistas no tema. Como demostra Brito (1998 pg 67).

As dificuldades de aprendizagem em Matemática podem estar relacionadas a impressões negativas oriundas das primeiras experiências do aluno com a disciplina, à falta de incentivo no ambiente familiar, à forma de abordagem do professor, a problemas cognitivos, a não entender os significados, à falta de estudo, entre outros fatores. De acordo com os Parâmetros Curriculares Nacionais da Matemática para o Ensino Fundamental (BRASIL,1997, p. 15),

Pergunta Geral

Quais são os principais dificuldades no processo de ensino e aprendizagem da matemática no ensino fundamental II das Escolas Estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus, Amazonas, no ano de 2022.

Perguntas Especificas:

Quais são as dificuldades metodológicas no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022?
Quais são as dificuldades pessoais no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022?
Quais são as dificuldades familiares no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022?

OBJETIVOS DA INVESTIGAÇÃO

Objetivo Geral

Analisar as dificuldades no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022?

Objetivos Específicos:

Identificar as dificuldades metodológicas no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus- Amazonas no ano de 2022;

Analisar as dificuldades pessoais no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022;

Verificar as dificuldades familiares no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022;

Justificativa

A principal justificativa da pesquisa é analisar as dificuldade do processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II nas metodologias utilizadas, dificuldades pessoais e apoio familiar. Investigar esse tema é de fundamental pertinência para nossa formação profissional, bem como para apresentar alternativas e solução dos nossos conhecimentos acadêmicos e pedagógicos.

Atualmente o tema as dificuldades no processo do ensino e aprendizagem em Matemática tem sido instrumento de investigação, palestras, encontros, seminários e congresso, com o objetivo de descobrir as origens de tantos problemas no ensino desta disciplina.

Esta pesquisa terá um valor significativo para que toda comunidade escolar possa refletir sobre as dificuldades no processo de ensino e aprendizagem em matemática dos alunos do 7º do ensino fundamental II das escolas estaduais Waldemiro Perez Lustosa e São Luiz de Gonzaga no Município de Manaus-Amazonas no ano de 2022.

Limitações da Pesquisa

É necessário conhecer a historia de vida dos alunos, suas vivências de aprendizagens fundamentais, suas condições sociológicas, psicológicas e culturais.

Identificação das Variáveis

As dificuldades no processo de ensino e aprendizagem em matemática

Definição conceitual das variáveis

Segundo D’Ambrósio (1993) as dificuldades de ensino e aprendizagem podem ser consideradas como responsável por diversidade de problemas educacionais. É bastante ampla e complexa, pode abranger dificuldades pedagógicas, pessoais, familiares e sociais, entre outros.

Definição operacional das variáveis

A definição operacional das variáveis para o tema “As dificuldades no processo de ensino e aprendizagem em matemática” refere-se à descrição clara e mensurável de como essas dificuldades serão identificadas, avaliadas ou observadas em um estudo. Aqui está uma possível abordagem:

Variável: Dificuldades no ensino da matemática

Definição operacional: As dificuldades enfrentadas pelos professores durante a prática pedagógica em matemática, medidas por meio de entrevistas, questionários ou observações em sala de aula. Esses aspectos podem incluir desafios relacionados à abordagem de conteúdos, utilização de recursos didáticos, estratégias pedagógicas ou interação com os alunos.

Variável: Dificuldades na aprendizagem da matemática

Definição operacional: Obstáculos enfrentados pelos alunos na compreensão, aplicação ou retenção de conteúdos matemáticos. Esses desafios podem ser identificados por meio de avaliações diagnósticas, análise de desempenho em exercícios ou provas, e relatos dos próprios alunos sobre os fatores que dificultam o aprendizado (como ansiedade matemática ou falta de interesse).

Variável: Fatores contextuais

Definição operacional: Elementos externos que podem influenciar as dificuldades no ensino e aprendizagem, como infraestrutura escolar, formação docente, metodologias utilizadas e apoio familiar. Esses fatores podem ser mensurados por meio de questionários aplicados a professores, alunos e responsáveis.

Variável: Estratégias de superação das dificuldades

Definição operacional: Práticas e intervenções realizadas por professores e alunos para mitigar os desafios enfrentados, avaliadas pela análise de projetos pedagógicos, implementação de metodologias ativas ou o uso de tecnologias educacionais.

Caso deseje expandir ou detalhar essas definições operacionais, posso ajudar a ajustá-las com base em contextos específicos ou objetivos de pesquisa.

Hipótese de investigação

As dificuldades no processo de ensino e aprendizagem em Matemática estão relacionadas a fatores como a falta de metodologias pedagógicas adequadas, baixa motivação dos alunos, insuficiência na formação docente, e contextos socioculturais que desfavorecem o engajamento com a disciplina.

Possíveis desdobramentos dessa hipótese:

Metodologias pedagógicas inadequadas: O uso de métodos tradicionais de ensino, sem conexão com a realidade dos alunos, pode dificultar a compreensão e a aplicação prática de conceitos matemáticos.
Fatores emocionais e motivacionais: Ansiedade matemática e desinteresse dos alunos podem impactar negativamente o aprendizado.
Formação e capacitação docente: Professores que não recebem formação continuada em metodologias inovadoras têm maior dificuldade em adaptar o ensino às necessidades dos alunos.
Condições socioeconômicas e culturais: Alunos em situações de vulnerabilidade social podem ter menos acesso a recursos educacionais, o que agrava as dificuldades em Matemática.

CAPITULO II

2 MARCO TEÓRICO

A fundamentação teórica se exprime no embasamento teórico da pesquisa, ou seja, como define Vergara (2010, p. 33) “fundamentação teórica é a sustentação referencial do tema com base em outros estudos realizados por autores que se ocuparam do mesmo tema”.

2.1 MATEMÁTICA

A matemática é abstrata e desencarnada – mas é real. A matemática tem uma existência objetiva, fornecendo estrutura para esse universo e qualquer universo possível, independente e transcendendo a existência de seres humanos ou de quaisquer seres (ALMOULOUD, 2017).

A matemática humana é apenas uma parte da matemática abstrata e transcendente. Portanto, a prova matemática permite descobrir verdades transcendentes do universo. A matemática é parte do universo físico e fornece estrutura racional para ele. Existem séries de Fibonacci em flores, espirais logarítmicas em caracóis, fractais em cordilheiras, parábolas em home runs e bolas em direção ao gol (NACARATO, et. al., 2004).

Na forma esférica de estrelas, planetas e bolhas, razão para qualquer ser possível. Aprender matemática é, portanto, aprender a linguagem da natureza, um modo de pensamento que teria que ser compartilhado por quaisquer seres altamente inteligentes em qualquer lugar do universo. Porque a matemática é desencarnada e a razão é uma forma de matemática. Lógica matemática, a própria razão é desencarnada (FIORENTINI et. al., 2018).

Mas quanto mais se aplica o que se sabe sobre a ciência cognitiva para entender a estrutura cognitiva da matemática, mais se torna claro que a matemática como ciência abstrata é real (HULIN, 2016).

A matemática humana, o único tipo de matemática que os seres humanos conhecem, não pode ser uma subespécie de uma matemática abstrata e transcendente. Em vez disso, parece que a matemática como se conhece surge da natureza do cérebro humano e da experiência incorporada. Como consequência, todas as partes parecem falsas, por razões que se desconhece. Talvez o maissurpreendente seja que a descoberta que muitas das ideias matemáticas fundamentais são inerentemente metafóricas por natureza: a linha numérica, onde os números são conceituados metaforicamente como pontos em uma linha; álgebra de classes de Boole, onde a formação de classes de objetos é conceituada metaforicamente em termos de operações e elementos algébricos: mais, tempos, zero, um e assim por diante; lógica simbólica, onde o raciocínio é conceituado metaforicamente no cálculo usando símbolos; funções trigonométricas, onde os ângulos são conceituados metaforicamente como números; o plano complexo, onde a multiplicação é conceituada metaforicamente em termos de rotação (PARRA; SAIZ, 1996; SADOVSKY, 2007).

E como veremos, Prado (2000) estava certo sobre a centralidade da metáfora conceitual para uma compreensão completa do infinito na matemática. Existem dois conceitos finitos em matemática – um literal e um metafórico. O conceito literal (“in finitude” – falta de um fim) é chamado “infinito potencial”. É simplesmente um processo que continua sem fim, como contar sem parar, estender o segmento alinho indefinidamente ou criar polígonos com mais e mais lados. Ideias não metafóricas são necessárias neste caso.

O infinito potencial é uma noção útil na matemática, mas o evento principal está em outro lugar. A ideia de “infinito real”, onde o infinito se torna uma coisa – um conjunto infinito, um ponto no infinito, um número transfinito, a soma de uma série infinita – é o que é realmente importante (VALLADARES, 2003).

A finitude real é fundamentalmente em uma ideia metafórica, como Prado (2000) suspeitava. A surpresa foi que todas as formas do infinito real – pontos no infinito, infinitas seções, números transfinitos e assim por diante – parecem ser casos especiais de apenas uma metáfora básica do infinito. Isso é tudo menos óbvio e será discutido longamente no decorrer do livro. Como aprendemos cada vez mais sobre a natureza do reconhecimento matemático humano, o Romance da Matemática se dissolveu diante de nossos olhos. O que surgiu em seu lugar uma imagem ainda mais bonita – uma imagem do que realmente é a matemática-matemática (PRADO, 2000). O ensino de matemática visa tornar o educando capaz de explicar o meio próximo e remoto que o cerca e atuar sobre ele, desenvolvendo para tanto o espírito de investigação, invenção e iniciativa; o pensamento lógico e a noção da universalidade das leis científicas e matemáticas. Com base neste conceito, o ensino da matemática no Brasil deveria ser, então, preparar o aluno para um mundo científico, pois os objetivos explícitos refletem a imagem de aluno com profundos conhecimentos matemáticos em nosso meio (SOARES, 2001).

A educação científica constitui uma área da educação que envolve problemas peculiares, os quais a distinguem de outros campos de atuação da escola. Ensinar a ler e escrever, por exemplo, envolve a transmissão de conhecimentos sobre um objeto acabado — um sistema de escrita já determinado — e de domínio público, assim comoo desenvolvimento da habilidade de usar bem esse sistema (SOARES, 2001).

A educação científica, por outro lado, envolve a transmissão de conhecimento sem construção, frequentemente desconhecidos do público em geral, o desenvolvimento da habilidade de usar esses conhecimentos e, além disso, o desenvolvimento de um modo de conhecer também especializado, que permite a criação de novos conhecimentos científicos (NACARATO, et. al., 2004).

2.1.1 A Aprendizagem em Matemática

O modelo vigente de ensino de matemática, concretizado pela prática educacional corrente, parece tratar o ensino como um problema principalmente de transmissão de informações e, ocasionalmente, de utilização dessas informações para resolver problemas já resolvidos por outros através de rotinas para solução de problemas já praticadas com o professor (FIORENTINI et. al., 2018).

Então que matemática ensinar? No que diz respeito ao ensino e à aprendizagem da Matemática é possível delinear um esquema interpretativo, Neste esquema, duas dimensões são fundamentais relativas ao processo de aprendizagem segundo Soares (2001, p. 6):

A primeira dimensão respeita ao modo como o conhecimento é incorporada no conjunto dos fatos, dos conceitos e das generalizações já integradas e realizadas pelo aluno. Nos extremos desta dimensão se tem ou uma aprendizagem mecânica ou uma aprendizagem significativa. A segunda dimensão respeita ao itinerário através do qual os conhecimentos e capacidades são adquiridos. Nos extremos se tem uma aprendizagem por descoberta ou de uma aprendizagem por recepção.

A aprendizagem mecânica caracteriza-se pelo fato do conhecimento ser adquirido de forma isolada, sem ligação com o que já se conhece. Para reter na memória o contributo é necessário recorrer a uma repetição mecânica e estereotipada, uma vez que não existe relação entre aquele e a estrutura cognitiva já desenvolvida. Pode-se acrescentar que tal conhecimento facilmente cai no esquecimento (desde que não utilizado frequentemente) por permanecer isolado no conjunto dos conhecimentos adquiridos. Aqui a leitura poderia ser dinamizada como forma fundamental de retenção de conhecimento (HULIN, 2016).

A aprendizagem significativa, caracteriza-se pelo fato do novo material a aprender poder ser associado e vir de fato associado aos conceitos e competências já adquiridas e, portanto, poder ser incorporado, não de forma isolada mas de forma bem relacionada, no corpo de conhecimentos já existente. A rede de relações que assim se constitui facilita quer a evocação que a utilização do conhecimento por meio da leitura (PARRA; SAIZ, 1996).

Não se trata, na maior parte dos casos, de se ser o primeiro a descobrir qualquer coisa, isto é, em sentido absoluto, mas antes em sentido relativo, ou seja, como se fosse o primeiro a fazê-lo. Isto significa que a solução do problema ou a demonstração da verdade de uma afirmação não são comunicados ao aluno. Uma autêntica descoberta, ainda que no sentido relativo, exige a formulação de hipóteses viáveis e também a validação das mesmas (NACARATO, et. al., 2004),

A aprendizagem por recepção caracteriza-se pela falta de autonomia na construção de um conceito, de um processo de resolução, etc. Todos os conhecimentos provêm da transmissão cultural ou da comunicação direta (FIORENTINI et. al., 2018). (HULIN, 2016).

A forma com se definem as finalidades do ensino da Matemática parece ter consequências nas concepções que se desenvolvem. De uma forma geral pode ser definida pela sua importância na vida. “Se os requisitos da vida do dia a dia determinassem o conteúdo dos programas de Matemática, haveria com certeza muito pouca Matemática neles” (DIENES, 1960, cit. por ORTON e FROBISHER, 1996, p. 3).Também é muita vez referida pelo seu valor em ensinar pessoas a pensar e resolver problemas. No entanto, não existe evidência de que estudar Matemática é a melhor maneira de treinar o pensamento ou que uma “dieta pesada” de matemática escolar produz melhores pensadores lógicos ou que existem conteúdos matemáticos mais válidos que quaisquer outros noutras áreas do saber. Poderão ser referidas outras razões para ensinar matemática, que possivelmente serão base de outro tipo de concepções. O fato de que os nossos alunos têm o direito de conhecer quão importante é a matemática presente no nosso mundo atual e de que esta é parte da nossa herança cultural (PRADO, 2000).

Se a linguagem nos capacita para comunicar, então a matemática também nos habilita com extensões da linguagem – a informação é por vezes melhor expressa emgráficos, tabelas, símbolos algébricos transmitindo-nos um significado conciso de relações globais tal como numa fórmula ou diagramas por vezes permitem modos mais fáceis de aceder a ideias que outras formas. A matemática pode ser apreciada por si mesma – existe um elemento estético na matemática. Apreciar a matemática e criar o gosto de fazer matemática como qualquer outra coisa deve ser uma das finalidades principais (ORTON e FROBISHER, 1996).

Schoenfeld (1992) caracteriza a Matemática como uma atividade essencialmente social, na qual a comunidade de praticantes (matemáticos) se envolve na Science of patterns, sistematicamente examinando e procurando regularidades abstratas que tanto podem ser reais como imaginárias, visuais ou mentais.

Na perspectiva do social construtivismo, Ernest (1996, p. 25), “identifica a Matemática como sendo uma instituição social que resulta da formulação e resolução de problemas pelo Homem”. O conhecimento matemático não está contido em textos ou outros materiais, nem em qualquer reino ideal. O conhecimento objetivo da Matemática reside nas regras, convenções, compreensões e significados dos membros da sociedade e nas suas interações e conseqüentemente nas instituições sociais.

Nas discussões sobre os fundamentos da Matemática Davis e Hersh (1991, p.299) apresentam “três dogmas padrão: platonismo, formalismo e construtivismo”. No primeiro um matemático não tem nada a inventar uma vez que tudo já existe e apenasnecessita ser descoberto.

No formalismo não há objetos matemáticos, esta apenas consiste em axiomas, definições e teoremas, enquanto Matemática pura não tem qualquer significado nem qualquer valor de veracidade. Os construtivistas, opondo-se aos outros, consideram Matemática genuína apenas a que pode ser obtida por uma construção finita. Assim, deste ponto de vista “a atividade dos que estão a aprender matemática, desde que produtiva, envolvendo a formulação e resolução de problemas não é qualitativamente diferente da atividade dos matemáticos profissionais” (ERNEST, 1996, p. 27).

Quando as crianças chegam à educação formal já possuem um grande conjunto de conhecimento anterior, capacidades, crenças econceitos que significativamente influenciam a forma como percepcionam o ambiente, organizam e interpretam a informação. Este conhecimento afeta a sua capacidade de recordar, raciocinar, resolver problemas e adquirir novos conhecimentos (BRANSFORD, 2000).

A forma como essas ideias interferem ou não na sua atividade matemática na aula é muito da responsabilidade do professor e as concepções destes também implicam na definição das tarefas e consequentemente nas expectativas que os alunos vão desenvolver. “O que os professores consideram ser o objeto de estudo influencia significativamente o modo como ensinam” (DAVIS e PETTITT, 1994).

2.1.2 Visão dos Professores de Matemática

Muitos professores veem a matemática escolar apenas em termos de conteúdo. As competências são adquiridas em tais casos fortuitamente, já que não existem experiências de aprendizagem especialmente pensadas para promover o seu desenvolvimento (NACARATO, et. al., 2004).

Outros veem a matemática como uma exploração no mundo desconhecido dos símbolos e estão convencidos que a matemática escolar, através do estudo de competências e conhecimentos matemáticos, é uma preparação para esse mundo, não uma parte dele (FIORENTINI et. al., 2018).

Tais professores não reconhecem as investigações como fazendo parte da experiência matemática das crianças até que sejam universitários ou até mesmo apenas quando se dedicarem a uma pós-graduação. Para outros, ainda, compreendeapenas competências e conhecimentos e a finalidade da matemática escolar é transmitir estas ideias (HULIN, 2016).

Existe também um grande número de professores que acreditam que as investigações constituem parte essencial da experiência matemática de todas as crianças e defendem que a matemática escolar deve refletir a natureza da matemática como uma atividade exploratória disponível para todos. Desta forma, para os professores de matemática que o ensino de matemática depende da pesquisa e da capacidade de investigação. Tal é o caso de Ernest (1996, p. 87):

Dado que uma parte fundamental da matemática é a formulação e resolução de problemas, e que esta é uma atividade acessível a todos, daqui decorrem importantes consequências para a educação. Entre estas consequências, (…) incluem-se as seguintes: – A matemática escolar para todos deve estar essencialmente relacionada com a formulação e resolução de problemas; – A inquirição e a investigação devem ocupar um lugar central no currículo de matemática; – O fato de a matemática ser uma construção falível e em permanente evolução deve ser explicitamente aceite e incorporado no currículo; A pedagogia utilizada deve ser centrada nos processos e na inquirição, caso contrário, existe contradição com as implicações anteriores.

Um resultado destes princípios é que a matemática para todos passa a ser Matemática por todos. A perspectiva de incluir nos processos educativos tarefas de cariz investigativo não é pacífico e igualmente entendido por todos. Mesmo considerando que a pedagogia de inquirição é a mais adequada, Ernest (1996a) distingue várias formas de abordar as a sua integração na prática curricular.

Uma das vertentes integra as investigações como um tema adicional, mas em que os conteúdos são prevalecentes. Embora de formas diferentes tanto a perspectiva“old humanist” como a “technological pragmatist”, partilham uma visão absolutista da Matemática e valorizam as atividades investigativas como uma aplicação não rotineirado conhecimento ou como problemas práticos que conduzem a resultados concretos (NACARATO, et. al., 2004)

Outra das vertentes referidas é a da adoção das investigações como abordagem pedagógica de todo o currículo e não como algo adicional. Esta perspectiva é partilhada pelo que designa de “progressive educators” e de “public educators”. No primeiro caso as investigações são entendidas em termos dos processos dos alunos, os ambientes de aprendizagem cuidadosamente estruturados e os professores entendidos como gestores e facilitadores da aprendizagem. Distinguem-se dos “public educators” na medida em que apenas abordam temas de Matemática pura ou questões “seguras”. Estes acrescentam uma dimensão político- social às abordagens investigativas, incluindo o trabalho de grupo e a discussão, a autonomia e incentivando a possibilidade dos alunos seguirem os seus caminhos na formulação da metas a atingir. Em todos os casos referidos a diferenciação centra-se sobre a tarefa proposta. Davis (1994) assinala que a diferenciação pode ocorrer pela tarefa proposta ou pelo produto obtido. No primeiro caso entende-se que se proponha aos alunos conjuntos de tarefas consistentes com o seu nível de conhecimentos, de compreensão ou competência.

Na diferenciação por produtos obtidos, as tarefas podem ser mais abertas e o grau de controle sobre o trabalho a desenvolver é passado para os alunos podendo se desenvolvido a diversos níveis de complexidade (DAVIS, 1994).

A abordagem realizada partiu do ponto de vista de implementadores do currículo, especialistas, matemáticos, professores problematizando a forma como definem as finalidades do ensino da Matemática, o entendimento desta como ciência e a adoção por parte dos professores de perspectivas que possibilitem uma realização de atividades investigativas (DAVIS, 1994).

A implementação deste tipo de tarefas no ensino/aprendizagem da Matemáticatem também de ultrapassar outro tipo de obstáculos. Estes advêm do efeito socializante do contexto implicando que muitos professores, apesar de terem diferentes crenças sobre a Matemática e o seu ensino, tendem a adaptar práticas semelhantes aos seus colegas de escola (PARRA; SAIZ, 1996).

Os constrangimentos e oportunidades resultantes do contexto social de ensino fazem com que os professores afastem as suas intenções e práticas pedagógicas dasteorias que adaptam (PARRA; SAIZ, 1996).

O contexto social tem uma poderosa influência devido a certo número de fatores entre os quais estão às expectativas de outros, nomeadamente dos alunos, dos pais, dos colegas professores e dos superiores hierárquicos. Esta influência também resulta do currículo institucionalizado: os manuais, a organização curricular, a avaliação e o sistema global de ensino. (ERNEST, 1996, p.35-36).

No que respeita às convicções dos alunos acerca da Matemática, estudos realizados por Frank (1992) caracterizam-nas da forma que se apresenta na tabela a seguir:

Quadro 1 – Convicções dos alunos acerca da matemática

O que é…?	Com se entende…	O que se faz…
Matemática é calculo	As quatro operações básicas, memorização de tabuadas e algoritmos.	Fazer matemática é seguir regras eaprender a memorizar
Os problemas de matemática são questões que se resolvem rapidamente e em poucos passos	Tarefas de rotina em que se podemaplicar os algoritmos Aritméticos ou algébricos	Algo está errado com eles ou com o problema se este demorava mais de 5-10 minutos a resolver
O objetivo de fazer matemática éobter respostas certas	Dicotomia entre certo ou erradoque era legitimado pelo professor	Atenção centrada apenas no resultado
O papel dos alunos de matemática é receber conhecimentos e demonstrar que os adquiriu	Receber conhecime ntos passivamente e obter respostascertas	Ter atenção na aula, ler o livro adotado e fazer os trabalhos de casa.
O papel do professor de matemática é transmitir conhecimentos e verificar que os alunos os adquiram	Explicar e dar a matéria do livroadotado	Explicar bem a matéria, confirmar que os alunos adquiram os conhecimento.

Fonte: Frank (1992, p. 33).

Um aluno com este tipo de convicções poderá ser um aluno de sucesso caso lhe seja solicitado à resolução rápida e eficiente de exercícios. É natural que reaja negativamente se lhe forem propostas atividades de investigação e que revele insegurança, solicitando o apoio e elucidação do professor (DAVIS, 1994).

Concepções de alunos acerca da natureza da matemática são também apresentadas por Schoenfeld (1992) reforçando a ideia de que existe apenas uma resposta correta, que um problema tem uma única forma de se resolver, um aluno que entenda a matéria aplica a forma correta em pouco tempo e dos alunos vulgares não se pode esperar que compreendam a Matemática mas apenas que a memorizem. Acrescenta o fato de os alunos entenderem a atividade matemática como uma atividade solitária, que a Matemática aprendida na escola tem pouco ou nada a ver com a vida real e que a demonstração é irrelevante nos processos de descoberta ou invenção.

A resistência dos alunos perante atividades investigativas é bem justificada quando nos confrontamos com sistemas de concepções deste tipo. No entanto, a introdução deste tipo de tarefas no currículo poderá contribuir para alterar progressivamente as concepções e criar condições para uma aprendizagem mais interessante (FIORENTINI et. al., 2018).

Convencendo os estudantes de que o seu sucesso reside, não tanto na obtenção de respostas corretas, mas antes na elaboração de conjecturas sustentáveise na construção de argumentos que convençam os outros de que as suas conjecturas são razoáveis, um professor pode sustentar o raciocínio matemático, quando as coisas se tornam mais difíceis (MASON, 1996, p. 81).

Algumas investigações realizadas problematizam o conceito de atitude e concepção dos alunos e fornecem-nos dados que importa considerar mesmo que estes respeitem a outros níveis de ensino. Matos (1991) investiga as atitudes e concepções de alunos de 8º ano em relação à Matemática.

O estudo sugere uma dualidade na visão que os alunos têm da Matemática: há por um lado uma Matemática prática ou automatizada e por outro uma Matemática do raciocínio. Estas duas concepções coexistem nos diversos alunos mas aparecem com uma importância relativa diferente. As concepções dos alunos estão relacionadas com a atividade matemática por eles realizada mas tendem a ser vistas como características da própria Matemática (MASON, 1991).

A Matemática pode surgir como imposta do exterior e, nesse caso, ela aparece com um conjunto de regras que se aplicam em situações bem definidas. Mas também pode ser entendida como expressão da individualidade e, nesse caso, é algo que se elabora e pensa. Uma grande fixação dos alunos nas preocupações de cunho escolar (nomeadamente a avaliação) tende a reforçar uma visão pragmática desta disciplina, dificultando a evolução de ideias dos alunos (PONTE, MATOS e ABRANTES, 1998, p. 204-205).

Um dos aspectos analisados por Abrantes (1994) no estudo sobre os efeitos do currículo desenvolvido pelo projeto MAT789 é a evolução das concepções dos alunos a respeito da Matemática.

Os estudos de caso sugerem que a evolução das concepções dos alunos está fortemente relacionada com as experiências de aprendizagem que viveram no âmbito do currículo e que a visão dos alunos sobre a Matemática condiciona o modo como se envolvem nas tarefas matemáticas. Além disso, fornece exemplos de relação estreita entre a evolução das concepções e de aspectos cognitivos e afetivos como se tornar competente em vários aspectos do estudo desta disciplina ou verificar que, em Matemática, há lugar para uma variedade de estilos pessoais de trabalhar (MATOS, 1991).

Este estudo mostra ainda que a falta de discussão explícita sobre o que é a Matemática, à luz das experiências dos alunos, torna muito difícil que eles reflitam sobre essas experiências e sejam capazes de desenvolver uma concepção pessoal coerente sobre a Matemática e uma visão crítica fundamentada sobre o ensino e aprendizagem desta disciplina. (PONTE, MATOS e ABRANTES, 1998, p. 206).

Se do ponto de vista da concepção do que é Matemática e da sua aprendizagem a introdução de atividades investigativas no currículo adquire todo o significado, a estruturação dessas atividades e a forma como são apresentadas às crianças deverá ter em consideração as convicções destes e por objetivo uma reflexão, desde muito cedo, sobre o que é a Matemática, a partir das experiências de aprendizagem proporcionadas (MASON, 1991).

2.2 DIFICULDADES EM MATEMÁTICA

As dificuldades de matemática são comuns entre alunos de todas as séries do ensino fundamental até o ensino médio no Brasil. Embora as deficiências de desenvolvimento e aprendizagem sejam fontes significativas dessas dificuldades, o desempenho em matemática está fortemente relacionado ao status socioeconômico dos alunos (PARRA; SAIZ, 1996).

Quando se avalia a aprendizagem matemática em exames nacionais deveria se levar em conta a renda familiar, o nível de pobreza no bairro em que o aluno reside e a escolaridade dos pais. Em média, alunos de famílias de baixa renda desfavorecidas desempenham uma matemática substancialmente pior do que suas contrapartes de famílias de alta renda. Alunos pobres têm uma probabilidade 1,5 vezes maior de ter uma deficiência de aprendizado e duas vezes mais chances de repetir uma série e, eventualmente, abandonar o ensino médio do que seus colegas não-pobres. A taxa de pobreza nos Brasil é muito alta, afetando milhões de alunos emidade escolar (SADOVSKY, 2007).

Alunos de minorias, como negras, especiais, são desproporcionalmente representadas em populações de baixa renda, resultando em disparidades significativas de classe social e social na aprendizagem de matemática. As consequências do fraco desempenho em matemática são sérias para o funcionamento diário e o avanço da carreira profissional (PRADO, 2000).

Uma forte conquista matemática em todas os alunos é importante para atender às necessidades de nossa sociedade cada vez mais tecnológica e para a igualdade da força de trabalho A competência em matemática está associada à entrada nas disciplinas (ciência, tecnologia, engenharia e matemática) no ensino superior, bem como nas ocupações relacionadas ao ensino tecnológico (VALLADARES, 2003).

A diferença de renda no desempenho em matemática é bem documentada no ensino fundamental e médio. As raízes dessa lacuna são plantadas bem antes dos alunos começarem a escola. As oportunidades de aprendizado e as experiências sociais, juntamente com o aprendizado básico e as habilidades cognitivas, contribuem para o aprendizado de matemática das crianças desde a infância (VITTI, 1999).

O número de competências que as crianças trazem para a escola preparou o terreno para o aprendizado de matemática complexa. A competência numérica (também conhecida como conhecimento numérico ou ‘sentido numérico’ ”) envolve a compreensão de números e relações numéricas (VALLADARES, 2003).

Um aluno deve representar coleções como “conjuntos de indivíduos”, representando simultaneamente o todo e suas unidades constituintes. Esse conceito é essencial para a competência numérica verdadeira, incluindo a capacidade de reconhecer o valor numérico de pequenas quantidades sem contar, discriminar entre e entre quantidades, fazer julgamentos sobre as magnitudes de pequenos números, contar atentamente objetos e executar cálculos simples de adição e subtração. A competência numérica envolve a capacidade de visualizar números em uma linha numérica e compreender que cada número é um a mais que o número anterior (PARRA; SAIZ, 1996).

Os componentes principais do número (por exemplo, representações exatas de pequenas numerosidades e representação aproximada de numerosidades maiores) se desenvolvem sem instrução formal (SADOVSKY, 2007).

Pensa-se que essas fundações pré-verbais fornecem uma base para o aprendizado de habilidades numéricas mais complexas, envolvendo palavras numéricas, comparações numéricas e contagem. No entanto, esses fundamentos pré- verbais não são suficientes. A maioria dos alunos com dificuldades de matemática noensino fundamental e mais tarde parece ter problemas particulares com os sistemas de números verbais ou simbólicos, que são fortemente influenciados por experiênciase instruções precoces (PRADO, 2000).

Enquanto os alunos com deficiências na matemática são especificamente incluídas na definição de Dificuldades de Aprendizagem, raramente as dificuldades de aprendizagem dos alunos levam os mesmos a serem encaminhadas para avaliação.

Em muitos sistemas escolares, os serviços de educação especial são fornecidos quase que exclusivamente com base nas deficiências de leitura das crianças (BACHELARD, 2018).

Mesmo após serem identificadas como deficientes na aprendizagem de matemática poucos alunos recebem avaliação e correção substanciais de suas dificuldades aritméticas. Essa negligência relativa pode levar pais e professores a acreditar que problemas de aprendizagem na aritmética não são muito comuns, ou talvez não muito sérios. No entanto, aproximadamente 46,00% dos alunos apresentam déficits matemáticos significativos e entre os alunos classificados como deficientes em aprendizagem, as dificuldades aritméticas são tão difundidas quanto os problemas de leitura. Isso não significa que todas as dificuldades de leitura são acompanhadas de problemas de aprendizagem aritmética, mas significa que os déficits em matemática são generalizados e precisam de atenção e preocupação equivalentes (HULIN, 2016).

Os efeitos do fracasso matemático ao longo dos anos de escolaridade, juntamente com o analfabetismo matemático na vida adulta, podem prejudicar seriamente a vida diária e as perspectivas profissionais. No mundo de hoje, o conhecimento matemático, o raciocínio e as habilidades não são menos importantes do que a capacidade de leitura (ALMOULOUD, 2017).

Tal como acontece com as dificuldades de leitura dos alunos, quando existem dificuldades matemáticas, elas variam de leve a grave. Também há evidências de que os alunos manifestam diferentes tipos de deficiências em matemática (FIORENTINI et. al., 2018).

Infelizmente, as pesquisas que tentam classificá-las ainda não foram validadasou amplamente aceitas; portanto, é necessário cuidado ao considerar as descrições de diferentes graus de deficiência matemática (NACARATO, et. al., 2004) Ainda assim, parece evidente que os alunos experimentam intensidades não apenas diferentes de dilemas matemáticos, mas também tipos diferentes, o que exigia várias ênfases na sala de aula, adaptações e, às vezes, até métodos divergentes (FIORENTINI et. al., 2018).

Alguns alunos com dificuldades de aprendizagem têm uma excelente compreensão dos conceitos de matemática, mas são inconsistentes no cálculo. Eles não são confiáveis ao prestar atenção ao sinal operacional, ao tomar emprestado ou transportar adequadamente e ao sequenciar as etapas em operações complexas(BACHELARD, 2018).

Esses mesmos alunos também podem ter dificuldade em dominar fatos numéricos básicos. Curiosamente, alguns dos alunos com essas dificuldades podem ser estudantes de matemática corretivos durante os anos elementares em que a precisão computacional é fortemente estressada, mas podem continuar a participar de turmas de honra em matemática superior, onde sua proeza conceitual é chamada para (NACARATO, et. al., 2004)

Claramente, esses alunos não devem ser acompanhados em aulas de matemática secundárias de baixo nível, onde continuarão apenas demonstrando esses espelhos descuidados e habilidades computacionais inconsistentes enquanto tiverem acesso negado aos conteúdos de nível superior dos quais são capazes (HULIN, 2016).

Como há muito mais na matemática do que o cálculo confiável de respostas corretas é importante acessar o amplo escopo das habilidades e não julgar a inteligência ou o entendimento observando apenas habilidades fracas de nível inferior. Muitas vezes, deve-se encontrar um equilíbrio delicado no trabalho com alunos com deficiência de aprendizagem, que incluem: (a) reconhecer suas fraquezas computacionais (b) manter um esforço persistente para fortalecer habilidades inconsistentes; (c) compartilhar uma parceria com o aluno para desenvolver sistemasde auto monitoramento e compensações; e, ao mesmo tempo, fornecendo o escopo completo e enriquecido do ensino de matemática (ALMOULOUD, 2017). Em algumas pesquisas sobre didática da matemática, a questão da preparaçãoda matemática para os alunos, está localizada no cruzamento entre dois campos teóricos não independentes, mas ainda assim distintos: a teoria da transposição didática, desenvolvida desde o início dos anos 1980 por Y Chevallard e a teoria das situações didáticas, iniciada por G. Brousseau (1986) no início da década de 1970 e desenvolvida por vários pesquisadores diferentes desde então (NACARATO, et. al., 2004)

Se alguém adota uma abordagem de ‘transposição didática’, introduz um sistema aberto para a análise que inclui, em particular, as instituições na fonte do conhecimento que se pretende ensinar e a instituição iniciada por esse ensino. Isso éfeito questionando a constituição e a vida desse conhecimento, mantendo-se particularmente atento à economia e à ecologia do conhecimento a ser ensinado. Questiona-se a possível viabilidade do conteúdo que se deseja promover, considerando as leis que governam o funcionamento do sistema de ensino (ALMOULOUD, 2017); (FIORENTINI et. al., 2018)..

Tenta-se prever as deformações pelas quais é provável que sejam submetidas; tenta-se garantir que o objeto possa viver e, portanto, se desenvolver dentro do sistema de ensino sem mudar drasticamente sua natureza ou se tornar corrompido.

2.2.1 Reforma da Matemática

A reforma da matemática moderna proporcionou uma base excelente. para o estudo desses fenômenos de transposição didática, e é, principalmente, o terreno escolhido por Y. Chevallard na primeira referência citada acima (HULIN, 2016).

Outras teorias analisam a evolução por meio de estudos realizados dentro e fora do campo da didática da matemática, bem como algumas teses de doutorado que estudaram a matematização progressiva da esfera econômica, os obstáculos encontrados, os debates e as negociações que surgiram em torno dessa matematização e suas implicações para o conteúdo do próprio ensino (BACHELARD, 2018).

Pode-se acrescentar que tal conhecimento facilmente cai no esquecimento (desde que não utilizado frequentemente) por permanecer isolado no conjunto dos conhecimentos adquiridos. Aqui a leitura poderia ser dinamizada como forma fundamental de retenção de conhecimento (PRADO, 2000).

A aprendizagem por descoberta põe a tônica no itinerário da aprendizagem e, mais precisamente, no seu caráter de processo independente e no fato de que a conquista da verdade de uma proposição se inicia por via autônoma. Não se trata, na maior parte dos casos, de se ser o primeiro a descobrir qualquer coisa, isto é, em sentido absoluto, mas antes em sentido relativo, ou seja, como se fosse o primeiro a fazê-lo. Isto significa que a solução do problema ou a demonstração da verdade de uma afirmação não são comunicados ao aluno. Uma autêntica descoberta, ainda queno sentido relativo, exige a formulação de hipóteses viáveis e também a validação das mesmas (HULIN, 2016).

Em alguns países, os órgãos de governança da educação sempre realizam exames específicos para diagnosticar os problemas do ensino, principalmente em relação ao vernáculo e ao ensino de matemática, o que no Brasil se resuma a uma avaliação da educação básica por meio de teste estanque. Nos Estados Unidos, por exemplo, um grupo de pesquisa chamado Grupo de Matemática Diagnóstica e Corretiva foi formado na Universidade da Califórnia no ano de 1982, com a tarefa principal de identificar as dificuldades encontradas pelos alunos e, em seguida, usar essas informações para desenvolver procedimentos corretivos para superar essas dificuldades (NACARATO, et. al., 2004).

Métodos de diagnóstico de dificuldades. Por exemplo, eles consideraram técnicas de entrevista, como fazer os alunos pensarem em voz alta, com os alunos sendo solicitados a verbalizar todas as ideias que vêm à sua mente durante a solução de um problema de matemática.

A variante dessa técnica, desenvolvida originalmentepor Jean Piaget, é a entrevista clínica. Isso difere de ‘pensar em voz alta’, pois o professor pode seguir os pensamentos de seus alunos fazendo perguntas aqui e durante o curso de solução do problema específico (FIORENTINI et. al., 2018).

As entrevistas com os alunos, embora deem indicações sutis da existência de dificuldades cognitivas, precisam ser complementadas por estudos mais amplos que indiquem a extensão dessas dificuldades na população em questão.

Portanto, o Grupo de Diagnóstico e Remédios planejou desenvolver um documento de teste que consistisse em perguntas de múltipla escolha, cujo desenho se baseasse em suspeitas de dificuldades conceituais com as perguntas formuladas a induzir erros conceituais (NACARATO, et. al., 2004)

Eles estavam cientes de que os erros encontrados podem vir de várias fontes, incluindo deficiências sensoriais, mentais, emocionais, motivacionais, culturais, sociais, de leitura ou de instrução.

Eles também estavam cientes das dificuldades conhecidas no nível escolar que ainda precisam ser diagnosticadas e ressarcidas adequadamente, conforme relatado pelo órgão de governança da educação no Estado da Califórnia e o relatório do Universidade da Califórnia.

Foi realizada uma investigação preliminar de diagnóstico matemático a 350 alunos do 5º ao 9º ano em agosto de 1982, usando perguntas que exigiam uma resposta por escrito, projetadas para provocar possíveis mal-entendidos e erros (FIORENTINI et. al., 2018).

O primeiro teste diagnóstico de múltipla escolha foi então projetado usando evidências da investigação preliminar para construir problemas que podem levar a erros observados. Esse Teste de Diagnóstico em Matemática foi implementado para os alunos do 5º ao 9º ano em 1983. Foi altamente bem-sucedido em discriminar estudantes de diferentes capacidades e desde então foi parcialmente modificado para um teste em julho de 984, substituindo ou modificando aquelas questões que eram discriminadoras menos bem-sucedidas (NACARATO, et. al., 2004).

2.3 ESCOLA PÚBLICA X ESCOLA PRIVADA

A escola é um espaço educativo, portanto seu trabalho tem que ser pensado erealizado de forma planejada. O projeto pedagógico é o instrumento que possibilita essa prática, na medida em que apresenta novos caminhos para as mais diversas situações que precisam ser resolvidas. Para Freire (2003) pensar sobre o planejamento educacional exige que partamos de uma concepção ampla de educação e que tenhamos como eixo os desafios da realidade e o comprometimento com a circunstância.

Freire (2003) ao pensar o planejamento educacional exige que partamos de uma concepção ampla deeducação, ou seja, que este planejamento esteja não só direcionado ao currículo escolar, mas também contextualizado com a realidade social em que o aluno e a escola estão inseridos.

Na escola pública esse planejamento é pensado, não pensando na realidade do aluno, mas na realidade da educação que se quer atingir. Já na escola privada, a concisão do aluno é fundamental nesta condicionalidade do planejamento; a condição do aluno é condição sine qua non para tal intento.

Em um trabalho substancial Maria et. al., (2009) faz um estudo comparativo do estilo de vida de adolescentes da cidade de Florianópolis, tanto da escola pública como da escola privada e chega à concussão que as diferenças são muito grandes, conforme Tabela 1:

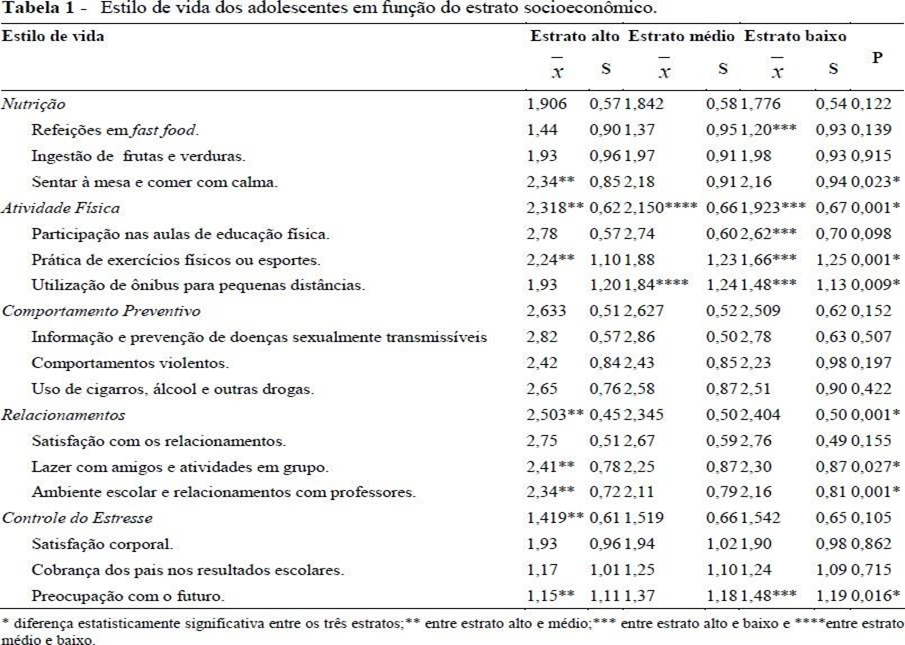
Fonte: Maria et. al. (2009, p.; 3)

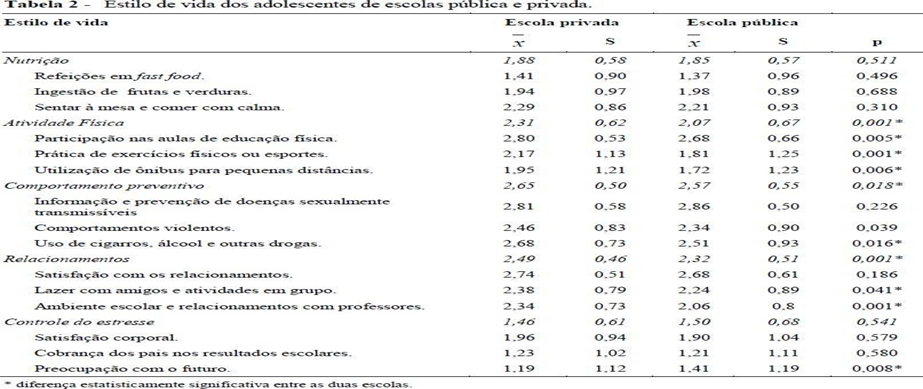
Fonte: Maria et. al. (2009, p; 4).

Ao analisar a tabela fica claro uma diferença significativa entre o extrato mais alto para o extrato médio e desse par o extrato baixo; mas a diferença do extrato alto para o extrato baixo é abissal, nas variáveis estudadas de nutrição, atividade física, comportamento preventivo, relacionamentos e controle do estresse. Logo após Maria et. al. (2009) apresenta mais duas tabelassem que compara Estilo de vida dos adolescentes de escolas pública e privada (Tabela 2) e Estilo de vidas dos adolescentes dos sexos masculino e feminino (Tabela 03) e nessas duas tabelas percebe-se claramente as diferenças entre os três extratos (alto, médio e baixo) o que caracteriza uma diferença entre alunos de escolas públicas e escolas particulares por seus extratos sociais.

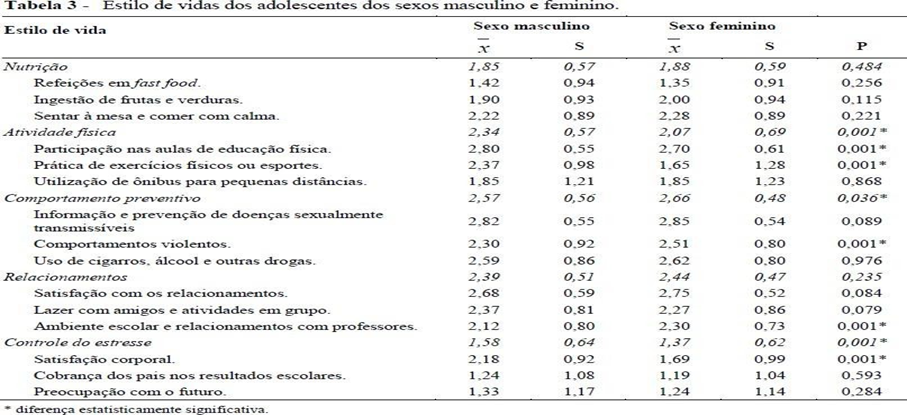
Fonte : Maria et al (2009. P.4)

Maria et. al. (2009) discute os resultados de suas descobertas, apontado que no caso do sexo, a proporção é quase igual e bem equilibrada dentro da amostra. Assim os resultados encontrados por Maria et. al. (2009) são muito parecidos com um estudo correlato de Perfeito et. al. (2008), que foi realizado nas mesmas organizaçõesescolares. No Estudo de Perfeito et. al. (2008) os alunos da escolas privadas representavam 61,30%, enquanto os da escola pública representavam 48,70% da amostra.

Desses alunos da escola privada no estudo de Perfeito et. al. (2008), 59,00% era do sexo masculino e 41,00% do sexo feminino. Já na escola pública, 52,00% eram do sexo feminino e, 48,00% do sexo masculino. Os estudos de Maria et. al. (2009) se encontram com o de Perfeito et. al. (2008) na questão do extrato social. Os alunos, deambos os estudos que estão na escola privada tendem a pertencer ao extrato social mais alto; já os da escola pública tendem a pertencer ao extrato social mais baixo; enquanto os do extrato social médio pertencem aos dois seguimentos: público e privado.

Já nas outras variáveis é nítida a diferença entre os estratos. Esse tipo de estudo deveria servir de embasamento para a formulação do planejamento educacional. Mas tanto Perfeito et. al. (2008) como Maria et. al. (2000 dizem que na escola pública não se usa nenhum tipo de estudo par formalizar o planejamento; na escola privada isso é olhado com mais cuidado).

O planejamento educacional tem um sentido mais amplo no campo da Gestão, pois este envolve as políticas educacionais em um nível macro, num contexto nacional, estadual e municipal. Está direcionado não apenas ao campo específico da Gestão Escolar, pois abrange todo o processo de fixação e implementação dos objetivos, além da política do planejamento e do campo administrativo da gestão. Teoricamente isso serve de base tanto na escola pública como na privada. Mas na realidade o que acontece é outra coisa

Em um estudo substancial sobre as diferenças entre a escola pública e a privada Souza (2011) fez descobertas muito interessantes sobre o que a escola representa para os alunos do Ensino Fundamental II. Souza (2011) pergunto: podem falar a respeito dessa aventura na escola: como foi? Quais os fatos mais marcantes? O que sobrou dela? Suas principais descobertas foram:

Tanto na escola pública como na privada os alunos encontram um mundo diferente de sua realidade; tudo é controlado. A escola parece uma prisão; com vigias nos portões; não é permitido a entrada de qualquer pessoa. E tudo isso parece muito estranho, por que há um corte na realidade externa. Só que na escola privada os pais de aluno são uma constante na escola; o mesmo não acontece na escola pública quando os pais, por várias razões. Não estão presentes constantemente na escola. Mas em ambas as escolas (pública e privada) os alunos se separam da vida, sendo obrigado a esquecerem do seu cotidiano, para vivem um novo cotidiano. São obrigadas a usarem uniforme, são controlados em seus horários, etc. Na escola pública o acesso à tecnologia é coletivo; na privada geralmente é individual.

Na maior parte dos casos, a escola pública leva em consideração as diferenças que existem entre os alunos: diferenças nas condições materiais de vida, diferenças nas experiências adquiridas fora da escola, diferenças de atitudes dos pais em relação à escola , etc. Na escola particular, essas diferenças são menos evidentes. O que acontece então? Tratar de forma igual àqueles que são desiguais “significa não apenas manter a desigualdade, mas até aumentá-la”: o que têm mais recursos avança mais, progridem mais, são selecionados para chegar à universidade, e a desigualdade aumenta ainda mais. Além dos conhecimentos das matérias escolares, a criança aprende valores e normas comportamentais, principalmente por meio das atitudes que é obrigada assumir na escola.

Assim, não apenas direcionado ás diretrizes do planejamento restrito a escola, o Planejamento Educacional envolve um processo de condução política, compreendendo as diversas instâncias dos Conselhos Educacionais e a questão social; de condução técnica, observando a implementação dos objetivos e os termos burocráticos que envolvem a gestão, condução administrativa que resulta no campo da própria administração desses eixos escolares.

Compreender a realidade da gestão escolar democrática nos dias atuais exige capacidade de pensamento relacional simultâneo, pois a realidade é pluridimensional, complexa e mutável. As instituições, como a realidade em que estão inseridas, se caracterizam ora por movimentos rápidos e lentos, ora de intensidade maior e por outras menores.

Essa duplicidade simultânea de movimentos se constrói, pelo menos em parte, pelo discurso institucional. Muitas vezes, o discurso aponta numa direção, mas as práticas concretas da instituição sinalizam outra. O discurso é avançado, a prática, conservadora e até reacionária. Nesse sentido, sabemos que a escola é um espaço público no qual convivem os mais diversos interesses.

Ela é também um espaço de conflitos. Essa pluralidade de perfil deve se constituir num rico debate interno, fundamentado na reflexão coletiva, na construção de consensos, com sentido explícito e um compromisso definido coletivamente e democraticamente. Logo entendemos que, gestão implica participação e participaçãoimplica a marca politica na escola. Contudo, participação é processo e não ação pontual, que necessita de uma compreensão dos fatores que constituem a realidade sócio histórica, politica e cultural, pois a realidade é complexa, muitas vezes, é diversa e até contraditória com o movimento aparente.

Mas a participação da comunidade na gestão da escola pública encontra um sem-número de obstáculos para concretizar-se, razão pela qual um dos requisitos básicos e preliminares para aquele que se disponha a promovê-la é estar convencido da relevância e da necessidade dessa participação, de modo a não desistir diante das primeiras dificuldades” (PARO, 2006, p. 16).

Sabemos que a gestão de pessoas, processos e estruturas é uma prática complexa e exige planejamento. Do contrario, a ação do gestor pode ter uma intencionalidade e direção coerentes com o projeto institucional e ainda assim pode ser compreendida pelo grupo de forma antagônica e ate contraditória a intenção do gestor, o que dificulta sobremaneira sua ação, ele fica sem saber de fato se o grupo acredita ou compreende aquilo que está sendo proposto ou aceita para não perder o emprego.

A gestão democrática na escola e nos sistemas de ensino torna-se um processo de construção da cidadania emancipada. Para tanto, e segundo Araújo (2010), são quatro (4) os elementos indispensáveis a uma gestão democrática: participação, pluralismo, autonomia e transparência.

A pratica da participação democrática dá a comunidade escolar um sentimento de cidadania que alimenta um desejo continuo da própria participação, gerando desta forma um comprometimento social. A gestão democrática necessita da participação direta nas tomadas de decisão. Segundo Paro (2006, p. 16):

A esse respeito, quando uso esse termo, estou preocupado, no limite, com aparticipação nas decisões. Isto não elimina, obviamente, a participação na execução; mas também não a tem como fim e sim como meio, quando necessário, para a participação propriamente dita, que é a partilha do poder, a participação na tomada de decisões.

A gestão democrática de uma escola vai muito além da eleição de seus diretores, da cultura escolar e da sala de aula. Implica atenção especial ás tendências do mundo atual, conscientizadas pelas pessoas que, além da velocidade, captam o sentido e a direção do movimento.

Como há múltiplos olhares e compreensões sobre fatos e propostas, quando a instituição tem uma equipe diretiva ou um colegiado, têm maiores possibilidades de discernir o movimento real da instituição e ações necessárias para produzirem as mudanças desejadas. É necessário na gestão democrática o agir de um corpo só e não como cabeças individuais.

Neste sentido se afirma o Projeto Político Pedagógico (PPP). A indagação inicial quando se busca firmar um conceito é: o que é projeto político-pedagógico. Na concepção etimológica do termo, a palavra projeto se origina do latim projectu, que tem o significado de lançar para diante, ou seja, tem o significado de prever o futuro, de criar os caminhos em busca de um objetivo. No sentido da escola a adoção de um projeto significa a busca para da realização de algo, ou seja, lança-se algo para que se caminhe adiante, com base especificamente na estrutura existente, buscando o possível. É visão de futuro que se quer alcançar diferente do que teve no passado e do que se tem no presente, como informa Gadotti (1996).

Todo projeto trabalha com a ruptura com o passado e o presente e se vale de esperanças de melhoria no futuro próximo. Assim quando se projeta algo significa a quebra do status quo para uma situação de risco em busca da ruptura de uma situação confortável com a finalidade de se adquirir uma nova estabilidade em função de que, do que se imagina seja melhor do que o que se tem.

Neste aspecto, o projeto político-pedagógico ultrapassa a simples existência de planos ensino e de atividades diversas. O projeto não pode ser encarado apenas como um documento em papel que vai ser guardado para serem apresentado às entidades de governança educacional como instrumento burocrático que cumpre apenas o que determina a legislação. Ele deve ser construído em uma ação coletiva e participativa de todos os segmentos da comunidade escolar.

Para Gadotti (1996), o PPP é o estabelecimento de um caminho, a necessária busca por uma direção. É uma ação coletiva e participativa intencional, que estabelece um compromisso formal da coletividade educacional com a escola que se quer construir. Por essa razão explícita, segunda a autora supracitada, o projeto pedagógico de uma escola funciona também como um firmamento de compromisso sociopolítico de toda a comunidade escolar de forma evidente, já que nele deve constar o tipo de sociedade que se quer atingir. E por que a denominação de projeto político. Político por que deve assumir o necessário comprometimento com a formação cidadã e como um modelo de sociedade. Para Saviani (1983, p. 93) “A grandeza política que deve estar contida no PPP acontece exatamente quando esse comprometimento de formação cidadã está no contexto pedagógico da escola”. Na dimensão pedagógica se localiza a verdadeira intenção da escola, que deve ter o vetor da formação cidadã do sujeito participativo responsável, compromissado, crítico e criativo. No sentido pedagógico, o PPP ganha à dimensão escolar quando define as ações educativas que devem ser implementada com o objetivo de se cumprir os propósitos e sua intenção de educar. Para Marques (2003), o PPP tem absolutamente indissociável, ou seja, no âmbito da escola não existe somente o projeto político e muito menos o projeto pedagógico de forma isolada. Assim é que o PPP é um processo intenso e dinâmico de espaço reflexivo que envolve uma discussão ampla dos problemas da escola, na busca de alternativas de solução compatíveis com a realidade da escola, entre sua intenção objetiva e subjetiva constitutiva de forma normativa. Para a autora, o PPP é o documento normativo que define a intencionalidade da escola no processo de educar e na sua visão de sociedade.

Para Betini (2005), a elaboração e aplicação do PPP evidencia a convivência democrática que cria os mecanismo de participação, visando uma ação coletiva de todos os componentes da comunidade escolar o que certamente acarreta a prática dacidadania, ou seja, é a perfeita interação entre a dimensão política e a dimensão pedagógica do espaço educativo na escola.

Já para Fonseca (2003) o projeto político-pedagógico, ao se efetivar no espaço escolar proporciona decisões democráticas e participativas, buscando instaurar uma forma de organização do trabalho escolar que evite situações conflituosas e casos elas existam que sejam amplamente discutidas e superadas, já que no espaço escolar democrático não existe condicionantes competitivas, corporativas e autoritárias, ou seja, o PPP, quebra a rotina da gestão autocrática, racionaliza a gestão administrativada escola eliminando a burocracia excessiva, o que certamente rompe com as relações impessoais e frias e, também acaba por os poderes de decisão centralizados. Desse modo, como informam Longhi e Bento (2006), o projeto político-pedagógico tem uma ligação intensa e dinâmica com a organização do trabalho escolar no âmbito pedagógico em dois (2) aspectos: o primeiro na organização do espaço escolar em toda a sua dimensão; e, em segundo lugar na organização da sala de aula.

Estes dois (2) aspectos do PPP, segundo os autores em voga, inclui a necessária interação com o contexto social que envolve a comunidade escolar como um todo e sua visão total de sociedade. Nesta interim, os referidos autores inferem que o PPP tem por objetivo central estabelecer o necessário procedimento de organização do trabalho pedagógico da escola como um todo.

A construção do projeto político-pedagógico não pode nem ser pensada sem que a escola goze de autonomia, de que a escola possa estabelecer seus próprios caminhos, de criar sua própria identidade. Ou seja, alguns pressupostos são básicos para a construção do PPP na escola. O primeiro é sem duvida autonomia, a liberdade de escolha e de possuir a sua própria visão de sociedade. Sem isso, não há PPP. O segundo é sem dúvida a identidade, ou seja, a escola tem que ter sua própria identidade e não se cópia de modelos estabelecidos. Suas caracterização própria é fundamental. O terceiro ponto necessário para a construção do PPP é sem dúvida originalidade, ou seja, o PPP tem que ser único, individual, com características próprias, considerando apenas aquilo que sua comunidade pensa (BAFFI, 2002).

Para Neto e Almeida (2000), o PPP tem a finalidade de buscar uma nova organização do espaço escolar e se torna um grande desafio para a comunidade escolar como um todo. Mas como enfrentar esse desafio? Em primeiro lugar se faz necessário que se tenha disposição para enfrentar o desafio. E ele começa com a busca do necessário aporte teórico que vai embasar a construção do PPP. Mas neste momento surge um indagação – qual seja? Se a construção do PPP pressupõe identidade e originalidade, como buscar o aporte teórico e metodológico em outras experiências? A resposta é simples: não se precisa abandonar a caracterização própria para se buscar o necessário aporte teórico que vai fundamentar o PPP.

Este aporte deve estar embasado em experiências acadêmicas e científicas de profundeza teórica no sentido de estabelecer os alicerces como base em uma teoria pedagógica crítica viável, que tenha ligação com a identidade e a originalidade da escola comprometida com uma visão moderna de educação, de democracia e de participação social na resolução de problemas de educação.

Mas esse aporte teórico terá que servir apenas de embasamento, já que a o PPP terá que ser originário do espaço do que Freitas (1991, p. 23) denomina de “chão da escola”, com a participação de todo o aparato comunitário que envolve a escola, dentre eles, professores e técnicos e sua representação – Congregação de Professores e Técnicos. Estudantes – Grêmio Estudantil, Funcionário, Pais e Comunidade em geral – Associação de Pais, Mestres e Comunitários. E, Gestão escolar com base em modelos de pesquisa. Para Gandin (s/d), esse procedimento inicial tem o significado de que a escola quer imprimir mudanças significativas em seu espaço escolar, concebendo um instrumento balizador de sua ação política e pedagógica e da sua organização escolar como um todo, criando o seu próprio modelo e não seguindo os ditames, seja do Ministério da Educação e/ou das Secretarias de Educação Estadual ou Municipal, já que não é papel destas instituições definir que modelo de escolar cada comunidade deve possuir. O mesmo autor infere:

O PPP está alinhado com produção PPP de uma qualidade que é, ao mesmotempo, política e técnica. Neste processo, é preciso não descuidar nem da elaboração de uma clara visão de mundo e nem da construção do conhecimento, tarefa precípua da escola; ambos devem estar relacionados intimamente.

Assim, para que se produza um documento ilustrativo da ação política e pedagógica que a escola vai proceder a partir do PPP a participação é estritamente imprescindível. E de toda a comunidade escolar. Cabe a gestão de a escola motivá- los e incentivá-los a participarem de forma efetiva da construção do PPP. Percebe- seque todos os autores citados chegam à mesma conclusão, o projeto político- pedagógica é um construção coletiva e participativa e não pode funcionar como um instrumento normativo burocrático apenas, mas sim funcionar como um propulsor da ação política e pedagógica da escola a partir de então.

Para se construir um PPP em uma escola se faz necessário que alguns princípios sejam abordados e considerados. O primeiro destes princípios faz referência a um princípio constitucional: o princípio da igualdade. Então durante a construção da PPP, o igualitarismo deve ser a base basilar como uma ideologia que, entre os valores que compõe a fórmula da legitimidade que atribui à igualdade, tomada em um ou outro de seus sentidos, Lugar de preponderância, assumindo que a igualdade é um conceito que tende a afirmar condições de uma tendência de longa duração que lhe aventura a qualificar de providencial, mas que não se efetiva na sociedades industriais (COMPARATO, 1998).

Assim a igualdade deve esta interligada com as condições de acesso e permanência na escola. Saviani (1983, p 63) infere que, a desigualdade está perfeitamente estabelecida quando se chega à escola, mas que no final a desigualdade inicial tem que se transformar em igualdade. O autor destaca:

Na realidade o processo educacional só ode se visto de forma conjunta buscando identificar a necessária distinção entre democracia no momento deentrada e no momento de partida, ou seja, considerando a desigualdade da entrada e a igualdade da saída.

Para Comparato (1998) a condição jurídica das pessoas iguala-se com a extinção do modo de produção feudal, ou seja, teoricamente, os ordenamentos jurídicos incorporam o princípio da igualdade, tão defendido na Revolução Francesa e na Declaração de Direitos Humanos no século XIII da própria Inglaterra, ou seja, os indivíduos são reconhecidos como igualmente aptos a fazer contrato, a comprar, a vender, a casar-se. Vem em seguida, ou juntamente, um processo de igualização dos direitos políticos. Em terceiro lugar, como nas sociedades capitalistas tornam- se mais produtivas e mais ricas, as disparidades extremas entre abundância e a penúria veem- se gradualmente suprimidas – ou melhor, são percebidas, pela maioria dos excluídoscomo algo que deve ser suprimido.

A esse quadro bastante otimista informado por Comparato (1998), pode-se acrescentar um último traço. As desigualdades de acesso aos bens públicos, como aeducação, por exemplo, que seriam também progressivamente diminuídos, a ponto de, em última instância, todos os membros da sociedade contemporânea poderem aspirar ao gozo de um mesmo tesouro cultural. Assim, os ordenamentos jurídicos, inclusive o do Brasil, incorporam o princípio da igualdade afirmam que as oportunidades devem ser iguais, ou seja, não deve se restringir apenas ao aumento da oferta para o atendimento da demanda, mas que a qualidade do atendimento seja a mesma. Não pode haver diferenciação entre escolas.

O segundo princípio é o princípio da qualidade, que não pode de forma alguma se constituir em privilégios de alguns. O desafio do sistema de ensino e notadamente da escola na construção de seus PPP é de reservar a necessária qualidade para todos.

Para Gadotti (1996), a qualidade que a escola pública deve buscar como objetivo central de sua ação pedagógica está centrada em duas (2) dimensões inseparáveis: a formal ou técnica e a política. A primeira é a atividade da escola propriamente dita, ou seja, são as metodologias e os instrumentos utilizados no dia a dia do trabalho escolar; a segunda (política) está centrada na questão da participaçãoou como informa Demo (1994, p. 14): “a competência humana do ser humano e buscarde sua própria história, deve está em perfeita harmonia com as finalidades históricas da sociedade”.

Assim, a qualidade do ensino está voltada ao desafio de fazer a história e o fazer da história tem que possuir identidade própria. Assim a qualidade formal está atrelada a qualidade política. A qualidade da escola precisa ser medida e essa medição está diretamente ligada aos seus índices de reprovação e evasão. Quanto menor forem eles, mas qualidade se terá no processo educativo como um todo. Assim, não basta garantir o acesso, é preciso que os resultados do processo ensino e aprendizagem sejam satisfatórios. O terceiro princípio é o da gestão democrática queestá garantida na Constituição Federal de 1988 e na Lei de Diretrizes e Bases da Educação Nacional – Lei Nº 9.394/1996 que envolve as dimensões pedagógica, administrativa e financeira. Esse princípio rompe com os modelos autoritários da gestão na escola, onde o gestor é o senhor de todo o processo decisório na escola. Para Dalbério (2008) a gestão democrática exige que os problemas da escola seja encarados de forma coletiva. É um problema de todos e por ser de todos tem a responsabilidade sobre ele.

Para Paro (2006) a gestão democrática modifica e provoca um reflexão sobre o processo decisório da organização escolar, ou seja, os problemas e suas alternativas de solução devem ser socializados. Esta socialização implica em participação e esta em uma ação coletiva que provoca mudança nos modelos consagrados na história da educação no Brasil. Tenório e Rozenberg (1997, p. 5)inferem sobre a participação:

A participação integra o cotidiano de todos os indivíduos. Ao longo da vida e em diversas ocasiões somos levados, por desejo próprio ou não, a participar de grupos e atividades. O ato de participar, tomar parte, revela a necessidade que os indivíduos têm em se associar na busca de alcançar objetivos que lhes seriam de difícil consecução ou até mesmo inatingíveis caso fossem perseguidos individualmente, de maneira isolada.

Alarcão (2001) concorda com Tenório e Rozenberg (1997) afirmando que a efetivação da gestão democrática envolve a participação de toda a comunidade escolar de forma direta ou por intermédio de seus representantes legais institucionalizados o que leva a um verdadeiro envolvimento nas decisões/ações administrativo-pedagógicas. Marques (1990, p. 21) afirma isso de forma absolutamente clara e didática:

A participação de todos os elementos da comunidade escolar, por exemplo, promove a necessária transparência no processo decisório, o que acaba por transformar as decisões legítimas. Também promove o necessário controle de todas as ações e atividades e, sobretudo, estabelece a contribuição para que todas as questões que de outra forma não entrariam em cogitação.

Assim se evidencia que implantar a gestão democrática, embora seja uma imposição legal contida no ordenamento jurídico brasileiro é um processo desafiador já que muda a postura da comunidade escolar que tem que adquirir uma postura crítica e da própria gestão que tem que dividir o processo decisório. .O quarto princípio norteador da construção de um PPP na escola é o princípio da liberdade, também um princípio constitucional. A liberdade está atrelada em todos os sentidos a autonomia. Ambos os casos (autonomia e liberdade), são inerentes ao trabalho pedagógico em si. Autonomia pressupõe normas que deve ser seguidas pelos atores da comunidadeescolar. Para Rios (1982, p. 77), a liberdade “é uma experiência de educadores e constrói-se na vivência coletiva, interpessoal”. Já a autonomia pressupõe decisões própria, escolhas de caminhos em que a identidade deve se estabelecer.

O quinto princípio e a valorização do magistério e o padrão de formação do magistério esteve sempre atrelado ao projeto de desenvolvimento industrial imposto a sociedade brasileira, ou seja, formavam-se professores para proferir formação de mão de obra que atendessem as premissas do desenvolvimento industrial, o que começou a mudar com o avento da Lei nº 9.394/1996.

Na realidade os novos enfoques da formação de professores no Brasil foi estabelecido pela Lei nº 9.394/1996 que imprimiu uma mudança completa nestas padrões formacionais, passando fazer parte das agências institucionais – secretáriasde educação em nível estadual e municipal que precisaram estabelecer convênios com as universidades Freitas (2008, p. 33) diz com muita propriedade:

Várias circunstâncias são responsáveis por esta situação, entre elas estão os requerimentos que a formação social brasileira (e suas conexões internacionais) impõem à questão educacional, de forma muito evidente em todos o processo.

Até mesmos para o leigo, nos últimos anos, uma nova terminologia esteve presente nos jornais e na televisão, assinalando os rumos de uma nova ordem mundial. Competitividade internacional; desregulamentação; Estado mínimo, informática, desemprego, redução do déficit público, recessão, etc., são exemplos.

O velho padrão de exploração da classe trabalhadora (que influenciou as mudanças educacionais dos anos 1970) encontra dificuldades para continuar gerando riqueza. Nos anos 1970, o padrão de exploração implicava ampla fragmentação das tarefas de produção, acompanhadas por rotatividade, de forma a baixar seus salários.Nesse processo a formação do trabalhador era bastante limitada e rapidamente conduzida no posto de trabalho, por observação direta ou por cursinhos rápidos no interior da fábrica. O que importava era o domínio de um conjunto limitado de tarefas realizadas dentro de certo ritmo.

O nível educacional da força de trabalho é, nesta perspectiva, apenas um elemento complementar e a pouca qualidade da escola não incomoda. Carvalho (2008, p. 56) complementa a análise sobre a década posterior (1980), inferido conclusões de suma importância:

A partir de meados da década de 1980, o Brasil sofreu influência de um movimento internacional, que procura redefinir as bases deste processo de exploração da classe trabalhadora a partir da introdução de novas tecnologiase de novas formas de organização do processo de trabalho. Este processo foi acompanhado por uma nova divisão de mercados que criou conglomerados regionais, sob a liderança de alguns países emergentes (por exemplo, Japão e Alemanha), onde a competitividade internacional definiu posições dos países membros. Entre outros fatores, fez parte do aumento desta competitividade à introdução e novas formas de organização do trabalho (por exemplo, tecnologia de grupo, células de produção, qualidade total) baseadas em novas tecnologias (em especial a microeletrônica). ,

Nestas novas formas, apontadas por Carvalho (2008), de organização da produção, o capital fixo (complexificou-se o velho padrão de exploração é superado1 e novas exigências são feitas para a organização do Estado, para o trabalhador, para a escola2. Maior capacidade de integração trabalho em equipe, mais democracia na condução do trabalho, caracterizada pelo maior envolvimento do trabalhador em certas decisões, maior capacidade de abstração, mais leitura, mais

matemática – entre outras – são requeridas. No entanto, as habilidades não podem ser rapidamenteimprovisadas na contratação do trabalhador. São habilidades típicas de serem desenvolvidas no aparato escolar – não no atual, mas em um reformulado. A qualidade da escola passa a interessar mais.

2.3.1 O Ensino da Matemática no Ensino Fundamental II

Como produto da reforma do ensino com o advento da Lei nº 9.394/1996 e da introdução dos Parâmetros Curriculares Nacionais de 1998 tanto no nível fundamentalcomo no nível médio, uma nova visão sobre o ensino da matemática foi criada no Brasil, ou seja, com a adoção de novas formas didáticas e de livros didáticos foi possível à concretização dos postulados de uma maneira diferente de conceber e trabalhar matemática em cada nesse nível (RODRIGO, et. al. 2013).

Tratando-se especificamente do ensino fundamental II, para se atingir os objetivos e com base no fato de que a proposta original seria necessariamente modificada na prática por diferentes circunstâncias, que precisariam ser reconhecidase documentadas (ERNEST, 2015).

Nesta perspectiva, as condições e regras que governavam a escola ficaram em segundo lugar. Embora o interesse tenha sido o tratamento dado pelos professores àmatemática nas salas de aula a partir do livro didático gratuito de matemática,

¹ No sentido hegeliano do termo, eliminar/conservar.

² Ver Paiva (2009). op. cit Freitas, L. C. Neotecnicismo e formação do educador, in Alves, N. Formação de professores: pesar e fazer. São Paulo: Cortez, 1992; Pinto, A. M. R. o mundo capitalista e as transformações do fordismo: a reabilitação da escola clássica na era das máquinas inteligentes. Tese de doutorado. PUC-SP, 1991.

Considerou-se necessário recuperar na análise não apenas aspectos de natureza didática, mas também outros com o professor, envolvido na definição da situação. A literatura atual sobre prática pedagógica em matemática relata várias pesquisa que tentam aproximar o desempenho do professor na sala de aula através do estudo de suas concepções ou crenças. Rodrigo et. al. (2013) apontam que as concepções de professores sobre educação matemática, sobre o valor do conteúdo e sobre os processos propostos pelo currículo os levam a interpretar, decidir e agir na prática, ouseja, selecionar livros didáticos, adotar estratégias de ensino, avaliar o processo de ensino-aprendizagem, entre outros (RODRIGO, et. al., 2013).

Por esse motivo, as influências que as concepções exercem sobre a As ações dos professores fizeram com que fossem considerados elementos chave para entender os processos de ensino-aprendizagem em matemática que eles dão na sala de aula. Assim, Ernest (2015) afirma que o ensino não terá sucesso a menos que os professores mudem de opinião sobre ensino e aprendizagem em matemática, e que essas mudanças andam de mãos dadas com um processo de reflexão sobre o processo de ensino em matemática.

Como se estar explicitamente localizado na escola, deve-se apontar duas restrições importantes que a distinguem do início de outros contextos designados como aprendizado natural (como família ou sociedade): uma restrição temporária: o aprendizado deve ser realizado em tempo determinado estabelecido pela instituição e aprovado legalmente; restrição epistemológica em que o conhecimento adquirido naaprendizagem escolar deve estar em conformidade com um conhecimento de referência: conhecimento matemático. Portanto, não se pode considerar que o processo de aprendizagem em matemática seja supostamente análogo ao que poderia ser realizado em outras áreas da Escola (campo da expressão oral ou escrita, expressão plástica, expressão musical, expressão geral), mas depende do conhecimento colocado em jogo (ERNEST, 2015).

A matemática é a essência de todos os fenômenos didáticos. Assim uma questão é fundamental para o ensino de matemática e, conseqüentemente, para o aprendizado de matemática dos alunos. De acordo com Brousseau (2018, p. 5): “Conhecer matemática” não é apenas conhecer definições e teoremas para reconhecer a oportunidade de usá-las e aplicá-las, é “lidar com problemas” que, em um sentido amplo, inclui encontrar boas perguntas e encontrar soluções.

Uma boa reprodução, pelo aluno, da atividade matemática exige que ele intervenha na referida atividade, o que significa que ele formula afirmações e prova proposições, que ele constrói modelos, linguagens, conceitos e teorias, que ele as testa e as troca. com os outros, reconhecer aqueles que são construídos de acordo com a cultura matemática e levar aqueles que são úteis para continuar sua atividade (ERNEST, 2015).

A grande maioria dos trabalhos de pesquisa realizados na área de Didática da Matemática lida com a aprendizagem matemática dos alunos, o que mostra sua enorme relevância para esse domínio do conhecimento científico. Os modelos teóricos que se apresenta não têm mais valor para nos servir como um conjunto de princípios que explicam o fenômeno da aprendizagem matemática, eles oferecem quadros de referência para interpretar os comportamentos dos alunos, bem como as intervenções e decisões do professor, permitindo-nos responder à questão: como ocorre a aprendizagem matemática? (BROUSSEAU, 2018).

Para facilitar o estudo de aspectos relacionados à aprendizagem do aluno, é estabelecida uma relação complementar entre a Didática da Matemática e o domínio da psicologia, uma vez que a abordagem psicológica é um instrumento indispensável para esclarecer o modelo do funcionamento cognitivo do sujeito em relação com conhecimento e, assim, questionar as tese empiristas que sustentam as práticas dos professores, correndo o risco de simplificar os modelos teóricos das várias concepções existentes sobre a aprendizagem matemática dos alunos. Assim duas concepções se destacam atualmente no Brasil no ensino da matemática? O empirismo e o construtivismo. A primeira concepção (empirismo) é baseada em uma concepção espontânea presente na maioria dos professores: o aluno aprende o que o professor explica na aula e não aprende nada com o que ele não explica Brousseau (2018).

É uma concepção que dificilmente se torna explícita, mas que é muito difundida entre os membros de toda a comunidade educacional no Brasil. Piaget (1973) chamou de empirista esse tipo de concepção baseada na concepção filosófica de mesmo nome que sustenta que a experiência é a única forma de conhecimento.

Sob esse conceito, o discurso do professor é registrado no aluno, que não é considerado capaz de criar conhecimento. Seu aprendizado é considerado como uma transferência dos conhecimentos fornecidos pelo professor, é limitado para receber bem o conteúdo (PIAGET, 1973).

Assim, o conhecimento matemático, enunciado e explicado pelo professor, é impresso de maneira direta e imediata no aluno e, se houver outra intervenção além da palavra do professor, os objetos matemáticos os verão ou tocarão. Como consequência. Neste modelo há um grande abuso de apresentações ostensivas no ensino. A ostensão é o procedimento privilegiado para a introdução precoce de noções matemáticas. Assim, por exemplo, no ensino fundamental II, o conteúdo deste nível de ensino é apresentado aos alunos de maneira ostensiva (BROUSSEAU, 2018).

No ideal empirista, professor e aluno não devem estar errados: o erro está relacionado ao fracasso, e impede de alcançar o sucesso em sua tarefa. Portanto, oserros podem criar maus hábitos nos alunos, eles podem substituir a resposta correta (PIAGET, 1973).

As causas do erro são geralmente declaradas pelos professores em termos delacunas, deficiências e noções parcialmente assimiladas. Portanto, o aluno deve ter poucas chances de encontrar o erro. “Você tenta criar uma espécie de barreira ao erro. Aceitar erros para canalizá-los e posteriormente evacuá-los colocaria profundamente em dúvida o sistema de ensino”. Nesta hipótese, o ensino ideal consistirá em um curso em que o professor não cometerá erros, seguido de perguntas ou tarefas em que o aluno tenha a oportunidade de responder corretamente, verificando se ele entendeu perfeitamente. No entanto, se aceitar que, para fazer matemática, o aluno deve resolver problemas, deve-se considerar normal conviver com a incerteza: confusão, dúvida, tentativa e erro estão no cerne da aprendizagem da matemática. Os alunos devem superar muitas dificuldades, mas acima de tudo, muitos erros (MARGOLINAS, 2013, p. 179); (BROUSSEAU, 2018).

Os professores precisam entendê-los como algo necessário, porque somente se os detectarem e tiverem consciência de sua origem, eles colocarão meios para superá-los. “Quem pratica ciência sabe bem que sua força não provém de infalibilidade intrínseca, mas contrária à sua capacidade incessante de autocorreção”.Essa forma de ensino é a mais usada no Brasil, apesar do que diz os PCNs (LEVY apud MARGOLINAS, 2013, p. 170)

Com relação ao construtivismo, se sabe que muito conhecimento pode ser transmitido de uma geração para outra sem muito esforço, com pouca consciência de sua aquisição, como se todas as pessoas estivessem impregnados deles, por simplesimitação, enquanto para outros se precisa de uma construção real e de uma intençãodeterminada de aprender (BROUSSEAU, 2018).

Considerar que o aprendizado de um determinado conhecimento supõe uma atividade própria do sujeito é aproximar-se da corrente construtivista. Em anos recentes, estar-se imersos no desenvolvimento e aplicação da teoria construtivista. Em todo o seu desenvolvimento, há uma idéia fundamental que o preside: aprender matemática significa construir matemática (MARGOLINAS, 2013, p. 179).

As hipóteses fundamentais nas quais essa teoria se baseia, extraídas da psicologia genética e da psicologia social, podem ser resumidas da seguinte forma: 1ª Hipótese: A aprendizagem é baseada na ação. Ideia fundamental no trabalho de Piaget (1973): “É a partir da ação que o pensamento procede em seu mecanismo essencial, constituído pelo sistema de operações lógicas e matemáticas” (PIAGET, 1977, p. 26).

Assim o termo ação é frequentemente usado nos domínios pedagógicos edidáticos, atribuindo-lhe o significado de realizar manipulações em certos materiais. No entanto, o termo ação em matemática vai mais longe, trata-se de antecipar ações concretas, ou seja, sobre a construção de uma solução que possa dispensar mesmo do manuseio de objetos reais, seja porque os objetos não estão disponíveis ou porque eles são muito numerosos e seriam muito caros de manusear (BROUSSEAU, 2018).

As ações às quais está se referindo nesta primeira hipótese, embora possam ter sua origem em manipulações reais anteriores, que poderiam evocar mental ou atéverbalmente o sujeito, nem sempre precisam ser identificadas com manipulações eficazes. Em qualquer caso, a solução matemática (a ação matemática) se opõe à solução prática (a ação na coisa real): a ação nos objetos reais frequentemente leva à realização de uma verificação, enquanto a ação matemática, mesmo que não seja usa um procedimento especializado, está situado no nível de uma antecipação BROUSSEAU, 2018).

No ensino fundamental II, necessariamente, os alunos participarão da construção do conhecimento matemático por meio de ações concretas e eficazes em objetos reais e testarão a validade ou invalidez de seus procedimentos de manipulação desses objetos (BROUSSEAU, 2018).

Essas ações ajudarão o aluno a apropriar-se dos problemas, a entender a natureza das perguntas, a configurar uma reapresentação da situação proposta.

Também será nesse nível que eles começarão a antecipar resultados matemáticos relacionados a situações ausentes ou mesmo não realizados (simplesmente evocadas), mas sobre as quais eles têm certas informações. Eles descobrirão que o conhecimento matemático os isentará de realizar ações concretas em objetos reais (PIAGET, 1973)

Margolinas (2013) assegura que uma das funções da matemática é permitir a antecipação dos resultados de uma ação. O termo antecipação tem um duplo significado: previsão e garantia de validade dessa previsão. Basta revisar a atividade para verificar se o conhecimento matemático nos dá a capacidade de construir uma solução de tipo intelectual que exclua ações efetivas sobre objetos.

O fato de a ação ser entendida no sentido de uma verdadeira antecipação não significa que a manipulação seja excluída no inventário, muito pelo contrário. Eles permitem que os alunos desde o início apropriem-se do problema, entendam a natureza da questão, facilitem a construção de representações que, posteriormente, em situações análogas, possam ser formuladas ou evocadas mentalmente e permitirão realizar ações no sentido matemático do termo: construção de diagramas, cálculos, etc.

Além disso, a manipulação é um meio pelo qual os alunos nesse nível podem validar suas soluções, confirmar suas antecipações sobre um determinado problema, verificar a relevância de uma resposta; embora com o tempo, em cursos superiores, seu conhecimento matemático o facilite a obter verificações que não exigirão que sejam eficazes em objetos reais (MARGOLINAS, 2013, p. 179). (BROUSSEAU, 2018).

2ª Hipótese: A aquisição, organização e integração do conhecimento do aluno passa por estados transitórios de equilíbrio e desequilíbrio, no decurso dos quais o conhecimento anterior é questionado. Se esse desequilíbrio for superado, isso implica uma reorganização do conhecimento. O novo conhecimento está sendo integrado ao conhecimento anterior, apoiado nos processos de assimilação e acomodação (BROUSSEAU, 2018).

Trata-se de aplicar o modelo facilitado pela teoria do equilíbrio de Piaget (1973). No curso da ação em um determinado meio, as contradições aparecem no sujeito como produto dos desequilíbrios e devem modificar suas representações, produzindo o que Piaget (1973) chamou de acomodação, que basicamente envolve uma modificação no assunto causada pelo meio (perturbação). Reciprocamente, as transformações realizadas pelo sujeito para responder aos distúrbios modificam sua organização do ambiente, produzindo um processo de assimilação. O jogo da dupla acomodação/assimilação está no centro dos mecanismos dos processos de equilíbrio. A aprendizagem, portanto, não se reduz à simples memorização, a uma justaposição de saber fazer ou a condicionamento, aprende-se raramente de uma só vez; Aprender envolve começar de novo, sentir falta de si mesmo, repetir, mas repetir a compreensão do que é feito e por que é feito (MARGOLINAS, 2013, p. 179); (BROUSSEAU, 2018).

. 3ª Hipótese conhecida contra conhecimentos prévios. É uma idéia fundamental da epistemologia de Bachelard sobre o conhecimento científico, adotada por Brousseau (2018) para explicar a formação de obstáculos na aprendizagem da matemática: “O uso e a destruição de conhecimentos anteriores fazem parte do ato de aprender” (BROUSSEAU, 2018, p. 120).

O aprendizado prévio dos alunos deve ser levado em consideração para a construção de novos conhecimentos, uma vez que este não é produzido do zero, suaelaboração está sujeita a adaptações, interrupções e reestruturações, às vezes radicais, de conhecimentos anteriores. Aprende-se com e também contra o que já se sabe. O novo conhecimento só pode ser obtido modificando os anteriores e não pela simples acumulação destes nos existentes. No ensino fundamental II, como os alunosestão bem próxios do fim de sua formação fundamental, elas já sao capazes de construir mais do que um domínio muito limitado de conhecimentos matemáticos. Dado que a noção de obstáculo é de extrema importância para o aprendizado de matemática (BROUSSEAU, 2018).

4ª Hipótese: Conflitos cognitivos entre membros do mesmo grupo social podem facilitar a aquisição de conhecimento. Ideia básica da psicologia social apoiada no trabalho de Vygotsky (1989), que considerou necessário levar em consideração o queum indivíduo pode fazer com a ajuda de outros, uma vez que a aprendizagem ocorre em um ambiente social em que as interações são abundantes, horizontal (criança- criança) e vertical (criança-adulto).

A eficácia dos conflitos sociocognitivos é justificada, segundo Blaye (2014), uma vez que: – Eles permitem ao aluno tomar conhecimento de outras respostas que não as suas, o que os obriga a descentralizar sua resposta inicial. – A necessidade derealizar regulamentos sociais. , para chegar a um consenso, implica que o aluno é mais cognitivamente ativo – A resposta diferente dos demais é portadora de informações e chama a atenção do sujeito para aspectos da tarefa que ele não havia

considerado. Assim, os conflitos sociocognitivos causam um duplo desequilíbrio: devido às diferentes respostas dos sujeitos; desequilíbrio interindividual, devido à consciência de diferentes respostas, o que convida o sujeito a duvidar de sua própria resposta (BLAYE, 2014).

2.3.2 Principais Ferramentas Digitais para o Ensino de Matemática

Pode haver uma tendência para ensinar matemática informando os alunos sobre as propriedades associadas, exigindo que aprendam as propriedades e, em seguida, concluam exercícios que mostram que aprenderam os fatos (MONTENEGRO, 2005).

Tal abordagem pode significar que poucas tentativas são feitas para encorajar os alunos a fazer conexões lógicas e explicar seu raciocínio. Embora seja importante que os alunos tenham um bom conhecimento de fatos matemáticos, se eles desejam desenvolver seu pensamento espacial e intuição, uma variedade de abordagens são benéficas. Por exemplo, alguns fatos podem ser introduzidos informalmente, outros desenvolvidos dedutivamente ou descobertos por meio de exploração. Para ensinar matemática de forma eficaz para alunos de qualquer idade ou habilidade, é importante garantir que os alunos entendam os conceitos que estão aprendendo e as etapas envolvidas em processos específicos, em vez de os alunos apenas aprenderem as regras (MONTENEGRO, 2005).

Abordagens de ensino mais eficazes incentivam os alunos a reconhecer as conexões entre diferentes formas de representar ideias matemáticas dentro das áreasda matemática. A evidência sugere que é provável que isso ajude os alunos a reter conhecimentos e habilidades e lhes permita abordar novos problemasmatemáticos com alguma confiança (CASTRO, 2010).

Ao planejar abordagens para o ensino e aprendizagem da matemática, é importante garantir que a oferta nos primeiros anos do fundamental incentive os alunos a desenvolver um entusiasmo pelo assunto, proporcionando oportunidades para investigar ideias espaciais e resolver problemas da vida real (MONTENEGRO, 2005).

Também é necessário garantir que haja uma boa compreensão dos conceitos básicos e da linguagem da matemática a fim de fornecer bases para trabalhos futuros e permitir que os alunos considerem problemas matemáticos e comuniquem ideias

Os alunos devem ser encorajados a usar descrições, demonstrações e justificativas, a fimde desenvolver as habilidades de raciocínio e a confiança necessárias para apoiar o desenvolvimento de uma habilidade de seguir e construir provas matemáticas (CASTRO, 2010).

Para muitos alunos, o ensino da matemática requer abordagens de ensino semelhantes às usadas nos anos anteriores. Uma abordagem formal e dedutiva ao aprendizado da matemática precisa ser tratada com muito cuidado para ser apropriada para todos os alunos (SANTOS, 2017).

Com alunos mais capacitados, é possível estimular uma maior compreensão da necessidade de definições e das leis da lógica dedutiva. Isso pode incluir noções do lugar dos axiomas, uma apreciação da importância da prova, a compreensão de algumas provas e a capacidade de construir as próprias provas simples. Para todos os alunos, deve haver ênfase na resolução de problemas envolvendo aplicações da vida real de habilidades matemáticas (MONTENEGRO, 2005).

A matemática no Currículo Nacional pode ser ensinada com pouco uso de recursos práticos, mas esta não é necessariamente a melhor maneira de fazê-lo. É útil considerar a matemática como um assunto prático e fornecer oportunidades para os alunos usarem uma variedade de recursos para explorar e investigar propriedadesde formas e fatos matemáticos (ALVARES, 2016).

Deve-se dar atenção especial às maneiras pelas quais os recursos de TIC, cada vez mais disponíveis nas escolas, podem ser usados para melhorar o ensino ea aprendizagem da matemática. O uso de matemática dinâmica permite que o professor ou alunos individuais gerem e manipulem problemas matemáticos rapidamente e explorem relações usando uma variedade de exemplos (SANTOS, 2017).

A Figura 1 envolve o uso de software de matemática dinâmica para explorar os vários “centros” de um triângulo. Embora o uso de tal software possa estimular o ensino da geometria, deve-se notar que nem sempre está claro quais interpretações os alunos fazem dos objetos geométricos encontrados dessa maneira. Há também a possibilidade de que a oportunidade proporcionada pelo software de testar uma miríade de diagramas através do uso da função ‘arrastar’, ou de confirmar conjecturas por meio de medições (que também se ajustam conforme a figura é arrastada), pode reduzir a necessidade percebida de prova dedutiva (CASTRO, 2010).

Figura 1 – Uso de software em matemática

Fonte: Castro (2010)

Outro software também pode ser inestimável. O logotipo pode ser usado para descrever viagens e investigar propriedades de formas (Figura 2). Os pacotes de desenho de gráfico são úteis para coordenar e geometria de transformação. Todos esses recursos podem ser usados individualmente pelos alunos ou para aulas com toda a classe usando um quadro branco interativo (CASTRO, 2010).

Figura 2 – Logotipo de software

Fonte: Castro (2010)

As diversas tecnologias de comunicação formam hoje um complexo ecossistema comunicativo. Isso estabelece os meios entre sujeitos, grupos e instituições. E a velocidade dessa comunicação dentro de um contexto social onde as relações estão virtualizadas causa medo e preocupação, principalmente na tecnologia como Inteligência Artificial, mas todas as inovações representam um novo e audacioso despertar para a humanidade e traz mudanças de conceitos e valores e quebra de paradigmas que norteiam o seguimento da sociedade (AYDIN, 2015).

O termo tecnologia educacional nos remete ao emprego de recursos tecnológicos como ferramentas para aprimorar o ensino e a aprendizagem promovendo mais desenvolvimento sócio educacional e melhor acesso a informação.O grande aparato que traz inúmeros benefícios sociais educacionais é o computador (TOLEDO, 2008).

Essa tecnologia representa na educação a criação de processos metodológicos, capacidades, competências e conhecimento que permite melhorar ascondições de vida nos seus diferentes aspectos sociais, econômicos, pessoais, etc. O avanço da tecnologia provoca um grande impacto na sociedade e resulta em inovações que proporcionam melhor nível de vida ao ser. A luta por uma prática pedagógica mais libertadora deve se estender as outras frentes da sociedade. Desta forma, o educador, “ao repensar a educação, está também repensando a sociedade. Não existe uma igualdade entre política e educação: existe uma identidade” (FREIRE, 1996, p. 67).

Assim as práticas educativas educação tecnológica deve ter como característica a interação entre todos os envolvidos no processo, mediados pelo conhecimento e isso se inicia pela aplicação de metodologias ativas. É esse o contexto que dimensiona e dá sentido e significado a prática dos professores seja em que nível de ensino ela ocorra, com o objetivo de construir o conhecimento geral e também de natureza institucional. O mundo de hoje está caracterizado como a sociedade da informação, o que significa uma maior intensidade da comunicação e um aumento noritmo das transformações, o que tem como consequência novas configurações no contexto social, cultural e político o que certamente envolve a atividade educativa quecomeça a se construir pela metodologia ativa no ensino de informática, ciências de comutação, análise de sistemas e outros cursos correlatos (BERBEL, 2011).

Desta forma, a educação tecnológica é um processo intenso de crescimento qualitativo de todos os envolvidos, inclusive e, principalmente do professor que se inicia com metodologias ativas que tem o objetivo de proporcionar o seu desenvolvimento técnico-profissional no contanto direto com o cotidiano escolar, cujafinalidade é apresentar uma instituição que ensine ao aluno que vê o professor, comouma referência, já que a educação acompanha o ser humano, durante toda a vida. Durkheim (2008, p. 41) assim define a educação:

A educação é a ação exercida, pelas gerações adultas, sobre as gerações que não se encontrem ainda preparadas para vida social; tem por objetivo suscitar e desenvolver, na criança, certo número de estados físicos, intelectuais e morais, reclamadas pela sociedade política, no seu conjunto, epelo meio especial a que a criança, particularmente se destina.

Da definição de Durkheim(2008) podem-se extrair duas (2) ideias importantes: a educação é ao mesmo tempo múltipla e una; e a educação consiste na socialização metódica das novas gerações. E o metodologias ativas é o momento inicial para que o futuro professor tenha contato com essas duas ideias que compõem o pensamento do autor supracitado. Qual o sentido do conhecimento de base disciplinar de base disciplinar numa que exige cada vez mais competências globais para a abordagem integrada dos problemas? Assim é necessário que um programa de pesquisa envolva o trabalho interdisciplinar com base em metodologias e técnicas e técnicas de integração contidas no currículo. As consequências de uma integração são amplamente positivas já que produz ao indivíduo a percepção de sua importância no contexto participando ativamente das atividades alcançando assim a finalidade precípua do programa. No momento onde se constrói um consenso em torno da necessidade de transformar práticas, em favor de um trabalho mais dinâmico e mais ágil, mais eficiente e focada em resultados, ganha nova importância a questão do currículo da transdisciplinaridade e educação tecnológica para a criação de um ótimo clima organizacional. O impacto disso é significativo (CARVALHO, 2008).

A travessia das práticas convencionais para um modelo radicalmente novo custa tempo e esforço, mas precisa ser feita. As técnicas de pesquisa que abordam a estratégia metodológica para enfrentar as mudanças vêm crescendo nos últimos anos, mas os aspectos humanos não têm sido suficientemente valorizados (MALHEIROS, 2004).

Na medida em que se alteram as condições sociais, econômicas e políticas, também vão se modificando as maneiras de análise de concepção dos modelos de pesquisa e sua ação, fora as formas clássicas de se organizar, em função de fatores específicos e um tanto rígidos como especialização do trabalho já que outras concepções foram surgindo nas últimas décadas (CARVALHO, 2008).

Essas novas ideias de analisar e projetar a pesquisa tem girado em torno de temas às vezes ambíguos e fluidos, como a multidisciplinaridade, mas por isso mesmo, capaz de retratar, mas fielmente a verdadeira natureza ou necessidade da modernidade (MALHEIROS, 2004).

Para se ter uma ideia aproximada da problemática que envolve a questão do currículo da transdisciplinaridade e educação tecnológica na atualidade, longe se vai à expectativa de buscar essa compreensão apenas nos estreitos limites da própria pesquisa em si (AZEVEDO, 2011).

Há que se delinear essa compreensão a partir de variáveis especiais que remeteram para a configuração da complexidade da situação que hoje é vivenciada. E mais: se, por outro lado, está à sociedade da informação e os seus novos enfoques pessoais e organizacionais mais outro lado estão às características históricas da sociedade brasileira impregnadas no tecido das estruturas organizacionais arcaicas. Assim, as minhas experiências na disciplina currículo da transdisciplinaridade e educação tecnológica valeu pelo momento histórico que envolveu o contexto do trabalho e da pesquisa, buscando apresentar algo que se traduzisse na evolução dosprocedimentos de pesquisa no contexto atual por meio de sua própria história (BAKI, 2018).

A assimilação das teorias compreendidas requer mais e mais ser complementadas, pela aplicação dessas teorias aos processos históricos subjacentesà realidade na qual vive e sobre o qual possivelmente terá de atuar (BAROODY, 2013).

As salas de aula como experiência docente permitem adquirir a informação, osmétodos e as técnicas científicos e pedagógicos de base, bem como a formação pessoal e social adequadas ao exercício da função, numa perspectiva de educaçã permanente que permitiu a reconversão e mobilidade para os diferentes níveis de ensino em que se atua, nomeadamente o necessário complemento de formação profissional (BAKI, 2018)..

Estas experiências permitem uma preparação científico-pedagógica quer no da articulação teórico-prática quer em práticas metodológicas afins das que o educador e o professor vierem a utilizar no seu cotidiano. Ao se utilizar certos elementos da racionalidade do modelo de escola que se tem, pode-se apontar para o fato de não superação absoluta do modelo referido. Infere-se que tal modelo é retomado em determinados momentos históricos. Avança em relação a ele na medida em que apresenta os elementos de um modelo de sistema social em função de uma abordagem pré-sistêmica (BAROODY, 2013).

O enfoque dado na produção do conhecimento se fez numa referência teórica bastante presente. No entanto, há indícios de um enfoque inovador, principalmente devido às várias referências da área de estudos sociais, buscando a discussão de temas importantes no contexto (PAIS, 2018).

Outro enfoque é do da aproximação com os problemas da vida de cada aluno, uma vez que os livros introduzem o elemento “comportamento” na discussão, apesar de não aprofundar sua análise.

A abordagem construída permite (re)conhecer as influências das teorias, assim como suas extensões e permanências.

A concepção deEducação e a importância de sua presença no mundo como desafio de humanizaçãodas sociedades desembarcam no século XXI, na pauta das discussões de todos os países civilizados do planeta, sem, no entanto, terem uma definição nem uma identidade real, pois, como afirmou Freire (1996, p. 85), “o mundo não é. O mundo está sendo”. Apenas a compreensão, através da análise crítica do movimento histórico, permite-nos perceber a dinâmica do processo educacional e, desta forma, reconstruir a epistemologia do materialismo histórico dialético, e reflexivamente nos percebermos como sujeitos da história.

A configuração da atividade educativa caracteriza-se pela interação de sujeitos,mediados pelo conhecimento, contextualizados pelas dimensões históricas, política, social e cultural. É o contexto que dimensiona e dá sentido e significado à interação entre sujeitos, construindo e desconstruindo as subjetividades envolvidas, sejam elasde natureza individual ou coletiva, e, inclusive, de natureza institucional (FREIRE, 1996)

O contexto contemporâneo aponta para uma sociedade da informação, o que significa uma maior intensidade da comunicação e um aumento no ritmo das transformações, e, conseqüentemente, os contextos social, político e cultural têm novas configurações, gerando novas subjetividades e atingindo também o foco mediador da atividade educativa: o conhecimento. As subjetividades estão imersas em um dinâmico espaço-tempo configurada em rede, onde as informações e a comunicação não têm centro, e, portanto, o professor já não ocupa o centro do processo, e sim, é simplesmente um ator com mais experiência, tendo maiores condições de aprender e, portanto, de coordenar o acesso às informações e articular os processos de comunicação (CALHEIROS, 2009).

Nos novos tempos, as instituições de ensino em todos os níveis deverão ser organizações que tenham capacidade de aprender. Para isso ocorrer, será necessárioque os professores criem espaços de aprendizagem, sejam capazes de trabalhar com múltiplas linguagens (verbal, imagética, escrita, corporal, etc.) e elaborem atividades que desenvolvam a intersubjetividade e a comunicação com o outro, esteja ele próximo ou distante (CANAVARRO, 2013).

O novo professor precisará, no cotidiano, criar condições para a vivência dos contextos por parte dos alunos e propiciar também a convivência entre os sujeitos. Será uma nova pedagogia, que se denomina pedagogia da diferença, a qual se estrutura a partir do diferente na diferença, enfatizando as singularidades, tanto de natureza espaço-temporal como no âmbito das subjetividades. Este será o novo perfil docente e esta deverá ser a nova escola no mundo contemporâneo: uma escola centrada nos homens e nas mulheres, enquanto expressões do ser humano (BORBAe PENTEADO, 2011).

Ainda assim as relações mais notáveis e humanas entre professores e alunos apresentadas ao longo da história das atividades escolares são os fundamentos de toda ação pedagógica, pois, toda atividade educativa é uma relação entre sujeitos (CANAVARRO, 2013).

2.3.3 Uso da Tecnologia no Ensino da Matemática

De acordo com os padrões de excelência no ensino de matemática definidos na Base Nacional Curricular Comum (BNCC) (2015), os professores de matemática

precisam criar um ambiente que maximize as oportunidades de aprendizado dos alunos; para que eles possam incentivar o aprendizado autodirigido, modelar o raciocínio e o raciocínio matemáticos e fornecer feedback proposital e oportuno. Nos últimos anos, as novas tecnologias forneceram aos professores de matemática de todos os níveis de ensino mais oportunidades para abordar essa excelência. O uso de equipamentos de TI e as tecnologias associadas juntos fornecem uma dessas oportunidades (LEMOS, 2010; CANAVARRO, 2013).

Tablet, PC ou aparelhos de telefonia celular são laptops equipados com uma tela sensível ao toque e um estilo para permitir que o usuário escreva ou manipule a tela. Embora estejam disponíveis na educação desde o final do século XX, os custos e a dificuldade de uso percebida significam que todo o seu potencial raramente foi investigado. Nas escolas, os professores ao usarem para aprimorar suas palestras inferem a vida dos alunos, cujo uso de Ti é fundamental. Na sala de aula, Silva e Oliveira (2017) afirmam que este tipo de equipamento é uma tecnologia de fácil adoção que pode ter efeitos positivos na atenção e na aprendizagem do aluno.

Na educação básica, esses equipamentos também foram mostrados como facilitadores úteis da comunicação com alunos online remotos, permitindo que professores e alunos usem a escrita eletrônica para fornecer e receber conhecimentose habilidades (CERCONI e MARTINS, 2014).

A partir dos resultados da pesquisa, a percepção da tecnologia sugere que, quando os alunos usam equipamentos de TI se tornam parte integrante da lição, que o ambiente da sala de aula fica mais eficaz do que o formato tradicional, e que isso éem parte devido à ênfase crescente nos aspectos sociais da aprendizagem e nos processos que os alunos realizam quando fazem sentido.

Torres (2017), em uma reflexão sobre as práticas dos alunos da denominada geração da TI, acredita que, à medida que a educação dos alunos se torna virtual, essa mudança promove o uso de próteses de pensamento e continua a transformar as expectativas dos alunos em seus ambientes de aprendizagem.

Koehler (2019), em sua estrutura de tecnologia, pedagogia e conhecimento de conteúdo, propõem uma maneira de pensar que inclui o papel crítico do contexto na integração efetiva da tecnologia. Por exemplo, as disciplinas matemáticas dependem muito do uso de símbolos e gráficos em que o professor tradicionalmente escreve ou desenha à mão para explicar conceitos matemáticos passo a passo para os alunos.

Os recursos exclusivos de TI permitem que o usuário escreva facilmente informações simbólicas e gráficas eletronicamente e fornece ao professor uma ferramenta para explorar diferentes caminhos para uma solução ou para ajustar uma aula com base na reação da audiência. Com base nessa flexibilidade, os recursos de TI e suas tecnologias relacionadas permitem novos e mais rápidos métodos de entrega e comunicação para o ensino de matemática (BORBA et al., 2020).

Isso significa que, para o ensino, as experiências de aprendizado dos alunos podem incluir formatos de texto simples em todas as alternativas simbólicas e gráficas a serem criadas e disseminadas rapidamente. Koehler (2019) começou sua a pesquisar a utilidade e a funcionalidade dos Tablet e PCs em 2004, (um dispositivo conectado a USB com uma caneta para permitir que o usuário desenhasse ou escrevesse na tela) eram usados para ensinar grandes grupos de palestras estudandomatemática no primeiro ano. No final de 2006, o USQ financiou um projeto para investigar melhor seu potencial em grandes cursos de matemática e estatística no primeiro ano. Em 2007, o projeto foi estendido para além do ensino de matemática e,até o momento, a pesquisa envolveu um total de 10 funcionários, incluindo outras disciplinas.

Como política governamental, uso de TI em sala de aula deu-se início após um grande esforço, iniciado na década de 1990, para implementar o uso da tecnologia matemática nas salas de aula do ensino fundamental e médio em uma tentativa considerável entre os pesquisadores de educação matemática de analisar tantotentativas teóricas e empíricas de integração da tecnologia nas práticas da sala de aula (CANNONE et al., 2008).

No entanto, apesar desse nível de esforço, as dificuldades são realmente persistentes, apesar do contínuo apoio governamental dado à integração há mais de 20 anos. A complexidade da gênese instrumental tem sido amplamente subestimada em pesquisa e inovação em TI na educação, até bem recentemente. Essa a integração de tecnologias digitais na educação matemática como “marginal” e propõe quatro razões principais, segundo Meirelles (2018, p. 33):

A fraca legitimidade educacional das tecnologias de computador em oposição à sua alta legitimidade social e científica.

A subestimação de questões ligadas à informatização do conhecimento matemático. Processos complexos governam a transformação (transposição, como é chamado na pesquisa) do conhecimento matemático no contexto da sala de aula.

A oposição dominante entre as dimensões técnica e conceitual da atividadematemática. ,

A subestimação da complexidade dos processos de instrumentação. Por enquanto, esse problema pode ser formulado como uma falha no reconhecimento adequado de toda a extensão das novas demandas matemáticas e tecnológicas impostas aos alunos.

Esse conjunto de problemas aponta, em parte, para uma falha em teorizar adequadamente a complexidade de apoiar os alunos a desenvolver um relacionamento fluente e eficaz com a tecnologia na sala de aula – por eficaz, entende- se ajudar os alunos a se envolver, desenvolver e articular entendimentos de matemática. Procedimentos, estruturas e relacionamentos através da tecnologia e deacordo com o tempo e o status desse processo. Além disso, os valores ligados ao conhecimento matemático dificilmente podem permanecer invariantes sob a transformação tecnológica; do contrário, como Meirelles (2018, p. 133) coloca, “o preço que precisa ser pago para transformar objetos complexos em instrumentos matemáticos eficientes pode ser justificado?”.

As maneiras pelas quais o conhecimento matemático é transformado pela presença do computador são uma preocupação há muitos anos, começando com projetos com o Logo na década de 1980, e cada vez mais foca-se nas transformações epistemológicas do conhecimento dos alunos nas interações com computadores nas salas de aula de matemática para uma discussão sobre os tipos de software que têm o potencial de permitir essa transformação. Por exemplo, as experiências dos alunos com variáveis matemáticas podem ser transformadas encontrando-as como “entradas” em programas de Logo cujos valores podem ser facilmente alterados com efeitos observáveis imediatos; quantidades intensivas como taxas – notoriamente difíceis por causa de sua abstração – podem tornar-se “objetos” a serem manipuladosem muitos ambientes de computador; e conjecturas podem ser testadas através da construção de sistemas de geometria dinâmica, transformando assim os primeiros encontros com provas de exercícios procedimentais na validação para exercícios exploratórios na explicação (VASCONCELLOS, 2020).

Essas transformações de significados matemáticos gerados em contextos de integração exigem uma concepção de entendimento matemático e de conhecimento matemático, que justamente explique a especificidade das situações e as contingências de expressão matemática em ferramentas e tecnologias e nas comunidades em que estão inseridas (VITI, 1996).

Essa visão em desenvolvimento do conhecimento matemático ajuda a entenderas atividades que vem sendo pesquisado em uma variedade de situações bem diferentes: atividades com adultos nos locais de trabalho, bem como com estudantese tecnologias digitais (MEIRELLES, 2018).

Procura-se, portanto, elaborar um relato teórico unificado de como as concepções de matemática podem estar situadas – em termos de linguagem e conectividade e com o contexto de sua gênese, meios de expressão e uso (isto é, com os artefatos, objetivos e objetivos). discurso que faz parte da atividade) – e ainda assim são abstratos, pois se estendem além das preocupações imediatas até concepções mais gerais de conhecimento, ou seja, podem ser mapeadas em partes da matemática formal (VASCONCELLOS, 2020).

A marginalização da tecnologia pelas escolas produz atenção para a necessidade de uma análise mais precisa do papel do professor nesses novos e mutáveis contextos didáticos (LEMOS, 2010).

A legitimidade do computador tem sido frequentemente justificada em termos de facilidade de uso, relativa simplicidade de sua adoção e exagero de seu potencial (como se, aliás, o computador – é algo que pode ser considerado sem problemas como um elemento em um contexto educacional estático e sem resposta, ou que diretamente ofereça essa ou aquela ligação) (CANNONE et al., 2008).

Com demasiada frequência, os alunos são deixados por conta própria, explorando tarefas matemáticas para si mesmos por meio de suas interações com o computador, enquanto os professores lutam para interpretar o que fazem em termos matemáticos (LEMOS, 2010).

Além disso, as transformações do conhecimento matemático na presença da tecnologia podem ou não ser julgadas como desejáveis do ponto de vista educacional: depende do valor do conhecimento transformado como percebido, talvez de forma diferente, por professores e alunos (BORBA et al., 2020).

Assim, mesmo que os alunos possam se envolver e sentir que a atividade é legítima do ponto de vista deles, ela ainda pode representar um problema de legitimidade para o professor, uma vez que o que é expresso pelos alunos – e como – deve ser reconhecido como matemático dentro o discurso do sistema institucional deaprendizagem da matemática (CERCONI e MARTINS, 2014).

2.3.4 Transmissão e Aprendizagem de Informações

A abordagem de transmissão de informações para aprendizagem com computadores tem suas origens no trabalho de B.F. Skinner com instrução programada nas décadas de 1950 e 1960. Apesar das mudanças consideráveis na tecnologia e nas ideias sobre como as pessoas interagem e aprendem com ela, principalmente com o advento da Internet, a abordagem de transmissão de informações para a aprendizagem ainda tem uma influência profunda nas TIC (FREITAS, 2017).

Ele vê a aprendizagem de uma perspectiva de informação: a aprendizagem surge da maneira como os dados são codificados e transformados pelas pessoas emsuas tentativas de dar sentido ao mundo e às suas experiências nele. Essa visão progressiva da transmissão de dados, derivada da teoria da informação, é baseada em uma epistemologia kantiana que assume que o indivíduo recebe dados do mundo externo e processa esses dados categorizando-os. O seguinte relato da transmissão progressiva de dados foi adaptado de Boisot (1995).

A primeira linha de interceptação de dados do mundo externo é por meio dos cinco sentidos da visão, audição, paladar, olfato e tato. A totalidade do mundo externo não pode ser capturada, então os dados são codificados, isto é, simultaneamente selecionados e categorizados (FLORES, 2012).

A categorização é perceptiva ou conceitual. As categorizações perceptivas surgem da codificação de atividades que estão enraizadas principalmente em estímulos locais e imediatos por meio dos sentidos. Por si só, as categorizações perceptivas fornecem apenas uma classificação limitada e fragmentária dos fenômenos imediatamente disponíveis (BIGGE, 2017).

Mas eles são enriquecidos com uma interação constante com categorizações conceituais. As categorizações conceituais surgem de atividades de codificação dependentes de estímulos não locais originados na memória e na experiência, ou seja, complexidades de dados que representam conceitos genéricos como objetos, situações, eventos e ações (DE PAULA et al., 2012).

As interações entre as duas categorizações significam que a percepção nunca está totalmente livre de um contexto conceitual, em outras palavras, a codificação perceptual de dados sensoriais invoca o conhecimento teórico anterior. O uso de conceitos reduz muito a quantidade de informações que o sistema cognitivo precisa codificar. Assim como a codificação, a conceituação por meio da abstração é um processo seletivo que oferece mais economia em dados e categorias (CUTRIM e LIMA, 2015).

A abstração envolve a escolha de categorias que melhor capturem um atributo perceptivo. Além de certo nível de abstração, agrupamentos de relacionamentos às vezes adquirem coesão independentemente dos atributos perceptivos dos quais surgem (BORBA e PENTEADO, 2011).

Esses agrupamentos podem, por sua vez, tornar-se formas simbólicas que podem ser corrigidas para codificar e economizar ainda mais. Por meio da codificação simbólica, novas estruturas podem ser construídas a partir de elementos que se referem a outras estruturas mais complexas, sem ter que representar seus detalhes (CALHEIROS, 2009)

Todo o processo progressivo é baseado em economias no manuseio de dados: reduzindo a quantidade que deve ser tratada como atributos e o número de categorias às quais deve então ser atribuída. Os teóricos da educação reconhecerão isso essencialmente como uma reformulação laboriosa do construtivismo. Todo o processoconstitui aprendizagem, de fazer seleções e categorizações progressivas dos dados disponíveis até que sejam significativos para a pessoa envolvida. Os dados são codificados e tornam-se informações, integrados e contextualizados com o que foi previamente aprendido, a informação torna-se conhecimento. A intervenção propositalpode acontecer a qualquer momento por meio da agência do aluno, de outros indivíduos ou da tecnologia (COSCARELLI, 2015).

2.3.5 Pressupostos sobreo Papel da Tecnologia

A abordagem da transmissão de informações para o aprendizado, por sua vez, gera suposições adicionais sobre o papel da tecnologia no processo. As transformações da informação são mediadas pela intervenção no processo de aprendizagem por meio de uma tarefa ou atividade e transações associadas. Em ambientes educacionais formais, professores, colegas e outros atores educacionais esociais, utilizando uma variedade de recursos humanos e materiais, medeiam à intervenção. Mesmo em situações de autoaprendizagem e educação à distância, a mediação humana na forma de designers instrucionais, por exemplo, está apenas a alguns passos do aluno (BOISOT, 1995).

O papel da tecnologia na intervenção é visto em termos de aumento da produção ou agregação de valor. Em termos econômicos, produção significa tudo o que acontece a um objeto ou conjunto de objetos que aumenta seu valor (CULP et al.,2013).

Essa ação geralmente é uma mudança na forma, mas pode ser uma mudança no espaço ou no tempo. Os dados são economizados ao convertê-los em informações. A informação não é um fator de produção em seu direito próprio; é o resultado da economia de dados (RIBEIRO, 2005).

Os próprios dados são a entrada para a atividade produtiva. Informações para uma pessoa são dados para outra. A tecnologia pode agregar valor à aprendizagem em vários pontos: na fonte perceptual, na extensão da gama sensorial, nos processos de codificação, seleção, categorização e abstração, e nas intervenções e transações educacionais. A implicação é que as coisas serão feitas com mais eficiência, eficácia ou de novas maneiras (MEIRELLES, 2018).

A tecnologia pode estender a quantidade de dados que um indivíduo pode acessar do mundo externo, muito além do que está imediatamente disponível aos sentidos e do que pode ser prontamente processado pela mente humana (ALMEIDA, 2016).

O sensoriamento remoto e a microscopia eletrônica, por exemplo, estendem as escalas, a resolução e as velocidades nas quais as configurações espaciais podem ser exploradas. A tecnologia também fornece os meios para desenvolver códigos maisdiscriminantes, permitindo a diferenciação e integração de estímulos sensoriais. Outra suposição aqui é que o desenvolvimento dessas tecnologias baseia-se no conhecimento dos fenômenos físicos que é de natureza teórica e, portanto, conceitual;em outras palavras, os dados são tão bons quanto os modelos teóricos nos quais a tecnologia se baseia (FLORES, 2012).

A tecnologia da informação é notável pela quantidade de dados que pode disponibilizar, pela massa de dados que pode manipular e pela velocidade com que pode fazê-lo. Afeta o que pode ser encontrado, o que é procurado, onde é procurado e como é avaliado. O valor é agregado aos dados por meio dos processos de codificação, seleção, categorização e abstração que os transformam em informações úteis para quem os recebe. Esta é a transferência de informações como um processo de construção. Mas também pode envolver a desconstrução (LANKSHEAR et al.,2000).

Os dados podem existir como conhecimento tácito em práticas e fluxos já constituídos. Para se tornar informação, esse conhecimento deve ser desprovido de contexto e transformado em algo abstrato. A informação, neste sentido, é um conhecimento desconcretizado, em vez de dados brutos processados. Por meio de uma desconcretização posterior, de acordo com regras formais, as informações podem ser representadas como itens discretos de dados (DE PAULA et al., 2012).

Além de agregar valor aos processos, a tecnologia da informação também podeser usada para modelar e simular a realidade e suas abstrações. Tal como acontece com a ampliação da faixa sensorial, os resultados dessas atividades dependem dos modelos teóricos usados para gerá-las (CUTRIM e LIMA, 2015).

2.3.6 Agregando Valor às Intervenções e Transações Educacionais

A percepção sensorial e a conceitualização por meio da codificação, seleção, categorização e abstração podem ser aprimoradas pela tecnologia, mas acontecem dentro de um contexto social. Em termos educacionais, o contexto é fornecido por meio de intervenções e transações (CULP et al., 2013).

A transação educacional pode envolver dar e receber informações, o desempenho de certas habilidades, a construção de conhecimento, interação social eautoexpressão, incluindo a expressão de crenças e criatividade (COSCARELLI, 2015).

Grande parte do uso diário das TIC envolve fazer as coisas com maior eficiência e eficácia, especialmente trabalhando com informação, habilidade e conhecimento. Na literatura de TIC na educação, há muitos exemplos de agregação de valor a intervenções e transações de rotina em todas as disciplinas (AZEVEDO, 2008).

Exemplos de inovação, de fazer as coisas de maneiras genuinamente novas, são menos comuns. Pode haver abordagens inovadoras para acesso em termos de ampliação da participação e tornar o conteúdo mais compreensível, e de qualidade em termos de melhoria do conhecimento e compreensão (COSCARELLI, 2015).

Mas a maioria das reivindicações de inovação está associada à criatividade, envolve as dimensões sociais e expressivas da aprendizagem e abrange as preocupações culturais mais amplas de contexto, significado e discurso (CANNONE et al., 2008).

As qualidades inovadoras têm mais probabilidade de estar associadas à maneira como os atores sociais envolvidos na situação educacional trabalham com atecnologia, do que com a própria tecnologia (COSCARELLI, 2015).

A perspectiva mais ampla engloba as formas simbólicas da linguagem, das imagens e, principalmente do ponto de vista tecnológico, da multimídia. Os cinco sentidos da visão, audição, paladar, olfato e tato são revisitados em busca de maneiras pelas quais possam ser adaptados por meio da tecnologia para proporcionar experiências educacionais (CALHEIROS, 2009)

O design multimídia é uma extensão do design instrucional. Ambos utilizam princípios educacionais e de design, mas enquanto o design instrucional se preocupa principalmente com o texto, o design multimídia se preocupa com a interação de texto,imagem e som. A realidade virtual adiciona outras experiências sensoriais à mistura, mas ainda não faz parte da experiência educacional convencional (BORBA e PENTEADO, 2011).

1.3.6.1 Implicações para o ensino

A visão da aprendizagem da transmissão de informações é uma forma de construtivismo baseada na epistemologia kantiana, que assume que o indivíduo recebe dados do mundo externo e processa esses dados categorizando-os (BIGGE, 2017).

Assume que os dados são entidades objetivas que, por meio dos sentidos, entram na mente. O ato de construção está localizado na mente. Além disso, se os dados forem entidades objetivas, eles podem ser pré-especificados e sua assimilação quantificada (BAKI, 2018).

Os pressupostos incorporados nesta visão impactam em questões como: comoensina-se sobre informação e comunicação e suas tecnologias associadas, como usamos as TIC em nosso ensino e onde no currículo essas responsabilidades devemestar localizadas. A ênfase aqui na informação, comunicação e tecnologias associadas é deliberada. Indiscutivelmente, esta é a arena através da qual deveria serpossível definir a noção de professor especialista em TIC. Que conhecimento e experiência esse professor teria? Por definição, este é um campo transdisciplinar, ouseja, opera entre as disciplinas (LANKSHEAR et al., 2000)

O especialista compreenderia os fundamentos das teorias da informação e da comunicação e sua relação com as teorias de aprendizagem e ensino. Uma compreensão da teoria e da prática educacional permitiria que ele ou ela tomasse decisões sobre o que é educacionalmente desejável (ALMEIDA, 2016).

Uma base sólida em estudos culturais e de mídia forneceria um contexto para a informação na sociedade e as formas como ela é comunicada. Ele ou ela também entenderia os fundamentos da ciência da computação, saberia algo sobre o design de multimídia educacional e ambientes virtuais de aprendizagem e os tipos de transaçãoeducacional que eles suportam (BOISOT, 1995)

Poucos professores têm essas credenciais; não existem cursos para fornecê- los. A maioria dos professores de TIC chega ao trabalho por caminhos circulares. Mesmo se eles tivessem a formação de especialista ideal, raramente há uma oportunidade de utilizar tal conhecimento de uma forma coerente, uma vez que a responsabilidade por algumas, mas não todas, as partes especializadas de TIC estão espalhadas em outro lugar no currículo. Em vez disso, a visão amplamente aceita, mas raramente articulada, da transmissão de informações da aprendizagem levou a uma preocupação com a eficiência e eficácia na transmissão e no processamento deinformações (BIGGE, 2017).

Freqüentemente, os dois conflitam com o resultado de que há uma falta geral de clareza sobre o que constitui um benefício educacional das TIC. Isso, por sua vez,levou a um foco seletivo em certos resultados mensuráveis, notadamente na proficiência no uso da tecnologia, ou seja, com habilidades (BORBA e PENTEADO, 2011).

Como acontece com qualquer tecnologia, existe um conjunto de conhecimentosprocedimentais que deve ser aprendido e colocado em prática. Isso pode ser adquiridopor meio de treinamento, mas só será aprimorado e aperfeiçoado com o uso constanteem situações profissionalmente relevantes. A obsessão com habilidades em detrimento do desenvolvimento de uma teoria viável de TIC na educação, um conteúdo acadêmico significativo para o especialista em TIC e um nicho curricular para TIC tem restringido os sistemas de educação em todo o mundo. Todas as disciplinas usam TIC (RIBEIRO, 2005).

Assim como é possível dizer algo sobre o papel do especialista em TIC, também deveria ser possível dizer algo sobre as coisas que os especialistas da área precisam abordar em suas disciplinas (CALHEIROS, 2009)

Um paradoxo da informação é que quem sabe muito sobre um assunto tem mais consciência do que não sabe do que quem sabe menos. Quanto mais um indivíduo sabe, mais ciente ele ou ela está sobre as informações que precisa adquirir. Aqueles que possuem informações estão em melhor posição para exigir informações do que aqueles que não às possuem, daí a importância do conhecimento metacognitivo. Já foi dito que a educação deve proteger da informação: em outras palavras, deve fornecer ao indivíduo os meios para fazer escolhas informadas e discriminatórias sobre a informação e a forma como ela é usada (MACDONALD, 2008).

Fazer escolhas discriminatórias exige que os professores reexaminem as premissas fundamentais nas quais suas disciplinas se baseiam e como o acesso à quantidade e variedade cada vez maior de informações e à tecnologia para trabalhar com elas está desafiando essas premissas. Eles podem então estar em melhor posição para ajudar os alunos a compreender alguns assuntos fundamentalmente importantes e inter-relacionados, tais como: a natureza das disciplinas, suas metodologias e como eles usam as informações; formas de abordar a validade e procedência da informação, como é corroborada e suas limitações; os valores culturais e sociais que sustentam a informação e seu uso; frameworks para conectar ideias e conceitos de diferentes disciplinas (COSCARELLI, 2015).

Há poucas evidências de que esse exame do assunto de dentro para fora esteja ocorrendo. Não só há uma variação considerável no uso de TIC em diferentes disciplinas, há novamente uma preocupação com conhecimentos e habilidades procedimentais: conhecimento de software e aplicativos e proficiência em usá-los (CULP et al., 2013).

As representações de software de muitos professores não especialistas são idiossincráticas, fragmentárias e transitórias, com links aprendidos de maneira imperfeita e suposições falsas, que se manifestam no que Hale (2008) chama de ‘hazyspace‘. Não surpreendentemente, esses professores estão preocupados com o fato de que as habilidades de seus alunos são mais avançadas. Sempre haverá alunoscom mais capacidade técnica do que seus professores.

Eles têm tempo e correm riscos. Se a educação é vista como uma parceria, deve-se reconhecer que os alunos trazem para ela muitas habilidades cruas. O que os professores trazem é sabedoria e orientação. Eles têm o conhecimento artesanal de ensino e aprendizagem. Eles são os especialistas e entusiastas em seus assuntos. Eles fornecem os contextos nos quais os alunos entendem as informações. Eles ajudam os alunos a entender quem eles são como indivíduos e em relação aos outros (MARTINS, 2009).

A abordagem de transmissão trata a informação como ‘bytes‘ que podem ser montados e desmontados, sua assimilação na aprendizagem medida e quantificada de certas maneiras, com formas concomitantes de responsabilização que dão origem a ênfases particulares no ensino. Ele pertence à geração de software educacional deestímulo-resposta, exercício e prática. Porque tem alguma utilidade, e porque as inter- relações entre a teoria da informação e a teoria educacional raramente são exploradas, a transmissão de informações tornou-se enraizada em procedimentos e pedagogias como formas complexas de, por exemplo, incorporadas (como se faz as coisas aqui) incorporadas (em rotinas sistêmicas, papéis e procedimentos formais) e conhecimento institucional codificado (veiculado por signos e símbolos) (DE PAULA et al., 2012).

No entanto, será evidente a partir do que precede que a abordagem de transmissão de informações para a aprendizagem tem sérias limitações: é teoricamente inadequada, é epistemologicamente limitada e, como estreita as percepções do campo, é educacionalmente restritiva. As inadequações práticas da abordagem dão origem a formas muito específicas de lidar com a informação e a comunicação e, como se viu, estas, por sua vez, têm impacto nas concepções sobre a natureza das disciplinas relativas à informação e comunicação e do professor especialista em TIC e como ele ou ela trabalha com as TIC (FLORES, 2012).

Hoje em dia, o software é cada vez mais inteligente e intuitivo; é adaptável ao usuário e ao contexto no qual está sendo usado. Uma infraestrutura de redes globais reduziu a linearidade e a dependência do caminho dos fluxos de informação (MEIRELLES, 2018).

Em breve, a World Wide Web será estruturada semanticamente, onde os agentes de software realizarão tarefas sofisticadas, feitas sob medida para as necessidades dos usuários individuais (FREITAS, 2017).

Foram propostas novas concepções de construtivismo que estão mais de acordo com os desenvolvimentos tecnológicos e com o pensamento atual sobre a natureza da aprendizagem (MEIRELLES, 2018).

Um deles é o seguinte como resultado da maneira como os indivíduos estão em constante interação com seu ambiente. Nesta visão, os dados não são objetivos, mas são o resultado de transações do ambiente humano (FREITAS, 2017).

O ato de construção, a seleção da informação, não é algo que a mente faz no processamento de todos os dados que recebe por meio dos sentidos, mas é constituído na interação e, portanto, pode ser denominado construtivismo teórico da ação (MACDONALD, 2008).

Ao vincular o conhecimento à ação, o construtivismo teórico da ação é compatível com a teoria transacional do conhecimento de Dewey, onde as transações estão situadas social e culturalmente (BOISOT, 1995).

Em vez de ver as pessoas e a natureza em oposição, Dewey apud Freitas (2017) acreditava em sua unidade fundamental. Ele rejeitou as doutrinas kantiana e cartesiana que respectivamente defendiam a existência das coisas em si mesmas e uma mente autoconsciente que existe independentemente de um reino extra mental. Para Dewey apud Freitas (2017), a experiência é a função de hábitos, de ajustes e reajustes ativos, de coordenação e atividades, ao invés de estados de consciência. Nesta visão, as ideias humanas e o ambiente em que são geradas têm uma relação recíproca (ALMEIDA, 2016).

Dewey foi fortemente influenciado pelas implicações filosóficas das ideias de Darwin sobre evolução e seleção natural. A estrutura sociocultural que agora acomoda o pensamento de Dewey apud Freitas (2017) é compatível com a síntese evolutiva moderna que liga a evolução biológica e a mudança cultural. Isso inclui as mudanças feitas pelos organismos em seus ambientes por meio de uma série de pressões de seleção auto induzidas. No caso da espécie humana, essas atividades incluem a cultura no sentido mais amplo. Em tal síntese, a teoria evolucionária precisa de uma moeda – adequação neste caso – por meio da qual as adaptações ao meio ambiente podem ser medidas. Uma moeda correspondente na teoria sociocultural pode ser a informação (LANKSHEAR et al., 2000).

A informação, neste sentido, não é simplesmente uma mercadoria transmitida;é parte integrante da construção e reconstrução constante do significado entre as pessoas e seu ambiente (MEIRELLES, 2018).

Uma extensão moderna do pensamento de Dewey apud Freitas (2017) é a educação como intersubjetividade prática, que vê a educação como um processo de aculturação, não um processo unilateral no qual a cultura é transferida de um para o outro, mas um processo co-construtivo no qual ambos os participantes desempenham um papel ativo (BIGGE, 2017).

O ponto de partida não está no comportamento individual dos participantes, mas no campo intersubjetivo com o qual eles interagem, campo que ao mesmo tempo é estabelecido pela cooperação intersubjetiva (MEIRELLES, 2018).

As mudanças provocadas no indivíduo predispõem-no a reagir em situações futuras de uma forma mais específica – as predisposições adquiridas que Dewey apud Freitas (2017) chamou de hábitos.

A intersubjetividade prática requer revisitar a epistemologia, a metodologia e apedagogia relativas à informação e à tecnologia agora disponíveis. Por exemplo, o ensino especializado em TIC pode envolver o exame das teorias que sustentam as aplicações de computador em disciplinas e as suposições que fazem sobre a natureza do conhecimento. Pode desafiar a forma como os aplicativos de software legitimam, ignoram ou até deslegitimam métodos epistemológicos, como dedução, interpretaçãopor indução, intuição e introspecção (MARTINS, 2009).

E, dado que a percepção do conhecimento como um estoque objetivamente ordenado de fatos intrinsecamente ordenados está se tornando um artefato em constante mudança de julgamento intersubjetivamente mediado, o especialista pode explorar a relação entre informação e diferentes formas de conhecimento – racional, objetivo, tácito, problemático, experiencial e assim por diante (BAKI, 2018).

2.3.7 O Futuro das TICs e da Educação

As TIC são um dos símbolos mais visíveis da globalização e inovação educacional e é frequentemente apresentada como uma causa e um impulsionador consequente para a inovação educacional e mudança (BIGGE, 2017).

As TIC nas políticas de educação foram identificadas, partindo de uma lógica econômica, uma lógica social e uma racional educacional, para uma lógica catalítica. Dentro desses discursos, as TIC são frequentemente apresentadas como inevitáveis e cada vez mais onipresente (BORBA e PENTEADO, 2011).

As TIC têm sido utilizadas até agora para aprimorar o ensino e a aprendizagem, inclui a promoção, a pesquisa, o envolvimento da comunidade acadêmica e administração, além de colocar computadores pessoais nas mãos dos alunos e em direção à tecnologia móvel, o mundo virtual e computação em nuvem entre outros argumentam, no entanto, que o determinismo tecnológico satura muitos das futuras visões educacionais promovidas por formuladores de políticas, indústria e até mesmo alguns pesquisadores (BIGGE, 2017).

Mais e mais pesquisadores tem recomendado cautela ao falar das possibilidades de novas tecnologias e ao assumir que um determinado meio ou tecnologia trazem automaticamente resultados de aprendizagem específicos, uma vez que há nada é inerente à tecnologia que garante automaticamente a aprendizagem (CANNONE et al., 2008).

Quatro grandes vertentes podem ser distinguidas em relação à pesquisa em TIC e educação: (1) pesquisa voltada para políticas em TIC na educação, (2) Pesquisa e Desenvolvimento de Tecnologia (PDT) no campo de tecnologias de aprendizagem, (3) pesquisa sobre ferramentas de Design Instrucional (DI) baseadas em computadore (4) pesquisa sobre o uso pedagógico das TIC (FREITAS, 2017).

A pesquisa orientada para políticas sobre TIC na educação é normalmente conduzida sob a autoridade do Ministério da Educação – MEC, e organizada em programas de pesquisa como TIC na Educação, Educação Online e o Monitor de TIC. No Brasil, as escolas são responsáveis pela inovação de seu próprio ensino, incluindo o uso das TIC, enquanto o governo estimula e facilita essa inovação (COSCARELLI, 2015).

Em comparação com outros países ocidentais, a infraestrutura técnica disponível nas escolas brasileiras é regular. Existem cerca de 10 alunos por computador e todas as escolas estão conectadas à Internet. Um ponto de atençãoespecial tem sido e ainda é a escolaridade dos professores no que diz respeito às suas competências em TIC, mas nos últimos anos foram feitos progressos razoáveis a este respeito (CULP et al., 2013).

Num futuro próximo, as políticas serão principalmente direcionadas para a resolução de dois problemas persistentes, nomeadamente, a falta contínua de materiais de aprendizagem digitais de alta qualidade e acessíveis nas escolas e as dificuldades com a aplicação das TIC de forma a realmente melhorar os processos deensino e aprendizagem. A PDT no domínio das tecnologias de aprendizagem trata principalmente do fato de o desenvolvimento de conteúdos de aprendizagem de alta qualidade em quantidade suficiente se revelar extremamente difícil (CUTRIM e LIMA,2015).

Requer um tempo considerável, grandes orçamentos e conhecimentos de design e desenvolvimento que estão apenas disponíveis. A linha de pesquisa dominante concentra-se em permitir a reutilização de materiais de aprendizagem. A ideia básica é que, uma vez feito, o conteúdo de aprendizagem pode ser usado muitas vezes em muitos ambientes instrucionais diferentes. Se o conteúdo de aprendizagem for dividido em pequenos pedaços modulares chamados objetos de aprendizagem, osdesenvolvedores serão capazes de combinar e recombinar esses objetos para criar um novo conteúdo de aprendizagem (FLORES, 2012).

Os padrões de tecnologia de aprendizagem têm como objetivo garantir que os objetos de aprendizagem sejam desenvolvidos, organizados e distribuídos de maneirauniforme. Tais padrões dificilmente tratam de questões pedagógicas, porque se afirmaque a padronização deve ser pedagogicamente neutra (KENSKI, 2007).

No entanto, mesmo uma abordagem neutra deve oferecer a oportunidade de implementar a mais ampla variedade possível de métodos de ensino de tal forma quea reutilização ainda seja garantida. Na Universidade de Campinas – UNICAMP, umaestrutura instrucional genérica para objetos de aprendizagem foi descrita por meio de uma Linguagem de Modelagem Educacional), que está atualmente em processo de padronização pelo grupo Learning Design de o IMS Global Learning Consortium (KÜBLER, 2019).

Terceiro, a pesquisa em ferramentas de DI baseadas em computador estuda como as TIC podem ajudar designers ou professores a realizar o processo de DI, ou seja, a aplicar o ciclo ADDIE (Análise, Projeto, Desenvolvimento, Implementação e Avaliação) de maneira eficaz e eficiente (LEMOS, 2010).

Van Merriënboer e Martens (2002) descrevem uma série de ferramentas para analisar tarefas ou conteúdos e projetar planos para aulas ou programas de treinamento (ou seja, ferramentas de pré-autoria), para desenvolver materiais de instrução, e para implementar e avaliar a instrução (ou seja, ferramentas de pós- autoria) (KÜBLER, 2019).

À semelhança do que acontece com a PDT no domínio das tecnologias de aprendizagem, o principal objetivo desta linha de investigação é tornar mais rápido e barato o processo de desenvolvimento de conteúdos de aprendizagem de qualidade. Finalmente, a pesquisa sobre o uso pedagógico das TIC estuda principalmente como as TIC podem melhorar os processos de ensino e aprendizagem (KENSKI, 2007).

Embora a maioria dos pesquisadores provavelmente concorde que as TIC per se não podem melhorar os processos instrucionais, deve ficar claro que as TIC podem, pelo menos em princípio, permitir o uso de métodos instrucionais inovadores que podem ajudar a tornar a aprendizagem mais eficaz, eficiente e atraente (MAIA e TORRES, 2018).

Isso se aplica tanto às estratégias de entrega, que são métodos instrucionais para transmitir a instrução ao aluno e/ou para receber e responder à entrada do aluno, quanto às estratégias organizacionais, que são métodos instrucionais para organizar as tarefas de aprendizagem e os conteúdos que têm foi selecionado para a instrução. Por exemplo, as TIC podem permitir a colaboração entre os alunos que estão distribuídos no espaço ou no tempo (ou seja, permitir uma estratégia de entrega que, sob determinadas circunstâncias, não seria possível sem as TIC) ou permitir que os alunos trabalhem, na sala de aula, em um ambiente de simulação que permite estudar os efeitos de diferentes políticas sobre o crescimento econômico de um país (ou seja,uma estratégia organizacional que nunca poderia ser aplicada em sala de aula sem ouso das TIC) (MENDES e BARTON, 2017).

2.3.8 Dificuldades no uso da Tecnologia no Ensino da Matemática

O rápido desenvolvimento tecnológico mudou a forma de conceber as sociedades. As Tecnologias de Informação e Comunicação (TIC) permitiram o acesso a enormes volumes de informação de forma imediata e além dos limites do espaço e do tempo. A chamada sociedade do conhecimento longe de ter sobrecarregado a instituição escolar, possibilitou que ela se tornasse um cenário renovado para aprender a lidar com essas informações (MAIA e TORRES, 2018).

As tecnologias digitais tornaram-se elementos onipresentes, com interesse geral em que os alunos aprendam a usar essas tecnologias desde a escola. Tal expansão tecnológica alterou a forma de conceber a escola e a incorporação das TIC ao contexto escolar parece ser fundamental para responder à configuração do novo papel do professor no contexto de ensino; uma vez que promovem a renovação metodológica e motivam os alunos de forma diferente dos métodos tradicionais (LEMOS, 2010).

Da mesma forma, a irrupção tecnológica na instituição escolar tem proporcionado um interesse crescente pela formação de professores em tecnologias de informação e comunicação. O professor tem que assumir o papel tradicional, mas também precisa criar novas situações de aprendizagem que motivem os alunos a aprender. Tal demanda evidencia novos desafios ao saber profissional do professor (KENSKI, 2007).

Flores (2012) valoriza a importância das TIC como ferramentas que permitem o desenvolvimento do conhecimento pedagógico do conteúdo (CPC). Nesse sentido, desenvolveu um modelo de conhecimento pedagógico no qual incluem o conhecimento tecnológico como essencial para o desenvolvimento das disciplinas em sala de aula. Eles chamam de Conhecimento Tecnológico-Pedagógico do Conteúdo (CTPC). Esse conhecimento contém dimensões pessoais e tácitas que só se tornam explícitas através da prática e da reflexão. Até agora, verificou-se um processo gradual de introdução de recursos tecnológicos em sala de aula, mas não se sabe precisamente se essas ferramentas têm sido utilizadas como um recurso integrado no currículo, o que implica seu uso efetivo no design, mas também no Desenvolvimento de programação em sala de aula (KÜBLER, 2019).

Especula-se que o uso das TIC pode facilitar a aquisição de uma nova gama de habilidades, competências e experiências para professores qualificadosNo entanto, apesar dos esforços na formação inicial e continuada de professores, não é comum a utilização plena das TIC integradas no currículo. Isso pode ser devido à existência de barreiras que impedem sua integração na sala de aula. Algumas dessasbarreiras estão relacionadas às atitudes e crenças dos professores sobre a utilidadeda tecnologia no ensino (KENSKI, 2007).

2.3.9 Atitudes e Crenças em Relação às TICs

Para entender o uso que os professores fazem de qualquer tecnologia, é importante saber não apenas que conhecimento ela produz ou as barreiras que a limitam. Nesse sentido, também precisamos conhecer as crenças e atitudes subjacentes às práticas educativas em sala de aula; pois são eles que determinam sua aplicação (MENDES e BARTON, 2017).

O sucesso de sua integração nesse contexto. De alguma forma, se o próprio uso das TIC representa uma mudança, então as crenças dos professores também devem mudar e indicam que os professores não devem apenas ter habilidades para manusear essas ferramentas; mas também uma atitude positiva em relação à sua integração (MEIRA, 2019).

O reconhecimento por parte dos professores de uma utilização positiva das TICinfluencia uma atitude positiva em relação à sua incorporação na sala de aula. Esta atitude positiva baseia-se na consideração da tecnologia como elemento-chave para alcançar melhores resultados de aprendizagem, o que por sua vez aumenta a possibilidade de usá-la nos processos de ensino (MAIA e TORRES, 2018).

Outras pesquisas enfatizam as atitudes como chave para prever o uso, aceitação e satisfação dos professores que as integram em sua prática educacional enfatizam que atitudes negativas podem constituir uma barreira para a integração das TIC na sala de aula. Em relação às crenças, alguns estudos destacam que elas determinam a forma como as tecnologias são utilizadas nos processos de ensino. Kübler (2019), conclui que eles desempenham um papel importante nas práticas educativas e contribuem para a integração das tecnologias, especialmente as crenças atribuídas ao seu valor quando se trata de alcançar objetivos de ensino (LEMOS, 2010).

No entanto, não há correlação significativa entre as crenças dos professores esuas práticas quando se trata de integrar tecnologia (Judson, 2006); porque embora os professores demonstrem atitudes positivas, não está claro qual é o valor específico de suas crenças (LEMOS, 2010).

CAPÍTULO III

MARCOS MEDOTOLÓGICO

Conforme Lakatos e Marconi (2013, p. 83), “o método é o conjunto das atividades sistemáticas e racionais que, com maior segurança e economia, permite alcançar o objetivo – conhecimentos válidos e verdadeiros”.

Projeto de Pesquisa

A pesquisa foi realizada nas Escolas Estaduais Waldemiro Lustosa (Figura 3) e São Luiz de Gonzaga Figura 4). A Escola Estadual Waldemiro Lustoza se localiza na Rua Alberto Rangel, 33 Compensa. A Escola Estadual São Luiz de Gonzaga se localiza R. Cinco de Setembro, 1 – São Raimundo.

Figura 3 – Escola Estadual Waldemiro Lustoza

Fonte: Arquivo Pessoal da autora

Figura 4 – Escola Estadual São Luiz de Gonzaga

Fonte: Arquivo Pessoal da autora

Os bairros da Compensa e de São Raimundo ficam na zona oeste de Manaus. O bairro de São Raimundo surgiu praticamente com a fundação de Manaus dada a sua proximidade com o Forte de São José do Rio Negro. O bairro da Compensa surgiu no final da década de 1960, por meio de um proceso de invasão de terras herdadas da famosa viúva Borel.

Essa senhora herdou uma gleba de terras imensa e não teve condições de manter uma vigilância sobre a área. As pessoas que aportaram na cidade, pós início da Zona Franca de Manaus, sem um lugar fixo para morar e fugindo do aluguel passaram a ocupar o local que já no ínício da década de 1970 já era um bairro que precisa de todo o aparato estrutural, o que foi rápidamente na administração do prefeito Frank Lima. O bairro de São Raimundo se juntou em torno do antigo matadouro de Manaus.

O bairro da Compensa é um bairro de clase média que passa por intensos problemas como a questão da segurança, sendo considerado um bairrs que abriga os chefes de uma famosa facção criminosa.

O bairro da compensa possui toda a infraestrutrura urbana, comercio pujante, rede de serviços bem consolida, pequenas indústrias e am alguns locais até pequenas hortas. O serviço de agua e luz atende todas as residências e os transportes urbanos são bem consistentes.

O bairro do São Raimundo é um dos mais antigos da cidade de Manaus e surgiu ainda no século XIX, quando a cidade passava por momento pujante do Ciclo da Borracha e depois passou pelas agruras do térmico do segundo Ciclo da Borracha. Onome foi dado em função do sincretismo religio

Enfoque da pesquisa

Essa pesquisa apresenta um enfoque quali-quantitativo. Assim, o processo interativo do enfoque quali-quantitativo do estudo significa que as amostras geralmente são conduzias pela teoria em maior ou menor grau.

O enfoque será qualitativo define padrões de validade na pesquisa que são ainda mais desafiadores devido à necessidade de incorporar tanto o rigor quanto a subjetividade, bem como a criatividade no processo científico. Além disso, métodos qualitativos díspares adotam diferentes critérios avaliativos. Como discernir a qualidade na pesquisa quali-quantitativa dentro de uma estrutura tão ambígua e intangível? O que distingue a ciência da pseudociência? As pesquisas tornam-se tão diversificadas que as diretrizes gerais de validade são impossíveis ou existem critérios específicos que cruzam diferenças metodológicas e filosóficas?

Forbes et al. (2009) argumentaram que garantias específicas de conhecimento transcendem fronteiras filosóficas e metodológicas. Embora reconheçam a diversidade de tradições qualitativas, aliadas às infinitas suposições dos investigadores, acreditavam que a busca de critérios comuns de bondade é necessária e digna de pesquisa qualitativa.

Assim o enfoque na pesquisa como quali-quantitativo passou por inúmeras transformações para fortalecer a contribuição única que essa tradição científica oferece ao conhecimento do desenvolvimento. As conceituações iniciais de validade foram aplicadas diretamente a partir de padrões de confiabilidade e validade de pesquisas quantitativas ou experimentais, baseadas em uma filosofia positivista (FORBES ET AL, 2009).

Considerou-se que as definições tradicionais de confiabilidade e validade são aplicáveis e reconhecidas como marcas de referência pelas quais a qualidade de toda a pesquisa pode ser julgada. A confiabilidade se referia à estabilidade das descobertas, enquanto a validade se ressentia da veracidade das descobertas.

A incompatibilidade desses termos com as premissas e princípios subjacentes à pesquisa de qualidade qualitativa resultou na tradução de termos mais alinhados com a perspectiva interpretativa. A resposta à necessidade de convencer a comunidade científica dominante e um tanto hostil sobre os méritos da pesquisa qualitativa que levou Forbes et al. (2009) a um atoleiro epistemológico, ao traduzir a validade interna à credibilidade, a validade externa à transferibilidade, a confiabilidade e os objetivos da atividade para confirmação.

O que transferibilidade e confiabilidade significam para a pesquisa qualitativa? Como esses critérios podem ser garantidos? A pesquisa qualitativa é generalizável? Quem deve confirmar os resultados: o participante, o investigador ou um especialista externo? Por um lado, argumentou-se que a pesquisa qualitativa é uma abordagem alternativa para o desenvolvimento do conhecimento, mas, ao mesmo tempo, defendiam-se padrões de validade da abordagem tradicional. Apesar da incongruência entre epistemologia quantitativa e metodologia qualitativa, padrões traduzidos de validade provaram ser critérios úteis para demonstrar o rigor e a legitimidade da pesquisa qualitativa

Desenho da investigação (abordagem metodológica)

Um dos grandes problemas de um projeto de pesquisa é a infinidade de metodologias de pesquisa, dificultando a seleção de um desenho de pesquisa apropriado para um estudo específico.

É necessário fazer um estudo aprofundado da (s) metodologia (s) escolhida (s), para executar boas práticas de pesquisa. Muitas vezes, os autores se contradizem, oque exige que os pesquisadores exercitem escolhas bem informadas, tornem sua escolha conhecida e substanciada.

Neste projeto de pesquisa tem-se a intenção de falar de comparar as dificuldade no ensino da matemática em função da didática dos profesores na escola pública e na escola privada com base na experiência do seu autor e revisão de literatura, além de uma pesquisa de campo.

Assim definiu-se o desenho desta investigação como fenomenológico que nasceu pós Primeira Guerra Mundial, quando a Europa estava em ruínas. Freudenthal (2013, p. 54) capta a situação com vivacidade: a ordem social do capitalismo europeu havia sido abalada por suas “raízes pela carnificina da guerra e suas consequências turbulentas”.

As ideologias das quais essa ordem habitualmente dependia, os valores culturais pelos quais governava, também estavam em tumulto profundo. A ciência parecia ter diminuído para um positivismo estéril, uma obsessão míope com a

categorização dos fatos; a filosofia parecia dividida entre tal positivismo, por um lado, e um subjetivismo indefensável, por outro; formas de relativismo e irracionalismo eram desenfreadas, e a arte refletia essa desconcertante perda de orientação (FREUDENTHAL, 2013).

No contexto dessa crise ideológica, o filósofo alemão Edmund Husserl (1859- 1938) “procurou desenvolver um novo método filosófico que emprestasse certeza absoluta. a uma civilização em desintegração. Embora as origens da fenomenologia possam ser rastreadas até Kant e Hegel, Freudenthal (2013) considera Husserl como “a fonte da fenomenologia no século XX. Husserl apresenta sua filosofia com as bases e condições de uma ciência rigorosa. Porém, como dar rigor ao raciocínio filosófico em relação a coisas tão cambiantes e variáveis como as coisas do mundo real (SCHUTZ, 2009).

Para evitar que a verdade filosófica também fosse provisória, a solução, para Husserl, é que ela deveria referir-se às coisas como se apresentam na experiência deconsciência, estudadas em suas essências, em seus verdadeiros significados, de ummodo livre de teorias e pressuposições, despidas de seus acidentes próprios do mundo real, do mundo empírico objeto da ciência. Buscando restaurar a “lógica pura” e dar rigor à filosofia, argumenta a respeito do principio da contradição na Lógica (FREUDENTHAL, 2013).

O método fenomenológico contribuiu fortemente para o desenvolvimento de correntes filosóficas, como o existencialismo, e de correntes científicas, como as que nos permitem analisar as experiências humanas nos muitos aspectos na sua vida psíquica e na vida social. Percebemos que o conceito de significação se torna chave, superando-se as amarras, por exemplo, da psicologia e da sociologia positivistas. Temos que significação é a produção humana de sinais, é o meio pelo qual uma pretendida objetivação ganhe sua peculiaridade e um objeto, na perspectiva teórica de um certo estudo, seja-nos historicamente identificado. A primeira tratava (e trata) o psiquismo como uma mera soma de elementos bioquímicos, fisiológicos e anatômicos, reduzindo-o a algo neuropsicológico, onde o psíquico não é objeto em si,mas um conjunto de efeitos psíquicos de causas não psíquicas (FREUDENTHAL, 2013).

Com a fenomenologia, a psicologia ganhou autonomia científica e pode estudar uma série de fenômenos ligados à consciência que são dotados de significação própria. Também eram irrelevantes para a psicologia tradicional certos fenômenos como os lapsos (as chamadas parapraxias) e os sonhos, mas que para a psicologia dinâmica ganham marcante significação. A sociologia positivista, por sua vez, tratava(e trata) a sociedade como uma mera soma de ações dos indivíduos causando o social. Com a fenomenologia, surge a sociologia como ciência autônoma e pode estudar os fatos sociais como uma realidade observável distinta do psíquico (FREUDENTHAL, 2013).

A fenomenologia busca o início real de todo o pensamento filosófico e deve, quando estiver completamente desenvolvida, acabar onde todas as Filosofias tradicionais começam. Ela pretende ser o suporte das demais filosofias. Seu lugar é além, ou melhor, antes de todas as distinções entre realismo e idealismo (SCHUTZ, 2009).

Ele se assegura de sua especificidade em relação às duas únicas dimensões nas quais, até então, foi possível empreender uma análise do tempo: a psicologia e afilosofia em conformidade ao uso da época – A teoria do conhecimento.

Nas Investigações Lógicas Husserl aceita ainda (mesmo que de má vontade) considerar seu trabalho como uma espécie de “psicologia descritiva”, ele declara, ao contrário que se trata de resolver as dificuldades profundas vinculadas à oposição entre a subjetividade do ato do conhecimento e a objetividade do conteúdo e do objeto do conhecimento (a verdade e o ser) (SCHUTZ, 2009).

Husserl formula uma “crítica do conhecimento”, ou ainda, ele exige uma fenomenologia do conhecimento. Todavia, o que a fenomenologia é, ela mesma, em “sentido rigoroso e próprio”, um difícil e obscuro equilíbrio entre duas negações.

Quando Husserl insiste na relação de seu pensamento com a teoria do conhecimento, é antes de tudo para negar que aquele seja uma psicologia; e, quando nega que seu pensamento seja uma psicologia “em sentido rigoroso e próprio”, deixa por aqui mesmo entender que seja, apesar disso, em um certo sentido (e num sentido novo e indefinido) uma “psicologia”, ou seja, que não é pura e simplesmente uma reiteração do kantismo.

Neste ponto é bom distinguir entre o delineamento da pesquisa e as técnicas de coleta e análise de dados a serem utilizadas. […]. Uma variedade muito rica de situações problemáticas apresenta-se nas organizações FREUDENTHAL, 2013).

Estas oportunidades ou problemas podem ser explorados e analisados de forma mais completa por meio de métodos e técnicas. Assim este estudo foi feito em livros, revistas e artigos eletrônicos.

Vergara (2011, p. 38), por analogia “a revisão integrativa é a atividade de localização e consulta de fontes diversas de informação escrita orientada pelo objetivo explicito de coletar materiais mais genéricos ou mais específicos a respeito de um tema”. Os resultados foram analisados a luz da bibliografia existente em contraponto a opinião da autora.

Alcance

Esse estudo contribui para uma maior compreensão das causas e dos fatores que influenciam as dificuldades de ensino e aprendizagem. Isso pode envolver aspectos cognitivos, emocionais, sociais, pedagógicos e estruturais no ambiente educacional.

População e Amostra

População 240 alunos do 7º ano das Escolas Estadual Waldemiro Lustoza e São Luiz de Gonzaga e 5 Amostra, 20% dos alunos (60), sendo 30 alunos por escola e 100% dos professores (6); 3 por escola.

A amostragem teórica exige a construção de teorias interpretativas a partir dosdados emergentes e a seleção de uma nova amostra para examinar e elaborar a teoria. É a principal estratégia para a abordagem teórica fundamentada, que foi usadanesta investigação qualitativa que requer interpretação.

O saldo relativo dependeu da questão da pesquisa e do estilo escolhido de análise e interpretação dos dados. É importante reconhecer que a essência da abordagem qualitativa é que ela é naturalista – estudando pessoas reais em ambientes naturais e não em isolamento artificial.

Portanto, a amostragem levou em consideração não apenas as característicasdos indivíduos, mas também as influências temporais, espaciais e situacionais, ou seja, o contexto do estudo, levando o pesquisador há considerar o quadro mais amplo:esses indivíduos expressariam uma opinião diferente se fosse entrevistado na próxima semana ou no próximo mês? Será que eles se sentiriam diferentes se fossementrevistados em casa ou no escola? Devo estudar quando estão sob estresse ou relaxados?

Não existe uma resposta correta para essas perguntas, assim como não há uma maneira perfeita de amostrar, mas a influência que esses fatores podem ter na confiabilidade dos resultados deve ser reconhecida.

Técnica e Instrmentos de recolha de dados

O instrumento será o questionário e a técnica de coleta de dados será da entrevista individual que não se caracteriza por um diálogo comum com uso de um questionário escrito (também conhecido como questionário de autoadministração) que é uma ferramenta de coleta de dados na qual são apresentadas perguntas escritas que devem ser respondidas pelos respondentes de forma escrita.

Um questionário escrito pode ser administrado de diferentes maneiras, como por exemplo: Enviar questionários por correio com instruções claras sobre como responder às perguntas e pedir respostas por correio; Reunir todos ou parte dos entrevistados em um local ao mesmo tempo, dando instruções orais ou escritas e permitiendo que os respondentes crenchan os questionários; ou entregar questionários.

Neste caso especifico, em função da pandemia, os questionários foram distribuídos via WhatsApp justamente para facilitar as respostas em tempo hábil. A pesquisa será de campo. Para Cruz Neto (2006, p. 87) é a pesquisa de campo, através da qual se realiza uma busca minuciosa, para averiguar a realidade de um caso concreto junto à testemunha ou à pessoa contatada; investigação e estudo minucioso e sistemático com o fim de estabelecer fatos ou princípios relativos aos casos concretos e, em especial, junto às pessoas contatadas e às testemunhas; várias dessas pesquisas de campo são realizadas em consultórios, gabinetes ou salas nos quais aquelas pessoas são levadas para serem entrevistadas (DA MATTA, 2018).

Diante dos fatos a pesquisa será uma pesquisa social estratégica (MINAYO, 2007, p. 26), sobre a inclusão de autistas na escola regular com uso da musicoterapia em um novo contexto sociocultural como agente facilitador ou não de dificuldades e sofrimentos. Segundo Minayo (2007, p. 27), a pesquisa estratégica teria a “finalidade de lançar luz sobre determinados aspectos da realidade”, mesmo não prevendo soluções práticas para os mesmos, sendo “particularmente adequada às investigações sobre educação”. Serão usados discursos e representações socialmente construídas como material indispensável à investigação e o viver de professores e pais de alunos, assim, será privilegiado a fala, o vivido, o sentido e o simbolizado pelo indivíduo que sente necessidade de explicar suas experiências (JOVCHELOVITCH, 2015, p. 45).

Adotando, portanto, a Metodologia Qualitativa, como estratégia de abordagem, por ser ela capaz de “incorporar o significado e a intencionalidade como fundamentais às construções humanas, contidas em seus atos, relações e estruturas sociais” (MINAYO, 2007, p. 10). O fato de esta metodologia permitir a proximidade entre entrevistado e entrevistador, será decisório em nossa escolha, visto que, “autor e intérprete fazem parte do mesmo contexto”.

Ou seja, o investigador também é morador da cidade escolhida para o estudo como os sujeitos a serem investigados, além de possuir outras características em comum com seus entrevistados.

Sendo assim, caberá ao investigador tratar cuidadosamente de suas impressões e interpretações acerca do material colhido, partindo da proposta de Velho apud Da Matta (2018, p. 45), de que “o processo de estranhar o familiar torna-se possível quando somos capazes de confrontar intelectualmente, e mesmo emocionalmente, diferentes versões e interpretações existentes a respeito de fatos, situações”.

O investigador, então, vai se esforçar em transformar o “Exótico em familiar eo Familiar em exótico”, Desta forma, através da observação direta realizada no próprio ambiente de trabalho dos entrevistados, pode-se captar a estrutura, procedimentos e pensamentos imperantes na escola, marcados por uma nova política administrativa, comentada e questionada, tanto pelos profissionais, quanto pelos alunos.

A entrevista identificará a eficácia do uso de tecnologias em sala de aula com a aplicação de dois questionários elaborados para coletar evidências de professores e alunos sobre suas experiências e conhecimentos em TIC e usar no ensino, suas atitudes em relação ao valor das TICs para o ensino e aprendizado, o treinamento que receberam e, quando relevante, seus motivos para ampliar o uso das TIC.

Assim, a entrevista semiestruturada teria a qualidade de elucidar de maneira mais ampla possível às interrogações que o pesquisador pretende investigar no trabalho de campo m(CRUZ NETO, 2006, p. 57).

Procedimentos de Recolha de Dados

A entrevista foi realizada por etapas. Na primeira etapa foram ouvidos ao entrevistados da Escola Estadual Waldemiro Lustoza. Na segundo etapa, os entrevistados da Escola Estadual São Luiz de Gonzaga.

Técnica de Análise de Dados

A análise interativa dos dados da pesquisa serão rastreados e apresentados em forma de gráficos dinâmicos para análise de dados em geral, originado pelo estatístico John Tukey citado por Moraes (2014).

Uma excelente revisão das origens dessas idéias é apresentada na coleção deartigos editados por Cleveland e McGill (1988) apud Moraes (2014), e discussões precoces de métodos específicos são contidas nos artigo.

4 MARCO ANÁLITICO

Segundo Lakatos e Marconi (2013, p. 176), a análise dos resultados é entendida como sendo: “é a fase da pesquisa realizada com intuito de recolher informações prévias sobre o campo de interesse. O levantamento de dados é feito de duas maneiras: pesquisa de campo (ou de fontes primárias) e pesquisa bibliográfica (ou de fontes secundárias).

4.1 ORGANIZAÇÃO DOS RESULTADOS

A seguir serão descritos todos os resultados da pesquisa

4.1.1 Escola Estadual Waldemiro Lustos

A evolução resultante do dinamismo social força a instituição escolar a se adaptar às constantes mudanças para responder às demandas sociais e educacionais emergentes e foi isso que ocorreu com a Escola Estadual Waldemiro Lustoza que sofreu rupturas, e a principal é que a escola não perdeu seu prestígio na área, tanto em suas dimensões temporais quanto espaciais.

As necessidades do sistema educacional são frequentemente debatidas; Assim, Aos professores nesta situação em que a crise escolar está sendo discutida continuamente, muitas vezes se veem confusos, com um certo sentimento de solidãoe, às vezes, com a ideia de que o que é ensinado na escola vai contra o que é vivenciado fora dela.

A verdade é que a Escola Estadual Waldemiro Lustoza, como todas as escolas públicas, precisa de mudanças profundas, como não poderia ser de outra forma, em uma sociedade que mudou e está mudando muito. Portanto, vê-se que é necessária uma mudança qualitativa na maneira de entender o ensino.

A Escola Estadual Waldemiro Lustoza tem um problema e, para sua solução, exige, entre outras coisas,um papel ativo dos professores antes dela e explorar os laços de relação entre escolae meio ambiente.

Pode-se inferir disso tudo que a evolução social excede a adaptabilidade do sistema educacional. Assim, embora a gestão da escola tenha conhecimento dos problemas que afetam a instituição escolar: baixa motivação (por parte dos alunos e do corpo docente), conflitos escolares mal resolvidos, absenteísmo, normalização da violência, multiplicidade de funções dos professores.

Esses problemas fizeram com que os diferentes profissionais enfrentassem seu trabalho todos os dias, imaginando qual seria o verdadeiro significado de seu trabalho na sala de aula, sem saber até que ponto seu grau de envolvimento poderia ocorrer. na resolução de problemas socioeducativos e, em muitos casos, não se sentindo capaz de enfrentá-los.

A escola, ocupada em cumprir os requisitos curriculares estabelecidos pelo sistema, não tem tempo, nem meios, nem profissionais preparados para lidar com esses problemas.

Se os problemas estruturais do sistema educacional já são preocupantes, aqueles que afetam diretamente o risco de exclusão na escola não são menos preocupantes, o que geralmente é determinado pela inadequada adaptação da instituição escolar, pela baixa dotação de recursos ou pelo baixo envolvimento dos alunos. professores, podendo encontrar um clima de desespero ao abordar o problema relacionado ao comportamento perturbador, falta de motivação, absentismoe agressividade.

Os professores estão vivendo o dia-a-dia dos alunos, conhecem os problemas, mas em muitas ocasiões eles não têm tempo ou o treinamento mais adequado para enfrentá-los.

Portanto, as necessidades e deficiências dos professores devem ser conhecidas para fornecer soluções.

Desta forma, na pesquisa realizada com os professores de matemática da Escola Estadual Waldemiro Lustoza, duas variáveis foram estudadas: a primeira diz respeito ao perfil do profissional de ensino que atua na disciplina matemática; o segundo quanto a sua didática no sentido de entender as dificuldades dos alunos emrelação a aprendizagem em matemática.

Perfil dos professores da Escola Waldemiro Lustoza

Assim, quando ao sexo dos entrevistados, o gráfico 1, apresenta os resultadosconsolidados

Gráfico 1 – Sexo dos entrevistados na Escola Estadual Waldemiro Lustoza

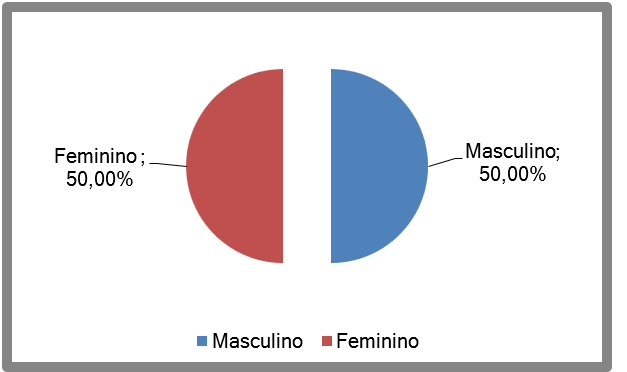
Fonte: Pesquisa de campo (2023)

Como se pode observar no gráfico 1, 50,00% dos professores entrevistados são do sexo masculino e 50,00% do sexo feminino. Isso denota, uma paridade entre os sexos que combina perfeitamente com dados do Censo Demográfico brasileiro de 2010 que aponta uma pequena diferença no número de mulheres (50,80%) contra 49,20% de homens. Essa pequena diferença entre os gênero não faz diferença algumas, mas é diferente quando o tema mercado de trabalho para professores de matemática que tem maioria masculina com cerca de 69,6%, seguindo a lógica do mercado de trabalho no Brasil, conforme aponta Lemos (2016, p. 86):

O mercado de trabalho no Brasil, ainda é um mercado com predominância dosexo masculino. Em 2015, 59,00% da população empregada no mercado formal era do sexo masculino e, apenas 41,00% do sexo feminino, denotando, ainda que, as mulheres apesar dos avanços, ainda não estão emcondições de igualdade com os homens. Também, é importante ressaltar queo IBGE (2015) aponta que as mulheres ainda recebem cerca de 40,00% a menos dos que os homens em atividades correlatas.

No caso, especifico deste estudo, a busca por informações que apresentem números consolidados da distribuição por sexo de profesores de matemática foi uma tarefa bastante hercúlea, por que quase nenhum estudo apresenta essa consolidação. Apenas um estudo do MEC (2012), demostra essa consolidação quando apresenta cerca de apenas 30,00 de mulheres ocupando funções docente em matemática.

Confirma-se, portanto, a afirmativa de Lemos (2016) de que a maioria dos professoresde matemática do ensino fundamental II são do sexo masculino, o que não representaum distorção significativa, até por que, o mercado de trabalho como um todo ainda é predominantemente masculino. Segundo Probst (2016, p. 3):

No Brasil, as mulheres são 41,00% da força de trabalho, mas ocupam somente 24,00% dos cargos de docência na área de exatas, seja em qual nível for. O balanço anual da Gazeta Mercantil revela que a parcela de mulheres nos cargos executivos das 300 maiores empresas brasileiras subiude 8,00%, em 1990, para 13,00%, em 2000. No geral, entretanto, as mulheresbrasileiras recebem, em média, o correspondente a 71,00% do salário dos homens. Essa diferença é mais patente nas funções menos qualificadas. No topo, elas quase alcançam os homens. Os estudos mostram que no universodo trabalho as mulheres são ainda preferidas para as funções de rotina. De cada dez pessoas afetadas pelas lesões por esforço repetitivo (LER), oito sãomulheres.

Como se pode observar, nas palavras de Probst (2016), o mercado de trabalho, ainda é bastante caracterizado pela presença masculina, destacando-se que 41,00% é ocupado por mulheres e 59,00% por homens.

Desta forma, a presença masculina no mercado de trabalho docente de matemática no ensino fundamental II é muito forte,ainda, não obedecendo à proporção populacional levantada no último Censo do IBGE (2010) que apontou 51,00% de mulheres e 49,00 de homens.

Quando presença de mulheres na docência de matemática em um estudo substancial de Barbosa (2016) são apresentados dados que reforçam a ideia de que a docência de matemática é um campo eminentemente masculino, Barbosa (2016, p.709), quando o autor apresenta o depoimento de uma professora de matemática que faz referência ao preconceito de uma menina estudar matemática dizendo ““Quando eu comecei, eles achavam que menino aprendia melhor matemática do que menina. Eu até falei para minha mãe: Então eu sou uma aberração da natureza, né? Porque sou mulher e gosto de matemática”.

Assim fica evidente que a própria concepção original e social de que pessoas do sexo feminino não nasceram para estudar ciências exatas e que essa é uma atividade masculina, que levou a professora entrevistada por Barbosa (2016) a questionar sua própria normalidade.

Gráfico 2 – Idade dos entrevistados na Escola Estadual Waldemiro Lustoza

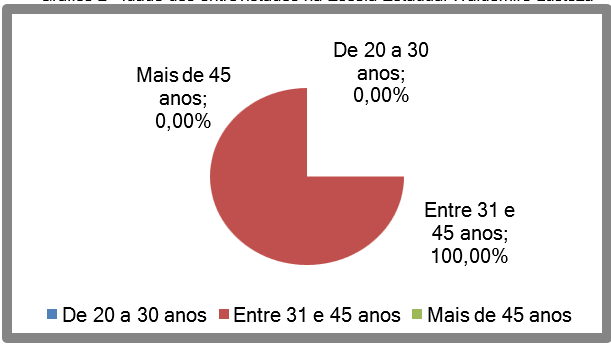
Fonte: Pesquisa de campo (2023)

Na questão da idade (Gráfico 2), 100,00% dos professores entrevistaos na Escola Estadual Waldemiro Lustoza estão na Faixa etaria entre 31 e 45 anos de idade, o que denota certa maturidade. Normalmente, a distribuição etária (por idade) de uma população é feita em três faixas: Jovens (até 19 anos); adultos (de 20 até 59) anos; Idosos ou terceira idade (de 60 anos em diante). No mundo atual os países podem ser classificados como jovens- quando têm mais de 50,00% da população na faixa etária jovem, ou como maduros se têm mais de 50,00% de adultos.

Ferreira (2018) explica que os países jovens são aqueles nos quais as taxas de natalidade e de mortalidade são mais elevadas e, consequentemente, é menor a média de vida dos habitantes.

Os países maduros são os que possuem menores índices de natalidade e de mortalidade, apresentando uma média de vida mais elevada. Entretanto, ressalta-se que existem países que não são classificados nem como jovens tampouco como maduros. Este é o caso do Brasil que se encontra em fase de transição para maturidade.

Com intuito de tornar mais concreta essas afirmações, Ferreira (2018) apresenta no quadro 3, alguns exemplos de países que são classificados como (jovem, em transição e maduro).

Quadro 2 – Distribuição etária da população em alguns países (em %)

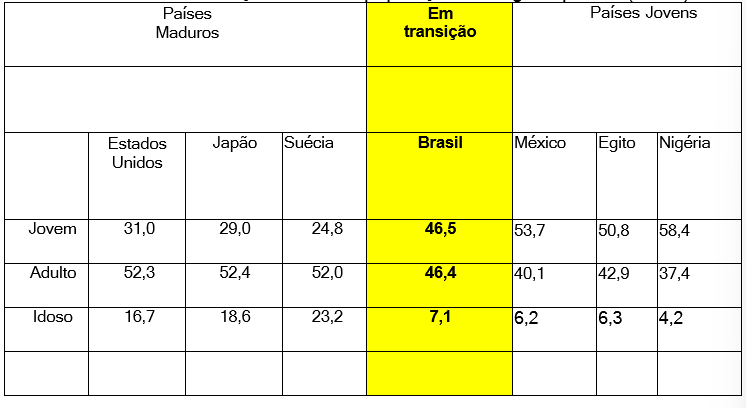
Fonte: FERREIRA (2018) Adaptado da ONU (Organização das Nações Unidas – 2017).

Como se observa no quadro 3 países como Japão, Estados Unidos e Suécia têm predominância de adultos e idosos, o que denota um problema de ordem econômico-previdenciário. Ou seja, cada vez mais, o número de contribuintes do seguro social é menor, causando déficit orçamentário.

Em todos os países do chamado Primeiro Mundo existe um Estado assistencialista. Todavia, a sua origem encontra-se na chamada socialdemocracia3, que prevalece ou prevaleceu durante décadas em alguns países – como a Alemanha, Suécia, Dinamarca, Inglaterra e outros -, e acabou influenciando os demais Estados das nações capitalistas desenvolvidas.

Mas, o grande problema do Estado do Bem-Estar Social está concentrado exatamente no orçamento crescente para atender as necessidades da população beneficiária, principalmente a quantidade crescente de idosos, que necessitam mantero nível de seus ganhos quando se aposentam; precisam de um sistema de saúde eficiente etc., e, como a população de idosos é crescente nos países desenvolvidos e, a população contribuinte está se estagnado, o orçamento cresce, necessitando de aumento de impostos para evitar o déficit das contas públicas. Lopes (2013, p. 81) citao exemplo da Suécia:

Na Suécia, o país que levou mais longe o Welfare State, os gastos públicos aumentaram de 31,00% do Produto Nacional Bruto (PNB) em 1980 para o pico de 67,00% em 2002 – a mais alta proporção de qualquer país capitalista.Só que já em 2006, estes gastos tinham diminuído para 61,00%, havendo uma tendência de queda maior devido às políticas de privatização e diminuição dos impostos e dos gastos públicos. Ou seja, o Estado diminui sua atuação, o que causou uma grande reação da População. Isso ocorreu, em toda a Europa e, vem se intensificando, com a população reagindo ferozmente, com protestos imensos.

O Brasil é um país de transição para a maturidade, exatamente como apontou os dados da pesquisa com os professores da Escola Estadual Waldemiro Lustoza. Sua população aos poucos está envelhecendo, resultado do declínio da mortalidadee da natalidade, com um aumento da faixa etária superior a 60 anos e uma diminuição relativa da faixa jovem, de pessoas com menos de 20 anos. Nos anos 1970, a estrutura da população brasileira era de um país jovem; já em 1991 era a de um país em transição e, já nos anos 2000 o Brasil está muito perto de ser um país adulto. As consequências são evidentes e, a sociedade tem cobrado do governo uma ação maior, principalmente a elite capitalista que exige mudanças profundas no seguro social do país, como ocorreu em 2019.

³ A socialdemocracia consiste numa política trabalhista ou numa forma de governo que se caracteriza pela união entre o partido político no poder e os sindicatos de trabalhadores.

Mas essa mudança no seguro social, não diminuiu privilégios; pelo contrário, os manteve como o seguro social de judiciário e do legislativo, além dos militares, que não sofreram nenhuma agrura da propalada reforma da previdência que atacou apenas o Regime Geral, pessoas que ganham até 3,0 salários mínimos e funcionários públicos comuns.

No caso dos professores foi atacado duramente a questão da idade mínima e da peculiaridade o seguro social para professores do sexo feminino. Koraly (2017, p. 167), ao analisar a proposta de reforma da previdência instituída pelo governo Temer foi taxativo em afirma que essa não considerou dados demográficos substanciais queo sistema neoliberal impõe determinantes como:

Alguns estudiosos consideram negativa para a economia de um país a predominância da faixa etária jovem em sua população total. Segundo eles, a elevada proporção de jovens constituiria um peso para os adultos, que teriam que sustentá-los. Essa tarefa, porém, não poderia ser bem cumprida em virtude da baixa produtividade dos adultos, já que nesses países a industrialização e a mecanização do campo são escassas. Em consequência, haveria necessidade de uma boa parte dos jovens trabalharem, prejudicando assim seus estudos. sós costuma ser considerado um círculo vicioso, pois esses jovens, ao se tornarem adultos, terão baixa especialização, não podendo, portanto, sustentar as demais faixas etárias (jovens e velhos).

Se com os jovens acontece isso, um país adulto sofre do mesmo problema, pois, ao contrário do que ocorre nos países subdesenvolvidos e de elevadas taxas de natalidade e mortalidade, nos quais há um número excessivo de jovens em relação aos adultos (que, teoricamente, são os que trabalham e mantêm os demais), nos países industrializados e com baixas taxas de natalidade e mortalidade, o problema demográfico mais sério é o envelhecimento da população.

Assim a presença substancial de adultos na docência de matemática no ensino fundamental II, na Escola Estadual Waldemiro Lustoza acaba por se transformar em algo bastante positivo, pois são certamente pessoas que já alcançaram a maturidade e estão prontas para lidar com os problemas de aprendizagem.

Com relação ao tempo de atuação o Gráfico 3 resume os dados colhidos:

Gráfico 3 – Tempo de formação dos professores que atuam na Escola Estadual Waldemiro Lustoza

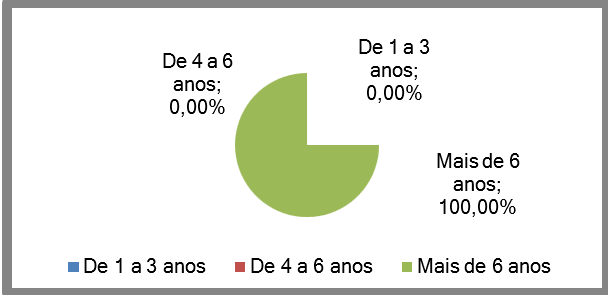
Fonte: Pesquisa de campo (2023)

Com relação ao tempo de formação dos professores de matemática que atuam na Escola Estadual Waldemiro Lustoza, 100,00% deles já estão formados há mais de 6 anos. Isso se coaduna perfeitamente com o acréscimo de vagas oferecidas no curossuperiores do Brasil pós Lei de Diretrizes e Bases da Educação Nacional – LDB nº 9.394/1996.

No Estado do Amazonas, até o ano 2000, os cursos de licenciatura em matemática era um exclusividade da Universidade Federal do Amazonas – UFAM< que possuia muitas limitações de vagas, principalmente para atender a demanda do interior do Amazonas. A partir do ano 2000, com a implementação da Universidade do Estado do Amazonas – UEA, esse acréscimo do número de vagas foi exponencial para a realidade da época. Mas, não se podem esquecer o aspecto político em funçãodos aspectos técnicos, que devem exigir de quem planeja a visão da totalidade sociale da totalidade histórica, considerado como domínio privilegiado das ciências.

Desta forma, a proposta da interdisciplinaridade fez uma análise histórica do processo de formação de professores no Amazonas, observando que ela só passa a existir de forma mais sistemática a partir da década de 1960, com a efetivação da Universidade Federal do Amazonas e, intensificada a partir da década de 1980, relatando que antes desses períodos a preparação para a docência era incipiente no Amazonas, notadamente no interior do Estado.

Mas, é importante ressaltar o que diz a Secretaria Municipal de Educação de São Paulo (1990, p. 27) apud Lima (2015, p. 133), em um trabalho intitulado “Uma revisão da educação do educador” que observa que o processo de formação de professores no Brasil obedeceu duas correntes específicas: europeia, adotada pela Universidade de São Paulo, e a norte-americana, introduzida no Instituto Tecnológicoda Aeronáutica (ITA) de São José dos Campos, na Universidade Federal de Viçosa(MG) e na Universidade Federal do Rio de Janeiro.

Neste percebe-se que a política de formação de professores foi integrada napolítica nacional geral de desenvolvimento, que com seus princípios, objetivos e instrumentos de ação, dão racionalidade ao ato de educar. A universidade cabe participar com eficiência no todo do processo, respondendo ativamente às necessidades que lhe cabe atender. Nessa medida, a universidade faz parte do amplo processo em que o Estado vai intervir. Ou seja, o Estado vem em socorro do sistema liberal-burguês, mantendo em suas universidades os recursos suficientes para a preparação de quadros que serão absorvidos pelo sistema.

Então ao se encarregar da preparação desse efetivo especializado, o Estado desobriga o sistema produtivo desses custeios, socializando-os na medida em que os assumem as expensas dos tributos (fonte natural dos recursos do Estado). É uma forma de auxiliar diretamente o processo de acumulação. Logo, não é apenas capitalfísico e social que o Estado garante no processo de acumulação, facilitando a tarefa de expansão do capital. O Estado age igualmente na formação e na acumulação do novo capital – o capital humano -, socializando os custos de sua formação e especialização.

Esse processo se solidificou pelas políticas pós 1930, é que o ensino superior sempre representou, para os interesses do Estado uma etapa fundamental na preparação da mão-de-obra qualificada.

A importação de técnicas fundamentais no ideário liberal, seja para a educação, seja para os demais setores da Política Social, corresponde, na verdade, à força indutora da modernização imposta pelo capitalismo mundial e faz parte da lógica inserida nos processos de acumulação transnacionalizada do capital e na divisão internacional do trabalho. Então as reformas procedidas nas legislações nacionais tinham por objetivo central estabelecer os mecanismos de interesse do capital, inclusive com a plena utilização dos instrumentos de comunicação de massa solidificados durante a década de 1940.

Mesmo diante de tal providência, o Estado do Amazonas, a partir do ano 2000 com sua ação de reorientação curricular deveriam estar associada às ações de formação permanente dos educadores. As duas são faces de um mesmo ensino. Durante toda a sua gestão, o secretário Vicente Nogueira manteve a formação continuada dos educadores, tendo como princípios básicos: 1 – o educador é o sujeito de sua prática, cumprindo a ele cria-la e recriá-la; 2 – A formação do educador deveinstrumentalizá-lo para que ele crie e recrie a sua prática através da reflexão sobre o seu conteúdo; 3 – A formação do educador deve ser constante, sistematizada, porquea prática se faz e se refaz; 4 – A prática pedagógica requer a compreensão da própriagênese do conhecimento, ou seja, de como se dá o ato de conhecer; 5 – O programa de formação de educadores é condição para o processo de reorientação curricular daescola; 6 – O programa de formação de educadores tem como eixo básicos: a fisionomia da escola que se quer, enquanto horizonte da nova proposta pedagógica; a necessidade de suprir elementos de formação básica aos educadores, nas diferentes áreas do conhecimento humano; A apropriação pelos educadores, dos avanços científico-tecnológicos do conhecimento humano, que possam contribuir paraa qualidade da escola que ser quer.

São múltiplas as modalidade de formação permanente. Todavia, a proposta básica de formação buscou garantir o princípio ação/reflexão/ação, quer dizer, os educadores partiam da discussão da sua prática, expressavam seus pressupostos teóricos, aprofundavam a avançavam seus fundamentos, reconstruindo então sua prática, na perspectiva da educação transformadora.

O trabalho central de formação foi realizado nos grupos de formação. Esse trabalho já se encontra relatado quando a seus resultados em um trabalho da própria Universidade do Estado do Amazonas do ano de 2008.

O grupo de formação ofereceu ao educador momentos de troca, nos quais foivalorizado o se social, afetivo e cognitivo. Assim, pois, resgatou-se a identidade pessoal e profissional do educador ao mesmo tempo em que se lhe ofereceu a oportunidade de encontrar-se a sim mesmo no grupo e fora dele. Os temas que emergiram da discussão foram estudados na perspectiva da construção coletiva do conhecimento. Buscou-se a socialização do heterogêneo, seu confronto e a possiblidade de romperem posturas cristalizadas. Observação, registro, reflexão, síntese, avaliação e elaboração de planos foram instrumentos metodológicos do grupo de formação.

No final de 2008, 80,00% dos municípios do Amazonas, já tinham seus grupos de formação permanente, com a participação de 75,00% de todos os educadores das redes municipal e estadual de educação. Paralelo esse processo de aprimoramento dos professores, A Universidade do Estado do Amazonas – UEA, criou também cursos de formação de novos professores, para o atendimento da demanda crescente por este tipo de profissional no interior do Estado do Amazonas, tão carente, de profissionais gabaritados, basta verificar que até o ano 2000, somente 35,00%, segundo dados da própria Secretaria de Educação do Estado do Amazonas, dos professores, possuíam curso superior.

Gráfico 4 – Escolas em que atual os professores entrevistados na Escola Estadual Waldemiro Lustoza

Fonte: Pesquisa de campo (2023)

O Gráfico 4 aponta que 50,00% dos professores entrevistados na Escola Estadual Waldemiro Lustoza atuam em duas redes de ensino (50,00% respectivamente). Ou seja, trabalham tanto na esfera estadual quanto na esfera municipal. Isso denota que os professores precisam trabalhar em duas frentes em função de que não conseguem se sustentar trabalhando somente em uma rede de ensino como seria o ideal.

Didática

No início dos anos 1970, a Teoria das Situações Didáticas (TSD) foi uma das primeiras, ao que parece, a indicar a necessidade de uma abordagem científica específica para os problemas do ensino e aprendizagem da matemática.

Nesse sentido, pode-se dizer que ela realizou uma revolução copernicana no campo da educação matemática. Ela propões uma metodologia que começa a questionar o conhecimento matemático, como é implicitamente assumido nas instituições de ensino: o que é geometria, o que é estatística, o que é números decimais, o que está contando, o que é álgebra etc. etc.

Em seguida, propões modelos epistemológicos específicos de conhecimento matemático –As situações– que devem ser testadas experimentalmente: uma noção matemática só pode ser analisada na medida em que aparece como solução para uma situação. Este é o princípio metodológico fundamental do TSD: um conhecimentomatemático é representado por uma situação que envolve problemas que podem serresolvidos da melhor maneira possível usando esse conhecimento.

Assim, apareceu um novo modelo geral de matemática como uma alternativa aos conceitualistas mais comumente usados – explícita ou explicitamente – no ensino de matemática. Seguindo o TSD, a matemática é descrita em termos de situações e consiste principalmente em lidar com problemas em um sentido amplo.

Com base nestes princípios foi indagados aos professores que trabalham com matemática na Escola Estadual Waldemiro Lustoza o seguinte questionamento: Comoo professor de matemática deve direcionar o aprendizado do seu aluno nas aulas de matemática? Os entrevistados responderam:

Ensinar matemática não é considerado como ensinar ideias, noções ou conceitos matemáticos, mas como ensinar e aprender uma atividade humana situada, realizada em instituições concretas. Além disso, uma situação inclui a razão de ser ou racional que dá sentido à atividade matemática realizada (ENTREVISTADO PROFESSOR 1).

Ensinar matemática contém restrições institucionais que fornecem e limitama aplicação do conhecimento matemático correspondente. Portanto, o ensinode matemática muda as antigas questões centrais do ensino de matemática: Como os alunos aprendem matemática? e o que podemos fazer para melhorar o aprendizado deles? Quais são as condições necessárias para uma situação implementar o conhecimento matemático específico que ela define? E, “Como as situações podem ser projetadas e seu desenvolvimento gerenciado em uma determinada instituição educacional? (ENTREVISTADOPROFESSOR 2),

Assim, a opinião dos entrevistados levou a uma mudança nas noções usadas para estudar os processos de aprendizagem e ensino e, além disso, no modo particular de questionar a realidade educacional. Eles direcionaram os problemas, os modelos utilizados e o sistema a ser estudado, para combater a dificuldades de aprendizagem que o estudo de qualquer fenômeno didático precisa questionar modelos epistemológicos comuns da matemática. Chama-se isso de Programa Epistemológico como o novo paradigma de pesquisa no ensino de matemática, originado por essas suposições que situam a modelagem da atividade matemática no centro do estudo de qualquer fenômeno didático, segundo Gascón (2008).

No segundo questionamento foi perguntando aos professores de matemática que atuam na Escola Estadual Waldemiro Lustoza: Alguns métodos de ensino de matemática são mais eficazes que outros? Por quê? Os entrevistados em sua totalidade responderam que sim e justificaram suas respostas no fato de o uso de metodologias ativas, proporciona um melhor aprendizado.

A aprendizagem ativa passa pelo reconhecimento que esta ocorre apenas quando há compreensão, que se baseia no conhecimento já existente, enfatizando a importância dos sujeitos terem controle da sua própria aprendizagem, não só como sujeitos ativos, mas também desenvolvendo um conjunto de capacidades que lhes permitam predizer o desempenho em diversas tarefas e monitorizar o nível de compreensão (MITRE, et al, 2008).

Este conjunto de atividades (cognitivas ou associativas) de suporte da aprendizagem ativa tem sido estudado e referenciado, depois da aplicação deste conceito como capacidades do aluno gerar seu próprio conhecimento. Para além de tudo, a nova ciência da aprendizagem está a começar a fornecer conhecimento para melhorar significativamente as capacidades das pessoas para se tornarem aprendentes ativos que procuram compreender assuntos e estão melhor preparados para transferir o que aprenderam para novos problemas e novos cenários (GALANTEe BRITO, 2008).

Neste contexto, é fundamental sublinhar a importância de repensar o que se ensina, como é ensinado e como a aprendizagem é avaliada A ênfase na compreensão conduz a uma das principais características do processo de aprendizagem, tal como é concebido atualmente: no sentido mais geral as pessoas constroem novo conhecimento e compreensão do que aprendem com base no que jáconhecem e nas crenças que subjazem (VALENTE, s/d)

Assim a aprendizagem se consubstancia no modelo de metodologia ativa pois tem o sentido no processo de conhecer. Fialho (2011, p. 124) já se referia que o construtivismo é o paradigma mais significativo na investigação em educação e que

apesar da metáfora da construção de estruturas a partir de conhecimentos anteriores, possivelmente formatadas por tarefas específicas ser comum, existem várias formas de entender o construtivismo. Esses princípios se coadunam nas organizações em função de “o conhecimento não é passível de ser recebido quer pelos sentidos ou pela comunicação. O conhecimento é ativamente construído pelo sujeito cognoscitivo”.

No combate as dificuldades de aprendizagem de matemática, ambos os entrevistados resultaram a importância de uma relação muito próxima com seus alunos para que eles tenham certa tranquilidade para continuarem estudando. Trata- se da relação afetiva entre aluo do professor.

O aluno com dificuldades de aprendizagem em matemática, principalmente vaiconstituindo conceitos de simpatia e antipatia, ou seja, do gosto e do não gosto, disso ou daquilo, que estão diretamente ligados aos parceiros (colegas) e seus superiores (profissionais do ensino). Surge aqui a questão da valorização dos sentimentos de inferioridade ou superioridade. Neste estágio se destacam “as relações individuais ea autovalorização”, segundo Angelini (2013, p. 56).

Assim o aluno adquire sentimentos de gosto ou não gosto e esses sentimentos surgem em acordo com o atendimento de seus interesses e valores, ou seja, a simpatia ocorre quando a identificação de interesses e no contrário surge à antipatia. Segundo Angelini (2013, p. 56): “para que haja simpatia é necessário que exista um mínimo de equilíbrio ou enriquecimento mútuo”. Algumas pessoas falam demais, exigindo que todos foquem a escutá-las, outras são dominadoras e outras ainda são egoístas. As trocas afetivas que se estabelecem nessas pessoas, por existirem esforços, são deficitárias e, de maneira geral, não provocam sentimentos de simpatia. Assim, “haverá mais simpatia quanto menos deficitárias foram as trocas afetivas. A antipatia é gerada quanto às trocas afetivas não proporcionam enriquecimento mútuo” (ANGELINI, 2013, p. 56-7).

Quanto a prática de memomrização, os entrevistados foram enfáticos ao admitirem que essa é uma atitude comum, embora eles tentem combate-la a todo custo. Mas trata-se de um sistema cultural que vem desde o inicio dos estudos dos alunos, ou seja, desde a educação infantil e esse procedimento é muito díficl de ser combatido.

Gascón (2008), diz que para combater a memorização se faz necessário a aplicação de um Programa Epistemológico, em que as atividades matemáticas realizadas na escola não podem ser adequadamente interpretadas sem levar em consideração os fenômenos relacionados à reconstrução da matemática nas instituições de ensino.

Precisa-se, portanto, ir ao local onde esses fenômenos iniciam, isto é, as instituições de produção do conhecimento matemático. Essa é a primeira contribuição da teoria da transposição didática. Se querer-se entender (e assim modelar demaneira apropriada) que tipo de atividade matemática é realizada na escola, precisa-se conhecer os outros tipos de atividades matemáticas que motivam e justificam o ensino e a aprendizagem da primeira.

Desta forma, os professores entrevistados na Escola Estadual Waldomiro Lustoza acham que podem ajudar os seus alunos a aprenderem a aprender matemática, justamente por que, segundo eles mesmos disseram, precisam saber as atividades matemática são interpretadas nas diferentes instituições. Assim, os fenômenos didáticos não podem ser separados dos fenômenos relacionados à produção e ao uso da matemática.

Para os professores entrevistados na Escola estadual São Luiz de Gonzaga as atividades matemáticas realizadas na escola são então integradas ao domínio mais amplo do estudo das práticas matemáticas institucionalizadas. O domínio da didática vai além das instituições educacionais para todas as que adotam qualquer tipo de manipulaçãodo conhecimento matemático. Pode-se dizer que a didática da matemática – como hoje é considerada pelo Programa Epistemológico – estuda a cognição matemática no sentido das condições que tornam possível a produção e o desenvolvimento de conhecimentos matemáticos em instituições sociais (GASCÓN, 2008).

Com relação ao uso da criatividade em matematica, os entrevistados foram taxativos em dizer que sim. Entretanto, a novidade criadora, em grande parte, constitui um remanejamento de um conhecimento já existente. É um acréscimo só possível a partir do que se conhece. Copérnico, Darwin, Newton, Einstein e todos os outros cientistas criadores desenvolveram seus trabalhos a partir de pesquisas realizadas por outros cientistas. Muitas vezes as pessoas que propõem a novidade, aquilo que muda o que já existe, não são bem aceitas por seus contemporâneos. A maioria das pessoas prefere a segurança do que se conhece à incerteza do desconhecido. Por isso reagem a novidade: Copérnico foi acusado de blasfemo. Galileu quase foi queimado vivo, Darwin foi perseguido pelo clero. Em muitos casos, as pessoas criadoras só são reconhecidas depois da morte (FERNANDES, 2006).

O pensamento inovador por ser exploratório, por aventurar-se, por buscar o desconhecido, o risco e a incerteza. Já o pensamento não-criador é mais cauteloso,mais metódico, mais organizado, mais conservador. Prefere o que já existe ao novo. A inovação pode manifestar-se em todos os campos e todas as pessoas podem ser criativas, em maior ou menor grau: o cientista que procura uma nova forma de energia;a mãe que inova na educação de seus filhos; o aluno que inventa novas maneiras de aprender mais facilmente matemática; o motorista que percorre um novo caminho para fugir ao congestionamento; o cozinheiro que cria novas receitas culinárias, o compositor que cria uma nova música. O processo da inovação é único e complexo, mas, para fins deste trabalho, pode-se identificar no ato criador cinco (5) fases: primeira apreensão, preparação, incubação, iluminação e verificação.

Nas escolas de ensino fundamental, os obstáculos à criatividade e a inovação são a disciplina e a ordem exagerada, em prejuízo da iniciativa individual e da espontaneidade; o excesso de importância atribuída à distinção entre os sexos, etc. No ensino médio, a valorização de comportamentos convencionais e atitudes com base em regras, em prejuízo das manisfestações de sensibilidade, e o excesso de exigências formais na apresentação de trabalhos, são alguns dos fatores que prejudicam a criatividade. No ensino superior, enfatiza-se a aquisição de conhecimentos já acumulados, a obrigatoriedade de leituras, currículos rigorosos, etc.,em detrimentos da criatividade. Agora com o advento das monografias, este formalismo está cada vez mais exagerado, pois regras são mais importantes do que a capacidade criativa do aluno (FERNANDES, 2006).

Outra variável identificada como fonte das dificuldades dos alunos na aprendizagem matemática esta relacionada, segundos os professores entrevistados na Escola Estadual Waldomiro Lustoza. Para eles, a história dos alunos com a matemática transforma isso em um aversão a disciplina. Para combater essa história e tentar criar um novo momento histórico dos alunos com a matematica, os professores entrevistados Consideram que qualquer problema didático contém algumas atividades matemáticas que estão sendo produzidas, ensinadas, aprendidase praticadas. Mesmo que essas atividades matemáticas ocorram em uma instituição concreta (geralmente educacional), sua forma de existência e evolução dependem principalmente de restrições educacionais relacionadas ao processo de transposição didática.

Esse processo, apontado pela primeira vez por Chevallard (1985), atua sobre as mudanças necessárias que um corpo de conhecimentos e seus usos precisam receber para serem aprendidos na escola. Ele introduz uma distinção entre: (1) conhecimento matemático original ou acadêmico, como é produzido por matemáticos ou outros produtores; (2) conhecimento a ser ensinado oficialmente prescrito pelo currículo; (3) conhecimento como é realmente ensinado pelos professores em suas salas de aula e (4) conhecimento como é realmente aprendido pelos alunos. Ao serem indagados sobre se o ensino deve enfatizar os conceitos matemáticos ou como esses conceitos são aplicados no mundo real, os profesores entrevistados na Escola Estadual Waldomiro Lustoza disseram que sim, por quê, no contexto de um ambiente de ensino que se torna cada vez mais instável e imprevisível, dada à vertiginosa alteração de demandas sociais e estimulações tecnológicas, o primeiro alerta para a sobrevivência é bem claro: “nada é mais perigoso do que o sucesso de ontem”. (TOFFLER, 1990, p. 14).

O fundamento da aprendizagem ativa é a cultura da inovação. Todas as instituições têm cultura. Melhor dizendo, todas as organizações vivem dento de uma determinada cultura. A cultura abrange a maneira de gestão (agir, pensar e sentir) de uma instituição. Maneira de agir que pode ter aspectos comuns e aspectos diferentes em relação à maneira de agir de outros instituições. A forma de organização social de uma instituição, portanto, também faz parte de sua cultura. Assim cultura é a herança que o grupo social transmite a seus membros através da aprendizagem e daconvivência social (SOARES, 2011).

4.1.2 Os alunos da Escola Waldemiro Lustosa

Os alunos da Escola Estadual Waldemiro Lustoza são alunos que residem próximo da escola ou, em sua grande maioria no bairro da Compensa, onde a escola está localizada. Com relação ao gênero dos alunos entrevistados na Escola Municpal São Pedro:

Gráfico 5 – Sexo dos alunos entrevistados na Escola Estadual Waldemiro Lustoza

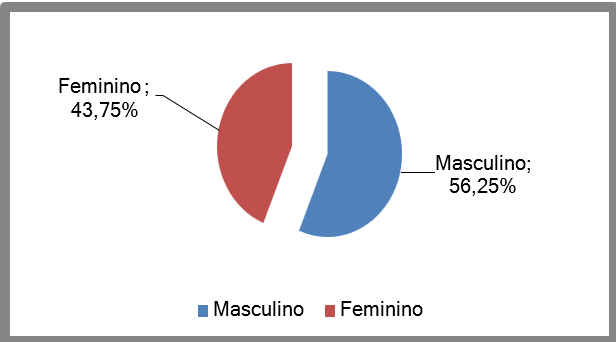
Fonte: Pesquisa de campo por google classroom (2020)

O gráfico 5 aponta 56,25% dos alunos da Escola Estadual Waldemiro Lustoza são do sexo masculino e 43,75% são do sexo feminino. Esse resultado se coaduna perfeitamente com os números apresentados no Censo Escolar (2018) que dizia que 53,00% dos alunos Ensino Fundamental era do sexo masculino e 47,00% do sexo feminino. A diferença apresentada na pesquisa em voga não é significante.

Gráfico 6 – Idade dos alunos entrevistados na Escola Estadual Waldomiro Lustoza

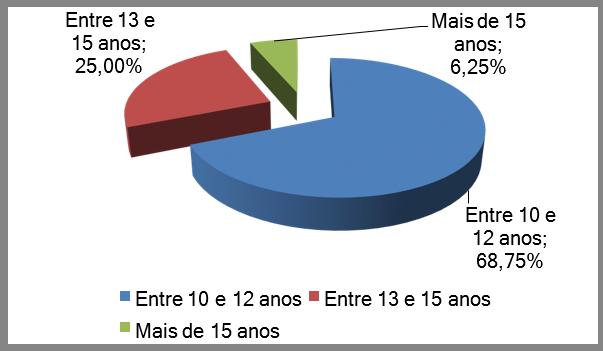
Fonte: Pesquisa de campo (2023)

Com relação a idade (Gráfico 6) percebe-se claramente que 68,75% estão na idade correta na 7º ano do ensino fundamental II. Enquanto 31,25% estão fora da idade para o 7º ano do ensino fundamental II, sendo que, 25,00% possuem entre 13 e 15 anos de idade e 6,25% possuem mais de 15 anos.

Esse fator acontecem por dois motivos: reprovação ou abandono. O Brasil apresenta, de forma agravada, algumas características próprias de países em desenvolvimento, entre as quais as enormes desigualdades na distribuição da renda e as imensas deficiências no sistema educacional. Constata-se, deste modo, que esses dois problemas estão obviamente associados. Não é possível, hoje em dia, aumentar substancialmente a renda de adultos sem instrução, nem conseguir educar adequadamente crianças cujas famílias vivem à beira da miséria. Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE, 2018), o Brasil conta hoje com mais de 60,0 milhões de alunos nos ensinos fundamental e médio.

Esse dado seria animador se o quadro geral não fosse bem diferente: as escolas públicas, onde estão matriculados 89% dos alunos, são de baixa qualidade. Sabe-se que o sucesso que muitos países vêm tendo no que se refere à educação de seu povo deve-se a muitos fatores, entre eles uma política que concede a educação como prioridade para o seu desenvolvimento. Isso sem dúvida eleva os índices de reprovação e abandono, por que os alunos precisam ajudar suas famílias no sustentoda casa e na maioria das vezes não possuem nenhum tipo de ajuda familiar nos estudos (LIMA, 2015).

1. O ensino de Matemática segundo os alunos da Escola Estadua Waldemiro Lustoza

Levar em conta o processo de ensino da matemática significa que o estudo de qualquer problema didático precisa adotar um ponto de vista particular (modelo) sobreas práticas matemáticas envolvidas. Por exemplo, qual é esse conteúdo que estar-seconsiderando? Para que serve? Existe algo em matemática acadêmica? De que maneira? Em que práticas? Como se tornou um conhecimento a ser ensinado? Em que práticas matemáticas escolares está (ou poderia ser) incluída? Que tipo de restrições isso impõe ao desenvolvimento das práticas de alunos e professores?

Com base nestes pressupostos se indagou aos alunos da Escola Estadual Waldemiro Lustoza: você acredita que a didática dos professores ajuda no seu desenvolvimento e na sua aprendizagem em matemática? Por que?

Gráfico 7 – Ajuda da didática no desenvolvimento da aprendizagem dos alunos entrevistados na Escola Estadual Waldomiro Lustoza

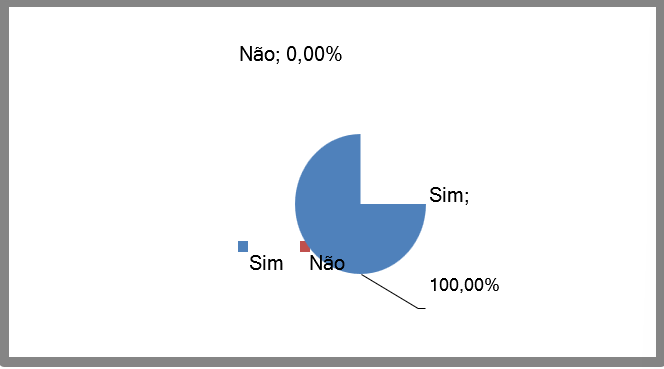
Fonte: Pesquisa de campo (2023)

Assim, 100,00% dos alunos foram taxativos informando que a didática é fundamental para a aprendizagem, Nas respostas dos por ques eles acham isso, ficou latente que a didática destaca a relatividade institucional do conhecimento e situa problemas didáticos em nível institucional, além das características individuais dos sujeitos das instituições.

Sua principal consequência é que a minoria da análise de qualquer problema didático não pode ser limitada à consideração de como os alunos aprendem (e os professores ensinam) matemática.

Deve incluir todas as etapas do processo de transposição didática, incluindo dados provenientes de cada uma das instituições envolvidas como base empírica. Nesse sentido, podemos dizer que os fenômenos de transposição didática estão no cerne de qualquer problema didático.

Gráfico 8 – Uso de tecnologia nas atividades de matemática

Fonte: Pesquisa de campo (2023)

Com relação ao uso de tecnologia nas aulas de matemática, 100,00% dos alunos entrevistados disseram que essse uso é fundamental, pis vive-se atualmente a era da informação e com ela nada prescinde deste uso. Alguns depoimentos são fundamentais;

Usamos tecnologia em tudo, por quê não nas aulas de matemática (ENTREVISTADO ALUNO 1);

È fundamental que se use tecnologia nas aulas de matemática, pois aprenderemos mais rápido (ENTREVISTADO ALUNO 2);

A tecnologia funciona como ajuda para que possamos resolver os problemas (ENTREVISTADO ALUNO 3);

Acho legal por que em tudo tem tecnologia por que não nas aulas de amatemática (ENTREVISTADO ALUNO 4);

Sem dúvida que é fundamental (ENTREVISTADO ALUNO 5);

Acho muito importante mesmo ((ENTREVISTADO ALUNO 6).

Assim, evidencia-se que o aumento da mídia digital interativa catapultou o professor-interações dos alunos, desde o modelo tradicional da Web 1.0 até um novo mundo interativo pós-Web 2.0 com uso de aplicativos educacionais que fomentam a aprendizagem. Uma tecnologia instrucional a muitos educadores vem sendo discutidafrequentemente na literatura educacional.

Por exemplo, Leron e Hazzan (2008) ofereceram uma comparação abrangentede transferência de conhecimento em curso de matemática via uso de tecnologia versus curso tradicional, descobrindo que os alunos que usaram tecnologia produziram melhor conhecimento e transferam r resultados. Esses resultados foram atribuídos em grande parte ao senso de comunidade encontrado no uso de tecnologia.O uso de equipes virtuais, mesmo além das encontradas foi um aprimoramento pedagógico que possibilitado tecnologias instrucionais.

Por fim se indagou como os alunos julgam o seu desempenho a partir da utilização de novos modelos didáticas apresentadas pelo professor de matemática como julga o seu desempenho após a aplicação do mesmos

Gráfico 9 – Uso de tecnologia nas atividades de matemática

Fonte: Pesquisa de campo por google classroom (2020)

Como se pode perceber o Gráfico 9 apresenta 43,75% dos alunos entrevistados na Escola Estadual Waldemiro Lustoza consideram seu desempnho bom após as mudanças didáticas apresentadas pelos professores; 25,00% acham que seu desempenho foi ótimo; e 31,25% dizem que foi regular. Isso se confirma pela Teoria Antropológica da Didática, Chevallard (1997) que surgiu como uma consequência natural do desenvolvimento da teoria da transposição didática.

Ele afirma que a atividade matemática deve ser interpretada (ou seja, modelada) como uma atividade humana entre outras, em vez de considerá-la apenascomo a construção de um sistema de conceitos, o uso de uma linguagem e/ou um processo cognitivo (no sentido da ciência cognitiva).

Assim o professor debe tomar a atividade matemática institucionalmente concebida como seu principal objeto de pesquisa. Portanto, deve especificar explicitamente que tipo de modelo geral está sendo usado para descrever o conhecimento matemático e as atividades matemáticas, incluindo a produção e difusão do conhecimento matemático.

Em seguida foram aplicados dois testes aos anos da Escola Estadual Waldomiro Lustoza. O primeiro se referia a operação com potencia e o segundo as operações polinominais.

Com relação ao componente curricular frações foi aplicado um teste para verificar o nível de aprendizado. Esse teste foi composto de 10 questões sobre operações com frações do 7º ano do ensino fundamental II. As questões foram divididas em questões fáceis (4 questões), medianas (4 questões) e difíceis (2 questões). Para efeito de avaliação, foi considerada como ‘acerto’, se o aluno acertasse todas as questões; e, ‘errado’ se o aluno errasse pelo menos uma questão. Os resultados estão sintetizados no quadro 4 abaixo:

Quadro 4 – Teste com operações com potencia E. M. Waldemiro Lustoza

Nível	Alunos Escola Estadual Waldemiro Lustoza
Nível	Acertou	Errou
Fácil	29	1
Mediano	26	6
Difícil	2	28

Fonte: Teste aplicado pela autora (2023)

Os resultados dos testes aplicados aos alunos considerandos e níveis de questões (fácil, médio e difícil). No nível fácil 29 alunos acertaram todas as questões e apenas 1 não acertou todas as questões; no nível mediano, 26 alunos acertaram todas questões e 6 erraram pelo menos uma questão; e no nível difícil só 2 alunos acertaram todas as questões; e 28 erraram pelo menos 1 questão. Percebe-se que 93,75% dos alunos dominam as questões fáceis; 62,50% dominam as questões medianas; e, apenas 12,50% dos alunos dominam as questões mais difíceis com relação a operação com frações. Neste sentido conclui-se que o nível de aprendizagem dos alunos neste componente curricular (operações com frações) encontram-se oscilando entre o nível elementar (fácil) e mediano (médio). Nas questões mais complexas uma maioria significativa não conseguiu resolver as questões.

Com relação as operações polinominais, os alunos da Escola Municipal Waldemiro Lustoza foram submetidos a um teste nas mesmas proporções que foram submetidos ao teste de operações com frações. Só que neste segundo teste a distribuição de graus de dificuldades foi: 3 questões fáceis; 4 questões medianas e 3 questões difíceis. O quadro 5 sintetiza os resultados.

Quadro 5 – Teste com operações polinominais E. M. São Pedro

Nível	Alunos Escola Estadual Waldemiro Lustoza
Nível	Acertou	Errou
Fácil	30	0
Mediano	27	3
Difícil	2	28

Fonte: Teste aplicado pelo autora (2023)

Como se pode observar no quadro 5, nas questões fáceis, nenhum aluno Errou qualquer questão; no nível mediano 27 acertaram as 4 questões e, 3 erraram pelo menos 1 questão; no nível difícil, apenas 2 acertaram todas as 3 questões e 28 erraram pelo menos 1 questão. Assim se infere que 100,00% dos alunos dominam questões de operações polinominais no nível elementar; 81,25% dominam questões no nível mediano; e, apenas 12,50% dos alunos dominam questões complexas.

Isso representa que os alunos testados na Escola Estadual Waldemiro Lustozaoscilam entre o nível elementar de conhecimento e o nível mediano, o que pode representar solução de continuidade no ensino, pois já deveriam dominar o nível maiscomplexo destes componentes currrriculares.

Neste sentido faz necessário uma intervenção dos professores de matemática com o objetivo de incentivar a aprendizagem colaborativa que tem sido um modelo pedagógico popular em uma variedades de domínios, com uso de parcerias entre alunos que dominam os componentes curriculares aliados a tecnologia da informação.Pesquisas anteriores sobre esse modelo pedagógico eficazes levaram a diretrizes de design detalhadas, planejamento habilidoso, coordenação e implementação de currículo, pedagogia e nova tecnologia, segundo Ramos (2015).

Apesar de uma crescente acumulação de conhecimento na área, tem havido pouca influência das tecnologia da informação nas aulas de matemática na prática escolar real. Na verdade, alguns estudos mostraram que os alunos que trabalham emum ambiente relatam que aprenderam mais rápido e passaram a dominar certos conhecimentos que detinham somente no nivel elementar.

4.1.3 Escola Estadual São Luiz de Gonzaga

A Escola Estadual São de Gonzaga é É uma escola tradicional na cidade de Manaus, muito respeitada por seus resultados em um passado recente. Sempre se destacou nos eventos em que participou como jogos escolares e desfiles da semana da pátria.

Escola por ser uma estrutura rígida, hierarquizada e centralizada, ou seja, com as características típicas de um órgão da administração público, está localizada na Rua 5 de Setembro, São Raimundo. Manaus – Amazonas – Brasil. A escola possui580 alunos matriculados, segundo o Censo Educacional de 2022.

No entanto, o advento do planejamento estratégico fez com que as lideranças do órgão percebessem a necessidade de flexibilização dessa estrutura rígida, combinando-se a isso o rompimento com aspectos tradicionais da cultura interna, a modificação de processos e a descentralização do poder de decisão.

A Instituição se reveste das características de uma burocracia: extensa departamentalização, regras e regulamentos bastante formalizados, autoridade centralizada (comunicação descendente), tarefas operacionais altamente padronizada (alta especialização), margem estreita de controle e processo decisório que acompanha a cadeia de comando.

As atividades técnico-científicas da Instituição são desempenhadas por uma categoria de servidores e funcionários especializados, com formação secundária e superior, todavia, a operacionalização dos processos internos da escola requer, em grande parte, cargos simples, rotineiros e padronizados.

Combina-se a isso a adesão estrita ao princípio da cadeia de comando: uma linha contínua de autoridade, que se estende do topo da organização até o escalão mais inferior, deixando claro quem se reporta a quem. Isso assegura a existência de uma hierarquia formal de autoridade, em que cada pessoa é controlada e supervisionada por um único superior (unidade de comando).

Estes dois conceitos, observáveis na estrutura organizacional da Instituição, implicam em um terceiro conceito: a margem de controle, ou seja, a quantidade de subordinados que o gestor consegue dirigir com eficácia e eficiência.

Este aspecto permitiu deduzir que a restrita margem de controle torna mais complexa a comunicação vertical na Instituição. Entende-se, assim, que os diversos níveis de hierarquia reduzem a velocidade da tomada de decisões e tendem a isolar a alta administração, fomentando ainda uma supervisão rígida demais, que desencoraja a autonomia, a criatividade e a versatilidade do funcionário.

Com base na pesquisa a missão da organização é: “promover a Educação de excelência, visando à formação do cidadão crítico e autônomo comprometido com o desenvolvimento social, científico e tecnológico do País”.Assim é cristalina a missão da Instituição para seus colaboradores, que trabalham no ato de sua integração compondo as definições da organização, contudopara que a missão se promova leva um tempo e exigirá muito comprometimento de todos os colaboradores.

Visão é o modelo mental de um estado ou situação altamente desejável, de uma realidade futura possível para a organização, (COSTA, 2007). Para Chiavenato (1999) é da imagem que os funcionários de uma organização têm a respeito do que desejam para esta, bem como, suas aspirações e comportamentos condizentes. A visão da organização: “consolidar a escola como uma instituição de educação por excelência no Estado do Amazonas”.

Da mesma forma que foi trabalhada a missão, a organização tem esse comprometimento de trabalhar com seus colaboradores, para que fique claro o propósito da visão, que deve ser conhecida por todos e aplicadas por eles de forma que possam utilizar como ferramenta para a busca dos objetivos daInstituição.

Valores são características, virtudes, qualidades da organização que podem ser objeto da avaliação, como se estivessem em uma escala, como gradação entre avaliações extremas. São atributos realmente importantes para a organização, virtudes que se pretende preservadas e incentivada às quais deve ser dado mérito (COSTA, 2007).

Conforme Chiavenato (2005), a intenção estratégica da organização é constituída por seus propósitos, das competências essenciais para que possa trilhar seu destino e de sua ideologia central que é o conjunto de princípios e valores que dão os limites da ação da organizaçãoDe acordo com a organização os valores são: valorização humana foco no aluno: colocasse as necessidades do aluno como nossa

maior prioridade, flexibilidade e agilidade; responsabilidade e justiça: somos comprometidos com o sucesso de cadatarefa, fazendo melhor o que já é bom; – ética: conduzimos nossos serviços de forma integra. nossa conduta para com alunos, professores e comunidade devem gerar a mais completa credibilidade.

A organização tem trabalhado forte na divulgação com os seus valores com palestras e identificando nos setores com placas informativas explorando dos seus dirigentes e colaboradores para que juntos alcancem o conhecimento desempenho com excelência.

Os princípios são aqueles pontos e tópicos os quais a organização não está disposta a mudar, aconteça o que acontecer (COSTA, 2007). Então o principal princípio é educar com qualidade.

Já quanto aos objetivos e metas afirma Costa (2007, p. 209): objetivos e metas referem-se aos parâmetros-chaves, qualitativos ou quantitativos, que se pretende atingir ou manter um dado momento ou período de tempo futuro estabelecido. Podem ser marcos finais ou intermediários, eles são como as placas de quilometragem nas estradas a servem para indicar se o caminho escolhido está correto e se está sendo percorrido no espaço, no tempo e na forma combinada.

Neste sentido a organização tem como objetivo se tornar uma escola de referência no Estado do Amazonas, mas para isso a organização precisa trabalhar e explorar o desempenho de seus colaboradores. Como meta ela busca sempre melhorar os índices de aprovação para 95% de seu alunado. Seus objetivos e metas estão de acordo com o conceito de Costa (2007), mas havendo a necessidade de melhorar e trabalhar seus colaboradores, no sentido de uma interação constante.

Perfil dos Professores da Escola Estadual São Luiz de Gonzaga

Assim, quando ao sexo dos entrevistados, o gráfico 1, apresenta os resultadosconsolidados

Gráfico 10 – Sexo dos entrevistados na Escola Estadual São Luiz de Gonzaga

Fonte: Pesquisa de campo (2023)

Como se pode observar no gráfico 10, 50,00% dos professores entrevistados na Escola Estadual São Luiz de Gonzaga são do sexo masculino e 50,00% do sexo feminino. Essa constatação seguiu os parêmetros do Censo Demográfico do Brasil de2010 que apontou que 50,80% da população brasileira é composta de mulheres, enquanto que 49,20% é composta de homens. Ramos (2015, p. 133) fala dessa composição com muita propriedade: “No Brasil até o ano de 1990, a prevalencia do sexo masculino nos censos demográficos era uma constante. Isso mudou, com a lógica se invertendo, embora, ainda muito próximas uma da outra”.

O autor faz referencia clara ao fato de que todos os censos (o primeiro foi realizado no ano de 1972) sempre tiveram uma prevalencia do sexo masculino. Mas a partir dos anos de 1990, Isso realidade começou a mudar, com a aproximação do sexo feminino em relação ao sexo masculino, chegando no ano de 2010 a ultrapssar, embora ainda muito próxima uma da outra, Mas sem dúvida que a realidade demográfica de gênero no Brasil mudou.

Gráfico 11 – Idade dos entrevistados na Escola Estadual São Luiz de Gonzaga

Fonte: Pesquisa de campo (2023)

Na questão da idade dos entrevistados na Escola Estadual São Luiz de Gonzaga(Gráfico 11), 100,00% dos professores se localizam na faixa etaria entre 31 e 45 anos de idade, seguindo a mesma premissa da Escola Estadual Waldemiro Lustoza, ou seja, são professores já com maturidade profissional e na vida.

Não resta dúvida que, a maturidade profissional é o determinante da quantidade de energia necessária para as atividades cognitivas e comportamentais no exercício da profissão de profesor. A maturidade acadêmica, definida como a produção de energia necessária para as atividades acadêmicas”, segundo Bozanoglu (2014) requer vários fatores, um dos que se pensa ser a escolha da profissão. As profissões na sociedade moderna permitem que os indivíduos alcancemuma posição e status dentro de seu ambiente, ao mesmo tempo que lhes dá acessoà liberdade financeira, ajudando-os a se realizarem e a darem sentido às suas vidas. Os indivíduos precisam ser eficazes nas decisões de escolher essas atividades importantes de suas vidas.

O principal objetivo da escolha de carreira de profesor como o ponto de viragem na vida de um indivíduo é planejar um futuro satisfatório. Para que os indivíduos possam fazer suas escolhas profissionais, eles devem ter os níveis de maturidade profissional adequados. A maturidade profissional foi definida por Kİng (1989) apud Bozanoglu (2014, p. 234) como a capacidade do indivíduo de escolher uma profissão que seja apropriada e realista para ele.

Quando a profissão de professor foi escolhidade acordo com os interesses, habilidades, valores, expectativas e traços de personalidade de um indivíduo, a saúde espiritual, a vida profissional e pessoal do indivíduo seriam afetadas positivamente; e isso também contribuiria para a qualidadee os padrões de vida do indivíduo.

Indivíduos com níveis adequados de maturidade profissional também devem estar cientes de que, para atingir os objetivos planejados no futuro, são obrigados a ter competência acadêmica. Um indivíduo neste estado de consciência seria capaz de se motivar para o sucesso. Segundo Marzano (2013, p. 144), existe uma relação positiva entre motivação e realização. Se um aluno está motivado para aprender um tópico, então seu desempenho naquele tópico aumentaria. Um aluno com maior desempenho estaria um passo mais perto de sua futura profissão.

Gráfico 12 – Tempo de formação dos professores que atuam na Escola Estadual São Luiz deGonzaga

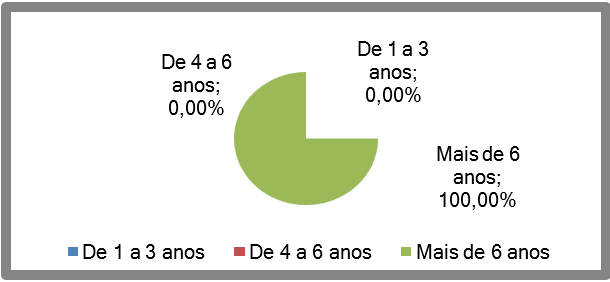
Fonte: Pesquisa de campo (2023)

Seguindo os ditames do que foi identificado na Escola Estadual Waldemiro Lustoza, os professores da Escola Estadual São Luiz de Gonzaga também já possuemmais de 6 anos de formados. Isso é bom, por que como já dito, até o ano de 2000, a responsabilidade na formação de professores de matemática no Estado

do Amazonasera tão somente da UFAM. A partir do ano 2000, com o advento da UEA, essa responsabilidade passou a ser dividida entre a UEA e a UFAM e, a partir do ano de 2008, algunas universidades particulares também começaram a formar professores em todas as áreas, inclusive professores de matemática.

Gráfico 13 – Escolas em que atual os professores entrevistados na Escola Estadual São Luiz de Gonzaga

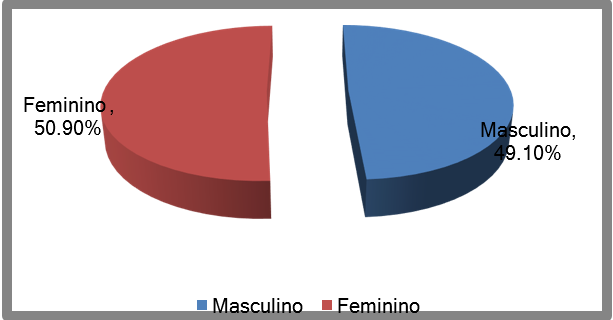
Fonte: Pesquisa de campo (2023)

O Gráfico 13 aponta que 70,00% dos professores entrevistados na Escola o e, apenas 30,00% atual na rede municipal de ensino, ou seja, 100% dos professores entrevistados na Escola Estadual Castela Branco atuam nas duas redes de ensino. Isso é uma constante no magisterio brasileiro, já que os salarios aviltantes, obrgiam os professores a trabalharem em pelo menos dois empregos e as vezes em três, sendo 2 em um rede pública e outro em outra rede pública. Isso acaba por ter influênci diretana qualidade do ensino, conforme aponta Lemos (2016, p. 56): “o fato de terem que trablahr em 3 empregos, transforma sua atuação em rotineira se fazer a diferença, porque está cansado muitas das vezes”.

Didática

Ficou evidente nas entrevistas realizadas com os professores de matemática da Escola Estadual São Luiz de Gonzaga que eles convivem com alunos ativos, capazes de viver em um mundo cheio de conflitos e de resolver problemas complicados. A escola tem uma parte da responsabilidade de educar essas pessoas.

Atualmente os professores não estão mais trabalhando nas condições restritas de um currículo escolar unificado. Oficialmente, eles têm a oportunidade de aplicar sua criatividade ao ensino. Mas o condicionamento ao longo de vários anos, que produziu os professores estereotipados, sobrevive e, portanto, a transformação do sistema educacional prossegue lentamente.

Deixaram bem claro que se necesita de uma mudança fundamental na concepção do trabalho da Escola Estadual São Luiz de Gonzaga. Essa mudança é uma transição do ambiente de estufa (onde o aluno vive em dois mundos quase separados – na escola dentro e fora) para a criação de um clima escolar que não separa o aluno de seu ambiente ou experiências externas da escola.

Essa transição não é realizada sem dificuldades e não é realizada geralmente, mas frequentemente apenas localmente e de forma descoordenada. Para fazer a transição, não basta apenas alterar os documentos pedagógicos, mas é preciso preparar os professores para essas mudanças.

Durante o período em que os alunos estão em contato com a matemática, eles são bombardeados com um enorme número de impulsos diferentes. A quantidade ea intensidade das informações que os alunos enfrentam continuam crescendo. No momento, a principal dificuldade não é a acessibilidade desse conhecimento, mas simo cisalhamento.

O único objetivo geralmente reconhecido da escola hoje em dia é entregar aos alunos o máximo de informações possível, de preferência na forma de conhecimento esquematicamente ordenado. Teoricamente, esse objetivo deveria perder sua posição. Mas a realidade da escola é diferente. É muito mais simples e mais facilmente mensurável para um professor ensinar aos alunos (incluindo futuros professores) habilidades e conhecimentos sem compreensão do que ensiná-los com compreensão,a capacidade de usar seu conhecimento e de ser independente e autoconfiante.

Os alunos da Escola Estadual São Luiz de Gonzaga

Os alunos da Escola Estadual São Luiz de Gonzaga são alunos da Zona Oeste de Manaus em sua grande maioria, moradores do Bairro de São Raimundo e comporta alunos do bairro. Mas também existem alunos dos bairros adjacentes como os bairros

da Glória, Aparecida, Santo Antônio, Compensa, Vila Marinho, Santo Agostinho, Lirio do Vale e Ponta Negra. Mas alguns alunos também pertencem a outros bairros como os bairros da Alvorada, Chapada e Flores, conjuntos Residencias Dom Pedro, Kissia, Ipase, Augusto Montenegro, Conjunto Ajuricaba, Campos Elysios, Manauara, etc.

Gráfico 14 – Sexo dos alunos entrevistados na Escola Estadual São Luiz de Gonzaga

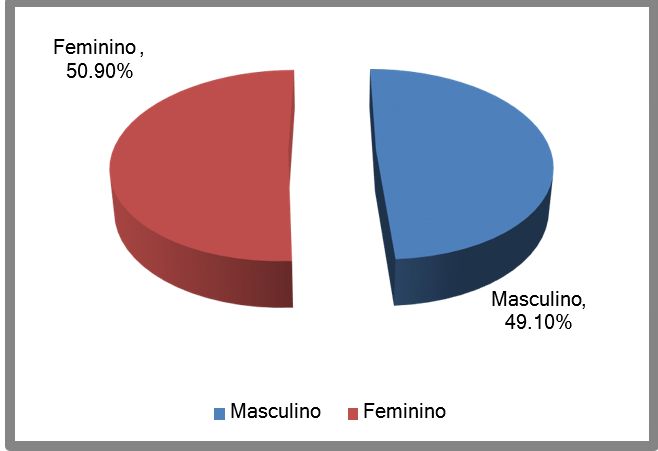
Fonte: Pesquisa de campo (2023)

O gráfico 5 aponta 50,90% dos alunos da Escola Estadual São Luiz de Gonzaga são do sexo feminino e 49,10 são do sexo masculino. Esse resultado está perfeitamente dentro do que o Censo Demográfico de 2010 apntou (50,80% – sexo feminino e, 49,20% – sexo masculino). Já o Censo Educacional de 2018 apontou que 53,00% dos alunos Ensino Fundamental era do sexo masculino e 47,00% do sexo feminino. Desta forma, os números são quase que iguais.

Gráfico 15 – Idade dos alunos entrevistados na Escola Estadual São Luiz de Gonzaga

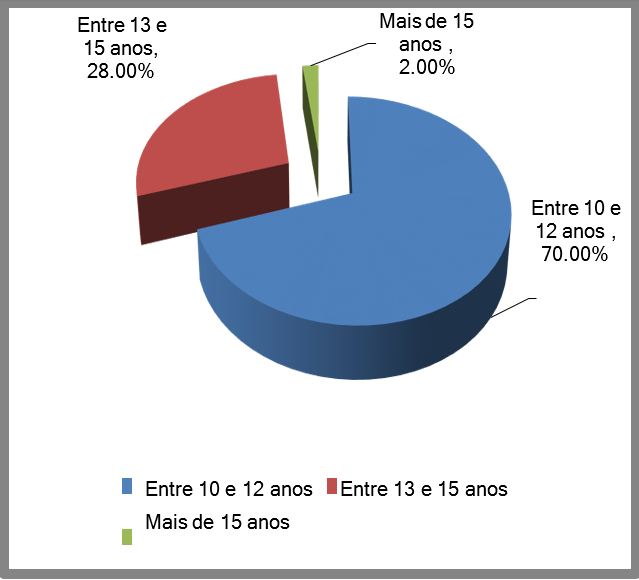
Fonte: Pesquisa de campo (2023)

Com relação a idade (Gráfico 15) os números da Escola Estadual São Luiz de Gonzagas ao praticamente iguais ao da Escola Estadual Waldomiro Lustoza. Percebe-se que 70,00% dos alunos estão na idade certa e, 30,00 não estão na idade certa no 7º ano do Ensino Fundamental II. Os motivos são os mesmos: reprovação em algum momento da vida estudantil e/ou abandono em algum momento também.

O Ensino da matemática segundo os alunos da Escola Estadual São Luiz de Gonzaga.

Gráfico 16 – Ajuda da didática no desenvolvimento da aprendizagem dos alunos entrevistados naEscola Estadual São Luiz de Gonzaga

Fonte: Pesquisa de campo (2023)

Percebe-se que 100,00% dos alunos (Gráfico 16) da Escola Estadual São Luizde Gonzaga disseram que a didática é de suma importancia. A didática é arte de ensinar; o procedimento pelo qual o mundo da experiência e da cultura é transmitido pelo educador ao educando, nas escolas ou em obras especializadas, ou seja, é um conjunto de teorias e técnicas relativas à transmissão do conhecimento. Sobre esta questão conceitual da didática, se posiciona Libâneo (2002, p. 129):

Os enfoques sobre o papel da didática na atividade escolar variam de acordo com as tendências pedagógicas, sendo possível encontrar na prática educacional pelos menos três: o tradicional, o renovado-tecnicista e o sociopolítico. O trabalho refere-se à didática assentada na transmissão cultural, concebendo o aluno como um ser receptivo/passivo, atribuindo um caráter dogmático aos conteúdos e métodos da educação; o renovado- tecnicista corresponde à versão modernizada da escola nova, acentuando o caráter prático-técnico do ensino e, assim, sua neutralidade face às questõessociais; finalmente, o sociopolítico assume uma postura crítica em relação aos dois anteriores, por acentuar a relevância dos determinantes sociais na educação e, assim, as finalidades sociopolíticas da escola.

O autor em voga faz uma ampla análise da didática por meio dessas três tendências pedagógicas, deixando que se perceba que cada uma possui vantagens edesvantagens próprias, mas enfatiza que a “do ponto de vista pedagógico didático, o que se crítica nos enfoques analisados é a separação entre os aspectos material/formal do ensino, ou seja, entre a valorização da transmissão dos conteúdos e o modo de aquisição desses conteúdos” (LIBÂNEO, 2002, p. 132).

Charlot (2004, p. 153) enfatiza que o importante na configuração da didática “éa interação de sujeitos, mediados pelo conhecimento, contextualizados pelas dimensões históricas, política, social e cultural”. Ou seja, é o contexto que dimensiona e dá sentido e significado à interação entre sujeitos, construindo e desconstruindo as subjetividades envolvidas, sejam elas de natureza individual ou coletiva, e, inclusive, de natureza institucional.

Este contexto contemporâneo aponta para uma sociedade da informação, o que significa uma maior intensidade da comunicação e um aumento no ritmo das transformações, e, conseqüentemente, os contextos social, político e cultural têm novas configurações, gerando novas subjetividades e atingindo também o foco mediador da atividade educativa: o conhecimento.

As subjetividades estão imersas em um dinâmico espaço-tempo configurada em rede, onde as informações e a comunicação não têm centro, e, portanto, o professor já não ocupa o centro do processo, e sim, é simplesmente um ator com mais experiência, tendo maiores condições de aprender e, portanto, de coordenar o acesso às informações e articular os processos de comunicação.

A didática precisa, no cotidiano, criar condições para a vivência dos contextos por parte dos alunos e propiciar também a convivência entre os sujeitos. É uma nova pedagogia, que se denomina pedagogia da diferença, a qual se estrutura a partir do diferente na diferença, enfatizando as singularidades, tanto de natureza espaço- temporal como no âmbito das subjetividades.

Libâneo (2002, p. 133) observa com muita clareza e objetividade: “O trabalho formativo, portanto, supõem elementos pedagógico-didáticos como fatores específicos do ensino, sempre socialmente contextualizados; supõe o professor atuando como mediador entre o aluno as matérias, entre um sujeito motivado e interessado no saber e os conteúdos culturais vivos, problematizados no confronto com a realidade social”.

Para Gramsci (1991, p. 132), “compreender a relação sujeito-objeto é compreender como o ser humano se relaciona com as coisas, com a natureza, com avida. Este problema, central em todas as ciências, pode ser compreendido a partir dediferentes abordagens. A dialética pode ser uma delas, principalmente a dialética marxista” que, aparece no pensamento de Karl Marx como uma tentativa de superação da dicotomia, da separação entre o sujeito e o objeto.

A didática não é mais do que isso: um modelo dialético de transmissão do conhecimento. Freire (1996) fala em reconstrução, pois apresenta o sistema se demolindo, em destruição e que, para se fazer educação, para se conscientizar, é preciso lutar contra o atual sistema. Para ele:

O educador, ao repensar a educação, está também repensando a sociedade.Não existe uma igualdade entre política e educação: existe uma identidade. O ato educativo é essencialmente político. O papel do educador é um papel político. Sempre que o educador deixou de “fazer política”, escondido atrás de um pseudo-neutralidade da educação, estava fazendo, com a sua omissão, a política do mais forte, a política da dominação. Não existe educação neutra: ou faz-se uma pedagogia do oprimido ou uma pedagogia contra ele (FREIRE, 1996, p. 67).

Assim, o processo de ensinar (didática) é um processo dinâmico que implica a superação da contradição educador-educando. Uma ação didática limitada à transmissão do conhecimento vira um depósito de ideias. A interação é essencial à própria docência, no sentido original da busca, da procura, de constantes inquietações, de dúvidas. Um professor que transmite sempre os mesmos conteúdossignifica que ele cessou de buscar, instalando-se em verdades prontas, adquiridas, pré-fabricadas. Freire (1996, p. 72) ensina:

A prática educativa progressista que liberta que problematiza, já não pode ser o ato de depositar, ou de narrar, ou de transferir, o de transmitir conhecimentos e valores aos educandos, meros pacientes, à maneira do processo comum. O educador não deve ser apenas o que educa, mas o que enquanto educa é educado, em diálogo com o educando que, ao ser educado, também educa. Ambos se tornam sujeitos do processo em que crescem juntos e em que os argumentos da autoridade já não valem. Em que, para ser-se, funcionalmente, se necessita de estar sendo com as liberdades e não contra elas. De forte cunho político, a tarefa do professor ultrapassava os muros escolares e avançava à sociedade como um todo. Não bastava o conhecimento das ciências, das Artes, da Literatura, das metodologias específicas e das Ciências da Educação, era preciso ter-se um projeto de emancipação social e um saber político/ideológico e, por isso, o educador era também um intelectual orgânico a serviço da mudança das condições materiais e culturais da sociedade da época. O professor poderia assumir uma postura que tornava os conteúdos escolares secundários diante da necessidade de construção de uma compreensão crítica da realidade ou, poderia enfatizar nos conteúdos, sua condição de meio para essa mesma compreensão crítica e emancipadora do mundo em que seus alunos vivem. Eram opções a serem escolhidas.

Neste sentido, a didática desempenha, pois, um papel de suma importância nareprodução das relações sociais. Enquanto atividade mediadora no interior das práticas sociais, a educação concorre para a manutenção ou o questionamento da divisão social do trabalho. Ideologicamente, tanto contribui para a reprodução, quanto para sua problematização, pois a realidade, sendo contraditória, engendra um processo educativo também contraditório.

A atitude paternalista do professor que quer ensinar a verdade, como se ele fosse o dono dela, querendo dar a consciência crítica como se ele fosse o único possuindo, só pode tornar o aluno impotente para o ato pedagógico (didática), para aaquisição dessa consciência crítica.

Gráfico 17 – Uso de tecnologia nas atividades de matemática

Fonte: Pesquisa de campo por google classroom (2020)

Com relação ao uso de tecnologia nas aulas de matemática, 100,00% dos alunos entrevistados na Escola Estadual São Luiz de Gonzagadisseram que esse uso é fundamental, pis vive-se atualmente a era da informação e com ela nada prescinde deste uso.

A necessidade de repensar a educação deste novo contexto é a alavanca que impulsiona a necessária mudança no sentido de, segundo Zaballa (2008, p. 33-34):

Planejar a atuação de uma maneira suficientemente flexível para permitir a adaptação às necessidades dos alunos em todo o processo de ensino/aprendizagem;

Contar com as contribuições e os conhecimentos dos alunos, tanto no início das atividades como durante sua realização, ou seja, os conhecimentos dos alunos são de suma importância na construção do processo ensino- aprendizagem;

Ajudá-los a encontrar sentido no que estão fazendo para que conheçam oque têm que fazer, sintam que podem fazê-lo e que é interessante fazê-lo, ouseja, contextualizar o conhecimento é função do professor;

Estabelecer metas ao alcance dos alunos para que possam ser superadascom o esforço e a ajuda necessários; .

Oferecer ajudas adequadas, no processo de construção do aluno, para os progressos que experimenta e para enfrentar os obstáculos com os quais sedepara;

Promover atividades mental auto estruturante que permita estabelecer o máximo de relações com o novo conteúdo, atribuindo-lhe significado no maiorgrau possível e fomentando os processos de meta cognição que lhe permitam assegurar o controle pessoal sobre os próprios conhecimentos e processos durante a aprendizagem;

Estabelecer um ambiente e determinadas relações presididos pelo respeitomútuo e pelo sentimento de confiança, que promovam a autoestima e o autoconceito;

P romover canais de comunicação que regulem os processos de renegociação, participação e construção;

Potencializar progressivamente a autonomia dos alunos na definição de objetivos, no planejamento das ações que os conduzirão a eles e em sua realização e controle, possibilitando que aprendam a aprender;

Avaliar os alunos conforme suas capacidades e seus esforços, levando em conta o ponto pessoal de partida e o processo através do qual adquirem conhecimento e incentivando a auto avaliação das competências como meiopara favorecer as estratégias de controle e regulação da própria atividade.

Assim, pode dizer que a construção do conhecimento não é um processo unilateral, mas dependente da participação de todos, em uma atitude construtivista onde o professor é aquele que também aprende e o aluno também pode ensinar, independente da modalidade de ensino, presencial ou à distância. 80,00% dos entrevistados disseram que usam o computador e as lousas eletrônicas, além de outros recursos disponíveis com tablets ; os outros 20,00% disseram que não usam nenhuma tecnologia.

Gráfico 18 – São Luiz de Gonzaga – Uso de tecnologia nas atividades de matemática

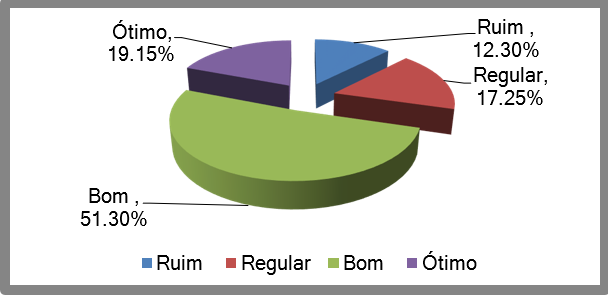
Fonte: Pesquisa de campo (2023)

O São Luiz de Gonzaga apresenta que dos alunos 51,30% dos entrevistados na Escola Estadual São Luiz de Gonzaga acham bom; 19,15%, 17,25% acham regular. E, 12,30% acham ruim. Pode haver uma tendência para ensinar matemática com uso de tecnología informando aos alunos as propriedades da disciplina e, em seguida, apresentar exercícios que mostram que aprenderam os fatos. Tal abordagem pode significar que poucas tentativas são feitas para encorajar os alunos a fazer conexões lógicas e explicar seu raciocínio. Mas o importante é usar a tecnología da informação, ja que esse é um proceso ireversível.

Da mesma forma da Escola Estadual Waldemiro Lustoza, também na Escola Estadual São Luiz de Gonzaga aplicados dois testes. O primeiro se referia a operação com frações e o segundo as operações polinominais.

Quadro 6 – Teste com operações com potencia E. E São Luiz de Gonzaga

Nível	Alunos Escola Estadual Waldomiro Lustoza
Nível	Acertou	Errou
Fácil	30	0
Mediano	22	8
Difícil	1	29

Fonte: Teste aplicado pelo autor (2020)

O quadro 6 apresenta o resultado dos testes com o componente curricular operações com frações na Escola Estadual São Luiz de Gonzaga. No nível fácil 30 alunos acertaram todas as questões e, nenhum errou nenhuma questão; no nível mediano, 22 alunos acertaram todas questões e 8 erraram pelo menos uma questão; e no nível difícil só 1 alunos acertou as duas questões formuladas; e 29 erraram pelo menos 1 das questões formuladas.

Percebe-se que 100,00% dos alunos dominam as questões fáceis; 73,33% dominam as questões medianas; e, apenas 6,25% dos alunos dominam as questões mais difíceis com relação a operação com frações. A conclusão é a mesma da Escola Estadual Waldomiro Lustoza, ou seja, os alunos da escola Estadual Castel Branco em relação ao componente curricular operações com frações, encontram-se oscilando entre o nível elementar (fácil) e mediano (médio). Nas questões mais complexas, apenas 1 aluno conseguiu resolver as duas questões formuladas.

Com relação as operações polinominais, os alunos da Escola Estadual São Luiz de Gonzaga, também foram submetidos a um teste nas mesmas proporções que foram submetidos ao teste de operações com frações e nas mesmas condições da Escola Estadual Waldomiro Lustoza, ou seja, 3 questões fáceis; 4 questões medianas e 3 questões difíceis. O quadro 7 sintetiza os resultados

Quadro 7 – Teste com operações polinominais E. E São Luiz de Gonzaga

Níve l	Alunos Escola Estadual Waldomiro Lustoza
Níve l	Acerto u	Errou
Fácil	28	2
Mediano	27	3
Difícil	1	29

Fonte: Teste aplicado pelo autor (2020)

O quadro 7 sintetiza os resultados do testes aplicados aos alunos da Escola Estadual São Luiz de Gonzaga com relação a operações com polinomios. Nas questões fáceis, 28 alunos acertaram todas as questões e 2 erraram pelo menos 1 questão; no nível mediano 27 acertaram as 4 questões e, 3 erraram pelo menos 1 questão; no nível difícil, apenas 1 acertou todas as 3 questões e 29 erraram pelo menos 1 questão. Assim, 87,50% dominam questões polinominais no nível elementar;81,25% dominam no nível mediano; e apenas 6,25% dominam no nível mais complexo.

Da mesma forma que na Escola Estadual Waldemiro Lustoza, os alunos da Escola Estadual São Luiz de Gonzaga, encontra-se entre o nível elementar e medianonestes componentes curriculares, o que denota a necessidade imediata de intervenção dos professores de matemática para que os alunos não tenham problemas futuramente.

Segundo Ramos (2015), numerosos estudos examinaram os fatores determinantes do desempenho acadêmico em matemática. Esse interesse é impulsionado pela relevância da matemática tanto para a educação formal quanto para a vida cotidiana. No entanto, desde os primeiros anos de educação, muitos alunos enfrentam o fracasso em matemática. Os componentes afetivo-motivacionais dos alunos (ou seja, motivação, crenças de autoeficácia, prazer, ansiedade e utilidade percebida ou valor da matemática) e as estratégias que eles usam para aprender matemática (ou seja, abordagens de aprendizagem) impactam em seu desempenho, independentemente de sua capacidade cognitiva habilidade ou conhecimento prévio.

Ramos (2015) fala que estudos anteriores relatam que os alunos experimentam uma ampla gama de emoções enquanto estão envolvidos em situações de aprendizagem. Consequentemente, os componentes afetivo-motivacionais não se referem simplesmente a gostar ou não gostar da matemática, mas sim a utilidade ou valor percebido da matemática, autoeficácia matemática, motivação intrínseca, ansiedade matemática e prazer. Assim percebe-se claramente nos testes apresentados na Escola Estadual São Luiz de Gonzaga que o problema está diretamente não ligado a questão didática, poisse eles dominam os níveis elementares e medianos, por que não dominam também os níveis complexos? Assim, chega-se a conclusão de que o problema está ligado aoque Ramos (2015) chama de ‘valor’ que é a utilidade percebida que se refere às crenças dos alunos sobre o uso prático e aplicabilidade da matemática atualmente e em relação ao seu futuro, ou seja, estudam somente para pasar, por que nãoconseguem ver valor na matemática.

Essas percepções de alto valor estão associadas à aquisição de novos conhecimentos. Alunos que percebem a matemática como úteis são mais motivados para aprender, praticar, estudar e empregar estratégias de autorregulação chave do que os alunos que percebem a matemática como menos útil. Isso ficou evidente tanto na Escola Estadual Waldemiro Lustoza bem como na Escola Estadual São Luiz de Gonzaga.

5. CONCLUSÃO

O processo de ensino e aprendizagem da Matemática no Ensino Fundamental II enfrenta desafios que são multifacetados, envolvendo fatores pedagógicos, socioculturais e emocionais. Para superá-los, é essencial adotar uma abordagem integrada que promova a aprendizagem significativa, conecte a Matemática com a realidade dos alunos e invista na formação contínua dos professores. A aplicação de práticas inovadoras e inclusivas pode tornar a Matemática mais acessível e interessante, contribuindo para um processo de ensino mais eficaz.

É preciso avaliar o ensino de matemática enquanto espaço de educação. Muitas são as contradições, incoerências e fracassos na sua prática. Acredita-se estar evidente que a escola, pelos resultados que produz, tem falhado em sua função específica. Entre os aspectos político-ideológico e técnico-formal não parece claro que é básico ensinar conhecimento para que o aluno possa gestar cidadania competente. Também não parece estar claro como garantir ao aluno a apropriação do que lhe é imprescindível conhecer.

O processo de uso de recursos tecnológicos segue o princípio básico da intercomunicação no sentido de alavancar esforços para uma construção coletiva que possibilite o restabelecimento dos valores que justifique a importância dos aspectos fundamentais da matemática.

A integração das TIC no ensino da matemática no Ensino Fundamental ii pode ser uma estratégia eficaz para superar muitas das dificuldades enfrentadas. No entanto, para que isso ocorra, é essencial que haja: Formação contínua para professores sobre como integrar tecnologias de forma pedagógica. Disponibilidade de infraestrutura tecnológica adequada nas escolas. Planejamento cuidadoso para que as TIC sejam usadas como complemento às práticas pedagógicas, e não como substituto do ensino presencial.

Dessa forma, o uso das TIC pode não apenas facilitar o aprendizado de matemática, mas também contribuir para o desenvolvimento de habilidades digitais e promover maior engajamento entre os alunos.

Aplicado, em sua grande maioria nas escolas particulares como ação educativa, que incorpora como princípio a pedagogia da interatividade, funciona como um processo de relativização que implica considerar as múltiplas referências que cooperam para a realização de um objetivo. Nisto se encontra com o ensino de matemática nas escolas públicas.

Assim a convencionalidade do ensino de matemática não rege só as relações entre os signos da disciplina e o mundo, mas está presa também a valores sociais, econômicos, ideológicos, políticos religiosos. Dependendo de contextos desse tipo, opróprio sentido da palavra muda.

Desta forma, este estudo, proporcionou uma reflexão e um alerta sobre a indicação clara de que as transformações organizacionais da escola podem causar impactos significativos na cultura educacional sem uma administração planejada desses impactos, e seus reflexos prováveis sobre a produtividade dos alunos. Para os profissionais da educação deve pretender ser um novo componente de ajuda na busca do sucesso escolar porque supõe a adoção de um espírito de pesquisa, justamente porque nem tudo se reduz ao conhecido, ao programado, àquilo que é. Oprocesso de uso de recursos tecnológicos produz o comprometimento com aquilo quese quer algo se torne. No âmbito educacional é fundamental. Com Relação ao desempenho dos alunos após o uso de TIs na sala de aula, ficou evidenciado no trabalho que esses melhoram bastante seja na escola pública ou na particular. As origens dos alunos de comunidades carentes determinam suas histórias de vida, moldando um conceito de moral, de valores, de sua religiosidade, de aspirações, de ascensão social, configurando uma visão do mundo bem próxima, diferenciada, portanto, das pessoas que compõem o comum da sociedade urbana e que estudam na escol particular.

Suas concepções de vida são diferentes devido a fatores determinantes que lhe são peculiares. Suas inteligências estão voltadas para sobrevivência, nos seus cotidianos, e não para o seu questionamento e superação. Suas culturas o impedem de ver além, num horizonte mais amplo, aspectos que lhes dariam uma nova abertura com dimensão diferente de vida.

Tem-se consciência de que o trabalho com o processo de uso de recursos tecnológicos no ensino só se consolida, no âmbito educacional, a partir da prática docente, e, em função desta postura, conduzimos este estudo. As decisões nunca são tomadas unilateralmente, cabendo à totalidade dos profissionais da escola escolher aforma como o fazer educativo se desenvolverá.

Por fim o presente estudo examinou o valor preditivo da aprendizagem dos alunos de forma comparativa nas escolas públicas base na aprendizagem e abordagens profundas e superficiais para aprender sobre o desempenho em matemática em uma amostra de alunos de 7º ano do Ensino Fundamental.

Os resultados obtidos no presente estudo apoiaram parcialmente as previsõesiniciais, com todo o conjunto de variáveis explicando uma pequena, mas significativa quantidade de variação em desempenho em matemática. Embora todas as variáveis estivessem significativamente correlacionadas com o desempenho em matemática, na análise empreendida com aplicação de testes em operações com fraçoes e operações polinominais em 3 níveis de dificuldades (fácil, meidiano e difícil) para a aprendizagem foram preditores estatisticamente significativos. Especificamente, como o prazer dos alunos em matemática aumentou quando percebem que acertaram os problemas dos níveis fácil e mediano. Mas reduziu bastante quando perceberam que erraram no grau díficil nas escolas públicas.

Essas descobertas são consistentes com pesquisas internacionais anteriores realizadas em diferentes estágios educacionais, que relataram o valor preditivosignificativo de variáveis afetivo-motivacionais, como atitudes de aprendizagem,hábitos de aprendiza

6. RECOMENDAÇÕES

O relato expresso neste estudo significa que o ensino de matemática, por mais democrática que seja como a estudada aqui, não tenha problemas, nem mesmo que a totalidade de profissionais esteja trabalhando numa linha dialética – realidade do aluno/planejamento, a ser realizado: certamente a escola ainda está no início de uma jornada, na qual deve acreditar.

No campo educacional, a matemática tem vetor no entendimento de que a educação é tarefa de transformação e, não significa uma postura ingênua no sentido de que somente através da escola a mudança pode ocorrer, mas de que, através dela, com posturas consensuais a respeito do papel político-social dos que nela atuam, estaremos colaborando de forma consciente para a construção de uma escola crítica. É necessário acordar o educador adormecido. É necessário que se tenha claro o papel de educador. São necessários que se assuma responsabilidades de agentes da mudança.

Do momento em que esses canais passam a funcionar e a comunidade escolar começa a atingir seus objetivos, decorre um processo de retroalimentação, modificando sua concepção de mundo até então estritamente empírica. Se o aluno conserva sua visão de mundo é porque não está havendo a ação indispensável à retroalimentação.

Da mesma forma, há falha no processo se o indivíduo abandona sua concepção de mundo. Isto indica que houve seccionamento/ruptura, desgarrando- se da sua estrutura antiga. Se, entretanto, há uma modificação na sua concepção de mundo é porque o processo está funcionando, havendo, por conseguinte, produtividade provocada pela eficiência do sistema montado.

Torna-se necessário controlar e avaliar a ação do sistema, possibilitando sua constante retroalimentação, ou seja, o entendimento do conceito de educação permanente, que, neste processo circular cumulativo, modificará a própria matriz social do aluno. O círculo de ação vai-se ampliando, refletindo-se no meio em que ela vive o que provocará profundas e alterações no seu contesto sociocultural, garantindoassim a dinâmica de um processo de mudança que venha melhorar a configuração do mundo de comunidades care

REFERÊNCIAS

ABRAMI, P. C. Compreender e promover o uso de aprendizagem complexa usando a tecnologia. Educacional Pesquisa e avaliação, 7, 113-136, 2017.

ABRANTES, P. O trabalho de projeto e a relação dos alunos com a Matemática: A experiência do projeto MAT789 (tese de doutoramento, Universidade de Lisboa). Lisboa: APM, 1994.

ABRANTES, P., CUNHA LEAL, L. e PONTE, J. P. Investigar para aprender matemática: Textos selecionados (pp. 1-4). Lisboa: Projeto PMT e APM, 1998.

ALARCÃO, I. Escola reflexiva e nova racionalidade. Artigo, 2001. Disponível em

ALMEIDA, L. S. Cognição e aprendizagem: como a sua aproximação conceptual pode favorecer o desempenho cognitivo e a realização escolar. Psicologia:Teoria, Investigação e Prática, I (1), 17-32, 2016.

ALMOULOUD, A. S. Fundamentos da didática da matemática. 2ª ed. São Paulo: Editora UFPR, 2017.

ALVARAES, M. K. A. Efeitos dos sistemas de álgebra computacional em atitudes em relação à matemática. Hacettepe University Journal of Education, 35, 13-26, 2016.

ALVES, L.; BRITO, M. O Ambiente MOODLE como Apoio ao Ensino Presencial. Actas do 12º Congresso Internacional da Associação Brasileira de Educação a Distância–ABED, 2015.

AMAZONAS. Universidade do Estado Amazonas – UEA. Formação de professores no Estado do Amazonas. Manaus: UEA, 2008.

ANGELINI, N. Ensino Fundamental: programa de aprendizagem Belo Horizonte: Programa de Assistência Brasileiro-Americano, 2013.

ANTUNES, A. As redes municipais de educação diante da pandemia. Fiocruz, 2020. Rio de Janeiro: Disponível em https://portal.fiocruz.br/noticia/redes- municipais- de-educacao-diante-da-pandemia. Acesso em 25 de mar de 2023

ARIFA, F. N. Desafios na implementação do estudo da política doméstica durante a emergência da Covid-19 Informações Breve: Um Breve Estudo de Questões Reais e Estratégicas, XII (7 / I), 6, 2020.

ARRUDA, E. P. Educação remota emergencial: elementos para políticas públicas na educação brasileira em tempos de Covid-19. Em Rede, v. 7, n. 1, p. 257-275, 2020

.AYDIN, E. O uso de computadores na educação matemática: uma mudança de paradigma da instrução assistida por computador para a programação do aluno. The Online Journal of Educational Technology, 4 (2), 27-34, 2015. Disponível em http://www.tojet.net/volumes/v4i2.pdf Acesso em 14 de mar de 2023.

AZEVEDO, J. Educação Tecnológica. Porto Alegre: Asa, 2011.

BACHELARD, G. La formation de l’esprit scientifique: contribution à unepsychanalyse de la connaissance objective. 36ª ed. Paris: Vrin, 2018.

BAFFI, M. A. T. O planejamento em educação: revisando conceitos para mudar concepções e práticas. Artigo. 2002. Disponível em http://ww.aedb.br/faculdades/ped/conteudo/gestao_escolar/O_planejamento_em_Ed ucacao_revisando_conceitos.pdf Acesso em 23 de mar de 2023.

BAKI, A. Educação matemática com TICs: da teoria à prática. 4 ed. São Paulo: Harf Publicações Educacionais, 2018.

BANDURA, A. Autoeficácia: O exercício de controle. Belo Horizonte: Freeman, 2007.

BANDURA, A. Auto-eficácia: Rumo a uma teoria unificadora da mudança comportamental. Psychological Review, 84 (2), 191-215.

BARBOSA, L. A. L; Masculinidades, feminilidades e educação matemática: análise de gênero sob ótica discursiva de docentes matemáticos. Educ. Pesqui., São Paulo, v. 42, n. 3, p. 697-712, jul./set. 2016.

BAROODY, A. J. Problemas, resolução e comunicação. 2 ed. São Paulo: Hucitec, 2013.

BASKIN, C.; WILLIAMS, M. Integração das TIC nas escolas: Onde estamos agora e o que vem a seguir? Australasian Journal of Educational Technology, 22 (4), 455- 473, 2006.

BAUMAN, Z. Modernidade e ambivalência na educação na Pandemia da COVID- 19. São Paulo: Polity Press, 2020. By country. Disponível em:

<https://www.coe.int/en/web/cepej/compilation-comments>. Acesso em 25 de mar de2023.

BELLONI, M. L. O que é mídia e educação. 2 ed. Campinas, v.29. n. 104, 2018.

BERBEL, N. A. N. As metodologias ativas e a promoção da autonomia de estudantes. Semina: Ciências Sociais e Humanas, Londrina, v. 32, n. 1, p. 25-40, jan./jun. 2011.

BETA, F. G. Pesquisa sobre as barreiras à adoção das TIC pelos professores. Disponível em http://partners.becta.org.uk/page_documents/research/barriers.pdf. Acesso em 21 de jan de 2023.

BETINI, G. A. A construção do projeto político-pedagógico da escola. Artigo. EDUC@ação – Rev. Ped. – UNIPINHAL – Esp. Sto. Do Pinhal – SP, v. 01, n. 03,

jan./dez.2005. Disponível em http://www.escolapadrereus.com.br/portal/JP/JP_texto_01.pdf Acesso em 23 de jan de 2023.

BIGGE, M. L. Teorias da aprendizagem para professores. São Paulo: Editora Pedagógica e Universitária, 2017.

BIZELLI, J. L.; HEREDERO, E. S. Educação e inovação: o desafio da Escola Brasileira. Revista Tendéncias Pedagogicas (Universidad Autónoma de Madrid), v. 28, p. 55-66, 2016.

BLAYE, A. Aprendizagem matemática São Paulo: Rodrigues Alves, 2014.

BOISOT, M. H. Espaço de informação. A Framework for Learning in Organizations, Institutions and Culture (Londres, Routledge), 1995.

BOLTER, D. J. Espaço para escrever: o computador, o hipertexto e a história da escrita. New Jersey: Lawrence Earlbaum, 1991.

BORBA, M. C.; PENTEADO, M. G. Informática e educação matemática. Belo Horizonte: Autêntica, 2011.

BORBA, M. de C; SILVA, R. S. R. da; GADANIDIS, G. Fases das tecnologias digitais em Educação Matemática: sala de aula e internet em movimento. São Paulo: Autêntica Editora, 2020.

BOZANOGLU, I. Escala de motivação acadêmica: desenvolvimento, confiabilidade, validade. Jornal da Faculdade de Ciências da Educação da Universidade de São Paulo, 37 (2), 83-98, 20, 2014.

BRANSFORD, J. D., et al. Anchored instruction: Why we need it and how technology can help. In D. Nix & R. Sprio (eds), Cognition, education and multimedia. Tradução Renato Machado de Lima. LHillsdale, NJ: Erlbaum Associates. 2009.

BRASIL. Censo Demográfico 2010. Brasília: IBGE, 2010. Disponível em http://www.ibge.gov.br Acesso em 30 de jan de 2023.

BRASIL. Estatística docente do Brasil. Brasília: MEC, 2012. Disponivel em http://www.mec.gov.br Acesso em 30 de jan de 2023.

BRASIL. Instituto Brasileiro de Geografia e Estatística – IBGE. Censo Demográfico. Brasília: IBGE, 2010. Disponível em http://www.ibge.gov.br Acesso em 30 de jan de 2023.

BRASIL. Instituto Brasileiro de Geografia e Estatística – IBGE. Pesquisa Nacional de Amostra de Domicílios. Brasília: IBGE, 2018. Disponível em http://www.ibge.gov.br Acesso em 30 de jan de 2023.

BROUSSEAU, G. Fundamentos e Métodos da Didáctica da Matemática. In: BRUN,

J. Didática das Matemáticas. Tradução de: Maria José Figueiredo. Lisboa: Instituto Piaget, 2013.

CALHEIROS, D. DA S. Utilização das tecnologias da informação e comunicação no contexto da Web 2.0 na prática docente. Dissertação de mestrado. Universidade Federal de Alagoas, 2009. Versão digitalizada.

CANAVARRO, A. P. Concepções e práticas de professores de matemática: três estudos de caso. 2013 Dissertações (Mestrado em Educação) – Departamento de Educação da Faculdade de Ciências, Universidade de Lisboa, Lisboa, 2014.

CANNONE, G.; ROBAYNA, M. S.; MEDINA, M. M. P. O ensino da matemática e as novas Tecnologias da Informação e da Comunicação (TIC): estudo de caso de um grupo professores de ensino fundamental, Ciclo I, em Tenerife – Espanha. Zetetiké, v. 16, n. 30, p. 107-138, 2008. Disponível em:<http://www.fae.unicamp.br/revista/index.php/zetetike/article/view/2517>. Acesso em: 25 de mar de 2023.

CARLSON, S.; FIRPO, J. Integrando computadores ao ensino: descobertas de um programa de 3 anos em 20 países em desenvolvimento. Em L. R Vandervert,

L. V. Shavinina & R. A. Cornell (Eds.), Educação cibernética: O futuro do Ensino à Distância. Larchmont, NY: Mary Ann Liebert, Inc, 85-114, 2011

CARVALHO, M. S. Tecnologia educacional. São Paulo: Pioneira, 2008.

CASTRO, K. Interpretações dos alunos de um ambiente de geometria dinâmica. São Paulo: Atlas, 2010.

CERCONI, F. B. M.; MARTINS, M. A. Recursos tecnológicos no ensino de matemática: considerações sobre três modalidades. In: IV Simpósio Nacional de Ciência e Tecnologia. Ponta Grossa, Paraná, 27 a 29 de novembro de 1014. Disponível em http://sinect.com.br/anais2014/anais2014/artigos/ensino-de- matematica/01409358155.pdf, acesso em 11 de mar de 2023

CHARLOT, B. A mistificação pedagógica. 4ª. ed. Rio de Janeiro: Zahar, 2004. CHEN, P.; MAO, L.; NASSIS, G. P.; HARMER, P.; AINSWORTH, B. E.; LI, F.

Coronavirus disease (COVID-19): The need to maintain regular physical activity

while taking precautions. J Sport Health Sci. 2020;9:103-4.

CHEVALLARD, Y . Do conhecimento acadêmico ao conhecimento. Campinas-SP: Papirus, 1985.

CHEVALLARD, Y . Familiar e problemático, a figura do professor, Pesquisa em Didática da Matemática 17 (3), 17–54, 1997.

CHIAVENATO, I. Gestão de Pessoas. Rio de Janeiro: Elsevier, 1999.CHIAVENATO,

I. Gestão de Pessoas. Rio de Janeiro: Elsevier, 2005.

COELHO, T. O que é indústria cultural. 9 ed. São Paulo: Brasiliense, 2011.

COFFEY, A.; ATKINSON, P. Dando sentido aos dados qualitativos. Thousand Oaks: Sage Publications, 1996.

COMPARATO, F. K. O princípio da igualdade e a escola. Artigo. Fundação Carlos Chagas, n. 104, 1998. Disponível em http://publicacoes.fcc.org.br/ojs/index.php/cp/article/view/716 Acesso em 23 de março de 2023.

COSCARELLI, C. V. Alfabetização e letramento digital. In: COSCARELLI, Carla V.; RIBEIRO, Ana. E. (Org.). Letramento digital: aspectos sociais e possibilidades pedagógicas. Belo Horizonte: Autêntica, 2015

COSTA, E. A. Gestão estratégica da Instituição que temos para a Instituição que queremos. 2º ed. São Paulo: Saraiva, 2007.

COSTA, P.; CLARKE, S.; JENKINS, I. As habilidades de tecnologia da informação e comunicação dos alunos e seu uso durante o treinamento de professores. Revista de Tecnologia da Informação para a Formação de Professores. 9 (1), 9-22, 2010. .

CROOK, C. Aprendizagem como prática cultural. IN: M.K. Lea & K. Nicoll (Eds.), Aprendizado Distribuído: Abordagens Sociais e Culturais da Prática (pp. 152-169). Londres: RoutledgeFalmer, 2014.

CRUZ NETO, O. Trabalho de campo como descoberta e criação. In: M. C. de S. Minayo (org). Pesquisa social: teoria, método e criatividade. Petrópolis: Vozes, 2006.

CUBAN, L. KIRKPATRICK, H, & PECK, C. Tecnologias de alto acesso e baixo uso em salas de aula do ensino médio: Explicando um aparente paradoxo. Americna Educational Research Journal, 38, 4, 813-834, 2019.

CULP, K.M., HONEY, M. E MANDINACH, E. Uma retrospectiva em vinte anos de educação política de tecnologia. Artigo, 2013. Disponivel em. http://www.nationaledtechplan.org/participate/ 20years.pdf Acesso em 1 de abr de 2023.

CUTRIM, R. dos. S.; LIMA, F. R. Educação e tecnologias: inter-relações entre teoria e práticas pedagógicas no processo de ensino e aprendizagem no ensino fundamental. Cad. Ed. Tec. Soc., Inhumas, v. 8, n.2, p. 148-165, 2015.

D’AMBRÓSIO, Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.

DA MATTA, R. Fundamentos da pesquisa social. 3 ed. Porto Alegre: Artes Médicas, 2018.

DARIDO DA CUNHA, M.; BIZELLI, J. L. Inovações tecnológicas e contexto escolar: reflexões necessárias. Revista Ibero-Americanade Estudos em Educação,v. 10, p. 50-66, 2015. Disponível em:<http://seer.fclar.unesp.br/iberoamericana/article/view/7772/5350>.Acesso em: 10 de março de 2023.

DAVID, L. COV CHEN, P.; MAO, L.; NASSIS, G. P.; HARMER, P.; AINSWORTH, B.

E.; LI, F. Coronavirus disease (COVID-19): The need to maintain regular physical activity while taking precautions. J Sport Health Sci. 2020;9:103-4.

DAVIS, A. Aprendizagem matemática. São Paulo: Key Stage, 1994.DAVIS, A.

DAVIS, F. Um modelo de aceitação de tecnologia para testar empiricamente novos sistemas de informação do usuário final: teoria e resultados. Tese de doutorado, Sloan School of Management, MassachusettsInstitute of Technology, 1986.

DAVIS, P. J. HERSH, R. A experiência matemática. Lisboa: Gradiva,1991.

DE PAULA, J. B.. FREITAS, D. B. de S. TIC’s na educação nacional: avanços e retrocessso. São Paulo: Campus, 2012.

DEMO P. Educação e qualidade. Campinas, Papirus,1994.

DRENT, M.; MEELISSEN, M. Quais fatores obstruem ou estimulam os educadores de professores a usar TIC de forma inovadora? Computadores e Educação, vol.51, no.1, pp. 187-199, 2008.

DURKHEIM, e. Sociologia. São Paulo: Contexto, 2008.

EARLE, R.S. A integração da tecnologia instrucional na educação pública: promessas e desafios. ET Magazine, vol. 42, no. 1, pp. 5-13, 2012.

ERNEST, P. O impacto das crenças no ensino de matemática. São Paulo: Summus, 2015.

FENICHEL, O. Resistência: um conceito psicológico aplicado na sociedade. São Paulo: Summus, 2000.

FENNEMA, E.; SHERMAN, J. A. Escalas de Atitudes em Matemática Fennema- Sherman: Instrumentos projetados para medir as atitudes em relação à aprendizagem da matemática por homens e mulheres. Catálogo de documentos selecionados em psicologia, 6 (1), 31-38, 2016.

FERNANDES, M. da C. V. A inserção da mulher docência de matemática: uma questão de gênero. Dissertação apresenta ao Programa de Pós-Graduação em Educação da Universidade Federal da Paraíba para obtenção do titulo de Mestre. João Pessoa: UFPB, 2006. Versão digitalizada.

FERREIRA, A. O mercado de trabalho. Artigo. 2008. Disponível em Disponível em http://www.portaldoenvelhecimento.org.br Acesso em 30 de jan de 2023.

FERREIRA, Ao. Dicionário Básico da Língua Portuguesa. 6 ed. Rio de Janeiro: Nova Fronteira, 2015.

FIALHO. F. A. P. Introdução às Ciências da Cognição. Florianópolis: Insular. 2011.

FIORENTINI, D.; SOUZA JR. A.; MELO, G. A. Saberes docentes: um desafio para acadêmicos e práticos. In: GERALDI, C. M. G.; FIORENTINI, D.. PEREIRA, E. M. (Orgs). Cartografias do Trabalho Docente: professor(a)-pesquisador(a), p. 307-35, Campinas, ALB e Mercado de Letras, 2018.

FLORES, A. Aprendendo e ensinando com tecnologia. Teaching Children Mathematics, 308-310, 2012.

FONSECA, H. Os processos matemáticos e o discurso em atividades de investigação na sala de aula. (Tese de mestrado, Universidade de Lisboa). Lisboa: APM, 2000.

FONSECA, M. O projeto político-pedagógico e o plano de desenvolvimento da escola: duas concepções antagônicas de gestão escolar. Artigo. Cad. Cedes, Campinas, v. 23, n. 61, p. 302-318, dezembro 2003. Disponível em http://www.cedes.unicamp.br Acesso em 30 de jan de 2023.

FORBES, D. A.; KING, K. M.; KUSHNER, K. E.; LETOURNEAU, N. L.; MYRICK, A.

F.; PROFETTO-MCGRATH, J. Evidência garantida na pesquisa qualitativa. Journal of Advanced Nursing, 29, 2009.

FREIRE, P. Pedagogia do oprimido. Petrópolis: Vozes, 1996.

FREITAS, C. et. al. Tecnologias de informação e comunicação na aprendizagem. São Paulo: Moderna, 2017.

FREITAS, L. C. Organização do trabalho pedagógico. Palestra proferida no V11 Seminário Internacional de Alfabetização e Educação. Novo Hamburgo, agosto de 1991 (mimeo).ANDIN, Luís Armando. Projeto político-pedagógico: construção coletiva do rumo da escola. Arti. s/d. Disponível em zonaws.com/academia.edu.documents/20175695/6_gandin.pdf?AWSAccessKeyId= AKIAJ56TQJRTWSMTNPEA&Expires=1473950356&Signature=bixznTqp09xDi4%2 F3u2TEaIt%2BFYE%3D&response-content-disposition=inline%3B filename%3DProjeto_Politico-Pedagogico_construcao_c.pdf Acesso em 10 de abr de 2023.

FREITAS, P. F.; ANDRADE, A. A hora da ação. Revista Timaster, São Paulo, 26 ago. 2016. Disponível em: http://www.revistamaster.com.br Acesso em 30 de jan de 2023.

FREUDENTHAL, H. Fenomenologia. São Paulo: Saraiva, 2013.

GADOTTI, M. Projeto Político Pedagógico: modelo de gestão participativa. Petrópolis: Vozes, 1996.

GALANTE. A. C.; BRITO, J. L. N. e S. Aplicação da tecnologia de sistemas de suporte à decisão no planejamento urbano municipal: uma proposta para o município de Macaé. Revista de Sistemas de Informação nº. 01 Jan./Jun. 2008.

GALINDO, D.; MORAES, V. As percepções dos alunos sobre o suporte

relacionado às TIC em estágios de ensino. Journal of Computer Assisted Learning. 17, 396-408, 2011.

GASCÓN, J .Evolução da didática das matemáticas como disciplina científica. São Paulo: Ática, 2008.

GIL, A. C Método e técnicas de pesquisa. São Paulo: Summus, 2010.

GRAMSCI, A. A concepção dialética da história. Rio de Janeiro: Civilização, 1991.

HALE, G. Hazyspace: para re-compreender o usuário, British Journal of Educational Technology, 29 (2), 185-186, 2008.

HOFFMANN, J. Avaliação Mediadora: uma prática em construção da pré-escola à Universidade. 10 ed., Porto Alegre: Mediação, 2006.http://www.ia.udrrj.br/ppgea/conteúdo/conteudo-2008-2/2 www.ia.udrrj www.ia2 2/2/SF%20e%20nova%20racionalidade.pdfAcesso em 30de jan de 2023.

HULIN, M. Epistemologia e didattica della matematica. La matematica e la sua Didattica, Bologna, n. 4, p. 621-655, 2016.

JOHNSON, B. S.; KURLAN, M. D. ; KAPLAN, E K. Tecnologia da informação nas escolas. J Am Acad Child Adolesc Psychiatry. 2009.

JONES, A. Uma revisão da literatura de pesquisa sobre barreiras à adoção de TIC por Professores. Agência Britânica de Comunicações Educacionais e Tecnologia. Recuperado em maio 20, 2014. Disponível em http://www.becta.org.uk. Acesso em 30 de jan de 2023.

JOVCHELOVITCH, S. Representações sociais da pesquisa científica. Petrópolis: Vozes, 2015.

KENSKI, V. M. Educação e tecnologias: o novo ritmo da informação. Campinas, SP: Papiros, 2007

KIBBIN, W. F. R. Os impactos macroeconômicos globais do Covid-19: sete cenários. Disponível Em: http://henryjenkins.org Acesso em 30 de jan de 2023.

KOEHLER, N.C. Ensino da matemática com uso de TI. São Paulo: Summus, 2019. KORALY, J. Previdência; retrocesso ou avanço. São Paulo: Rodrigues Alves, 2017.

KÜBLER, H-D. Competência de mídia – dimensões de uma frase de efeito. In: Schell, Fred; Stolzenburg, Elke. Noções básicas e ação educativa. São Paulo: KoPäd Verlag, 2019.

LAMBIC, D.; LIPKOVSKI, A. Medir a influência das atitudes dos alunos no processo de aquisição de conhecimento em matemática. Croatian Journal of Education, 14.187-205, 2012.

LANKSHEAR, C.; PETERS, M.; KNOBEL, M. Informação, conhecimento e

aprendizagem: algumas questões enfrentadas pela epistemologia e educação na era digital. Journal of Philosophy of Education, 34 (1), 17-40, 2000.

LEMOS, K. P. Brasil do século XXI. São Paulo: Pioneira, 2016. LEMOS, M. de S. Aprendizagem criativa. São Paulo: Pioneira, 2010.

LEMOS, M. L. O mercado de trabalho do Brasil: participação das mulheres brasileiras no mercado de trabalho na história do Brasil. Brasília: Biblioteca Digital da Câmara dos Deputados do Brasil. Disponível em http://www.hd.camara.gov.br Acesso em 30 de jan de 2023.

LERON, U. E.; HAZZAN, O. O mundo segundo Johnny: uma perspectiva de enfrentamento no ensino de matemática. Estudos Educacionais em Matemática 32, 265-292, 2008.

LÉVY, P. As tecnologias da inteligência. Rio de Janeiro: Ed. 34, 2013.

LIBÂNEO, J. C. Democratização da escola pública: a pedagogia crítico-social dos conteúdos. São Paulo: Loyola, 2002.

LIMA, P. de C. SCHALLENBERGER, C. O movimento de emancipação da família e da instituição. São Paulo. Rodrigues Alves, 2006.

LIMA, S, R. de. A formação de professores no Brasil. São Paulo: Saraiva, 2015.

LONGHI, S. R. P.; BENTO, K. L. B. Projeto político-pedagógico: uma construção coletiva. Artigo. Revista de divulgação técnico-científica do ICPG Vol. 3 n. 9 – jul.- dez./2006 ISSN 18072836. Disponível em http://www.hd.camara.gov.br Acesso em 30 de jan de 2023.

LOPES, R. G. Psicologia da pessoa idosa. São Paulo: Summus, 2013. LUCKESI, C. C. Avaliação da aprendizagem escolar. 4 ed. São Paulo: Cortez, 2015.LUFT, P. C. Mini Dicionário Luft. 10 ed. São Paulo: Ática, 2016.

MACDONALD, S. Informação para inovação. Gerenciando a mudança de uma perspectiva de informação (Oxford, Oxford University Press), 2008.

MAIA, C. P.; TORRES, C. S. Crenças pedagógicas dos professores e seu planejamento e conduta de aulas em sala de aula mediadas por computador. British Journal of Educational Technology, vol. 39, não. 5, pp. 807–828, 2018.

MALHEIROS, A. P. dos S. A produção matemática dos alunos em um ambiente de modelagem. 2004. Dissertação (Mestrado em Educação Matemática) – Instituto de Geociências e Ciências Exatas, Universidade Estadual Paulista, Rio Claro, 2004.

MARCONI, Marina de Andrade; LAKATOS, Eva Maria. Técnicas de pesquisa: planejamento e execução de pesquisas, amostragens e técnicas de pesquisa, elaboração, análise e interpretação de dados. 5ª ed. São Paulo: Atlas, 2010.

MARGOLINAS, C. Situações, meios, conexões. Analise Da atividade do professeur. Em Dorier, J.-L. Et. al. (Eds.) Acts of the 11e École d’Été de Didactique des Mathématiques – Corps, em torno de 2001, p. 141-156. Grenoble: La Pensée Sauvage

– Edições, 2013.

MARIA, W. B.; GUIMARÃES, A. C. de A.; MATIAS, T. S. Estilo de vida de

adolescentes de escolas públicas e privadas de Florianópolis-SC. R. da Educação Física/UEM Maringá, v. 20, n. 4, p. 615-623, 4. trim. 2009.

MARQUES, L. R. O projeto político pedagógico e a construção da autonomia e da democracia na escola nas representações sociais dos conselheiros. Artigo. Educ. Soc. Campinas, vol. 24, n. 83, p. 577-597, agosto 2003. Disponível em http://www.scielo.br/pdf/%0D/ccedes/v23n61/a03v2361.pdf Acesso em 30 de jan de 2023.

MARQUES, M. O. Projeto pedagógico: A marca da escola. In: Revista Educação e Contexto. Projeto pedagógico e identidade da escola no 18. ljuí, Unijuí, abr./jun. 1990. MARTINS, N. E. Um currículo básico para a telemática na formação de professores. São Paulo: Summus, 2009.

MARZANO, R. O que funciona nas escolas: traduzindo a pesquisa em ação. Association for Supervision and Curriculum Development (ASCD), 2013.

MASON, J. O “quê”, o “porquê” e o “como” em matemática. In P. Abrantes, L. Cunha Leal e J. P. Ponte (Orgs.), Investigar para aprender matemática: Textos selecionados (pp. 89-105). Lisboa: Projeto MPT e APM, 1996.

MATOS, J. F. Logo na Educação Matemática: Um estudo sobre as concepções e atitudes dos alunos. (tese de doutoramento, Universidade de Lisboa). Lisboa: APM, 1991.

MEDEIROS, C. S. Integrar as TIC como uma ferramenta integral de ensino e aprendizagem em cursos de formação inicial de professores. Issues in Educational Research, 15 (1), 101-113. Recuperado em 20 de outubro de 2015, Disponível em http: //www.iier.org.au/iier15/steketee.htm Acesso em 30 de jan de 2023.

MEIRA, J. M. Uso de tecnologia por professores iniciantes: desenvolvimento de professores de primeiro ano e o efeito do contexto institucional no uso da tecnologia de ensino de novos professores com os alunos. Journal of Research on Technology in Education, vol. 39, no. 3, pp. 245–261, 2019.

MEIRELLES, F. Aprendizagem em rede. São Paulo: Pioneira, 2017. MEIRELLES, F. O uso de TI no ensino. São Paulo: Contexto, 2018.

MEIRELLES, F. O uso de TI’s na escola pública brasileira: realidade e contexto. São Paulo, Summus, 2014.

MEIRELLES, C. de A. B.; PORTO, C. P.; MOREIRA, T.; HOFFMANN, L. M.A.

Metodologias ativas de ensino-aprendizagem na formação profissional em saúde: debates atuais. Ciência & Saúde Coletiva, 13(Sup 2):2133-2144, 2008.

MENDES, A.; BARTON, W. Uma investigação dos fatores que afetam o uso das TIC para o ensino nas escolas. 18ª Conferência sobre Sistemas de Informação, 2017.

MINAYO, M. C. de S. Pesquisa Social. 4ª ed. São Paulo: Saraiva, 2007. MITRE, S. M.; BATISTA, R. S.; MENDONÇA, J. M. G. de.; PINTO, N. M. de M.;

MONTENEGRO, G. A.. Inteligência visual e 3-D. São Paulo: Edgard Blücher, 2005. MORAES, R. Análise de conteúdo. São Paulo: Contexto,2014.

MOREIRA, D.; SOUZA, M. Primeiras reflexões de professores-alunos sobre tecnologia da informação e comunicação e aprendizagem em sala de aula: implicações para a formação inicial de professores. Journal of ComputerAssisted Learning, 21, 130-142, 2011.

MOUZA, J. T. J. Identificando discriminantes variáveis entre professores que integram totalmente computadores e professores com limitado integração. Computadores e Educação, vol. 51, nº 4, pp. 1523-1537, 2016.

NACARATO, A. M.; PASSOS, C. L. B.; FIORENTINI, D.; BRUM, E. D.; MEGID,

M. A.; FREITAS, M. T. M.; MELO, M. V.; GRANDO, R. C.;MISKULIN, R. S. Saberes

Docentes em Matemática: uma análise da prova do Concurso Paulista de 2003. Trabalho apresentado na 7º ENCONTRO PAULISTA DE EDUCAÇÃO MATEMÁTICA. São Paulo: USP e SBEM-SP, 2004, 26 p.

NETO, A. C.; ALMEIDA, M. D. De. Educação e Gestão Descentralizada: Conselho Diretor, Caixa Escolar, Projeto Político-Pedagógico. Artigo. Em Aberto, Brasília, v. 17,n. 72, p. 35-46, fev./jun. 2000. Disponivel em http://www.inep.gov.br Acesso em 15 dedez

de 2022.

ORTON, A., FROBISCHER, L. Ensaios de Matemática. São Paulo: Saraiva, 1996. PAIS, L. C. Didática da Matemática; uma análise da influência francesa. 2. ed. Belo Horizonte: Autêntica, 2018.

PALTRIDGE, S. Como a competição ajuda a Internet. OECD Observer, 201, agosto

/ setembro, 26, 1996.

PARO, V. H, 1945- Gestão democrática da escola pública/Vitor Henrique Paro. – 4 .ed. – São Paulo : Ática, 2006.

PARRA, C.; SAIZ, I. Didática da Matemática: reflexões psicopedagógica. Porto Alegre, Artmed (Artes Médicas). 1996.

PEDRO, A. A história da humanidade. São Paulo: Atlas, 2009.

PERALTA, H.; COSTA, F. A. Competência e confiança dos professores em relação ao uso das TIC. Revista de Ciências da Educação, vol. 3, pp. 75-84, 2017.

PERFEITO, R. B. et al. Avaliação das aulas de Educação Física na percepção dos alunos de escolas públicas e particulares. Revista da Educação Física/UEM, Maringá, v. 19, n. 4, p. 489-499, out./dez. 2008.

PETTITT, D. Matemática: São Paulo: Key Stages, 1994.

PIAGET, J. Para onde vai à educação? Rio de Janeiro: Livraria José Olympo Editora/Unesco, 1973.

PRADO, I. G. Ensino de matemática: o ponto de vista de educadores e de seus alunos sobre aspectos da pratica pedagógica. Rio Claro 2000. Tese de Doutorado

– Educação Matemática, Universidade Estadual Paulista, Instituto de Geociência e Ciências exatas (UNESP).

PROBST, E. R. A evolução da mulher no mercado de trabalho. Artigo. Disponível em http://www.icpg.com.br Acesso em 30 de jan de 2023.

RAMOS, G. T. C. Conhecimentos e habilidades metacognitivas em alunos com abordagem profunda à aprendizagem: Evidências de resolução de problemas matemáticos. Journal of Psychodidactics, 20 (2), 209-226. doi: 10.1387 /

RevPsicodidact.13060, 2015.

RAMOS. A. P. Censo Demográfico 2010: diagnóstico brasileiro do século XXI. São Paulo: Atlas, 2016.

RAMOS. S. L. Como o Brasil vem lidando com o coronavírus. Artigo, 2020. Financial Times, disponível em https://www.ft.com/content/cc1f650a-91c0-4e1f-b990- ee8ceb5339ea Acesso em 30 de jan de 2023.

RANGASWAMY, A.; GUPTA, E. S. Adoção e difusão da inovação no ambiente digital: algumas oportunidades de pesquisa. São Paulo Summus, 2010.

RIBEIRO, O, J. Educação e novas tecnologias: um olhar para além das técnicas. In: COSCARELLI, Carla V.; RIBEIRO, Ana. E. (Org.). Letramento digital: aspectos sociais e possibilidades pedagógicas. Belo Horizonte: Autêntica, 2005. p. 86-97.

RIOS, T. Significado e pressupostos do projeto pedagógico. In: Série Ideias. São Paulo, FDE,1982.

RODRIGO, M.; RODRÍGUEZ, A. E MARRERO, J. As teorias implícitas. Uma abordagem ao conhecimento cotidiano. Porto Alegre: ArtMed, 2013.

ROECH, William J. Administração por objetivos. 4ª. ed. São Paulo: Atlas, 2013.

ROESCH, P. Pesquisa por objetivo. São Paulo: Pioneira, 2013. ROGERS, E. M. Difusão de inovações. Nova York: Free Press, 2013.

ROZELL, E. J.; GARDNER, W. L. Sucesso e fracasso relacionados ao computador: um campo longitudinal estudo dos fatores que influenciam o desempenho relacionado ao computador. Computadores em Humanos Behavior, vol. 15, não. 1, pp. 1-10, 2009.

RUSSELL, M. Como o uso da tecnologia pelos professores varia por posse e longevidade. Journal of Educational Computing Research, vol. 37, não. 4, pp. 393- 417, 2015.

SABINO-SILVA, R.; JARDIM, A. C. G.; SIQUEIRA, W. L. Coronavirus COVID-19

impacts to dentistry and potential salivary diagnosis. Clin Oral Investig. 2020;24(4):1619-162116.

SADOVSKY, P. Falta fundamentação didática no ensino da matemática.Nova Escola. São Paulo, Ed. Abril, Jan./Fev. 2007.

SALOMON, G. Em M. Eraut (Ed.), The International Encyclopedia of

EducationalTechnology, Oxford: Pergamon Press, 167-170, 2009.

SANTAELLA, L. Linguagens líquidas na era da mobilidade. São Paulo: Paulus, 2007.

SANTOS, B. de S. Tudo o que é sólido desmancha no ar. In: TOSTES, Anjuli e FILHO, Hugo Melo (Org.) Quarentena: reflexões sobre a pandemia e depois. Bauru: Editora Canal 6 Editora, 2020.

SANTOS, P. Práticas de ensino remoto na pandemia: espaço, tempo e corporeidade/Luciana Piccoli e Patricia Camini; ilustrações de Eloá Guazzelli. – Erechim: Edelbra, 2020.la. São Paulo: Loyola, 2017.

SAVIANI, D. Para além da curvatura da vara. In: Revista Ande no 3. São Paulo, 1982.

SCHILER, J. Trabalhando com TIC: Percepções dos diretores australianos, Journal of Educational Administração, vol. 41, no. 3, pp. 171-185, 2013.

SCHLEMMER, E. A aprendizagem com o uso das tecnologias digitais: viver e conviver na virtualidade. Série-Estudos – Periódico do Mestrado em Educação da UCDB. Campo Grande-MS, n. 19, p. 103-126, jan./jun. 2015.

SCHOENFELD, A. Ensinando matemática: a investigação como parte da experiência matemática dos alunos do 2º ciclo. (tese de Mestrado, Universidade de Lisboa). Lisboa: APM, Serrazina, L. 1992.

SCHUTZ, A. Fenomenologia e relações sociais: Textos Escolhidos de Alfred Schutz. (org. e introdução de Helmut R. Wagner). Rio de Janeiro: 2009.

SEVERINO, A. J. Metodologia do Trabalho Científico. São Paulo: Cortez, 2016.

SHERRY, L.; GIBSON, D. O caminho para a liderança do professor em tecnologia educacional. Questões contemporâneas em tecnologia e formação de professores, vol. 2, não. 2, pp. 178-203, 2012.

SILVA, A. Direito à Educação em Tempos de Pandemia. Belo Horizonte: Sind Rede – BH, 2020. Disponível em http://redebh.com.br/confira-os-videos-do- seminário- direito-a-educacao-e-desafios-em-tempos-de-pandemia/. Acesso em 12 de mai de 2022.

SILVA, M. da G M. da. De navegadores a autores: a construção do currículo no mundo digital. In: Anais do ENDIPE. Belo Horizonte. 2010.

SILVA, R L.. OLIVEIRA, R P. Ensino da matemática por meio de TICs. São Paulo: Atlas, 2017.

SILVERMAN, D. Interpretando dados qualitativos. (3ª ed.). Londres: Publicações Sage, 2006.

SMARKOLA, C. Preditores de aceitação de tecnologia entre professores-alunos e professores experientes em sala de aula. Journal of Educational Computing Research, 37 (1), 65-82, 2007.

SOARES, E. EAD, palavra proibida. Educação online, pouca gente sabe o que é.Ensino remoto, o que temos para hoje. Mas qual é mesmo a diferença? Revista Docência e Cibercultura, Sessão Notícias. Rio de Janeiro, 2021. Disponível em: https://www.e- publicacoes.uerj.br/index.php/re-doc/announcement/view/1119. Acesso em 25 de abr de 2022.

SOARES, M. DOS S. Metodologias Ágeis Extreme Programming e Scrum para o Desenvolvimento de Software. Universidade Presidente Antônio Carlos, s/d. Lafaiete, MG, 2011.

SOARES, P. O. Educação cristã: a história da humanidade a partir do século X. São Paulo: Pioneira, 2001.

SOUZA, B. e outros. Cuidando, escola! São Paulo, Brasiliense, 2011.

SOUZA, S. H. Fatores críticos para a adoção bem-sucedida de tecnologia: uma lista de verificação baseada nas descobertas. Tecnologia Educacional, vol. 32, não. 1, pp. 57-58, 2010.

TAYLOR, L. Como os alunos-professores desenvolvem sua compreensão do ensino usando as TIC. Journal of Education for Teaching. 30 (1), 43-56, 2014.

TENÓRIO, F. G. ROZEMBERG, J. E. Gestão pública e cidadania: metodologias participativas em ação. Cadernos de Gestão Pública e Cidadania. Fundação Getúlio Vargas, 1997. Disponível em http://bibliotecadigital.fgv.br/ojs/index.php/cgpc/article/viewFile/43833/42694 Acesso em 23 de mar de 2023.

TEO, M. N. Educação e tecnologia. São Paulo: Moderna, 2008. r

THOMPSON, J. A educação 1.0 está pronta para alunos da web 2.0? Inove: Journal of Online Education.Fischler School of Education and Human Services da Nova Southeastern University. 3 (4), recuperado em 13 de outubro de 2007, em http://www.innovateonline.info/index.php?view=article&id=393 Acesso em 25 de mar de 2023.

TO, K. K.; TSANG, O. T.; LEUNG, W. S.; TAM, A. R.; WU, T. C.; LUNG, D. C.; et

al.

Temporal profiles of viral load in pos-terior oropharyngeal saliva samples and serum antibody responses during infection by SARS–CoV-2: an observational cohort study. Lancet Infect Dis. 2020;pii: S1473-3099(20)30196-1.13.

TOFFLER, A. Gestão da modernidade. São Paulo: McGraw Hill, 1990.

TOLEDO, M. da S. Metodologias ativas como fonte de aprendizagem. São Paulo: Senai-SP, 2008.

TOMEI, L. A. Desafios do ensino com tecnologia em todo o currículo: problemas e soluções. Londres: IRM Press (IGI Global), 2015;

TORRES, M. D. Práticas de alunos em matemática. Jornal de educação.28-35, 20, 2017

VALENTE, J. A. Aprendizagem ativa no Ensino Superior: a proposta da sala de aula invertida. Depto. de Multimeios, Nied e GGTE – Unicamp & Ced – PucSP. s/d. VALLADARES, R. C. O jeito matemático de pensar. Rio de Janeiro: Editora Ciência moderna Ltda. 2003.

VAN MERRIËNBOER, J. J. G.; MARTENS, R. Ferramentas baseadas em computador para design instrucional. Tecnologia Educacional, Pesquisa e Desenvolvimento, 50 (4), Edição Especial, 2002.

VASCONCELLOS, R. P. M. et al. Reflexões sobre o uso de Tecnologias Digitais em tempos de pandemia na educação básica da rede pública de ensino. EDUCAÇÃO PRESENCIAL E A DISTÂNCIA: DESAFIOS E REFLEXÕES, p. 103 – 116, 2020.

VEEN, W.; WRAKKING, B. Homo Zappiens: educando na era digital. Porto Alegre: Artmed, 2009.

VERGARA, S. C. Projeto e relatórios de pesquisa em administração. 4 ed. São Paulo: Atlas Editora, 2011.

VERGARA, Sylvia. Metodologia da Pesquisa. São Paulo: Summus, 2010.

VILLAVICENCIO, F. T.; BERNARDO, A. B. I. Emoções acadêmicas positivas moderam a relação entre autorregulação e desempenho acadêmico. British Journal of Educational Psychology, 83 (2), 329-340.doi: 10.1111 / j.2044-

8279.2012.02064, 2013.

VITTI, C. M. Matemática com prazer, a partir da história e da geometria. 2 ed. Piracicaba – São Paulo. Editora UNIMEP. 1999.

VITTI, A. Compreensão de Enunciados Escritos em Provas de Matemática, p. 34, 1996.

VYGOTSKY. L. S. A formação social da mente. São Paulo: Martins Fontes, 1989.

WANG, Y. Quando a tecnologia encontra as crenças: as percepções dos professores de formação inicial sobre o papel dos professores na sala de aula com os computadores. Journal of Research on Technology in Education. 35 (1), 150–161, 2012.

WILLIAMS, M. D. (2003). Integração da tecnologia na educação. Em Tan, S.C. & Wong, F.L. (Eds.), Ensino e aprendizagem com tecnologia, pp. 17-31: Uma perspectiva Nacional. São Paulo: Prentice Hall, 2013.

WILLIANS, M. Nativos digitais, imigrantes digitais. No horizonte. 9 (5), 1-6, 2006.

WOLNEY, L. V. P. Implementando Tecnologias Informáticas: Percepções e Práticas dos Professores. Revista de Tecnologia e Formação de Professores. 14 (1), 173-207, 2016.

AS DIFICULDADES NO PROCESSO DE ENSINO E APRENDIZAGEM EM MATEMÁTICA PARA OS ALUNOS DO 7º ANO ENSINO FUNDAMENTAL II DAS ESCOLAS ESTADUAIS WALDEMIRO PEREZ LUSTOZA E SÃO LUIZ DE GONZAGA, LOCALIZADAS NA ZONA OESTE DA CIDADE DE MANAUS-AM/BRASIL NO ANO DE 2022

CAPÍTULO I: MARCO INTRODUTÓRIO

CAPITULO II

2 MARCO TEÓRICO

2.1 MATEMÁTICA

2.1.1 A Aprendizagem em Matemática

2.1.2 Visão dos Professores de Matemática

2.2.1 Reforma da Matemática

2.3.1 O Ensino da Matemática no Ensino Fundamental II

2.3.2 Principais Ferramentas Digitais para o Ensino de Matemática

2.3.3 Uso da Tecnologia no Ensino da Matemática

2.3.4 Transmissão e Aprendizagem de Informações

2.3.5 Pressupostos sobreo Papel da Tecnologia

2.3.6 Agregando Valor às Intervenções e Transações Educacionais

2.3.7 O Futuro das TICs e da Educação

2.3.8 Dificuldades no uso da Tecnologia no Ensino da Matemática

2.3.9 Atitudes e Crenças em Relação às TICs

CAPÍTULO III

4 MARCO ANÁLITICO

4.1.1 Escola Estadual Waldemiro Lustos

4.1.2 Os alunos da Escola Waldemiro Lustosa

4.1.3 Escola Estadual São Luiz de Gonzaga

5. CONCLUSÃO

6. RECOMENDAÇÕES

REFERÊNCIAS

SADOVSKY, P. Falta fundamentação didática no ensino da matemática.Nova Escola. São Paulo, Ed. Abril, Jan./Fev. 2007.

APÊNDICE

Apêndice – Questionário para os professores