REGISTRO DOI: 10.5281/zenodo.7735100
Yves-Garnard Irilan1
Paul André2
Resumo
O método das diferenças finitas é uma técnica de derivação numérica utilizado para resolver problemas de valor de contorno, ou valor inicial, envolvendo equações diferen ciais. O presente trabalho consiste na resolução de equações diferenciais pelo método de diferenças finitas do problema de uma placa aquecida. O objetivo é determinar a distribuição de temperatura para as condições de contorno fornecido do problema.
Palavras-chave
Equações diferenciais, diferenças finitas, Métodos matemáticos .
1 Introdução
Equações diferenciais são equações matemáticas usadas para prever o comportamento de sistemas. A evolução do fenômeno pode ser descrita através de uma modelagem com as grandezas que definam o problema resolvendo a equação diferencial (ou sistema de equações diferenciais) que caracteriza determinado processo ou sistema, pode-se extrair informações relevantes sobre os mesmos e, possivelmente, prever o seu comportamento. Muitas leis físicas como: Leis de Newton para o resfriamento dos corpos, Equações de Maxwell, Equações de Navier-Stokes e Equações da Mecânica Quântica de Schrödinger são escritas por equações diferenciais parciais que relacionam o espaço e suas derivadas com o tempo. Neste trabalho, as equações governantes são as de continuidade de momento e de energia e de condição de fronteira que são descritos no problema.
2 Conceitos gerais sobre Equações Diferencias Parciais
Uma equação diferencial parcial (EDP) de segunda ordem geral é dada por
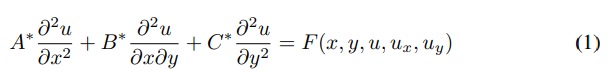
onde u = u(x, y) e A∗, B∗e C∗podendo ser funções de x, y, u, ux e uy. Neste trabalho usaremos a notação
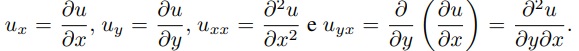
Quando A∗, B∗e C∗forem funções de x e y apenas e F for linear nas variáveis u, ux e uy a EDP geral de segunda ordem acima poderá ser escrita como:
Auxx + Buxy + Cuyy + Dux + Euy + F u + G = 0 (2)
e agora A, B, C, D, E, F e G podem1ser funções de x e y apenas. Quando G = 0 dizemos que a EDP é homogênea. A partir dos coeficientes A, B e C da equação (2) podemos classificar a EDP em:
1. Hiperbólicas: Este caso ocorre quando B2 − 4AC > 0;
2. Parabólicas: Este caso ocorre quando B2 − 4AC = 0 e
3. Elípticas: Este caso ocorre quando B2 − 4AC < 0.
A nossa função u é definida como u : R2 ⊇ Ω → R e nos problemas de EDP sempre temos restrições na fronteira de Ω, que é o domínio de u. Estas restrições são chamadas de condições de contorno, que podem ser dos três tipos mais conhecidos na literatura:
1. Condição de Dirichlet impõe que na fronteira de Ω, ( notação para fronteira = ∂Ω) a função u é conhecida, isto é, u(∂Ω) = f(x, y), onde f é dada.
2. Condição de Neumann impõe que na fronteira de Ω, especificamos a derivada normal de u, isto é, especificamos
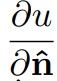
onde n é o vetor normal unitário à fronteira de Ω. A titulo de ilustração, explicitamos
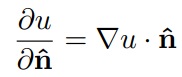
3. Condição de Robin impõe que na fronteira de Ω seja especificada uma combinação linear de u e
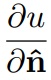
isto é,
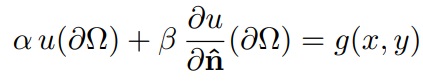
onde g é uma função conhecida.
3 Problemas físicos onde se aplicam estas EDP’s
(a) EDP Elíptica: A EDP elíptica mais conhecida é a equação de Poisson, onde A = C = 1, G = −f(x, y) e B = D = E = F = 0 (e assim B2 − 4AC < 0). Portanto pela equação (1) esta EDP ficará:
uxx + uyy = f(x, y).
Equações deste tipo surgem no estudo de vários problemas de física independentes da variável tempo t, tais como a distribuição de calor estacionária em uma região plana, a energia potencial de um ponto em um plano submetido a forças gravitacionais no plano e problemas bidimensionais estacionários envolvendo fluidos incompressíveis. No estudo da distribuição de calor estacionária em uma região plana temos que ter f(x, y) = 0, e assim temos, fazendo u = T, o problema 3 desta lista que é a equação de Laplace:
Txx + Tyy = 0.
(b) EDP Parabólica: O exemplo mais clássico deste tipo de EDP é a equação do calor ou difusão, onde a temperatura u = u(x, t) é dada pela EDP:
ut = α2uxx,
onde α é uma constante, 0 < x < ℓ e t > 0. Aqui explicitamos as condições de Dirichlet: u(0, t) = u(ℓ, t) = 0 e u(x, 0) = f(x), para 0 ≤ x ≤ ℓ. Note que aqui, comparando com a equação (1), temos que A = −α2, B = C = D = G = F = 0 e E = 1 sendo assim B2 − 4AC = 0. Este problema pode ser visto como a difusão (propagação) do calor numa barra de comprimento ℓ ao longo do tempo t.
(c) EDP Hiperbólica: Agora temos a equação da propagação de uma onda, como exemplo mais clássico da EDP Hiperbólica. Aqui u = u(x, t) é dada pela solução da EDP:
utt − α2uxx = 0,
onde α é uma constante.
Aqui explicitamos as condições de contorno mais utilizadas para se resolver esta EDP: u(0, t) = u(ℓ, t) = 0 para t > 0. E ainda u(x, 0) = f(x) e
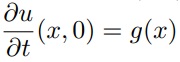
para 0 ≤ x ≤ ℓ. Perceba que aqui, pela equação (1), temos que A = −α2, B = D = E = F = G = 0 e C = 1. Então, de fato, B2 − 4AC > 0.
4 O método das diferenças finitas
Esta técnica baseia-se essencialmente na aproximação numérica das derivadas que aparecem nas EDP’s. Estas aproximações são feitas usando-se diferenças.
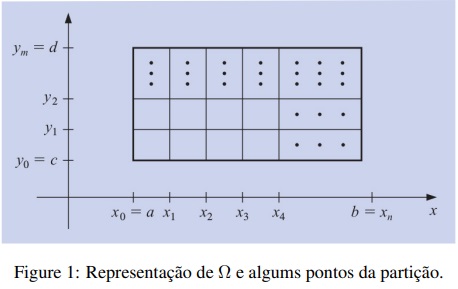
Suponha que estejamos interessados em resolver uma EDP num domínio Ω retangular, isto é, Ω = {(x, y) ∈ R2: a ≤ x ≤ b e c ≤ y ≤ d}. O procedimento se inicia através de uma partição de Ω do seguinte modo: primeiro fazemos uma partição P do intervalo [a, b] em (n + 1) pontos de modo que se tenha a = x0 < x1 < x2 < . . . < xn−1 < xn = b e ainda se tenha cada um desses n subintervalos com amplitude h constante, isto é,
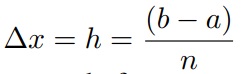
constante e assim xi = a + ih, para todo i = 0, 1, . . . , n. Do mesmo modo fazemos uma partição Q do intervalo [c, d] em (m + 1) pontos afim de que c = y0 < y1 < y2 < . . . < ym−1 < ym = d e ainda se tenha cada um dos m subintervalos de amplitude q constante, isto é,
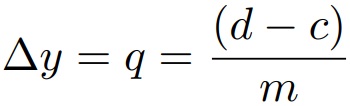
constante, e analogamente temos que yj = c + jq, para todo j = 0, 1, . . . , m. Na figura 1 abaixo temos uma representação esquemática desta partição de Ω.
As análises que se seguem servem para se avaliar a derivada de uma função com relação a x, isto é, com relação a primeira variável. As derivadas com relação às outras variáveis seguem de modo análogo.
Sabemos, do caso contínuo, que a derivada de uma função é dada por:
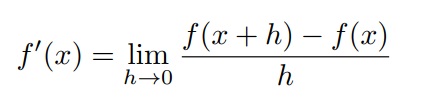
mas na partição do intervalo [a, b] não se aplica esta definição, pois entre xi e xi+1 não se tem pontos x para se avaliar na função f.
O mais próximo que podemos chegar desta operação é, se usarmos, xi − xj = h, então:
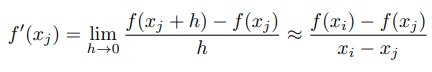
Usando série de Taylor para se avaliar o erro cometido nesta análise, temos:
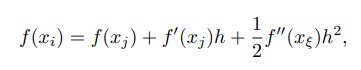
onde2ξ ∈ [xj , xi]. Assim
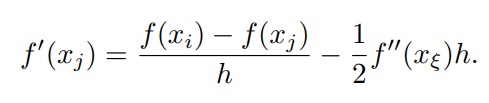
Como f′′(ξ) é constante concluimos que o erro que cometemos ao calcular f′(xj ) desta maneira é da ordem de h, isto é, quanto menor h menor o erro.
Sejam xi−1, xi e xi+1 três pontos consecutivos da partição P. Assim definimos:
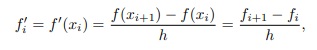
como sendo a derivada avançada de f em xi. E do mesmo modo definimos:
Note que podemos melhorar a ordem da aproximação da derivada fazendo uma combinação das séries de Taylor para fi+1 e fi−1, do seguinte modo
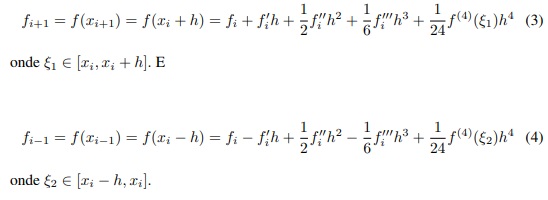
Fazendo a subtração da equação (3) pela equação (4), teremos:
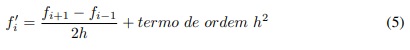
E definimos (5) (excetuando o termo h2, pois h ≪ 1) como sendo a derivada central de f no ponto xi. Agora somando as equações em (3) e (4), obtemos uma expressão para a derivada segunda de f no ponto xi, dada por:

como, em geral, h ≪ 1, então o termo h2na equação (6) é desprezado.
Finalmente se temos uma função u = u(x, y) definida em Ω e queremos calcular suas derivadas parciais atráves da técnica de diferenças finitas, procedemos assim para a derivada primeira:
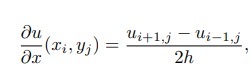
onde definimos a notação ui+1,j = u(xi+1, yj ).
E para a derivada segunda com relação a x, procedemos assim:
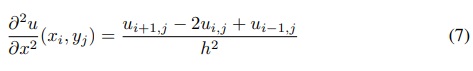
lembre que h = ∆x.
E para a derivada primeira com relação a y, teremos, analogamente:
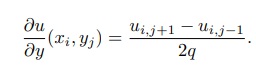
E para a derivada segunda com relação a y, temos:
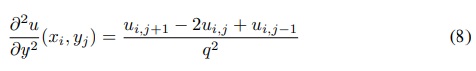
pois q = ∆y.
A titulo de ilustração, iremos apresentar como fica a derivada parcial mista, isto é,
a derivada
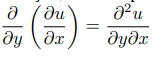
usando diferenças finitas.
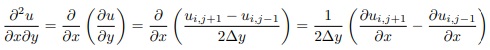
Assim
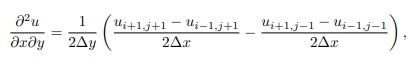
ou simplesmente
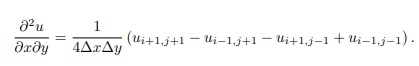
Onde é sempre bom lembar que ui,j = u(xi, yj).
5 Problema prática resolvendo a equação de Laplace no domínio não retangular e com as condições de temperatura na fronteira.
O nosso objetivo é resolver a equação de Laplace,

no domínio não retangular Ω e com as condições de temperatura na fronteira como se vê na figura 2.
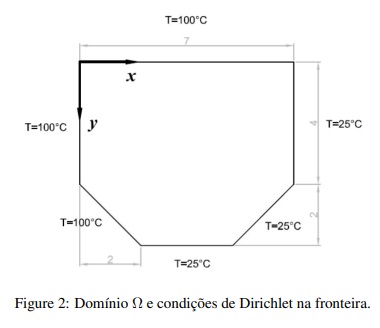
A discretização de Ω foi feita de modo que ∆x = ∆y = constante, assim, se colocarmos N subintervalos na direção do eixo x e M subintervalos na direção do eixo y, deveremos ter
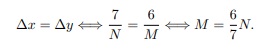
Assim N deve ser múltiplo de 7 ou M ser múltiplo de 6.
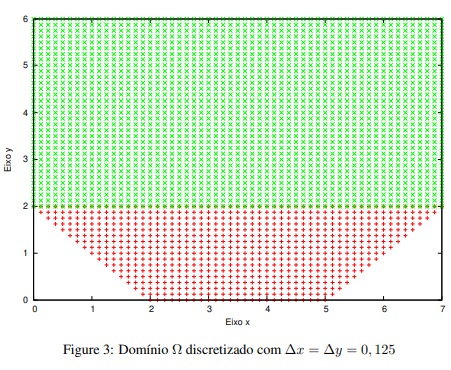
A figura 3 abaixo3 foi feita usando N = 56 subintervalos na direção do eixo x e portanto M = 48 subintervalos na direção do eixo y e assim teremos ∆x = ∆y = 0, 125. Note que o dominio Ω pode ser visto como a união de dois conjuntos: um retangular e outro formado por um trapézio. Note ainda que com estas quantidade de subintervalos nas direções x e y, temos que as coordenadas (x, y) dos vértices do
trapézio serão dadas por: A(2N/7, 0), B(5N/7, 0), C(N, 2M/6) e D(0, 2M/6). E as coordenadas dos vértices do retângulo serão dadas por: E(N, M), F(0, M), D e C. Na figura 3 abaixo temos os nós internos e da fronteira da dicretização do domínio Ω onde se vê a distinção da parte retangular e da parte do trapézio.
Na figura 4 abaixo mostramos como fica a partição de Ω com N = 280 subinterva los no eixo x e portanto M = 240 subintervalos no eixo y e então ∆x = ∆y = 0, 025. Note que já praticamente não mais se distingue os nós internos, isto é, temos uma região interna praticamente “totalmente” preenchida. A figura 4 foi feita sem mais distinção das duas regiões retangulares e do trapézio.
Utilizando-se das equações (7) e (8) obtidas por diferenças finitas para as derivadas
segundas de T = T(x, y), temos que a equação de Laplace pode ser escrita como:
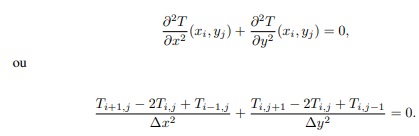
Como queremos que ∆x = ∆y, então nosso problema será resolver o sistema linear:
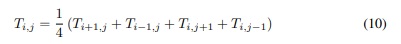
para todo 1 ≤ i ≤ (N − 1) e 1 ≤ j ≤ (M − 1), onde Ti,j = T(xi, yj ). Note ainda que este sistema dado por (10) possuirá (N − 2)(M − 2) equações. Pois como se verá nas condições de contorno logo abaixo, nos pontos de coordenadas: (i, 0) e (i, N) para 0 ≤ i ≤ M, e para os pontos (0, j) e (M, j) para 0 ≤ j ≤ N, já se conhece o valor de Ti,j . Logo basta resolvermos o sistema (10) para os nós internos à malha. Assim, por exemplo, se N = 56 e M = 48 então teremos 2484 equações e 2484 incógnitas, que são as temperaturas nos nós internos da malha, a se determinar.
Para montar este sistema na forma A · T = b, irei considerar a malha completa, isto é, irei considerar o domínio de solução da EDP como sendo Y = Ω ∪ X, onde X são os dois triângulos retângulos que faltam na figura 3 (ou figura 2), logo Y é o retângulo maior de dimensões 7 cm por 6 cm. Como os pontos de X não irão participar, por diferenças finitas, para a solução da EDP (exceto os pontos das hipotenusas destes triângulos), irei impor que Ti,j = 0, para os pontos interiores a X, do seguinte modo:
Suponha, agora, que sejam dados M subintervalos de P, na direção do eixo x, assim, 0 ≤ i ≤ M e N subintervalos4na direção do eixo y, assim, 0 ≤ j ≤ N. Quanto às coordenadas dos vértices, nosso primeiro triângulo retângulo (o da esquerda) possui as coordenadas para seus vértices: (0, 0),(2M/7, 0) e (0, 2N/6). O segundo triângulo retângulo (o da direita) possui as coordenadas: (5M/7, 0),(M, 0) e (M, 2N/6). Sendo assim podemos localizar os pontos da hipotenusa do primeiro triângulo retângulo com a equação da reta:
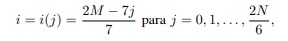
logo para a região interna ao primeiro triângulo, basta fazermos Ti,j = 0, para cada j = 0, 1, . . . ,
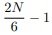
fazemos i variar entre 0 e
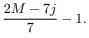
Analogamente para os pontos internos ao segundo triângulo, basta fazermos Ti,j = 0, para cada j = 0, 1, . . . ,
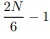
fazemos i variar entre 0 e
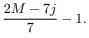
e M – 1.
Deste modo e pelas condições de contorno dadas na figura 2, temos, para os lados
do retângulo Y, as condições de contorno:

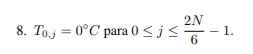
Para as diagonais dos triângulos X, fazemos: Ti,j = 100, 0◦C para
i=
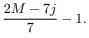
onde
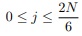
(diagonal esquerda, note que assim o nó inferior desta diagonal é tal que
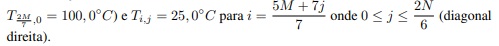
Feito isso, devemos explicitar a matriz e os vetores do nosso sistema A · T = b. Da equação (10) temos que:
−4Ti,j + Ti+1,j + Ti−1,j + Ti,j+1 + Ti,j−1 = 0
e montando as equações para os pontos internos ao retângulo Y, isto é, fazendo 1 ≤ i ≤ (M − 1) e 1 ≤ j ≤ (N − 1), temos:
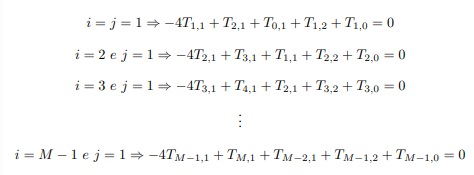
Assim por diante, isto é, para cada j = 2, 3, …, N − 1 fazemos i variar entre 1 e (M − 1). Logo o vetor das incógnitas5 T de nosso sistema (10) será um vetor coluna com (N − 2)(M − 2) coordenadas do tipo
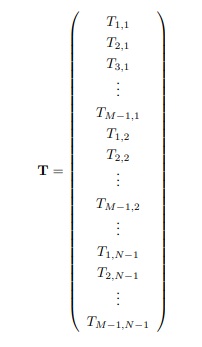
Deste modo A será uma matriz quadrada de ordem (N − 2)(M − 2) e temos para i = j = 1, o vetor linha ℓ1, como sendo a primeira linha de A :
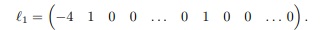
Para i = 2 e j = 1 temos a segunda linha de
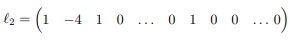
Para i = 3 e j = 1 temos a terceira linha de A.
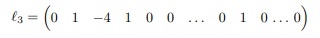
Para i = 4 e j = 1 temos a quarta linha de A
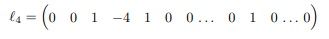
Assim por diante até i = M − 1 e j = 1 e aqui temos a (M − 1)−ésima linha de A que é
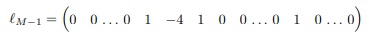
Seja agora i = 1 e j = 2 então temos o vetor linha ℓM de A que é
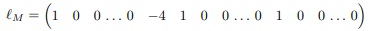
Para i = j = 2 temos a linha (M + 1) de A que é:

Para i = 3 e j = 2 temos a linha (M + 2) de A que
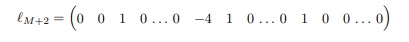
E para i = M − 1 e j = 2 temos a linha (2M − 2) de A que
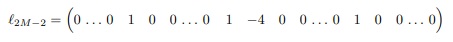
Este processo segue até a última linha de A que é
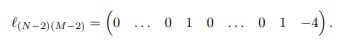
Finalmente o vetor b das constantes deste sistema será o vetor coluna formado pelas condições de contorno, isto é,

veja que aqui aparecem também alguns zeros, este fato, se deve pois estaremos em algum momento calculando Ti,j em função apenas de nós internos à malha.
Espero que o leitor tenha percebido que na matriz A = [aij ] sempre temos, em cada linha, o número −4 na diagonal e os demais termos iguais a zero ou um de modo que esta matriz ficará estritamente diagonalmente dominante, isto é, α < 1, para todo i = 1, . . . ,(M − 1), onde
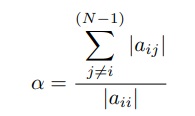
Assim os métodos de Gauss-Jacobi e Gauss-Seidel estudados no curso irão solucionar este sistema (10), isto é, os métodos irão convergir para a solução do sistema. Veja que dá muito trabalho montar este sistema, ou seja, alocar cada entrada desta matriz e vetores. Sendo assim não resolvemos o sistema no programa temp.f90 de forma a explicitar esta matriz e vetores, porém resolvemos o sistema (10) de forma iterativa, isto é, coloquei o programa para resolver a equação que se vê no sistema (10) num lupe de 60000 iterações. Aqui vale ressaltar que para esta quantidade de iterações foi necessária para a convergência do método de Gauss-Seidel uma vez que refinei por cinco vezes vezes a malha e o resultado final não mudou. Veja os resultados gráficos que se seguem.
6 RESULTADOS
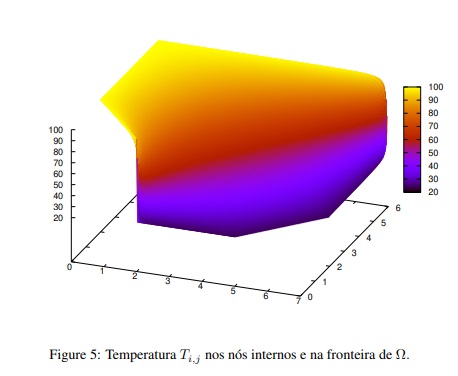
Na figura 5, a titulo de ilustração, apresento o gráfico da superfície em R3 formada pelos pontos (xi, yj , T(xi, yj )), para ∆x = ∆y = 0, 025 e maxiter = 40000 iterações.
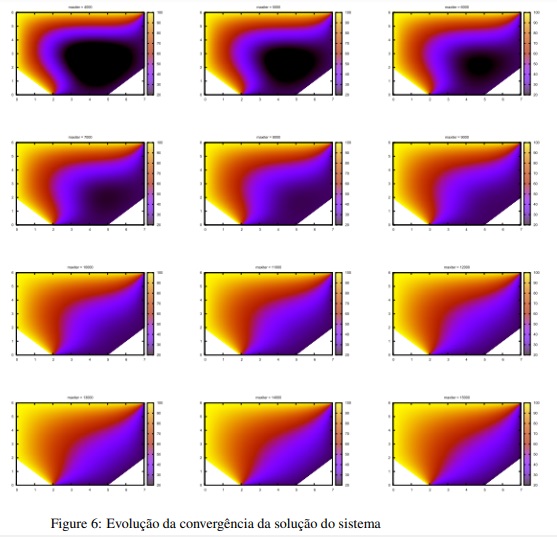
Na figura 6 abaixo apresentamos uma sequência de imagens que mostram a evolução da solução do sistema (10) a partir de uma variação do número natural maxiter, que no meu programa temp.f90 representa o número máximo de iterações do algoritmo Gauss-Seidel que está sendo utilizado para se resolver este sistema.
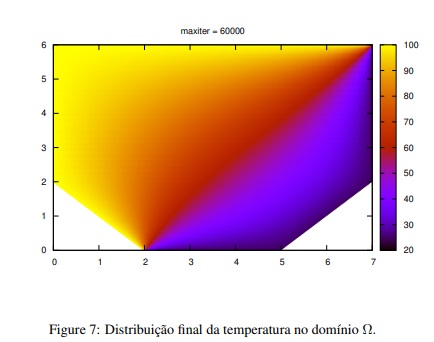
Na figura 7 temos a solução final do sistema (10). Aqui utilizamos maxiter = 60000, perceba que na figura 7 já não há muita diferença da imagem da figura 6, onde maxiter = 40000, mas mesmo assim utilizamos este maxiter = 60000 para garantir de fato a convergência da solução do sistema (10).
Veja a animação movie.gif nos arquivos enviados onde se mostra mais claramente a evolução da solução do sistema (10).
7 Conclusão
Neste trabalho, foi utilizado o método das diferenças finitas para resolver um problema de valor de contorno e valor inicial, envolvendo equações diferenciais parciais. Assim, este método foi eficaz para solucionar as equações de modelos a parâmetros definidos. Apresentamos um resumo dos conceitos gerais acerca das Equações Diferenciais, no qual destacamos uma aplicação através de um exemplo prático. Além disso, buscamos, nas bibliografias, reunir, de forma clara, os principais conceitos e resultados relacionados à teoria das Equações Diferenciais Parciais. Aqui, também expomos de forma sucinta, o conceito o método das diferenças finitas de modo a nos servir de ferramenta na resolução de nosso problema. De modo geral, estivemos interessados no estudo da Equação do calor, sobre a qual apresentamos fundamentos, Com este fim, apresentamos uma análise de qualidades físicas do som produzido da distribuição de temperatura sobre uma placa.
8 Agradecimentos
Agradecimento especial ao IFSC
Referências
[1] Métodos Numéricos para Engenharia, Steven C. Chapa e Raymond P. Canale, Ed. McGraw-Hill, 5a Ed., 2008.
[2] ASCHER, U. M.; GREIF, C. A first course in numerical methods. Philadelphia: SIAM, 2011.
[3] BURDEN, R. L.; FAIRES, J. D. Análise numérica. São Paulo: Cengage Learning, 2008.
[4] FORTUNA, A. O. Técnicas computacionais para dinâmica dos fluidos: conceitos básicos e aplicações. 2. ed. São Paulo: EDUSP, 2012.
[5] Cálculo Numérico Computacional, Teoria e Prática – Dalcídio Moraes Cláudio, Jussara Maria Marins – Atlas (1996).
[6] Ruggiero MG, Lopes Vd. Cálculo Numérico: Aspectos Teóricos e Computacionais. São Paulo: Makron Books; 2004.
[7] CHAPRA, S. C., Métodos Numéricos Aplicados com MATLAB para Engenheiros e Cientistas, Grupo A, 2013.
3Mas em geral estes coeficientes são constantes.
4Aqui estamos supondo a existência de um ponto ξ em [xj , xi] ⊂ R.
5O mapeamento dos nós dos pontos da fronteira podem ser vistos com mais detalhe no arquivo temp.f90 ou na letra (b) desta questão 03.
6Agora
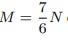
e N deve ser multipo de 6, pois foi assim que fiz no meu programa temp.f90
7Deste modo na verdade teremos entradas Ti,j = 0, neste vetor, que são as temperaturas nos pontos interiores a X, mas isto não afetará a solução do sistema. Sendo assim iremos assumir estes pontos como incógnitas também.
1, 2 Instituto Federal de Santa Catarina Câmpus Caçador-Av. Fahdo Thomé
