REGISTRO DOI: 10.5281/zenodo.12639786
Johnny Luis Mércuri; Bruna Karla Pereira de Souza Castro; Israel Nunes Pimentel do Nascimento; Auricelio Carneiro de Morais; Claudenice Teixeira Magalhães
Resumo
O presente artigo, tem por objetivo principal analisar o problema de maximizar o volume na construção de uma caixa qualquer sem tampa, utilizando uma folha retangular para essa construção. Para tal, buscou-se analisar qual seria a medida ideal do corte a se realizar nos vértices de uma determinada folha aplicando ferramentas de cálculo diferencial.
Palavra-chave: Otimização, Calculo Diferencial, Volume Máximo.
Abstract
The main objective of this article is to analyze the problem of maximizing the volume in the construction of any box without a lid, using a rectangular sheet for this construction. To this end, we sought to analyze what would be the ideal measurement of the cut to be performed at the vertices of a given sheet by applying differential calculation tools.
Keywords: Optimization, differential calculation, maximum volume.
1- Introdução
O Cálculo Diferencial e Integral apresenta aplicações que permeiam várias áreas do conhecimento, como nas ciências exatas e biológicas. Surgindo no século XVII de forma independente nos trabalhos publicados por Newton e Leibniz, como apontado por Melchiors e Soares (2013), tem por objetivo principal o estudo de limites, derivadas e integrais de funções de uma ou várias variáveis.
De acordo com Eves (2004, p. 417) “… com essa invenção a matemática criativa passou a um plano superior e a história da matemática elementar essencialmente terminou”, pois antes do seu desenvolvimento os matemáticos ficavam restritos a questões de contagem, medições e descrição como apontado por Melchiors e Soares (2013).
Em matemática os conceitos de derivação são aplicados principalmente na solução de problemas que possam ser descritos por funções, onde, por meio de métodos de derivação pode-se analisar o comportamento da mesma e obter possíveis valores de máximos e mínimos.
O presente artigo tem por objeto principal analisar uma folha de medida qualquer e aplicando métodos de cálculo, obter o valor de corte ideal a se realizar nessa folha afim de maximizar o volume na construção de uma caixa qualquer sem tampa.
2- Metodologia
A fim de solucionar o problema proposto, o de obter uma expressão que descreva a medida do corte ideal de uma folha retangular para maximizar a construção de uma caixa sem tampa, buscou-se realizar uma pesquisa bibliográfica sobre o problema e aplicar métodos de cálculo para apresentar a solução.
3- Desenvolvimento
Tomando uma folha retangular com y unidade de medida de um dos lados e x unidade de medida o outro, tem-se a seguir a representação dessa folha com as respectivas medidas dos lados.
Figura 1 – Folha retangular
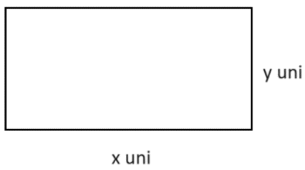
Querendo obter uma expressão geral para maximizar o volume da caixa construída, adotou-se a representação da unidade por “uni”, onde a mesma pode variar dependendo do problema abordado.
Para se construir uma caixa, deve-se realizar cortes nos vértices da folha, esses cortes devem ter a mesma medida, para que ao se dobrar a folha, após o corte, a altura das laterais se mantenha as mesmas. A figura a seguir, traz em vermelho (pontilhado) onde se deve realizar o corte, em azul onde se deve realizar a dobra após o corte.
Figura 2 – Folha retangular com marcações
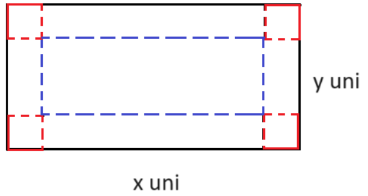
Definindo o corte a se realizar nos vértices por z , a seguir tem-se os valores respectivos das laterais, o que proporciona a elaboração de uma expressão que descreve o volume da caixa em função de x, y e z. Para facilitar e evitar a sobrecarga de notação, a partir deste ponto será omitido a unidade de medida “uni” e será inserida somente no resultado do problema.
Figura 3 – Folha retangular com medidas de corte
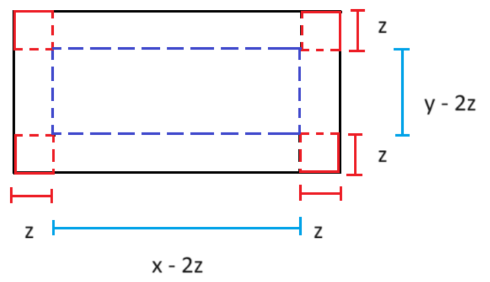
O volume da caixa, após o corte é representado pela expressão a seguir.
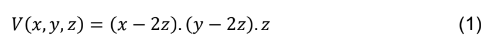



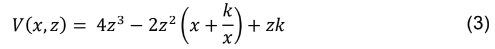

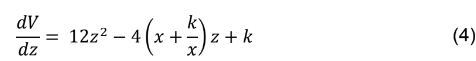

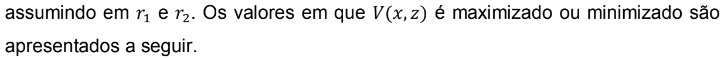
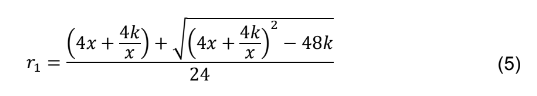
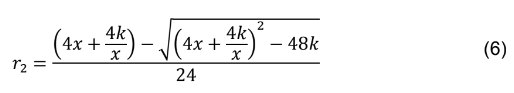
4- Discussão dos resultados
Verificou-se que ao realizar cortes nos vértices de uma determinada folha retangular de medidas x e y , na unidade de medida específica desejada, apresenta uma medida ideal de corte, a fim de maximizar o volume de uma caixa sem tampa.


5- Conclusão

Pode-se notar que o corte a se realizar apresenta uma limitação, em específico para o lado menor da folha, pois o corte não pode ser maior que a metade da medida desse lado menor.
Portanto, dada uma folha retangular de medidas conhecidas, pode-se realizar cortes nos vértices a fim de construir uma caixa sem tampa de volume máximo o que proporciona um melhor aproveitamento de espaço da mesma e a redução no desperdício de material.
6- Referências
FLEMMING, Diva Marilia; GONÇALVES, Mirian Buss. Cálculo A. ed. Pearson, 6 Ed, 2006.
MELCHIORS, Angeline; SOARES, Maricelia. História do cálculo diferencial e integral. Maiêutica. Ensino de Física e Matemática, v. 1, n. 1, 2013.
EVES, Howard Whitley. Introdução à história da matemática. Unicamp, 2004.
